1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с параметром из ЕГЭ прошлых лет
Задание
1
#6329
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых система [begin{cases} (x-2a-2)^2+(y-a)^2=1\
y^2=x^2end{cases}]
имеет ровно четыре решения.
(ЕГЭ 2018, основная волна)
Второе уравнение системы можно переписать в виде (y=pm x). Следовательно, рассмотрим два случая: когда (y=x) и когда (y=-x). Тогда количество решений системы будет равно сумме количества решений в первом и во втором случаях.
1) (y=x). Подставим в первое уравнение и получим: [2x^2-2(3a+2)x+(2a+2)^2+a^2-1=0quad(1)] (заметим, что в случае (y=-x) мы поступим так же и тоже получим квадратное уравнение)
Чтобы исходная система имела 4 различных решения, нужно, чтобы в каждом из двух случаев получилось по 2 решения.
Квадратное уравнение имеет два корня, когда его (D>0). Найдем дискриминант уравнения (1):
(D=-4(a^2+4a+2)).
Дискриминант больше нуля: (a^2+4a+2<0), откуда (ain (-2-sqrt2;
-2+sqrt2)).
2) (y=-x). Получаем квадратное уравнение: [2x^2-2(a+2)x+(2a+2)^2+a^2-1=0quad (2)] Дискриминант больше нуля: (D=-4(9a^2+12a+2)>0), откуда (ain
left(frac{-2-sqrt2}3; frac{-2+sqrt2}3right)).
Необходимо проверить, не совпадают ли решения в первом случае с решениями во втором случае.
Пусть (x_0) – общее решение уравнений (1) и (2), тогда [2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=2x_0^2-2(a+2)x_0+(2a+2)^2+a^2-1] Отсюда получаем, что либо (x_0=0), либо (a=0).
Если (a=0), то уравнения (1) и (2) получаются одинаковыми, следовательно, имеют одинаковые корни. Этот случай нам не подходит.
Если (x_0=0) – их общий корень, то тогда (2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=0), откуда ((2a+2)^2+a^2-1=0), откуда (a=-1) или (a=-0,6). Тогда вся исходная система будет иметь 3 различных решения, что нам не подходит.
Учитывая все это, в ответ пойдут:

-0,6right)cupleft(-0,6; -2+sqrt2right)]
Ответ:
(ainleft(frac{-2-sqrt2}3; -1right)cupleft(-1;
-0,6right)cupleft(-0,6; -2+sqrt2right))
Задание
2
#4032
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых система [begin{cases}
(a-1)x^2+2ax+a+4leqslant 0\
ax^2+2(a+1)x+a+1geqslant 0 end{cases}]
имеет единственное решение.
(ЕГЭ 2018, СтатГрад, 19 апреля 2018)
Перепишем систему в виде: [begin{cases}
ax^2+2ax+aleqslant x^2-4\
ax^2+2ax+ageqslant -2x-1
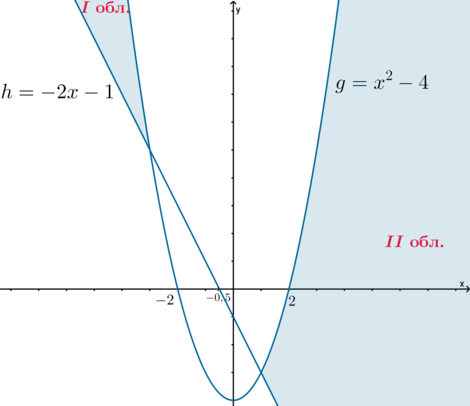
end{cases}] Рассмотрим три функции: (y=ax^2+2ax+a=a(x+1)^2), (g=x^2-4), (h=-2x-1). Из системы следует, что (yleqslant g), но (ygeqslant
h). Следовательно, чтобы система имела решения, график (y) должен находиться в области, которая задается условиями: “выше” графика (h), но “ниже” графика (g):
(будем называть “левую” область областью I, “правую” область – областью II)
Заметим, что при каждом фиксированном (ane 0) графиком (y) является парабола, вершина которой находится в точке ((-1;0)), а ветви обращены либо вверх, либо вниз. Если (a=0), то уравнение выглядит как (y=0) и графиком является прямая, совпадающая с осью абсцисс.
Заметим, что для того, чтобы исходная система имела единственное решение, нужно, чтобы график (y) имел ровно одну общую точку с областью I или с областью II (это значит, что график (y) должен иметь единственную общую точку с границей одной из этих областей).
Рассмотрим по отдельности несколько случаев.
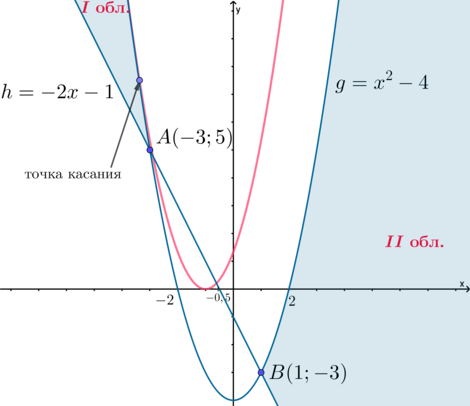
1) (a>0). Тогда ветви параболы (y) обращены вверх. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) касалась границы области I или границы области II, то есть касалась параболы (g), причем абсцисса точки касания должна быть (leqslant
-3) или (geqslant 2) (то есть парабола (y) должна коснуться границы одной из областей, которая находится выше оси абсцисс, раз парабола (y) лежит выше оси абсцисс).
(y’=2a(x+1)), (g’=2x). Условия касания графиков (y) и (g) в точке с абсциссой (x_0leqslant -3) или (x_0geqslant 2): [begin{cases}
2a(x_0+1)=2x_0\
a(x_0+1)^2=x_0^2-4 \
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right. end{cases}
quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right.\[1ex]
a=dfrac{x_0}{x_0+1}\[1ex]
x_0^2+5x_0+4=0 end{cases}] Из данной системы (x_0=-4), (a=frac43).
Получили первое значение параметра (a).
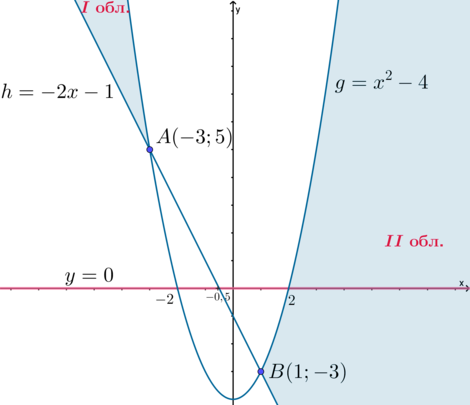
2) (a=0). Тогда (y=0) и видно, что прямая имеет бесконечное множество общих точек с областью II. Следовательно, это значение параметра нам не подходит.
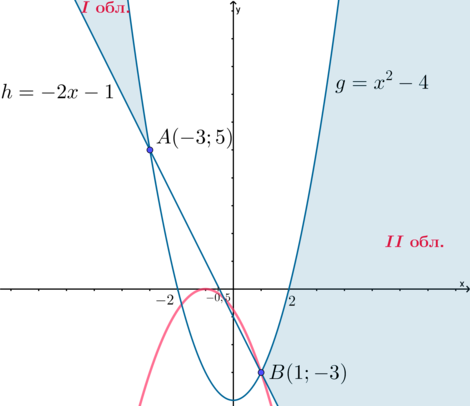
3) (a<0). Тогда ветви параболы (y) обращены вниз. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) имела одну общую точку с границей области II, лежащей ниже оси абсцисс. Следовательно, она должна проходить через точку (B), причем, если парабола (y) будет иметь еще одну общую точку с прямой (h), то эта общая точка должна быть “выше” точки (B) (то есть абсцисса второй точки должна быть (<1)).
Найдем (a), при которых парабола (y) проходит через точку (B): [-3=a(1+1)^2quadRightarrowquad a=-dfrac34] Убеждаемся, что при этом значении параметра вторая точка пересечения параболы (y=-frac34(x+1)^2) с прямой (h=-2x-1) – это точка с координатами (left(-frac13; -frac13right)).
Таким образом, получили еще одно значение параметра.
Так как мы рассмотрели все возможные случаи для (a), то итоговый ответ: [ain left{-dfrac34; dfrac43right}]
Ответ:
(left{-frac34; frac43right})
Задание
3
#4013
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых система уравнений [begin{cases}
2x^2+2y^2=5xy\
(x-a)^2+(y-a)^2=5a^4 end{cases}]
имеет ровно два решения.
(ЕГЭ 2018, СтатГрад, 26 января 2018)
1) Рассмотрим первое уравнение системы как квадратное относительно (x): [2x^2-(5y)x+2y^2=0] Дискриминант равен (D=9y^2), следовательно, [x_{1,2}=dfrac{5ypm 3y}4quadRightarrow quad x_1=2y, quad x_2=dfrac12y] Тогда уравнение можно переписать в виде [(x-2y)cdot (2x-y)=0] Следовательно, всю систему можно переписать в виде [begin{cases}
left[begin{gathered}begin{aligned} &y=2x\[1ex]
&y=0,5xend{aligned}end{gathered}right.\[1ex]
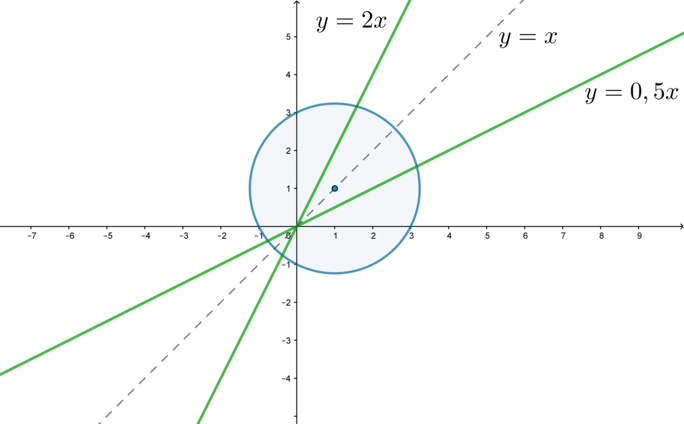
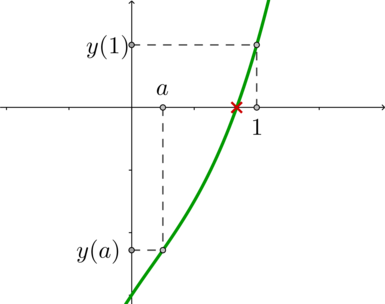
(x-a)^2+(y-a)^2=5a^4end{cases}] Совокупность задает две прямые, второе уравнение системы задает окружность с центром в ((a;a)) и радиусом (R=sqrt5a^2). Чтобы исходное уравнение имело два решения, нужно, чтобы окружность пересекала график совокупности ровно в двух точках. Вот чертеж, когда, например, (a=1):
Заметим, что так как координаты центра окружности равны, то центр окружности “бегает” по прямой (y=x).
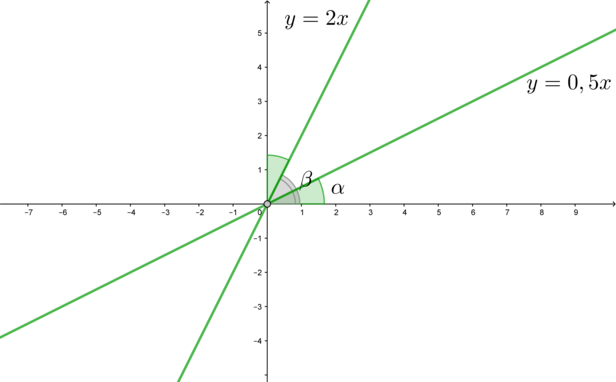
2) Так как у прямой (y=kx) тангенс угла наклона этой прямой к положительному направлению оси (Ox) равен (k), то тангенс угла наклона прямой (y=0,5x) равен (0,5) (назовем его (mathrm{tg},alpha)), прямой (y=2x) – равен (2) (назовем его (mathrm{tg},beta)). Заметим, что (mathrm{tg},alphacdot
mathrm{tg},beta=1), следовательно, (mathrm{tg},alpha=mathrm{ctg},beta=mathrm{tg},(90^circ-beta)). Следовательно, (alpha=90^circ-beta), откуда (alpha+beta=90^circ). Это значит, что угол между (y=2x) и положительным направлением (Oy) равен углу между (y=0,5x) и положительным направлением (Ox):
А так как прямая (y=x) является биссектрисой I координатного угла (то есть углы между ней и положительными направлениями (Ox) и (Oy) равны по (45^circ)), то углы между (y=x) и прямыми (y=2x) и (y=0,5x) равны.
Все это нам нужно было для того, чтобы сказать, что прямые (y=2x) и (y=0,5x) симметричны друг другу относительно (y=x), следовательно, если окружность касается одной из них, то она обязательно касается и второй прямой.
Заметим, что если (a=0), то окружность вырождается в точку ((0;0)) и имеет лишь одну точку пересечения с обеими прямыми. То есть этот случай нам не подходит.
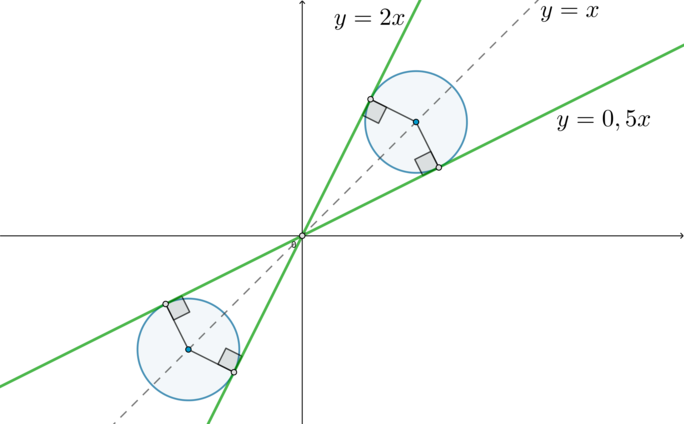
Таким образом, для того, чтобы окружность имела 2 точки пересечения с прямыми, нужно, чтобы она касалась этих прямых:
Видим, что случай, когда окружность располагается в третьей четверти, симметричен (относительно начала координат) случаю, когда она располагается в первой четверти. То есть в первой четверти (a>0), а в третьей (a<0) (но такие же по модулю).
Поэтому рассмотрим только первую четверть.
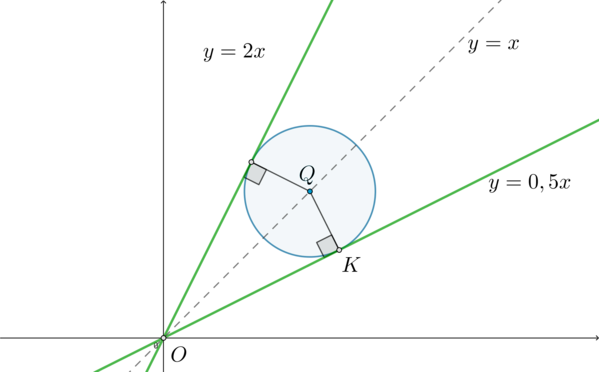
Заметим, что (OQ=sqrt{(a-0)^2+(a-0)^2}=sqrt2a), (QK=R=sqrt5a^2). Тогда [OK=sqrt{2a^2-5a^4}] Тогда [mathrm{tg},angle
QOK=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}] Но, с другой стороны, [mathrm{tg},angle QOK=mathrm{tg},(45^circ-alpha)=dfrac{mathrm{tg},
45^circ-mathrm{tg},alpha}{1+mathrm{tg},45^circcdot
mathrm{tg},alpha}] следовательно, [dfrac{1-0,5}{1+1cdot 0,5}=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}
quadLeftrightarrowquad a=pm dfrac15] Таким образом, мы уже сразу получили и положительное, и отрицательное значение для (a). Следовательно, ответ: [ain {-0,2;0,2}]
Ответ:
({-0,2;0,2})
Задание
4
#3278
Уровень задания: Равен ЕГЭ
Найдите все значения (a), для каждого из которых уравнение [25^x-(a+6)cdot 5^x=(5+3|a|)cdot 5^x-(a+6)(3|a|+5)]
имеет единственное решение.
(ЕГЭ 2017, официальный пробный 21.04.2017)
Сделаем замену (t=5^x, t>0) и перенесем все слагаемые в одну часть: [t^2-bigg((a+6)+(5+3|a|)bigg)cdot t+(a+6)(3|a|+5)=0] Получили квадратное уравнение, корнями которого по теореме Виета являются (t_1=a+6) и (t_2=5+3|a|). Для того, чтобы исходное уравнение имело один корень, достаточно, чтобы полученное уравнение с (t) тоже имело один (положительный!) корень.
Заметим сразу, что (t_2) при всех (a) будет положительным. Таким образом, получаем два случая:
1) (t_1=t_2): [a+6=5+3|a| quadLeftrightarrowquad 3|a|=a+1 quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} & 3a=a+1\
&3a=-a-1 end{aligned} end{gathered} right. \
a+1geqslant 0 end{cases}quadLeftrightarrowquad
left[begin{gathered}begin{aligned} & a=dfrac12\[2ex]
&a=-dfrac14 end{aligned} end{gathered} right.]
2) Так как (t_2) всегда положителен, то (t_1) должен быть (leqslant
0): [a+6leqslant 0 quadLeftrightarrowquad aleqslant -6.]
Ответ:
((-infty;-6]cupleft{-frac14;frac12right})
Задание
5
#3252
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [sqrt{x^2-a^2}=sqrt{3x^2-(3a+1)x+a}]
имеет ровно один корень на отрезке ([0;1]).
(ЕГЭ 2017, резервный день)
Уравнение можно переписать в виде: [sqrt{(x-a)(x+a)}=sqrt{(3x-1)(x-a)}] Таким образом, заметим, что (x=a) является корнем уравнения при любых (a), так как уравнение принимает вид (0=0). Для того, чтобы этот корень принадлежат отрезку ([0;1]), нужно, чтобы (0leqslant
aleqslant 1).
Второй корень уравнения находится из (x+a=3x-1), то есть (x=frac{a+1}2). Для того, чтобы это число было корнем уравнения, нужно, чтобы оно удовлетворяло ОДЗ уравнения, то есть: [left(dfrac{a+1}2-aright)cdot
left(dfrac{a+1}2+aright)geqslant 0quadRightarrowquad
-dfrac13leqslant aleqslant 1] Для того, чтобы этот корень принадлежал отрезку ([0;1]), нужно, чтобы [0leqslant dfrac{a+1}2leqslant 1
quadRightarrowquad -1leqslant aleqslant 1] Таким образом, чтобы корень (x=frac{a+1}2) существовал и принадлежал отрезку ([0;1]), нужно, чтобы (-frac13leqslant aleqslant 1).
Заметим, что тогда при (0leqslant aleqslant 1) оба корня (x=a) и (x=frac{a+1}2) принадлежат отрезку ([0;1]) (то есть уравнение имеет два корня на этом отрезке), кроме случая, когда они совпадают: [a=dfrac{a+1}2quadRightarrowquad a=1] Таким образом, нам подходят (ain left[-frac13; 0right)) и (a=1).
Ответ:
(ain left[-frac13;0right)cup{1})
Задание
6
#3238
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [xsqrt{x-a}=sqrt{6x^2-(6x+3a)x+3a}]
имеет единственный корень на отрезке ([0;1].)
(ЕГЭ 2017, резервный день)
Уравнение равносильно: [xsqrt{x-a}=sqrt{3a(1-x)}] ОДЗ уравнения: [begin{cases} xgeqslant 0\ x-ageqslant 0\3a(1-x)
geqslant 0end{cases}] На ОДЗ уравнение перепишется в виде: [x^3-a(x^2-3x+3)=0]
1) Пусть (a<0). Тогда ОДЗ уравнения: (xgeqslant 1). Следовательно, для того, чтобы уравнение имело единственный корень на отрезке ([0;1]), этот корень должен быть равен (1). Проверим: [1^3-a(1^2-3cdot 1+3)=0 quadRightarrowquad a=1.] Не подходит под (a<0). Следовательно, эти значения (a) не подходят.
2) Пусть (a=0). Тогда ОДЗ уравнения: (xgeqslant 0). Уравнение перепишется в виде: [x^3=0 quadRightarrowquad x=0] Полученный корень подходит под ОДЗ и входит в отрезок ([0;1]). Следовательно, (a=0) – подходит.
3) Пусть (a>0). Тогда ОДЗ: (xgeqslant a) и (xleqslant 1). Следовательно, если (a>1), то ОДЗ – пустое множество. Таким образом, (0<aleqslant 1) и при этих (a) ОДЗ: (aleqslant xleqslant
1). Следовательно, если корень подойдет по ОДЗ, то он попадет и в отрезок ([0;1]).
Рассмотрим функцию (y=x^3-a(x^2-3x+3)). Исследуем ее.
Производная равна (y’=3x^2-2ax+3a). Определим, какого знака может быть производная. Для этого найдем дискриминант уравнения (3x^2-2ax+3a=0): (D=4a(a-9)). Следовательно, при (ain (0;1]) дискриминант (D<0). Значит, выражение (3x^2-2ax+3a) положительно при всех (x). Следовательно, при (ain (0;1]) производная (y’>0). Следовательно, (y) возрастает. Таким образом, по свойству возрастающей функции уравнение (y(x)=0) может иметь не более одного корня.
Следовательно, для того, чтобы корень уравнения (точка пересечения графика (y) с осью абсцисс) находился на отрезке ([a;1]), нужно, чтобы [begin{cases} y(1)geqslant 0\
y(a)leqslant 0 end{cases}quadRightarrowquad ain [0;1]] Учитывая, что изначально в рассматриваемом случае (ain (0;1]), то ответ (ain (0;1]).
Итоговый ответ, полученный объединением ответов во всех трех случаях: [ain [0;1]]
Ответ:
([0;1])
Задание
7
#3267
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [sqrt{1-4x}cdot ln(9x^2-a^2)=sqrt{1-4x}cdot ln (3x+a)]
имеет ровно один корень.
(ЕГЭ 2017, основная волна)
Данное уравнение можно переписать как [begin{cases}
sqrt{1-4x}cdot ln dfrac{(3x-a)(3x+a)}{3x+a}=0\[2ex]
3x+a>0end{cases} quadLeftrightarrowquad
begin{cases}
sqrt{1-4x}cdot ln (3x-a)=0\
3x+a>0end{cases}] Система имеет два корня:
1) (x_1=frac14), если он удовлетворяет (3x+a>0) и (3x-a>0): [begin{cases}
dfrac34+a>0\[1ex]
dfrac34-a>0end{cases} quadLeftrightarrowquad
-dfrac34<a<dfrac34]
2) (x_2=frac{a+1}3), если он удовлетворяет (3x+a>0) и (1-4xgeqslant 0): [begin{cases}
a+1+a>0\[1ex]
1-dfrac43a-dfrac43geqslant 0end{cases}quadLeftrightarrowquad
-dfrac12<aleqslant -dfrac14]
Рассмотрим случаи, когда данная система имеет ровно один корень. Пусть (x_1ne x_2), то есть (ane -frac14).
1. Пусть (x_1=frac14) – единственное решение системы.
(x_1) будет корнем, если (-frac34<a<frac34), (x_2) не будет корнем, если (ain
left(-infty;-frac12right]cupleft(-frac14;+inftyright)). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain left(-dfrac34;-dfrac12right]cupleft(-dfrac14;dfrac34right)] 2. Пусть (x_2=frac{a+1}3) – единственное решение системы.
(x_1) не будет корнем, если (ain
left(-infty;-frac34right]cupleft[frac34;+inftyright)), (x_2) будет корнем, если (-frac12<aleqslant -frac14). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain varnothing]
Пусть (x_1=x_2). Тогда (a=-frac14). Заметим, что при этом значении что (x_1), что (x_2) являются решением, следовательно, оно нам подходит.
Итоговый ответ: [ain left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)]
Ответ:
(ain
left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)
)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите все значения параметра k, при каждом из которых уравнение имеет хотя бы одно решение на интервале
2
Найдите все значения k, при каждом из которых уравнение
имеет хотя бы одно решение на отрезке
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 4. (Часть C).
3
Определите, при каких значениях параметра a уравнение
имеет ровно два решения.
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
4
Найдите все значения параметра a, при каждом из которых уравнение
имеет корни, но ни один из них не принадлежит интервалу (4; 19).
5
Найдите все значения параметра a, при каждом из которых уравнение
имеет хотя бы один корень на отрезке [5; 23].
Пройти тестирование по этим заданиям
165 задач с параметрами
1. Линейные уравнения и приводимые к ним уравнения с параметрами.
2. Квадратичные и сводимые к ним уравнения с параметрами.
3. Уравнения с параметрами, содержащие модуль.
4. Системы уравнений с параметрами.
5. Иррациональные уравнения с параметрами.
6. Линейные неравенства и неравенства, приводимые к линейным. Системы неравенств.
7. Квадратичные неравенства с параметрами.
8. Иррациональные неравенства с параметрами.
9. Уравнения и неравенства с параметрами, содержащие логарифмы.
10. Тригонометрические уравнения, неравенства и системы уравнений с параметрами.
Задание 17. Уравнения и неравенства с параметром
Существует ровно три генеральных метода решения задач 17:
- Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;
- Графический метод — привлечение чертежа. Во многих задачах 17 достаточно начертить графики функций — и решение становится очевидным;
- Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.
Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.
Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)
Глава 1. Графический подход § 1. Вебинар по задачам 18: модуль и окружности 















Задачи с параметрами на ЕГЭ по математике
Задача с параметрами – одна из самых сложных в ЕГЭ по математике Профильного уровня. Это задание №18
И знать здесь действительно нужно много.
Научиться строить графики всех элементарных функций (и отличать по внешнему виду логарифм от корня квадратного, а экспоненту – от параболы).
И после этого – учимся решать сами задачи №18 Профильного ЕГЭ.
Вот основные типы задач с параметрами:
Еще одна задача с параметром – повышенного уровня сложности. Автор задачи – Анна Малкова
И несколько полезных советов тем, кто решает задачи с параметрами:
1. Есть два универсальных правила для решения задач с параметрами. Помогают всегда. Хорошо, в 99% случаев помогают. То есть почти всегда.
— Если в задаче с параметром можно сделать замену переменной – сделайте замену переменной.
— Если задачу с параметром можно решить нарисовать – рисуйте. То есть применяйте графический метод.
2. Новость для тех, кто решил заниматься только алгеброй и обойтись без геометрии (мы уже рассказывали о том, почему это невозможно). Многие задачи с параметрами быстрее и проще решаются именно геометрическим способом.
Эксперты ЕГЭ очень не любят слова «Из рисунка видно…» Ваш рисунок – только иллюстрация к решению. Вам нужно объяснить, на что смотреть, и обосновать свои выводы. Примеры оформления – здесь. Эксперты ЕГЭ также не любят слова «очевидно, что…» (когда ничего не очевидно) и «ёжику ясно…».
3. Сколько надо решить задач, чтобы освоить тему «Параметры на ЕГЭ по математике»? – Хотя бы 50, и самых разных. И в результате, посмотрев на задачу с параметром, вы уже поймете, что с ней делать.
4. Задачи с параметрами похожи на конструктор. Разобрав много таких задач, вы заметите, как решение «собирается» из знакомых элементов. Сможете разглядеть уравнение окружности или отрезка. Переформулировать условие, чтобы сделать его проще.
На нашем Онлайн-курсе теме «Параметры» посвящено не менее 12 двухчасовых занятий. Кстати, оценивается задача 18 Профильного ЕГЭ в 4 первичных балла, которые отлично пересчитываются в тестовые!
источники:
http://www.berdov.com/ege/parametr/
http://ege-study.ru/ru/ege/materialy/matematika/zadachi-s-parametrami-na-ege-po-matematike/
Муниципальная учебно-исследовательская
конференция старшеклассников
«Ломоносовские чтения»
Направление математика
Параметр в заданиях ЕГЭ по математике.
Исследовательская работа
Выполнена учеником 11 класса
МОУ «Средняя общеобразовательная
школа № 7», МО «Котлас»,
Архангельской области
Шергиным Тимуром Олеговичем
Научный руководитель – учитель
МОУ «Средняя общеобразовательная
школа № 7», МО «Котлас»,
Архангельской области
Курдюкова Ольга Васильевна
г. Котлас, 2015
Оглавление
Введение 3
Глава 1 Основные понятия 5
§1Что такое параметр 5
§2 Что означает «решить задачу с параметром» 6
§3 Основные типы решения задач с параметрами 6
§4Основные способы решения задач с параметрами 7
Глава 2 Основные способы решения задач с параметрами 8
§1 Аналитический способ 8
§2 Графический способ 12
§3 Решение относительно параметра 15
Заключение 22
Литература 23
Приложение 1 Результаты социологического опроса в 9, 11 классах 24
Приложение 2 Список задач с параметром 25
Введение.
Задачи с параметром — одна из самых интересных и многогранных тем в математике. Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры у школьников, но их решение вызывает у них значительные затруднения. Это связано с тем, что каждое уравнение с параметрами представляет собой целый класс обычных уравнений, для каждого из которых должно быть получено решение.
Актуальность данной темы очевидна. Ведь уравнения и неравенства с параметром стали привычной частью вступительных экзаменов ЕГЭ (задание № 18), на ГИА (задание № 23) и на вступительных экзаменах в вузы. И хотя они нередко представлены в многочисленных пособиях для абитуриентов, в школьной практике такие задачи встречаются редко.
Осенью 2015 года мы провели социологический опрос. Решили выяснить, будут ли выпускники 2016 года решать на ГИА и ЕГЭ по математике задания с параметром (см.приложение 1). Результаты нашего исследования неутешительные. Из 80 респондентов 50 (т.е. 63%) сообщили, что не будут решать задания такого типа. Учащиеся выпускных классов не до конца понимают, что каждое невыполненное задание на экзамене лишает их возможности получить высокие баллы и быть конкурентно способными на вступительных экзаменах в ВУЗы. В связи с этим мы и решили изучить задания последних лет с параметрами на ЕГЭ по математике.
Цель данной работы: изучение основных способов решения уравнений и неравенств с параметром.
Для достижения поставленной цели необходимо решить следующие задачи:
1) сбор и обработка материала по данной теме;
2) систематизировать различные методы решения;
3) провести мастер-классы по решению уравнений с параметром в 11 классах;
4) разработать список заданий по данной теме ( в помощь учителю и ученику).
Объект исследования: уравнения и неравенства с параметром.
Предмет исследования: методы решения уравнений и неравенств, содержащих параметр.
Методы исследования:
- Изучение специальной литературы по данному вопросу: энциклопедии, справочники и учебные пособия, Интернет-ресурсы
- Анкетирование
- Проведение мастер класса
- Обработка полученных данных(составление обобщающих таблиц, диаграмм,)
- Работа в компьютерных программах MicrosoftWord, Excel, MicrosoftPowerPoint
Глава 1 Основные понятия.
§1 Что такое параметр.
Толковый словарь определяет параметр как величину, характеризующую какое — нибудь основное свойство машины, устройства, системы или явления, процесса. (Ожегов С.И. , Шведова Н.Ю. Толковый словарь русского языка.Москва. 1999). Рассмотрение параметров — это всегда выбор. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и др. Перед выбором мы стоим и в различных жизненных ситуациях. Вспомним сказку: В чистом поле стоит столб, а настолбу написаны слова: «Кто поедет от столба сего прямо, тот будет голоден и холоден; кто поедет в правую сторону, тот будет здрав и жив, а конь его будет мертв; а кто поедет в левую сторону, тот сам будет убит, а конь его жив и здрав останется!» Иван-царевич прочел эту надпись и поехал в правую сторону, держа на уме: хоть конь его и убит будет, зато сам жив останется и со временем сможет достать себе другого коня. (“Иван-царевич и серый волк” Русская народная сказка). Здесь от выбора зависит жизнь Ивана-царевича.
Что такое параметр в математике?Если вы вспомните некоторые основные уравнения (например, kx+l=0, ax²+bx+c=0), то обратите внимание, что при поиске их корней значения остальных переменных, входящих в уравнения, считаются фиксированными и заданными. Все разночтения в существующей литературе связаны с толкованием того, какими фиксированными и заданными могут быть эти значения остальных переменных.
Поскольку в школьных учебниках нет определения параметра, возьмем за основу следующий его простейший вариант.
Определение: параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Независимость параметра заключается в его «неподчинении» свойствам, вытекающим из условия задачи. Например, из неотрицательности левой части уравнения |x|=a–1 не следует неотрицательность значений выражения a–1, и если a–1<0, то мы обязаны констатировать, что уравнение не имеет решений.
§2 Что означает «решить задачу с параметром».
Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.
Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.
§3. Основные типы задач с параметрами.
Тип 1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.
Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успех и при решении задач всех других основных типов.
Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).
При решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени.
Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).
Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.
Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Например, найти значения параметра, при которых:
1) уравнение выполняется для любого значения переменной из заданного промежутка;
2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.
Многообразие задач с параметром охватывает весь курс школьной математики (и алгебры, и геометрии), но подавляющая часть из них на выпускных и вступительных экзаменах относится к одному из четырех перечисленных типов, которые по этой причине названы основными.
§4 Основные способы решения задач с параметром.
Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.
Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
Перейдем теперь к демонстрации указанных способов решения задач с параметром.
Глава 2. Основные способы решения задач с параметром
§1 Аналитический способ.
Универсальных методов решения уравнений и неравенств с параметрами не существует. Одно из немногих исключений – линейные уравнения и неравенства.
Пример 1. Решить уравнение а(а – 2)х = а – 2.
Решение.Перед нами линейное уравнение, имеющее смысл при всех допустимых значениях а. Будем его решать «как обычно»: делим оби части уравнения на коэффициент при неизвестном. Но всегда ли возможно деление? Нет. Делить на ноль нельзя. Придется рассмотреть отдельно случай, когда коэффициент при неизвестном равен нулю. Получим:
1).а= 2, тогда уравнение примет вид 0 ∙ х = 0, х – любое число;
2).а = 0, тогда 0 ∙ х = -2, уравнение корней не имеет;
3).а ≠ 0, а ≠ 2, тогда
а(а – 2)х = а – 2 ,
х = ,
х = .
Ответ: 1) еслиа ≠ 0, а ≠ 2, то х = .
2) если а = 2, то х – любое число;
3) если а = 0, то корней нет.
Отмечу сразу, что запись ответа – важнейший этап решения, отличающий задачу с параметром от других задач. Ответ в задаче с параметром – это описание множества ответов к задачам, полученным при конкретных значениях параметра.
Пример 2. Решить неравенство (а + 3)х< 4а – 1.
Решение. Рассмотрим случаи:
1) а + 3 = 0, а = -3, тогда неравенство примет вид 0 ∙ х< -13, неравенство решений не имеет;
2) а + 3 > 0, а> -3, тогда
3) а + 3 < 0, а< -3, тогда
Ответ: 1) если а = -3, то решений нет;
2) если а> -3, то
3) если а< -3, то
Другое важное исключение — уравнения и неравенства, связанные с квадратичной функцией.
Пример 3. Решить неравенство ах2< 4.
Решение. Здесь три случая:
1).если а = 0, то получаем неравенство 0 ∙ х2< 4, решением которого является любое число;
2).если а< 0, тогда ах2< 4 для всех х, поскольку ах2 ≤ 0;
3).если а> 0, тогда х2<, откуда
< 0, или иначе:
< 0; пользуясь методом интервалов, заключаем, что
<х<
.
Ответ: 1) еслиа ≤ 0, то х – любое число;
2) еслиа> 0, то х;
.
Пример 4. Решить неравенство (х – 4а)(х + а – 5) ≤ 0.
Решение. Решим неравенство методом интервалов. Для этого необходимо оставить на числовой оси два числа: 4а и 5 – а. Но в каком порядке? Рассмотрим случаи:
- 4а = 5 – а, что возможно приа = 1; неравенство примет вид:
(х – 4)2≤ 0х = 4;
2) 4а> 5 – а, что возможно приа> 1; число 4а на координатной оси расположено правее числа 5 – а.
х [5 – a; 4a]
3) 4а< 5 – а, что возможно при а< 1
х [4a; 5 – a]
Ответ: 1) еслиа = 1, то х = 4;
2) еслиа> 1, то х [5 – a; 4a];
3) еслиа< 1, то х [4a; 5 – a].
Пример 5. Решить уравнение (а – 2)х2 + (2а – 3)х + а + 2 = 0.
Решение. Рассмотрим два случая:
- а = 2, получим линейное уравнение х + 4 = 0, откуда х = -4;
- а ≠ 2, получим квадратное уравнение. Рассмотрим дискриминант:
D = (2а – 3)2 – 4(а – 2)(а + 2) = 4а2 – 12а + 9 – 4а2 – 8а + 8а + 16 =
= -12а + 25
Далее, если D< 0, -12а + 25< 0, а>, тогда уравнение не имеет корней;
если же D ≥ 0, а ≤ , то
.
Ответ: 1) еслиа = 2, то х = -4;
2) если а>, то корней нет;
3) если а ≤ , то
.
При решении задач с параметрами нередко применяются те же самые приемы, что и при решении обычных задач. Так, в следующем примере мы используем разложение на множители.
Пример 6. Решить неравенство х + 9а ≥ 10.
Решение. Перепишем неравенство в виде: х + 9а — 10 ≥ 0. Рассмотрим случаи:
- а = 0, тогда х ≥ 0;
- а>0, тогда ОДЗ: х ≥ 0
Замена:
t2 —
Учитывая, что х ≥ 0, имеем
- а< 0, тогда х ≤ 0 и х + 9а — 10
< 0, что противоречит условию.
Ответ: 1) еслиа = 0, то х[0; +
);
2) если a> 0, то ;
3) еслиа< 0, то решений нет.
При решении примера 7 мы воспользовались преобразованиями модуля.
Пример 7.Решить уравнение x|x – 4| = a.
Решение. Воспользуемся равносильностью:
- Пусть а > 0, тогда х > 0. Перепишем уравнение в виде:
Так как х> 0 и а> 0, то корень первого уравнения х = 2 – , посторонний. Корни второго уравнения определены и положительны при
0<а ≤ 4.
2) Пустьа< 0, тогда х< 0. Перепишем уравнение в виде:
3) Пустьа = 0, тогда х = 0 или х = 4.
Ответ: 1) еслиа = 0, то х = 0 и х = 4;
2) если 0<а ≤ 4, то х = 2 + и х = 2 ±
;
3) еслиа> 4, то х = 2 + ;
4) еслиа< 0, то х = 2 – .
Пример 8: Найдите все значения а, при каждом из которых уравнение имеет хотя бы один корень. (С5 ЕГЭ 2012г.)
Рассмотрим функции и
Функция
1.Пусть , тогда
(раскрываем модуль со знаком минус)
,
. Получаем, что угловой коэффициент функции
равен 4 либо 12, (так как может быть одинаковый знак в зависимости от числа х.) При таких значениях график функции возрастает (так как коэффициент больше 0)
2.Пусть , тогда
,
Получаем, что угловой коэффициент функции
равен -4 либо -12. При таких значениях график функции убывает (так как коэффициент меньше 0)
3.При х=0, тогда Получаем, что
=
Функция
возрастает при
и убывает при
, поэтому
=
Исходное уравнение имеет один корень, когда
откуда
, либо
, где а=-5.
Ответ: -5,
§2 Графический способ.
Алгоритм графического решения уравнений с параметром:
-Находим область определения уравнения.
-Выражаем α как функцию от х.
-В системе координат строим график функции α (х) для тех значений х, которые входят в область определения данного уравнения.
-Находим точки пересечения прямой α =с, с графиком функции α (х). Если прямая α =с пересекает график α(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение
c = α(х) относительно х.
-Записываем ответ.
Рассмотрим на примерах:
Пример1: Решить уравнение |x2 — 2x — 3| = a в зависимости от параметра а.
Решение. Понятно, что при а ≥ 0:
Но все ли корни подходят? Чтобы выяснить это, построим график функцииа = |x2 — 2x — 3|. Количество корней можно увидеть на рисунке 1, мысленно проводя прямые линии, соответствующие значениям а. Получим:
- если a< 0, то корней нет;
- еслиа = 0 и а> 4, то два корня.
Найдем эти корни:
При а = 0 получим x2 — 2x — 3 = 0, и х1 = -1, х2 = 3; при а> 4 это корни уравнения x2 — 2x – 3 – а = 0.
3) если 0 <a< 4 – все четыре корня подходят;
4) приа = 4 – три корня:
x2— 2x— 3 = 4 x2 — 2x — 3 = — 4
x2— 2x — 7 = 0 x2 — 2x + 1 = 0
х = 1
Ответ: 1) если a< 0, то корней нет;
2) если а = 0, то х1 = -1, х2 = 3;
3) если 0 <a< 4, то х1,2,3,4 = 1;
4) если а = 4, то х1 = 1, х2,3 = 1;
5) если а> 4. то х1,2 = 1 .
Пример 2: Найдите все значения а, при каждом из которых уравнение имеет единственный корень. ( С5 ЕГЭ 2013г.)
Запишем уравнение в виде и рассмотрим две функции
и
.
Рассмотрим функцию , преобразовывая подкоренное выражение, получим:
.
Таким образом, получаем.функцию, графиком которой является полуокружность с радиусом 2 в центре с точкой (-1;0), лежащей в верхней полуплоскости.
Графиком функции является прямая с угловым коэффициентом -а, проходящая через точку М (4;2)
Уравнение имеет единственный корень, если графики функций имеют одну общую точку (т.е. прямая касается или пересекает полуокружность в единственной точке).
Рассмотрим рисунок: 1. Прямая МС является касательной к полуокружности, следовательно, МС и полуокружность пересекаются в единственной точке. Так как МС параллельна оси ОХ ( У точки М (4,2) и С(-1,2)), то угловой коэффициент равен нулю. Таким образом, найдено первое значение а=0, при котором уравнение имеет один единственный корень.
2. Проведем прямую через точки М(4;2) и А(-3;0) ( так как координаты известны). Прямая МА пересекает график полуокружности в двух точках, но такая ситуация не удовлетворяет условию задачи. Поэтому надо найти значения углового коэффициента, при которых вышеназванное условие не выполняется. Чтобы найти значения –а подставим координаты точек М и А в функцию.
-4а+16а+2=2 3а+4а+2=0
12а=0 7а=-2
а=0. а=
Получаем, -а=0 и –а=.
При условии прямые имеют с графиком две общие точки, а это не удовлетворяет условию задачи.
3. Проведем прямую МВ через точки М(4;2) и В(1;0). Чтобы найти значения –а подставим координаты точек М и А в функцию.
3а+4а+2=0 -а+4а+2=0
7а=-2 3а=-2
а= а =
Получаем –а= и –а=
. При условии
прямые имеют с графиком одну общие точки и это удовлетворяет условию задачи.
Ответ: а=0,
§3 Решение относительно параметра.
Если степень неизвестного слишком высока, а степень параметра не превосходит двух, то здесь эффективен метод решения уравнения (неравенства) относительно параметра.
Пример 1.Решить уравнение 2х3 – (а + 2)х2– ах + а2 = 0.
Решение. Перепишем уравнение в виде
2х3 – ах2 — 2х2 – ах + а2 = 0
а2 – (х2 + х)а + 2х3 — 2х2 = 0
Решим уравнение относительно параметра а.
D = (х2 + х)2 – 4(2х3 — 2х2) = х2(х + 1)2 – 8х2(х – 1) = х2(х2 + 2х + 1 – 8х + 
Тогда (а – х2 + х)(а – 2х) = 0
Осталось решить полученные уравнения относительно х.
х2 – х – а = 0 а – 2х = 0
имеет корни при
D = 1 + 4а ≥ 0 х =.
4а ≥ -1
а ≥ —
т.е. при а ≥ —
приа< — корней нет.
Ответ: 1) если а< — , то корней нет; 2) если а ≥ —
, то
, х3 =
Пример 2.Решить уравнение 3х4 + х3 – 2(а + 1)х2 + 3ах – а2 = 0.[1]*
Решение. Заменим уравнение как квадратное по отношению к параметру а:
3х4 + х3 – 2ах2 – 2х2 + 3ах – а2 = 0
—а2 – (2х2 – 3х)а + 3х4 + х3 – 2х2 = 0
а2 + (2х2 – 3х)а – 3х4 – х3 + 2х2 = 0
D = (2х2 – 3х)2 – 4(2х2 – х3 – 3х4) = х2(2х – 3)2 – 4х2(2 – х– 3х2) =
= х2(4х2 – 12х + 9 – 8 + 4х + 12х2) = х2(16х2 – 8х + 1) = х2(4х – 1)2
а1 = х2 + х
а2 = -3х2 + 2х Тогда
(а – х2 – х)(а + 3х2 – 2х) = 0
а – х2 – х = 0 3х2 – 2х + а = 0
х2 + х – а = 0 D = 4 – 12а
D = 1 + 4аD ≥ 0 при а ≤
D ≥ 0 при а ≥ —
Произведя развертку по параметру а, получили
Ответ: 1) приа< — ,
;
2) при, то
,
;
3) приа >, то
.
Приведем примеры решения еще нескольких заданий С5 из контрольно измерительных материалов ЕГЭ:
1.Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно 4 решения.
Преобразуем данную систему:
Пусть t = y – 3, тогда система примет вид:
Количество решений полученной системы совпадает с количеством решений исходной системы.
Построим графики уравнений (1) и (2) в системе координат Oxt.График первого уравнения – ромб, диагонали которого, равные 8 и 6, лежат на осях Ох и Оt, а графиком второго уравнения является окружность с центром в начале координат и радиусом r = |a|.
Система имеет 4 решения, так как графики уравнений системы пересекаются в четырех общих точках. Значит, окружность либо вписана в ромб, либо ее радиус удовлетворяет условию 3 < r < 4.В первом случае радиус окружности является высотой прямоугольного треугольника с катетами 3 и 4, откуда
Во втором случае получаем 3 <|a |< 4, откуда −4 < a < −3; 3 < a < 4.
Ответ: а = ± 2,4; −4 < a < −3; 3 < a < 4.
2.Найдите все значения , при каждом из которых уравнение
имеет хотя бы одно решение.
Введем замену поэтому
Перейдем к системе:
При подстановке выясняется, что ни при одном значении число
не является корнем уравнения.
Рассмотрим функцию , графиком является парабола, ветви которой направлены вверх. Следовательно, условие задачи выполнено если выполняется одно из трех условий: Эти условия соответствуют следующим способам расположения графика функции
:
1) Трёхчлен имеет два различных корня, и только больший из них лежит на промежутке (0; 1])(см.рис. 1), то есть
2) Трёхчлен имеет два различных корня, и только меньший из них лежит на промежутке (0; 1])(см.рис. 2), то есть
3)Трёхчлен имеет два корня, возможно, совпадающих, и оба лежат на промежутке
(0; 1])(см.рис. 3), то есть
Решим систему 1:
Решим систему 2:
Решим систему 3:
Ответ:
3.Найдите все значения , при которых уравнение
на промежутке
имеет ровно два корня.
Рассмотрим функции и
Проанализируем
на промежутке
При все значения функции
на промежутке
не положительны, а все значения функции
— положительны, следовательно, при
уравнение не имеет решений на промежутке
При функция
возрастает на промежутке
, Функция
убывает на этом промежутке, следовательно, уравнение
всегда имеет ровно одно решение на промежутке
, поскольку
На промежутке уравнение
принимает вид
Это уравнение сводится к уравнению
Будем полагать, что
, поскольку случай
был рассмотрен ранее. Дискриминант квадратного уравнения
поэтому при
это уравнение не имеет корней; при
уравнение имеет единственный корень, равный 2; при
уравнение имеет два корня.
Пусть уравнение имеет два корня, то есть Тогда оба корня меньше 5, поскольку при
значения функции
не положительны, а значения функции
положительны. По теореме Виета сумма корней равна 4, а произведение равно
Значит, больший корень всегда принадлежит промежутку
, а меньший принадлежит этому промежутку тогда и только тогда, когда
.
Таким образом, уравнение имеет следующее количество корней на промежутке
:1) Нет корней при
2) Один корень при
3) Два корня при
и
4) Три корня при
Ответ: ;
4.Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Если является корнем исходного уравнения, то и
является его корнем. Следовательно, уравнение имеет единственный корень, только если
то есть
Подставим значение
в исходное уравнение:
откуда либо либо
или
При исходное уравнение принимает вид:
Корнями этого уравнения являются числа
и
то есть исходное уравнение имеет более одного корня.
При и при
уравнение принимает вид:
При это уравнение сводится к уравнению
которое не имеет корней. При
получаем уравнение
которое имеет единственный корень.При
получаем уравнение
которое не имеет корней.
При и при
исходное уравнение имеет единственный корень. Ответ:
Заключение.
В процессе проделанной работы в соответствии с ее целями и задачами были получены следующие выводы и результаты:
1. Рассмотрели основные способы решения уравнений и неравенств с параметром:
— аналитический способ;
— графический способ;
— решение относительно параметра;
2. Графический метод является удобным и быстрым способом решения уравнений и систем уравнений с параметрами, но нельзя полностью представить себе сложность и нестандартность решения каждой задачи с параметром, изучая только графический способ. Нельзя научиться решать любые задачи с параметрами, используя какой-то алгоритм или формулы.
3. В заданиях ГИА по математике в 9 классе уравнения, системы уравнений с параметром проще, удобнее и нагляднее решать графическим способом. В связи с этим разработали ряд задач с параметром в помощь учителю и ученику. ( см. приложение 2) Разработанный ряд задач можно использовать на факультативах по математике при подготовке к ГИА, при подготовке к олимпиадам или для привития интереса к математике, совершенствования математической культуры, навыков дедуктивного мышления и творческих исследовательских способностей. Данный справочник предложен 9 классникам.
Без задач с параметрами, как правило, не обходятся олимпиады всех уровней, вступительные экзамены в наиболее престижные вузы, поэтому мы планируем продолжить работу над этой темой.
Литература
1. Алгебра. 9 класс. Учебник для учащихся общеобразовательных учреждений/ А.Г.Мордкович.- М.:Мнемозина, 2013;
2. Горнштейн П.И. «Задачи с параметрами. » Москва 2003г.;
3. Математика. 9 класс. Подготовка к ГИА – 2014: учебно-методические пособие/ Под ред.Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов-на-Дону: Легион, 2013г.;
4. Математика. Подготовка к ЕГЭ-2013 : учебно-методические пособие/ Под ред.Ф.Ф.Лысенко, С.Ю.Кулабухова. – Ростов-на-Дону: Легион, 2012г.;
5. Солуковцева Л. «Линейные и дробно-линейные уравнения и неравенства с параметрами. Москва.2007г.;
6. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. Пособие для 10 кл. сред.шк. – М.: Просвещение, 1989.;
7.ЯстребинецкийГ.А.«Уравнения и неравенства, содержащие параметры», 1972г.
Приложение 1
Результаты социологического опроса в 9, 11 классах
1. Будут ли выпускники 2016 года решать на ГИА и ЕГЭ по математике задания с параметром.
2. Причина, по которой не будут решать задания с параметром.
Приложение 2
Задание 23
Подготовительные задания
1. Постройте график функции и определите, при каких значениях параметра a прямая y = a не имеет с графиком общих точек.
2. Постройте график функции у = х² +1 и определите, при каких значениях параметра k прямая y = kx имеет с графиком ровно одну общую точку.
3. Постройте график функции у = |х – 1| + |х + 1| – 1 и определите, при каких значениях параметра k прямая у = kx имеет с графиком ровно одну общую точку.
4. Постройте график функции у = х² -2|х| и определите, при каких значениях параметра а прямая у = а имеет с графиком ровно две общих точки.
5. Постройте график функции
и определите, при каких значениях параметра а прямая у = а имеет с графиком ровно
две общие точки.
Тренировочные задания.
1. При каких отрицательных значениях с прямая у = сх – 9 имеет с параболой у = х² + 5х ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
2. Постройте график функции
Определите, при каких значениях k прямая у = k будет пересекать построенный график в трех точках.
Зачетные задания.
1. Постройте график функции . Определите, при каких значениях параметра k прямая у = kx имеет с этим графиком ровно одну общую точку.
2. Постройте график функции и определите при каких значениях параметра а прямая у = а не имеет с графиком общих точек.