На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 18 задания. Объясняется тема об обработке числовой информации в электронных таблицах.
Содержание:
- ЕГЭ по информатике 18 задание объяснение
- Решение 18 задания ЕГЭ
- Исполнитель Робот
18-е задание: «Обработка числовой информации в электронных таблицах»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение обрабатывать вещественные выражения в электронных таблицах
Решение 18 задания ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Исполнитель Робот
18 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
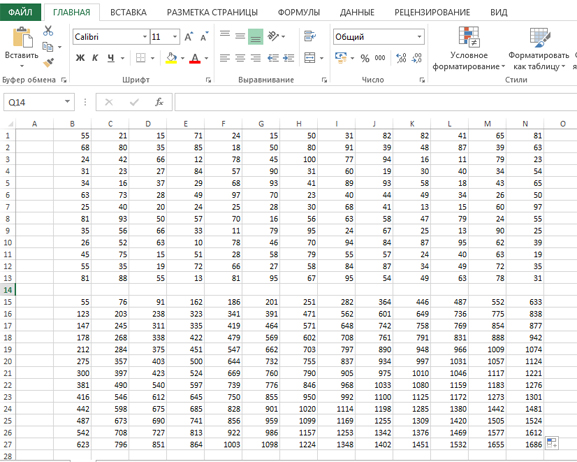
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:

Ответ: 1204 | 502
Решение подобного задания смотрите в следующем ниже разборе.
📹 YouTube здесь
Видеорешение на RuTube здесь
18_1:
Задание выполняется с использованием прилагаемых файлов
Исходные данные записаны в файле (выше) в виде электронной таблицы прямоугольной формы.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой НИЖНЕЙ клетки в правую ВЕРХНЮЮ. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
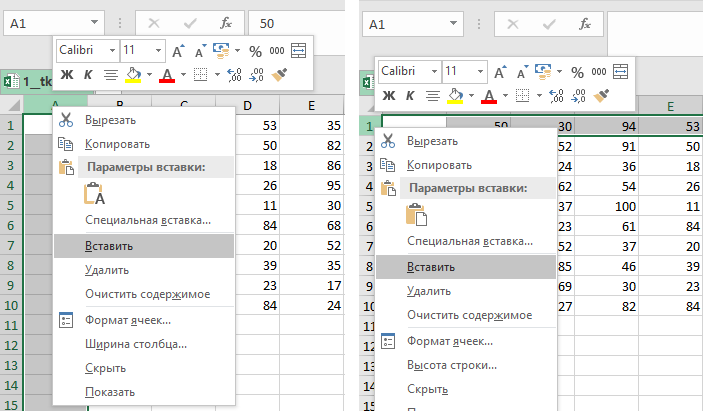
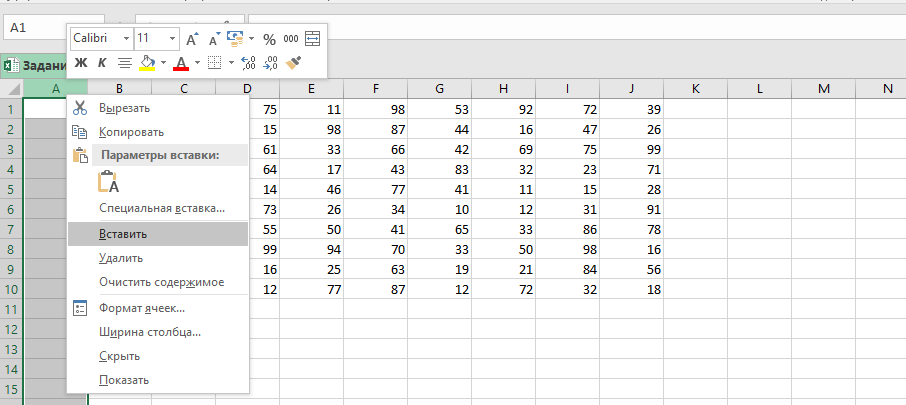
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
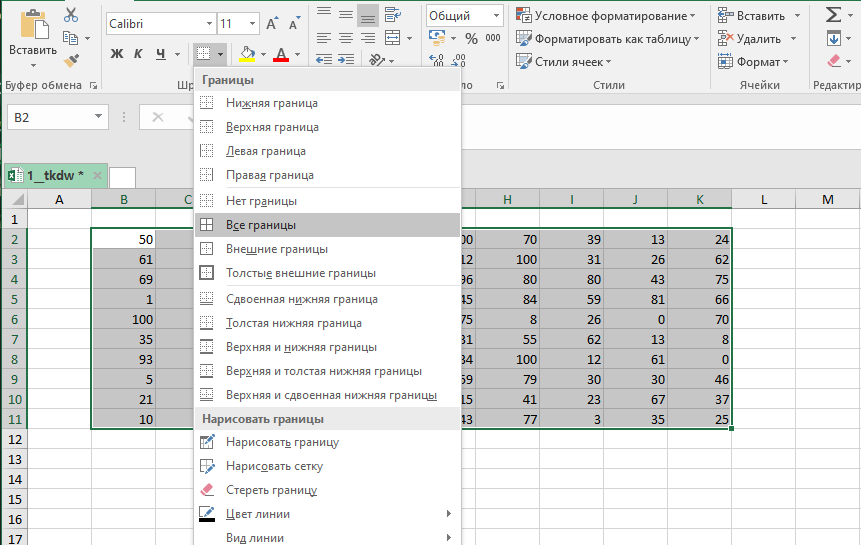
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — верхняя правая ячейка
J12результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
=J1
J12 Робот мог, либо двигаясь из ячейки I12, либо из J13. I12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка I1). Ну и поскольку дальше он попадет только в ячейку J12, то необходимо прибавить значение этой ячейки. Поскольку значение уже просчитано для результирующей таблицы, то мы и будем его брать именно с результирующей таблицы. То есть введите формулу для ячейки I12:=I1+J12
I12, будет такой же и для всех оставшихся ячеек верхней строки.I12 в диапазон ячеек A12:H12:J13. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — J2) и добавим значение ячейки, в которую он пойдет дальше — ячейка J12 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=J2+J12
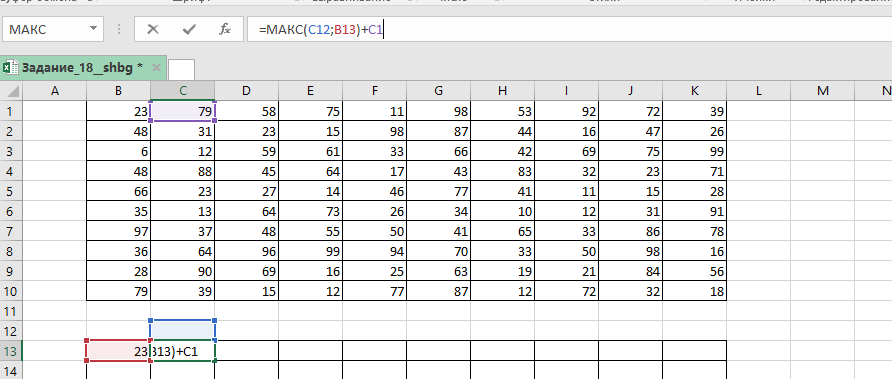
J13 подходит для всех ячеек данного столбца.J13 в диапазон ячеек J14:J21:I12 и J13 Робот мог попасть, также двигаясь из ячейки I13. Рассмотрим ее.I13 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I2), и затем у него альтернатива движения: либо в ячейку I12, либо в J13. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Для этого надо выбрать максимум из I12 и J13 и добавить к текущему значению. Введите формулу в I13:
=I2+МАКС(I12;J13)
I13, использовав маркер копирования, во все оставшиеся ячейки таблицы:I13 на =I2+МИН(I12;J13).Ответ: 1133 | 522
18_2:
Задание выполняется с использованием прилагаемых файлов
При попытке зайти на клетку со стеной Робот разрушается. Исходные данные записаны в файле в виде электронной таблицы прямоугольной формы. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю, не разрушившись. Известно, что такой путь существует. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
L25результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке исходной таблицы —L12. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
формула для L25:
=L12
L12 Робот мог, либо двигаясь из ячейки K12, либо из L11. К12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка K12). Ну и поскольку дальше он попадет только в ячейку L12, то необходимо прибавить значение этой ячейки.K25:=ЕСЛИ(И(L25>0;ИЛИ(K12<=100;K12>=500));K12+L25;0)
Если выполняются одновременно два условия: L25>0 И либо K12<=100 либо K12>=500, то собираем монету с текущей ячейки (K12) и добавляем монету с L25, так как там нет стены (L25>0)
K25 будет такой же и для всех оставшихся ячеек строки.K25 в диапазон ячеек A25:J25.L24. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — L11) и добавим значение ячейки, в которую он пойдет дальше — ячейка L25 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=ЕСЛИ(И(L25>0;ИЛИ(L11<=100;L11>=500));L11+L25;0)
Если выполняются одновременно два условия: L25>0 И либо L11<=100 либо L11>=500, то собираем монету с текущей ячейки (L11) и добавляем монету с L25, так как там нет стены (L25>0)
L24 в диапазон ячеек L14:L23.K24 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — K11), и затем у него альтернатива движения: либо в ячейку L24, либо в K25. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки, нет ли там стены. Для этого введите формулу в K24:=ЕСЛИ(И(K11>100;K11<500);0;ЕСЛИ(И(L24=0;K25=0);0;ЕСЛИ(L24=0;K11+K25; ЕСЛИ(K25=0;K11+L24;K11+МИН(L24;K25)))))
Здесь логика формулы следующая: если текущее значение ячейки соответствует стене, то записываем 0; ИНАЧЕ — если обе ячейки, в которые может двигаться Робот, — стены, то записываем в текущую ячейку 0; ИНАЧЕ — если ячейка справа — стена, то двигаемся вниз, собирая по пути монеты; ИНАЧЕ — если ячейка снизу — стена, то двигаемся вправо, собирая по пути монеты; ИНАЧЕ — выбираем минимальное значение из соседних ячеек и собираем монеты.
K24, использовав маркер копирования, во все оставшиеся ячейки таблицы:МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.
Ответ: 1492 640
18_3:
Задание выполняется с использованием прилагаемых файлов
Робот может двигаться только вниз и вправо. Для сбора денег у Робота есть контейнеры вместимостью 8 монет каждый. С каждой клетки Робот забирает наибольшее количество контейнеров, полностью заполненных монетами. Если контейнер не заполнен до конца, а монеты в клетке кончились, робот высыпает из него монеты перед переходом в следующую клетку. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
J21результирующей таблицы. Робот просто соберет монеты, которые находится в этой ячейке исходной таблицы —J10, если наберется целое число контейнеров (значение кратное 8). Если целое число контейнеров не набирается, — то робот забирает только то, что набралось в контейнеры (8* ЧАСТНОЕ от деления монет на 8). Поэтому для ячейки возьмем значение из исходной таблицы, проверяя его на кратность 8. Введите формулу:
формула для J21:
=ЕСЛИ(ОСТАТ(J10;8)=0;J10;8*ЧАСТНОЕ(J10;8))
J20. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка J9). При этом будем проверять значение на кратность 8 и действовать так же, как описано в предыдущем пункте. Ну и поскольку дальше Робот попадет только в ячейку J21, то необходимо прибавить значение этой ячейки.формула для J20: =ЕСЛИ(ОСТАТ(J9;8)=0;J9+J21;8*ЧАСТНОЕ(J9;8)+J21)
J20 будет такой же и для всех оставшихся ячеек столбца.J20 в диапазон ячеек J12:J19.I21. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — I10). Проверим заполненность контейнеров, и добавим значение ячейки, в которую Робот пойдет дальше — ячейка J21 (берем значение из результирующей таблицы, поскольку оно уже просчитано):формула для I21:
=ЕСЛИ(ОСТАТ(I10;8)=0;I10+J21;8*ЧАСТНОЕ(I10;8)+J21)
I21 в диапазон ячеек A21:H21.I20 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I9), проверяя заполненность контейнеров, и затем у него альтернатива движения: либо в ячейку J20, либо в I21. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки на заполненность контейнеров. Для этого введите формулу в I20:формула для I20:
=ЕСЛИ(ОСТАТ(I9;8)=0;I9+МАКС(J20;I21);8*ЧАСТНОЕ(I9;8)+МАКС(J20;I21))
I20, использовав маркер копирования, во все оставшиеся ячейки таблицы.МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.Ответ: 1144 448
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа и 4 команды проверки условия. Команды-приказы: вверх, вниз, влево, вправо. При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится, и программа прервётся.
Другие 4 команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно, снизу свободно, слева свободно, справа свободно. Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно. В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно). В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА <снизу свободно ИЛИ справа свободно>
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
ЕСЛИ <снизу свободно>
ТО вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
2
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа и 4 команды проверки условия.
Команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится, и программа прервётся.
Другие 4 команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно | снизу свободно | слева свободно | справа свободно |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка А1)?
НАЧАЛО
ПОКА < слева свободно ИЛИ сверху свободно >
ЕСЛИ < слева свободно >
ТО влево
ИНАЧЕ вверх
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Источник: Демонстрационная версия ЕГЭ—2013 по информатике.
3
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх , вниз
, влево
, вправо
.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно | снизу свободно | слева свободно | справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции. Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ЕСЛИ снизу свободно
ТО
вниз
КОНЕЦ ЕСЛИ
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
4
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх , вниз
, влево
, вправо
.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно | снизу свободно | слева свободно | справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободнo
ТО
вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
5
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх вниз
влево
вправо
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно | снизу свободно | слева свободно | справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в данной клетке и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
ЕСЛИ справа свободно ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Пройти тестирование по этим заданиям
12 задание ЕГЭ по информатике обычно решает только половина выпускников. Оно правда такое сложное? Нет, если заранее изучить каждый из трех прототипов. Из этой статьи вы узнаете, как справиться с Редактором, Роботом и Чертежником — и как можно сделать это еще проще, используя программирование.
Прототипы задания 12 и их сложности
12 задание ЕГЭ по информатике относится к повышенному уровню сложности. На экзамене за него можно получить один первичный балл.
Это задание — часть блога «Алгоритмизация». Чтобы решить его, нужно уметь работать с алгоритмами и анализировать их. В этом задании могут встретиться три прототипа заданий: Редактор, Робот и Чертежник. Причем Редактор встречается на экзамене в последнее время чаще других прототипов.
Редактор — это прототип на работу с цепочками цифр или букв. Нам дают алгоритм и строку, содержащую некоторое количество знаков. Нужно узнать, какая строка получится после выполнения программы или посчитать количество символов в строке.
Если решать подобные задания аналитически, нужно искать закономерности изменения цепочки, чтобы получить ответ. Именно в этом и заключается сложность задания, ведь не все могут правильно найти нужную закономерность.
Робот — прототип на работу с клетчатой плоскостью и алгоритмом. Вам дают алгоритм и плоскость, содержащую 36 клеток. Нужно найти количество клеток, удовлетворяющее определенному условию. Сложность в том, что ученики начинают проверять все 36 клеток. Делать это не нужно, если проанализировать алгоритм из условия.
Чертежник — прототип на работу с алгоритмом, где исполнитель перемещается по координатной плоскости. Чаще всего в таких заданиях в алгоритме есть пропуски в командах. Нужно найти наибольшее количество повторений цикла. Сложностей обычно здесь не так много, основная — невнимательность при выполнении вычислений.
Самостоятельно подготовиться к ЕГЭ непросто. На то, чтобы разобраться со всеми темами, понадобится много времени. Но и это не решит проблему! Например, если вы запомнили какое-то решение из интернета, а оно оказалось неправильным, можно на пустом месте потерять баллы. Если хотите научиться решать все задания ЕГЭ по информатике, обратите внимание на онлайн-курсы MAXIMUM! Наши специалисты уже проанализировали сотни вариантов ЕГЭ и подготовили для вас вас максимально полезные занятия.
Приходите к нам на консультацию — вы сможете пройти диагностику по выбранным предметам ЕГЭ, поставить цели и составить стратегию подготовки, чтобы получить на экзамене высокие баллы. Все это абсолютно бесплатно!
Редактор — как решать?
Задания с прототипом «Редактор» можно решать как аналитически, так и с помощью компьютера, если у вас все хорошо с программированием. Мы рассмотрим с вами оба способа решения и убедимся, что они дают одинаковые ответы.
Пример 1 (Редактор)
Исполнитель Редактор получает на вход строку цифр и преобразовывает ее.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 88 идущих подряд цифр 4? В ответе запишите полученную строку.
Аналитическое решение
Алгоритм сначала заменяет в цепочке цифр все четверки на единицы. Потом начинает заменять назад единицы на четверки, но как только в цепочке образуются 3 четверки, алгоритм заменяет их на единицу. Порядок замены имеет значение при поиске ответа, поэтому его нужно обязательно учитывать. Также важно, что замена выполняется всегда в начале цепочки.
Сначала уберем по возможности все четверки из цепочки.
88 / 3 = 29 и 1 в остатке.
Получается, что из цепочки уйдет 29 блоков по 3 четверки и образуется 29 единиц, 1 четверка останется в цепочке в самом конце.
Теперь будем последовательно убирать единицы из цепочки.
29 “1” + 1 “4”
1 “4” + 27 “1” + 1 “4”
2 “4” + 25 “1” + 1 “4”
3 “4” + 23 “1” + 1 “4”
24 “1” + 1 “4”
Как только в цепочке появились 3 четверки, алгоритм заменил их назад на единицу. Суммарно из цепочки ушло 5 единиц. Это действие будет повторяться циклически, поэтому можно посчитать, сколько блоков по 5 единиц уйдет из цепочки.
29 / 5 = 5 и 4 в остатке
Получается, что в цепочке останется 4 единицы и 1 четверка.
11114 → 4114 → 444 → 1
В итоге в цепочке останется только единица.
Решение с помощью компьютера
В самом задании у нас уже написана программа. Остается перевести ее на конкретный язык программирования. Напишем программу на Python.
Она будет выглядеть следующим образом:
Создаем строку, содержащую 88 четверок. Далее запускаем цикл, который будет проверять, есть ли в строке 3 четверки или 2 единицы. Пропиваем условие и замену в строке. Важно в методе replace() указать третий параметр, который отмечает, сколько замен нужно выполнить. По умолчанию replace() сразу заменит все цифры в строке, а нам нужно выполнять замены по одной.
При запуске данной программы мы также получим ответ 1.
Ответ: 1
Пример 2 (Редактор)
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
На вход приведенной ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 25 цифр 1, 45 цифр 2 и 10 цифр 3, расположенных в произвольном порядке.
Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы.
Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.
Аналитическое решение
Цифры 1, 2 и 3 находятся в строке в произвольном порядке. Все, что нам нужно сделать, чтобы получить ответ — это понять, сколько цифр образовалось в результате замен.
Каждую единицу алгоритм заменит на тройку. Если изначально было 25 единиц, то в результате замен образуется 25 троек, и их сумма будет равна 25 * 3 = 75.
Каждую двойку алгоритм заменит на 2 единицы. Изначально было 45 двоек, значит, в результате замен образуется 90 единиц. Их сумма будет равна 90.
Каждую тройку алгоритм заменит на 2 тройки. Было 10 троек, станет 20. Сумма составит 20 * 3 = 60.
Итоговая сумма всех цифр цепочки будет равна 75 + 90 + 60 = 225.
Решение с помощью компьютера
Перенесем алгоритм на язык программирования Python.
Получаем следующую программу:
Сначала мы задали строку, содержащую знак “>” и нужное количество всех цифр. Далее в цикле проверяем наличие знака “>” и цифр и выполняем замену. Как только программа вышла из цикла, считаем количество единиц, двоек и троек в строке — и находим сумму. При запуске программы также получается ответ 225.
В данном задании написание программы может занять больше времени, чем аналитическое решение. Поэтому всегда оценивайте временные затраты на написание кода.
Ответ: 225
Робот — как решать?
Второй прототип, который включает в себя 12 задание ЕГЭ по информатике — Робот. Этот прототип точно придётся решать аналитически, поэтому давайте разбираться, как сделать это с минимальными затратами времени.
Пример 3 (Робот)
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа и 4 команды проверки условия.
Команды-приказы: вверх, вниз, влево, вправо
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится, и программа прервется.
Другие 4 команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно, снизу свободно, слева свободно, справа свободно
Цикл
ПОКА < условие > команда
Выполняется, пока условие истинно, иначе происходит переход на следующую строку.
Если РОБОТ начнет движение в сторону стены, то он разрушится, и программа прервется.
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ уцелеет и остановится в той же клетке, с которой он начал движение?
НАЧАЛО
ПОКА < снизу свободно > вправо
ПОКА < справа свободно > вверх
ПОКА < сверху свободно > влево
ПОКА < слева свободно > вниз
КОНЕЦ
Решение
Чтобы не проверять все 36 клеток плоскости, нужно проанализировать программу. В алгоритме 4 цикла, но нам важен только последний. Робот будет выполнять действия и остановится только в той клетке плоскости, где слева есть стена, так как в последнем цикле мы проверяем именно это условие. Поэтому необходимо проверить только те клетки, где слева есть стена. В остальных клетках плоскости Робот просто не сможет остановиться, поэтому и начинать движение из них мы тоже не будем.
Проверяем по алгоритму 12 отмеченных клеток.
Из всех отмеченных клеток нам подойдет только клетка В5. Если начать движение из нее, Робот вернется в эту же точку. Остальные клетки не подойдут, так как Робот либо разобьется, либо остановится в другой клетке.
Ответ: 1
Прототип Чертежник — как решать?
Последний прототип, который составители включили в 12 задание ЕГЭ по информатике — это Чертежник. Здесь при решении важно правильно составить систему уравнений и найти наибольший/наименьший делитель двух чисел. Посмотрим, как это сделать.
Пример 4 (Чертежник)
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и величины смещения в первой из повторяемых команд неизвестны):
В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?
Решение
Чтобы решить это задание, необходимо обозначить неизвестными пропуски в алгоритме.
Далее составим систему уравнений. Нам известно, как перемещался Чертежник, и сказано, что он вернулся в начальную точку. Получается, его перемещение равно 0.
Теперь мы можем найти n — наибольшее количество повторений цикла. Число n должно быть делителем как 24, так и 16, то есть нам нужно найти НОД(24, 16). Он равен 8. Это и будет ответом к заданию.
Ответ: 8
Что нужно запомнить?
- Если вам попадется Редактор, можете написать программу, которая найдет ответ вместо вас. Но всегда рассчитывайте, что будет рациональнее: аналитическое решение или компьютерное. Если останется время, можно проверить себя вторым способом.
- Решая задание с Роботом, не нужно проверять все клетки — это долго. Проанализируйте алгоритм и проверяйте только те клетки, которые действительно могут подойти под условия.
- Чтобы разобраться с Чертежником, внимательно составляйте систему уравнений. Ищите НОД, если нужно найти наибольшее количество повторений цикла.
- Если в конце экзамена осталось время, вернитесь к заданию и проверьте его — ребята часто теряют баллы из-за невнимательности. Особенно рекомендую перепроверить Робота — решите его заново.
Теперь вы знаете, как решать 12 задание ЕГЭ по информатике! Обязательно прочитайте наш гайд по этому экзамену, если хотите разобраться с остальными темами и заданиями. Там вы найдете структуру экзамена, актуальные прототипы, тематические блоки и лайфхаки от наших преподавателей. Желаем удачи в подготовке 🙂
Динамическое
программирование. Робот – сборщик монет
Разбор задания № 18 КЕГЭ 2021
Проверяемые элементы содержания:
Умение обрабатывать
вещественные выражения в электронных таблицах.
Использование инструментов
решения статистических и расчётно-графических задач.
Проверяемые
умения или способы действий: представлять и
анализировать табличную информацию
(повышенный уровень, время – 6
мин)
|
Задание повышенного уровня сложности проверяет знания и |
|||
|
использовать для расчетов в таблицах |
|||
|
таблицу значениями с использованием формул, |
|||
|
Кроме того, это задание проверяет умение применять методы динамического |
|||
|
программирования при решении задач с |
|||
|
При выполнении этого задания важно построить правильную |
|||
|
модель процесса, аккуратно описать |
|||
|
интерпретировать |
|||
|
Динамическое |
|||
|
разбиения на несколько |
|||
|
Самым простым примером будут числа Фибоначчи — чтобы |
|||
|
число в этой последовательности, нам нужно |
|||
|
первые два, затем четвертое таким же |
|||
|
далее. |
|||
|
Решение задачи динамическим программированием должно |
|||
|
● |
|||
|
условии); |
|||
|
● значение начальных состояний. |
|||
|
В задачах данного типа “динамическое программирование” |
|||
|
означает оптимальную |
|||
Общие сведения:
|
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель |
|
перемещаться по клеткам, выполняя за одно |
|
или вниз. По команде вправо Робот перемещается |
|
команде вниз – в соседнюю нижнюю. При |
|
разрушается. Перед каждым запуском Робота |
|
достоинством от 1 до 100. Посетив клетку, Робот |
|
относится |
Информационные ресурсы:
1. Теория:
Обработка числовой информации
2. Задания
для тренировки: Задания 18. Робот-сборщик монет
За да ние № 18 (ФИПИ ДЕМО КЕГЭ-2021)
|
Определите максимальную |
||||||||||||
|
собрать Робот, пройдя из левой верхней |
||||||||||||
|
два |
||||||||||||
|
Исходные данные |
||||||||||||
|
ячейка |
||||||||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|||
|
1 |
51 |
21 |
93 |
48 |
45 |
100 |
67 |
39 |
18 |
29 |
||
|
2 |
57 |
43 |
97 |
51 |
92 |
10 |
93 |
32 |
19 |
58 |
||
|
3 |
63 |
16 |
31 |
16 |
78 |
88 |
90 |
72 |
37 |
67 |
||
|
4 |
10 |
57 |
64 |
25 |
96 |
50 |
81 |
65 |
91 |
69 |
||
|
5 |
99 |
43 |
95 |
7 |
40 |
76 |
18 |
34 |
5 |
65 |
||
|
6 |
35 |
19 |
71 |
77 |
64 |
38 |
62 |
56 |
10 |
2 |
||
|
7 |
100 |
57 |
27 |
26 |
51 |
33 |
100 |
11 |
53 |
1 |
||
|
8 |
11 |
79 |
49 |
46 |
37 |
69 |
80 |
31 |
25 |
39 |
||
|
9 |
22 |
71 |
20 |
23 |
11 |
12 |
39 |
16 |
64 |
34 |
||
|
10 |
4 |
25 |
87 |
84 |
30 |
48 |
77 |
13 |
40 |
33 |
Решение:
1.
В первой строке таблицы и в первом столбце вычислим значения с
нарастающим итогом, т.е.
a.
в ячейку L1 введём формулу =A1,
b.
в M1 =L1+B1, с помощью автозаполнения копируем формулу из M1
в диапазон ячеек N1:U1;
c.
в L2 =L1+A2, с помощью автозаполнения копируем
формулу из L2 в диапазон ячеек L3:L10;
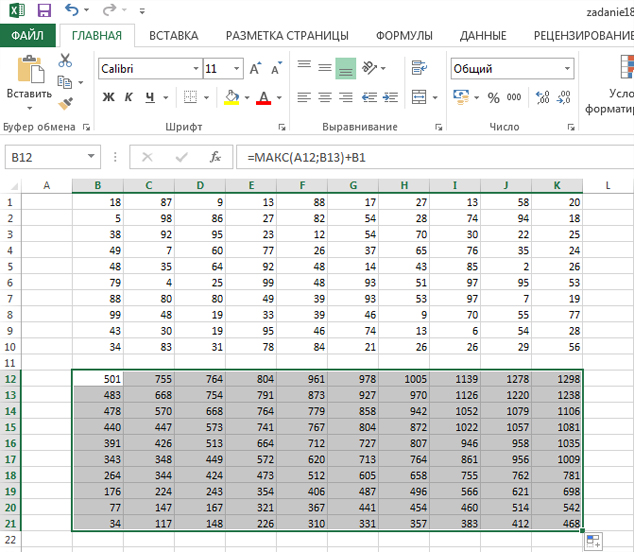
2.
Для поиска максимальной суммы в ячейку M2 введём формулу
=MAX(M1;L2)+B2
3.
С помощью автозаполнения скопируем формулу из M2 в
диапазон ячеек
M2:U10. Получим таблицу:
В ячейке U10 находится искомое
число: max = 1204.
4.
Для поиска минимальной суммы в ячейку M2 введём формулу
=MIN(M1;L2)+B2
5. С помощью автозаполнения скопируем формулу из M2 в
диапазон ячеек
M2:U10. Получим таблицу:
|
Задание 18 № |
|
|
Дан квадрат 15 × 15 клеток, в каждой клетке которого |
|
|
правом верхнем углу квадрата |
|
|
одну клетку влево, вниз или по |
|
|
робот не может. Необходимо переместить |
|
|
сумма чисел в клетках, через которые прошёл |
|
|
была максимальной. |
|
|
Исходные данные |
Решение:
1. В
первой строке таблицы и в первом столбце вычислим значения с нарастающим
итогом, т.е.
a.
в ячейку O17 введём формулу =O1,
b.
в N17 =O17+N1, с помощью автозаполнения копируем (справа
налево) формулу из N17 в диапазон ячеек A17:M17;
c.
в O18 =O17+O2, с помощью автозаполнения копируем (сверху
вниз) формулу из O18 в диапазон ячеек O19:O21;
2.
Для поиска максимальной суммы в ячейку N18 введём формулу
=MAX(N17;O17;O18)+N2
3. С помощью
автозаполнения скопируем (по диагонали влево вниз) формулу из N18 в
диапазон ячеек A18:N31. Получим таблицу:
Разбор заданий № 24. Готовимся к итоговой
аттестации 2021. Лещинер, В.Р.[2]
|
Вариант № 1 |
|
|
Определите максимальную |
|
|
собрать Робот, пройдя из левой нижней |
|
|
два |
|
|
Исходные данные |
|
|
ячейка |
Решение:
1.
В последней строке таблицы и в первом столбце вычислим
значения с нарастающим итогом, т.е.
a.
в ячейку N12 введём формулу =A12,
b.
в O12 =N12+B12, с помощью автозаполнения копируем формулу
из O12 в диапазон ячеек P12:Y12;
c.
в N11 =N12+A11, с помощью автозаполнения копируем формулу
из N11 в диапазон ячеек N1:N10;
2.
Для поиска максимальной суммы в ячейку O11 введём формулу
=MAX(N11;O12)+B11
3.
С помощью автозаполнения скопируем формулу из O11 в
диапазон ячеек O1:Y11. Получим таблицу:
В ячейке Y1 находится
искомое число: max = 1439.
4.
Для поиска минимальной суммы в ячейку O11 введём формулу
=MIN(N11;O12)+B11
5. С
помощью автозаполнения скопируем формулу из O11 в диапазон ячеек O1:Y11.
Получим таблицу:
|
Вариант № 2 |
|
|
Определите максимальную |
|
|
собрать Робот, пройдя из правой нижней |
|
|
два |
|
|
Исходные данные |
|
|
ячейка |
Решение:
1.
В последней строке таблицы и в последнем столбце
вычислим значения с нарастающим итогом, т.е.
a.
в ячейку Y12 введём формулу =L12,
b.
в X12 =Y12+K12, с помощью автозаполнения копируем формулу
из X12 в диапазон ячеек N12:W12;
c.
в Y11 =Y12+L11, с помощью автозаполнения копируем формулу
из Y11 в диапазон ячеек Y1:Y10;
2.
Для поиска максимальной суммы в ячейку X11 введём формулу
=MAX(X12;Y11)+K11
3.
С помощью автозаполнения скопируем формулу из X11 в
диапазон ячеек
N1:X11. Получим таблицу:
В ячейке N1 находится
искомое число: max = 1345
4.
Для поиска минимальной суммы в ячейку X11 введём формулу
=MIN(X12;Y11)+K11
5. С помощью автозаполнения скопируем формулу из X11 в
диапазон ячеек
N1:X11. Получим таблицу:
Задание № 18.1
|
Определите максимальную |
|
собрать Робот, пройдя из правой верхней |
|
два |
|
Исходные данные |
|
ячейка |
Решение:
1. В первой строке таблицы
и в последнем столбце вычислим значения с нарастающим итогом, т.е.
a.
в ячейку U1 введём формулу =J1,
b.
в T1 =U1+L1, с помощью автозаполнения копируем формулу
из T1 в диапазон ячеек L1:S1;
c.
в U2 =U1+J2, с помощью автозаполнения копируем формулу
из U2 в диапазон ячеек U3:U10;
2. Для поиска максимальной суммы в ячейку T2 введём формулу
=MAX(T1;U2)+I2
3.
С помощью автозаполнения скопируем формулу из T2 в
диапазон ячеек L2:T10. Получим таблицу:
В ячейке L10 находится
искомое число: max = 1133.
4.
Для поиска минимальной суммы в ячейку T2 введём
формулу =MIN(T1;U2)+I2
5.
С помощью автозаполнения скопируем формулу из T2 в
диапазон ячеек L2:T10. Получим таблицу:
Привет! Мы добрались до 18 задания из ЕГЭ по информатике 2021.
Это задание снова решается с помощью компьютера.
Восемнадцатое задание направлено на обработку вещественных чисел с помощью таблиц. Мы с вами будет использовать программу Excel от компании Microsoft.
Перейдём к к тренировке решения 18 задания из ЕГЭ по информатике 2021.
Задача (Стандартная)
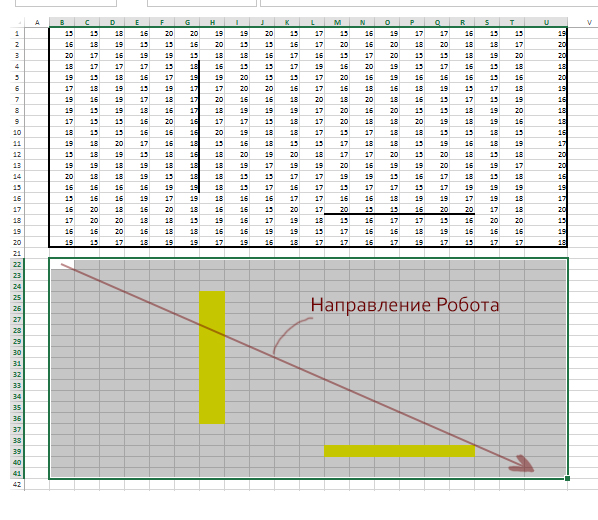
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монеты с собой; это также относится к начальной и конечной клетке маршрута Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
Решение:
Открываем файл к данной задачке.
В начале найдём максимальную сумму.
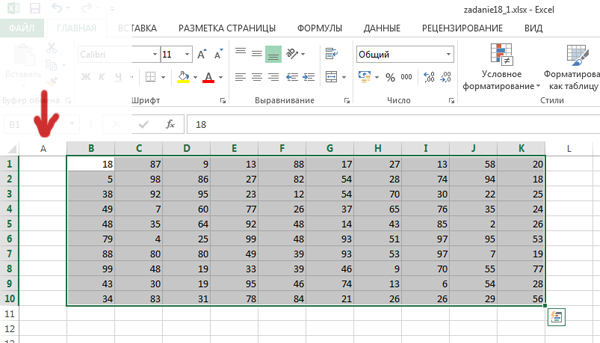
Выделяем область всех ячеек, где написаны числа, вырезаем её и вставляем на столбец правее. Это нужно для того, чтобы при составлении формулы решения не было ошибок.
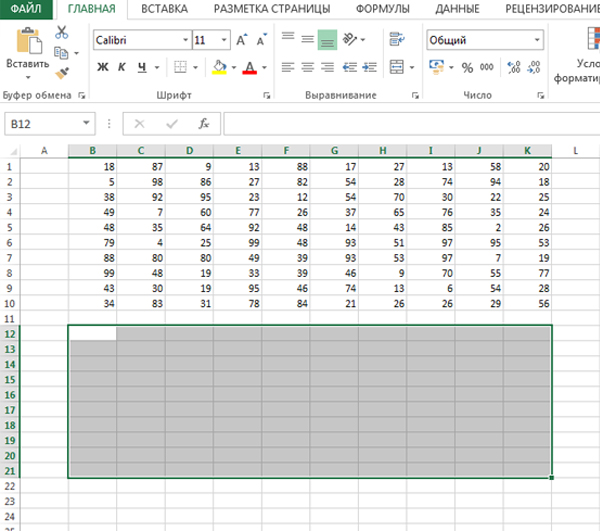
Обозначим мысленно ту область, где мы будем составлять наше решение, пропустив одну или две строчки снизу. По размеру область будет такая же.
В каждой ячейке этой области будет лежать максимальная cумма, которую может собрать Робот, дойдя до этой клетки. Т.к. Робот идёт в верхнюю правую клетку, то, соответственно, в ячейке K12 будет находится нужный нам ответ.
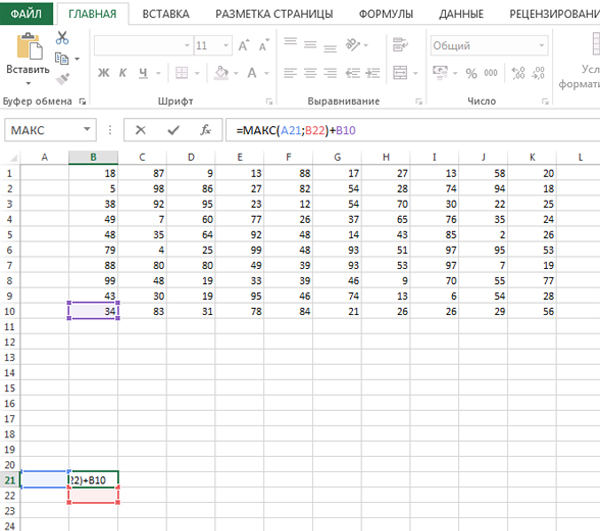
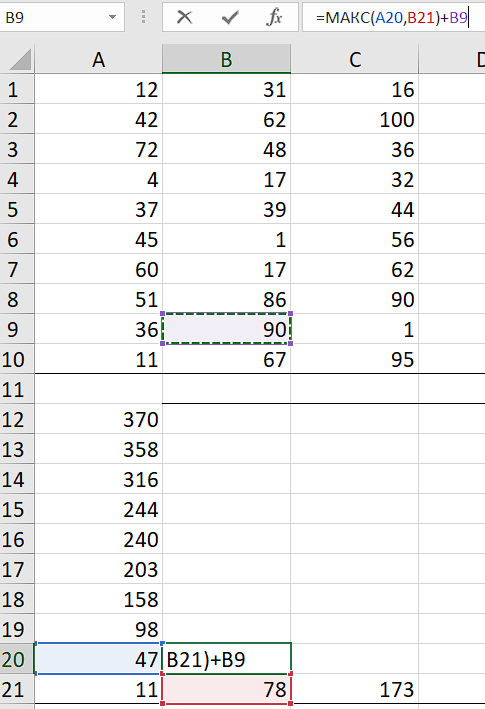
Наш Робот идёт из левой нижней клетки. Поэтому формулу, решающую эту задачу, составим сначала для ячейки B21.
Кликаем на ячейку B21 и пишем формулу:
=МАКС(A21;B22)+B10
Примечание: Чтобы в ячейке начать писать формулу, нужно поставить знак «=».
В любую ячейку нашей области можно попасть либо слева, либо снизу (Т.к. составляем формулу для любой ячейки, то не играет роли, что в данная ячейка угловая). Поэтому для ячейки B21 мы берём предыдущий результат — либо из левой ячейки, либо из правой ячейки, в зависимости от того, где собранная сумма больше.
Эту роль исполняет функция МАКС(). Она помогает выбрать откуда нужно идти, чтобы сумма всегда была максимальна.
Плюс, мы должны добавить сумму для данной ячейки к максимальной сумме предыдущей клетки. Поэтому в формулу дописываем ячейку B10
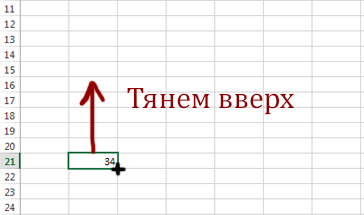
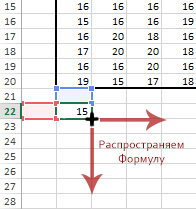
После того, как составили формулу для одной ячейки B21, можно распространить формулу на всю область.
Подносим мышку к правому нижнему углу. Как только появился чёрный крестик, кликаем левую кнопку мыши, и тянем вверх на 10 строчек вверх.
После того, как столбец готов, выделяем этот столбец, и аналогично, распространяем его на всё пространство.
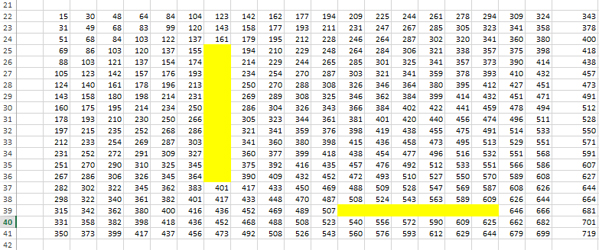
В итоге получается такая картина:
Видим, что в ячейке K12 значение 1298. Это значение нам и нужно.
Аналогичным образом ищется минимальное значение, только в формуле вместо функции МАКС будет использоваться функция МИН.
Минимальное значение получилось 589.
Ответ: 1298589
Посмотрим ещё одну интересную задачу из примерны задач ЕГЭ по информатике нового образца 2021.
Задача (со стенками)
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел
Решение:
Открываем файл в программе Excel.
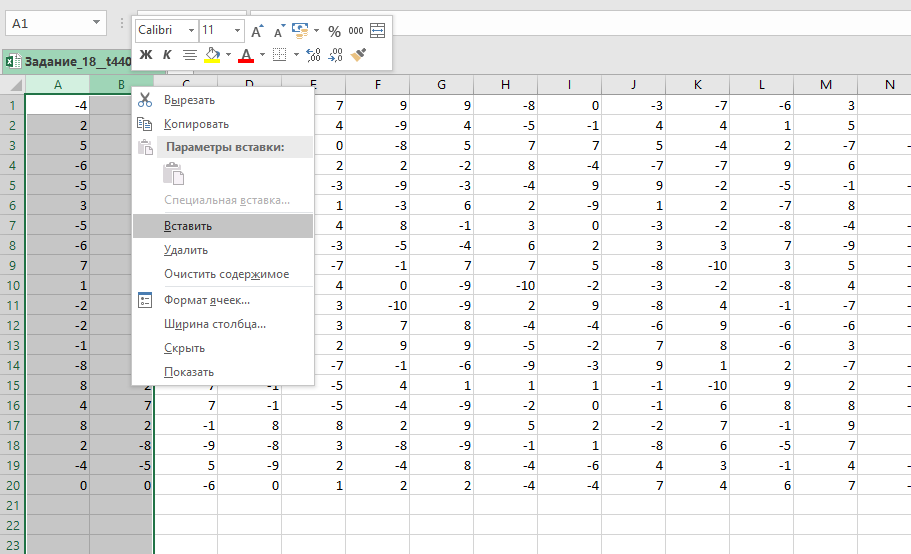
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
Распространим формулу на всё пространство, не трогая закрашенные клетки.
Получается такая картина:
В ячейки для первой закрашенной области, Робот может попасть только сверху! Поэтому пишем формулу для ячейки H25:
=H24+H4
Распространяем формулу по всему закрашенному столбцу.
В ячейки для второй закрашенной области, Робот может попасть только слева! Поэтому пишем формулу для ячейки М39:
=L39+M18
Распространяем формулу по всей закрашенной строчке.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 721.
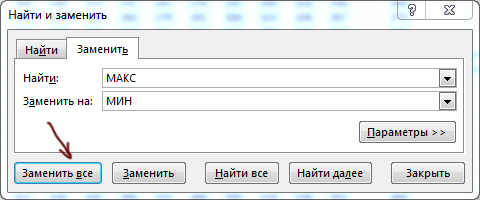
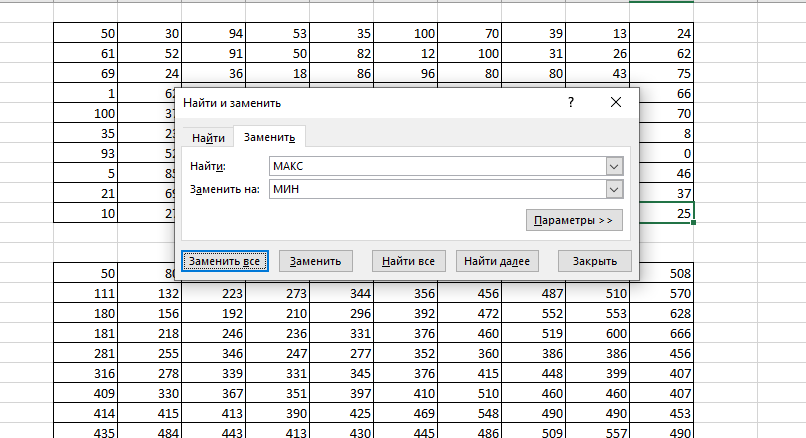
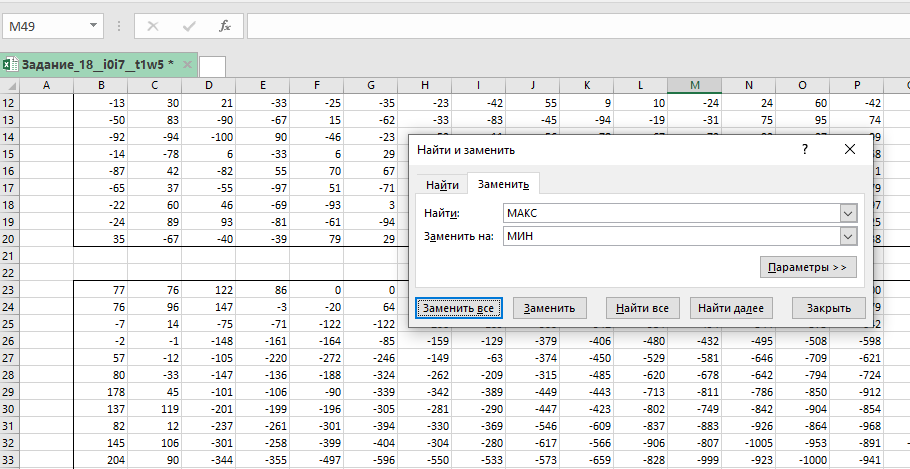
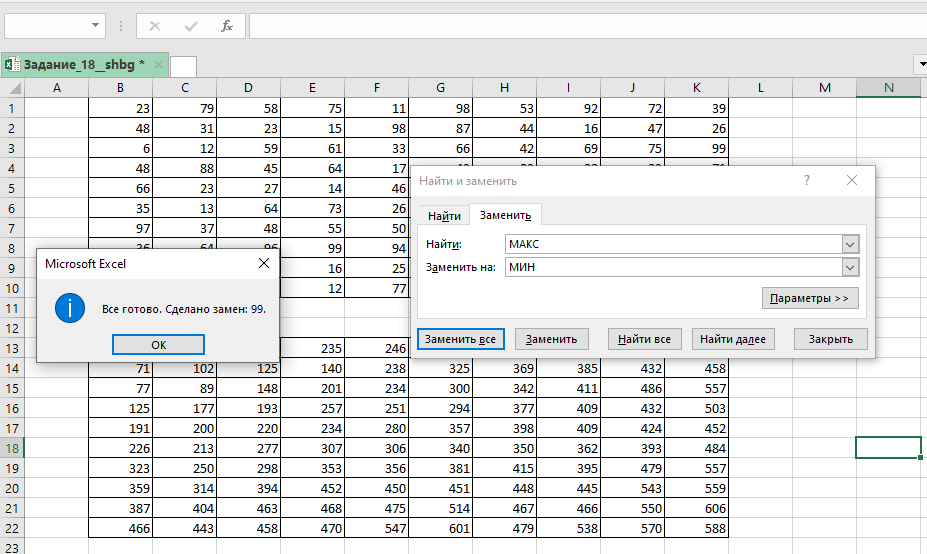
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 640.
Ответ:
Задача (Два Робота)
Квадрат разлинован на N×N клеток (2 < N < 19). В каждой клетке лежат
монеты, количество которых соответствует записанному числу. Количество
монет не может быть меньше 1.
Два исполнителя – ВЕРХ и НИЗ – существуют на одинаковых полях. Первый
имеет две команды – вверх и вправо, второй – вниз и вправо, которые,
соответственно, перемещают исполнитель на одну клетку вверх, вниз или
вправо. Исполнитель ВЕРХ начинает движение в левой нижней ячейке,
исполнитель НИЗ – в левой верхней.
Откройте файл. Какой из исполнителей соберет большее количество монет в результате
своей работы, если известно, что каждый из них запрограммирован собрать
максимальное количество монет?
Исходные данные представляют собой электронную таблицу размером N×N,
каждая ячейка которой соответствует клетке квадрата.
Пример:
| 1 | 8 | 8 | 4 | 10 |
| 10 | 1 | 1 | 3 | 2 |
| 1 | 3 | 12 | 2 | 8 |
| 2 | 3 | 5 | 6 | 11 |
| 3 | 19 | 14 | 11 | 5 |
Для указанных входных данных ответом является комбинация из названия
исполнителя и количества собранных монет
ВЕРХ84
Решение:
Перенесём таблицу чисел на один столбец вправо.
Найдём, сколько соберёт монет исполнитель ВЕРХ.
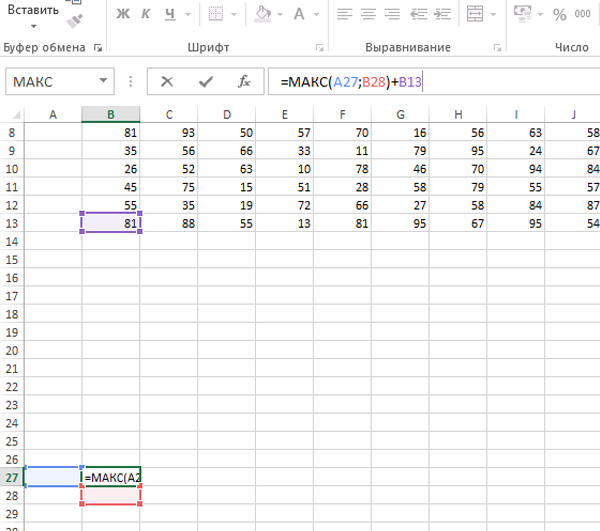
Исполнитель «ВЕРХ» начинает идти с левой нижней клетки. Поэтому первую формулу мы зададим для клетки B27. Эта ячейка является нижней левой клеткой для области, где мы будем составлять решение.
Напишем в ячейке B27:
=МАКС(A27;B28)+B13
Распространим формулу на всё пространство.
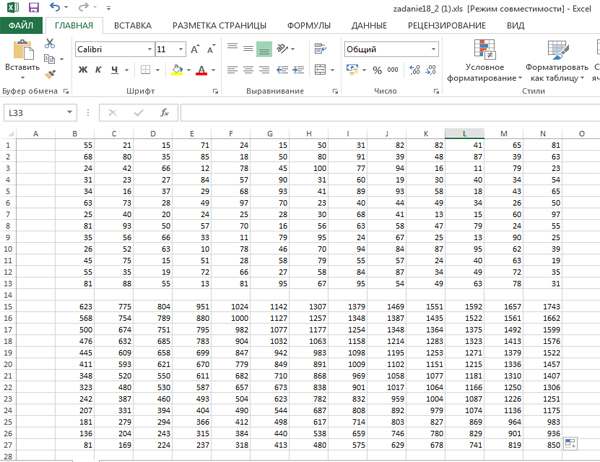
Когда исполнитель пройдёт всё поле, в ячейке N15 будет находится ответ. Максимальное количество монет, которое может собрать исполнитель ВЕРХ будет 1743.
Теперь найдём максимальное количество монет, которое может собрать исполнитель НИЗ.
Решать будем аналогичным образом, удалив все следы от предыдущего исполнителя.
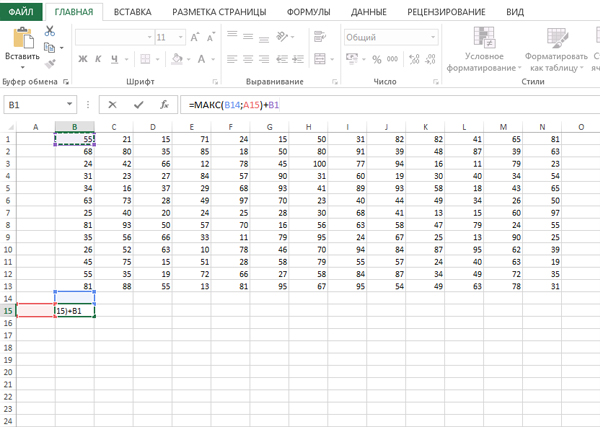
Т.к. исполнитель НИЗ стартует с левой верхней клетки, то мы сначала составим формулу для ячейки B15. Эта клетка олицетворяет левую верхнюю ячейку для области, где будет происходить решение.
=МАКС(B14;A15)+B1
В любую ячейку мы можем попасть либо сверху, либо слева. Это не относится к боковым и угловым ячейкам, но формула будет работать и для них.
При составлении максимальной суммы для любой ячейки, мы выбираем максимальное значение суммы из двух предыдущих ячеек + добавляем значение для этой ячейки.
Распространим формулу на всё пространство.
В ячейке N27 будет максимальное значение для исполнителя НИЗ. Получилось 1686.
Видим, что у исполнителя ВЕРХ получилось собрать больше монет.
Ответ: ВЕРХ1743
Спасибо за ваши советы, не знаю как без них бы я готовился к экзамену, не сдавайтесь и продолжайте помогать нам, молодёжи, удачи!
Тема 18.
Обработка вещественных выражений в электронных таблицах
18
.
01
Робот-сборщик монет (Стандарт)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
обработка вещественных выражений в электронных таблицах
18.01Робот-сборщик монет (Стандарт)
18.02Робот-сборщик монет (Стенки)
18.03Робот-сборщик монет (Котики)
18.04Робот-сборщик монет (Ямы)
18.05Робот-сборщик монет (Смешанное)
18.06Шахматные фигуры
18.07Последовательность чисел
18.08Нестандартные прототипы
Решаем задачи
Задание выполняется с использованием прилагаемых файлов.
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от до
.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней
клетки в правую нижнюю. В ответ запишите два числа друг за другом через пробел — сначала максимальную сумму,
затем минимальную.
Исходные данные представляют собой электронную таблицу размером , каждая ячейка которой соответствует
клетке квадрата.
Вложения к задаче
Показать ответ и решение
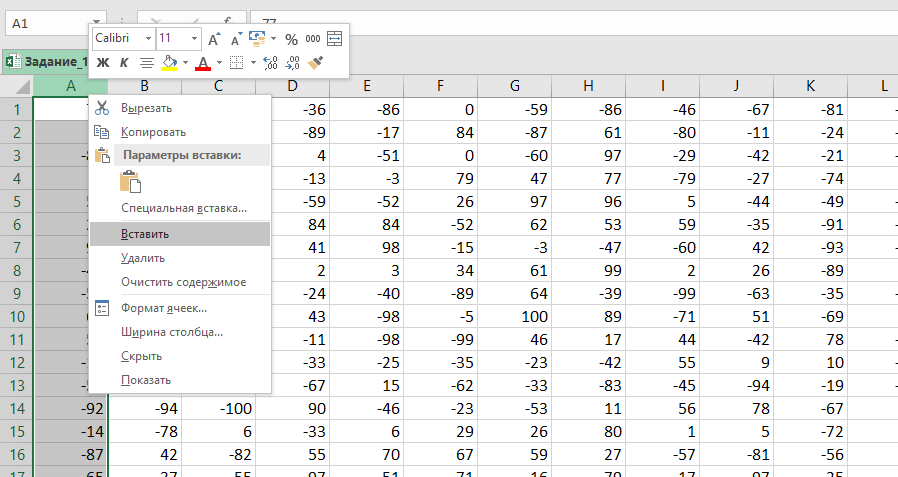
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить) и пустую строку перед
самой первой (нажимаем правой кнопкой мыши на строку и выбираем Вставить).
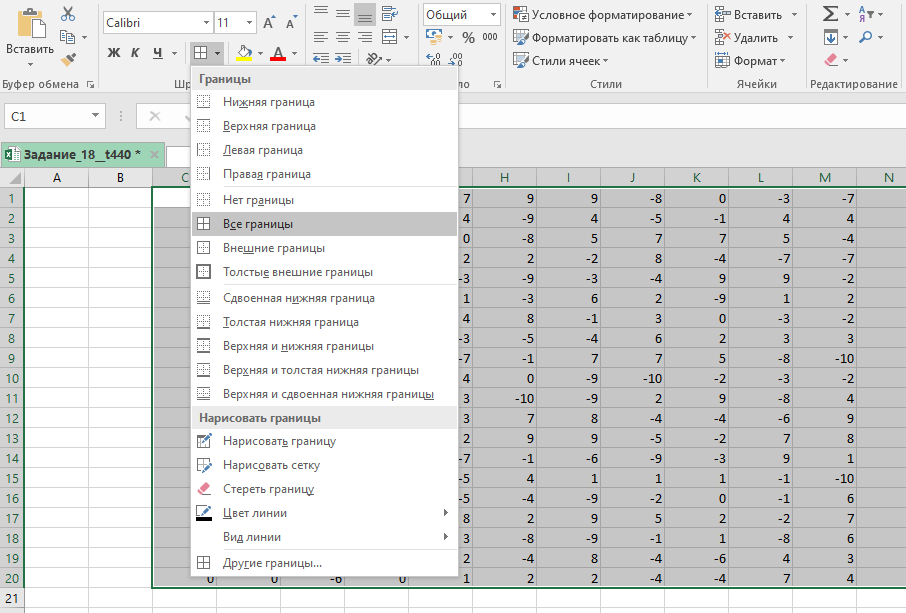
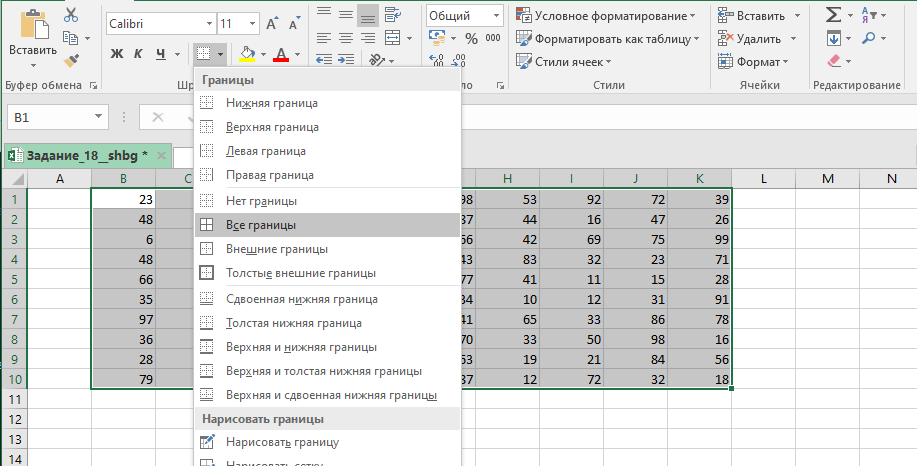
Выделим всю таблицу и добавим границы.
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
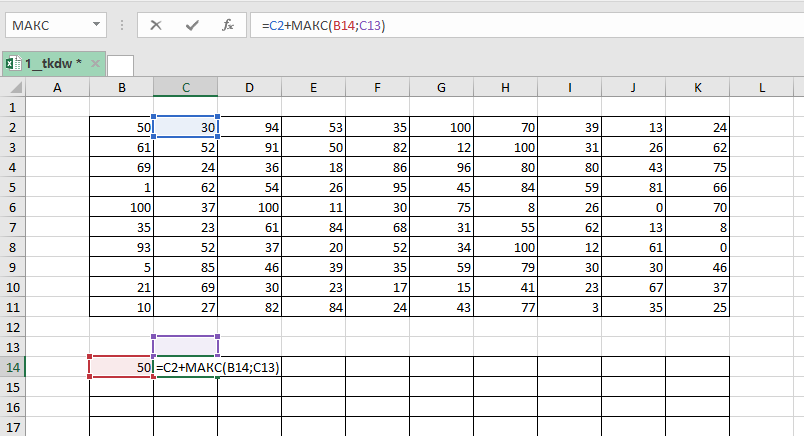
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =C2+МАКС(B14;C13)
Копируем её на всю таблицу. Выписываем значение из правой нижней ячейки. Заменим все МИН на
МАКС.
Запишем в ответ сначала максимальное количество монет, затем через пробел — минимальное.
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на клеток
. Робот стоит в левом нижнем углу. Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо
Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу
квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от
до . Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите минимальную денежную сумму и максимальную денежную сумму, которую может собрать
Робот. В ответ запишите два числа друг за другом без разделительных знаков — сначала минимальную сумму, затем
максимальную сумму.
Исходные данные представляют собой электронную таблицу размером , каждая ячейка которой соответствует
клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:
Вложения к задаче
Показать ответ и решение
Скопируем табличку вниз. Очистим ее. Вставим левое нижнее число из изначальной ячейки.
Далее левую сторону и нижнюю заполняем как: предыдущее значение + значение из старой ячейки.
Потом встаем в ячейку по диагонали вправо вверх и пишем основную формулу для подсчета:
Также поступаем с минимальной суммой — заменяем в формулах на МИН. Пишем ответ.
Дан квадрат клеток, в каждой клетке которого записано целое число. В левом верхнем углу стоит некая фигура.
За один ход она может переместиться в пределах квадрата либо вправо (на одну или две клетки), либо вниз (на одну или
две клетки). Необходимо переместить фигуру в правый нижний угол так, чтобы сумма чисел в клетках, в которых она
останавливалась (включая начальную и конечную), была максимальной.
В ответ запишите максимально возможную сумму.
Вложения к задаче
Показать ответ и решение
Добавляем 2 пустых столбца (выделяем столбцы и
, нажимаем правой кнопкой и выбираем Вставить).
Выделим всю таблицу и добавим границы.
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
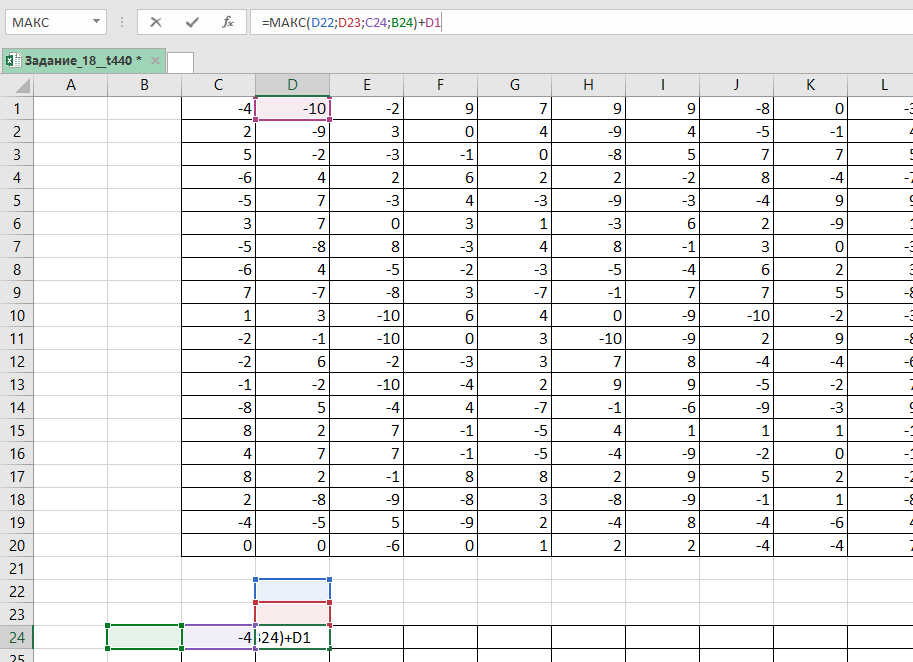
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =МАКС(D22;D23;C24;B24)+D1
Копируем её на всю таблицу.
Выписываем значение из правой нижней ячейки в ответ.
Дан квадрат клеток, в каждой клетке которого записано целое число. В левом верхнем углу квадрата
стоит робот. За один ход робот может переместиться на одну клетку вправо, вниз или по диагонали вправо
вниз. Выходить за пределы квадрата робот не может. Определите максимальную и минимальную сумму
чисел в клетках, которую может собрать Робот (включая начальную и конечную клетки), пройдя из левой
верхней клетки в правую нижнюю. В ответе укажите одно число – сумму максимальной и минимальной
сумм.
Вложения к задаче
Показать ответ и решение
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить).
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
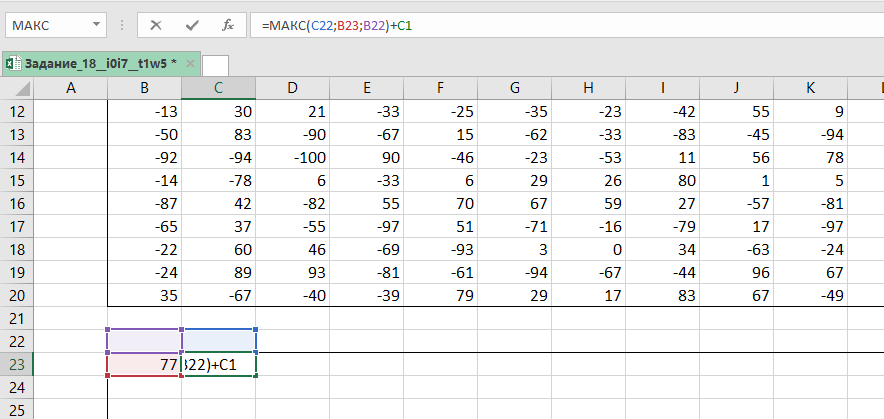
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =МАКС(C22;B23;B22)+C1
Копируем её на всю таблицу. Выписываем 1909 из правой нижней ячейки. Заменим все МИН на МАКС.
В правой нижней ячейке получим -1473.
Запишем в ответ сумму двух полученных значений: 1909 + (-1473) = 436.
Задание выполняется с использованием прилагаемых файлов.
Квадрат разлинован на клеток
. Исполнитель Робот может перемещаться по клеткам, выполняя
за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от до
.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из
левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала
максимальную сумму, затем минимальную.
Вложения к задаче
Показать ответ и решение
Добавляем пустой столбец (нажимаем правой кнопкой мыши на столбец и выбираем Вставить).
Выделим всю таблицу и добавим границы.
Копируем таблицу и с помощью специальной вставки () вставляем только её формат.
В начало маршрута (в нашем случае ) записываем значение левой верхней клетки данной нам таблицы. В клетку
записываем формулу =МАКС(C12;B13)+С1
Копируем её на всю таблицу. Выписываем значение из правой нижней ячейки. Заменим все МИН на
МАКС.
Запишем в ответ сначала максимальное количество монет, затем — минимальное (без разделительных
знаков).
Квадрат разлинован на N N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за
одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Откройте файл. Определите минимальную денежную сумму и максимальную денежную сумму, которую
может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без
разделительных знаков — сначала минимальную сумму, затем максимальную сумму.
Исходные данные представляют собой электронную таблицу размером N N, каждая ячейка которой соответствует
клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:
Вложения к задаче
Показать ответ и решение
Исходная таблица:
Заполним новую таблицу начиная с левой нижней клетки. Далее для каждой ячейки будем брать сумму той же ячейки
из исходной таблицы и минимальное/максимальное из клеток слева и снизу новой таблицы.
Минимум:
Первым ответом получаем 1059.
Максимум:
Вторым ответом будет 2216.
Квадрат разлинован на клетки. Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение
одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку,
по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от до
.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Для приведенного ниже квадрата определите минимальную денежную сумму и максимальную денежную
сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа
друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную сумму. Для вашего
удобства таблица была прикреплена в виде файла.
Вложения к задаче
Показать ответ и решение
Заполним новую таблицу начиная с левой нижней клетки. Далее для каждой ячейки будем брать сумму той же ячейки из
исходной таблицы и минимальное/максимальное из клеток слева и снизу новой таблицы.
Минимум:
Первым ответом получаем .
Максимум:
Вторым ответом будет .
Квадрат разлинован на 4 × 4 клетки. Исполнитель Робот может перемещаться по клеткам, выполняя за одно
перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю
правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот
разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 0 до 100.
Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута
Робота.
Для приведенного ниже квадрата определите минимальную денежную сумму и максимальную денежную
сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа
друг за другом без разделительных знаков — сначала минимальную сумму, затем максимальную сумму.
Показать ответ и решение
Заполним новую таблицу, начиная с левой нижней клетки. Далее для каждой ячейки будем брать сумму той же ячейки из
исходной таблицы и минимальное/максимальное из клеток слева и снизу новой таблицы.
Минимум:
Первым ответом получаем 22.
Максимум:
Вторым ответом будет 52.