Версия для печати и копирования в MS Word
1
Колесо имеет 25 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 167692.
2
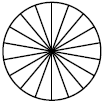
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 18°?
3
Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
4
Колесо имеет 10 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
5
Колесо имеет 45 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
6
Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
7
Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
8
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 12°?
9
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 15°?
10
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 20°?
11
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 20°?
Источник: Досрочная волна ЕГЭ−2022 по математике
-
ЕГЭ по математике (база) 2023
- /
-
Задание 10
- /
- Задача 17
- /
Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите величину наим…
Разбор сложных заданий в тг-канале:
Сложность:
Среднее время решения: 33 сек.
ЕГЭ по математике (база) 2023 задание 10: номер 17 | tf5bm | Колесо имеет 18 спиц. Углы ме…
25
Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите величину наименьшего угла (в градусах), который образуют две соседние спицы.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите величину наименьшего угла (в градусах), который образуют две соседние спицы.
От столба высотой 29 м к дому натянут провод, который крепится на высоте 5 м от земли. Расстояние от дома до столба 7 м. Найдите длину провода. Ответ дайте в метрах.
Пол комнаты, имеющий форму прямоугольника со сторонами 6 м и 2.7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 9 см и 20 см. Сколько потребуется таких дощечек…
Пожарную лестницу длиной 25 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 7 м. На какой высоте расположено окно? Ответ дайте в метрах.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Подобные треугольники
Два треугольника называются подобными, если углы одного треугольника соответственно равны углам другого треугольника, а стороны одного треугольника соответственно пропорциональны сторонам другого треугольника.
Подобие треугольников обозначается значком «∼». Запишем подобие двух треугольников:
△ A B C ∼ △ A 1 B 1 C 1
Соответственные стороны двух подобных треугольников – это стороны, которые лежат напротив равных углов.
Пары равных углов:
∠ A и ∠ A 1
∠ B и ∠ B 1
∠ C и ∠ C 1
Пары соответственных сторон:
B C и B 1 C 1
A C и A 1 C 1
A B и A 1 B 1
Представьте себе, что на смартфоне или планшете вы открыли изображение треугольника. Вы захотели получше его рассмотреть и увеличили изображение. Сам треугольник увеличился, но его пропорции сохранились (он не сплюснулся, не вытянулся, просто стал больше). Вот такие два треугольника: исходный и увеличенный будут подобными. Масштаб увеличенной картинки изменился в k. Это число k будет являться коэффициентом подобия этих треугольников.
Коэффициент подобия k это число, равное отношению соответственных сторон подобных треугольников.
k = A 1 B 1 A B = A 1 C 1 A C = B 1 C 1 B C
- Если стороны большего треугольника относить к сторонам меньшего треугольника, то коэффициент подобия k > 1.
- Если стороны меньшего треугольника относить к сторонам большего треугольника, то коэффициент подобия k < 1.
Отношение периметров подобных треугольников равно коэффициенту подобия.
P △ A 1 B 1 C 1 P △ A B C = k
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S △ A 1 B 1 C 1 S △ A B C = k 2
Признаки подобия треугольников
Первый признак подобия треугольников (по двум углам)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
∠ A = ∠ A 1 ∠ B = ∠ B 1 | ⇒ △ A B C ∼ △ A 1 B 1 C 1
Второй признак подобия треугольников (по двум сторонам и углу между ними)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
∠ A = ∠ A 1 A 1 B 1 A B = A 1 C 1 A C = k | ⇒ △ A B C ∼ △ A 1 B 1 C 1
Третий признак подобия треугольников (по трём сторонам)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
A 1 B 1 A B = A 1 C 1 A C = B 1 C 1 B C = k ⇒ △ A B C ∼ △ A 1 B 1 C 1
Задачи про часы и стрелки
В задании 17 ОГЭ встречаются задачи, в которых необходимо найти угол между часовой и минутной стрелкой. Давайте разберёмся, как их решать.
Часовой циферблат – это окружность.
Градусная мера всей окружности равна 360 ° .
Стрелки – стороны центральных углов.
На окружности 60 маленьких делений и 12 больших.
Каждое маленькое деление отсекает от окружности дугу, градусная мера которой равна 360 ° 60 = 6 ° .
Каждое большое деление отсекает от окружности дугу, градусная мера которой равна 360 ° 12 = 30 ° .
Можно рассуждать, что одна большая дуга содержит пять маленьких, то есть её градусная мера равна 6 ° ⋅ 5 = 30 ° .
Задачи про колесо со спицами
В задании 17 ОГЭ встречаются задачи, в которых дано колесо со спицами и требуется определить либо угол между соседними спицами (если дано количество спиц), либо количество спиц (если дан угол между соседними спицами). Будем разбираться, как такие задачи решать.
Пусть у нас есть колесо, в котором n спиц. Тогда эти спицы образуют n равных центральных углов α .
Формула, которая связывает количество спиц и угол между двумя соседними:
α ⋅ n = 360 °
Задачи на лестницу и ступеньки
В задаче данного типа дана лестница, состоящая из n ступенек. Каждая ступенька характеризуется своей высотой (вертикальный отрезок) и длиной (горизонтальный отрезок). Сама лестница характеризуется своей длиной (отрезок AC), высотой (отрезок BC) и отрезком AB.
Высота всей лестницы – количество ступенек, умноженное на высоту одной ступеньки. Длина всей лестницы – количество ступенек, умноженное на длину одной ступеньки. Для нахождения длины лестницы необходимо применить теорему Пифагора.
Задачи на нахождение длин и площадей
Теоретический и практический материал по нахождению площадей треугольников и четырехугольников можно найти в уроках 3 и 4 модуля геометрия.
Перейти по ссылкам:
- Площадь треугольника
- Площадь равностороннего треугольника
- Площадь прямоугольного треугольника
- Площадь параллелограмма
- Площадь ромба
- Площадь прямоугольника
- Площадь квадрата
- Площадь трапеции
© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
Две подруги Оля и Таня задумались о том, как рассчитать площадь поверхности зонта.
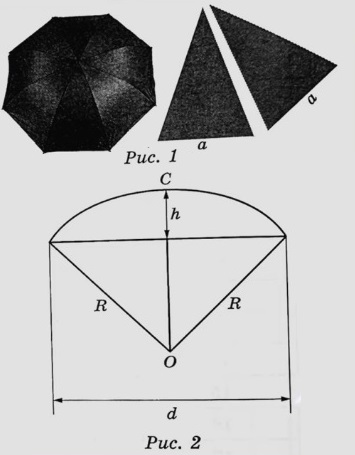
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Оля и Таня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 108 см.
Источник: ОГЭ Ященко 2023 (36 вар)
Задание 1
Длина зонта в сложенном виде равна 27 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,8 см.
Решение
Найдём треть длины спицы, отняв от длины всего зонта длину ручки:
27 см – 6,8 см = 20,2 см
Если это треть, то вся спица в 3 раза больше:
20,2·3 = 60,6 см
Ответ: 60,6.
Задание 2
«Поскольку зонт сшит из треугольников, – рассуждала Оля, – площадь его поверхности можно найти как сумму площадей треугольников». Вычислите площадь поверхности зонта методом Оли, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 59 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение
По первому условию зонт состоит из 12 треугольников с основанием а = 28 см и высотой h = 59 см.
Площадь одного такого треугольника:
S_{Delta}=frac{1}{2}ah=frac{1}{2}cdot 28cdot 59=14cdot 59=826
Найдём площадь поверхности зонта, методом Оли, округлив до ДЕСЯТКОВ:
Sповерхности = 12·SΔ = 12·826 = 9912 ≈ 9910 см2
Ответ: 9910.
Задание 3
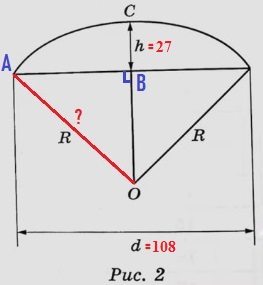
Таня предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС = R (рис. 2). Ответ дайте в сантиметрах.
Решение
Нам необходимо найти гипотенузу R в прямоугольном треугольнике АВО. АВ равно половине d:
AB = d/2 = 108/2 = 54
Т.к. по условию ОС = R, то:
ОВ = ОС – h = R – 27
По теореме Пифагора найдём ОА = R:
ОА2 = АВ2 + ОВ2
R2 = 542 + (R – 27)2
R2 = 2916 + R2 – 54R + 729
R2 – R2 + 54R = 3645
54R = 3645
R = 3645/54 = 67,5
Ответ: 67,5.
Задание 4
Таня нашла площадь купола зонта как площадь поверхности сферического сегмента по формуле S = 2πRh‚ где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Тани. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
Решение
S = 2πRh
π ≈ 3,14
R = 67,5
h = 27
Найдём площадь и округлим до целого:
S = 2πRh = 2·3,14·67,5·27 = 54·3,14·67,5 = 11445,3 ≈ 11445 см2
Ответ: 11445.
Задание 5
Рулон ткани имеет длину 20 м и ширину 90 см. На фабрике из этого рулона были вырезаны треугольные клинья для 15 зонтов, таких же, как зонт, который был у Оли и Тани. Каждый треугольник с учётом припуска на швы имеет площадь 850 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение:
Найдём площадь рулона ткани в см2:
S = 20м х 90см = 2000см х 90см = 180000 см2
Помня, что в одном зонте 12 треугольников найдём сколько ушло ткани на 15 зонтов:
S1 = 15·12·850 = 153000 см2
Найдём сколько см2 ткани рулона ушло в обрезки:
S2 = S – S1 = 180000 – 153000 = 27000 см2
Найдём сколько это процентов от начального рулона:
frac{27000}{180000}cdot 100%=frac{27}{180}cdot 100%=frac{3}{20}cdot 100%=frac{3 cdot 100}{20}%=frac{3 cdot 5}{1}%=15%
Ответ: 15.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 63
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на прямоугольный треугольник, использование тригонометрических функций. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
Использование тригонометрических функций
Прямоугольный треугольник
27238. В треугольнике ABC угол C равен 90º, AC = 4,8, . Найдите AB.
27244. В треугольнике ABC угол C равен 90º, BC = 4, sin A = 0,5. Найдите AB.
27242. В треугольнике ABC угол C равен 90º, AC = 4, Найдите AB.
27240. В треугольнике ABC угол C равен 90º, AC = 4, cos A = 0,5. Найдите AB.
27249. В треугольнике ABC угол C равен 90º, BC = 4, tg A = 0,5. Найдите AC.
27247. В треугольнике ABC угол C равен 90º, BC = 2, Найдите AC.
27243. В треугольнике ABC угол C равен 90º, AC = 8, tg A = 0,5. Найдите BC.
27250. В треугольнике ABC угол C равен 90º, AC = 24, BC = 7. Найдите sin A.
27268. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, Найдите AH.
27269. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, sin A = 0,5. Найдите BH.
27270. В треугольнике ABC угол C равен 90º, BC = 5, . Найдите высоту CH.
27277. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, Найдите BH.
27336. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, BH = 4. Найдите sin A.
27339. В треугольнике ABC угол C равен 90º, высота CH равна 20, BC = 25. Найдите sin A.
27342. В треугольнике ABC угол C равен 90º, высота CH равна 24, BH = 7. Найдите sin A.
27431. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, sin A = 2/3. Найдите AB.
27271. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, . Найдите AH.
27272. В треугольнике ABC угол C равен 90º, CH — высота, BC = 5, cos A = 7/25. Найдите BH.
27273. В треугольнике ABC угол C равен 90º, BC = 8, cos A = 0,5. Найдите высоту CH.
27280. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, cos A =1/6. Найдите BH.
27337. В треугольнике ABC угол C равен 90º, CH — высота, BC = 25, BH = 20. Найдите cos A.
27340. В треугольнике ABC угол C равен 90º, высота CH равна 4, BC = 8. Найдите cos A.
27343. В треугольнике ABC угол C равен 90º, высота CH равна 7, BH = 24. Найдите cos A.
27432. В треугольнике ABC угол C равен 90º, CH — высота, AH = 12, cos A = 2/3. Найдите AB.
27265. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A =1/5. Найдите AH.
27266. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A = 5. Найдите BH.
27267. В треугольнике ABC угол C равен 90º, AB = 13, tg A = 1/5. Найдите высоту CH.
27341. В треугольнике ABC угол C равен 90º, высота CH равна 4, Найдите tg A.
27344. В треугольнике ABC угол C равен 90º, высота CH равна 8, BH = 4. Найдите tg A.
27357. В треугольнике ABC угол C равен 90º, CH — высота, AH = 27, tg A = 2/3. Найдите BH.
27358. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, tg A = 2/3. Найдите AH.
27789. В треугольнике ABC угол C равен 90º, угол A равен 30º, Найдите высоту CH.
27790. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 2. Найдите AH.
27791. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 4. Найдите BH.