Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
Математика ЕГЭ 2014 (система задач из открытого банка заданий)
Задания В13
Текстовые задачи
Материалы подготовили:
Корянов А. Г. (г. Брянск); e-mail: akoryanov@mail.ru Надежкина Н.В. (г. Иркутск); e-mail: nadezhkina@yahoo.com
СОДЕРЖАНИЕ
|
Введение |
1 |
|
|
I. Задачи на движение |
2 |
|
|
1. |
Движение по прямой дороге |
3 |
|
2. |
Движение по замкнутой дороге |
8 |
|
3. |
Движение по реке |
9 |
|
4. |
Движение протяженных тел |
13 |
|
5. |
Средняя скорость |
15 |
|
II. Задачи на работу |
16 |
|
|
1. |
Явный объем работы |
16 |
|
2. |
Неявный объем работы |
19 |
|
III. Задачи на проценты |
21 |
|
|
1. Части и проценты |
21 |
|
|
2. |
Процентное сравнение величин |
22 |
|
3. |
Сложные проценты |
23 |
|
IV. Задачи на концентрацию |
25 |
|
|
V. Задачи на арифметическую про- |
28 |
|
|
грессию |
||
|
VI. Задачи на геометрическую про- |
31 |
|
|
грессию |
||
|
Дополнительные задачи |
31 |
|
|
Решения заданий-прототипов |
46 |
|
|
Ответы |
66 |
|
|
Список и источники литературы |
68 |
Элементы содержания, проверяемые заданиями В13: уравнения.
Проверяемые требования (умения) в
заданиях В13: моделировать реальные ситуации на языке алгебры, составлять уравнения по условию задачи; исследовать построенные модели с использованием аппарата алгебры.
Введение
Данное пособие является тринадцатым в серии пособий для подготовки к части В ЕГЭ по математике и посвящено решению задачи В13 – так называемой «текстовой задачи». Среди задач пособия есть
изадачи «на движение», и задачи «на работу», и задачи «на проценты и сплавы»,
изадачи «на прогрессию».
Задачи эти, можно сказать, весьма стандартные и традиционные – подобные задачи решали в свое время, наверное, не только мамы и папы, но и бабушки и дедушки современных школьников. Задачи, казалось бы, еще и несложные – уровня основной школы. И вроде бы особых вопросов это задание части В вызывать не должно.
В то же время, согласно «краткому анализу выполнения задания в 2012 году» [2], на реальном экзамене для задания В13 «Средний процент правильных ответов — 49,6%… Высокий процент тех, кто даже не приступал к решению». Опытные репетиторы формулируют это так: «Когда 11-классники приходят готовиться к ЕГЭ, большинство не просто не решает В13. Они задачу даже не читают, сразу говорят – такие задачи решать не умею».
Сложность выполнения данного задания для современных школьников нашла свое отражение и в том, что в новейшей демоверсии варианта ЕГЭ по математике задача В13 имеет новый номер В14 и относится уже ко «второй части» варианта.
А ведь большинство задач В13 решается по вполне четким алгоритмам с использованием ясных и понятных формул
|
17.11.2013. www.alexlarin.net |
1 |

Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
исхем. По опыту авторов, научить решать большинство задач В13, содержащихся в открытом банке, можно практически любого выпускника. Безусловно, при этом определяющими факторами являются желание и стремление ученика, а также математическая и методическая грамотность преподавателя, его умение четко и ясно изложить на первых порах именно алгоритмы решения. Без первых удачных опытов у ученика не пройдет страх перед текстовыми задачами, а для этих опытов, на наш взгляд, нужны именно четкие алгоритмы.
Именно в решении этих вопросов и призвано помочь данное пособие. В качестве практического материала авторами были использованы задачи «от составителей» из «открытого банка заданий» [6], а также некоторые задачи из контрольных измерительных материалов прошлых лет.
Структура пособия такова, что задачи из «открытого банка заданий», наряду с фиксированным номером из открытого банка заданий (он расположен в скобках непосредственно перед текстом задачи), имеют также собственную тройную нумерацию внутри каждого раздела. Все типы задач из «открытого банка заданий» систематизированы по содержанию. Каждый тип задачи представлен тремя задачами (первая из этих трех задач и есть прототип данного типа задач), что позволяет учащемуся при необходимости неоднократно проверить себя, а учителю — использовать дополнительные задания в виде отдельных, уже готовых трех вариантов для домашних или проверочных работ. Таким образом, первое число в тройной нумерации каждой задачи означает номер раздела, второе число – номер типа задачи внутри раздела, третье число — номер задачи внутри типа (или номер варианта).
Для первых задач каждого типа представлены подробные решения, для всех задач есть ответы.
Мы постарались сделать так, чтобы пособие было полезно и для ученика практически любого уровня подготовки,
идля учителя, и для репетитора. Ответы
и решения задач-прототипов представлены отдельно для того, чтобы в конкретном экземпляре пособия можно было легко оставить только нужную форму ответов или решений для проверки либо самопроверки. Например, в экземплярах пособий, предлагаемых для уверенных в своих силах учеников, можно вообще убрать и ответы, и решения. Для менее уверенных в своих силах учащихся можно оставить только решения задачпрототипов. Для учителя и репетитора необходимы как раз ответы ко всем задачам для упрощения процесса проверки и оценки домашних и самостоятельных работ.
I.Задачи на движение
Если нет специальных оговорок, то движение считается равномерным, при этом пройденный путь определяется по формуле:
S t,
где S – расстояние, пройденное телом;
– скорость движения тела; t – время движения тела.
Отсюда S и t S .
Все величины (расстояние, скорость, время) считаются положительными:
S 0; 0; t 0.
Указанные величины должны быть в одной системе единиц.
|
Расстояние |
Скорость |
Время |
|
км |
км/ч |
ч |
|
м |
м/с |
с |
|
м |
м/мин |
мин |
Скорость с разными единицами измерения
1 км/ч 1000 м 5 м/с ; 3600 с 18
90 км/ч 90 5 м/с = 25 м/с; 18
|
17.11.2013. www.alexlarin.net |
2 |
Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
1 м/с 18 км/ч ; 5
10 м/с 10 18 км/ч = 36 км/ч 5
1 км/ч 1000 м 50 м/мин; 60 мин 3
30 км/ч 30 50 м/мин = 500 м/мин; 3
1 м/мин 3 км/ч;
50
100 м/мин 100 3 км/ч = 6 км/ч. 50
Повороты движущихся тел, переходы на новый режим движения считаются происходящими мгновенно.
Время движения и расстояние, пройденное телом (при постоянной скорости)
– прямо пропорциональные величины:
t1 S1 . t2 S2
Скорость движения и расстояние, пройденное телом (при постоянном времени)
– прямо пропорциональные величины:
1 S1 .2 S2
Скорость движения и время движения (при постоянном расстоянии) – обратно пропорциональные величины:
1 t2 .2 t1
1.Движение по прямой дороге
При решении задач на равномерное движение часто встречаются две ситуации.
Если начальное расстояние между объектами равно S , а скорости объектов
1 и 2 , то:
а) при движении объектов навстречу друг другу время, через которое они
встретятся, равно t S ;
1 2
б) при движении объектов в одну сторону ( 1 2) время, через которое пер-
|
вый |
объект догонит второй, равно |
||
|
t |
S |
. |
|
1 2
Пример 1. Поезд, пройдя 450 км, был остановлен из-за снежного заноса. Через полчаса путь был расчищен, и машинист, увеличив скорость поезда на 15 км/ч, привел его на станцию без опоздания. Найдите первоначальную скорость поезда, если путь, пройденный им до остановки, составил 75% всего пути.
Решение. Так как 75% 0,75, то весь путь составил 450:0,75 600 км. Пусть первоначальная скорость поезда равна х км/ч. После остановки скорость поезда составила (x 15) км/ч.
450 ч – время движения поезда до x
остановки.
600 450 150 (км) – расстояние, пройденное поездом после остановки.
150ч – время движения поезда по-
x15
сле остановки.
|
Поезд стоял |
1 |
часа, поэтому |
|||||
|
2 |
|||||||
|
450 |
1 |
150 |
|||||
|
ч – фактическое время |
|||||||
|
x |
2 |
x 15 |
|||||
движения поезда.
600 ч – время движения поезда по x
расписанию.
Так как поезд прибыл без опоздания, то составим и решим уравнение
|
450 |
1 |
150 |
600 |
. |
|||||||||
|
2 |
x 15 |
||||||||||||
|
x |
x |
||||||||||||
|
1 |
150 |
150 |
. |
||||||||||
|
2 |
|||||||||||||
|
x 15 |
x |
Умножим обе части уравнения на
2x(x 15) 0.
x(x 15) 300x 300(x 15). x2 15x 300x 300x 4500. x2 15x 4500 0.
Квадратное уравнение имеет один положительный корень 60. Следовательно, первоначальная скорость поезда равна 60 км/ч.
|
17.11.2013. www.alexlarin.net |
3 |
Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
Для решения подобных задач удобно составить таблицу, используя так называемую «схему S t ». За неизвестное в дальнейшем всегда будем обозначать то, что требуется найти в условии. Рассмотрим движение после остановки по расписанию и фактически.
|
Расстояние |
Скорость |
Время |
||||
|
(км) |
(км/ч) |
(ч) |
||||
|
По расписа- |
150 |
x |
150 |
|||
|
нию |
x |
|||||
|
Фактически |
150 |
x 15 |
150 |
|||
|
x 15 |
||||||
Так как после остановки поезд затратил
|
на |
1 |
часа меньше, чем по расписанию, |
||||||
|
2 |
||||||||
|
150 |
150 |
1 |
||||||
|
то |
составим уравнение |
. |
||||||
|
x 15 |
||||||||
|
x |
2 |
Это уравнение уже решено выше и имеет один положительный корень 60.
Ответ: 60 км/ч.
***
1.1.1.(прототип 99588) Из двух городов,
расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
1.1.2.(112399) Из двух городов, расстояние между которыми равно 480 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 75 км/ч и 85 км/ч?
1.1.3.(112453) Из двух городов, расстояние между которыми равно 260 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 50 км/ч и 80 км/ч?
***
1.2.1.(прототип 99589) Из городов A и B,
расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
1.2.2.(112459) Из городов A и B, расстояние между которыми равно 440 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 4 часа на расстоянии 240 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч. 1.2.3.(112511) Из городов A и B, расстояние между которыми равно 450 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 240 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
***
1.3.1.(прототип 99595) Два пешехода от-
правляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
1.3.2.(113377) Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 425 метрам?
1.3.3.(113437) Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 2 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 400 метрам?
***
1.4.1.(прототип 99590) Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
1.4.2.(112519) Расстояние между городами A и B равно 440 км. Из города A в город B со скоростью 50 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со ско-
|
17.11.2013. www.alexlarin.net |
4 |
Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
ростью 80 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах. 1.4.3.(112799) Расстояние между городами A и B равно 550 км. Из города A в город B со скоростью 50 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 75 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
***
1.5.1.(прототип 99591) Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.
1.5.2.(112801) Расстояние между городами A и B равно 330 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 75 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 180 км от города A. Ответ дайте в км/ч.
1.5.3.(113079) Расстояние между городами A и B равно 450 км. Из города A в город B выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 70 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 240 км от города A. Ответ дайте в км/ч.
***
1.6.1.(прототип 26580) Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.
1.6.2.(5957) Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и вело-
сипедист. Известно, что в час автомобилист проезжает на 110 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл
впункт В на 5,5 часов позже автомобилиста. Ответ дайте в км/ч.
1.6.3.(39175) Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 65 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл
впункт В на 4 часа 20 минут позже автомобилиста. Ответ дайте в км/ч.
***
1.7.1.(прототип 26581) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А
вВ. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. 1.7.2.(5639) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 240 км. На следующий день он отправился обратно в А со скоростью на 1 км/ч больше прежней. По дороге он сделал остановку на 1 час. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. 1.7.3.(39213) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 180 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А
вВ. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
***
1.8.1.(прототип 26582) Велосипедист выехал с постоянной скоростью из горо-
|
17.11.2013. www.alexlarin.net |
5 |
|
Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи |
||||||||
|
да А в город В, расстояние между кото- |
рость второго, и прибыл к финишу на |
|||||||
|
рыми равно 98 км. На следующий день |
2 часа раньше второго. Найти скорость |
|||||||
|
он отправился обратно со скоростью на 7 |
велосипедиста, пришедшего к финишу |
|||||||
|
км/ч больше прежней. По дороге он сде- |
первым. Ответ дайте в км/ч. |
|||||||
|
лал остановку на 7 часов. В результате он |
*** |
|||||||
|
затратил на обратный путь столько же |
1.10.1.(прототип 26584) Два велосипеди- |
|||||||
|
времени, сколько на путь из А в В. |
ста одновременно отправились в 88- |
|||||||
|
Найдите скорость велосипедиста на пути |
километровый пробег. Первый ехал со |
|||||||
|
из А в В. Ответ дайте в км/ч. |
скоростью, |
на |
3 |
км/ч |
большей, |
|||
|
1.8.2.(5627) Велосипедист выехал с по- |
чем скорость второго, и прибыл к фини- |
|||||||
|
стоянной скоростью из города А в город |
шу на 3 часа раньше второго. Найти ско- |
|||||||
|
В, расстояние между которыми равно 80 |
рость велосипедиста, пришедшего к фи- |
|||||||
|
км. На следующий день он отправился |
нишу вторым. Ответ дайте в км/ч. |
|||||||
|
обратно со скоростью на 2 км/ч больше |
1.10.2.(5661) Два велосипедиста одно- |
|||||||
|
прежней. По дороге он сделал остановку |
временно |
отправились |
в |
96- |
||||
|
на 2 часа. В результате он затратил на об- |
километровый пробег. Первый ехал со |
|||||||
|
ратный путь столько же времени, сколько |
скоростью, |
на |
4 |
км/ч |
большей, |
|||
|
на путь из А в В. Найдите скорость вело- |
чем скорость второго, и прибыл к фини- |
|||||||
|
сипедиста на пути из А в В. Ответ дайте в |
шу на 4 часа раньше второго. Найти ско- |
|||||||
|
км/ч. |
рость велосипедиста, пришедшего к фи- |
|||||||
|
1.8.3.(39257) Велосипедист выехал с по- |
нишу вторым. Ответ дайте в км/ч. |
|||||||
|
стоянной скоростью из города А в город |
1.10.3.(39349) Два велосипедиста одно- |
|||||||
|
В, расстояние между которыми равно |
временно |
отправились |
в |
224- |
||||
|
154 км. На следующий день он отправил- |
километровый пробег. Первый ехал со |
|||||||
|
ся обратно со скоростью на 3 км/ч боль- |
скоростью, |
на |
2 км/ч |
большей, |
||||
|
ше прежней. По дороге он сделал оста- |
чем скорость второго, и прибыл к фини- |
|||||||
|
новку на 3 часа. В результате он затратил |
шу на 2 часа раньше второго. Найти ско- |
|||||||
|
на обратный путь столько же времени, |
рость велосипедиста, пришедшего к фи- |
|||||||
|
сколько на путь из А в В. Найдите ско- |
нишу вторым. Ответ дайте в км/ч. |
|||||||
|
рость велосипедиста на пути из А в В. |
*** |
|||||||
|
Ответ дайте в км/ч. |
1.11.1.(прототип 99592) Из городов A и |
|||||||
|
*** |
B одновременно навстречу друг другу |
|||||||
|
1.9.1.(прототип 26583) Два велосипеди- |
выехали мотоциклист и велосипедист. |
|||||||
|
ста одновременно отправились в 240- |
Мотоциклист приехал в B на 3 часа |
|||||||
|
километровый пробег. Первый ехал со |
раньше, чем велосипедист приехал в A, а |
|||||||
|
скоростью, |
на |
1 км/ч |
большей, |
встретились они через 48 минут после |
||||
|
чем скорость второго, и прибыл к фини- |
выезда. Сколько часов затратил на путь |
|||||||
|
шу на 1 час раньше второго. Найти ско- |
из B в A велосипедист? |
|||||||
|
рость велосипедиста, пришедшего к фи- |
1.11.2.(113083) Из городов A и B одно- |
|||||||
|
нишу первым. Ответ дайте в км/ч. |
временно навстречу друг другу выехали |
|||||||
|
1.9.2.(5675) Два велосипедиста одновре- |
мотоциклист и велосипедист. Мотоцик- |
|||||||
|
менно отправились в 154-километровый |
лист приехал в B на 10 часов раньше, чем |
|||||||
|
пробег. Первый ехал со скоростью, на 3 |
велосипедист приехал в A, а встретились |
|||||||
|
км/ч большей, |
чем скорость |
второго, и |
они через 55 минут после выезда. Сколь- |
|||||
|
прибыл к финишу на 3 часа раньше вто- |
ко часов затратил на путь из B в A вело- |
|||||||
|
рого. Найти скорость велосипедиста, |
сипедист? |
|||||||
|
пришедшего к финишу первым. Ответ |
1.11.3.(113101) Из городов A и B одно- |
|||||||
|
дайте в км/ч. |
временно навстречу друг другу выехали |
|||||||
|
1.9.3.(39301) Два велосипедиста одно- |
мотоциклист и велосипедист. Мотоцик- |
|||||||
|
временно |
отправились |
в |
80- |
лист приехал в B на 4 часа раньше, чем |
||||
|
километровый пробег. Первый ехал со |
велосипедист приехал в A, а встретились |
|||||||
|
скоростью, на 2 км/ч большей, чем ско- |
они через 50 минут после выезда. Сколь- |
|||||||
|
17.11.2013. www.alexlarin.net |
6 |
Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
ко часов затратил на путь из B в A велосипедист?
***
1.12.1.(прототип 99593) Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
1.12.2.(113105) Товарный поезд каждую минуту проезжает на 400 метров меньше, чем скорый, и на путь в 270 км тратит времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
1.12.3.(113153) Товарный поезд каждую минуту проезжает на 300 метров меньше, чем скорый, и на путь в 420 км тратит времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
***
1.13.1.(прототип 99594) Расстояние меж-
ду городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
1.13.2.(113155) Расстояние между городами A и B равно 630 км. Из города A в город B выехал автомобиль, а через 2 часа следом за ним со скоростью 60 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
1.13.3.(113369) Расстояние между городами A и B равно 348 км. Из города A в город B выехал автомобиль, а через 1 час следом за ним со скоростью 85 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
***
1.14.1.(прототип 26578) Из А в В одно-
временно выехали два автомобилиста.
Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста. Ответ дайте в км/ч.
1.14.2.(5619) Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 42 км/ч, а вторую половину пути — со скоростью, на 28 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
1.14.3.(39049) Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 55 км/ч, а вторую половину пути — со скоростью, на 6 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
***
1.15.1.(прототип 26579) Из А в В одно-
временно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
1.15.2.(5617) Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути — со скоростью 96 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите
|
17.11.2013. www.alexlarin.net |
7 |

Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
скорость первого автомобиля, если известно, что она больше 57 км/ч. Ответ дайте в км/ч.
1.15.3.(39099) Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути — со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 50 км/ч. Ответ дайте в км/ч.
2.Движение по замкнутой дороге
Если длина замкнутой дороги равна S , а скорости объектов 1 и 2 , то:
а) при движении объектов в разных направлениях время между их встречами
вычисляется по формуле t S ;
1 2
б) при движении объектов в одном направлении время между их встречами
вычисляется по формуле t S
1 2
( 1 2).
Пример 2. На соревнованиях по кольцевой трассе один лыжник проходит круг на 2 мин быстрее другого и через час обошел его ровно на круг. За какое время каждый лыжник проходит круг?
Решение. Пусть S м – длина кольцевой трассы и x м/мин и y м/мин – скорости первого и второго лыжников соот-
ветственно (x y). Тогда S мин и S мин x y
– время, за которое проходит круг первый и второй лыжники соответственно. Из первого условия получаем уравнение
|
S |
S |
2. Так как скорость удаления |
|
|
y |
|||
|
x |
первого лыжника от второго лыжника равна (x y) м/мин, то из второго усло-
вия имеем уравнение S 60. Решим x y
систему уравнений
|
S |
S |
2, |
||||||||||||||||
|
x |
||||||||||||||||||
|
y |
||||||||||||||||||
|
y |
1 |
|||||||||||||||||
|
x |
. |
|||||||||||||||||
|
S |
||||||||||||||||||
|
S |
60 |
|||||||||||||||||
|
Сделаем замену |
S |
a |
и |
S |
b, |
тогда |
||||||||||||
|
x |
y |
|||||||||||||||||
|
система уравнений примет вид |
||||||||||||||||||
|
b a 2, |
||||||||||||||||||
|
1 |
1 |
|||||||||||||||||
|
1 |
. |
|||||||||||||||||
|
b |
||||||||||||||||||
|
a |
60 |
1 |
1 |
1 |
||||||||||||||
|
Получаем уравнение |
. |
|||||||||||||||||
|
a 2 |
||||||||||||||||||
|
a |
60 |
|||||||||||||||||
|
Умножим обе части |
уравнения на |
|||||||||||||||||
|
60a(a 2) 0. |
60(a 2) 60a a(a 2). a2 2a 120 0.
Квадратное уравнение имеет один положительный корень a 10, тогда b 12. Значит, первый лыжник проходит круг за
10минут, а второй лыжник – за 12 минут.
Ответ: 10 мин; 12 мин.
***
2.1.1.(прототип 99596) Два мотоцикли-
ста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
2.1.2.(113443) Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 22 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч больше скорости другого?
2.1.3.(113589) Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 5 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 5 км/ч больше скорости другого?
|
17.11.2013. www.alexlarin.net |
8 |

Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
***
2.2.1.(прототип 99598) Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
2.2.2.(113665) Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. 2.2.3.(114153) Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
***
2.3.1.(прототип 99599) Из пункта A кру-
говой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
2.3.2.(114157) Из пункта A круговой трассы выехал велосипедист, а через 40 минут следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а еще через 36 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
2.3.3.(114653) Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость
мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
***
2.4.1.(прототип 99600) Часы со стрелка-
ми показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
2.4.2.(114665) Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?
2.4.3.(114781) Часы со стрелками показывают 6 часов 40 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?
3.Движение по реке
Если объект движется по течению реки, то его скорость равна по теч. соб. теч.
Если объект движется против течения
реки, то его скорость равна
против теч. соб. теч.
Собственная скорость объекта (скорость в неподвижной воде) равна
соб. по теч. пр. теч. .
2
Скорость течения реки равна
теч. по теч. пр. теч. .
2
Скорость движения плота равна скорости течения реки.
Пример 3. Катер спустился вниз по течению реки на 50 км, а затем прошел в обратном направлении 36 км, что заняло у него на 30 минут больше времени, чем по течению. Какова собственная скорость катера, если скорость течения реки 4 км/ч?
Решение. Пусть собственная скорость катера равна х км/ч, тогда его скорость по течению реки равна (x 4) км/ч, а против течения реки (x 4) км/ч. Время движе-
ния катера по течению реки равно 50 x 4
ч, а против течения реки – 36 ч. x 4
|
17.11.2013. www.alexlarin.net |
9 |

Корянов А.Г., Надежкина Н.В. Задания В13. Текстовые задачи
|
Так |
как |
30минут |
1 |
ч, |
то согласно |
||||
|
2 |
|||||||||
|
условию задачи |
составим |
уравнение |
|||||||
|
36 |
50 |
1 |
. |
Умножим |
обе части |
||||
|
x 4 |
|||||||||
|
x 4 |
2 |
уравнения на (x 4)(x 4) 0.
72(x 4) 100(x 4) (x 4)(x 4). x2 28x 704 0.
D 142 704 900 302 . 4
x1 14 30 16; x2 14 30 44 (ис-
ключаем, так как x 0).
Итак, собственная скорость катера равна 16 км/ч.
Ответ: 16 км/ч.
Пример 4. Моторная лодка прошла по течению реки 36 км, а против течения 48 км, затратив на весь путь столько времени, сколько надо на прохождение 90 км по озеру. Найдите собственную скорость лодки, если скорость лодки равна 3 км/ч.
Решение. Пусть собственная скорость лодки составляет х км/ч. Составим таблицу.
|
Расстояние |
Скорость |
Время |
||||||||||||||||
|
(км) |
(км/ч) |
(ч) |
||||||||||||||||
|
Против |
48 |
x 3 |
48 |
|||||||||||||||
|
течения |
x 3 |
|||||||||||||||||
|
По |
36 |
x 3 |
36 |
|||||||||||||||
|
течению |
x 3 |
|||||||||||||||||
|
По озеру |
90 |
x |
90 |
|||||||||||||||
|
x |
||||||||||||||||||
|
Согласно |
условию |
задачи |
составим |
|||||||||||||||
|
уравнение |
36 |
48 |
90 |
|||||||||||||||
|
. |
||||||||||||||||||
|
x 3 |
x 3 |
|||||||||||||||||
|
x |
||||||||||||||||||
|
6 |
8 |
15 |
. |
|||||||||||||||
|
x 3 |
x 3 |
|||||||||||||||||
|
x |
||||||||||||||||||
|
Умножим |
обе |
части |
уравнения на |
|||||||||||||||
|
x(x 3)(x 3) 0. |
||||||||||||||||||
|
6x(x 3) 8x(x 3) 15(x 3)(x 3). |
||||||||||||||||||
|
D |
x2 6x 135 0. |
|||||||||||||||||
|
32 135 144 122 . |
||||||||||||||||||
|
4 |
||||||||||||||||||
|
x1 3 12 15; x2 |
3 12 9 (не удовле- |
|||||||||||||||||
|
творяет условию x 0). |
Значит, собственная скорость моторной лодки равна 15 км/ч.
Ответ: 15 км/ч.
***
3.1.1.(прототип 26585) Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
3.1.2.(5703) Моторная лодка прошла против течения реки 195 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 14 км/ч. Ответ дайте в км/ч.
3.1.3.(39353) Моторная лодка прошла против течения реки 60 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 8 км/ч. Ответ дайте в км/ч.
***
3.2.1.(прототип 26586) Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
3.2.2.(5691) Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
3.2.3.(39371) Моторная лодка прошла против течения реки 221 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.
***
3.3.1.(прототип 26587) Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в
|
17.11.2013. www.alexlarin.net |
10 |
Задания В13: Текстовые задачи.
Похожие учебники:
Пожаловаться
2013
Математика. ЕГЭ 2014. Задания В1 — Корянов А.Г., Надежкина Н.В.
2013
Математика. ЕГЭ 2014. Задания В12 — Корянов А.Г., Надежкина Н.В.
2013
Математика. ЕГЭ 2014. Задания В4 — Корянов А.Г., Надежкина Н.В.
2014
Математика. ЕГЭ 2014. Задания В14 — Корянов А.Г., Надежкина Н.В.
На чтение 1 мин Просмотров 2 Опубликовано 7 марта, 2023
Подготовка к ЕГЭ-2014 по математике. Решение заданий В13. Решение и ответы на задачи на официальном сайте источника онлайн.
В презентации приведены решения текстовых задач — прототипов В13 из открытого банка заданий ЕГЭ по математике.
Варианты ответов и решение задачи — МАТЕРИАЛЫ ТУТ: https://nsportal.ru/shkola/algebra/library/2013/08/20/podgotovka-k-ege-2014-po-matematike-reshenie-zadaniy-v13
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
ЕГЭ 2014, Математика, Задания В13, Корянов А.Г., Надежкина Н.В., 2013.
Данное пособие является тринадцатым в серии пособий для подготовки к части В ЕГЭ по математике и посвящено решению задачи В13 — так называемой «текстовой задачи». Среди задач пособия есть н задачи «на движение», и задачи «на работу». и задачи «на проценты и сплавы», и задачи «на прогрессию».
Примеры.
Из городов А и В. расстояние между которыми равно 440 км. навстречу друг другу одновременно выехали два автомобиля и встретились через 4 часа на расстоянии 240 км от города В. Найдите скорость автомобиля, выехавшего из города А. Ответ дайте в км/ч.
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 2 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 400 метрам?
Расстояние между городами А и В равно 435 км. Из города А в город В со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся? Ответ дайте в километрах.
СОДЕРЖАНИЕ
Введение
I. Задачи на движение
1. Движение по прямой дороге
2. Движение по замкнутой дороге
3. Движение по реке
4. Движение протяженных тел
5. Средняя скорость
II. Задачи на работу
1. Явный объем работы
2. Неявный объем работы
III. Задачи на проценты
1. Части и проценты
2. Процентное сравнение величин
3. Сложные проценты
IV. Задачи на концентрацию
V. Задачи на арифметическую прогрессию
VI. Задачи на геометрическую прогрессию
Дополнительные задачи
Решения заданий-прототипов
Ответы
Список и источники литературы.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ 2014, Математика, Задания В13, Корянов А.Г, Надежкина Н.В., 2013 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ 2014, Математика, Задания В13, Корянов А.Г, Надежкина Н.В., 2013
— pdf — Яндекс.Диск.
Дата публикации: 29.06.2014 06:31 UTC
Теги:
ЕГЭ по математике :: математика :: Корянов :: Надежкина
Следующие учебники и книги:
- ЕГЭ, Математика, Методические рекомендации, Ященко И.В., Семенов А.В., Высоцкий И.Р., 2013
- ЕГЭ, Математика, Экзаменационная работа, 2014
- ЕГЭ, Математика, Решение уравнений в целых числах, Власова А.П., Латанова Н.И., Евсеева Н.В.
- ЕГЭ, Математика, Вступительные испытания, Подготовка к ЕГЭ, Лаппо Л.Д., Попов М.А., 2014
Предыдущие статьи:
- ЕГЭ, Математика, Тематические тренировочные задания, Уровень В, С, Лаппо Л.Д., Попов М.А., 2014
- ЕГЭ, 3000 задач с ответами по математике, Все задания группы В, Семенов А.Л., Ященко И.В., Высоцкий И.Р., Посицельская М.А., 2014
- ЕГЭ, 3000 задач с ответами по математике, Все задания группы В, Семенов А.Л., Ященко И.В., Высоцкий И.Р., Гущин Д.Д., 2013
- ЕГЭ, 1000 задач с ответами и решениями по математике, Все задания группы С, Сергеев И.Н., Панферов В.С., 2014
У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.
Расскажи друзьям
Ищи САЙТ в Яндексе и Google по слову:
vpr-klass или впр-класс
Сохрани сайт в закладки — нажми Ctrl+D
|
Версия для печати
ЕГЭ по математике 2014 — задание в13.
Рассмотрим задание егэ по математике из диагностической работы 2014 года — под номером в13. Скачать решение. |
|
Категория: Учебные материалы, ЕГЭ по математике 2017 — решение заданий, подготов | |
|
Оставь свой комментарий! |
Интересно
ГИА (ОГЭ) по математике
Много разных решений
Тесты ГИА онлайн.
Видео — ГИА 2013: геометрия
Видео — ГИА 2012
Видео — Демо-вариант 2012.
Решение Демо-варианта 2013 года (2014 года).
Задача №1, Вычислить.
Задача №2, Числа и прямая.
Задача №3, Сравнение чисел.
Задача №4, Уравнения.
Задача №5, Графики и формулы.
Задача №6, Прогрессии.
Задача №7, Упростить выражение.
Задача №8, Неравенства, системы неравенств.
Задача №9, Задания по геометрии.
Генератор вариантов ГИА 2014
ЕГЭ по математике
Много разных решений.
Онлайн тесты.
Видео уроки ЕГЭ по математике.
Генератор вариантов ЕГЭ 2014
Книги, справочники
Решение демо варианта ЕГЭ по математике 2014
Задания B1, задача.
Задания B2, диаграммы.
Задания B5, уравнения.
Задания B8, производная.
Задания B10, вероятность.
ОГЭ по информатике
Видео уроки
Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям |
sitemap.xml
Онлайн видео уроки для подготовки к ЕГЭ 2014 по математике.
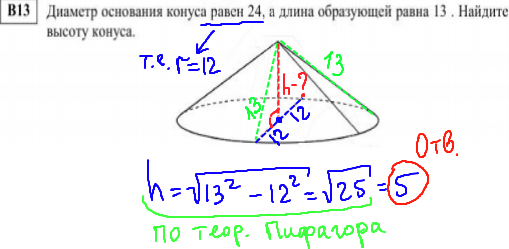
Задание В13
- Назначение: Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
- Часть 2: с кратким ответом в виде целого числа или конечной десятичной дроби.
В видео разобраны задания В13, подобранные в соответствии с демоверсией ЕГЭ 2014 по математике.
Проверяются знания и умения:
– Прямые и плоскости в пространстве;
– Многогранники;
– Тела и поверхности вращения;
– Измерение геометрических величин.
Первое задание в видео уроке подробно объясняется учителем; перед объяснением второго задания предлагается поставить воспроизведение на паузу и решить его самостоятельно, затем снять с паузы с свериться с решением учителя.
Видео уроки ЕГЭ от создателей курса
Домашний репетитор ЕГЭ 2014 по математике