Задания 15 егэ 2021 образцы вариантов с решениями - Помощь в подготовке к экзаменам и поступлению

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Всё варианты 15 задания математика ЕГЭ Профиль 2021

Всё варианты 15 задания математика ЕГЭ Профиль 2021admin2021-09-24T15:26:55+03:00

Источник

1. Решите неравенство:

$left ( 9^x -2cdot 3^{x+1} right )^2+14left ( 9^x-2cdot 3^{x+1} right )+45geq 0$

Решение:

Замена: $9^x -2cdot 3^{x+1} = t;$

подберем корни уравнения по теореме Виета: t_1=-5, t_2=-9.

$left [begin{array}{c}tleq -9 \tgeq -5end{array}right.;$ вернемся к переменной

$left [begin{array}{c}9^x-2cdot 3^{x+1}leq -9 \9^x-2cdot 3^{x+1}geq -5end{array}right.;$ $left [begin{array}{c}9^x-2cdot 3 cdot 3^x +9 leq 0 \9^x-2cdot 3 cdot 3^{x}+5 geq 0end{array}right.;$

сделаем замену 3^x=z, тогда

$left [begin{array}{c}z^2-6z+9leq 0 \z^2-6z+5geq 0end{array}right.Leftrightarrowleft [begin{array}{c}left ( z-3 right )^2 leq 0 \left ( z-1 right )left ( z-5 right ) geq 0end{array}right.Leftrightarrow$

$Leftrightarrowleft [begin{array}{c}z= 3 \zleq 1 \zgeq 5end{array}right.;$ $left [begin{array}{c}3^x=3 \3^xleq 1 \3^xgeq 5end{array}right.;$

функция y=3^x монотонно возрастает, поэтому

$left [begin{array}{c}3^x=3^1 \3^xleq 3^0 \3^xgeq 3^{log_35}end{array}right.Leftrightarrowleft [begin{array}{c}x=1 \xleq 0 \xgeq log_35end{array}right.$

Ответ: $x in left ( -infty ; 0 right ]cup left{ 1 right} cup left [ log_35;+infty right )$

2. Решите неравенство:

$displaystyle frac{3^x}{3^x-3}+frac{3^x+1}{3^x-2}+ frac{5}{9^x-5cdot 3^x+6}leq 0$

Решение:

$displaystyle frac{3^x}{3^x-3}+frac{3^x+1}{3^x-2}+ frac{5}{9^x-5cdot 3^x+6}leq 0$

Заменив получим:

$displaystyle frac{t}{t-3}+frac{t+1}{t-2}+ frac{5}{t^2-5t+6}leq 0,$

Упростим знаменатель третьей дроби. По теореме, обратной теореме Виета, числа 2 и 3 — корни квадратного трехчлена

значит,

${ t}^2-5t+6=left(t-2right)(t-3),$

$displaystyle frac{t}{t-3}+frac{t+1}{t-2}+ frac{5}{left(t-2right)cdot (t-3)}leq 0,$

$displaystyle frac{tleft(t-2right)+left(t+1right)left(t-3right)+5}{left(t-2right)(t-3),}leq 0,$

$displaystyle frac{2t^2-4t+2}{left(t-2right)(t-3)}leq 0,$

$displaystyle frac{2{left(t-1right)}^2}{left(t-2right)left(t-3right)}leq 0$

Решив неравенство с помощью метода интервалов, получим:

Сделаем обратную замену: t= 3^x

$left[ begin{array}{c}3^x=1, \2leq 3^xleq 3 end{array}right. , left[ begin{array}{c}3^x=3^0 \3^{{{log}_3 2 }}leq 3^xleq 3^1 end{array},right.$ а так как функция y=3^x монтонно возрастает на R, то

$left[ begin{array}{c}x=0 \{{log}_3 2leq xleq 1 } end{array}right.$

Ответ: $0 cup [{{log}_3 2; ;1 }]$

3. Решите неравенство:

${{log}_{12x^2-5x-2} (4x+1)leq 0 }$

Решение:

${{log}_{12x^2-5x-2} (4x+1)leq 0 }$

1) Найдем ОДЗ.

$left{ begin{array}{c}12x^2-5x-2textgreater 0 \12x^2-5x-2ne 1 \4x+1textgreater 0 end{array}right.$

Решим первое неравенство этой системы:

Найдем корни квадратного трехчлена:

$D =25+ 96=121={11}^2$

$left[ begin{array}{c}x=frac{5-11}{24} \x=frac{5+11}{24} end{array}right. , left[ begin{array}{c}x=-frac{1}{4} \x=frac{2}{3} end{array}right.$

$12x^2-5x-2=12(x+frac{1}{4})(x-frac{2}{3}),$ тогда

при $left[ begin{array}{c}xtextless -frac{1}{4} \xtextgreater frac{2}{3} end{array}right.$

Второе условие системы:

Решим уравнение

$D=25+ 144= 169 ={13}^2$

$left[ begin{array}{c}x=frac{5-13}{24} \x=frac{5+13}{24} end{array}right. , left[ begin{array}{c}x=-frac{1}{3} \x=frac{3}{4} end{array}right.$

Значит, $left{ begin{array}{c}xne -frac{1}{3} \xne frac{3}{4} end{array}right.$

Третье условие:

$xtextgreater -frac{1}{4}.$

Вернемся к системе, задающей ОДЗ:

$left{ begin{array}{c} left[ begin{array}{c}xtextless -frac{1}{4} \xtextgreater frac{2}{3} end{array}right. \left{ begin{array}{c}xne -frac{1}{3} \xne frac{3}{4} end{array}right. \xtextgreater -frac{1}{4} end{array}right.$ ${{stackrel{ }{Leftrightarrow }}}left{ begin{array}{c}xtextgreater frac{2}{3} \xne -frac{1}{3} \xne frac{3}{4} \xtextgreater -frac{1}{4} end{array}right.$ , ${{stackrel{ }{Leftrightarrow }}}left{ begin{array}{c}xtextgreater frac{2}{3} \xne frac{3}{4} end{array}right.$ ${{stackrel{ }{Leftrightarrow }}}left[ begin{array}{c}frac{2}{3}textless xtextless frac{3}{4} \xtextgreater frac{3}{4} end{array}right..$ Это ОДЗ.

2) Вернемся к исходному неравенству:

${{log}_{12x^2-5x-2} (4x+1)leq 0 },$

${{log}_{12x^2-5x-2} (4x+1)leq {{log}_{12x^2-5x-2} 1 } }$

Неравенство равносильно системе:

$left{ begin{array}{c}left[ begin{array}{c}left{ begin{array}{c}12x^2-5x-2textgreater 1 \4x+1leq 1 end{array}right. \left{ begin{array}{c}12x^2-5x-2textless 1 \4x+1geq 1 end{array}right. end{array}right. \left[ begin{array}{c}frac{2}{3}textless xtextless frac{3}{4} \xtextgreater frac{3}{4} end{array}right. end{array}right.{{stackrel{ }{Leftrightarrow }}}left{ begin{array}{c}left[ begin{array}{c}left{ begin{array}{c}12x^2-5x-3textgreater 0 \4xleq 0 end{array}right. \left{ begin{array}{c}12x^2-5x-3textless 0 \4xgeq 0 end{array}right. end{array}right. \left[ begin{array}{c}frac{2}{3}textless xtextless frac{3}{4} \xtextgreater frac{3}{4} end{array}right. end{array}right.stackrel{ }{Leftrightarrow }left{ begin{array}{c}12x^2-5x-3textless 0 \left[ begin{array}{c}frac{2}{3}textless xtextless frac{3}{4} \xtextgreater frac{3}{4} end{array}right. end{array}right.$

${{stackrel{ begin{array}{c} \ end{array}}{Leftrightarrow }}}left{ begin{array}{c}12left(x+frac{1}{3}right)left(x-frac{3}{4}right)textless 0 \left[ begin{array}{c}frac{2}{3}textless xtextless frac{3}{4} \xtextgreater frac{3}{4} end{array}right. end{array} right.{{stackrel{ }{Leftrightarrow }}} left{ begin{array}{c}xtextless frac{3}{4} \left[ begin{array}{c}frac{2}{3}textless xtextless frac{3}{4} \xtextgreater frac{3}{4} end{array}right. end{array}right., {{stackrel{ }{Leftrightarrow }}} frac{2}{3}textless xtextless frac{3}{4}$

Ответ: $left(frac{2}{3}; ;frac{3}{4}right)$

4. Решите неравенство:

${16}^x-2cdot 4^x+23left({16}^x-2cdot 4^{x+1}right)+112geq 0$

Решение:

Сделаем замену: ${16}^x-2cdot 4^{x+1}=t,$

Получим:

найдем корни квадратного трехчлена:

D= ${23}^2-4cdot 112=529-448=81=9^2$

$left[ begin{array}{c}t=frac{-23-9}{2} \t=frac{-23+9}{2} end{array}right.$ , $left[ begin{array}{c}t=-16 \t=-7 end{array}right.$ , тогда

$left[ begin{array}{c}tleq -16 \tgeq -7 end{array}right..$

Сделав обратную замену t= ${16}^x-2cdot 4^{x+1},$ получим

$left[ begin{array}{c}{16}^x-2cdot 4^{x+1}leq -16 \{16}^x-2cdot 4^{x+1}geq -7 end{array}right.$

Заменив ${ 4}^x=m, mtextgreater 0,$ получим $left[ begin{array}{c}left{ begin{array}{c}m^2-8m+16leq 0 \mtextgreater 0 end{array}right. \left{ begin{array}{c}m^2-8m+7geq 0 \mtextgreater 0 end{array}right. end{array}right. Leftrightarrow$

$Leftrightarrow left[ begin{array}{c}left{ begin{array}{c}{left(m-4right)}^2leq 0 \mtextgreater 0 end{array}right. \left{ begin{array}{c}left(m-1right)left(m-7right)geq 0 \mtextgreater 0 end{array}right. end{array}right.{{stackrel{}{Leftrightarrow}}}left[ begin{array}{c}m=4 \left{ begin{array}{c}left[ begin{array}{c}mleq 1 \mgeq 7 end{array}right. \mtextgreater 0 end{array}right. end{array}right.{{stackrel{}{Leftrightarrow}}}$

${{stackrel{}{Leftrightarrow}}}left[ begin{array}{c}m=4 \0textless mleq 1 \mgeq 7 end{array}right.$

Вернемся к переменной х:

$m={ 4}^x,$ получим совокупность $left[ begin{array}{c}4^x=4 \0textless 4^xleq 1 \4^xgeq 7 end{array}right.$

${{stackrel{}{Leftrightarrow}}}left[ begin{array}{c}4^x=4^1 \4^xleq 4^0 \4^xgeq 4^{{{log}_4 7 }} end{array}right.{{stackrel{ }{Leftrightarrow }}}left[ begin{array}{c}x=1 \xleq 0 \xgeq {{log}_4 7 } end{array}right.,$

$x in (-infty ; ;left.0right]cup left{1right}cup left[{{log}_4 7 }; ;infty )right.$

Мы воспользовались тем, что
функция y=4^x монотонно возрастает на R, то есть на множестве действительных чисел.

Ответ: $(-infty ; ;left.0right]cup left{1right}cup left[{{log}_4 7 }; ;infty )right.$

5. (Резервный день) Решите неравенство:

$displaystyle frac{1}{3^x-1}+frac{9^{x+frac{1}{2}}-3^{x+3}}{3^x-9}geq 3^{x+1}$

Решение:

$displaystyle frac{1}{3^x-1}+frac{3cdot 3^{2x}-27cdot 3^{x}+3}{3^x-9}geq 3cdot 3^{x}$

Замена:

$displaystyle frac{1}{t-1}+frac{3t^2 -27t+3}{t-9} geq 3t$

$displaystyle frac{1}{t-1}+3tcdot frac{t-9}{t-9}+frac{3}{t-9} geq 3t$

$displaystyle frac{1}{t-1}+3t+ frac{3}{t-9} geq 3t$

(Выделили целую часть в левой части неравенства),

$displaystyle frac{1}{t-1}+frac{3}{t-9} geq 0$

$displaystyle frac{t-9+3t-3}{(t-1)(t-9)} geq 0$

$displaystyle frac{4t-12}{(t-1)(t-9)} geq 0$

$displaystyle frac{t-3}{(t-1)(t-9)} geq 0$

Метод интервалов:

$left[begin{array}{c}1textless tleq 3\t textgreater 9end{array}right.$

Вернемся к переменной x:

$left[begin{array}{c}1textless 3^{x} leq 3\3^{x}textgreater 9end{array}right.Leftrightarrowleft[begin{array}{c}0textless x leq 1\xtextgreater 2end{array}right.,$

так как функция y=3^x монотонно возрастает.

Ответ:

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задача 15 ЕГЭ-2021 Решение неравенств» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
10.03.2023

Источник

10.10.2018

Практический сборник всех прототипов задания 15 из ЕГЭ по математике в 2021 году профильного уровня. Подробно разбираемся как решать любые задания такого типа на ЕГЭ.

Решение других заданий ЕГЭ по математике

Каждое задание содержит решение и правильный ответ, благодаря которому вы можете проверить себя.

Обсудить решение заданий вы можете в комментариях ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Источник

Автор

Задание №15 реального ЕГЭ 2021 года по математике профильный уровень.

Разбор и решение задания:

Тренировочные варианты ЕГЭ по математике с ответами:

Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами

Образцы заданий ЕГЭ 2021 по математике профильный уровень резервного дня 29 июня

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Тип 14 № 508319

Решите неравенство

Аналоги к заданию № 508319: 517423 511507 Все

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.

Классификатор алгебры: Неравенства рациональные относительно показательной функции

Методы алгебры: Замена — сумма или разность

Кодификатор ФИПИ/Решу ЕГЭ: 2.2.9 Метод интервалов

Источник

Задание 15. Вариант 12. ЕГЭ 2021 из 36 вариантов

Задание 15. Решите неравенство

Решение.

1. Запишем ОДЗ неравенства:

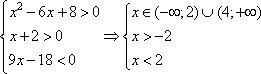
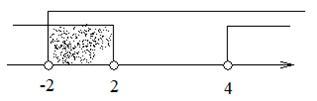
2. Преобразуем неравенство:

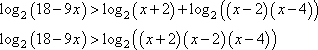
При одинаковых основаниях логарифмов можно перейти к их подлогарифмическим выражениям. Учитывая, что основание 21, то знак неравенства остается без изменения:

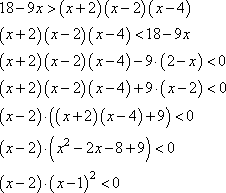
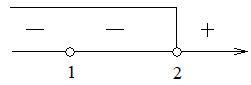
3. Пересечение с ОДЗ дает окончательное решение:

Ответ:

Источник


3370	Оценки экспертов решений задания 15 ЕГЭ по математике профильного уровня. Задание № 15 – это текстовая задача с экономическим содержанием. Решение	Критерии оценивания решений задания 15 ЕГЭ по математике профильного уровня ! Примеры оценивания реальных работ 2016-2021 гг # Приведены типы заданий с развёрнутым ответом, используемые в КИМ ЕГЭ по математике и критерии оценки выполнения заданий с развёрнутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку

3365	В июле 2026 года планируется взять кредит в размере 880 тыс. руб. Условия возврата таковы: – каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; – с февраля по июнь необходимо выплатить часть долга; – в июле 2027, 2028 и 2029 годов долг остается равным 880 тыс. руб. – суммы выплат 2030 и 2031 годов равны; – к июлю 2031 года долг будет выплачен полностью Найдите разницу между первым и последним платежами Решение	В июле 2026 года планируется взять кредит в размере 880 тыс. руб ! ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 15 Москва, Центр

3289	В июле 2022 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы: — каждый январь долг увеличивается на 15 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей. Найдите наибольшее значение S , при котором каждая из выплат будет меньше 3 млн рублей Решение	В июле 2022 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число ! Тренировочная работа №1 по МАТЕМАТИКЕ 10-11 класс 27.01.2022 Вариант МА2100109 Задание 15

3237	Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160 000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 25 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций? Решение	Сергей хочет купить пакет акций быстрорастущей компании ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 18 Задание 15 # Приведенорешениепрототипаcolor{blue} text{Приведено решение прототипа 2872}задачи- аналога 2872

2872	Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций? Решение	Александр хочет купить пакет акций быстрорастущей компании ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 15 Задание 15 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 17

2762	15 июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы: — 11-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца; -15-числа 15-го месяца долг составит 100 тысяч рублей; -к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей Решение	15 июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев ! 36 вариантов ФИПИ Ященко 2022 Вариант 33 Задание 15 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 23 Задание 17

2759	Планируется выдать льготный кредит на целое число миллионов рублей на четыре года. В середине каждого года действия кредита долг заёмщика возрастает на 25 % по сравнению с началом года. В конце 1-го и 2-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 3-го и 4-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 9 млн рублей Решение	Планируется выдать льготный кредит на целое число миллионов рублей на четыре года ! 36 вариантов ФИПИ Ященко 2022 Вариант 32 Задание 15 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 22 Задание 17

2734	По бизнес-плану четырёхлетний проект предполагает начальное вложение — 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в первый и второй годы, а также целое число m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся Решение	По бизнес-плану четырёхлетний проект предполагает начальное вложение ! 36 вариантов ФИПИ Ященко 2022 Вариант 28 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 18 Задание 17 # Задача-Аналог 1514

2692	15 января планируется взять кредит в банке на 11 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 4 % по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что на шестой месяц кредитования выплата составит 25 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования? Решение	15 января планируется взять кредит в банке на 11 месяцев ! Статград — Тренировочная работа №1 для 10 класса 28.01.2021 Профильный уровень Вариант МА2000309 Задание 17

2682	Евгений хочет купить пакет акций компании. 15 февраля он отложил определённую сумму денег и планирует откладывать такую же сумму денег 15 числа каждого месяца. Первого февраля пакет акций стоил 195 000 рублей. Первого числа каждого месяца пакет акций дорожает на 40 %. Какую наименьшую сумму нужно Евгению откладывать каждый месяц, чтобы через некоторое время купить желаемый пакет акций? Решение	Евгений хочет купить пакет акций компании ! Тренировочная работа №2 по математике 11 класс Статград 16-12-2020 профильный уровень Вариант МА2010209 Задание 17

Источник