ЕГЭ Профиль №9. Прямая
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Прямая
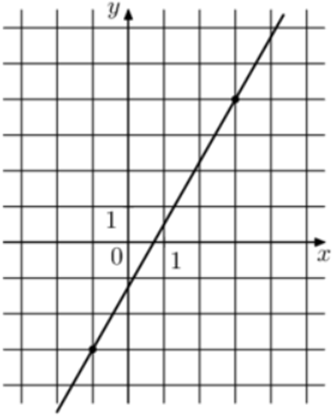
| Задача 1. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 5} right).)
Ответ
ОТВЕТ: — 10. |
 |
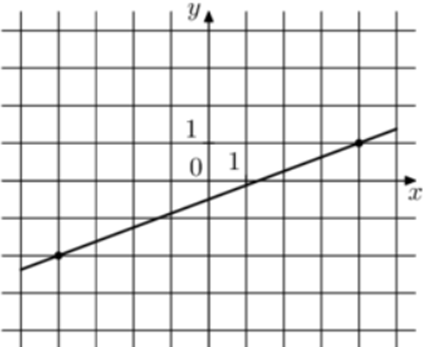
| Задача 2. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( {12} right).)
Ответ
ОТВЕТ: 4. |
 |
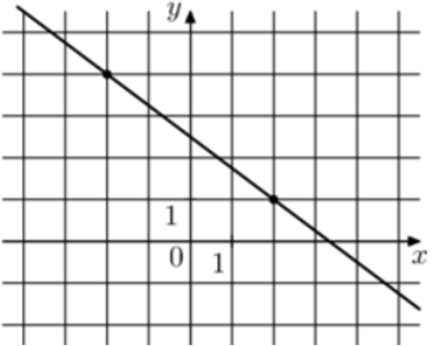
| Задача 3. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 16} right).)
Ответ
ОТВЕТ: 14,5. |
 |
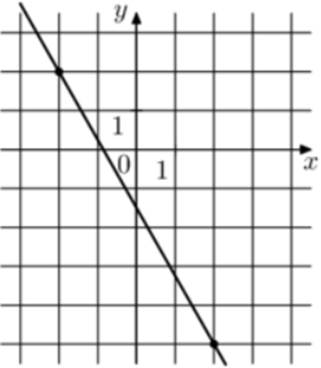
| Задача 4. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите (fleft( { — 16} right).)
Ответ
ОТВЕТ: 26,5. |
 |
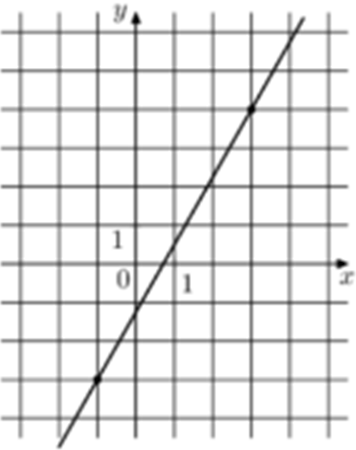
| Задача 5. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = — 13,5.)
Ответ
ОТВЕТ: — 7. |
 |
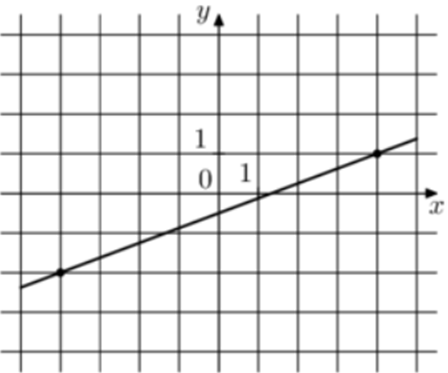
| Задача 6. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = 4,75.)
Ответ
ОТВЕТ: 14. |
 |
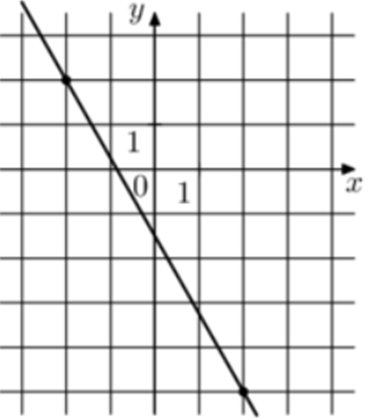
| Задача 7. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = 16.)
Ответ
ОТВЕТ: — 10. |
 |
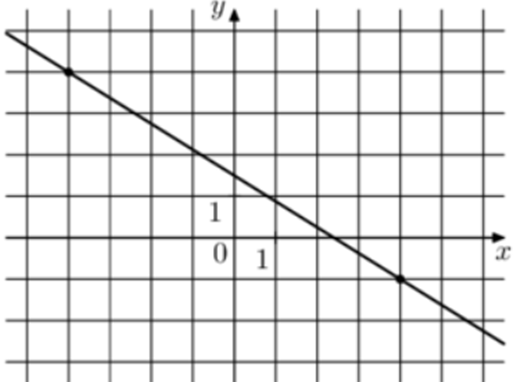
| Задача 8. На рисунке изображён график функции (fleft( x right) = k,x + b.) Найдите значение x при котором (fleft( x right) = — 7,25.)
Ответ
ОТВЕТ: 14. |
 |
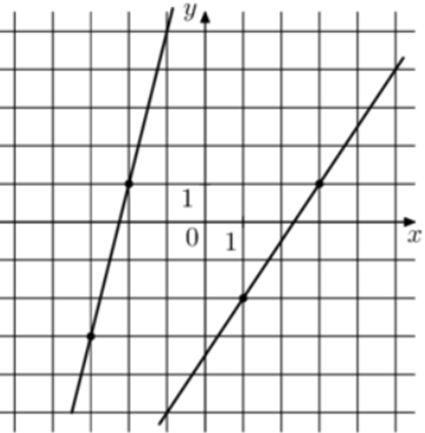
| Задача 9. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 5. |
 |
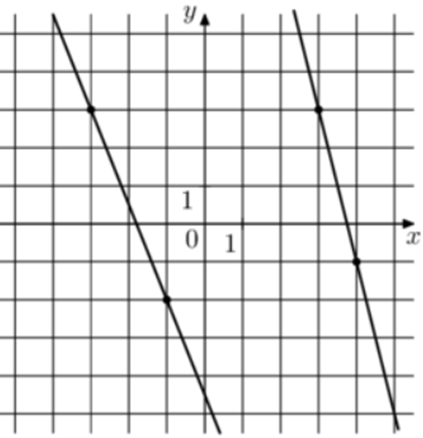
| Задача 10. На рисунке изображены графики функций вида (fleft( x right) = k,x + b.) которые пересекаются в точке А. Найдите абсциссу точки А.
Ответ
ОТВЕТ: 13. |
 |
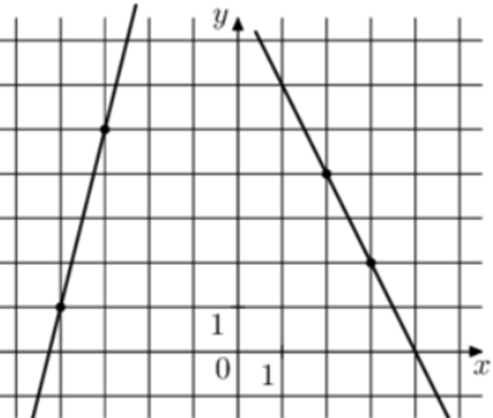
| Задача 11. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 11. |
 |
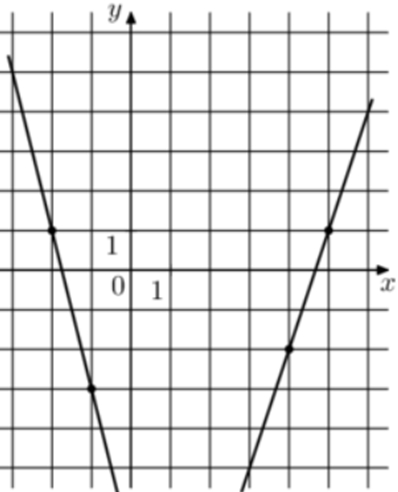
| Задача 12. На рисунке изображены графики функций вида (fleft( x right) = k,x + b.) которые пересекаются в точке А. Найдите ординату точки А.
Ответ
ОТВЕТ: — 11. |
 |
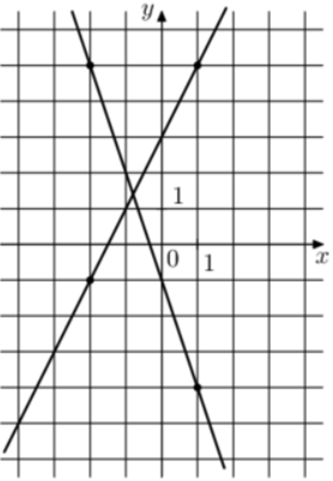
| Задача 13. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 0,8. |
 |
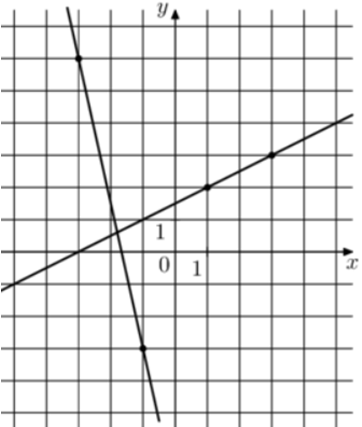
| Задача 14. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ
ОТВЕТ: — 1,8. |
 |
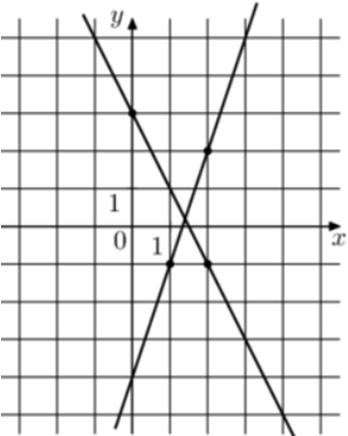
| Задача 15. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 0,2. |
 |
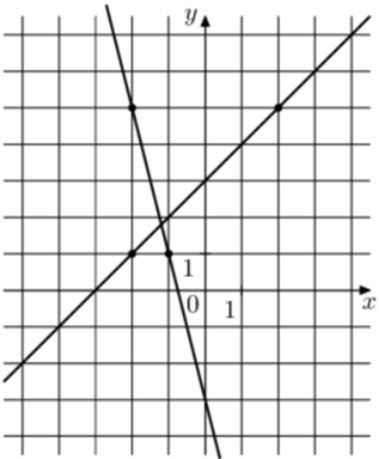
| Задача 16. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Ответ
ОТВЕТ: 1,8. |
 |
Поиск
Всего: 32 1–20 | 21–32
Добавить в вариант
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
Источник: ЕГЭ по математике 28.03.2022. Досрочная волна. ФИПИ. Вариант 4
Всего: 32 1–20 | 21–32
- ЕГЭ по математике профиль
Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.
Для успешного результата необходимо уметь выполнять действия с функциями.
Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы
| Скачать задания | Источник |
| Новые задания 9 | ФИПИ |
| Прототипы задания №9 | vk.com/mathegeexam |
| Скачать задания | vk.com/ekaterina_chekmareva |
| → Теория → Задачи → Шпаргалка |
vk.com/abel_mat |
| Линейная функция | math100.ru |
| Парабола | |
| Гипербола | |
| Логарифмическая и показательная функции | |
| Иррациональные функции | |
| Тригонометрические функции |
Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:
3.3.1 Линейная функция, её график
3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
3.3.3 Квадратичная функция, её график
3.3.4 Степенная функция с натуральным показателем, её график
3.3.5 Тригонометрические функции, их графики
3.3.6 Показательная функция, её график
3.3.7 Логарифмическая функция, её график
Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:
При отработке данного задания будут полезны книги:
Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля
Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств
Связанные страницы:
Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи в разделе контакты
💡 Если Вы — учитель математики, то Вы можете создавать готовые карточки для учеников с индивидуальными заданиями и с ответами для отработки заданий на графики функций. Данные задачи доступны в Конструкторе бесплатно.
|
3. На рисунке изображён график функции y=3x^2+bx+c . Найдите f(6) . [Ответ: 10] |
Смотреть видеоразбор похожего >> |
|
4. На рисунке изображён график функции y=ax^2+12x+c . Найдите f(7) . [Ответ: -74] |
Смотреть видеоразбор похожего >> |
|
5. На рисунке изображён график функции y=ax^2+bx+12 . Найдите f(-7) . [Ответ: 19] |
Смотреть видеоразбор похожего >> |
|
6. На рисунке изображён график функции y=ax^2+bx+c . Найдите f(1) . [Ответ: 49] |
Смотреть видеоразбор похожего >> |
|
7. На рисунке изображён график функции y=ax^2+bx+c , где числа a , b и c — целые. Найдите f(-5) . [Ответ: -29] |
Смотреть видеоразбор похожего >> |
|
8. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите f(0.1) . [Ответ: -17] |
Смотреть видеоразбор похожего >> |
|
9. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите, при каком значении x значение функции равно -4.4 . [Ответ: -12.5] |
Смотреть видеоразбор похожего >> |
|
10. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите f(-3.5) . [Ответ: 6] |
Смотреть видеоразбор похожего >> |
|
11. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите значение x , при котором f(x) = 10 . [Ответ: 0.6] |
Смотреть видеоразбор похожего >> |
|
12. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите k . [Ответ: 1] |
Смотреть видеоразбор похожего >> |
|
13. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
14. На рисунке изображён график функции f(x)=b+log_ax . Найдите f(frac{1}{9}) . [Ответ: 3] |
Смотреть видеоразбор похожего >> |
|
15. На рисунке изображён график функции f(x)=b+log_ax . Найдите значение x , при котором f(x)=-11 . [Ответ: 64] |
Смотреть видеоразбор похожего >> |
|
16. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите f(26) . [Ответ: -2] |
Смотреть видеоразбор похожего >> |
|
17. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите значение x , при котором f(x)=4 . [Ответ: 82] |
Смотреть видеоразбор похожего >> |
|
18. На рисунке изображён график функции f(x) = a^x+b . Найдите f(-2) . [Ответ: 22] |
Смотреть видеоразбор похожего >> |
|
19. На рисунке изображён график функции f(x) = a^x+b . Найдите значение x , при котором f(x) = 77 . [Ответ: -4] |
Смотреть видеоразбор похожего >> |
|
20. На рисунке изображён график функции f(x) = a^{x+b} . Найдите f(4) . [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
21. На рисунке изображён график функции f(x) = a^{x+b} . Найдите значение x , при котором f(x) = 64 . [Ответ: 8] |
Смотреть видеоразбор похожего >> |
|
22. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите f(8.41) . [Ответ: 8.7] |
Смотреть видеоразбор похожего >> |
|
23. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите значение x , при котором f(x)=-6.75 . [Ответ: 7.29] |
Смотреть видеоразбор похожего >> |
|
24. На рисунке изображены графики функций f(x)=-4x+22 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
25. На рисунке изображены графики функций f(x)=-6x-28 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 38] |
Смотреть видеоразбор похожего >> |
|
26. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 0.2] |
Смотреть видеоразбор похожего >> |
|
27. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 20] |
Смотреть видеоразбор похожего >> |
|
28. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -2.08] |
Смотреть видеоразбор похожего >> |
|
29. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: -2.4] |
Смотреть видеоразбор похожего >> |
|
30. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -11.3] |
Смотреть видеоразбор похожего >> |
|
31. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: 6.8] |
Смотреть видеоразбор похожего >> |
|
32. На рисунке изображены графики функций f(x) = 2x^2+16x+30 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: -9] |
Смотреть видеоразбор похожего >> |
|
33. На рисунке изображены графики функций f(x) = -2x^2-3x+1 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: -13] |
Смотреть видеоразбор похожего >> |
|
34. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите абсциссу точки A. [Ответ: 3.24] |
Смотреть видеоразбор похожего >> |
|
35. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите ординату точки A. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
36. На рисунке изображён график функции f(x) = asin{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
37. На рисунке изображён график функции f(x) = asin{x}+b . Найдите b . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
38. На рисунке изображён график функции f(x) = acos{x}+b . Найдите a . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
39. На рисунке изображён график функции f(x) = acos{x}+b . Найдите b . [Ответ: −1] |
Смотреть видеоразбор похожего >> |
|
40. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
41. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите b . [Ответ: −1,5] |
Смотреть видеоразбор похожего >> |
Слайд 1
«ЗАДАНИЕ № 9 В ЕГЭ 2022 ПРОФИЛЬНОГО УРОВНЯ» Зялалова З.А учитель математики МБОУ ВСОШ №4
Слайд 2
Задание №9 . «Анализ графиков» Прямая Парабола Гипербола Логарифмическая и показательная функции Иррациональные функции Тригонометрические функции
Слайд 3
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1
Слайд 4
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:
Слайд 5
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:
Слайд 6
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:
Слайд 7
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:
Слайд 8
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:
Слайд 9
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:
Слайд 10
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:
Слайд 11
На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение: Ответ: 4.
Слайд 12
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2
Слайд 13
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 14
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 15
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 16
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 17
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 18
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 19
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 20
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 21
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 22
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 23
По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:
Слайд 24
Прототип 1. (Прямая) На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения. 1 2 Решение: Уравнение прямой у = kx+b . 1) Первая прямая проходит через точки (-4;1) и (-2;4) , Решаем систему = > k=1,5; b=7 у =1,5х+7-уравнение 1 прямой. 2) Вторая прямая проходит через точки (-1;0) и (2;3) . Решаем систему = > k=1; b=1 Тогда у=х+1-уравнение 2 прямой. 3)Решим систему уравнений , х = -12.Тогда у = -11. Ответ:-11
Слайд 25
Прототип 2. (Парабола) На рисунке изображен график функции f(x)= x²+bx+c . Найдите f( -1 ) . Решение. Из рисунка видно, что график проходит через (3;2);(4;5);(5;4) В ычтем из 2 уравнения 1-е , п олучим7 a + b = Вычтем из 3уравнения 2 -е , получим 9 a + b=- Решив систему уравнений находим = -2 , b = 17. Тогда f(x )= — 2 x² + 17 x + c и f( 3 ) = 2, найдем ,что с = -31. f(x )= — 2 x²+ 17 x — 31, f( -1 ) =-2-17-31=-50 Ответ:-50
Слайд 26
Прототип 3 . (Парабола) На рисунке изображен график функции f(x)= ах ² + bx+c ,где числа , b и c -целые. Найдите абсциссу вершины параболы . Решение. Из рисунка видно, что график проходит через (3 ;-2);(2;1);(1;6) Тогда вычтем из 1 уравнения 2-е, получим 5a-b=- вычтем из 2 уравнения 3-е,получим 3 a-b=- Решив систему уравнений находим =1 , b =8. Абсцисса вершины параболы = — =-4 . Ответ:-4
Слайд 27
Прототип 4 . (Парабола) На рисунке изображены графики функций f(x )= 5х+9 и g(x)= ах ² + bx+c , которые пересекаются в точках А и В. Найдите абсциссу точки B Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3). Подставим координаты точки (-1;-3), получим -3=а- b -3. Отсюда а= b . g(x)= ах ² + а x -3. Подставим координаты точки (2;3 ), получим, что а=1. g(x)= х ² +x -3. Чтобы найти абсциссу точки ,нужно решить уравнение х ² +x -3 = 5х+9, х ² — 4 x — 12=0. По теореме Виета = -12, + = 4 По графику = -2, тогда =6. Ответ:6
Слайд 28
Прототип 5. (Гипербола) На рисунке изображен график функции f(x)= +a . Найдите f (0,25) Решение: График функции имеет горизонтальную асимптоту y = -2 , значит, а = -2 . ( График функции f(x ) = + a получается сдвигом графика функции f(x ) = вдоль оси Оу на величину |а| вверх, если а >0 и вниз если a<0 ) По графику а = -2 и проходит через точку (3;-3). -3 = -2 отсюда k = -3 .Значит, f(x ) = -2, f( 0,25 ) = -2= -14. Ответ:- 14
Слайд 29
Прототип 6 . (Гипербола) На рисунке изображён график функции вида f(x )= +c , где числа a, b и c — целые. Найдите f(13). Решение. График функции имеет горизонтальную асимптоту y = 2, значит, c = 2. График функции имеет вертикальную асимптоту x = 3 , значит, b = — 3. По графику f(2 ) = 1 , тогда +2=1, отсюда a = 1 . Таким образом, f(x ) = +2 Найдём f(13 ) = +2=2,1. f(13)=2,1. Ответ:2,1
Слайд 30
Прототип 7 . (Гипербола) На рисунке изображен график функции f(x)= . Найдите f . Решение. График функции имеет вертикальную асимптоту x = 2, значит, а = — 2. По графику а= -2 и проходит через точку (-3;-1). -1= , отсюда k = 5.Значит , f(x ) = , f = = 5: = -0,75. Ответ: -0,75
Слайд 31
Прототип 8. (Гипербола) На рисунке изображен график функции f(x)= . Найдите k Решение. Преобразуем данную функцию f(x)= f(x ) = Тогда, делаем вывод, что k- горизонтальная асимптота b -вертикальная асимптота График функции имеет горизонтальную асимптоту y=2, значит , k =2. Ответ:2
Слайд 32
Прототип 9 . (Гипербола) На рисунке изображен график функции f(x)= . Найдите a . Решение. График функции имеет горизонтальную асимптоту y=2, значит, k =2 . График функции имеет вертикальную асимптоту x=3, значит, b = — 3. По графику f( 5 )= 3, тогда 3= , отсюда а=-4. Ответ:-4 k-u горизонтальная асимптота b -вертикальная асимптота
Слайд 33
Прототип 10. ( Тригонометрическая функция ) На рисунке изображен график функции вида f(x )= cos(b π x+c )+d, где числа , b, c и d -целые. Найдите . Решение. По графику = -3 d = = = -1. |a|= = =2. По графику =2, c =0, T=2 T= = , то есть =2 , отсюда b=1 f (x)=2cos π x-1, f =f f , f =2cos π· -1 = 2cos π -1 = 2cos -1= -2cos 1= -2. Ответ:-2 Т=2
Слайд 34
Прототип 11.(Тригонометрическая функция) На рисунке изображён график функции вида f(x)= cos(b π x+c )+d, где числа , b, c и d -целые. Найдите . Решение. По графику = -3 d= = = -1. |a|= = =2. По графику = — 2 , c=0, T=2 T= = , то есть =2 , отсюда b=1 f(x )= — 2cos π x-1, f =f f , f = — 2cos π· -1 = — 2cos π -1 = — 2cos -1= 2cos 1= 0 . Ответ:0
Слайд 35
Прототип 12.(Иррациональная функция) На рисунке изображен график функции f(x)=k Найдите f(2,56) Решение. График этой функции проходит через точку (4;-3).Подставив координаты этой точки, получим -3= k , 2 k =-3, k =-1,5. f(2,56 ) =-1,5 Ответ:-2,4
Слайд 36
Прототип 13.(Логарифмическая функция) На рисунке изображен график функции f(x )=b+ x. Найдите значение х при котором f(x )=2. Решение. График функции f(x)= b+ x получается сдвигом графика функции f(x)= x. вдоль оси Оу на величину |b| вверх , если b > 0 и вниз если b <0 . По графику b = -2 и проходит через точку (3;- 1 ). -1= — 2 + , отсюда а =3 .Значит, f(x)= — 2 x , найдем х при котором f(x )= 2. 2=-2 x , x =4, значит, х=81. Ответ:81
Слайд 37
Прототип 14.(Показательная функция) На рисунке изображен график функции f(x )= . Найдите f (-5 ). Решение. График функции f(x)= получается сдвигом графика функции f(x)= вдоль оси Ох на величину | b | влево, если b>0 и вправо если b<0 . По графику b = — 1 и проходит через точку ( 3 ; 2 ). отсюда а = . Значит, f ( -5 )= = = Ответ:0,125
Скачать материал

Скачать материал


- Сейчас обучается 96 человек из 32 регионов


- Сейчас обучается 82 человека из 34 регионов


- Сейчас обучается 54 человека из 29 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Анализ графиков функций
Задание №9 -
2 слайд
Анализ графиков функций
Линейная функция
Квадратичная функция
Степенная функция
Показательная и логарифмическая функция
Тригонометрические функции
Кусочно-линейная функция
Комбинированные задачи -
3 слайд
Прототипы заданий
Найти аргумент по известному значению функции
Найти значение функции по известному значению аргумента
Найти координаты вершины параболы
Найти точку пересечения графиков двух функций
Найти один из параметров
Найти решение уравнения -
4 слайд
b = f(0)
b = f(0)
Линейная функция. График — прямая
Прямые параллельны тогда, когда их угловые коэффициенты равны
Прямые перпендикулярны тогда, когда произведение их угловых коэффициентов равно -1 -
5 слайд
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.
1
(-1;0)
(2;3)
(-4;1)
1 способ.
Система двух уравнений с двумя неизвестными
𝟏=𝟒𝒌+𝒃, 𝟒=−𝟐𝒌+𝒃
у=1,5х+7𝟎=−𝟏𝒌+𝒃, 𝟑=𝟐𝒌+𝒃
у=х+1Решим систему уравнений у=𝟏,𝟓𝒙+𝟕, 𝒚=𝒙+𝟏 .
х=-12
у=-11.Ответ:-11
(-2;4)
-
6 слайд
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.
1
k= 3 2
(-1;0)
(2;3)
(-4;1)
(-2;4)
2 способ.
Через tg α=k
k= 𝟑 𝟐 k= 𝟏
1=1,5·(-4)+ b 0=1·(-1)+ b,
b=7 b=1Решим систему уравнений у=𝟏,𝟓𝒙+𝟕, 𝒚=𝒙+𝟏 .
х=-12
у=-11.Ответ:-11
-
7 слайд
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.
1
(-1;0)
(2;3)
(-4;1)
(-2;4)
3 способ
Уравнение прямой, проходящей через 2 точки𝒙− 𝒙 𝟏 𝒙 𝟐 − 𝒙 𝟏 = 𝒚− 𝒚 𝟏 𝒚 𝟐 − 𝒚 𝟏
𝒙+𝟒 𝟐 = 𝒚−𝟏 𝟑 𝒙+𝟏 𝟑 = 𝒚 𝟑
Решим систему уравнений у=𝟏,𝟓𝒙+𝟕, 𝒚=𝒙+𝟏 .
х=-12
у=-11.Ответ:-11
-
8 слайд
Квадратичная функция
График — парабола
f(x)=ax2 + bx + c = a(x-x1)(x-x2) = a(x — m) 2+ n
-4
-3
-1
-1
-2 -
9 слайд
Определение коэффициента а в квадратичной функции по графику
f(x)=ax2
1
a==1
1
2
a==2
1
2
a= -= -2
1 -
10 слайд
На рисунке изображен график функции f(x)= 𝒂 x²+bx+c,
где числа a,b и c-целые. Найдите значение f(-12).
Решение.
f(x)= 𝒂(x-m)²+n,где m, n-координаты вершины параболы.
m= -4,n= -3, 𝒂 =1.
f(x)=(x-(-4))²+(-3),
f(x)=(x+4)²-3,
f(-12)=(-12+4)²-3,
f(-12)=61.
Ответ:61 -
11 слайд
𝑦=𝑎 𝑥−1 𝑥−4
с=4, а=1
𝑦= 𝑥 2 −5𝑥+4
𝑦 −12 =208
(1;0)
(4;0) -
12 слайд
На рисунке изображен график функции
f(x)= 𝒂 x²+bx+c. Найдите f(-1).
Решение: (3;2);(4;5);(5;4)9а+3b+c= 2, 16a+4b+c=𝟓, 25a+5b+c=4.
находим 𝒂=-2 ,b=17 с=-31
f(x)=- 2 x²+17x-31,
f(-1)=-2-17-31=-50
Ответ:-50 -
13 слайд
На рисунке изображен график функции f(x)=ах²+bx+c,где числа 𝒂 ,b и c-целые. Найдите абсциссу вершины параболы.
Решение.
Абсцисса вершины параболы найдем по формуле х 𝟎 = — 𝒃 𝟐𝒂
Из рисунка видно, что f(-3)=-2; f(-2)=1; f(-1)=6.Тогда
9а−3b+c= −2, 4a−2b+c=1, a−b+c=6 ;
вычтем из 1 уравнения 2-е, получим5a-b=-𝟑
вычтем из 2 уравнения 3-е,получим 3a-b=-𝟓.
Решив систему уравнений 5a−b=−𝟑, 3a−b=−𝟓; находим 𝒂=1 ,b=8.
Абсцисса вершины параболы х 𝟎 = — 𝒃 𝟐𝒂 =-4.
Ответ:-4 -
14 слайд
На рисунке изображены графики функций f(x)=5х+9 и g(x)= ах²+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B
Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3).
Подставим координаты точки (-1;-3), получим
-3=а- b-3.Отсюда а=b.
g(x)= ах²+аx-3.
Подставим координаты точки (2;3), получим, что а=1.
g(x)= х²+x-3.
Чтобы найти абсциссу точки ,нужно решить уравнение х²+x-3=5х+9,
х²-4x-12=0.
По теореме Виета х 𝟏 ·х 𝟐 =-12, х 𝟏 + х 𝟐 =4
По графику х 𝟏 =-2, тогда х 𝟐 =6.
Ответ:6 -
15 слайд
Степенная функция
-
-
-
-
19 слайд
Другой способ решения
-
20 слайд
На рисунке изображен график функции f(x)= 𝒌𝒙+𝒂 𝒙+𝒃 . Найдите k
Решение.
Преобразуем данную функцию
f(x)= 𝒌𝒙+𝒂 𝒙+𝒃 = 𝒌𝒙+𝒌𝒃−𝒌𝒃+𝒂 𝒙+𝒃 = 𝒌(𝒙+𝒃)−𝒌𝒃+𝒂 𝒙+𝒃 =𝒌+ 𝒂−𝒌𝒃 𝒙+𝒃 .
Илиf(x)=𝒌+ 𝒂−𝒌𝒃 𝒙+𝒃
График функции имеет горизонтальную асимптоту y=2,
значит, k=2.
Ответ:2 -
21 слайд
Логарифмическая и показательная функция
-
-
-
-
25 слайд
Кусочная функция
-
26 слайд
Тригонометрические функции
𝐴 = 𝑓 𝑚𝑎𝑥 −𝑓𝑚𝑖𝑛 2
𝐵= 𝑓 𝑚𝑎𝑥 +𝑓𝑚𝑖𝑛 2 -
-
28 слайд
11 На рисунке изображен график функции вида f(x)= 𝒂 cos(bπx+c)+d, где числа 𝒂,b, c и d-целые. Найдите 𝒇 𝟏𝟎𝟎 𝟑 .
Решение.
По графику 𝒇 𝒎𝒂𝒙 =𝟏,𝒇 𝒎𝒊𝒏 =-3
d= 𝒇 𝒎𝒂𝒙 + 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏−𝟑 𝟐 = -1. |a|= 𝒇 𝒎𝒂𝒙 − 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏+𝟑 𝟐 =2.
По графику 𝒂 =2, c=0, T=2
T= 𝟐𝝅 𝒃𝝅 = 𝟐 𝒃 , то есть 𝟐 𝒃 =2, отсюда b=1
f(x)=2cosπx-1,
f 𝟏𝟎𝟎 𝟑 =f 𝟗𝟔 𝟑 + 𝟒 𝟑 =𝒇 𝟑𝟐+ 𝟒 𝟑 =f 𝟒 𝟑 ,
f 𝟒 𝟑 =2cosπ· 𝟒 𝟑 -1 = 2cos 𝟒 𝟑 π-1 = 2cos π+ π 𝟑 -1= -2cos π 𝟑 −1= -2.
Ответ:-2Т=2
-
29 слайд
Ссылки для задания №9
✅Все НОВЫЕ Задания №9 ЕГЭ 2022 Профиль с сайта.. | ege314.ru | ОГЭ и ЕГЭ по математике 2022 (vk.com)
Задачи 9 ЕГЭ профильная математика, сортировка по темам (mathm.ru)
9. Функции и их свойства (ege314.ru)
Новое ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами. — math100.ru
Задание 9 ЕГЭ по математике. Графики функций (ege-study.ru)
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 779 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы



- 09.10.2022
- 205
- 20





Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация логистической деятельности на транспорте»
-
Курс повышения квалификации «Основы построения коммуникаций в организации»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Разработка эффективной стратегии развития современного вуза»
-
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
-
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
-
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
-
Курс профессиональной переподготовки «Управление качеством»
MATHM
>>
ЕГЭ
>>
ЕГЭ профиль
>>
Задача 9

ЗАДАЧА 9
сортировка
по темам
СПИСОК ТЕМ
Тема 1: График параболы
Тема 2: График гиперболы и корня
Тема 3: График модуля
Тема 4: Графики тригонометрических функций
Тема 5: График показательной функции и логарифма
Тема 6: Пересечение графиков
Задачи разделены на темы. Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.
Тема 1: График параболы.
посмотреть ответ
посмотреть решение
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
посмотреть ответ
посмотреть решение 1
посмотреть решение 2
видеоурок 1 по графику параболы
видеоурок 2 по графику параболы
Тема 2: График гиперболы и корня.
посмотреть ответ
посмотреть решение
видеоурок по графику гиперболы
посмотреть ответ
посмотреть решение
видеоурок по графику гиперболы
посмотреть ответ
посмотреть решение
видеоурок по графику гиперболы
посмотреть ответ
посмотреть решение
видеоурок по графику гиперболы
посмотреть ответ
посмотреть решение
видеоурок по графику корня
посмотреть ответ
посмотреть решение
видеоурок по графику корня
посмотреть ответ
посмотреть решение
видеоурок по графику корня
посмотреть ответ
посмотреть решение
видеоурок по графику корня
посмотреть ответ
посмотреть решение
видеоурок по графику корня
посмотреть ответ
посмотреть решение
видеоурок по графику корня
Тема 3: График модуля.
посмотреть ответ
посмотреть решение
видеоурок по графику модуля
посмотреть ответ
посмотреть решение
видеоурок по графику модуля
посмотреть ответ
посмотреть решение
видеоурок по графику модуля
посмотреть ответ
посмотреть решение
видеоурок по графику модуля
Тема 4: Графики тригонометрических функций.
посмотреть ответ
посмотреть решение
видеоурок 1 по графикам тригонометрических функций
видеоурок 2 по графикам тригонометрических функций
посмотреть ответ
посмотреть решение
видеоурок 1 по графикам тригонометрических функций
видеоурок 2 по графикам тригонометрических функций
посмотреть ответ
посмотреть решение
видеоурок 1 по графикам тригонометрических функций
видеоурок 2 по графикам тригонометрических функций
посмотреть ответ
посмотреть решение
видеоурок 1 по графикам тригонометрических функций
видеоурок 2 по графикам тригонометрических функций
посмотреть ответ
посмотреть решение
видеоурок 1 по графикам тригонометрических функций
видеоурок 2 по графикам тригонометрических функций
посмотреть ответ
посмотреть решение
видеоурок 1 по графикам тригонометрических функций
видеоурок 2 по графикам тригонометрических функций
Тема 5: График показательной функции и логарифма.
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
Тема 6: Пересечение графиков.
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
посмотреть ответ
посмотреть решение
Мастер-класс учителя математики
СП МБОУ СОШ №2 г Алагира Ревазовой Ж.Б.
по теме:
«Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»
2021г
«Расскажи мне и я забуду. Покажи мне и я пойму. Позволь мне сделать самому,
и я научусь»
Конфуций
Конфуций-древнекитайский проповедник, писатель, философ.
Сложно подготовить обучающихся к сдаче экзамена. Это большой труд. Но не надо бояться. Если вы хорошо знаете, объясняете, любите свой предмет и своих учеников, вы обязательно сможете подготовить их к ЕГЭ по математике.
Важный принцип — это логичность. В шутливой манере он говорит: «нормальные герои всегда идут в обход». Нужно учиться использовать наличный запас знаний, применяя различные «хитрости» и «правдоподобные рассуждения» для ответа наиболее простым и понятным способом.
Главная заповедь учителя – заметить даже самое маленькое продвижение ученика вперёд и поддержать его успех.
Цель мастер-класса:
•
показать приемы решения нового 9 задания по теме «Анализ графиков»
- развивать логическое мышление, память, познавательный интерес
1 9 задание
На рисунке изображены графики двух линейных функций. Найдите
ординату точек пересечения.
1
2
Решение
- Уравнение прямой у=kx+b. Первая прямая проходит через точки (-4;1) и (-2;4), k=.
- Вторая прямая проходит через точки (-1;0) и (2;3), k= . Найдем b,подставив координаты одной из точек в уравнение 0=1·(-1)+ b, b=1.Тогда у=х+1-уравнение2 прямой.
- Решим систему уравнений Вычтем из 1 уравнения 2 уравнение , получим 0=0,5х+6.Отсюда х=-12.Тогда у=-11.
Найдем b,подставив координаты одной из точек в уравнение 1=1,5·(-4)+ b, b=7.
у=1,5х+7-уравнение1 прямой.
Ответ:-11
9 задание
На рисунке изображен график функции f(x)= x²+bx+c,где числа a,b и c— целые. Найдите значение f(-12).
Решение.
f(x)= (x-m)²+n,где m, n-координаты вершины параболы.
m= -4,n= -3, =1.
f(x)=(x-(-4))²+(-3), f(x)=(x+4)²-3,
f(-12)=(-12+4)²-3, f(-12)=61.
Ответ:61
2
9 задание
На рисунке изображен график функции f(x)= +bx+c, где числа ,b и c-целые. Найдите значение f(4).
Решение.
f(x)=(x-m)²+n,где (m, n)-координаты вершины параболы. По графику m= -2,n= 11, = -2. (Введем новую систему координат через вершину параболы, тогда график функции f(x)= проходит через точку (2;-2).
Подставив в формулу f(x)= ,найдем а)
f(x)= — (x+2)²+11= — x²-2x+9,значит, = — 2, b=-2, c=9. Тогда f(4)= — +11= — 18+11= — 7.
Ответ:- 7
3
4 9 задание. На рисунке изображен график функции f(x)= x²+bx+c.
Найдите f(-1).
Решение.
Из рисунка видно, что график проходит через (3;2);(4;5);(5;4)
Вычтем из 2 уравнения 1-е, получим7a+b=
Вычтем из 3уравнения 2-е, получим 9a+b=-
Решив систему уравнений находим =-2 ,b=17.
Тогда f(x)=- 2x²+17x+c и f(3)=2, найдем ,что с=-31. f(x)=- 2x²+17x-31,
f(-1)=-2-17-31=-50
Ответ:-50
9 задание. На рисунке изображен график функции f(x)=ах²+bx+c,где числа ,b и c-целые. Найдите абсциссу вершины параболы.
Решение.
Абсцисса вершины параболы найдем по формуле = —
Из рисунка видно, что f(-3)=-2; f(-2)=1; f(-1)=6.Тогда
вычтем из 1 уравнения 2-е, получим5a-b=- вычтем из 2 уравнения 3-е,получим 3a-b=- Решив систему уравненийнаходим =1 ,b=8. Абсцисса вершины параболы = — =-4.
Ответ:-4
6
9 задание. На рисунке изображены графики функций f(x)=5х+9 и g(x)= ах²+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B
7
Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3).
Подставим координаты точки (-1;-3), получим
-3=а- b-3.Отсюда а=b. g(x)= ах²+аx-3.
Подставим координаты точки (2;3), получим, что а=1.
g(x)= х²+x-3.
Чтобы найти абсциссу точки ,нужно решить уравнение х²+x-3=5х+9,
х²-4x-12=0.
По теореме Виета =-12, +=4 По графику =-2, тогда=6.
Ответ:6
Решите 9 задание
На рисунке изображен график функции f(x)= x²+bx+c,где числа ,b и c— целые. Найдите значение дискриминанта уравнения f(x)=0.
Решение.
f(x)= (x-m)²+n,где m, n-координаты вершины параболы.
m=-3,n=3, =1. f(x)=(x-(-3))²+3 f(x)=(x+3)²+3,
f(x)=х²+6х+12, так как f(x)=0. то х²+6х+12=0
D=6²-4·1·12= -12.
Ответ:-12
8
9 задание
На рисунке изображен график функции вида = x+|bx+c|+d, где числа ,b, c и d-целые.
9
Найдите корень уравнения bx+c=0
Решение.
|bx+c|=0 в точке излома. Значит, bx+c=0 при х=2.
Ответ:2
9 задание.
На рисунке изображён график функции вида f(x)=ax + |bx + c| +d, где
числа a, b, c и d — целые. Найдите корень уравнения ax + d=0.
Решение.
|bx + c|=0 в точке излома при х=1,
Если х<1,то f(x)=ax -bx — c +d=(а-b)х+ d-с, где (а-b)-угловой коэффициент, (d-с)-ордината точки пересечения прямой с осью Ох.
По графику а-b=-4; d-с=5.
Если х>1,то f(x)=ax +bx + c +d=(а+b)х+с+ d, где а+b-угловой коэффициент, по графику а+b=2.
Продолжив прямую до пересечения с осью Оу, получим , что с+ d =-1.
10
5
-1
Решив эти системы получим,что
a=-1;b=3;c=-3;d=2. Подставив найденные значения в уравнение ax +d=0 , получим -x + 2=0,
х=2.
Ответ:2
11 На рисунке изображен график функции вида f(x)= cos(bπx+c)+d, где числа ,b, c и d-целые. Найдите .
Решение.
По графику =-3
d= = = -1. |a|= = =2.
По графику =2, c=0, T=2
T= = , то есть =2, отсюда b=1 f(x)=2cosπx-1,
f=ff,
f=2cosπ·-1 = 2cos π-1 = 2cos-1= -2cos1= -2. Ответ:-2
Т=2
9 задание. На рисунке изображен график функции f(x)=k Найдите f(2,56)
Решение.
График этой функции проходит через точку (4;-3).Подставив координаты этой точки, получим
-3=k ,
2k=-3, k =-1,5.
f(2,56)=-1,5
Ответ:-2,4
12
9 задание. На рисунке изображен график функции f(x)= +a. Найдите f (0,25)
Решение. График функции имеет горизонтальную асимптоту y=-2, значит, а=-2.
(График функции f(x)= +a получается сдвигом графика функции f(x)= вдоль оси Оу на величину |а| вверх, если а>0 и вниз если a<0)
По графику а= -2 и проходит через точку (3;-3).
-3= -2 отсюда k=-3.Значит,
f(x)= -2,
f(0,25)= -2= -14.
Ответ:- 14
13
9 задание. На рисунке изображен график функции f(x)= . Найдите f .
14
Решение.
График функции имеет вертикальную асимптоту x=2, значит, а= — 2.
(График функции f(x)= получается сдвигом графика функции f(x)= вдоль оси Ох на величину
|а| влево, если а>0 и вправо если a<0).
По графику а= -2 и проходит через точку (-3;-1).
-1= , отсюда k=5.Значит, f(x)= ,
f= =5: =-0,75.
Ответ:-0,75
9 задание. На рисунке изображён график функции вида f(x)=+c,
где числа a, b и c — целые. Найдите f(13).
Решение.
График функции имеет горизонтальную асимптоту y=2, значит, c=2.
График функции имеет вертикальную асимптоту x=3, значит, b= — 3.
По графику f(2)=1, тогда +2=1, отсюда a=1. Таким образом, f(x)= +2
Найдём f(13)=+2=2,1. f(13)=2,1.
Ответ:2,1
15
9 задание. На рисунке изображен график функции f(x)= . Найдите k
Решение.
Преобразуем данную функцию f(x)=
Или
f(x)=
График функции имеет горизонтальную асимптоту y=2, значит, k=2.
Ответ:2
16
9 задание. На рисунке изображен график функции
f(x)= . Найдите a
Решение.
Преобразуем данную функцию
f(x)=
Или
График функции имеет горизонтальную асимптоту y=2, значит, k=2.
График функции имеет вертикальную асимптоту x=3, значит,
b= — 3.
По графику f(5)=3, тогда 3=, отсюда а=-4. Ответ:-4
17
f(x)=
kx+a x+b
kx+kb k
a-kb
9 задание. На рисунке изображен график функции
f(x)=b+x.Найдите значение х при котором f(x)=2.
18
Решение.
График функции f(x)= b+x получается сдвигом графика функции f(x)= x. вдоль оси Оу на величину
|b| вверх, если b >0 и вниз если b <0.
По графику b = -2 и проходит через точку (3;-1).
-1= -2+, отсюда а=3.Значит,
f(x)= -2x, найдем х при котором f(x)=2. 2=-2x,
x=4, значит, х=81. Ответ:81
9 задание. На рисунке изображен график функции
f(x)=.Найдите значение х при котором f(-5).
19
Решение.
График функции f(x)= получается сдвигом графика функции f(x)= вдоль оси Ох на величину |b| влево, если b>0 и вправо если b<0.
По графику b= —1 и проходит через точку (3;2). отсюда а =.Значит,
f(-5)= ==
Ответ:0,125
9 задание. На рисунке изображён график функции вида f(x)= cos(bπx+c)+d, где числа ,b, c и d-целые. Найдите .
Решение.
По графику =-3
d= = = -1. |a|= = =2.
По графику =-2, c=0, T=2
T= = , то есть =2, отсюда b=1 f(x)=-2cosπx-1,
f=ff,
f=-2cosπ·-1 = -2cos π-1 = -2cos-1= 2cos1= 0. Ответ:0
20
- ПРОЕКТ. Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2022 года
- Статград. Новое ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
- Образовательный портал «СДАМ ГИА» Математика профильного уровня.
по МАТЕМАТИКЕ. Профильный уровень. ФИПИ
Хорошие результаты ЕГЭ и ОГЭ по математике позволяют выпускникам школы
успешно решить свои жизненные планы.
Нарисуйте пятиугольгик или треугольник
Мастер-класс был актуальным, полезным, интересным
Ничего нового на мастер- классе я для себя не узнал
Спасибо вам за то, что вы есть…























.png)

.png)


























































































