- ЕГЭ по математике профиль
Пробные и тренировочные варианты ЕГЭ 2022 по математике (база) из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (база)
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| Ягубов РФ | |
| Вариант 22 | скачать |
| Вариант 23 | скачать |
| Вариант 24 | скачать |
| Вариант 25 | скачать |
| Вариант 26 | скачать |
| Вариант 27 | скачать |
| Вариант 28 | скачать |
| vk.com/pro_matem | |
| variant 1 | разбор |
| variant 2 | разбор |
| vk.com/matematicalate | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
| variant 4 | скачать |
| variant 5 | скачать |
| variant 6 | скачать |
| variant 7 | скачать / разбор 1-13 |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике | |
| math100.ru (с ответами) по демоверсии 2021 года | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| Разные | |
| Вариант 1-5 | ответы |
Структура варианта КИМ ЕГЭ 2022 математика база
Экзаменационная работа включает в себя 21 задание с кратким ответом базового уровня сложности.
Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Ответом к каждому из заданий 1–21 является целое число, или конечная десятичная дробь, или последовательность цифр.
Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов № 1 в той форме, которая предусмотрена инструкцией по выполнению задания.
Распределение заданий варианта КИМ ЕГЭ по содержанию, видам умений и способам действий
В экзаменационной работе проверяется следующий учебный материал.
1. Математика, 5–6 классы.
2. Алгебра, 7–9 классы.
3. Алгебра и начала анализа, 10–11 классы.
4. Теория вероятностей и статистика, 7–9 классы.
5. Геометрия, 7–11 классы
Связанные страницы:
ЕГЭ математика — База 2022. Открытый банк заданий с ответами.
3 июня 2022
В закладки
Обсудить
Жалоба
Вариант собран по заданиям прошедшего ЕГЭ 3 июня.
Ответы прилагаются.
Экзаменационная работа включает в себя 21 задание.
На выполнение работы отводится 3 часа.
→ rm-ege2022-baza.pdf
→ Профильный уровень.
Каждое из заданий 1–21 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Каждое верно выполненное задание оценивается 1 баллом.
Перевод баллов в оценку
0-6 → 2
7-11 → 3
12-16 → 4
17-21 → 5
Источник: yagubov.ru
- ЕГЭ по математике
Пробные варианты ЕГЭ 2022 по математике базового уровня из различных источников.
Пробные варианты ЕГЭ 2022 по математике (базовый уровень)
| math100.ru (с ответами) по демоверсии 2022 года | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| ЕГЭ 100 баллов (с решениями) | |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| Ягубов РФ | |
| Вариант 22 | скачать |
| Вариант 23 | скачать |
| Вариант 24 | скачать |
| Вариант 25 | скачать |
| Вариант 26 | скачать |
| vk.com/matematicalate | |
| variant 1 | скачать |
| variant 2 | скачать |
| variant 3 | скачать |
| variant 4 | скачать |
| variant 5 | скачать |
| variant 6 | скачать |
Инструкция по выполнению работы
Экзаменационная работа включает в себя 21 задание.
На выполнение работы отводится 3 часа (180 минут).
Ответы к заданиям записываются по приведённым ниже образцам в виде числа или последовательности цифр. Сначала запишите ответы к заданиям в поле ответа в тексте работы, а затем перенесите их в бланк ответов № 1 справа от номера соответствующего задания.
Если ответом является последовательность цифр, как в приведённом ниже примере, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки.
При выполнении заданий можно пользоваться черновиком. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
После завершения работы проверьте, чтобы ответ на каждое задание в бланке ответов № 1 был записан под правильным номером
Связанные страницы:
В статье представлен полный разбор демонстрационной версии ЕГЭ 2022 по математике на базовом уровне. Надеемся, что данный разбор поможет подготовиться к решению базовых заданий, так как в демоварианте есть лишь ответы, но нет решений.
Разумеется, приступая к работе, внимательно читаем инструкцию, а в процессе решения используем справочный материал КИМа.
Задание 1
Сдавая экзамен, нужно решить одно задание на выбор, но мы будем рассматривать все варианты. Чтобы найти значение первого выражения, сначала выполним действия в скобках. 6,7 – 3,2 = 3,5 и умножим 3,5 на 2,4, получим 8,4. Не забываем, что ответ нужно записать, отводя на каждый символ по клеточке, то есть на запятую тоже отводим клеточку. Ответ:
Второй пример содержит обыкновенные дроби, решаем аналогично первому, сначала сложим дроби в скобках, общий знаменатель 66, это наименьшее общее кратное для чисел 33 и 22, получаем
8х2+13х3/66=55/66=5/6 , и теперь заменим деление умножением на взаимно обратное число («перевернем дробь-делитель»), 5/6 х 18/5 =3
Задание 2
Чтобы решить первую задачу, разделим 100 на 14,6, получаем приблизительно 6,8 (дальше делить не нужно, лишь потратим драгоценное время), поскольку можно купить целое число баночек, ответ: 6.
Для решения второй задачи вычислим, сколько денег потрачено на 1,6 кг моркови. Умножим 40 на 1,6, получим 64. Сдача со 100 рублей составит 36 рублей. Ответ: 36
Наконец, третья задача. Разделим 63 на 6, получаем 10,5. Полпачки клея не купишь, значит, придется покупать 11 пачек. Ответ: 11
Не забудьте, нужно решить один вариант, решайте тот, в котором больше всего уверены!
Задание 3
Первый вариант. Рост ребенка может составить 110 см, значит, А 4, толщина листа бумаги 0,2 мм, Б 3, автобус проедет 32 км, соответственно, В 1, и остается Г 2, что вполне отвечает здравому смыслу (9-10 этажный дом, считая по 3 м на этаж).
Ответ 4312
Во втором варианте А 3, Б 1, В 4 и Г 2.
Ответ 3142
Нужно уметь сравнивать различные единицы длины, массы и т.д., так как в реальном варианте может встретиться скорость, время и другие единицы измерения.
Задание 4
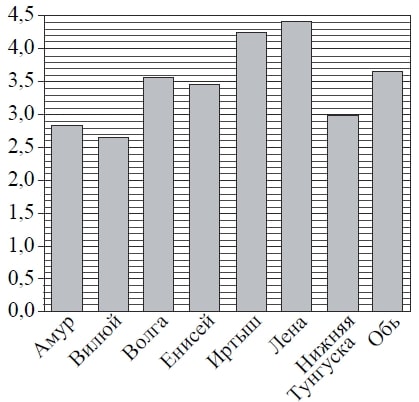
Первый вариант. Находим Амур и смотрим, сколько рек имеют длину больше, чем Амур. Это Волга, Енисей, Иртыш, Лена, Нижняя Тунгуска и Обь. Итого 6 рек. Амур на седьмом месте.
Ответ: 7
Во втором варианте просто выберем самый дешевый смартфон. Он стоит 6559 рублей.
Ответ: 6559
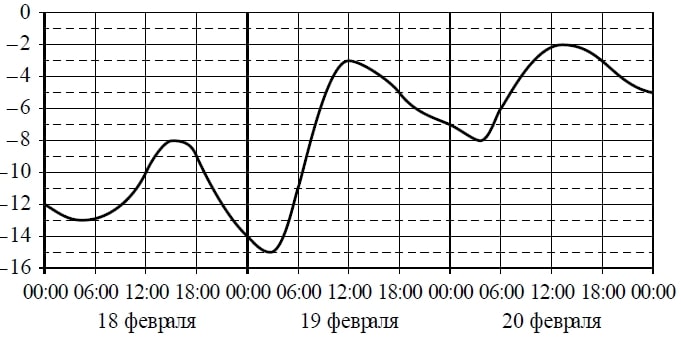
Третий вариант. Находим 19 февраля (выделено синим), находим максимальную температуру (красная точка).
Теперь нужно посмотреть, какой температуре она соответствует. Посередине между минус 4 и минус 2 градусами может быть только минус 3. Ответ: — 3
Задание 5
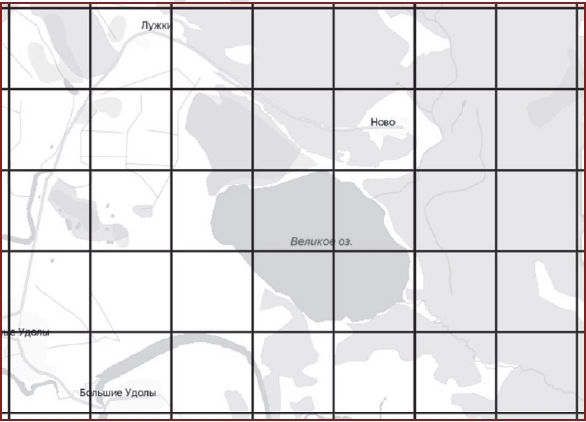
Две клеточки заполнены озером почти полностью, еще две примерно наполовину, и примерно на четверть еще одна. Значит, примерно 3 кв. километра, чуть больше или меньше, неважно.
Ответ: 3
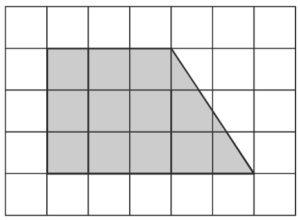
Перед нами трапеция, площадь равна произведению полусуммы оснований на высоту. Основания 5 и 3, высота 3, площадь 5+3/2 х 3=12
(Или просто считаем клеточки и их половинки)
Ответ: 12
Задание 6
Первый вариант. Найдем 13 процентов от 20 000. 20 000 : 100 =200, 200*13 = 2 600. Теперь вычтем налог из начисленного заработка, 20 000 – 2 600 = 17 400.
Ответ: 17400
Второй вариант. Так как 25 составляет одну треть всех выпускников, всего выпускников 25*3 = 75. Из них не сдавали физику 75-25=50.
Ответ: 50
Третий вариант. Составим уравнение. Пусть 5х гектар занимают зерновые, а 3х гектар овощные, тогда 5х+3х=24, 8х=24, х=24:8, получаем х=3. Зерновые занимают 5*3=15, а овощные 3*3=9.
Ответ: 9
Задание 7
Вариант 1. Представим 14 как 2*7. 29 х 79/ 27 х 78 сократим, получим 22*7=4*7=28.
Ответ: 28
Вариант 2. Сначала воспользуемся основным тригонометрическим тождеством sin2a+cos2a=1 0,64+ cos2a=1, cos2a=1-0,64, cos2a=0,36, таким образом cos a= 0,6 или -0,6, чтобы выяснить знак, построим единичную окружность, кстати, в КИМе указан именно такой угол.
Видим, что косинус данного угла отрицателен.
Ответ: -0,6
Вариант 3. Используем формулу сокращенного умножения
справа налево, получим (2 )2 – 1=4*13 – 1=51.
Ответ: 51
Вариант 4.
Смотрим в КИМе формулы, нам поможет подчеркнутая
используя ее справа налево, получаем:
log3(1,8*5)=log39 = 2, так как 32=9, логарифм числа по данному основанию равен показателю степени, в которую нужно возвести основание, чтобы получить данное число.
Ответ: 2
Задание 8
Просто подставляем значения и вычисляем.
Вариант 1. Р=72*5=49*5=245.
Ответ: 245
Вариант 2. g= ³√5*25*27 было бы нерационально и громоздко просто умножить выражение под корнем, поступим так: ³√5*5*5*3*3*3= ³√5³ *³√3³ =5*3=15
Ответ: 15
Задание 9
Вариант 1. 3х-3=34 основания равны, значит, равны и показатели, х-3=4, х=7
Ответ: 7
Вариант 2. 26=64, значит, log2(x-3)=log264, x-3=64, x=67
Ответ: 67
Вариант 3. Решаем квадратное уравнение, D=1-4*(-6)=25, х1,2 = 1+5/2, х1=3, х2= — 2, меньший -2
Ответ: -2
Задание 10
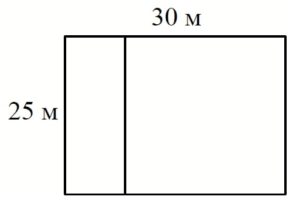
Вариант 1. Забор будет иметь две стороны по 30, две по 25 снаружи участка, и внутри разделяющий забор составит, как видно из чертежа, 25. Итого 60+50+25=135 метров.
Ответ: 135
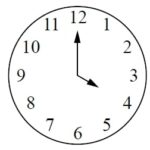
Вариант 2. Окружность составляет 360 градусов, на одно деление циферблата приходится 360:12=30 градусов. На 4 деления 30*4=120 градусов.
Ответ: 120
Задание 11
Несложные задании на вероятность.
Вариант 1. Всего 35 участников, из них россиян 7. Делим 7 на 35, получаем 0,2.
Ответ: 0,2
Вариант 2. Из условия следует, что в среднем исправны 97 лампочек из 100. Далее делим число исправных в среднем лампочек на число всех лампочек, 97:100=0,97.
Ответ: 0,97
Заметим, что если бы спрашивали вероятность того, что лампочка будет неисправной, нужно было бы разделить 3 на 100.
Задание 12
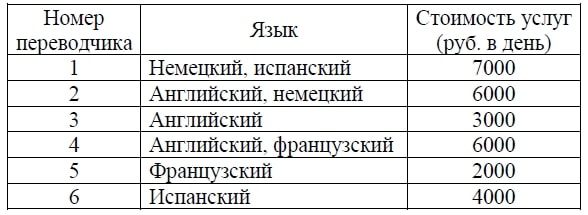
У данного варианта множество ответов, найдем один. Например, попробуем набрать нужные языки, а потом проверим стоимость. Нужный набор языков составят номера 2, 5 и 6. Услуги составят 6000+2000+4000=12000, что отвечает условию.
Ответ: 256
Другие ответы попробуйте подобрать сами.
Вариант 2
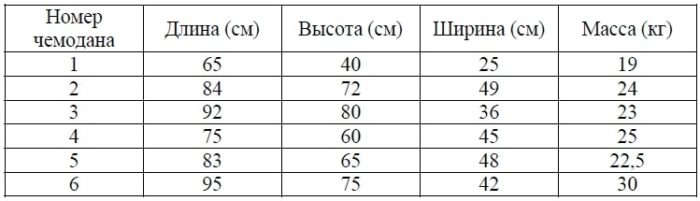
Проверим каждый чемодан, но сначала отбросим слишком тяжелые, это номера 2, 4, 6. Сумма трех измерений первого чемодана 65+40+25=130, подходит. Третий чемодан 92+80+36=208 не подходит, пятый 83+65+48=196 подходит.
Ответ: 15 или 51
Вариант 3
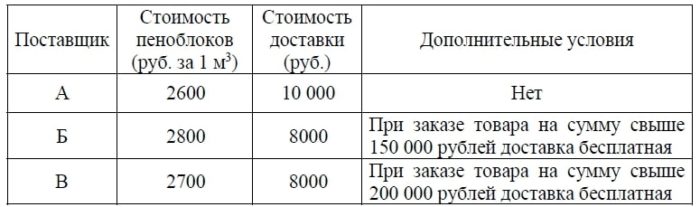
Считаем услуги каждого поставщика. Поставщик А: 70*2600=182 000 плюс за доставку 10000, получаем 192 000.
Поставщик Б: 70*2800=196 000, доставка будет бесплатной, но это все равно дороже, чем у А.
Поставщик В: 70*2700=189 000 плюс доставка 8000, итого 197 000. Самый дешевый поставщик обойдется в 192 000.
Ответ: 192 000
Задание 13
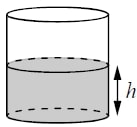
Вариант 1. Объем цилиндра равен произведению площади основания (круга) на высоту. Объем воды при переливании не изменится, а так как площадь круга равна числу пи, умноженному на радиус в квадрате, уровень уменьшится во столько же раз, во сколько площадь второго основания больше первого. А она больше в 42=16 раз. 80:16=5.
Ответ: 5
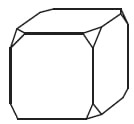
Вариант 2. Грани — это участки плоскостей. У кубика было 6 граней и 8 вершин, вместо каждой теперь грань, значит, 6+8 =14.
Ответ: 14
Задание 14
Для базового уровня задание довольно сложное, воспользуемся справочным материалом КИМа.
Если функция в точке возрастает, тангенс положительный, если убывает — отрицательный. Чем график круче, тем тангенс больше (по модулю). Тогда А соответствует значение под номером 2, В – 1, С – 4 и Д – 3.
Ответ: 2143
Вариант 2 гораздо легче. Разметим график для наглядности.
А: Участок от 0 до 1 минуты — температура не более 30, верно, соответствует 4.
Б: от 1 до 3 минут — соответствует 1, 2 и 3 явно не подходят, температура не падала и не была от 40 до 80.
В: от 3 до 6 минут — вот здесь рост от 40 до 80, значит, выбираем 3.
С: от 8 до 10 минут температура понижается, значит, 2.
Ответ: 4132
Максимум — на графике «холмик», минимум — «впадина», возрастает — при движении слева направо график вверх, убывает — вниз. Проще начать с номеров, подобрав к ним графики. 1 соответствует графику Б:
2 — графику Г
3 — графику В, а 4 графику А (на В при движении слева направо взбираемся в гору, а на А спускаемся)
Ответ: 4132
Задание 15
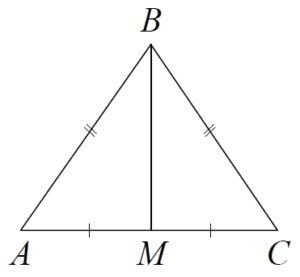
Почему-то номер 15 представлен всего одним вариантом. Ну, тем лучше. Так как треугольник равнобедренный (АВ=ВС), его медиана одновременно будет и высотой, то есть ВМ перпендикулярна основанию АС. Медиана делит сторону пополам, тогда АМ=10:2=5. Получился прямоугольный треугольник, по теореме Пифагора АМ2+ВМ2=АВ2, 25+ВМ2=169, ВМ2=144, ВМ=12.
Ответ: 12
Задание 16
Зато здесь целых три варианта.
Вариант 1.
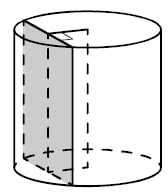
Сечение — прямоугольник, нужно найти его стороны. Одна из сторон равна высоте цилиндра, то есть образующей, 18, найдем вторую сторону.
Посмотрим на цилиндр сверху.
Ищем АВ, радиус АО=13, ОС=12, угол АСО прямой. Тогда АС находим по теореме Пифагора как корень квадратный из АО2-СО2, получаем корень из 169-144=25, корень из 25 будет равен 5, АВ = 2*5=10, тогда искомая площадь 18*10=180.
Ответ: 180
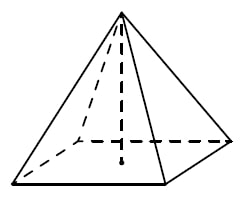
Вариант 2. Объем пирамиды равен одной трети от произведения площади основания на высоту пирамиды. Так как пирамида правильная, в основании квадрат со стороной 4, площадь 16. Найдем высоту.
Высота ОС2=АС2-АО2, АС2=17, ищем АО, АО равен половине АД, АД находим по теореме Пифагора как корень из 42+42=корень из 32, АО равен половине корня из 32. Корень не берется, но это не страшно.
АД= √32, АО=√32/2 , АО2 =32/4 =8
Находим ОС2=(√17 )2 –8=17-8=9, ОС=3,объем (16*3):3=16.
Ответ: 16
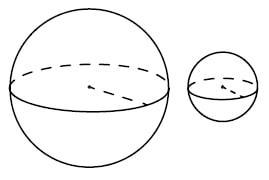
Вариант 3. Площадь поверхности шара
пропорциональна квадрату радиуса, поэтому если радиус большего шара в три раза больше радиуса маленького (9:3=3), то площадь будет больше в 32=9 раз.
Ответ: 9
Задание 17
Вариант 1. Сначала разберемся с числами. Логарифм десяти по основанию 2 равен степени, в которую нужно возвести 2, чтобы получить 10. Точно его не посчитать, но 23=8, значит, логарифм немножко больше 3. Подходит точка С, итак, С1.
Дробь 7/3 примерно равна 2,3. Подходит точка В, то есть В2.
Корень из 26 чуть больше 5, точка Д. Д3
И точка А соответствует числу 4. Проверим, будет 5/3, это примерно 1,6.
Ответ: 4213
Вариант 2. Проще всего не пытаться подбирать интервалы под неравенства, а просто аккуратно решить каждое неравенство.
А) 2х>=4
2x>=22
x>=2 соответствует интервалу 4. А4
Б)0,5х >=4
(1/2)х>=22
2— х >= 22
— х >=2
х <= -2 соответствует интервалу 3. Б3
В)0,5х<=4
решение «наоборот» чем в варианте Б, то есть х >= -2, интервал 2. В2
Ну и Г1.
Ответ 4321
Задание 18
Придется порассуждать логически.
Вариант 1.
Утверждение 1 — нет, не обязательно.
Утверждение 2 — да, верно, ведь всего получается 23 участника кружков при числе учащихся 20 человек.
Утверждение 3 — нет, неверно,
Утверждение 4 — да, верно, ведь на математику ходят всего 10 человек.
Ответ: 24
Вариант 2.
1 — верно, все деревья разные по высоте.
2 — нет, ясень ниже осины.
3 — нет, ясень выше рябины на 1 метр, дерево ниже ясеня может быть выше рябины.
4 — да, рябина ниже ясеня, все, что ниже рябины, автоматически ниже ясеня.
Ответ: 14
Задание 19
Задание придется решать подбором, чтобы не тратить драгоценное время экзамена, лучше оставьте его на конец работы.
Вариант 1.
Сначала выпишем трехзначные числа, сумма цифр которых равна 20, исключая варианты, где две цифры делятся на 3, а третья нет, так как сумма квадратов таких цифр не будет кратна 3. Затем проверим оставшиеся варианты. Получаем, например, числа776, 578, 884, 875, 974. Проверим каждое число на соответствие условию задачи. Так, проверим число 776. Сумма квадратов цифр данного числа составит 49+49+36=134 не подходит, число 875, 64+49+25=138, 138:3=46, 138 на 9 нацело не делится. Подходит.
Ответ: 875 (или другое число, их будет несколько, достаточно найти одно).
Вариант 2.
Для того, чтобы число делилось на 10, оно должно заканчиваться на 0. А чтобы оно не делилось на 20, надо, чтобы оно, разделенное на 10, было нечетным. Вначале можно подобрать карточки так, чтобы в конце числа был 0. Например, первое слагаемое 6, второе заканчивается на 7, третье тоже. Далее подберем числа так, чтобы результат, у которого убрали последний ноль, был нечетным. Получаем 6+27+357=390. На 10 делится, на 20 нет.
Ответ: 390 (найдите еще два ответа)
Вариант 3.
Чтобы число делилось на 12, оно должно делиться на 3 и на 4. Далее пригодится признак делимости на 4, согласно которому число делится на 4, если оно заканчивается двумя цифрами, образующими число, делящееся на 4. Так что отбросим последние цифры 1 и 3, остается 751576. Чтобы число делилось на 3, нужно, чтобы сумма его цифр делилась на 3. Проверим число, и если условие не выполнится, будем убирать мешающие цифры. В нашем случае придется удалить цифру 1.
Ответ: 75576
Задание 20
Вариант 1
Первый автомобиль проехал 350 км, следовательно, второй 120 км, так как все расстояние составляет 470 км. Скорость второго известна, 60 км/ч, а поскольку проехал он 120 км, время его движения составило 2 часа: 120 : 60=2. Значит, первый автомобиль находился в пути 5 часов – второй выехал через 3 часа после первого, и еще через 2 часа (как мы посчитали) они встретились. Итак, первый автомобиль за 5 часов проехал 350 км, скорость равна 350:5=70.
Ответ: 70
Вариант 2.
Пусть акции подорожали на Х процентов (процент – одна сотая) и до подорожания стоили А рублей. Значит, подорожавшие акции стоят А+Х*А, а подешевевшие стоят соответственно (А+Х*А) – Х(А+Х*А). Упростим второе выражение: А+ХА-ХА-Х2А=А-Х2А. Используем условие, что подешевевшие акции стали на 4 процента дешевле. Значит, они стоят 0,96 от первоначальной стоимости (1-0,04=0,96)
А-Х2А=0,96А сократим на А
1-Х2=0,96 получили квадратное уравнение
Х2=0,04, Х=0,2 (отрицательный корень отбросим, акции подешевели-подорожали на положительное число процентов)
Итак, 0,2 или 0,20 соответствует 20%.
Ответ: 20
Решение и ответы заданий демонстрационного варианта ЕГЭ 2022 по математике (базовый уровень). Демоверсия ФИПИ для 11 класса.
Задание 1.
Найдите значение выражения (6,7 − 3,2)·2,4.
ИЛИ
Найдите значение выражения
Задание 2.
Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?
ИЛИ
Килограмм моркови стоит 40 рублей. Олег купил 1 кг 600 г моркови. Сколько рублей сдачи он должен получить со 100 рублей?
ИЛИ
Для ремонта требуется 63 рулона обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 6 рулонов?
Задание 3.
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) рост ребёнка | 1) 32 км |
| Б) толщина листа бумаги | 2) 30 м |
| В) протяжённость автобусного маршрута | 3) 0,2 мм |
| Г) высота жилого дома | 4) 110 см |
ИЛИ
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ЗНАЧЕНИЯ |
| А) масса взрослого человека | 1) 8 т |
| Б) масса грузового автомобиля | 2) 5 г |
| В) масса книги | 3) 65 кг |
| Г) масса пуговицы | 4) 300 г |
Задание 4.
На диаграмме приведены данные о длине восьми крупнейших рек России (в тысячах километров). Первое место по длине занимает река Лена.
На каком месте по длине находится река Амур?
ИЛИ
В таблице представлены данные о стоимости некоторой модели смартфона в различных магазинах.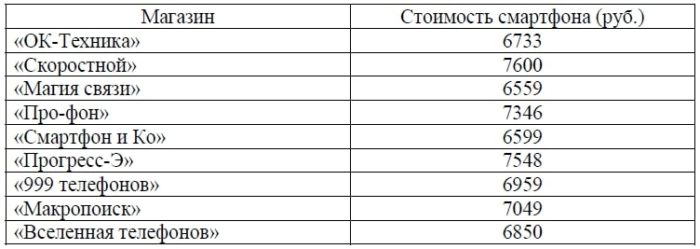
ИЛИ
На графике показано изменение температуры воздуха на протяжении трёх суток. На горизонтальной оси отмечены число, месяц, время суток в часах; на вертикальной оси — значение температуры в градусах Цельсия.
Определите по графику наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.
Задание 5.
На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображённого на плане. Ответ округлите до целого числа.
ИЛИ
План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.
Задание 6.
Ивану Кузьмичу начислена заработная плата 20 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13%. Сколько рублей он получит после уплаты подоходного налога?
ИЛИ
ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?
ИЛИ
Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 24 гектара и распределена между зерновыми и овощными культурами в отношении 5:3 соответственно. Сколько гектаров занимают овощные культуры?
Задание 7.
Найдите значение выражения
ИЛИ
Найдите cosα, если sinα = 0,8 и 90° < α <180°.
ИЛИ
Найдите значение выражения
ИЛИ
Найдите значение выражения log31,8 + log35.
Задание 8.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2·R, где I – сила тока (в амперах), R – сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если R = 5 Ом и I = 7 А.
ИЛИ
Среднее геометрическое трёх чисел: a, b и c – вычисляется по формуле . Вычислите среднее геометрическое чисел 5, 25, 27.
Задание 9.
Найдите корень уравнения 3x−3= 81.
ИЛИ
Найдите корень уравнения log2(x − 3) = 6.
ИЛИ
Решите уравнение x2− x − 6 = 0.
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Задание 10.
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
ИЛИ
Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
Задание 11.
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.
ИЛИ
Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной?
Задание 12.
Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.
Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день.
В ответе укажите какой-нибудь один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.
ИЛИ
В таблице приведены данные о шести чемоданах.
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера всех выбранных чемоданов без пробелов, запятых и других дополнительных символов.
ИЛИ
Строительная фирма планирует купить 70 м3 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.
Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
Задание 13.
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
ИЛИ
От деревянного кубика отпилили все его вершины (см. рисунок). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Задание 14.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A | 1) –4 |
| B | 2) 3 |
| C | 3) |
| D | 4) –0,5 |
В таблице под каждой буквой укажите соответствующий номер.
ИЛИ
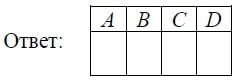
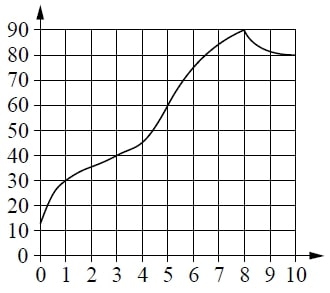
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси — температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 0–1 мин. | 1) Самый медленный рост температуры. |
| Б) 1–3 мин. | 2) Температура падала. |
| В) 3–6 мин. | 3) Температура находилась в пределах от 40°C до 80°C. |
| Г) 8–10 мин. | 4) Температура не превышала 30°C. |
В таблице под каждой буквой укажите соответствующий номер.
ИЛИ
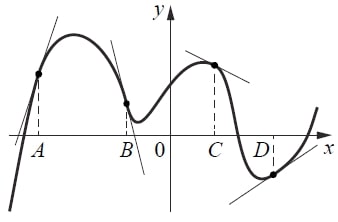
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1].
ХАРАКТЕРИСТИКИ
1) Функция имеет точку максимума на отрезке [−1; 1].
2) Функция имеет точку минимума на отрезке [−1; 1].
3) Функция возрастает на отрезке [−1; 1].
4) Функция убывает на отрезке [−1; 1].
В таблице под каждой буквой укажите соответствующий номер.
Задание 15.
В треугольнике ABC известно, что AB = BC = 13, AC =10. Найдите длину медианы BM.
Задание 16.
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
ИЛИ
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
ИЛИ
Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?
Задание 17.
На координатной прямой отмечены точки A, B , C и D.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
В таблице под каждой буквой укажите соответствующий номер.
ИЛИ
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
В таблице под каждой буквой укажите соответствующий номер.
Задание 18.
В классе учится 20 человек, из них 13 человек посещают кружок по истории, а 10 — кружок по математике. Выберите утверждения, которые верны при указанных условиях.
1) Каждый ученик этого класса посещает оба кружка.
2) Найдётся хотя бы двое из этого класса, кто посещает оба кружка.
3) Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике.
4) Не найдётся 11 человек из этого класса, которые посещают оба кружка.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ИЛИ
Во дворе школы растут всего три дерева: ясень, рябина и осина. Ясень выше рябины на 1 метр, но ниже осины на 2 метра. Выберите все утверждения, которые верны при указанных условиях.
1) Среди указанных деревьев не найдётся двух одной высоты.
2) Ясень, растущий во дворе школы, выше осины, растущей там же.
3) Любое дерево, помимо указанных, которое ниже ясеня, растущего во дворе школы, также ниже рябины, растущей там же.
4) Любое дерево, помимо указанных, которое ниже рябины, растущей во дворе школы, также ниже ясеня, растущего там же.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Задание 19.
Найдите трёхзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
ИЛИ
На шести карточках написаны цифры 2, 3, 5, 6, 7, 7 (по одной цифре на каждой карточке). В выражении
вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20. В ответе укажите какую-нибудь одну такую сумму.
ИЛИ
Вычеркните в числе 75157613 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно получившееся число.
Задание 20.
Расстояние между городами А и В равно 470 км. Из города А в город В выехал первый автомобиль, а через 3 часа после этого навстречу ему из города В выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города А. Ответ дайте в км/ч.
ИЛИ
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Задание 21.
Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в 3 раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?
ИЛИ
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
ИЛИ
В доме всего 14 квартир с номерами от 1 до 14. В каждой квартире живёт не менее одного и не более четырёх человек. В квартирах с 1-й по 12-ю включительно живёт суммарно 14 человек, а в квартирах с 11-й по 14-ю включительно живёт суммарно 12 человек. Сколько всего человек живут в этом доме?
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Незнайка → ЕГЭ → Математика → Базовая
Рейтинг: 475
Рейтинг: 471
Рейтинг: 466
Рейтинг: 434
Рейтинг: 422
Математика Базовый уровень
Об экзамене
Базовая математика – для слабаков, скажут одни, другие – для тупых гуманитариев, а третьи (те, что не снобы) просто используют ее в качестве разминки перед математикой профильной. Пусть гуманитарии не обижаются и не принимают все так близко к сердцу, самоирония должна быть. Просто, чтобы сдать базу, надо лишь ходить на уроки по математике и хотя бы немного слушать учителя. Никаких проблем не возникнет.
Структура
Экзаменационная работа состоит из одной части, включающей 20 заданий с кратким ответом базового уровня сложности. Ответом к каждому из заданий 1–20 является целое число или конечная десятичная дробь, или последовательность цифр.
На выполнение экзаменационной работы отводится 3 часа (180 минут).
Пояснения к оцениванию заданий
Правильное решение каждого из заданий 1–20 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби, или последовательности цифр. Максимальный первичный балл за всю работу – 20.
Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу.
Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Ознакомьтесь с подробной видеоинструкцией по использованию модуля.








































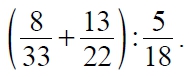
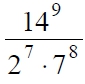
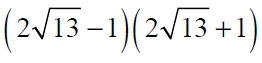
![Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1]. Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1; 1].](https://ege314.ru/wp-content/uploads/2020/08/Ustanovite-sootvetstvie-mezhdu-grafikami-funktsij-i-harakteristikami-etih-funktsij-na-otrezke-1-1..jpg)