Автономное учреждение профессионального
образования
Ханты-Мансийского автономного округа-Югры
«Сургутский политехнический колледж»
МЕТОДИЧЕСКОЕ
ПОСОБИЕ:
«Сборник
примерных экзаменационных работ для подготовки к итоговой аттестации по математике»
для студентов первого курса очной формы
обучения
обучающихся по программе подготовки специалистов
среднего звена
Сургут, 2021
Математика.
Методическое пособие «Сборник примерных экзаменационных работ для подготовки к
итоговой аттестации по математике»
© Сургутский
политехнический колледж, -2021 год.
Составители:
С.А. Гладышева,
преподаватель математики
И.А. Пелых, преподаватель
математики
Данный сборник составлен в соответствии с рабочей
программой по дисциплине «Математика» и содержит десять вариантов примерных
экзаменационных работ. Задания составлены в соответствии с рабочей программой, предназначенной для реализации образовательной программы среднего
общего образования в пределах освоения основной профессиональной
образовательной программы СПО на базе основного общего образования. Учебное пособие предназначено
для студентов колледжа первого курса и преподавателей.
Одобрено на
заседании методического объединения «Математика, информатика, физика».
Протокол № 8 от
12.05.2021 г.
Рекомендовано
к печати Методическим советом «Сургутский политехнический колледж».
Протокол
№ от 2021 г.
Пояснительная записка.
Данный сборник
предназначен для подготовки к итоговой аттестации по дисциплине «Математика»
студентов первого курса групп среднего и начального профессионального
образования.
Данное
методическое пособие может быть использовано преподавателями для подготовки
учащихся к экзамену по математике, а также студентами — для самоподготовки и
самоконтроля. Сборник состоит из 10 вариантов работ,
включающих следующие разделы дисциплины:
·
Взаимное расположение прямых и плоскостей в
пространстве;
·
Геометрические тела и поверхности. Объемы и площади
поверхностей геометрических тел;
·
Показательная, логарифмическая, степенная функции;
·
Основы тригонометрии;
·
Производная и ее приложение;
·
Интеграл и его приложения;
·
Практические задачи.
Экзаменационная
работа состоит из одиннадцати заданий. Эти задания разбиваются на 2 части. Первая
часть работы направлена на то, что бы проверить обязательный уровень
подготовки студентов, и включает в себя семь заданий по алгебре и началам
математического анализа и одно геометрическое задание, которые в совокупности
позволяют охватить проверкой значительный объём учебного материала. Для
решения заданий первой части достаточно уметь использовать основные
определения, владеть минимальным набором формул и алгоритмов. Задания по
геометрии требуют, помимо знания формул и умения ими пользоваться,
определенного уровня стереометрических представлений, умения работать с
изображениями пространственных конфигураций. В то же время уровень доказательности
при выполнении заданий предполагается минимальным.
Вторая часть работы содержит три более
сложных задания и нацелена на проверку усвоения материала курса на более
высоком уровне. Данная часть состоит из одного геометрического задания и двух
заданий по алгебре и началам анализа. Содержание заданий по геометрии соответствует
целям изучения геометрии в курсе «Математика», и для их решения достаточно пройденного
в курсе геометрического материала. От студентов, однако, не требуется владения
навыками сложных вычислений и преобразований, специальными приемами решения
уравнений и неравенств, хотя часть заданий предполагает наличие определенных
знаний и умений, приобретенных не только на первом курсе, но и в основной школе
(подстановка, формулы сокращенного умножения, уравнение прямой и т. п.).
Для получения отметки «3» (удовлетворительно)
студент должен набрать 12-15 баллов. Отметка «4» (хорошо) выставляется при
17-21 баллах. Отметка «5» (отлично) ставится за 22-24 балла. Каждый правильно
выполненный пример (задание) оценивается 1 баллом.
2. (4 балла) Решите
уравнения:
3. (3 балла)
Решите неравенство:
; 2)
; 3)
4. (4 балла)
Дана правильная четырехугольная пирамида
1.

2.
Назовите апофему;
3.
Назовите высоту пирамиды;
4.
Найдите площадь боковой поверхности пирамиды, если
АВ = 5см., SЕ = 10 см.
5. (2 балла) Найдите
производную функции:
1)
2)
6.
(2 балла) Найдите все первообразные функции:
1)
2)
7. (1 балл) В
магазине канцтоваров проходит распродажа. Ирина купила блокнот за 170 рублей с
учетом скидки, до распродажи он стоил 250 рублей. Определите процент скидки.
Часть 2
8.
В
правильной четырехугольной пирамиде апофема образует с плоскостью основания
угол 600. Высота пирамиды равна 6 см. Найдите площадь поверхности
пирамиды.
9.
Радиус
основания конуса равен 20 см; расстояние от центра основания до образующей
равно 12 см. Найдите площадь боковой поверхности конуса.
10. Решите
уравнение:
11.
Найдите
первообразную функции ,
график которой
проходит через начало координат.
2. (4 балла)
Решите уравнения:
3. (3 балла)
Решите неравенство:
; 2)
; 3)
;
4.

1.
Назовите осевое сечение конуса;
2.
Назовите образующую;
3.
Назовите высоту конуса;
4.
Найдите площадь боковой поверхности конуса, если диаметр
12 см., образующая 10 см.
5. (2 балла) Найдите
производную функции:
1)
2)
6.
(2 балла) Найдите все первообразные функции:
1)
2)
7. (1 балл) По тарифному плану «Просто как день» компания сотовой связи
каждый вечер снимает со счёта абонента 16 рублей. Если на счету осталось
меньше 16 рублей, то на следующее утро номер блокируют до пополнения счёта.
Сегодня утром у Лизы на счету было 700 рублей. Сколько дней (включая
сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?
Часть 2
8.
В
правильной треугольной пирамиде боковое ребро равно 10 см, а сторона основания
12 см. Найдите площадь полной поверхности пирамиды.
9.
Радиус
цилиндра равен 8 см. Через середину оси цилиндра проведена прямая, пересекающая
плоскость, содержащую нижнее основание цилиндра, на расстоянии 12 см от центра
нижнего основания. Эта прямая пересекает образующую цилиндра на расстоянии 2 см
от плоскости нижнего основания. Найдите высоту цилиндра.
10.
Решите
систему уравнений
11. Найдите
площадь фигуры, ограниченной осью абсцисс и графиком функции .
2. (4 балла)
Решите уравнения:
3. (3 балла)
Решите неравенство:
; 2)
; 3)
4.
(4 балла) Дан прямой круговой конус
1.

2.
Назовите образующую;
3.
Назовите радиус конуса;
4.
Найдите объём конуса, если радиус равен
4 см., высота 6 см.
5.
(2 балла) Найдите производную функции:
1)
2)
6.
(2 балла) Найдите все первообразные функции:
7.
(1 балл) На одну порцию рисовой каши требуется 40 грамм риса и 0,12 литра
молока. Какое наибольшее количество порций каши может приготовить столовая,
если в ее распоряжении есть 900 грамм риса и 3 литра молока?
Часть 2
8.
Основание
пирамиды – прямоугольный треугольник с катетами 6 см и 8 см. высота пирамиды
проходит через середину гипотенузы треугольника и равна гипотенузе. Найдите
боковые ребра пирамиды.
9. Высота
конуса равна 20 см, расстояние от центра основания до образующей равно 12 см.
Найдите объем конуса.
10.
Решите уравнение
11.
Найдите площадь фигуры, ограниченной
графиком функции
и осью абсцисс.
2. (4 балла)
Решите уравнения:
3. (3 балла)
Решите неравенство:
; 2)
; 3)
;
4.

1.
Назовите ось цилиндра;
2.
Назовите образующие;
3.
Назовите радиус цилиндра;
4.
Найдите объём цилиндра, если радиус равен
2 см., высота 5 см.
5. (2 балла)
Найдите производную функции:
1)
2)
6.
(2 балла) Найдите все первообразные функции:
7. (1
балл) Стоимость проезда в маршрутном такси составляет
20 руб. Какое наибольшее число поездок можно будет совершить в этом маршрутном
такси на 150 руб., если цена проезда снизится на 10%?
Часть 2
8. В
основании прямой призмы лежит ромб со стороной 10 см. Сторона основания удалена
от двух параллельных ей сторон противолежащей боковой грани соответственно на 5
см и 13 см. Найдите объем призмы.
9. Высота
цилиндра равна 12 см. Через середину образующей цилиндра проведена прямая,
пересекающая ось цилиндра на расстоянии 4 см от нижнего основания. Эта прямая
пересекает плоскость, содержащую нижнее основание цилиндра, на расстоянии 18
см от центра нижнего основания. Найдите радиус основания цилиндра.
10. Найдите
наименьшее и наибольшее значение функции на
отрезке [1;е].
11. Решите неравенство
.
2. (4 балла)
Решите уравнения:
3. (3 балла)
Решите неравенство:
; 2)
; 3)
;
4.
(4 балла) Дан прямой круговой цилиндр
1.
Назовите осевое сечение цилиндра;
2.
Назовите образующие;
3.
Назовите диаметр цилиндра;
4.
Найдите площадь боковой поверхности цилиндра, если
диаметр равен 2 см., высота 4 см.
5. (2 балла)
Найдите производную функции:
3)
4)
6.
(2 балла) Найдите все первообразные функции:
7.
Шоколадка
стоит 35 рублей. В воскресенье в супермаркете действует специальное
предложение: заплатив за две шоколадки, покупатель получает три (одну в
подарок). Какое наибольшее количество шоколадок можно получить, потратив не
более 200 рублей в воскресенье?
Часть 2
8.
Диагональ основания прямоугольного
параллелепипеда равна 10 см, а диагонали боковых граней см и
см. Найдите объем
параллелепипеда.
9.
Радиус цилиндра равен 8 см. Через середину оси
цилиндра проведена прямая, пересекающая плоскость, содержащую нижнее основание
цилиндра, на расстоянии 12 см от центра нижнего основания. Эта прямая
пересекает образующую цилиндра на расстоянии 2 см от плоскости нижнего
основания. Найдите высоту цилиндра.
10. Укажите
промежутки возрастания и убывания функции .
11.
Решите неравенство .
2.
(3 балла) Решите уравнения:
3.
(3 балла) Решите неравенство:
; 2)
; 3)
(3x+1)
.
4.
(4 балла) Дан куб АВСD
|
|
Укажите 1. 2. 3. 4. |
5.
(2 балла) Найдите производную функции:
1)
2)
6.
(2 балла) Найдите все первообразные
функции:
1)
f(x)= 4—
;
2)
f(x)=—
7.(1
балл) Железнодорожный
билет для взрослого стоит 720 рублей. Стоимость билета для школьника составляет
50% от стоимости билета для взрослого. Группа состоит из 15 школьников и 2
взрослых. Сколько рублей стоят билеты на всю группу?
Часть 2
8. Диагональ прямоугольного параллелепипеда
равна 18 см и составляет угол в 30 с плоскостью боковой
грани и угол в 45 с
боковым ребром. Найдите объём параллелепипеда.
9. Образующая
конуса наклонена к плоскости основания под углом 60°. В основание конуса
вписан треугольник, у которого одна сторона равна 8 см, а противолежащий угол
равен 30°. Определи площадь полной поверхности конуса.
10. Решите
уравнение:
11. Вычислите
интеграл:
2.
(4 балла) Решите уравнения:
3.
(3 балла) Решите неравенство:
; 2)
; 3)
(3x+1)
4. (4
балла) Дана правильная шестиугольная призма
|
|
Выясните 1. 2. 3. 4. |
5. (2 балла)
Найдите производную функции:
1)
6.
(2 балла) Найдите все первообразные функции:
1)
f(x)= 3—
;
2)
2) f(x)=
7. (1 балл) Футболка стоила 800 рублей. После снижения цены она стала
стоить 680 рублей. На сколько процентов была снижена цена на футболку?
Часть 2
8. Диагональ
осевого сечения цилиндра равна 48 см., угол между этой диагональю и образующей
равен 60. Вычислите объём цилиндра.
9. Сторона основания правильной треугольной
призмы равна 14см, высота призмы равна см. Вычисли объём и площадь поверхности призмы.
10. Решите уравнение: x-5
.
11. Найдите наименьшее значение функции у
= на отрезке
2. (4
балла) Решите уравнения:1
3. (3
балла) Решите неравенство:
; 2)
; 3)
(4x-1)
4.
(4 балла) Дана правильная треугольная призма
|
|
Выясните 1. 2. 3. 4. |
5.(2
балла) Найдите производную функции:
1)
6.(2
балла) Найдите все первообразные функции:
1)f(x)=
5—
;
2)
f(x)=
7. (1 балл) Налог на доходы составляет 13% от
заработной платы. После удержания налога на доходы Мария Константиновна
получила 9570 рублей. Сколько рублей составляет заработная плата Марии
Константиновны?
Часть 2
8. Основанием прямой призмы
является ромб, диагонали которого равны 2см и 8 см.
Большее диагональное сечение призмы равно 24. Вычисли объём призмы. (24
9. Образующая конуса наклонена к
плоскости основания под углом 60°. В основание конуса вписан треугольник, у
которого одна сторона равна 22 см, а противолежащий угол равен 30°. Определи
площадь полной поверхности конуса.
10. Решите уравнение: −8⋅
+12⋅
=0.
11. Исследуйте функцию и постройте ее
график: y = —
2. (4 балла) Решите уравнения:
3. (3 балла) Решите неравенство:
; 2)
; 3)
(3-2x)
4.(4 балла) Дан параллелепипед АВСD
|
|
Выясните взаимное расположение: 1. АВ и 2. 3. 4. |
5.(2 балла) Найдите производную
функции:
1)
2)
6.(2 балла)
Найдите все первообразные функции:
3)
f(x)=
7+
;
4)
2)
f(x)=
7. (1 балл) Тетрадь
стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при
покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?
Часть 2
8.
Высота правильной четырехугольной пирамиды равна 20 см, а боковое ребро —
16 см. Найдите площадь боковой поверхности пирамиды.
9.
Осевое сечение цилиндра квадрат, диагональ которого
равна 8см. Найдите объем этого цилиндра.
10. Решите уравнение:
11. Исследуйте
функцию и постройте ее график: y = —
2. (4
балла) Решите уравнения:
3.
(3 балла) Решите неравенство:
; 2)
; 3)
(2x-1)
4.
(4 балла) Дана правильная четырехугольная пирамида:
|
|
Укажите: 1.Основание 2.Апофему 3.Высоту 4.Вычислите |
5.(2
балла) Найдите производную функции:
1)
6.(2
балла) Найдите все первообразные функции:
1)f(x)=
7+
;
2) f(x)=
7. (1 балл) Среди 40000 жителей города 60% не интересуются футболом и
никогда не смотрят футбольные матчи по телевизору. Среди жителей,
интересующихся футболом, 80% смотрели по телевизору финал Лиги чемпионов.
Сколько жителей города смотрело этот матч по телевизору?
Часть 2
8.
Радиус основания конуса равен 20 см; расстояние
от центра основания до образующей равно 12 см. Найдите площадь боковой
поверхности конуса.
9.
Боковое
ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью
основания угол в 60°. Найдите объем пирамиды.
10.
Решите уравнение: —
11. Решите систему уравнений:
1)
;
;
, Ответ:
2)
;
;
=
Ответ:
4)
Ответ:
3.(3 балла) Решение неравенств:
1) ;
;
;
3x
3x
4x
х
Ответ:x
;
;
;
х=6
или х= — 1
Ответ:
3)
ОДЗ:
,
∞
Ответ:
3. (4 балла)
Дана правильная четырехугольная пирамида
1. 
2. Апофема-SE;
3. Высота пирамиды-SO;
4. Найдите площадь боковой поверхности пирамиды, если АВ = 5см., SЕ = 10 см.
Решение: ,
Ответ:
4. (2 балла)
Решение по нахождению производной функции:
1)
5. (2
балла) Решение по нахождению первообразных функции:
6. (1 балл) В
магазине канцтоваров проходит распродажа. Ирина купила блокнот за 170 рублей с
учетом скидки, до распродажи он стоил 270 рублей. Определите процент скидки.
Решение:
250р – 100% 1) х =
170р – х% 2) 100 — = 32(%) – составила скидка.
Ответ: 32%.
Часть 2
7.
В
правильной четырехугольной пирамиде апофема образует с плоскостью основания
угол 600. Высота пирамиды равна 6 см. Найдите площадь поверхности
пирамиды.

правильная пирамида FABCD
ABCD — квадрат
FM -апофема
FO – высота
пирамиды, 6 см
∟FMO = 600
Найти:
Решение:
1)
,
2)
Рассмотрим ∆ FOM.
Прямоугольный, так как FO – высота
пирамиды, ∟FOM = 900 .
По
условию угол между апофемой FM и основанием пирамиды равен 600
(∟FMO = 600)
=>
=>
=>
=>
=>
=>
=>
3)
По условию ABCD
– квадрат, точки О и М середины отрезков АС и CD
, ОМ — средняя линия => АD
= 2∙ОМ , АD =
4)
5)
6)
7)
Ответ:
8.
Радиус
основания конуса равен 20 см; расстояние от центра основания до образующей
равно 12 см. Найдите площадь боковой поверхности конуса.

круговой конус FABCD
ОC – радиус,
20 см
АО
– высота, ось конуса
АС
– образующая
FO –
расстояние от центра конуса до образующей, 12 см
∟FMO = 600
Найти:
Решение:
2)
Рассмотрим ∆ OFC
– прямоугольный, так как OF – расстояние от
центра конуса до образующей, ∟OFC
= 900 .
Используя
определение синуса угла=> =>
3)
Рассмотрим ∆ АOC
– прямоугольный, так как АО – высота, ось конуса, ∟АOC
= 900.
Используя
основное тригонометрическое тождество найдем косинус угла С:
Используя
определение косинуса угла=>
=>
=>
=>
4)
По условию ABCD
– квадрат, точки О и М середины отрезков АС и CD
, ОМ — средняя линия => АD
= 2∙ОМ , АD =
5)
Ответ:
9.
Решите
уравнение:
Решение:
Используем
формулу двойного аргумента:
Используя
основное тригонометрическое тождество, выразим косинус через синус:
Выполним
замену. Пусть , тогда
Вернемся
к замене:
нет решения, так как 3
[-1;1]
и
Ответ:
10. Найдите
первообразную функции , график которой проходит через начало
координат
Решение:
Найдем общий вид
первообразной:
Найдем константу с.
Так как график первообразной проходит через начало координат (0;0), то
составим уравнение:
с = 0
Составим
первообразную:
Ответ:
Справочные
материалы
|
Тригонометрия |
||||||||||||||||||||||||||||||||||||||
|
Решение
|
Тригонометрические
|
Формулы
Сумма и Формулы
Формулы преобразования в сумму: |
||||||||||||||||||||||||||||||||||||
|
Формулы |
||||||||||||||||||||||||||||||||||||||
|
Корни |
Степени |
|
Формулы |
|
||||||||||||||||||||||||||||||||||
|
2) 3) 4) 5) 6) |
|
1) alogab = b
|
Правила
2) 9) 10) 11)( 12) |
|||||||||||||||||||||||||||||||||||
|
Квадратное ax2 + bx + c = 0 D = b2 − 4ac Разложение ax2+bx+c=a (x—x1)(x—x2) |
Формулы умножения ( а + в )² = а² + 2ав + в² ( а — а² — |
|||||||||||||||||||||||||||||||||||||
|
Геометрия |
|
Треугольник
Теорема косинусов: Теорема синусов: Площадь
1. Сумма острых углов: 2. Теорема Пифагора: 3. Радиус описанной (R) и вписанной (r) окружности: (mс – 4. Площадь: Соотношения
Правильный многоугольник Сумма внутренних углов правильного n-угольника: Sn = 1800 Площадь правильного n-угольника: Pn – периметр : Круг
Lокр= 2πr Площадь круга и сектора: Sкруга = π
Цилиндр: Sбок=2πR·h, Sполн= Sбок + 2Sосн, V = Sосн·h, Sосн= πR2. Конус: Sбок= πRL, Sполн= Sбок + Sосн, V = Сфера, шар: V = |
Диагональ: Радиус описанной окружности: Периметр: Площадь:
Сумма углов: Соотношение сторон и диагоналей: Периметр:: Площадь:
Средняя линия ( m ):
Площадь:
Диагонали ромба взаимно перпендикулярны. Соотношения диагоналей и стороны: Радиус вписанной окружности: Площадь: Призма: Sбок=Росн·h, Sполн= Sбок + 2Sосн, V = Sосн·h. Прямоугольный параллелепипед, куб: Sбок=Росн·h, Sполн= Sбок + 2Sосн, V = abc. Пирамида: Sбок= cумма площадей боковых V = Правильная пирамида: Sбок = |
Список
литературы
1.
Алгебра и начала математического анализа. 10-11
кл.: учебник для для общеобразоват. учреждений : базовый и углубленный уровень
/ Ш.А.Алимов, Ю.М.Колягин, М. В. Ткачева [и др.]. – 4-е изд. – М.:
Просвещение, 2017. – 463 с.
2.
Математика в школе : научно-теоретический и
методический журнал. – Москва : ООО «Школьная пресса». – 2015-2019.
3.
Бутузов, В. Ф. Геометрия. Рабочая тетрадь 11 класс
: учебное пособие для общеобразоват. Организаций : базовый и углубленный
уровни /В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина. – 11-е изд. – Москва :
Просвещение, 2017. – 75 с. : ил.
4.
Геометрия : 10-11 кл.: учебник для общеобразоват.
организаций : базовый и углубл. уровни / Л. С.Атанасян [и др.]. – 4-е изд. –
Москва: Просвещение, 2017. – 256 с.
5.
Глазков, Ю.А. Геометрия. Рабочая тетрадь. 10 класс
: учебное пособие для общеобразоват. Организаций : базовый и углубленный уровни
/ Ю. А. Глазков, И. И. Юдина, В. Ф. Бутузов. – 11-е изд.. – Москва :
Просвещение, 2017 . – 95 с. : ил.
6.
Зив, Б.Г. Геометрия. Дидактические материалы.10
класс : учебное пособие для общеобразоват. организаций : базовый и углубленный.
– 16-е изд. – Москва : Просвещение, 2017. – 157 с. : ил.
7.
Математика в школе : научно-теоретический и
методический журнал. – Москва : ООО «Школьная пресса». – 2015-2019.
10-12. Чтение графика функции
Используя график функции у = f(x) (см. рис. ниже), определите и запишите ответ
10.1. Промежутки возрастания и убывания функции.
11.1. При каких значениях x
12.1. Наибольшее и наименьшее значения функции.
10.2. Промежутки возрастания и убывания функции.
11.2. Наибольшее и наименьшее значения функции.
12.2. При каких значениях x
10.3. Промежутки, на которых
11.3. Точки экстремума функции.
12.3. Наибольшее и наименьшее значения функции.
10.4. Нули функции.
11.4. Промежутки возрастания и убывания функции.
12.4. Наибольшее и наименьшее значения функции.
10.5. При каких значениях x функция y не имеет производной.
11.5. При каких значениях x выполняется
12.5. Наибольшее и наименьшее значения функции.
10.6. При каких значениях x выполняется
11.6. Промежутки возрастания и убывания функции.
12.6. При каких значениях x выполняется
10.7. При каких значениях x выполняется
11.7. Промежутки возрастания и убывания функции.
12.7. При каких значениях x выполняется
10.8. Область определения функции.
11.8. При каких значениях x выполняется
12.8. При каких значениях x выполняется
10.9. Область определения функции.
11.9. При каких значениях x выполняется
12.9. При каких значениях x выполняется
10.10. Область определения функции.
11.10. При каких значениях x выполняется 
12.10. Промежутки возрастания и убывания функции.
10.11. Область определения функции.
11.11. При каких значениях x выполняется
12.11. Промежутки возрастания и убывания функции.
10.12. Область определения функции.
11.12. При каких значениях x выполняется
12.12. Промежутки возрастания и убывания функции
.
10.13. Область определения функции.
11.13. При каких значениях x выполняется
12.13. При каких значениях x выполняется
10.14. При каких значениях x выполняется
11.14. При каких значениях x выполняется
12.14. Наибольшее и наименьшее значения функции.
10.15. Область определения функции.
11.15. При каких значениях x выполняется 
12.15. При каких значениях x выполняется
10.16. При каких значениях x выполняется
11.16. Промежутки возрастания и убывания функции.
12.16. Наибольшее и наименьшее значения функции.
10.17. При каких значениях x выполняется
11.17. Точки экстремума функции.
12.17. Промежутки возрастания и убывания функции.
10.18. При каких значениях x выполняется
11.18. Промежутки возрастания и убывания функции.
12.18. Наибольшее и наименьшее значения функции.
10.19. Область определения функции.
11.19. При каких значениях x выполняется
12.19. Точки экстремума функции.
10.20. При каких значениях x выполняется
11.20. При каких значениях x выполняется
12.20. Наибольшее и наименьшее значения функции.
Задания для подготовки к экзамену по математике для студентов 1 курса.
Основная часть
Вычислите значение выражения
1. 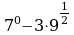
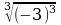
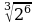
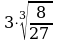
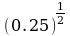
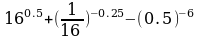
5. 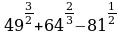
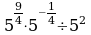
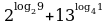
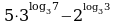
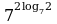
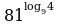
11. 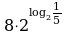
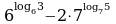
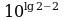
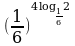
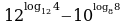
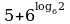
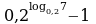
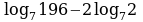
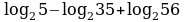
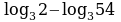
20. 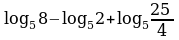
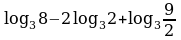
Найдите значение 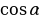
23. 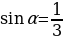
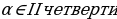
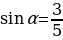
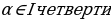
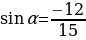
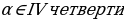
Найдите значение 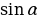
26.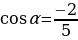
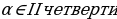
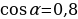
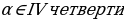
28.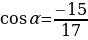
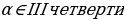
Решите уравнение
29. 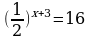
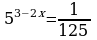
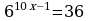
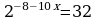
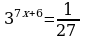
34. 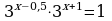
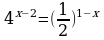
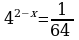
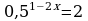
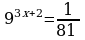
39. 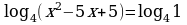
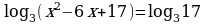
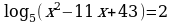
42. 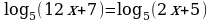
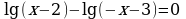
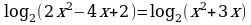
45. 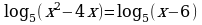
46. 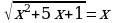
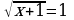
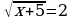
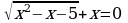
50. 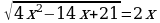
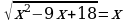
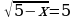
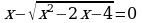
54. 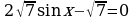
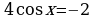
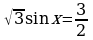
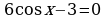
58.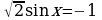
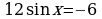
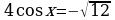
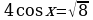
Решите неравенство
62. 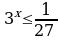
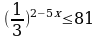
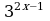
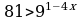
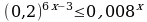
67.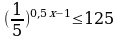
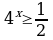
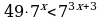
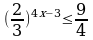
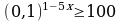
Упростить выражения
72. 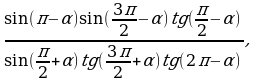
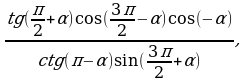
74. 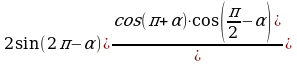
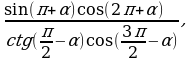
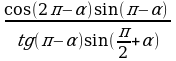
Найдите производную функции:
77. 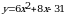
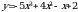
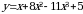
80. 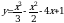
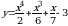
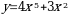
Найдите угловой коэффициент касательной к графику функции в точке с абсциссой 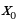
83. 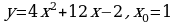
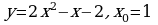
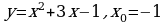
86. 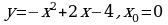
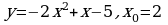
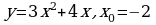
Точка движется прямолинейно по закону S(t) (S-путь в метрах, t-время в секундах) Вычислите скорость и ускорение тела в момент времени t.
89. 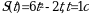
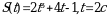
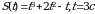
92. 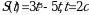
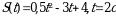
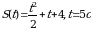
95. 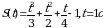
Найдите неопределенный интеграл
96. 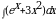
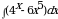
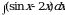
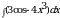
100. 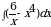
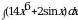
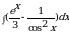
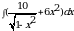
104. 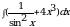
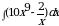
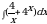
Точка движется прямолинейно так, что её скорость в момент времени t изменяется по закону v(t). Найдите путь, пройденный
107. V(t)=(10+2t)м/с c 3 по 5 секунду движения
108. V(t)=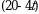
109. V(t)=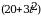
110. V(t)=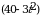
111. V(t)=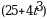
Найдите координаты вектора 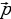
112. 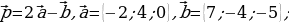
113. 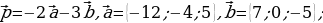
114. 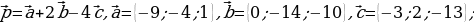
115. 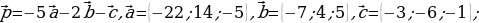
116. 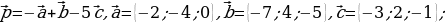
117. 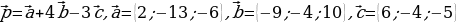
Решите задачи:
118. В коробке 35 шариков, из которых 13 белых, а остальные черные. Наугад выбирают один шарик. Какова вероятность, что он черный?
119. Петя включает телевизор. Телевизор включается на случайном канале. В это время по двенадцати каналам из тридцати трех показывают рекламу. Найдите вероятность того, что Петя попадет на канал, где реклама не идет.
120. В книге 58 страниц, на 10 из которых есть иллюстрации. Наугад открывают книгу. Найдите вероятность того, что она открыта на странице без иллюстрации.
121. В группе 30 студентов. За зачет получили оценку «3» четырнадцать человек, а остальные «4» и «5», причем четверок и пятерок одинаковое количество. Наугад выбирают фамилию ученика. Найдите вероятность того, что выбран ученик, получивший «5».
122. Для участия в конференции приехали 42 человека. В первый день выступают 12 человек, а в остальные три дня выступающих поровну. Какова вероятность того, что участник конференции выступает в третий день?
Решите задачи:
123. Диаметр цилиндра равен 4см, а высота 10см. Найти полную поверхность и объём цилиндра.
124. Длина окружности основания цилиндра равна 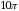
125. Площадь основания цилиндра равна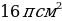
126. Высота цилиндра равна 10см, а площадь осевого сечения 80см. Найдите полную поверхность и объём цилиндра.
Дополнительная часть
Решите уравнения:
127. 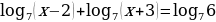
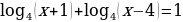
129. 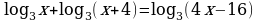
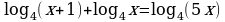
Найдите промежутки возрастания и убывания функции.
131. 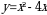
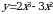
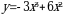
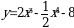
135. 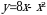
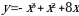
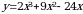
138. 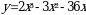
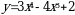
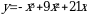
Найти область определения функции
141. 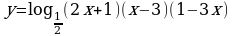
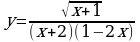
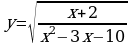
145. 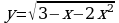
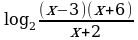
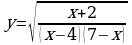
Найдите неопределенный интеграл
148. 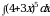
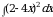
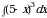
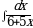
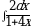
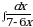
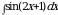
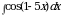
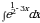
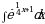
Решите задачи:
158.Каждое ребро прямоугольного параллелепипеда равно 6см, один из углов основания 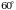
159.Диагональ основания куба равна 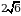
160.Каждое ребро прямой треугольной призмы равно 2. Найти полную поверхность и объём призмы.
161.Основанием прямой призмы является прямоугольный треугольник с катетами 9 и 12см. Наибольшая из площадей боковых граней равна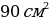
162. Основанием прямой призмы является прямоугольный треугольник с катетами 6 и 8см, боковое ребро равно 15см. Найти полную поверхность и объём призмы.
163. Основанием прямой призмы является ромб, диагонали которого 6 и 8см, а боковое ребро равно ребру основания. Найти полную поверхность и объём призмы.
164. Образующая конуса равна 8см и составляет с плоскостью основания угол 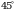
165. Образующая конуса равна 5см, а длина окружности основания 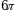
166. Диаметр основания конуса 16см, а образующая составляет угол 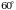
167. Диаметр основания конуса 12см. а высота 8см. Найти полную поверхность и объём конуса.
168. Угол при основании осевого сечения конуса 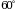
Найдите наибольшее и наименьшее значение функции на отрезке:
169. 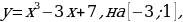
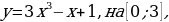
171. 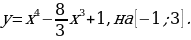
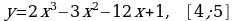
173. 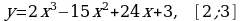
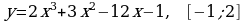
ЭКЗАМЕННАЦИОННЫЕ ЗАДАНИЯ
ПО МАТЕМАТИКЕ
Разработала: Донцова Валентина Викторовна
преподаватель ГАПОУ МО «КТК»
Пояснительная записка
Программа экзамена по математике за 1 семестр 1курса.
Экзамен в письменной форме из 10 заданий.
Продолжительность проведения экзамена – 5 часов.
Программа итогового экзамена по математике
Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем:
Тригонометрия:
Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.
Понятие степени:
Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.
3. Показательная функция:
Показательная функция. Свойства функций.
4. Стереометрия:
Многогранники.
Критерии оценки экзаменационной работы
|
Оценка «5» |
Оценка «4» |
Оценка «3» |
Оценка «2» |
|
90-100% (9-10 заданий) |
70-89% (7-8 заданий) |
50-69% (5-7 заданий) |
меньше 50% (меньше 5 заданий) |
Вариант 1
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 2
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 3
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 4
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 5
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 6
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 7
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 8
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 9
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 10
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 11
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 12
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 13
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 14
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 15
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 16
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
Вариант 17
1). Для функции f (х) = х3 + 2х2 – 1 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = х2 – 2. По графику определите:
а). Монотонность функции;
б). Минимальное (максимальное) значение функции
3). Для функции 
4).Вычислите:
5).Известно, что: 

6). Найдите значение выражения:
7).Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). В прямоугольном параллелепипеде длины сторон основания равны 3см и 4 см. Длина боковой грани равна 6 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 18
1). Для функции f (х) = 3х2 – х3 + 2 найдите f (0), f (1), f (-3), f (5).
2). Постройте график функции у = – х2 + 2. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4).Вычислите:
5). Известно, что:

6).Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
|
а) 9 |
б) |
в ) 0,008 |
|
г) |
д) |
е) |
10). Дан прямой параллелепипед. Длины сторон основания равны 10 см и 5 см. Высота основания равна 5 см. Найдите площадь боковой поверхности, площадь полной поверхности и объем параллелепипеда.
Вариант 19
1). Для функции f (х) = х3 -3х2 + 1 найдите f (0), f (-1), f (2), f (4).
2). Постройте график функции у = – х + 5. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции
3). Для функции 
4). Вычислите:

5). Известно, что 

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности прямого параллелепипеда равна 140 см2. Длины сторон основания параллелепипеда равны 4 см и 6 см. Найдите высоту, площадь полной поверхности и объем параллелепипеда.
Вариант 20
1). Для функции f (х) = 2х2 – х3 + 5 найдите f (0), f (1), f (3), f (-5).
2). Постройте график функции у = х – 7. По графику определите:
а). Монотонность функции;
б). Минимальное ( максимальное ) значение функции.
3). Для функции 
4). Вычислите:
5). Известно, что:

6). Найдите значение выражения:
7). Упростите выражения:
8). Сравните числа: а)
9). Вычислите
10). Площадь боковой поверхности куба равна 64 см2 Найдите сторону куба, площадь полной поверхности и объем куба.
-
Решить
уравнение
-
2)
3)
4)
5)
6)
7)

9)
10)
11)
12)
-
Составить
квадратное уравнение по его корням
1)
2)
3)
4)
5)
6)
-
Сократить
дробь
1)
2)
3)
4)
5)
6)
-
Решить неравенство
1)
2)
3)
4)
5)
6)
7)

9)
10
11)
12)
13)
14)
15)
16)
17)
18)
-
Найти
точки пересечения графика функции с
осями координат.
1)
2)
3)
4)
-
Определить
по чертежу точки пересечения графика
функции с осями координат.
а)
б)
в)
г)
-
Построить
график функции
и определить по чертежу значения
переменной
при которых функция отрицательна.
-
Построить
график функции
и определить по чертежу значения
переменнойпри которых функция положительна.
-
Найти
область определения функции.
Тригонометрия.
1.Найдите
значение выражения
,
если
2.Найдите
значение выражения
,
если
3.Найдите
значение выражения
,
если
4.Найдите
значение выражения
,
если
5.Найдите
значение выражения
,
если
6.Найдите
значение выражения
,
если
7.Найдите
значение выражения
,
если
8.Найдите
значение выражения
,
если
9.Найдите
значение выражения
,
если
10.Найдите
значение выражения
,
если
11.Найдите
значение выражения
,
если
12.Найдите
значение выражения
,
если
13.Найдите
значение выражения
,
если
14.Найдите
значение выражения
,
если
15.Найдите
значение выражения
,
если
16.Вычислите:
17.
Вычислите:
если
18.
Вычислите:
19.Найдите
значение выражения
,
если
20.
Найдите значение выражения
,
если
21.
Найдите значение выражения
,
если
22.
Найдите значение выражения
,
если
23.
Найдите значение выражения
,
если
24.
Найдите значение выражения
,
если
25.
Найдите значение выражения
,
если
26
.Вычислить
значения
если
,
.
27.
Определить знак выражения
1)
2)
3)
4)
5)
6)
7)

9)
28
. Вычислить:
29
.Упростить выражение:
1)
а)
;
б)
2)
а)
;
б)
3)
а)
б)
4)
а)
;
б)
.
5)
а)
;
б)
6)
а)
;
б)
.
7)
а)
;
б)
30.
Вычислить значения
если
1)
,
2)
,
.
31.
Вычислить значения
если
1)
,
2)
,
32.
Вычислить значения
,
если
1)
,
2)
,
33.
Вычислить
значения
,
если
1)
,
.
34.
Вычислить:
1)
,
если
,
.
б)
,
если
,
.
2)
а)
,
если
,
.
,
если
,
;
3)
а)
,
если
,
,
,
.
б)
,
если
,
;
35)
Упростить выражение:
1)
2)

3)
4)
5)
6)
36.
Доказать тождество
1)
2)
а)
Степени,
корни
Выполнить
действия со степенями и корнями:
1.
2.
3.
4.
5.
6.
7.
8.
9.
15. Найдите значение выражения:
при a=16
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Программа
итогового экзамена по математике
Раменское,
2013 г.
Пояснительная записка
Программа итогового экзамена по математике предназначена для студентов СПО.
Тест является основной формой проверки знаний за курс математики.
Объем теста – 20 заданий.
Продолжительность проведения экзамена – 5 часов.
Программа итогового экзамена по математике
Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем, согласно стандарта.
-
Тригонометрия:
Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.
-
Производная:
Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции.
-
Первообразная:
Основное свойство первообразной. Правила нахождения первообразных.
-
Понятие степени:
Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.
5. Показательная и логарифмическая функции:
Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций.
6. Стереометрия:
Многогранники. Тела вращения.
Критерии оценки контрольной работы
1 задание:
Степень с рациональным показателем – 1 балл
2 задание:
Степень с рациональным показателем – 1 балл
3 задание:
Свойства логарифмической функции – 1 балл
4 задание:
Основные тригонометрические формулы – 2 балла
5 задание:
Основные тригонометрические формулы–2 балла
6 задание:
Решение тригонометрических уравнений– 1 балл
7 задание:
Решение иррациональных уравнений – 2 балла
8 задание:
Решение показательных уравнений – 2 балла
9 задание:
Метод интервалов — Решение иррациональных уравнений – 1 балл
10 задание:
Свойства тригонометрических функций – 1 балл
11 задание:
Вычисление производных — 1 балл
12 задание:
Нахождение первообразной функции – 1 балл
13 задание:
Решение логарифмических уравнений – 1 балл
14 задание:
Нахождение максимального и минимального значений функции – 2 балла
15 задание:
Свойства тел в стереометрии – 1 балл
16 задание:
Площадь криволинейной трапеции – 3 балла
17 задание:
Построение графика логарифмической функции – 3 балла
18 задание:
Решение показательных неравенств — 3 балла
19 задание:
Многогранники — 3 балла
20 задание:
Тела вращения — 3 балла
Рекомендации для проверки (проведения) экзаменационного теста.
Тест состоит из 20 заданий.
Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и отметьте соответствующую ячейку в таблицу ответов.
Максимальный балл за тест – 35.
0 – 14 баллов — «2» («неудовлетворительно»)
15 – 19 баллов — «3» («удовлетворительно»)
21 – 29 баллов — «4» («хорошо»)
30 – 35 баллов — «5» («отлично» )
Ответы
Вариант 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
||||||||||||||||||
|
4 |
|
|
|
|
Вариант 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|||||||||||||
|
4 |
|
|
|
|
|
Вариант 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
|
|
|
Бланк ответов
экзаменационного теста
по математике
Ф.И.О.___________________________________________________
Группа № ________________________
Специальность ____________________
___ вариант.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
1 |
||||||||||||||||||||
|
2 |
||||||||||||||||||||
|
3 |
||||||||||||||||||||
|
4 |
Вариант 1
-
Вычислите 29
– 15.
-
2) 43 3) 73 4) 101.
-
Упростите выражение
.
-
5 2) 1 3) 10 4) 0.
3) Упростите выражение – 2
.
1) 2) 1 3) 8
4) 20.
4) Найдите значение , если
= -0,8 и
.
1) -0,6 2) 0,6 3) 0,2 4) 0,36
5) Упростите выражение 7cos2α – 5 + 7sin2α.
1) 1 + cos2α 2) 2 3) -12 4) 12.
6) Решите уравнение = 1.
1)2n, n
2)
3)
+2
n, n
4)
n, n
7) Укажите промежуток, которому принадлежит корень уравнения = -х.
1) 2) (35;37) 3) (-2;
4)
.

1) [-4;0) 2) [0;1) 3) [-∞;-4) 4) [4;6).
9) Решите неравенство ≤0.
1) (-∞;-2) [
) 2) [-2;
)
( 1;+∞) 3) (-∞;-2) 4) (-∞;-5)
(-2;
.
10) Найдите множество значений функции у =– 2.
1) [3;1] 2) (-∞;+∞) 3) [-1;1] 4) [-3;-1].
11) Найдите производную функции f(x) = .
1) -4 2) -8
3) 8
4)
.
12) Укажите первообразную функции f(x) = 2х + 4х3 – 1.
1) х2 + х4 – х 2) 2х2 + 4х4 3) 2 + 12х2 4) х2+х4.
13) Решите равнение +
=
.
1) 0 2) 4 3) 9 4) 15.
14) Найдите точки максимума функции у = х3 – 3х2 .
1) 0 2) 2 3) -2 4) 3.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1.
1) 5 2) 10 3) 3 4) 31.
16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х2, у = 0, х = 0, х = 2.
1) 8 2) 2 3) 5
4) 6
.
17) Укажите область определения функции у =.
1) (-∞;0)(2;+∞) 2) (-2;+∞) 3) (2;+∞) 4) (0;2).
18) Найдите наибольшее целое решение неравенства – 1
0.
1) 0 2) -1 3) 1 4) 2.
19) Площади двух граней прямоугольного параллелепипеда равны 56дм2 и 192дм2, а длина их общего ребра 8дм. Найдите объем параллелепипеда.
1) 840 2) 1029 3) 1344 4) 1210.
20) Образующая конуса равна 12см и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 384 2) 192 3) 24 4) 648.
Вариант 2
-
Вычислите 7 — 3∙
.
-
2) 8 3) -5 4) -17.
-
Упростите выражение
.
1) 1,2 2) 5 3) 4)
.
3) Упростите выражение +
—
.
1) 2 +2 2) 7 3) 3 — 6
4) 2.
4) Найдите значение, если
=
и 0
.
1) — 2)
3)
4)
.
5) Упростите выражение -3sin2α — 6 – 3cos2α.
1) 1 2) 2cosα 3) cosα + 4) -9 .
6) Укажите промежуток, которому принадлежит корень уравнения = -х.
1) 2) (-
;-10) 3)
4)
.
7) Решите уравнение = 1.
1) n, n
2)
3)
+2
n, n
4)
n,n
.

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).
9) Решите неравенство ≤ 0.
1) (-2;) 2) [-2;2)
(
;+∞) 3) (-∞;3) 4) (-∞;-2)
(
].
10) Найдите множество значений функции у = + 4.
1) [3;5] 2) (-∞;+∞) 3) [-1;1] 4) [-5;-3].
11) Найдите производную функции f(x) = .
1) 3 2)
3) -3
4) —
.
12) Укажите первообразную функции f(x) = 3х2 + 2х -4.
1) х3+ х2 — 4х 2) 6х + 2 3) х3+ х2 4) х2+ х – 4х.
13) Решите равнение +
=
1) 0 2) 11 3) 3 4) 12.
14) Найдите точку минимума функции у = х2 — 1.
1) -1 2) 1 3) -2 4) 0.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6.
1) 55 2) 7 3) 49 4) 11.
16) Вычислите площадь фигуры (S), ограниченной линиями у = х3 + 1, у = 0, х = 0, х = 2.
1) 8 2) 5 3) 6 4) 4.
17) Укажите область определения функции у =.
1) (-∞;0)(4;+∞) 2) (-4;+∞) 3) (4;+∞) 4) (0;4).
18) Найдите наименьшее целое решение неравенства – 1
0.
1) 0 2) 1 3) -1 4) 2.
19) Площади двух граней прямоугольного параллелепипеда равны 35см2 и 42см2, а длина их общего ребра 7см. Найдите объем параллелепипеда.
1) 840 2) 10290 3) 770 4) 210.
20) Образующая конуса равна 24см и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 3840 2) 1092 3) 5184 4) 648.
Вариант 3
1) Вычислите 2∙ – 0,90
1)10,9 2) 11 3) 9,1 4) 9.
2) Упростите выражение
-
2) 2 3) 0,7 4) 36.
3) Упростите выражение —
+
1) -1 + 2) -2 3) 0 4)
.
4) Найдите значение , если
= —
и
1) 2)
3)
4)
5) Упростите выражение -4sin2α +5 – 4cos2α
1) 1 2) 1 + 8sin2α 3) 1 + 8cos2α 4) 9.
6) Укажите промежуток, которому принадлежит корень уравнения = -х
1) 2) (-∞;-2) 3)
4)
.
7) Решите уравнение = -1
1) 2)0 3)
+2
n, n
4)
n, n

= 16
1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).
9) Решите неравенство ≥0
1) (-∞;-8] (
; 2) 2) [-8;
)
( 2;+∞) 3) (-∞; 2) 4) (-∞;-8)
(2; +∞

10) Найдите множество значений функции у = – 1
1) [-1;1] 2) (-∞;+∞) 3) [-2;0] 4) [0;2].
11) Найдите производную функции f(x) =
1) -18 2) 6
3) 18
4)
.
12) Укажите первообразную функции f(x) = 5х4 – 2х + 1
1) 5х5 – 2х2 + 1 2) 20х3 – х 3) х4 – 2х + х 4) х5 – х2 + х.
13) Решите равнение +
=
1) 15 2) 5 3) 4 4) 10.
14) Найдите точку максимума функции у = 4х – х4
1) 4 2) 2 3) -4 4) 0.
15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7
1) 19 2) 11 3) 121 4) 36.
16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х3, у = 0, х = 0, х = 1.
1) 1 2) 3)
4) 1
.
17) Укажите область определения функции у =.
1) (-3;+∞) 2) (-∞;0)(3;+∞) 3) (3;+∞) 4) (0;3).
18) Найдите наибольшее целое решение неравенства – 1
0.
1) 1 2) -1 3) 2 4) 0.
19) Площади двух граней прямоугольного параллелепипеда равны 20см2 и 45см2, а длина их общего ребра 5см. Найдите объем параллелепипеда.
1) 240 2) 120 3) 180 4) 4500.
20) Образующая конуса равна 18дм и составляет с плоскостью основания угол 300. Найдите объем конуса, считая = 3.
1) 3804 2) 2192 3) 2187 4) 6408.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ ИРКУТСКОЙ ОБЛАСТИ
Государственное бюджетное профессиональное образовательное учреждение Иркутской области
«Ангарский промышленно – экономический техникум»
(ГБПОУ ИО «АПЭТ»)
Авторская педагогическая разработка
(комбинаторная)
Сборник заданий для самостоятельной работы
для студентов дневного отделения
специальности 38.02.04 Коммерция (по отраслям)
|
Автор разработки: |
|
Майборская Светлана Владимировна, преподаватель ГБПОУ ИО «АПЭТ» |
Ангарск
2017 г.
ОДОБРЕНО цикловой комиссией
математических и естественнонаучных дисциплин
Протокол №____
от «____» ___________20
Председатель____________/Стогова Л.А./
Автор:
Майборская Светлана Владимировна, преподаватель ГБПОУ ИО «АПЭТ»
Аннотация: сборник заданий для самостоятельной работы разработан для студентов первого курса дневного отделения
специальности 38.02.04 Коммерция (по отраслям)
СОДЕРЖАНИЕ
Пояснительная записка 4
Методические указания к выполнению контрольной работы 5
Вопросы к контрольной работе 6
Основные источники 13
Дополнительные источники 13
-
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Сборник заданий для самостоятельной работы разработан для студентов первого курса дневного отделения специальности 38.02.04 Коммерция (по отраслям). Сборник составлен для учебной дисциплины «Математика: алгебра и начала математического анализа; геометрия» составлена на основе профессиональной образовательной программы ФГОС СПО по специальности 38.02.04 Коммерция (по отраслям) и предназначена для реализации требований к результатам освоения изучаемой дисциплины по ФГОС СПО.
Программа ориентирована на достижение следующих целей:
-
Формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
-
Развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
-
Овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения смежных естественно – научных дисциплин на базовом уровне и дисциплин профессионального цикла, для получения образования в областях, не требующих углублённой математической подготовки;
-
Воспитание средствами математики культуры личности, понимания значимости математики для научно – технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;
Основу сборника составляет содержание, согласованное с требованиями федерального компонента государственного стандарта среднего (полного) общего образования базового уровня.
Математика является фундаментальной общеобразовательной дисциплиной со сложившимся устойчивым содержанием и общими требованиями к подготовке обучающихся. Реализация общих целей изучения математики традиционно формируется в четырёх направлениях – методическое (общее представление об идеях и методах математики), интеллектуальное развитие, утилитарно – прагматическое направление (овладение необходимыми конкретными знаниями) и воспитательное воздействие.
Для экономического профиля более характерным является усиление общекультурной составляющей курса с ориентацией на визуально-образный и логический стили учебной работы.
В результате изучения предмета студенты должны усвоить, что математические понятия являются абстракцией свойств и отношений реального мира, обладают большой общностью, широкой сферой применимости, что сущность приложения математики к решению практических задач заключается в переводе задач на математический язык, решением их и интерпретации их результатов на язык исходных данных.
Входной контрольный срез
|
I вариант |
II вариант |
|
|
1) Вычислить: |
||
|
|
|
|
2) 2 % от x равны 18. Чему равен x? |
2) Чему равны 3 % от 27? |
|
3) Найти x: |
3) Найти y: |
|
|
|
|
|
|
4) Сократить дробь: |
||
|
|
|
|
|
5) Решить уравнения: |
||
|
а) x2 – 9=0 б) x2 + 3x = 0 в) x2 + 4x + 4 = 0 |
а) x2 + x – 6=0 б) x2 + 2x + 1 = 0 в) x2 – 25 = 0 |
|
|
6) Решить систему неравенств: |
||
|
|
|
|
|
7) Решить неравенство: |
||
|
x2 – 25 0 |
x2 – 16 |
Тема: «Производная и ее приложение»
|
I вар |
II вар |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Пределы
|
1 вариант |
2 вариант |
Тема: Производная
|
1 вариант |
2 вариант |
|
|
|
а) |
а) |
|
б) |
б) |
|
в) |
в) |
|
г) |
г) |
|
д) |
д) |
|
е) |
е) |
|
|
|
Вычислите скорость точки, движущейся прямолинейно по закону , в момент времени . Здесь S –путь (м), t – время (с). |
Точка движется прямолинейно по закону . Найдите скорость в момент времени . Здесь S –путь (м), t – время (с). |
|
|
|
|
|
|
|
|
|
|
|

































































































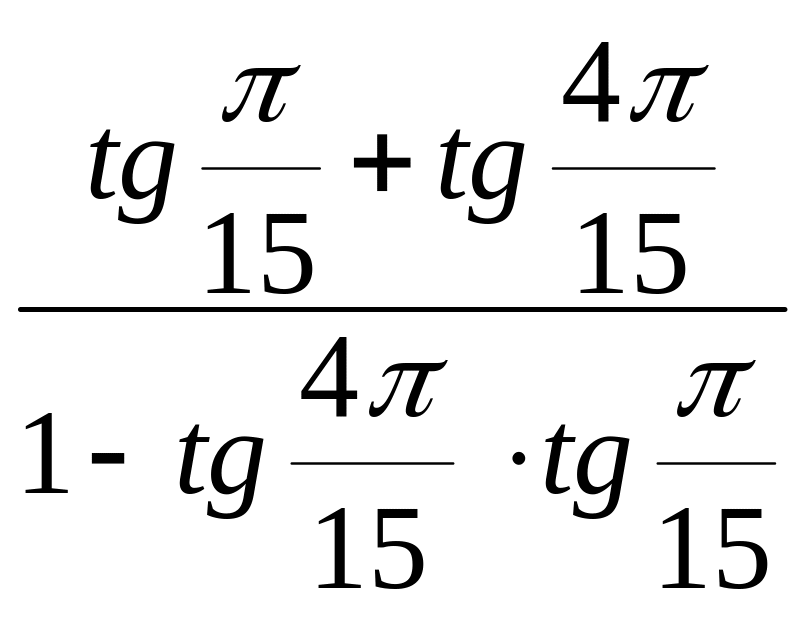

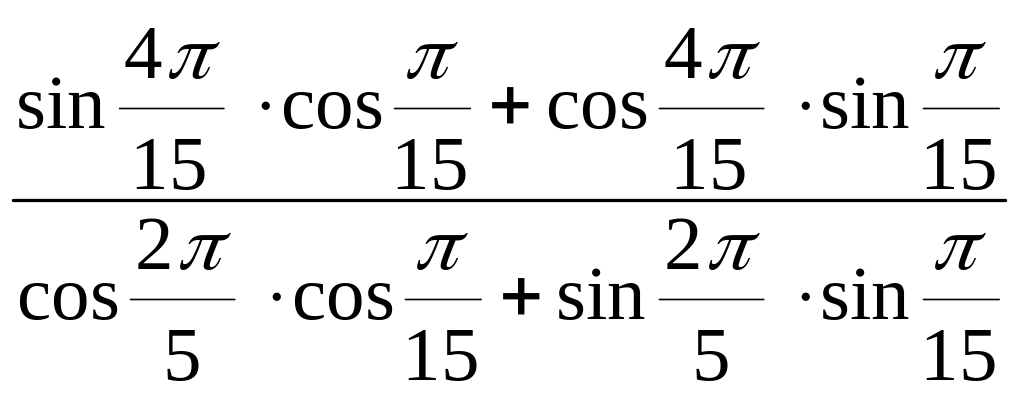
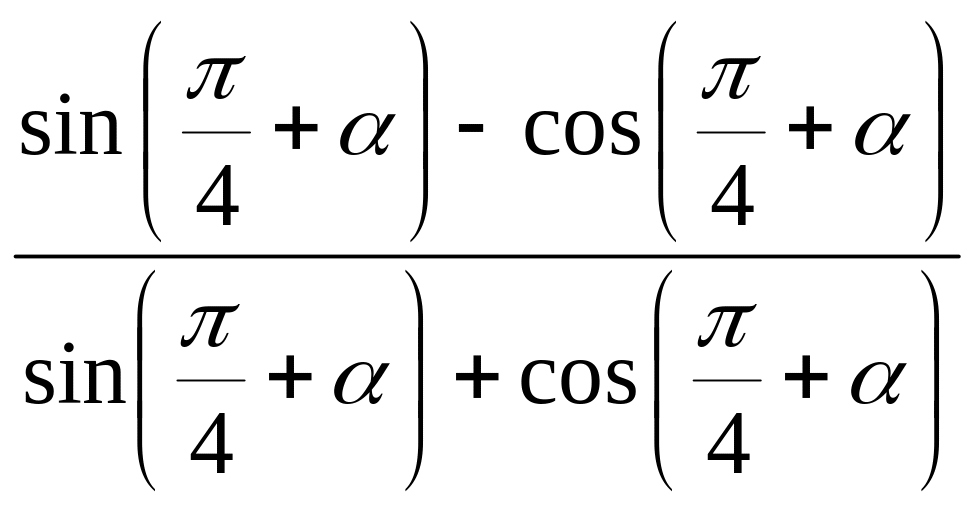

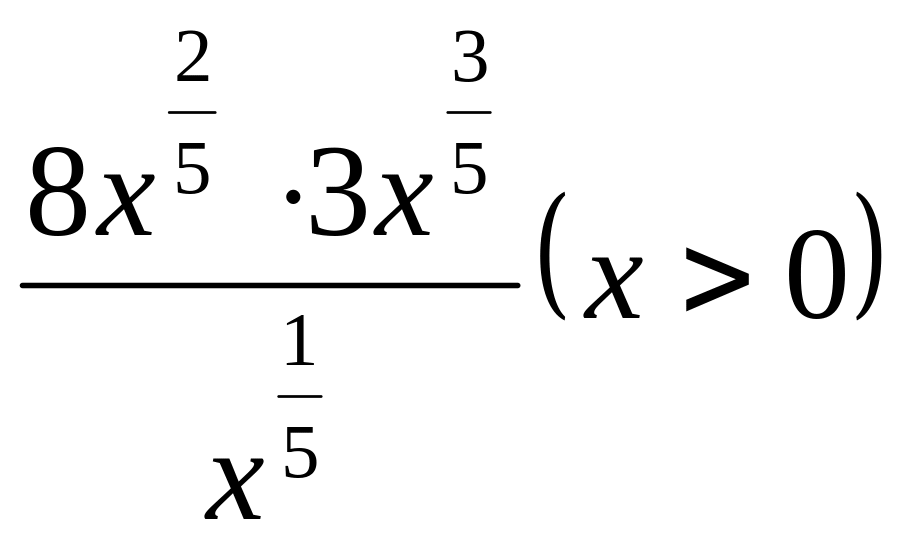

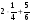
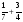
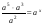
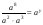
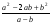
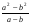
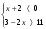
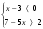
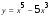
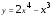
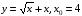
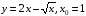
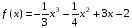
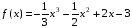
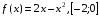
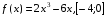
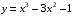
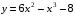
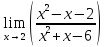
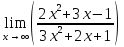
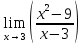
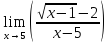
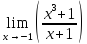

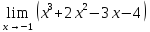
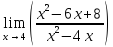
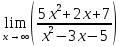
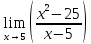
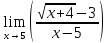
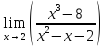
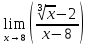
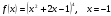
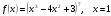
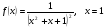
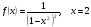
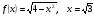
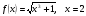
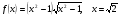
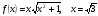
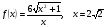
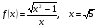
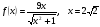
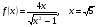
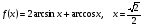
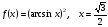 .
.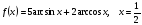 ;
; 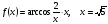 .
.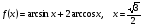 ;
; 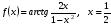 .
.