Вариант 1 6. Планиметрия
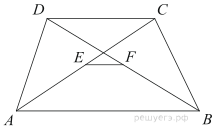
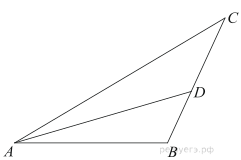
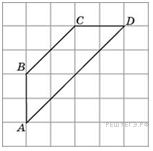
1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
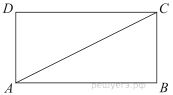
2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.
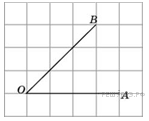
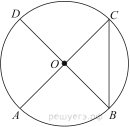
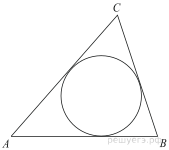
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2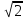
4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
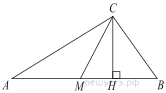
5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.
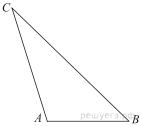
8. Найдите величину угла АВС. Ответ дайте в градусах.
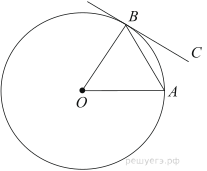
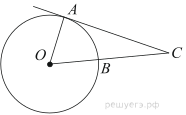
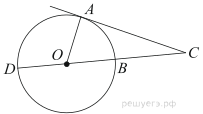
9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Вариант 2 6. Планиметрия
В 1. Сторона правильного треугольника равна 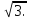
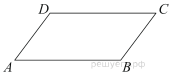
2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.
4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.
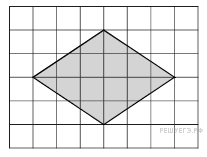
6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.
Вариант 3 6. Планиметрия
1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.
2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25. Найдите высоту АН.
4. В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.
5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А = . Найдите ВН.
6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите
8. Найдите площадь ромба, если его диагонали равны 4 и 12.
9. В треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН.
10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах
Вариант 4 6. Планиметрия
1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = . Найдите BH.
2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.
3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.
6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41
Найдите радиус окружности, вписанной в этот треугольник.
8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4, ВН = 4. Найдите
10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.
Вариант 5 6. Планиметрия
1. Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2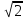
2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А = . Найдите АН.
4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
5. Катеты равнобедренного прямоугольного треугольника равны 2+ Найдите радиус окружности, вписанной в этот треугольник.
6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.
7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.
9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.
Вариант 6 6. Планиметрия
1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.
2. Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС= . Найдите
4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.
6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.
7. В треугольнике ABC угол C равен 90°, АС = 8, cos А = Найдите АВ.
8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
10. В треугольнике ABC угол ACB равен °, угол B равен
°, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Вариант 7 6. Планиметрия
1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. В треугольнике ABC AC = BC, AB = 22, tg А = . Найдите AC.
4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
5. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.
10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Вариант 8 6. Планиметрия
1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.
3. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
4. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.
6. В треугольнике ABC AC = BC, AB = 8, tg А = . Найдите AC.
7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.
8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.
9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47.
10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2
Вариант 9 6. Планиметрия
1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на
4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.
5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.
6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту
7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.
8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.
Вариант 10 6. Планиметрия
1. Найдите величину угла АВС. Ответ дайте в градусах.
2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.
3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.
4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А = . Найдите АВ.
5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.
6. Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.
7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
9. В треугольнике известно, что , , угол
равен 90°. Найдите радиус вписанной окружности.
10. В треугольнике АВС АС = ВС = 27 , — высота, sin ВАС =
. Найдите
|
6. Планиметрия |
||||
|
Вариант 1
|
Вариант 2
|
Вариант 3
|
Вариант 4
|
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
По теме: методические разработки, презентации и конспекты
Решение стереометрической задачи тремя различными способами
Здесь представлено на трех файлах моё решение решение задачи С2 (вариант 13) из пособия «МАТЕМАТИКА. Подготовка к ЕГЭ-2011» под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова. Эта-же задача встречается в пос…
Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Рассмотрим несколько геометрических задач, для решения которых необходимо вычислить те или иные расстояния или углы в пространст…
Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э…
Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Программа внеурочной деятельности «Практикум решения стереометрических задач». Пропедевтика стереометрических знаний на примере качественных стереометрических задач.
Всем известная трудность в изучении стереометрии, возникающая у учащихся 10 классов, в значительной степени объясняется низким уровнем развитием их пространственных представлений. Ученики теряю…
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
Скачать материал
Карточка
1
Карточка
2
Карточка
3
Карточка
4
Карточка
5
Карточка
6
Карточка
7
Карточка
8
Карточка
9
Карточка
10
Карточка
11
Карточка
12
Карточка
13
Карточка
14
Карточка
15
Карточка
16
Карточка
17
Карточка
18
Карточка
19
Карточка
20
Карточка
21
|
№ |
1 |
2 |
3(В9 |
4 |
5 |
|
1 |
9 |
0,6 |
3 |
8 |
45,90,60 |
|
2 |
7,5 |
0,8 |
12 |
2 |
90,45,60 |
|
3 |
10 |
0,75 |
5 |
214 |
60,90,90 |
|
4 |
8 |
0,8 |
5 |
1,5 |
90,45,60 |
|
5 |
9 |
0,6 |
2 |
120 |
90,45,60 |
|
6 |
9 |
0,5 |
2 |
8 |
90,45,90 |
|
7 |
8 |
0,6 |
4 |
8 |
90,45,60 |
|
8 |
6 |
-0,8 |
5 |
360 |
60,60,90 |
|
9 |
1,25 |
-0,75 |
10 |
22 |
90,60,30 |
|
10 |
4 |
2 |
2 |
27 |
90,45,90 |
|
11 |
6 |
-2 |
19 |
30 |
90,45,60 |
|
12 |
10 |
2 |
6 |
8 |
90,45,60 |
|
13 |
18 |
5 |
6 |
3 |
90,45,60 |
|
14 |
84 |
10 |
1,5 |
10 |
90,45,90 |
|
15 |
4 |
4,8 |
12 |
32 |
60,90,90 |
|
16 |
16 |
12 |
8 |
36 |
90,45,60 |
|
17 |
6 |
8 |
4 |
64 |
90,90,60 |
|
18 |
10 |
10 |
8 |
16 |
90,45,90 |
|
19 |
8 |
135 |
2 |
128 |
90,45,90 |
|
20 |
25 |
45 |
6 |
2 |
90,45,60 |
|
21 |
135 |
50 |
2 |
60,90,90 |
Скачать материал


- Сейчас обучается 96 человек из 32 регионов


- Сейчас обучается 82 человека из 34 регионов


- Сейчас обучается 54 человека из 29 регионов


Краткое описание документа:
Цель работы: Подготовка к ЕГЭ — решение геометрических задач.
Не секрет, что геометрические задачи при сдаче ЕГЭ вызывают затруднения у школьников. Для подговки к ЕГЭ предлагаю ключевые задачи по геометрии, встречающиеся в ЕГЭ (часть в).
В работе 21 вариант и ответы. Карточки можно использовать на уроках, на занятиях по поготовке к ЕГЭ.
Хорошо зарекомендовала себя парная работа: два ученика решаю каждый свой вариант, а потом объясняют решение соседу. Надеюсь, данная разработка поможет Вам. Успехов всем на ЕГЭ!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 779 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Оставьте свой комментарий
|
Вариант 1 |
|
Найдите высоту трапеции |
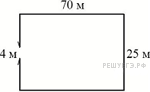
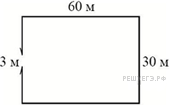
5. Задание 8 Два садовода, имеющие прямоугольные участки размерами 35 м на 40 м с общей границей, договорились и сделали общий прямоугольный пруд размером 20 м на 14 м (см. чертёж), причём граница участков проходит точно через центр. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода? |
Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°. |
6. Задание 13 Найдите объем многогранника, вершинами которого являются точки |
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. |
7. Задание 15 На клетчатой бумаге с клетками размером 1 см |
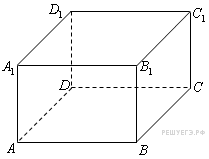
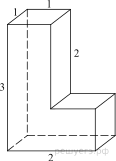
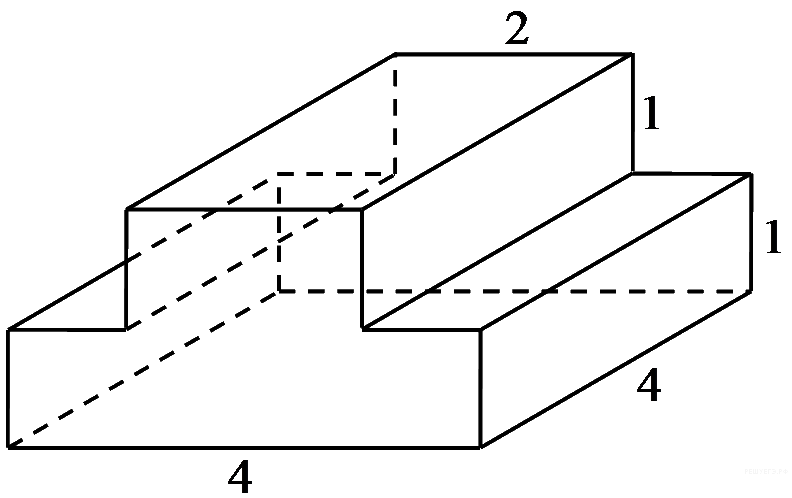
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
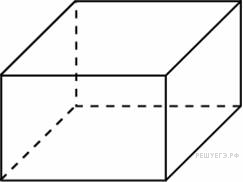
8. Задание 16 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. |
|
Вариант 2 |
|
На клетчатой бумаге с размером клетки |
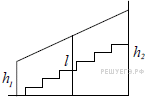
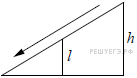
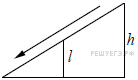
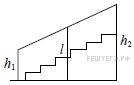
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 1,5 м, а наибольшая h2 равна 2,5 м. Ответ дайте в метрах. |
Площадь треугольника ABC равна4. DE — средняя линия. Найдите площадь треугольника CDE. |
Аквариум имеет форму прямоугольного параллелепипеда с размерами 60 см × 20 см × 50 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров. |
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь. |
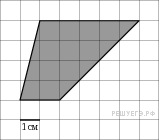
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см |
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. |
|
Вариант 3 |
|
Найдите высоту треугольника |
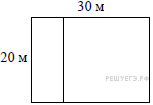
Дачный участок имеет форму прямоугольника со сторонами 20 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах. |
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне? |
Плоскость, проходящая через три точки A, B и C, разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше граней? |
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6. |
Найдите косинус угла . В ответе укажите значение косинуса, умноженное на |
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. |
|
Вариант 4 |
|
На клетчатой бумаге с размером клетки 1 |
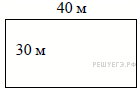
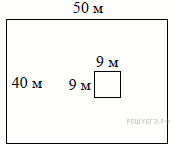
Дачный участок имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Размеры дома, расположенного на участке и также имеющего форму прямоугольника, — 9 м × 6 м. Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах. |
В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах. |
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах. |
Сторона правильного треугольника равна |
Хорда |
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда. |
ОТВЕТЫ
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Вариант 1 |
2 |
24 |
6 |
18 |
1260 |
10 |
14 |
5 |
|
Вариант 2 |
40 |
1 |
30 |
76 |
2 |
60 |
12 |
3 |
|
Вариант 3 |
5 |
6 |
2 |
92 |
120 |
7 |
-2 |
24 |
|
Вариант 4 |
2,5 |
38 |
0,5 |
110 |
1146 |
8000 |
105 |
48 |
Варианты для подготовки к ЕГЭ (задания по геометрии)
Вариант № 1
1. 
2. Электрику ростом 1,8 метра нужно поменять лампочку, закреплённую на стене дома на высоте 4,2 м. Для этого у него есть лестница длиной 3 метра. На каком наибольшем расстоянии от стены должен быть установлен нижний конец лестницы, чтобы с последней ступеньки электрик дотянулся до лампочки? Ответ запишите в метрах.
3. 
4. 
5. 
6.
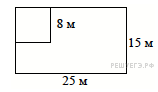
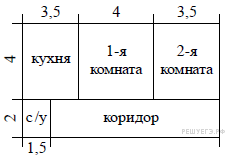
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин отгородил на участке квадратный вольер со стороной 8 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
7. 
8. 
9. Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 30 см. Сколько потребуется таких дощечек?
10. 
11. 
12. 
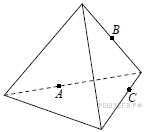
13. 
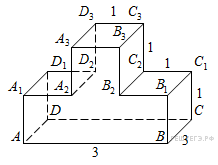
14. В прямоугольном параллелепипеде известно, что
,
,
. Найдите длину диагонали
.
15. 
16.
17. 
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
18. 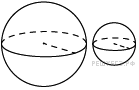
19. Площадь боковой поверхности цилиндра равна , а высота — 1. Найдите диаметр основания.
20. 
Ключ Вариант № 1
|
№ п/п |
Ответ |
|
1 |
1400 |
|
2 |
1,8 |
|
3 |
66 |
|
4 |
1 |
|
5 |
186 |
|
6 |
311 |
|
7 |
120 |
|
8 |
1 |
|
9 |
800 |
|
10 |
177 |
|
11 |
24 |
|
12 |
72 |
|
13 |
6 |
|
14 |
27 |
|
15 |
60 |
|
16 |
1200 |
|
17 |
11 |
|
18 |
9 |
|
19 |
2 |
|
20 |
93 |
Вариант № 2
1. 
2. 
3. 
4. Рыболовное хозяйство строит бассейн для разведения рыбы. Бассейн имеет форму прямоугольника со сторонами 4 м и 12 м. В центре бассейна находится техническая постройка, которая имеет форму прямоугольника со сторонами 2 м и 3 м. Найдите площадь оставшейся части бассейна.
5. 
6.
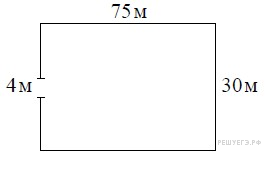
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 75 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе предусмотрен проезд шириной 4 м.
7. 
8. 
9. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
10. 
11. 
12. 
13.
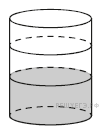
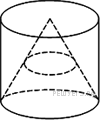
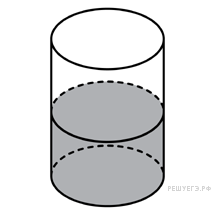
В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём сосуда 960 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
14. 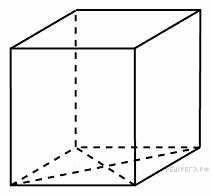
15. 
и
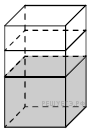
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
16. 
17. 
.
18. 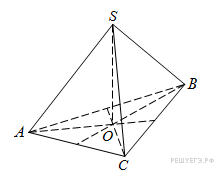
медианы основания
пересекаются в точке
. Площадь треугольника
равна 4; объем пирамиды равен 6. Найдите длину отрезка
.
19. 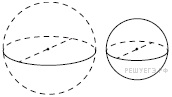
20.
К правильной шестиугольной призме с ребром основания 1 приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что основания совпали. Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Ключ
|
№ п/п |
Вариант № 1 |
Вариант № 2 |
|
1 |
1400 |
100 |
|
2 |
1,8 |
55 |
|
3 |
66 |
40 |
|
4 |
1 |
42 |
|
5 |
186 |
186 |
|
6 |
311 |
206 |
|
7 |
120 |
12 |
|
8 |
1 |
1919 |
|
9 |
800 |
120 |
|
10 |
177 |
1,1 |
|
11 |
24 |
17 |
|
12 |
72 |
63 |
|
13 |
6 |
120 |
|
14 |
27 |
42 |
|
15 |
60 |
11 |
|
16 |
1200 |
3200 |
|
17 |
11 |
2500 |
|
18 |
9 |
4,5 |
|
19 |
2 |
48 |
|
20 |
93 |
13 |