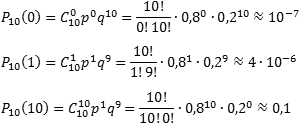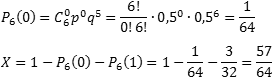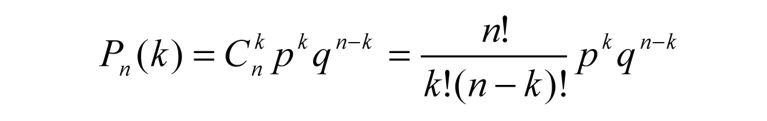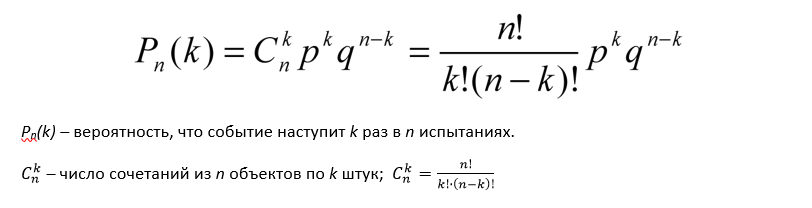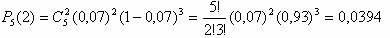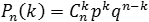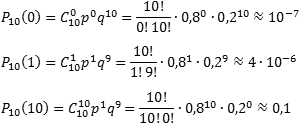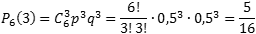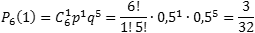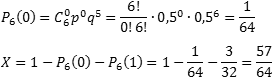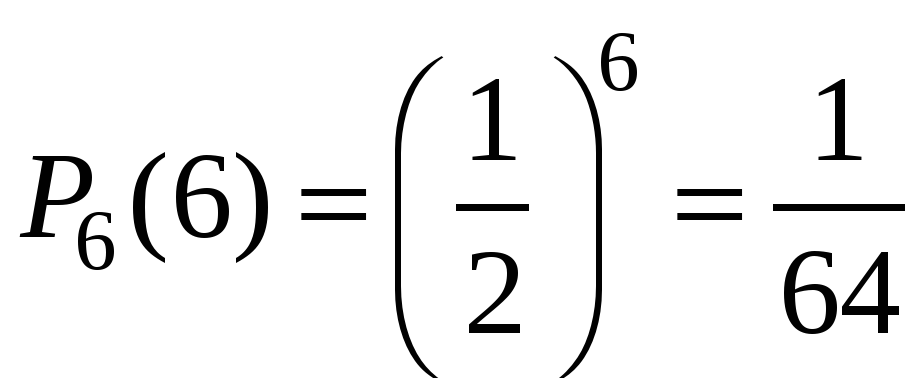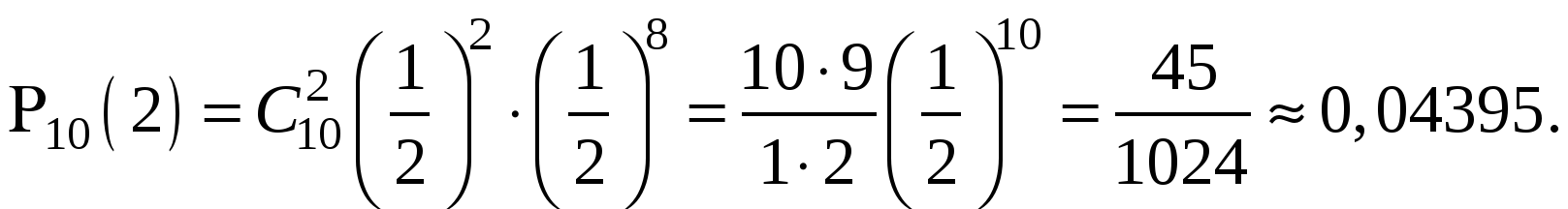Задания егэ на формулу бернулли - Помощь в подготовке к экзаменам и поступлению

« Методика решения сложных задач по теории вероятности с помощью
формулы Бернулли при подготовки к ЕГЭ».

Выполнила:
учитель математики

МКОУ СШ №2 г.Котельниково Волгоградской области

Пирожик Галина
Кирилловна

Цель работы:

·
научиться вычислять вероятности
событий с помощью формулы Бернулли

В результате выполнения практической
работы студент должен:

знать:

·
формулу Бернулли;

уметь:

·
вычислять вероятности событий с помощью формулы Бернулли.

В 2022 году в варианты ЕГЭ по математике профильного
уровня добавились новые задачи по теории вероятностей. По сравнению с теми,
которые раньше были в варианте, это повышенный уровень сложности и требует
применение более глубоких знаний по этой теме. При
решении вероятностных задач часто приходится сталкиваться с ситуациями, в
которых одно и тоже испытание повторяется многократно и исход каждого испытания
независим от исходов других. Такой эксперимент еще называется схемой
повторных независимых испытаний или схемой Бернулли.

Примеры
повторных испытаний:

1)
многократное извлечение из урны одного шара при условии, что вынутый шар после
регистрации его цвета кладется обратно в урну;

2)
повторение одним стрелком выстрелов по одной и той же мишени при условии, что
вероятность удачного попадания при каждом выстреле принимается одинаковой.

3)
бросание симметричной монеты n раз.

Схема Бернулли —
это когда производится n однотипных
независимых опытов, в каждом из которых может появиться интересующее нас
событие A, причем известна вероятность
этого события P(A)
= p. Требуется определить вероятность того, что при проведении n испытаний событие A появится
ровно k раз.

Поскольку
речь идет о испытаниях, и в каждом опыте вероятность события A одинакова,
то возможны лишь два исхода:

1. A — появление события A с
вероятностью p;

2. «не А» — событие А не появилось, что происходит с
вероятностью q = 1 − p.

Важнейшее
условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы
опытов мы ни проводили, нас интересует одно и то же событие A,
которое возникает с одной и той же вероятностью p.

Если же условия постоянны, можно точно определить вероятность
того, что событие A произойдет ровно k раз
из n возможных. Сформулируем этот факт в виде теоремы:

Теорема Бернулли.
Пусть вероятность появления события A в каждом опыте постоянна
и равна р. Тогда вероятность того, что в n независимых
испытаниях событие A появится ровно k раз,
рассчитывается по формуле:

где C_n^k — число
сочетаний, q = 1 − p.

Эта
формула так и называется: формула Бернулли.

Для
решения по формуле Бернулли надо вспомнить:

1)
определение факториала.

Факториал числа n (n!)— это произведение натуральных
чисел от 1 до n.

n!=1⋅2⋅3⋅…⋅(n−2)⋅(n−1)⋅n

Примеры для вычисления факториала числа:

1)
3! = 1*2*3 = 6 2) 4! = 1*2*3*4 = 24 3) 5! = 1*2*3*4*5 = 120 4)6!
= 1*2*3*4*5*6 = 720

Запоминаем

0! =
1 1! = 1

Свойство факториала n!=(n—1)!⋅n

1) 4! = (4-1)!*4= 3!*4; 2) 5! =(5-1)!*5=4!*5

2) Число сочетаний.

Число сочетаний из n по k элементов (обозначается ) очень
важное понятие в комбинаторике. Оно
показывает сколько существует вариантов выбора k элементов из множества n
элементов.
Число сочетаний вычисляется по формуле:

Примеры
для решени:

Разберем задачи на применение формулы для вычисления простых задач, решаемых по
формуле Бернулли

Задача1. Монету бросают 6
раз. Выпадение орла и решки равновероятно. Найти вероятность того, что орел
выпадет три раза.

Решение:

Событие A, когда выпадает
орел, вероятность этого события равна p = 0,5. Событию A противопоставляется
событие «не A», когда выпадает решка, что случается с
вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность
того, что орел выпадет k раз.

Таким
образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим
вероятность того, что орел выпал три раза, т.е. k = 3:

Ответ:
0,3125

Задача2. Монету бросают 6
раз. Выпадение орла и решки равновероятно. Найти вероятность того, что орел
выпадет не менее двух раз.

Решение:

Основная загвоздка — во фразе «не менее».
Получается, что нас устроит любое k,
кроме 0 и 1,
надо
найти значение суммы X = P₆(2) + P₆(3)
+ … + P₆(6).

Заметим,
что эта сумма также равна (1 − P₆(0) − P₆(1)),
т.е. достаточно из всех возможных вариантов «вырезать» те, когда орел выпал 1
раз (k = 1) или не выпал вообще (k = 0).
Поскольку P₆(1) нам уже известно, осталось найти P₆(0):

Ответ:0,890625

Задача 3. Монету
бросают 2 раза. Найти вероятность того, что «решка» выпадает хотя бы раз.

Решение:

Решка выпадет хотя бы раз (т. е. или раз из двух, или два из
двух)

p=0,5 – вероятность того,
что выпадет герба,

q=0,5 – вероятность того, что выпадет
решка.

Ответ: 0,75.

Задача 4. (ЕГЭ 2022) Симметричную монету бросают 10 раз. Во сколько
раз вероятность события «выпадет ровно 5 орлов» больше вероятности события
«выпадет ровно 4 орла»?

Решение:

Воспользуемся формулой Бернулли. Найдем вероятность события А,
состоящего в том, что при десяти бросаниях выпадет ровно 5 орлов:

Аналогично найдем вероятность события B, состоящего в том, что при
десяти бросаниях выпадет ровно 4 орла:

Количество вариантов, при которых выпадет ровно 5 орлов, равно

Количество вариантов, при которых выпадет ровно 4 орла, равно

Тогда

Ответ: 1,2

Задача 5. (ЕГЭ 2022) Стрелок стреляет по пяти одинаковым
мишеням. На каждую мишень дается не более двух выстрелов, и известно, что
вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько
раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности
события «стрелок поразит ровно 4 мишени»?

Решение:

Стрелок
поражает мишень с первого раза 0,6 а со второго выстрела 1-0,6=0,4;
Вероятность
поразить мишень равна 0,6+0,4∙0,6=0,84, не поразить 1-0,84=0,16

Вероятность
поразить 5 мишеней из 5 равна

Вероятность
поразить 4 мишени из 5 находим по формуле Бернулли:

=Р₂

$displaystyle frac{P_1}{P_2} = frac{0,84^5}{5 cdot 0,84^4 cdot 0,16}= frac{0,84}{0,8}=1,05$

Ответ: 1,05

Задачи
для самостоятельной работы:

1. Симметричную монету бросают 11 раз. Во сколько раз вероятность события
«выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Ответ: 1,4

2. Симметричную монету бросают 12 раз. Во сколько раз вероятность события
«выпадет ровно 4 орла» меньше вероятности события «выпадет ровно 5 орлов»?

Ответ: 1,6

3.Симметричную монету бросают 8 раз. Во сколько раз
вероятность события «выпало ровно 4 орла» больше вероятности события «выпадет
ровно 3~орла»?

Ответ: 1,25

4. Стрелок стреляет по пяти одинаковым мишеням.
На каждую мишень дается не более двух выстрелов, и известно, что вероятность
поразить мишень каждым выстрелом равна 0,5. Во сколько раз вероятность события
«стрелок поразит ровно 3 мишени» больше вероятности события «стрелок поразит
ровно 2 мишени»?

Ответ: 3.

Источник

Примеры решений задач на формулу Бернулли

Калькуляторы на формулу Бернулли

Обратите внимание на следующие разделы, где разобраны типовые задачи на формулу Бернулли. Вы можете решить или проверить вычисления своих заданий с помощью онлайн-калькуляторов. Теорию по этой теме можно найти в онлайн-учебнике.

Задача про партии в шахматы
Задача про выстрелы
Задача про мальчиков и девочек
Задача про лотерейные билеты
Задача о наивероятнейшем значении
Формула Пуассона

Еще: решаем в Excel по формуле Бернулли.

Понравилось? Добавьте в закладки

Схема Бернулли: решенные задачи

Задача 1. Из $n$ аккумуляторов за год хранения $k$ выходит из строя. Наудачу выбирают $m$ аккумуляторов. Определить вероятность того, что среди них $l$ исправных.
$n = 100, k = 7, m = 5, l = 3.$

Задача 2. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента;
б) не менее четырех элементов;
в) хотя бы один элемент.

Задача 3. Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?

Задача 5. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта.

Задача 6. Что более вероятно выиграть у равносильного противника: не менее двух партий из трёх или не более одной из двух?

Задача 7. а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4;
б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

Формула Пуассона: решенные задачи

Задача 4. С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия.

Задача 8. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено:
а) три ошибочно укомплектованных пакета;
б) не более трех пакетов.

Мы отлично умеем решать задачи по теории вероятностей

Решебник — когда задачи нужны быстро

Источник

Схема Бернулли. Примеры решения задач

5 июля 2011

Не будем долго размышлять о высоком — начнем сразу с определения.

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

A — появление события A с вероятностью p;
«не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.

Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C_n^k — число сочетаний, q = 1 − p.

Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):

Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:

герб выпадет три раза;

герб выпадет один раз;

герб выпадет не менее двух раз.

Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.

Таким образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим вероятность того, что герб выпал три раза, т.е. k = 3:

Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:

Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P₆(2) + P₆(3) + … + P₆(6).

Заметим, что эта сумма также равна (1 − P₆(0) − P₆(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P₆(1) нам уже известно, осталось найти P₆(0):

Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?

Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.

Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.

Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3):

[begin{array}{l}{P_{20}}left( 2 right) = C_{20}^2{p^2}{q^{18}} = frac{{20!}}{{2!18!}} cdot {0,2^2} cdot {0,8^{18}} approx 0,137\{P_{20}}left( 3 right) = C_{20}^3{p^3}{q^{17}} = frac{{20!}}{{3!17!}} cdot {0,2^3} cdot {0,8^{17}} approx 0,41end{array}]

Очевидно, P₂₀(3) > P₂₀(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.

Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.

P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.

Смотрите также:

Локальная теорема Муавра — Лапласа
Формула полной вероятности
Тест к уроку «Сложение и вычитание дробей» (легкий)
Сводный тест по задачам B12 (2 вариант)
Как решать задачи про летающие камни?
Задача C1: тригонометрические уравнения и формула двойного угла

Источник

Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»). Сегодня мы расскажем о том, как готовиться в 2021-2022 учебном году к ЕГЭ по профильной математике. В конце статьи вас ждёт бонус: вебинар по теории вероятности. Наш преподаватель Дмитрий Корабейников расскажет, как решать задания ЕГЭ по профильной математике 2022 года при помощи формулы Бернулли.

Хочешь БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.

Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.

В банке заданий ФИПИ появилось несколько новых задач по теории вероятностей. Часть из них крайне сложно решить без формулы, которую мало кто из одиннадцатиклассников знает. Это формула Бернулли. Выглядит она, конечно, страшновато:

Сейчас мы разберемся, что в ней значат все буквы и символы. А после решим задачу из банка ФИПИ с помощью этой формулы.

P_n(k) – вероятность, что событие наступит k раз в n испытаниях.
Например, человек открывает 7 (n = 7) коробок. В каждой коробке с какой-то вероятностью p может оказаться приз. И по формуле Бернулли можно найти вероятность, например, того, что приз окажется в 3 (k = 3) коробках из 7.

Таких сочетаний получилось 6 шт. Это мы сосчитали вручную. Так делать не всегда удобно: сочетаний может оказаться слишком много.

Наверняка не все знают, как считается так называемый факториал числа: n!
Нужно перемножить это число и все натуральные числа, идущие от 1 до этого числа. Поэтому, например,

Дальше нужно разобраться, что значат буквы p и q.

p и q – взаимообратные вероятности исхода какого-то события. Т.е. p + q = 1. Известный и понятный пример: шансы, что при броске монеты выпадет орел (p) или решка (q). Шанс выпадения орла p = 0,5. Шанс того, что орел не выпадет (а выпадет решка) q = 0,5. Всё сходится: p + q = 1.

Или такая ситуация: в коробке 7 красных карандашей и 3 синих. Обозначим вероятность случайно вытащить красный карандаш за p, а вытащить синий карандаш за q.
В этой ситуации p = 0,7 и q = 0,3; p + q = 1.

Со всеми обозначениями разобрались, давайте теперь решим реальную задачу. Это №10 из профильного ЕГЭ по математике 2022.

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Здесь вероятность выпадения орла p = 0,5. Тогда вероятность того, что орел не выпадет (а выпадет решка): q = 1 — p = 0,5.

Всего 10 бросков, т.е. будем рассматривать сочетания из 10 объектов: n = 10.

Далее нам предстоит сравнить два случая:
1) «выпадет ровно 5 орлов», т.е. из n = 10 объектов мы выбираем сочетания по 5, k = 5;
2) «выпадет ровно 4 орла», т.е. из n = 10 объектов мы выбираем сочетания по 4, k = 4.

Попробуйте решить пару подобных задач самостоятельно, и такие новые задачи по теорверу вас больше не смутят. Но сперва выучите формулу Бернулли:

Обожка поста: pixabay.com

Источник

10 июня 2022

В закладки

Обсудить

Жалоба

Формула Бернулли. Примеры решения задач по теории вероятностей

formula-bernuli.docx
formula-bernuli.pdf

Источник

Задача 1: Из n аккумуляторов за год хранения k выходит из строя. Наудачу выбирают m аккумуляторов. Определить вероятность того, что среди них l исправных.
n = 100, k = 7, m = 5, l = 3.

Решение: Имеем схему Бернулли с параметрами p=7/100=0,07 (вероятность того, что аккумулятор выйдет из строя), n = 5 (число испытаний), k = 5-3 =2 (число «успехов», неисправных аккумуляторов). Будем использовать формулу Бернулли (вероятность того, что в n испытаниях событие произойдет k раз).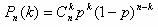
Получаем

Ответ: 0,0394.

Задача 2: Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента;
б) не менее четырех элементов;
в) хотя бы один элемент.

Решение: Имеем схему Бернулли с параметрами p = 0,2 (вероятность того, что элемент откажет), n = 5 (число испытаний, то есть число элементов), k (число «успехов», отказавших элементов). Будем использовать формулу Бернулли (вероятность того, что для n элементов отказ произойдет в k элементах):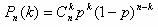
Получаем
а) 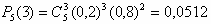— вероятность того, что откажут ровно три элемента из пяти.
б) 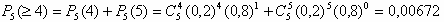— в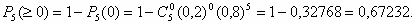ероятность того, что откажут не менее четырех элементов из пяти (то есть или четыре, или пять).
в) — вероятность того, что откажет хотя бы один элемент (нашли через вероятность противоположного события — ни один элемент не откажет).

Ответ: 0,0512; 0,00672; 0,67232.

Задача 3: Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?

Решение: Наивероятнейшее число побед k определяется из формулы

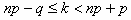
Здесь p =1/3 (вероятность победы), q = 2/3 (вероятность проигрыша), n — неизвестное число партий. Подставляя данные значения, получаем:

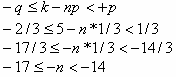
Получаем, что n = 15, 16 или 17.

Ответ: 15, 16, 17.

Калькуляторы на формулу Бернулли

Задача про партии в шахматы
Задача про выстрелы
Задача про мальчиков и девочек
Задача про лотерейные билеты
Задача о наивероятнейшем значении
Формула Пуассона

Еще: решаем в Excel по формуле Бернулли.

Полезная страница? Сохрани или расскажи друзьям

Схема Бернулли: решенные задачи

Формула Пуассона: решенные задачи

Мы отлично умеем решать задачи по теории вероятностей

Решебник — когда задачи нужны быстро

Категории раздела

Другое
[136]

Панорамы, статьи, идеи, предложения….

Программирование
[52]

Языки программирования, алгоритмы, программы

Немецкий язык
[19]

Тексты, задания, переводы

Обучение Фотошопу
[7]

Смотрим уроки, повторяем и тем самым учимся работать в программе Фотошоп!

Бесплатные программы
[36]

Все программы в данном разделе свободны для распространения.

Устройство компьютера
[5]

Из чего состоит компьютер?

ЕГЭ по математике
[9]

Разбор заданий по математике

SEO
[20]

Продвижение сайтов
[6]

Продвижение сайтов

ЕГЭ по русскому языку
[28]

Сочинения, билеты, тесты

ЕГЭ по физике
[29]

Разбор заданий/демоверсий и т.д.

Что-то новенькое
[0]

Время жизни сайта

Статистика

Онлайн всего: 1

Гостей: 1

Пользователей: 0

Друзья с Sape

Файлы/Документы

Информация:
Посетители, находящиеся в группе Гости,не могут скачивать файлы с данного сайта.

Формула Бернулли. Примеры решения задач.

	08.12.2013, 18:23
Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведенииn испытаний событие A появится ровно k раз. Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы. Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода: A — появление события A с вероятностью p; «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p. Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p. Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности. Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы: Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле: где C_n^k — число сочетаний, q = 1 − p. Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным. Задача Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10. Решение По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия. Таким образом, имеем: n = 10; p = 0,8; q = 0,2. Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10): Ответ 10⁻⁷; 4 · 10⁻⁶; 0,1 Задача Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что: герб выпадет три раза; герб выпадет один раз; герб выпадет не менее двух раз. Решение Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностьюq = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадетk раз. Таким образом, имеем: n = 6; p = 0,5; q = 0,5. Определим вероятность того, что герб выпал три раза, т.е. k = 3: Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1: Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы: X = P₆(2) + P₆(3) + … + P₆(6). Заметим, что эта сумма также равна (1 − P₆(0) − P₆(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P₆(1) нам уже известно, осталось найти P₆(0): Ответ 1) 5/16; 2) 3/32; 3) 57/64 Задача Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три? Решение Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8. Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8. Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3): Очевидно, P₂₀(3) > P₂₀(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая. Ответ P₂₀(3) > P₂₀(2) Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению. P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь. Расскажи друзьям:
Категория: ЕГЭ по математике \| Добавил: DaNcE-bOy \| Теги: Бернулли
Просмотров: 3427 \| Загрузок: 0 \| Рейтинг: 0.0/0

Добавлять комментарии могут только зарегистрированные пользователи.

[

Регистрация

Вход

]

Схема Бернулли возникает при повторных независимых испытаниях. Независимыми испытаниями называются такие, которые зависят друг от друга, и от результатов предыдущих испытаний. Они могут проводиться как в однотипных условиях, так и в разных. В первом случае вероятность появления какого-либо события во всех испытаниях одна и та же, во втором случае она меняется от опыта к опыту.

Пусть для каждого опыта вероятность появления события равна , вероятность противоположного события определяется зависимостью

Нужно найти вероятность появления события ровно раз в серии из испытаний. При этом следует отметить, что событие в серии опытов может чередоваться любым способом, главное чтобы исполнилась ровно раз.

Результаты испытаний для удобства обозначаем буквой в случае появления события и для противоположного.

Испытания в которых происходит раз и не происходит () раз по определению будут благоприятными. Их количество равно количеству способов выбора элементов с и определяется по формуле сочетания

Определим вероятность благоприятной комбинации (в серии из испытаний появления события ровно раз). Для простоты записи, рассмотрим случай, когда событие произошло в первых опытах и не состоялось в остальных . Схематично его можно обозначить следующим образом, а вероятность найти по теореме умножения вероятностей

для других благоприятных испытаний и вероятности будут такие же, только порядок их в серии из экспериментов будет постоянно меняться

Все благоприятные испытания являются попарно несовместимы, поэтому для нахождения общей вероятности их нужно просуммировать

или

Вывел ее впервые швейцарский математик Якоб Бернулли (1654 г.-1705 г.).

Если просуммировать вероятности всех испытаний в которых событие может произойти от нуля до раз в серии испытаний, то получим полную вероятность

Слагаемые этой суммы совпадают по виду с расписанием бинома Ньютона

Легко убедится, что

В литературе можно встретить термин «биномиальное распределение вероятностей», это как раз множество всех вероятностей, которые просуммированы выше.

Как последствия, из формулы Бернулли выводятся следующие формулы для популярных для практики задач:

1) вероятность появления события «хотя бы один раз» в серии из испытаний

2) вероятность появления события «хотя бы определенное количество раз» в серии из испытаний вычисляют по формуле

или согласно свойству биномиального разложения вероятностей

На основе данной зависимости вводят в рассмотрение сквозную функцию, которая дает возможность определить возможное количество появления события в серии из испытаний

По свойству сквозной функции множители при степени переменной () равны вероятности появления события в серии из опытов ровно раз. Это легко проследить по формуле суммирования вероятностей всех возможных испытаний по схеме Бернулли.

Если вероятности появления события в каждом опыте разные , а противоположного равны то по свойствам сквозной функции вероятность события произойти раз в серии из опытов равна множителю при в расписании функции по степеням

Она достаточно часто встречается при решении задач, в которых вероятности появления события в каждом последующем опыте меняются и позволяет при небольшом количестве появления события быстро найти вероятность (решение задачи).

Вероятное количество появлений события в схеме Бернулли лежит в интервале

Для применения схемы Бернулли нужно, чтобы выполнялись три условия:

1) опыты должны быть независимы между собой;

2) каждый опыт должен иметь два результата , и никаких других вариантов;

3) вероятность появления события должна быть одинаковой для каждого следующего опыта.

Рассмотрим решения типичных для данной схемы задач.

——————————

Пример 1. В тире стрелок проводит 7 выстрелов по мишени с вероятностью попадания каждого 0,8. Какова вероятность того, что будет: а) ровно 4 попадания б) не менее 5 попаданий в) не более двух попаданий.

Решение. а) проводится независимых друг от друга испытаний с вероятностью попадания в мишень в каждом из них . Вероятность того, что будет точно попаданий вычисляем по формуле Бернулли:

б) событие , которое заключается в том, что при выстрелах будет не менее 5 попаданий, можно рассматривать как сумму трех несовместных событий: – 5 попаданий из 7, событие – 6 попаданий с 7 и – все 7 выстрелов метки.

По формуле Бернулли находим вероятности событий

Тогда вероятность события равна сумме найденных вероятностей

в) Подобным образом, вероятность события – не более двух попаданий при семи выстрелах можно вычислить, как сумму вероятностей трех событий:

– 2 попадания из 7,

– 1 из 7 ,

– ни одного попадания из 7 выстрелов (7 промахов).

На практике студенты часто забывают рассматривать событие — подобное отсутствию попадений , поэтому не делайте подобных ошибок и хорошо запомните возможность возникновения такого варианта. Вероятности находим по знакомой уже формуле

Суммируя вероятности получим

Однако, события (не более двух попаданий при семи выстрелах) и (не менее 5 попаданий при семи выстрелах) противоположны друг другу, поэтому

——————————

Пример 2. Монета подбрасывают пять раз. Найти вероятность того, что герб выпадет не более трех раз.

Решение. Вероятность выпадения герба или решки считаем независимым событием с вероятностью . По аналогии с предыдущей задачей, искомая вероятность равна сумме трех следующих

Чтобы не искать столько слагаемых, из приведенных выше формул получим простую

——————————

Пример 3. Вероятность появления события в одном опыте равна 0,4. Сколько нужно провести опытов, чтобы вероятное количество появления события была равна 20.

Решение. Согласно условия выписываем данные

и проводим расчеты согласно неравенству

С него получим

три числа 49,50,51.

——————————

Пример 4. Три биатлониста независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого равна 0,9, для второго — 0,85, для третьего — 0,8. Найти вероятность того, что будут закрыты две мишени из трех.

Решение. Вероятности попадания для стрелков разные, поэтому применяем образующую функцию. Для нее входные данные примут значения

После подстановки и разложения в ряд получим

Искомая вероятность входит в расписание множителем при

Из этого примера также легко убедиться, что сумма всех множителей при степенях равна полной вероятности (единицы).

——————————

Схема Бернулли на практике не сложная, важно уловить как в вычислениях реализовать задачи вида «не более раз», «не менее раз», «ровно раз» с . Как только Вы это поймете, все остальное сведется к суммирования, умножению и возведения в степень.

Урок по теории вероятностей для 11 класса по теме: «Схема Бернулли. Формула Бернулли»

Корнюшина Татьяна Анатольевна
учитель математики, МБОУ «Гимназия №4», г. Брянск

Цель:

-формирование вероятностно-статистическое мышление учащихся;

-мотивация учащихся к изучению тем теории вероятностей;

-ознакомление с применением формулы Бернулли при решении задач.

Задачи:

-закрепить знания и умения решать комбинаторные задачи;

— формировать навыки применения схемы Бернулли при решении задач,

-формировать навыки решения задач по формуле Бернулли,

-развивать основные мыслительные операции учащихся: умение сравнивать, анализировать.

Тип урока: изучение нового материала.

Формы работы: фронтальная, индивидуальная, групповая.

Оборудование: компьютер, презентация.

Ход урока:

Актуализация знаний.

Вспомним основные понятия и формулы комбинаторики.

1. Что называется факториалом числа n?

Это произведение первых натуральных n чисел от 1 до n.

2.Сколькими способами можно расставить 4 различные книги на полке?

3! = 3·2·1

Это число перестановок из 3 элементов.

3. Сколькими способами можно распределить I, II, III места между 7 участниками соревнования?

7·6·5=210

Это число размещений из 7 элементов по 3.

4. Сколькими способами можно составить график дежурства 3 учащихся из 5?

Презентация (слайд 1)

5. Сформулируйте классическое определение вероятности.

Презентация (слайд 2)

Презентация (слайд 3)

Организационный момент.

(Сообщение темы, целей и задач урока)

Презентация (слайд 4)

Изучение нового материала.

При практическом применении теории вероятностей и математической статистики часто приходится встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или не появиться событие A, причем нас интересует не результат каждого опыта, а общее число появлений события A в серии опытов. Например, если производится серия выстрелов по одной и той же цели, то нас, как правило, интересует не результат каждого отдельного выстрела, а общее число попаданий. При этом результаты предыдущих опытов никак не сказываются на последующих.

Такая стандартная схема часто встречается и в самой теории вероятностей. Она называется схемой независимых испытаний или схемой Бернулли. Швейцарский математик XVII в. Якоб Бернулли объединил примеры и вопросы такого типа в единую вероятностную задачу-схему (работа «Искусство предположений» опубликована в 1713 году).

Историческая справка. Якоб Бернулли (27.12.1654, Базель, — 16.8.1705, там же) — профессор математики Базельского университета (1687) был выходцем из Голландии.

Вам дома надо было вычислить вероятность выпадения 6 на игральном кубике.

(Ученики называют результаты. Вывод: результаты могут зависеть и от размера кубика. от силы бросания и т.п.)

Несколько опытов называются независимыми, если вероятность исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. Например, несколько последовательных бросаний монеты — это независимые опыты. Несколько последовательных выниманий карты из колоды — независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются. В противном случае — это зависимые опыты.

Презентация (слайд 5)

Примеры.

Монета бросается n раз.

Из колоды извлекается карта n раз, причём каждый раз карта возвращается, колода перемешивается.

Исследуется n изделий некоторого производства, наугад выбранные, на качество.

Стрелок стреляет по мишени n раз и т.д.

Задание.

№1. Объясните, почему следующие вопросы укладываются в схему Бернулли. Укажите, в чем состоит «успех» и чему равны n и k.

а) Какова вероятность трехкратного выпадения «двойки» при десяти бросаниях игрального кубика?

б) Какова вероятность того, что при ста бросаниях монеты «орел» появится 73 раза?

в) Двадцать раз подряд бросили пару игральных кубиков. Какова вероятность того, что сумма очков ни разу не была равна десяти?

г) Из колоды в 36 карт вытащили три карты, записали результат и возвратили их в колоду, затем карты перемешали. Так повторялось 4 раза. Какова вероятность того, что каждый раз среди вытащенных карт была дама пик?

Решение. Ответы учащихся с использованием слайда 5 (парная работа).

Схема Бернулли предполагает, что один и тот же эксперимент повторяется в неизменных условиях, независимо, n раз; мы наблюдаем за появлением («успеха») или непоявлением («неудача») в каждом эксперименте одного и того же события А, вероятность появления которого в каждом эксперименте постоянна и равна p. Подсчитываем, сколько раз в серии из n повторных экспериментов произойдет событие А; k – это число «успехов» в серии из n испытаний.

а) Эксперимент – бросание кубика, число повторений n = 10.

Событие А – «выпало 2 очка» (Р(А)=const); успех – появление события А (появление двойки), число успехов k=3.

б) Эксперимент – бросание монеты, число повторений n = 100, событие А – «выпал орел» (Р(А)==const), успех – появление события А (появление «орла»), число успехов k=73.

в) Эксперимент – бросание двух кубиков одновременно, число повторений n =20, событие А – «сумма выпавших очков равна 10» (Р(А)==const), успех – появление события А (сумма выпавших очков оказалась 10); число успехов k = 0.

г) Эксперимент – извлечение одновременно трех карт из колоды 36 карт, число повторений n= 4, событие А – «среди извлеченных карт есть дама пик» (Р(А)==const), успех – появление события А (появление дамы пик в наборе); число успехов k= 4.

Ответ: а) n = 10, k=3; б) n =100, k =73; в) n = 20, k = 0; г) n = 4, k = 4.

Замечание. При решении этой задачи учащимся не нужно вычислять Р(А), достаточно сказать, что событие А имеет одну и ту же вероятность при каждом повторении эксперимента.

Презентация (слайд 6)

Решение заданий

Пример 1. Монета бросается 6 раз. Какова вероятность выпадения герба 0, 1, …6 раз?

Решение. Число опытов n=6. Событие А – «успех» – выпадение герба. Тогда .

;

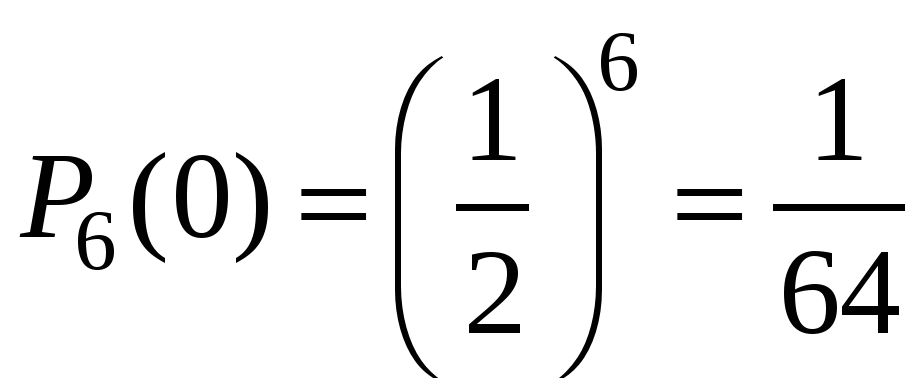
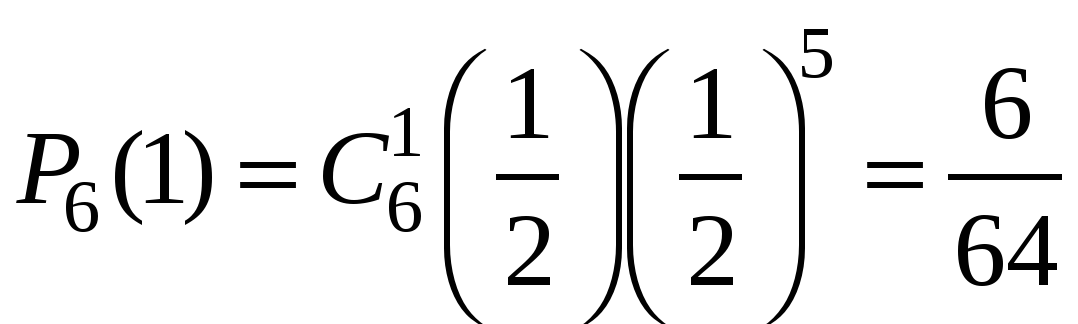
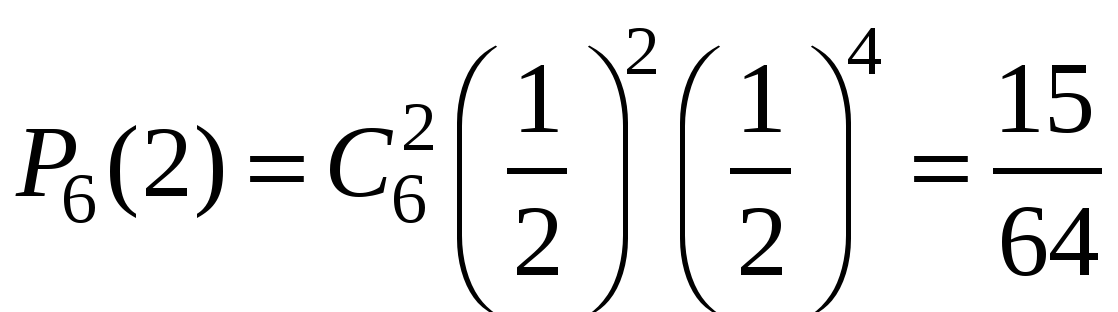
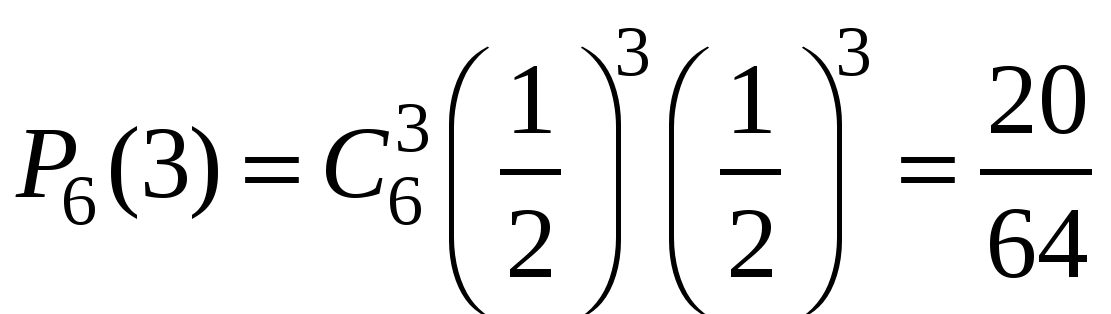
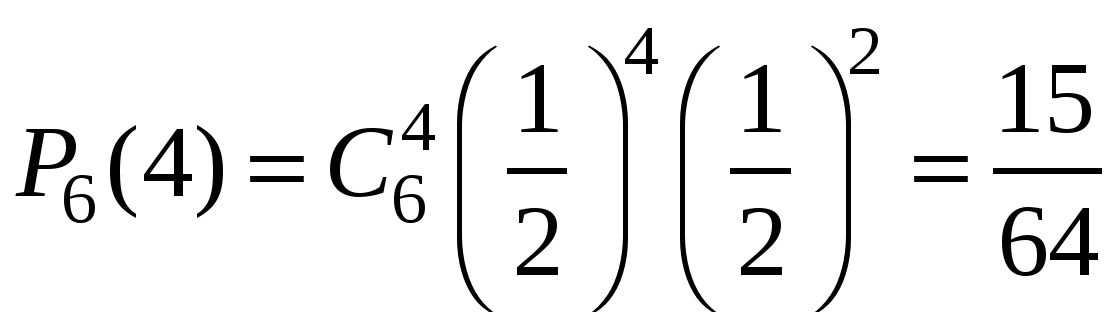
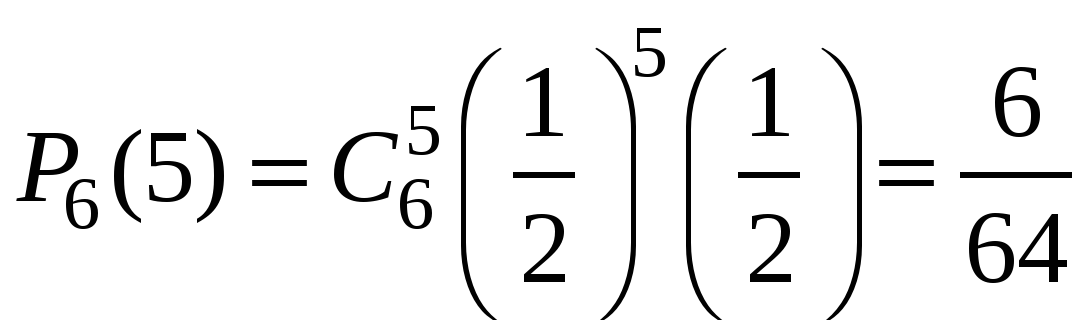
Очевидно, что наиболее вероятное число выпадений герба равно трём. Но далеко не каждый раз при шести бросаниях монеты герб выпадет ровно три раза! Вероятность говорит о том, что это будет происходить меньше, чем в трети случаях.

Пример 2. Монета бросается 10 раз. Какова вероятность двукратного появления герба?

Решение. Число опытов n=10, m= 2. Событие А – «успех» – выпадение герба. Тогда .

Ответ: 0,04395.

Пример 3. Вероятность того, что изделие не пройдет контроля, равна 0,125. Какова вероятность того, что среди 12 изделий не будет ни одного забракованного контролером?

Решение. Число опытов n=12, m=0. Событие А – «успех» – не будет ни одного забракованного. Тогда .

Ответ: 0,2514.

Домашнее задание

В следующих испытаниях найдите вероятности «успеха» и «неудачи».

а) Бросают пару различных монет. «Неудача» — выпадение двух «орлов».

б) Бросают игральный кубик. «Успех» — выпадение числа, кратного трем.

в) Бросают пару различных кубиков. «Неудача» — выпадение двух четных чисел.

г) Из 36 игральных карт берут 5. «Успех» — среди них нет дамы пик.

Решение.

а) Общее число исходов эксперимента n=2·2=4; вероятность «неудачи» ; вероятность «успеха» .

б) n=6; исходы, благоприятствующие «успеху» — выпадение 3 и 6 очков; ; вероятность «успеха» ; вероятность «неудачи» .

в) n=6·6=36; количество исходов, благоприятствующих «неудаче», (на каждом кубике 3 четные числа); вероятность «неудачи» ; вероятность «успеха» .

г) =376992; количество исходов, благоприятствующих «успеху», равно (выбираем карту из колоды без дамы пик);

вероятность «успеха» = = ,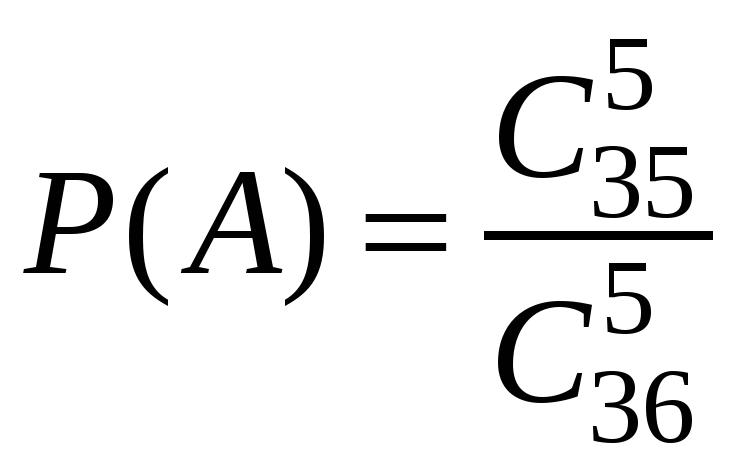

вероятность «неудачи» .

Подведение итогов

Источник

Задача №1.В Московской области при выращивании озимой ржи сорта Чулпан с применением почвозащитных технологий обработки почвы и средств химизации вероятность гибели более 92% всех сорняков равна 0,8. На опытном поле, разбитом на делянки, случайным образом выбрано 5 делянок. Найти вероятность того, что не менее, чем на двух из них погибнет более 92% сорняков.
Решение. Испытание состоит в проверке факта гибели более 92% сорняков на одной делянке. Общее число испытаний n = 5. Все испытания являются независимыми. Событие , которое может произойти или не произойти в каждом испытании — гибель более 92% сорняков. Вероятность р = 0,8, вероятность q = 0,2. Рассмотрим событие:
— более 92% сорняков погибнет не менее, чем на двух делянках из пяти.
Вероятность события в представляет собой вероятность того, что число m появлений события в пяти испытаниях будет больше или равно двум и меньше или равно пяти. Искомая вероятность равна

$P(B)=P(2leq mleq 5)=P_{5}(2)+P_{5}(3)+P_{5}(4)+P_{5}(5).$

Каждое из четырех слагаемых в последнем равенстве найдем по формуле Бернулли.
Решение будет более коротким, если рассмотреть событие bar{B} , противоположное событию . Событие bar{B} состоит в том, что более 92% сорняков погибнет менее, чем на двух делянках, т. е. или ни на одной, или на одной делянке. Воспользовавшись формулой (4) для определения вероятности противоположного события и теоремой сложения вероятностей несовместных событий, получим

$P(B)=P(2leq mleq 5)=1-P(0leq mleq 1)=1-(P_{5}(0)+P_{5}(1)).$

Вероятности $P_{5}(0)$ и $P_{5}(1)$ найдем по формуле Бернулли. Таким образом,

$P(B)=P(2leq mleq 5)=1-C_{5}^{0}p^{0}q^{5}-C_{5}^{1}p^{1}q^{4}=1-(0,2)^{5}-5cdot (0,8)^{1}cdot (0,2)^{4}=0,99328.$

Задача №2. Вероятность того, что из четырех кустов садовой земляники сорта Талисман, отобранных с некоторого участка случайным образом, хотя бы один куст поражен вилтом, равна 0,3439. Какова вероятность поражения вилтом одного куста земляники, если для всех кустов эта вероятность одинакова?
Решение. Испытание состоит в проверке одного куста земляники. Общее число испытаний n = 4. Испытания являются независимыми. Событие , которое может появится или не появится в каждом испытании, состоит в том, что проверенный куст поражен вилтом. Рассмотрим события:
— вилтом поражен хотя бы один куст из четырех кустов земляники;
bar{C} — ни один из четырех кустов не поражен вилтом.

Событие bar{C} противоположно событию . Используя формулу (4) для определения вероятности противоположного события и формулу (1), по которой найдем $P(bar{C})=P_{4}(0)$ , получим:

$P(C)=1-P_{4}(0)=1-q^{4}=0,3439,$

где q=1-p.
Решив уравнение $1-q^{4}=0,3439$ , найдем q = 0,9 ; отсюда получим p = 0,1.

Задача №3. Две электрические лампочки включены в цепь параллельно. Вероятность того, что при некотором повышении напряжения в цепи выше номинального перегорит только одна лампочка, равна 0,18. Найти вероятности перегореть для каждой из этих лампочек, если известно, что эти вероятности превосходят 0,7 и равны между собой.
Решение. Испытание состоит в проверке работы электрической лампочки. Общее число испытаний n =2. Испытания являются независимыми. Событие , которое может произойти или не произойти в каждом испытании, состоит в том, что при повышении напряжения в цепи лампочка не перегорит. Известна вероятность того, что не перегорит только одна лампочка (без указания, какая именно). Так как вероятности наступления события в каждом испытании равны между собой, то известна вероятность $P_{2}(1)$ , определяемая по формуле Бернулли. По условию $P_{2}(1)=0,18$ . Требуется найти вероятность р наступления события в каждом испытании.
По формуле Бернулли получим

$P_{2}(1)=C_{2}^{1}p^{1}q^{1}=2p(1-p)=0,18.$

Отсюда следует, что неизвестная вероятность р может быть найдена как корень квадратного уравнения $p^{2}-p+0,09=0$ . Это уравнение имеет два корня: $p_{1}=0,9$ и $p_{2}=0,1$ . По условию

Источник

Примеры решений задач на формулу Бернулли

Калькуляторы на формулу Бернулли

Схема Бернулли: решенные задачи

Формула Пуассона: решенные задачи

Решебник — когда задачи нужны быстро

Схема Бернулли. Примеры решения задач

Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Попробуйте решить пару подобных задач самостоятельно, и такие новые задачи по теорверу вас больше не смутят. Но сперва выучите формулу Бернулли:

Формула Бернулли. Примеры решения задач по теории вероятностей

Калькуляторы на формулу Бернулли

Схема Бернулли: решенные задачи

Формула Пуассона: решенные задачи

Решебник — когда задачи нужны быстро

Категории раздела

Реклама

Время жизни сайта

Статистика

Друзья с Sape

Ход урока:

Актуализация знаний.

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" height="261" src="https://fsd.videouroki.net/html/2017/09/30/v_59cfd18308cc5/v99695177_1_2.png" width="348" />

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" height="267" src="https://fsd.videouroki.net/html/2017/09/30/v_59cfd18308cc5/v99695177_1_3.png" width="356" />

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" height="279" src="https://fsd.videouroki.net/html/2017/09/30/v_59cfd18308cc5/v99695177_1_4.png" width="372" />

Организационный момент.

Изучение нового материала.

Примеры.

Задание.

Решение заданий

Домашнее задание

Подведение итогов