Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В основании правильной треугольной призмы ABCA1B1C1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A1C1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
2
В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.
3
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA = 5 : 3, на ребре BB1 — точка F так, что B1F : FB = 5 : 11, а точка T − середина ребра B1C1. Известно, что AD = 10, AA1 = 16.
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
4
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E = 6EA. Точка T — середина ребра B1C1. Известно, что AD = 12, AA1 = 14.
а) Докажите, что плоскость ETD1 делит ребро BB1 в отношении 4 : 3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD1.
5
Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна
Точка K — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)
Пройти тестирование по этим заданиям
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на построение сечений
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Важные факты и теоремы, необходимые для построения сечений
(blacktriangleright) Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются.
Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.
(blacktriangleright) Теорема о параллельности трех прямых: если (aparallel b, bparallel c), то и (aparallel c).
(blacktriangleright) Определение: прямая и плоскость параллельны, если они не имеют общих точек.
Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
(blacktriangleright) Определение: две плоскости параллельны, если они не имеют общих точек.
Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.
(blacktriangleright) Если две плоскости пересекаются, то их линия пересечения — прямая.
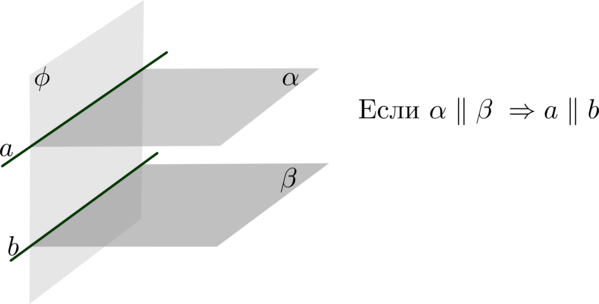
(blacktriangleright) Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)
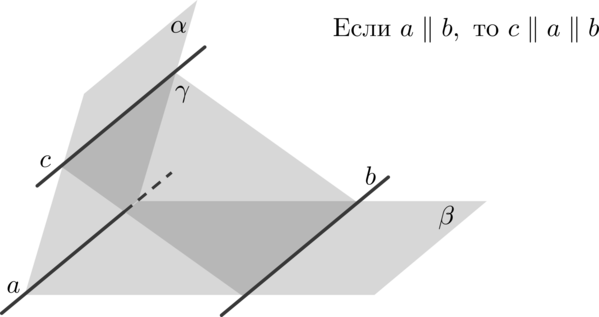
(blacktriangleright) Если плоскости (alpha) и (beta) пересекаются по прямой (a), а плоскости (beta) и (gamma) пересекаются по прямой (b), причем (aparallel b), то плоскости (alpha) и (gamma) пересекутся по прямой (cparallel aparallel b).
Задание
1
#999
Уровень задания: Легче ЕГЭ
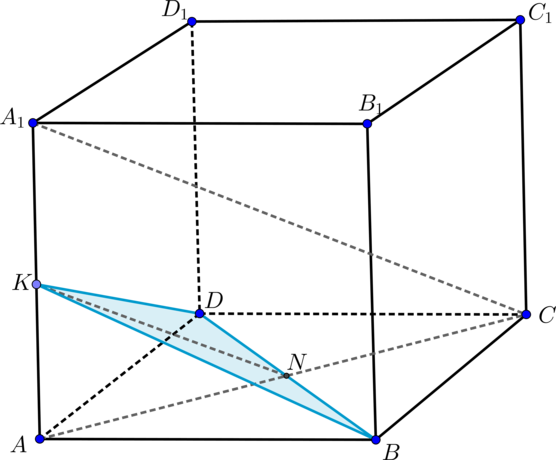
Дан куб (ABCDA_1B_1C_1D_1). Через точку (K), середину ребра (AA_1), и точку (B) проведите плоскость (alpha) параллельно диагонали (A_1C).
Т.к. (A_1Cparallel alpha Rightarrow A_1C) параллельна некоторой прямой, содержащейся в (alpha). Рассмотрим плоскость (AA_1C_1C), в которой находится (A_1C). Т.к. точка (Kin AA_1C_1C), то проведем в этой плоскости (KN parallel A_1C) (по теореме Фалеса (N) – середина (AC)).
Т.к. (ABCDA_1B_1C_1D_1) – куб, то (N) – точка пересечения диагоналей квадрата (ABCD), следовательно, (Nin BD). Таким образом, получили сечение (KBD) куба плоскостью (alpha).
Ответ:
Рисунок.
Задание
2
#3981
Уровень задания: Легче ЕГЭ
Дан куб (ABCDA_1B_1C_1D_1). На ребрах (AA_1) и (BC) отмечены точки (M) и (N) соответственно, причем (AM:MA_1=2:1), а (N) – середина (BC). Найдите сечение куба плоскостью (DMN).
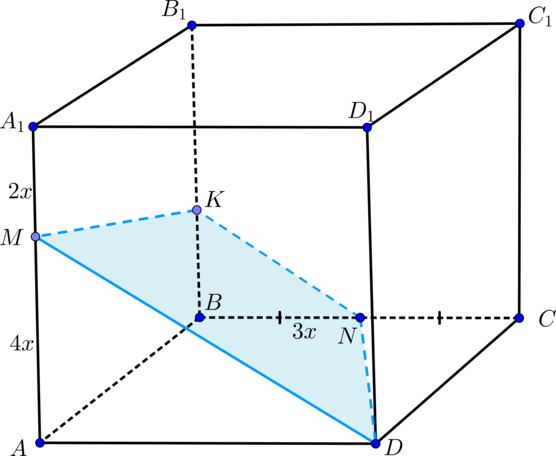
Т.к. грани (ADD_1A_1) и (BCC_1B_1) куба параллельны, то плоскость (DMN) пересечет их по параллельным прямым. Таким образом, проведем (NKparallel DM). Таким образом, (DNKM) – искомое сечение.
Необходимо найти точное расположение точки (K).
Обозначим ребро куба за (6x). Т.к. (bigtriangleup ADM sim
bigtriangleup BNK Rightarrow dfrac{BK}{AM}=dfrac{BN}{AD}
Rightarrow BK=2x). Таким образом, (BK:KB_1=1:2).
Ответ:
Рисунок.
Задание
3
#3804
Уровень задания: Равен ЕГЭ
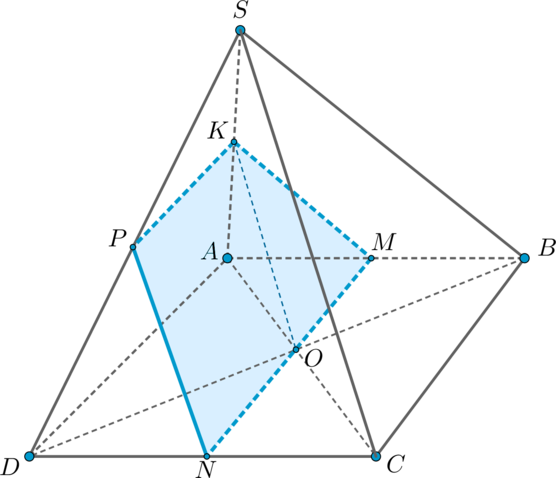
(SABCD) – четырехугольная пирамида, в основании которой лежит квадрат (ABCD), а две боковые грани (SAB) и (SAD) представляют собой прямоугольные треугольники с прямым углом (angle A).
1) Проведите плоскость (alpha) через точку пересечения диагоналей основания параллельно грани (SBC).
2) Найдите площадь сечения пирамиды плоскостью (alpha), если (SA=AB=a).
1) Пусть (ACcap BD=O). Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Заметим, что т.к. (angle SAB=angle SAD=90^circ Rightarrow
SAperp
(ABC)).
Проведем в плоскости (SAC) прямую (OKparallel SC). Т.к. (O) – середина (AC), то по теореме Фалеса (K) – середина (SA). Через точку (K) в плоскости (SAB) проведем (KMparallel SB) (следовательно, (M) – середина (AB)). Таким образом, плоскость, проходящая через прямые (OK) и (KM), и будет искомой плоскостью.
Необходимо найти сечение пирамиды этой плоскостью. Соединив точки (O) и (M), получим прямую (MN).
Т.к. (alphaparallel (SBC)),то (alpha) пересечет плоскость (SCD) по прямой (NPparallel SC) (если (NPcap SC ne varnothing), то (alphacap (SBC)ne varnothing), что невозможно ввиду их параллельности).
Таким образом, (KMNP) – искомое сечение, причем (KPparallel
ADparallel MN Rightarrow) это трапеция.
2) Т.к. все точки (K,M,N,P) – середины отрезков (SA, AB, CD, SD) соответственно, то:
а) (MN=AD=a)
б) (KP=dfrac{1}{2}AD=dfrac{a}{2})
в) (KM=dfrac{1}{2}SB=dfrac{asqrt2}{2})
Заметим, что по теореме о трех перпендикулярах (SBperp BC
Rightarrow KMperp MN). Таким образом, (KMNP) – прямоугольная трапеция.
(S_{KMNP}=dfrac{KP+MN}{2}cdot KM=dfrac{3sqrt2}{8}a^2)
Ответ:
1) Рисунок.
2) (dfrac{3sqrt2}{8}a^2)
Задание
4
#1003
Уровень задания: Равен ЕГЭ
Дана правильная треугольная пирамида (SABC) с вершиной (S). Проведите плоскость через середину ребра (AC) и точки пересечения медиан граней (ASB) и (CSB). Найдите площадь сечения пирамиды этой плоскостью, если (AB=21, AS=12sqrt2).
1) Пусть(K) – середина (AC), (SX, AL) – медианы грани (ASB), (CL,
SY) – медианы грани (CSB), (ALcap SX=M, CLcap SY=N). (SO) – высота пирамиды.
Найдем сечение пирамиды плоскостью (MNK).
Т.к. пирамида правильная, то (triangle SXY) – равнобедренный, (SM=SN=dfrac{2}{3}SX Rightarrow MNparallel XY Rightarrow
MNparallel (ABC)). Таким образом, плоскость (MNK) содержит прямую (MN), параллельную (ABC), следовательно, плоскость (MNK) пересечет плоскость (ABC) по прямой, параллельной (MN) (если это не так, то линия пересечения этих плоскостей (lcap MN=E Rightarrow Ein
(ABC)) и (Ein MN Rightarrow MN) не может быть параллельна ((ABC))).
Прямая, проходящая через точку (K) и параллельная (MN) (или (XY)) – это (AC). Следовательно, сечением является равнобедренный треугольник (ALC).
2) Пусть (LKcap SO=H). Тогда по теореме о трех перпендикулярах (HKperp AC) как наклонная ((HOperp (ABC), OKperp AC) как проекция). Следовательно, и (LKperp AC).
Тогда (S_{ALC}=dfrac{1}{2}ACcdot LK).
Рассмотрим (triangle SKB: BK=ABcdot
dfrac{sqrt3}{2}=dfrac{21sqrt3}{2} Rightarrow cos
B=dfrac{7sqrt3}{12sqrt2}).
Тогда по теореме косинусов для (triangle KLB):
(KL^2=dfrac{729}{4} Rightarrow KL=dfrac{27}{2})
Значит, (S_{ALC}=dfrac{567}{4}).
Ответ:
(dfrac{567}{4}).
Задание
5
#3792
Уровень задания: Сложнее ЕГЭ
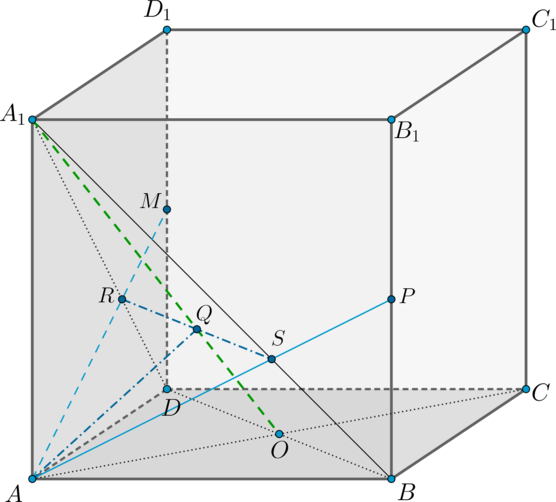
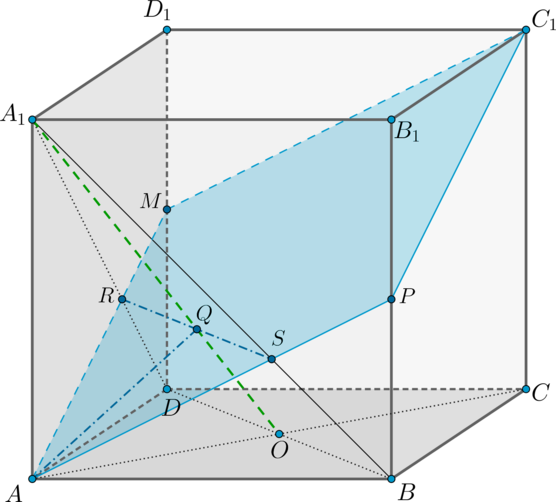
Дан куб (ABCDA_1B_1C_1D_1). Диагонали основания (AC) и (BD) пересекаются в точке (O). Найдите сечение куба плоскостью (alpha), проходящей через точку (A) перпендикулярно прямой (A_1O).
1) Если (A_1Operp alpha), то (A_1O) перпендикулярно двум пересекающимся прямым, лежащим в плоскости (alpha). Построим эти две прямые.
Рассмотрим плоскость (AA_1C_1C) ((A_1O) лежит в этой плоскости). Проведем в ней (AQperp A_1O). Теперь необходимо через их точку пересечения (точку (Q)) провести еще одну прямую перпендикулярно (A_1O).
Рассмотрим для этого плоскость (A_1BD) ((A_1O) лежит в этой плоскости). Проведем через точку (Q) прямую (RSperp A_1O). Т.к. по теореме о трех перпендикулярах (A_1Operp BD) как наклонная ((A_1Aperp (ABC), AOperp BD) – проекция), то (RSparallel BD).
2) Проведем прямые (AR) и (AS). Они могут пересечь либо сами ребра (DD_1) и (BB_1), либо их продолжения. Т.к. от этого зависит вид сечения, определим расположение точек (R) и (S).
Обозначим ребро куба за (a). Тогда (AO=dfrac{asqrt2}{2}=dfrac
a{sqrt2}). Рассмотрим прямоугольный (triangle AA_1O). Так как (AQperp A_1O), то по свойству прямоугольного треугольника (triangle AA_1Qsim triangle AA_1O). Следовательно, [dfrac{A_1Q}{AA_1}=dfrac{AA_1}{A_1O}] Так как по теореме Пифагора (A_1O=sqrt{a^2+frac{a^2}2}=dfrac{sqrt6 a}2), то [A_1Q=dfrac{AA_1^2}{A_1O}=dfrac{sqrt6}3a]
Так как (RSparallel BD), то (triangle A_1DOsim triangle A_1RQ), следовательно, [dfrac{A_1R}{A_1D}=dfrac{A_1Q}{A_1O}=dfrac{sqrt6}3:dfrac{sqrt6}2=
dfrac23] Аналогично (A_1S:A_1B=2:3).
Заметим, что (triangle AA_1Rsim triangle MDR) с коэффициентом подобия (2) ((A_1R:RD=2:1)), следовательно, (MD=frac12AA_1).
Аналогично (PB=frac12AA_1).
Таким образом, получили линии пересечения плоскостей (AA_1D_1) и (AA_1B_1) с плоскостью (alpha) – прямые (AM) и (AP).
3) Так как плоскости (AA_1B_1) и (DD_1C_1) параллельны, то плоскость (alpha) пересечет их по параллельным прямым. Следовательно, в плоскости (DD_1C_1) через точку (M) нужно провести прямую, параллельную (AP).
Так как (M) и (P) – середины (DD_1) и (BB_1), то (MC_1parallel
AP).
Таким образом, сечение куба плоскостью (alpha) – это четырехугольник (AMC_1P) (который, вообще говоря, является ромбом, так как (AM=AP=MC_1) и (MC_1parallel AP)).
Ответ:
Рисунок.
Задание
6
#2451
Уровень задания: Сложнее ЕГЭ
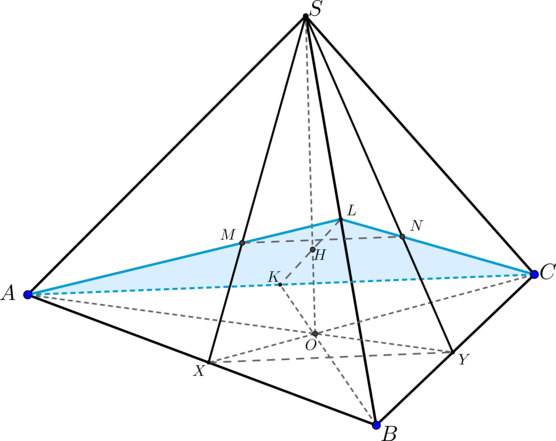
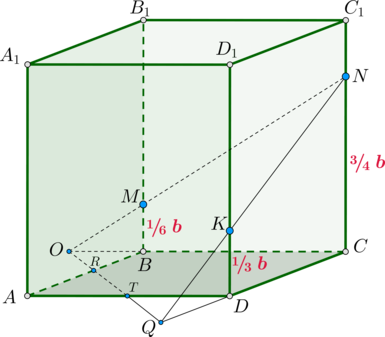
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1), в основании которого лежит квадрат (ABCD). На ребрах (BB_1), (CC_1), (DD_1) отмечены точки (M, N, K) соответственно так, что (BM:MB_1=1:5), (CN:NC_1=3:1), (DK:KD_1=1:2).
Найдите отношение отрезков, на которые делит плоскость (MNK) диагональ (AC).
Обозначим ребро основания за (a), а боковое ребро за (b). Тогда из условия задачи следует, что (BM=frac16b), (CN=frac34b), (DK=frac13b).
Найдем положение точек (R) и (T), в которых плоскость пересекает ребра (AB) и (AD) соответственно.
1) Продлим отрезки (NK) и (CD) до пересечения в точке (Q). Тогда (triangle QDKsim triangle QNC). Следовательно,
[dfrac{QD}{QC}=dfrac{KD}{NC} quad Rightarrow quad
dfrac{QD}{QD+a}=dfrac{frac13b}{frac34b}=dfrac49 quad
Rightarrow quad QD=dfrac45a.]
Аналогично из (triangle OMBsim triangle ONC) получаем, что [OB=dfrac27a.]
Соединив точки (Q) и (O), получим точки пересечения плоскости с ребрами (AB) и (AD).
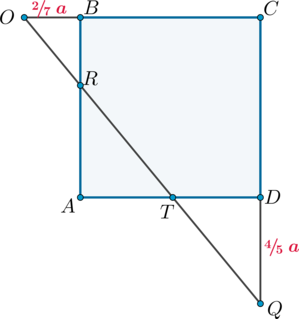
2) Рассмотрим основание.
(triangle OBRsim triangle OCQ), следовательно,
[dfrac{OB}{OC}=dfrac{BR}{CQ} quad Rightarrow quad
dfrac{frac27a}{frac97a}=dfrac{BR}{frac95a} quad Rightarrow
quad BR=dfrac25a.]
(triangle OBRsim triangle TAR), следовательно,
[dfrac{OB}{AT}=dfrac{BR}{AR}quad Rightarrow quad
dfrac{frac27a}{AT}=dfrac{frac25a}{frac35a} quad Rightarrow
quad AT=dfrac37a.]
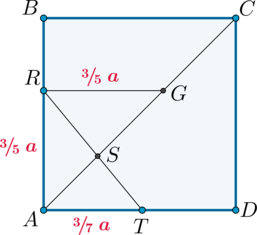
3) Для того, чтобы найти, в каком отношении (RT) поделит (AC), проведем прямую (RGparallel AD), (Gin AC).
Тогда (triangle ARG) – прямоугольный и (angle RAG=45^circ), то есть он равнобедренный и (RG=frac35a). Тогда по теореме Фалеса (AG:AC=AR:AB=3:5), следовательно, т.к. (AC=asqrt2), то (AG=frac{3sqrt2}5a).
(triangle ASTsim triangle RSG), следовательно,
[dfrac{AT}{RG}=dfrac{AS}{SG} quad Rightarrow quad
dfrac{frac37a}{frac35a}=dfrac{AS}{frac{3sqrt2}5a-AS} quad
Rightarrow quad AS=dfrac{sqrt2}4a.]
Тогда (SC=asqrt2-frac{sqrt2}4a=frac{3sqrt2}4a) и (AS:SC=1:3).
Ответ:
(1:3)
Теме «Построение сечения» в ЕГЭ по математике профильного уровня посвящается, как правило, несколько заданий. Они могут требовать от школьника как краткого ответа, так и полного развернутого решения. Если одним из ваших слабых мест являются именно задачи на сечения (в ЕГЭ при этом вы хотите получить конкурентные баллы), непременно стоит повторить или вновь разобраться в материале.
Сделать это наиболее эффективно вам поможет образовательный математический проект «Школково». Наши специалисты подготовили теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко справиться с решением задач на сечение.
Полезная информация
Для того чтобы выполнить построение сечений в ЕГЭ, нужно отметить точки пересечения пространственной фигуры с ребрами и произвести их соединение, начертив отрезки.
Необходимо запомнить
Производится соединение только двух точек, которые лежат в плоскости одной грани. Прежде чем приступить к решению задачи на построение сечений, полезно повторить материал о параллельных прямых. Сделать это вы можете, посетив раздел «Теоретическая справка».
Также необходимо запомнить, что пересечение секущей плоскости параллельных граней возможно только по параллельным отрезкам.
В том случае, когда в плоскости грани обозначена только одна точка, которая принадлежит плоскости сечения, следует отметить еще одну дополнительную. Для того чтобы это сделать, нужно определить точки пересечения прямых, которые уже построены, с теми, которые лежат в тех же гранях.
Выполнив построение сечений многогранников в задачах, которые представлены в нашем «Каталоге», вы сможете закрепить изученный материал и успешно справиться с подобным заданием на ЕГЭ в Москве.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
ЕГЭ Профиль №13. Площадь сечения
Скачать файл в формате pdf.
ЕГЭ Профиль №13. Площадь сечения
При нахождении угла между двумя плоскостями можно использовать теорему о площади ортогональной проекции многоугольника. При применении этого метода угол φ между плоскостями α и β можно вычислить, используя формулу (cos phi = frac{{{S_{пр}}}}{S}), где S — площадь многоугольника, лежащего в плоскости α, ({S_{пр}}) — площадь его ортогональной проекции на плоскость β. Следовательно, площадь многоугольника, лежащего в плоскости α равна (S = frac{{{S_{пр}}}}{{cos varphi }}.)
1В. Точки P и Q — середины рёбер AD и CC1 куба ABCDA1B1C1D1 соответственно.
а) Докажите, что прямые B1P и QB перпендикулярны.
б) Найдите площадь сечения куба плоскостью, проходящей через точку P и перпендикулярной прямой BQ, если ребро куба равно 2.
2В. В основании правильной треугольной пирамиды ABCD лежит треугольник ABC со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре AD отмечена точка T так, что AT : TD = 2 : 1. Через точку T параллельно прямым AC и BD проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
3В. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB = 4, BC = 3, AA1 = 2. Точки P и Q — середины рёбер A1B1 и CC1 соответственно. Плоскость APQ пересекает ребро B1C1 в точке U.
а) Докажите, что B1U : UC1 = 2 : 1.
б) Найдите площадь сечения параллелепипеда ABCDA1B1C1D1 плоскостью APQ.
ОТВЕТ: (frac{{11sqrt 3 }}{2}.)
4В. В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 6, а боковое ребро AA1 равно (4sqrt 3 ). На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
5В. Дан прямой круговой конус с вершиной M. Осевое сечение конуса — треугольник с углом ({120^ circ }) при вершине M. Образующая конуса равна (2sqrt 3 ). Через точку M проведено сечение конуса, перпендикулярное одной из образующих.
а) Докажите, что получившийся в сечении треугольник тупоугольный.
б) Найдите площадь сечения.
6В. В правильной треугольной пирамиде SABC сторона основания AB равна 24, а боковое ребро SA равно 19. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C.
б) Найдите площадь многоугольника, который является сечением пирамиды SABC плоскостью α.
7В. На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E : EA = 5 : 3, на ребре BB1 — точка F так, что B1F : FB = 5 : 11, а точка T — середина ребра B1C1. Известно, что (AB = 6sqrt 2 ), AD = 10, AA1 = 16.
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
8В. На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E = 6EA. Точка T — середина ребра B1C1. Известно, что (AB = 4sqrt 2 ), AD = 12, AA1 = 14.
а) Докажите, что плоскость ETD1 делит ребро BB1 в отношении 4 : 3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD1.
9В. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K — середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
10В. Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M.
а) Докажите, что MD : MD1 = 2 : 1
б) Найдите площадь сечения, если AB = 4, AA1 = 6.
11В. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ : QB = 1 : 2. Точка P — середина ребра AS.
а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
12В. В правильной треугольной пирамиде MABC боковые рёбра равны 10, а сторона основания равна 12. Точки G и F делят стороны основания AB и AC соответственно так, что AG : GB = AF : FC = 1 : 5.
а) Докажите, что сечение пирамиды плоскостью MGF является равнобедренным треугольником.
б) Найдите площадь сечения пирамиды плоскостью MGF.
13В. Через вершину S и диагональ BD основания правильной шестиугольной пирамиды SABCDEF проведена плоскость α.
а) Докажите, что расстояние от центра основания до этой плоскости в три раза меньше расстояния до этой плоскости от точки F.
б) Найдите площадь сечения пирамиды плоскостью α, если сторона основания равна (sqrt 3 ), а угол между боковой гранью и плоскостью основания равен ({60^ circ }).
ОТВЕТ: (frac{{3sqrt {30} }}{4}).
14В. Плоскость α проходит через сторону AB основания ABC правильной треугольной призмы ABCA1B1C1 и середину ребра B1C1.
а) Пусть M — точка пересечения плоскости α с прямой CC1. Докажите, что C1 — середина отрезка CM.
б) Найдите площадь сечения призмы плоскостью α, если все рёбра призмы равны 4.
15В. Плоскость α перпендикулярна основанию правильной треугольной пирамиды SABC с вершиной S и делит стороны AB и BC основания пополам.
а) Докажите, что плоскость α делит боковое ребро в отношении 1 : 3, считая от вершины S.
б) Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона основания равна 2, а высота пирамиды равна 4.
16В. Дана правильная четырёхугольная пирамида PABCD с вершиной в точке P. Через точку C и середину ребра AB перпендикулярно к основанию пирамиды проведена плоскость α.
а) Докажите, что плоскость ? делит ребро BP в отношении 2 : 1, считая от точки B.
б) Найдите площадь сечения пирамиды плоскостью α, если известно, что PA = 10, AC = 16.
17В. В правильной шестиугольной пирамиде с вершиной S стороны основания ABCDEF равны 6, а боковые рёбра равны 12. Точки K и M — середины рёбер и SF и SE соответственно.
а) Постройте сечение пирамиды плоскостью BKM.
б) Найдите площадь полученного сечения.
ОТВЕТ: (frac{{39sqrt {39} }}{4}).
18В. Точка M — середина ребра CD единичного куба ABCDA1B1C1D1. Через вершину A1 проведена плоскость, параллельная прямым AM и D1M.
а) Докажите, что эта плоскость проходит через середину ребра AB.
б) Найдите площадь сечения куба этой плоскостью.
ОТВЕТ: (frac{{sqrt 6 }}{2}).
19В. Дан параллелепипед ABCDA1B1C1D1 с основаниями ABCD и A1B1C1D1. Точки M и N — середины рёбер AD и CD соответственно, точка K лежит на ребре BB1, причём B1K : KB = 1 : 2.
а) Докажите, что плоскость, проходящая через точки M, N и K, делит ребро CC1 в отношении 2 : 7, считая от точки C.
б) Найдите площадь сечения параллелепипеда этой плоскостью, если параллелепипед ABCDA1B1C1D1 — правильная четырёхугольная призма, сторона основания ABCD равна (4sqrt 2 ), а боковое ребро равно 12.
ОТВЕТ: (frac{{140}}{3}).
20В. В правильной треугольной призме ABCA1B1C1 проведено сечение плоскостью, проходящей через середину M ребра AB, точку B1 и точку K, лежащую на ребре AC и делящую его в отношении AK : KC = 1 : 3.
а) Докажите, что эта плоскость проходит через середину ребра A1C1.
б) Найдите площадь сечения, если известно, что сторона основания призмы равна (4sqrt 2 ), а высота призмы равна (8sqrt 2 ).
ОТВЕТ: (3sqrt {195} ).
21В. Основание четырёхугольной пирамиды SABCD — параллелограмм ABCD.
а) Постройте сечение пирамиды плоскостью, проходящей через середину ребра AB параллельно плоскости SAD.
б) Найдите площадь полученного сечения, если площадь грани SAD равна 16.
22В. Основанием пирамиды SABCD с равными боковыми рёбрами является прямоугольник ABCD. Плоскость α проходит через сторону AB основания и середину высоты пирамиды.
а) Докажите, что плоскость α делит боковое ребро SD в отношении 1 : 2, считая от вершины S.
б) Найдите площадь сечения пирамиды плоскостью α, если AB = 6, AD = 8, а высота пирамиды равна 6.
23В. Через середину ребра AB куба ABCDA1B1C1D1 проведена плоскость, параллельная прямым BD1 и A1C1.
а) Докажите, что эта плоскость делит диагональ DB1 в отношении 3 : 5, считая от вершины D.
б) Найдите площадь полученного сечения, если ребро куба равно 4.
24В. Дан параллелепипед ABCDA1B1C1D1. Плоскость α проходит через прямую BA1 параллельно прямой CB1.
а) Докажите, что плоскость α делит диагональ AC1 параллелепипеда в отношении 1 : 2, считая от вершины A.
б) Найдите площадь сечения параллелепипеда плоскостью α, если он прямой, его основание ABCD — ромб с диагоналями AC = 10 и BD = 8, а боковое ребро параллелепипеда равно 12.
25В. Дана треугольная призма ABCA1B1C1. Плоскость α проходит через прямую BC1 параллельно прямой AB1.
а) Докажите, что плоскость α проходит через середину ребра AC.
б) Найдите площадь сечения призмы плоскостью α, если призма правильная, сторона её основания равна (2sqrt 3 ), а боковое ребро равно 1.
26В. Все рёбра правильной треугольной пирамиды SBCD с вершиной S равны 18. Основание O высоты SO этой пирамиды является серединой отрезка SS1, M — середина ребра SB, точка L лежит на ребре CD так, что CL : LD = 7 : 2.
а) Докажите, что сечение пирамиды SBCD плоскостью S1LM — равнобедренная трапеция.
б) Найдите площадь этой трапеции.
ОТВЕТ: (frac{{23sqrt {219} }}{4}).
27В. В правильном тетраэдре ABCD с ребром 10 на ребрах AD, BD и AC выбраны точки K, L и M так, что (KD = 4,;MC = 6,;;LD = 8.) Плоскость, проходящая через точки K, L и M, пересекает ребро BC в точке P.
а) Докажите, что (CP:PB = 9:1).
б) Найдите площадь четырехугольника MKLP.
28В. В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD со стороной 6. Противоположные боковые рёбра пирамиды попарно перпендикулярны. Через середины рёбер МА и МВ проведена плоскость α, параллельная ребру МС.
а) Докажите, что сечение плоскостью α пирамиды MABC является параллелограмм.
б) Найдите площадь сечения пирамиды МАВС плоскостью α.
ОТВЕТ: (frac{{9sqrt 3 }}{2}.)
29В. В правильной треугольной усеченной пирамиде ABCA1B1C1 площадь нижнего основания ABC в девять раз больше площади меньшего основания A1B1C1. Через ребро AB проведена плоскость α, которая пересекает ребро СС1 в точке N и делит пирамиду на два многогранника равного объёма.
а) Докажите, что точка N делит ребро СС1 в отношении 5 : 13, считая от вершины С1.
б) Найдите площадь сечения усеченной пирамиды плоскостью α, если высота этой пирамиды равна 13, а ребро меньшего основания равно 3.
30В. В правильной треугольной пирамиде SABC сторона основания AB равна 9, а боковое ребро SA равно (sqrt {43} ). На рёбрах AB и SB отмечены точки M и K соответственно, причём AM = 8, SK : KB = 7 : 3. Плоскость α перпендикулярна плоскости ABC и содержит точки M и K.
а) Докажите, что плоскость α содержит точку C.
б) Найдите площадь сечения пирамиды SABC плоскостью α.
ОТВЕТ: (frac{{3sqrt {73} }}{5}.)
31В. В правильной четырёхугольной пирамиде SABCD боковое ребро SA равно 12, а сторона основания AB равна 6. В боковых гранях SAB и SAD провели биссектрисы AL и AM соответственно.
а) Докажите, что сечение пирамиды плоскостью ALM делит ребро SC пополам.
б) Найдите площадь сечения пирамиды плоскостью ALM.
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Площадь сечения»
Открытый банк заданий по теме площадь сечения. Задания C2 из ЕГЭ по математике (профильный уровень)
Тригонометрические уравнения
Задание №1186
Тип задания: 14
Тема:
Площадь сечения
Условие
В правильном тетраэдре DABC с ребром 5 на рёбрах AD, BD и AC выбраны точки K, L и M соответственно так, что KD=MC=2, LD=4.
а) Постройте сечение тетраэдра плоскостью KLM.
б) Найдите площадь этого сечения.
Показать решение
Решение
а) Так как AK=AM=5-2=3, то triangle AKM равнобедренный.
Так как в этом равнобедренном треугольнике angle KAM=60^{circ}, то он равносторонний, то есть
KM=3. Тогда KM parallel DC, так как равны соответственные углы при прямых KM, DC и секущей AD.
Построим LN parallel DC. Так как в этом случае LN parallel KM, то точки K, L, N и M лежат в одной плоскости, то есть трапеция KLNM есть искомое сечение.
б) 1. triangle BLN sim triangle BDC, так как LN parallel DC. Следовательно, triangle BLN является равносторонним и LN=BN=BL =BD-LD=5-4=1.
2. triangle DKL=triangle CMN, так как DK=CM =2, DL=CN=4 и angle KDL=angle MCN=60^{circ}. Значит, KL=MN и KMNL — равнобедренная трапеция.
Опустим в ней высоту LH. Отсюда, KH =frac{KM-LN}2=frac{3-1}2=1.
3. По теореме косинусов для triangle KDL получим:
KL^2= KD^2+DL^2-2cdot KDcdot DLcdot cos 60^{circ}= 2^2+4^2-2cdot 2cdot 4cdot frac12= 12.
4. По теореме Пифагора LH= sqrt {KL^2-KH^2}= sqrt {12-1}= sqrt {11}.
5. S_{KMNL}= frac12(KM+LN)cdot LH= frac12(3+1)cdot sqrt {11}= 2sqrt {11}.
Ответ
2sqrt {11}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1185
Тип задания: 14
Тема:
Площадь сечения
Условие
В правильной четырёхугольной призме ABCDA_1B_1C_1D_1 сторона основания равна 9, боковое ребро равно 14. Точка K принадлежит ребру A_1B_1 и делит его в отношении 2:7, считая от вершины A_1.
а) Докажите, что сечение призмы плоскостью, проходящей через точки A, C и K, является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Показать решение
Решение
а) Плоскость сечения пересекает плоскость верхнего основания по прямой, проходя-щей через точку K и параллельной AC (по свойству параллельности плоскостей). Тогда плоскость AKC пересекает ребро B_1C_1 в точке L так, что KL parallel AC. Следовательно, искомым сечением будет трапеция AKLC.
KB_1parallel AB, B_1Lparallel BC, KLparallel AC. Значит, треугольники KB_1L и ABC подобны и являются равнобедренными прямоугольными треугольниками. Тогда KB_1=B_1L и A_1K=C_1L. Треугольники AA_1K и CC_1L равны, следовательно, AK=CL и трапеция AKLC — равнобедренная.
б) Найдём площадь трапеции AKLC.
A_1K=frac29A_1B_1 =frac29cdot 9=2.
Из triangle AA_1K,, AK = sqrt {AA_1^2+A_1K^2}= sqrt {14^2+2^2}= 10sqrt 2.
AC=ABsqrt 2=9sqrt 2; KL =frac79AC=frac79cdot 9sqrt 2=7sqrt 2.
Так как трапеция AKLC — равнобедренная, имеем
AH =frac{AC-KL}2=sqrt 2.
Из triangle AKH,, KH= sqrt {AK^2-AH^2}= sqrt {200-2}= sqrt {198}.
S_{AKLC}=frac{AC+KL}2cdot KH,= 8sqrt 2cdot sqrt {198}=48sqrt {11}.
Ответ
48sqrt {11}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1180
Тип задания: 14
Тема:
Площадь сечения
Условие
В правильной четырёхугольной призме ABCDA_1 B_1C_1 D_1 сторона основания равна 7, а боковое ребро — 12. На рёбрах A_1D_1, C_1D_1 и CB взяты точки F, К, L соответственно так, что A_1F=C_1K=CL=3.
а) Пусть P — точка пересечения плоскости FKL с ребром AB. Докажите, что FKLP — прямоугольник.
б) Найдите площадь сечения призмы плоскостью FKL.
Показать решение
Решение
а) Найдём положение точки P. Эта точка пересечения плоскости FKL и ребра AB, лежащего в плоскости ABCD.
Плоскость ABCD параллельна плоскости A_1B_1C_1D_1, в которой лежит отрезок KF. Плоскость FKL пересекает параллельные плоскости ABCD и A_1B_1C_1D_1 по параллельным прямым, отсюда KF parallel LP. Прямоугольные треугольники KD_1F и LBP равны по катету и острому углу D_1F=LB=4 и angle D_1FK=angle BLP как острые с соответственно параллельными сторонами).
Чтобы доказать, что четырёхугольник FKLP — прямоугольник, найдём длины его сторон и диагонали.
KF= PL= sqrt {KD_1^2+D_1F^2}= sqrt {16+16}= 4sqrt 2.
PF= LK = sqrt {LC^2+CC_1^2+C_1K^2}= sqrt {9+144+9}= sqrt {162}= 9sqrt 2. Противоположные стороны четырёхугольника попарно равны, значит, это параллелограмм. Проведём A_1A_2 parallel LF, тогда LF= A_1A_2 = sqrt {(LB-FA_1)^2+AB^2+AA_1^2} = sqrt {(BP-C_1K)^2+CB^2+CC_1^2}= PK. Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.
б) Пусть Q и R — точки пересечения прямой KF и прямых B_1C_1 и A_1B_1. Проведём прямые RL и QP, они пересекут рёбра CC_1 и AA_1 в точках M и N соответственно. Тогда RC_1=KC_1=CL, поэтому можно доказать, что равны треугольники RC_1M и MCL. Прямая RL, а значит, и плоскость FKL пересекают ребро CC_1 в его середине — точке M. Аналогично плоскость FKL пересекает ребро AA_1 в его середине —точке N.
В диагональном сечении CC_1A_1A, которое является прямоугольником, отрезок MN — средняя линия. В прямоугольнике MCAN противоположные стороны равны: MN=CA=7sqrt 2.
Сечение FKMLPN состоит из двух равных трапеций MKFN и MLPN, причём
мы доказали, что LK perp KF и LK perp LP. Высота каждой из этих трапеций равна frac{LK}2=frac{9sqrt 2}2.
S_{text{сечения}}= 2S_{MKFN}= 2cdot frac{KF+MN}2cdot frac{LK}2= (4sqrt 2+7sqrt 2)cdot frac{9sqrt 2}2= 99.
Ответ
99
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №985
Тип задания: 14
Тема:
Площадь сечения
Условие
В основании пирамиды DABC лежит правильный треугольник ABC со стороной 5. Ребро CD перпендикулярно плоскости основания. Точки K, L и M лежат на рёбрах AD, BD и AC соответственно. Известно, что AD=10, DK=4, CM=2 и KL parallel AB.
а) Постройте сечение пирамиды плоскостью KLM.
б) Найдите площадь этого сечения.
Показать решение
Решение
а) Построим MN parallel AB.
Так как KL parallel AB по условию, то KL parallel MN. Это означает, что точки K, L, N и M лежат в одной плоскости, то есть KLNM — искомое сечение.
б) 1. bigtriangleup MNC sim bigtriangleup ABC, так как MN parallel AB, то есть соответственные углы равны: angle CAB=angle CMN и angle CBA=angle CNM. Значит bigtriangleup MNC равносторонний, то есть CN=MN=CM=2.
2. Аналогично можно доказать, что bigtriangleup DKL sim bigtriangleup DAB, так как KL parallel AB. Значит, frac{KL}{AB}=frac{DK}{DA}=frac{2}{5}, KL=frac{2}{5}AB=frac{2}{5} cdot 5=2.
3. Так как KL parallel MN и KL=MN, то KLNM — параллелограмм.
4. bigtriangleup AMK sim bigtriangleup ACD, так как угол при вершине A общий и frac{AK}{AD}=frac{AM}{AC}=frac{3}{5}. Следовательно, MK parallel CD, так как соответственные углы равны (например, angle AKM=angle ADC). Отсюда, MK perp ABC, так как CD perp ABC. Значит, MK perp MN, то есть параллелограмм KLNM является прямоугольником.
5. По теореме Пифагора CD= sqrt{AD^2-AC^2}= sqrt{10^2-5^2}= 5sqrt{3}. Так как frac{MK}{CD}=frac{AM}{AC}=frac{3}{5}, то MK=frac{3}{5}CD=3sqrt{3}.
6. S_{KLNM}= MK cdot MN= 3sqrt{3} cdot 2= 6sqrt{3}.
Ответ
6sqrt{3}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №984
Тип задания: 14
Тема:
Площадь сечения
Условие
Дана правильная четырёхугольная пирамида SABCD, все рёбра которой равны.
а) Постройте сечение пирамиды плоскостью, проходящей через диагональ BD основания перпендикулярно грани SCD.
б) Найдите площадь этого сечения, если каждое ребро данной пирамиды равно 5.
Показать решение
Решение
а) Пусть K — середина ребра SC. Так как треугольники SDC и SBC равносторонние, то SC perp DK и SC perp BK (медиана равностороннего треугольника является его высотой). Значит, прямая SC перпендикулярна плоскости DKB. Так как SC perp DKB и SC subset CSD, то плоскость DBK перпендикулярна плоскости CSD. Треугольник DKB — искомое сечение.
б) Найдём площадь сечения. Высоты DK и BK в равносторонних треугольниках равны frac{5sqrt{3}}{2}. Диагональ BD квадрата ABCD равна 5sqrt{2}. В равнобедренном треугольнике DKB высота OK=sqrt{left ( frac{5sqrt{3}}{2}right )^2-left ( frac{5sqrt{2}}{2}right )^2}=frac{5}{2}. Площадь треугольника DKB равна frac{1}{2}DB cdot OK=frac{1}{2} cdot 5sqrt{2} cdot frac{5}{2}=frac{25sqrt{2}}{4}.
Ответ
frac{25sqrt{2}}{4}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №982
Тип задания: 14
Тема:
Площадь сечения
Условие
Дана правильная четырёхугольная пирамида SMNPQ с вершиной в точке S, сторона основания равна 5sqrt{3}, а плоский угол при вершине пирамиды равен 60^circ.
а) Постройте сечение пирамиды плоскостью, проходящей через диагональ NQ основания параллельно боковому ребру PS.
б) Найдите площадь сечения.
Показать решение
Решение
а) Обозначим через O точку пересечения диагоналей квадрата MNPQ.
В плоскости MSP проведем через точку O прямую OK parallel PS. Точку K соединим с точкой N и точкой Q, получим сечение NKQ, которое является искомым, так как содержит OK parallel PS и диагональ основания NQ, по признаку параллельности прямой и плоскости: плоскость NKQ параллельна ребру PS. Данное сечение представляет собой треугольник NKQ.
б) Треугольник NKQ — равнобедренный, NK=KQ. Это следует из равенства треугольников NKM и KMQ (по двум сторонам: MK — общая, NM=MQ и углу: angle KMQ=angle KMN). Точка O — середина NQ, NO=OQ. KO — медиана и, следовательно, высота. S_{NKQ}=frac{1}{2}NQ cdot KO.
Рассмотрим bigtriangleup SMQ, angle MSQ=60^circ, значит angle SMQ=angle SQM=60^circ, SM=SQ=MQ=5sqrt{3}. angle SOM=90^circ, точка K — середина SM (так как OK — средняя линия bigtriangleup PSM). Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. OK=frac{1}{2}SM=frac{5sqrt{3}}{2}. NQ — диагональ квадрата со стороной 5sqrt{3}. NQ=5sqrt{3} cdot sqrt{2}=5sqrt{6}.
S_{NKQ}= frac{1}{2}OK cdot NQ= frac{5sqrt{3} cdot 5sqrt{6}}{4}= frac{75sqrt{2}}{4}.
Ответ
frac{75sqrt{2}}{4}
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №959
Тип задания: 14
Тема:
Площадь сечения
Условие
В прямоугольном параллелепипеде ABCDA_1 B_1 C_1 D_1 стороны оснований AB и BC равны соответственно 8 и 5, а боковое ребро AA_1 равно 4. На ребре A_1 B_1 отмечена точка K, а на луче BC — точка F, причем A_1 K=KB_1 и BF=AB. Плоскость AKF пересекает ребро B_1 C_1 в точке P.
а) Докажите, что B_1 P:PC_1=4:1.
б) Найдите площадь сечения параллелепипеда плоскостью AKF.
Показать решение
Решение
а) Построим сечение параллелепипеда плоскостью AKF.
E — точка пересечения ребра DC и отрезка AF.
В плоскости ABB_1 проведем лучи AK и BB_1. AK пересекает BB_1 в точке Q. В плоскости BCC_1 проведем отрезок FQ. FQ пересекает B_1C_1 в точке P, а CC_1 в точке R. Пятиугольник AKPRE — искомое сечение.
KB_1 parallel AB, KB_1=frac{1}{2}A_1 B_1, значит KB_1 — средняя линия bigtriangleup ABQ, отсюда BB_1=QB_1, а так как BF parallel B_1 P, то B_1 P — средняя линия bigtriangleup FBQ, BF=8, B_1 P=frac{1}{2}BF=4. C_1 P=B_1C_1-B_1 P=5-4=1, следовательно, B_1 P:PC_1=4:1.
б) Прямоугольние треугольники ABQ, FBQ и ABF равны по двум катетам AB=BF=BQ=8, отсюда AQ=AF=QF=8sqrt{2}.
S_{AQF}=frac{a^{2}sqrt{3}}{4} как площадь равностороннего треугольника со стороной a.
S_{AQF}=frac{(8sqrt{2})^{2} cdot sqrt{3}}{4}=32sqrt{3},
S_{KQP}= frac{1}{4}S_{AQF}= frac{32sqrt{3}}{4}= 8sqrt{3}.
S_{AKPF}= S_{AQF}-S_{KQP}= 32sqrt{3}-8sqrt{3}= 24sqrt{3}.
bigtriangleup RCF sim bigtriangleup RC_1 P по первому признаку подобия (angle C=angle C_1=90^{circ}, angle1=angle2 как вертикальные). Из подобия следует frac{CF}{PC_{1}}=frac{FR}{PR}. По доказанному в а) PC_1=1, BF=AB=8, тогда CF=8-5=3 и frac{FR}{PR}=frac{3}{1}. Так как KP — средняя линия bigtriangleup AQF, то PF=frac{1}{2}QF=4sqrt{2}, FR=frac{3PF}{4}=frac{4sqrt{2} cdot 3}{4}=3sqrt{2}.
В равнобедренном прямоугольном треугольнике FCE FC=EC=3, тогда EF=3sqrt{2}. В bigtriangleup REFFR=EF=3sqrt{2}, angle RFE=60^{circ}, отсюда bigtriangleup REF — равносторонний.S_{REF}=frac{(3sqrt{2})^2sqrt{3}}{4}=frac{9sqrt{3}}{2}.
S_{AKPRE}= S_{AKPF}-S_{REF}= 24sqrt{3}-frac{9sqrt{3}}{2}= frac{39sqrt{3}}{2}.
Ответ
frac{39sqrt{3}}{2}
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №179
Тип задания: 14
Тема:
Площадь сечения
Условие
Образующая конуса равна диаметру его основания. В основание конуса вписан правильный шестиугольник. Через сторону этого шестиугольника и середину высоты конуса проведена плоскость alpha.
а) Докажите, что угол между плоскостью основания конуса и плоскостью alpha равен 45^{circ}.
б) Найдите площадь сечения плоскостью alpha шара, вписанного в конус, если радиус основания конуса равен 2.
Показать решение
Решение
а) Пусть радиус основания равен r, O — центр основания.
Рассмотрим правильный шестиугольник ABCDEF, OB=r, angle BOA=60^{circ}, bigtriangleup AOB — равносторонний, его высота OH=frac{OBsqrt{3}}{2}=frac{rsqrt{3}}{2}. Через прямую OH и высоту конуса OS проведем осевое сечение конуса, в сечении получим bigtriangleup SMN.
Пусть K — середина OS. bigtriangleup SMN — равносторонний (так как образующая конуса равна диаметру его основания) со стороной 2r. Тогда SO=frac{2rsqrt{3}}{2}=rsqrt{3}, OK=frac{rsqrt{3}}{2}, OK=OH, следовательно, прямоугольный bigtriangleup OHK — равнобедренный angle KHO=45^{circ}. Так как OH — проекция KH на плоскость основания конуса, OHperp AB по построению, то KHperp AB по теореме о трех перпендикулярах, следовательно, angle KHO — линейный угол двугранного угла между плоскостью alpha и плоскостью основания конуса. Значит, двугранный угол равен 45^{circ}, что и требовалось доказать.
б) Рассмотрим шар, вписанный в конус и осевое сечение, описанное выше. В сечении шара плоскостью MSN получим окружность, центр которой в точке Q (точке пересечения медиан bigtriangleup MSN), OQ:QS=frac{1}{2}, OS=rsqrt{3}=2sqrt{3}, SQ=frac{4}{3}sqrt{3}. SK=frac{1}{2}OS=sqrt{3}, QK=SQ-SK=frac{sqrt{3}}{3}=frac{1}{sqrt{3}}.
OQ=frac{1}{3}SO=frac{2sqrt{3}}{3}=QL — радиус вписанного шара. Пусть QQ’ perp HK, тогда bigtriangleup KQQ’ — прямоугольный и равнобедренный (angle QKQ’=45^{circ}), QQ’=frac{KQ}{sqrt2}=frac{1}{sqrt{6}}, Q’L^2=QL^2-(QQ’)^2=frac{7}{6}
Q’L — радиус круга, полученного в сечении шара плоскостью alpha. Тогда площадь сечения равна pi Q’L^2=frac76pi.
Ответ
б) frac{7}{6}pi.
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №168
Тип задания: 14
Тема:
Площадь сечения
Условие
Правильная треугольная пирамида SABC (ABC — основание) имеет боковое ребро SA=SB=SC=8 и сторону основания AB=BC=AC=12. На середине ребер SB и SC были соответственно взяты точки E и F. Плоскость alpha, которой принадлежит прямая EF, перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость alpha делит биссектрису основания пирамиды AA_1 в отношении 5:1, считая от точки A.
б) Вычислите площадь сечения пирамиды SABC плоскостью alpha.
Показать решение
Решение
а) EFparallel BC (как средняя линия bigtriangleup SBC) Rightarrow EFparallel ABC.
Сечение пересекает плоскость основания ABC в некоторой прямой PQ parallel EF.
Рассмотрим плоскость AA_1S.
Точка K — центр пересечения EF и A_1S, H — центр основания ABC, L – точка пересечения плоскости SAA_1 и прямой PQ.
begin{cases} PEF perp ABC \ SAA_1 perp ABC end{cases} Rightarrow KL perp ABC, KL parallel SH
FE — средняя линия bigtriangleup SBC, A_1K=KS, следовательно, A_1L=LH (т.к. A_1H – проекция прямой A_1S на плоскость основания).
Медиана AA_1 делится точкой H в соотношении: AH:HA_1=2:1Rightarrow AL:LA_1=5:1, ч.т.д.
б) Рассмотрим трапецию PEFQ.
EF = frac{1}{2} BC = 12:2 = 6
frac{PQ}{BC}=frac{AL}{AA_1}=frac{5}{6}
PQ=frac{5BC}{6}=frac{5cdot 12}{6}=10
AH=frac{2}{3} AA_1= frac{2}{3}sqrt{AB^2-(frac{1}{2}AB)^2}= frac{2}{3}cdot frac{sqrt{3}}{2}AB= frac{sqrt{3}cdot 12}{3}=4sqrt{3}
KL=frac{1}{2}SH= frac{1}{2}sqrt{SA^2-AH^2}= frac{1}{2}sqrt{8^2-(4sqrt{3})^2}=2
S_{PEFQ}=frac{1}{2}(EF+PQ)cdot KL= frac{1}{2}(6+10)cdot 2=16
Ответ
16
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
29
Ноя 2015
13 Задание (2022) (C2)СТЕРЕОМЕТРИЯ
Учимся строить сечения многогранников. Часть 2.
Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.
Вспомним, что сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат сторонам, а ребра — граням многогранника. Две соседние вершины принадлежат одной грани многогранника.
Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.
В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.
Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.
Постройте сечения, проходящие через точки .
Задание 1:
Подсказка. показать
Ответ. показать
Задание 2:
Подсказка: показать
Ответ: показать
Задание 3:
Подсказка: показать
Ответ: показать
Задание 4:
Подсказка: показать
Ответ: показать
Задание 5:
Подсказка: показать
Ответ: показать
Задание 6:
Подсказка: показать
Ответ: показать
Задание 7:
Подсказка: показать
Ответ: показать
Задание 8:
Подсказка: показать
Ответ: показать
Задание 9:
Подсказка: показать
Ответ: показать
Задание 10:
Подсказка: показать
Ответ: показать
Задание 11:
Подсказка: показать
Ответ: показать
И. В. Фельдман, репетитор по математике.
Для вас другие записи этой рубрики:
- Как найти расстояние от точки до прямой с помощью метода координат
- Угол между плоскостями. Метод координат. Задание 14
- Задание С2 из тренировочной работы 28 января 2014
- Видеолекция 9. «Метод координат. Задание С2. Расстояния в пространстве»
- Как построить чертеж в стереометрической задаче
- Видеолекция «Метод координат. Задание 14. Углы в пространстве»



.png)