Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д28 C1 № 2915
В безветренную погоду самолет затрачивает на перелет между городами 6 часов. Если во время полета дует постоянный боковой ветер перпендикулярно линии полета, то самолет затрачивает на перелет на 9 минут больше. Найдите скорость ветра, если скорость самолета относительно воздуха постоянна и равна
2
Задания Д28 C1 № 2940
В безветренную погоду самолет затрачивает на перелет между городами 6 часов. Если во время полета дует боковой ветер со скоростью перпендикулярно линии полета, то самолет затрачивает на перелет на несколько минут больше. Определите, на какое время увеличивается время полета, если скорость самолета относительно воздуха постоянна и равна
3
Задания Д28 C1 № 3279
Определите начальную скорость бруска, если известно, что после того, как он проехал 0,5 м вниз по наклонной плоскости с углом наклона 30° к горизонту, его скорость стала равна 3 м/с. Трением пренебречь. Ответ приведите в метрах в секунду.
4
Задания Д28 C1 № 3437
На последнем километре тормозного пути скорость поезда уменьшилась на 10 м/с. Определите скорость в начале торможения, если общий тормозной путь поезда составил 4 км, а торможение было равнозамедленным. Ответ приведите в метрах в секунду.
5
Задания Д28 C1 № 3441
На последнем километре тормозного пути скорость поезда уменьшилась на 10 м/с. Определите общий тормозной путь поезда, если скорость в начале торможения составляла 20 м/с, а торможение было равнозамедленным. Ответ приведите в километрах.
Пройти тестирование по этим заданиям
Тема 30.
Механика (Расчетная задача высокого уровня сложности+обоснование)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
механика (расчетная задача высокого уровня сложности+обоснование)
30.01Кинематика
30.02Динамика
30.03Законы сохранения в механике
30.04Статика
30.05Гидростатика
30.06Механические колебания
Решаем задачи
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи пренебрегаем силой сопротивления воздуха, также по условию задачи
соударения мгновенные и абсолютно упругие, можно сделать вывод о том, что при соударении энергия
не выделяется, поэтому в данной задаче можно использовать закон сохарнения энергии для
описания движения шарика. За нулевой уровень потенциальной энергии примем поверхность
земли.
4. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна
, поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.
Решение
Так как соударения абсолютно упругие, то траекторию можно перерисовать в виде параболы с
ветвями вниз.
Из Закона сохранения энергии скорость тела в начальный момент времени
Рассмотрим оси и
. По оси
начальная скорость
, при этом в высшей точки полета
она будет равна нулю, а время подъема будет равно половине время полета, следовательно, из
уравнений кинематики
Начальная скорость тела будет равна
Откуда начальная скорость по оси
А дальность полета () находится по формуле
Откуда
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Указано, что по горизонтали тело движется равномерно, а по вертикали — равноускоренно.
3. Указано, что тело является материальной точкой.
4. Обоснована возможность использования закона сохранения энергии.
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записаны законы кинематики
прямолинейного равномерного и равноускоренного движения, записан закон сохранения энергии,
записаны формулы кинетической и потенциальной энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тело движется
только под действитем силы тяжести с ускорением свободного падения, равным м/с
и
направленным вертикально вниз. Ось направлена вертикально вверх.
4. Так как сопротивление воздуха отсутствует, то полная механическая энергия тела не изменяется,
значит можно использовать закон сохранения энергии для описания движения тела. За нулевой уровень
потенциальной энергии примем поверхность земли.
5. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна
, поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.
Решение
По горизонтали тело пролетит
По вертикали
Так как по условию , то имеем
Скорость тела найдем из закона сохранения энергии
где – искомая величина,
– масса тела.
Откуда скорость тела перед падением с учетом (1)
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения закона сохраненя энергии.
3. Движение тела вдоль горизонтальной оси будет равномерным, а вдоль вертикальной оси –
равноускоренным с ускорением g.
4. Обоснована возможность применения к телу модели материальной точки.
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула для нахождения
пути тела при его равномерном движении вдоль горизонтальной оси и формула для пути
тела при его равноускоренном движении вдоль вертикальной оси, получены формулы для
движения тела с учетом начальных значений скоростей по осям и углу наклона вектора
начальной скорости к горизонту, записан закон сохранения энергии для нахождения скорости
тела в момент удара (или записано выражение для вертикальной составляющей вектора
скорости в момент удара, конечная скорость тела представлена в виде векторной суммы
горизонтальной и вертикальной составляющих, получено выражение для нахождения модуля вектора
конечной скорости тела в момент удара, записаны формулы кинетической и потенциальной
энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тело движется
только под действитем силы тяжести с ускорением свободного падения, равным м/с
и
направленным вертикально вниз. Ось направлена вертикально вверх. Так как сопротивлением
воздуха пренебрегаем, то описывать движение шарика будем с помощью закона сохранения
энергии, так как диссипативные силы отсутсвуют и действует только сила тяжести, которая
является потенциальной. За нулевой уровень потенциальной энергии примем поверхность
земли.
4. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна
, поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.
Решение
Запишем закон сохранения энергии
где – начальная скорость камня,
– масса камня.
Найдем начальную скорость камня
По условию скорость камня в начальный момент времени и конечный направлены под углом ,
отложим вектора этих скоростей из одной точки, при этом изменение скорости камня будет равно
величине . Будет треугольник, составленный на сторонах
,
, и
, при этом
будет лежать
напротив угла .
Откуда по теореме косинусов
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Указано, что по горизонтали тело движется равномерно, а по вертикали — равноускоренно.
3. Сказано, что тело является материальной точкой.
4. Обоснована возможность применения закона сохранения энергии.
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: законы кинематики прямолинейного
равномерного и равноускоренного движения, закон сохранения энергии, форулы кинетической и
потенциальной энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
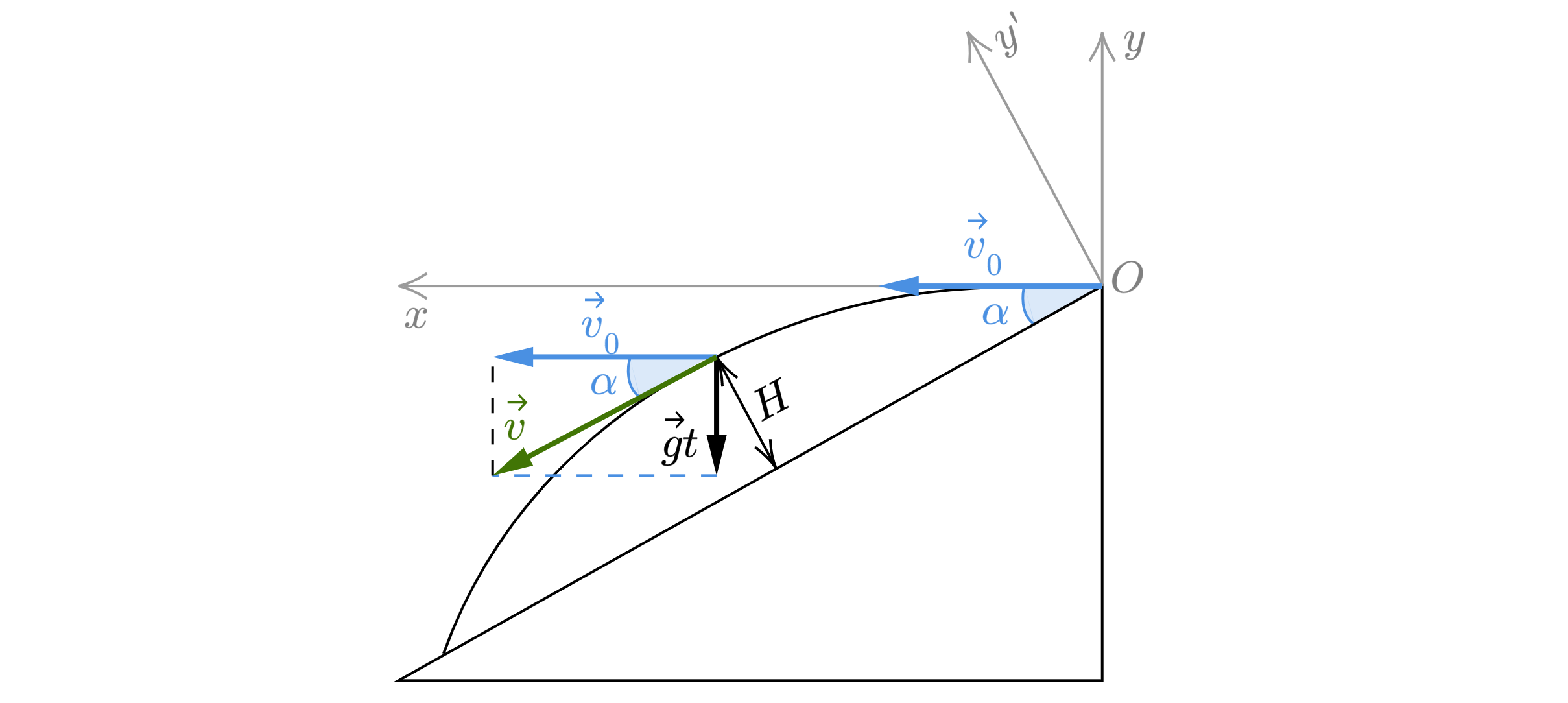
Из точки, находящейся над землёй, одновременно бросили два тела: одно вертикально вверх с начальной
скоростью м/с, второе — горизонтально с начальной скоростью
. Найти расстояние
между телами в тот момент, когда первое тело поднялось на максимальную высоту над
поверхностью земли. Второе тело в этот момент времени ещё не успело упасть на землю.
(«Росатом», 2012, 11)
Показать ответ и решение
I способ
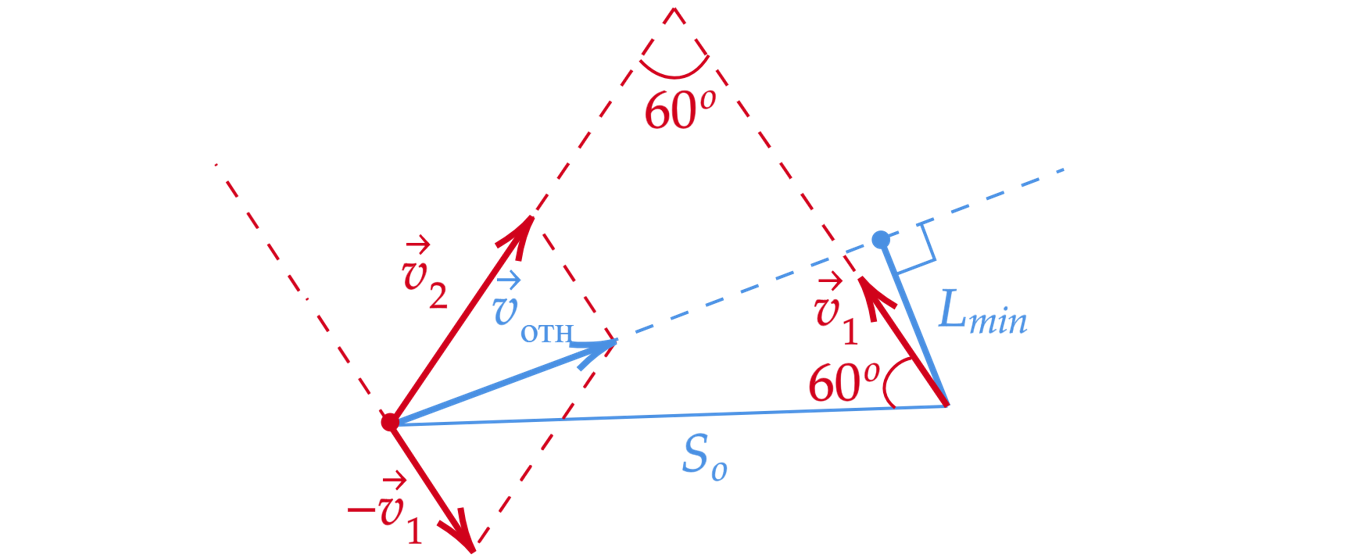
Перейдем в систему отсчета, связанную с первым кораблем.
Тогда относительная скорость равна
Чтобы найти угол рассмотрим треугольник со сторонами
Угол между сторонами
и
равен 60
По теореме косинусов
По
теореме синусов найдем
А угол равен
, значит, траектория относительного движения является
биссектрисой, а в равностороннем треугольнике она является еще и медианой, следовательно,
II способ
До момента пересечения траекторий корабли будут сближаться, после пересечения траекторий корабли
будут удаляться. Значит минимальное расстояние в точке пересечения траекторий. Так как скорость
второго в 2 раза больше, чем скорость первого, то он придет в точку пересечения в 2 раза быстрее, а
расстояние между кораблями будет равно половине траектории. Заметим, что треугольник
равносторонний (равнобедренный, с углом при пересечении одинаковых ребер 60 градусов), значит
длина траектории равна =20 км. Так как расстояние между кораблями равно
=10
км.
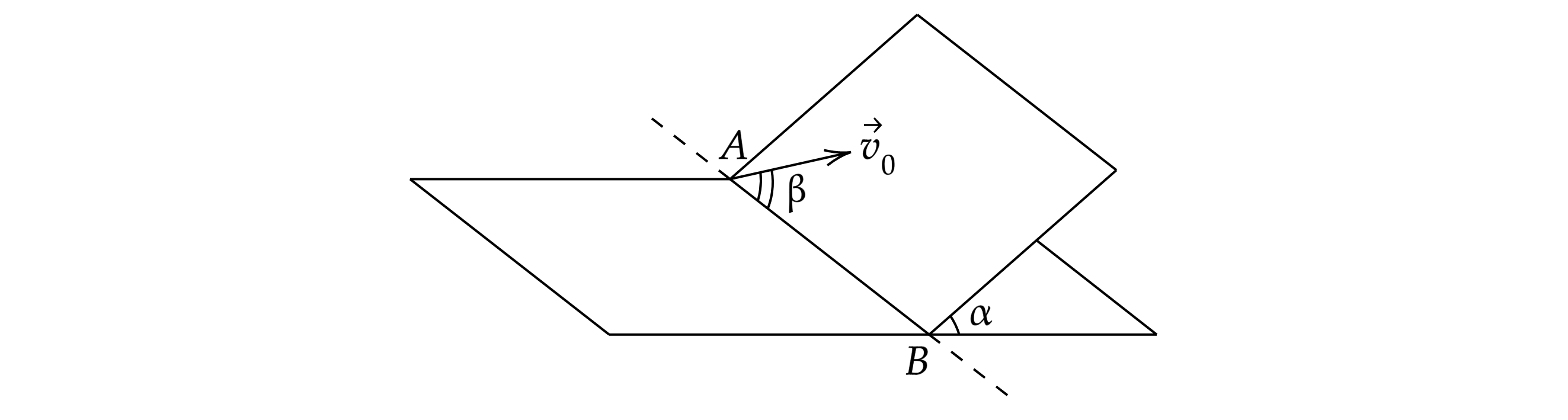
Наклонная плоскость пересекается с горизонтальной плоскостью по прямой . Угол между плоскостями
. Маленькая
шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью м/с под углом
к
прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной
плоскостью, найдите расстояние AB.
Сборник задач «1000 задач»
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в этой СО.
2. Движение тела поступательное, поэтому будем считать его материальной точкой.
3. В условии данной задачи пренебрегаем силой трения, поэтому тело движется только под действитем силы тяжести с
ускорением свободного падения, равным м/с
и направленным вертикально вниз. Ось
направлена перпендикулярно
прямой по наклонной плоскости. Ось
направим по прямой
.
4. Проекция ускорения на ось равна
, поэтому описывать движение по этой оси будем с помощью законов
прямолинейного равноускоренного движения. Проекция ускорения на ось равна 0, поэтому описывать движение по горизонтали
будем с помощью законов прямолинейного равномерного движения.
Решение
Ось направим по прямой
, ось
– вверх по наклонной плоскости перпендикулярно линии
. Найдем проекции
вектора ускорения свободного падения на оси
Движение по наклонной плоскости эквивалентно движению тела, брошенного под углом бета к горизонту, в поле тяжести с
ускорением .
Уравнения движения вдоль осей x и y:
В момент времени , соответствующий концу движения,
и
. Используя это условие для решения системы
уравнений, получаем
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Указано, что по выбранным координатным осям тело будет двигаться равноускоренно.
3. Обоснована возможность применения к телу модели материальной точки.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: формулы кинематики прямолинейного
равноускоренного и равномерного движения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Скорость мальчика при разгоне описывается уравнением:
где – конечная скорость,
– начальная скорость,
– ускорение,
– время движения.
Из этого уравнения можно выразить время разгона:
Расстояние, которое пробежит мальчик во время разгона равно:
Тогда на границе разгона расстояние от мальчика до ворот равно , а движение равномерное, значит, время движения
мальчика при равномерном движении равно:
Полное время движения
Из этой формулу видно, что меньше ускорение мальчика, тем больше время движения. Время движения не должно превышать
время опускания решетки . Для того, чтобы мальчик успел пробежать, необходимо, чтобы ворота опустились на высоту, не
превышающую рост мальчика , то есть время опускания ворот равно:
Максимальность времени движения мальчика (минимальность ускорения) будет достигнута при , то есть
Подставим числа из условия
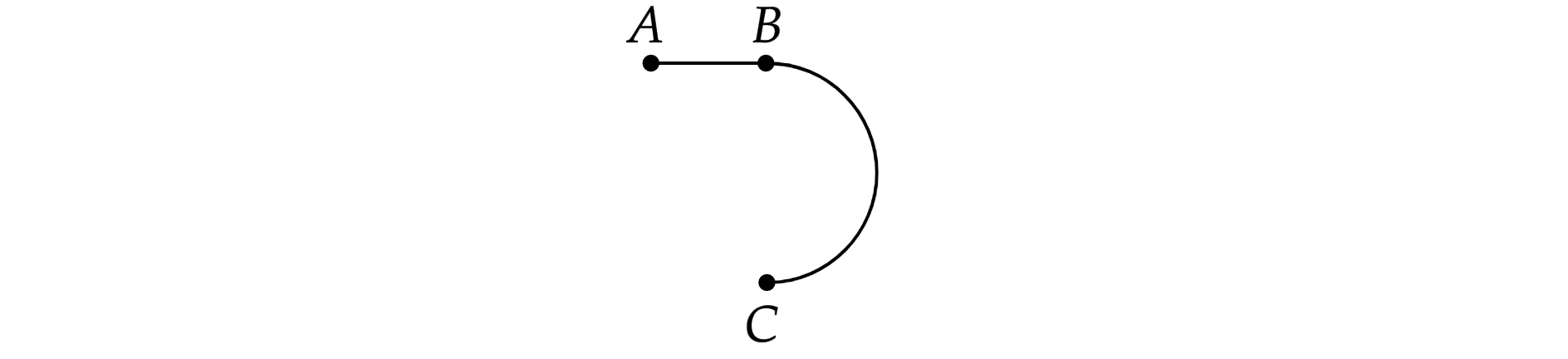
Стартуя из точки А (см. рисунок), спортсмен движется равноускоренно до точки В, после которой
модуль скорости спортсмена остаётся постоянным вплоть до точки С. Во сколько раз время,
затраченное спортсменом на участок ВС, больше, чем на участок АВ, если модуль ускорения на обоих
участках одинаков? Траектория ВС – полуокружность. Какие законы Вы использовали для описания
движения? Обоснуйте их применение к данному случаю.
Сборник задач «1000 задач»
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. На учаскте разгона тело движется прямолинейно с постоянным ускорением.
4. После окончания разгона тело будет с постоянной скоростью по окружности и будет обладать
центрострмеительным ускорением.
5. Движение тела на обоих участках будем описывать законами равноускоренного движения.
Решение
Рассмотрим прямолинейный участок. На нём ускорение определяется формулой:
Ускорение на прямолинейном участке определяется формулой
где – скорость в точке
,
– скорость в точке
, а
– время движения по
прямолинейному участку.
Так как спортсмен стартует из точки , то
и формулу можно преобразовать в
Рассмотрим движении по дуге окружности. Так как скорость спортсмена при движении по
полуокружности постоянна, то тангенциальная составляющая ускорения равна нулю и ускорение
при движении по окружности можно считать центростремительным, а его можно найти по
формуле:
где – радиус полуокружности.
С учетом того, что период обращения равен
При это период обращения равен движению по полному кругу, а в условии полуокружность, то –
пол периода, следовательно, , откуда
Так как по условию модули ускорений на участках равны, то приравнивая выражения для
ускорений, получим
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Сказано, что тело можно считать материальной точкой.
3. Сказано, что после прекращения разгона тело движется с постоянной скоростью по окружности и
обладает центростремительным ускорением.
4. Сказано, что описывать движение тела можно, используя законы равноускоренного движения.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записано уравнение скорости для
нахождения ускорения, записана формула центростремительного ускорения, использованы формулы
для описания движения по окружности).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
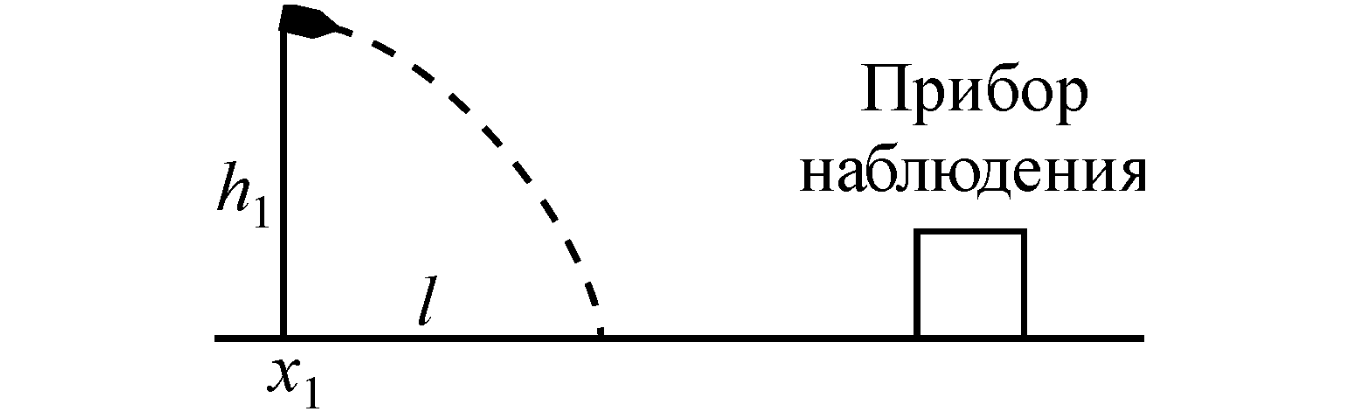
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и
высоту = 1655 м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на
расстоянии = 1700 м от места его обнаружения. Известно, что снаряды данного типа вылетают из
ствола пушки со скоростью 800 м/с. На каком расстоянии от точки взрыва снаряда находилась пушка,
если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на
одной горизонтали. Какие законы Вы использовали для описания движения? Обоснуйте их применение
к данному случаю.
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тело движется
только под действитем силы тяжести с ускорением свободного падения, равным м/с
и
направленным вертикально вниз. Ось направлена вертикально вверх.
4. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна
, поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.
Решение
Найдем горизонтальную проекцию скорости , где
– последние 3 секунды полета,
– начальная скорость полета,
– угол выстрела пушки.
где – вертикальная проекция скорости.
А значит в начальный момент времени вертикальная проекция скорости равна
Воспользуемся уравнением скорости для вертикальной оси
где – время падения снаряда.
Так как время подъема камня равно времени падения камня, то общее время полета равно , а
уравнения координаты на горизонтальную ось выглядит следующим образом
Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту,
достиг максимальной высоты 5 м и упал обратно на землю в 20 м от места броска. Чему равна
минимальная скорость камня за время полёта? Какие законы Вы использовали для описания движения?
Обоснуйте их применение к данному случаю.
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тело движется
только под действитем силы тяжести с ускорением свободного падения, равным м/с
и
направленным вертикально вниз. Ось направлена вертикально вверх.
4. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна
, поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.
Решение
В случае броска под некоторым углом, скорость будет раскладываться на 2 компонента
где – горизонтальная проекция скорости,
– вертикальная проекция скорости. Так как
горизонтальная проекция всегда постоянна, то для минимальности нужно, чтобы вертикальная
проекция была равна нулю, то есть в наивысшей точке полета. Воспользуемся уравнением скорости для
вертикальной оси
где – угол броска камня,
– время подъема камня на максимальную высоту. Подставим в
уравнение координаты на вертикальную ось
Выразим отсюда время подъема камня
Так как время подъема камня равно время падения камня, то общее время полета равно . По
горизонтальной оси скорость тела постоянна, а это означает, что путь, пройденный телом
равен
Выразим отсюда скорость по горизонтали
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Указано, что по горизонтали тело движется равномерно, а по вертикали — равноускоренно.
3. Сказано, что тело является материальной точкой.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записаны законы кинематики
прямолинейного равномерного и равноускоренного движения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
С некоторой высоты над поверхностью земли бросили груз без начальной скорости. Расстояние, которое
преодолел груз в последнюю секунду своего падения, оказалось на 10% больше пути, который он прошёл
в предыдущую секунду. Сколько времени падал груз? Ускорение свободного падения = 10 м/с
Сопротивлением воздуха пренебречь. Какие законы Вы использовали для описания движения?
Обоснуйте их применение к данному случаю.
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тело движется
только под действитем силы тяжести с ускорением свободного падения, равным м/с
и
направленным вертикально вниз. Ось направлена вертикально вниз.
4. Проекция ускорения на ось равна
, поэтому описывать движение по вертикали будем с
помощью законов прямолинейного равноускоренного движения.
Решение
Пусть всё время движения составляет секунд . Тогда за
секунд тело пройдет
за время
а за время
так как начальная скорость тела равна 0, то
Так как по условию
имеем
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Указано, что по вертикали тело движется равноускоренно.
3. Сказано, что тело является материальной точкой.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записаны законы кинематики
прямолинейного равноускоренного движения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тело движется
только под действитем силы тяжести с ускорением свободного падения, равным м/с
и
направленным вертикально вниз. Ось направлена вертикально вверх.
4. В условиях данной задачи проекция ускорения на ось равна 0, поэтому описывать движение
по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось
равна
, поэтому описывать движение по вертикали будем с помощью законов прямолинейного
равноускоренного движения.
Решение
1. Введем оси и
, по оси
мяч движется равномерно со скоростью
, а по оси
равноускоренно вниз с ускорением , при этом скорость движения в момент времени
равна
Откуда начальная скорость
2. Проанализируем, до какого момента мяч будет удаляться от склона, а будет удаляться до тех пор,
пока скорость не составит с горизонтом такой же угол, как и склон. Отложим вектора начальной и
конечных скоростей из одной точки, при этом изменение скорости камня будет равно величине .
Будет треугольник, составленный на сторонах ,
, и
, при этом
будет лежать напротив угла
(см. рис.)
Откуда тангенс угла
3. Введем ось перпендикулярную поверхности склона, тогда для это оси перемещение мяча по
:
Подставим значение из пункта 2:
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Указано, что по вертикали тело движется равноускоренно, а по горизонтали — равномерно.
3. Сказано, что тело является материальной точкой.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записаны законы кинематики
прямолинейного равномерного и равноускоренного движения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
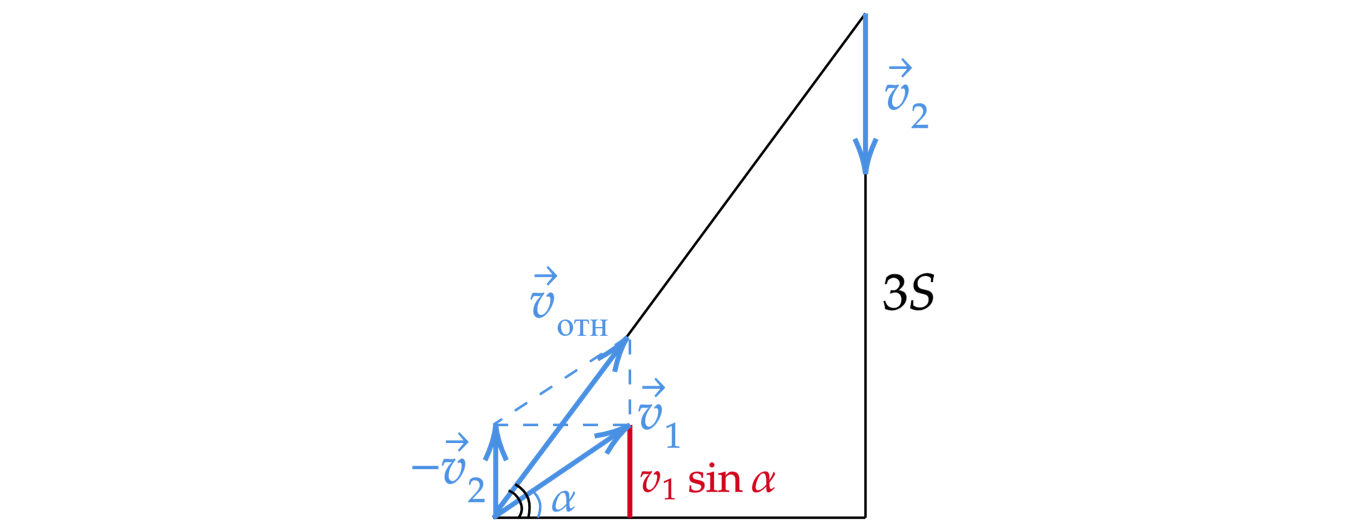
I способ
Перейдем в систему отсчета, связанную со вторым телом.
Если перейдем в систему отсчета, связанную со вторым, то первому телу надо будет пройти
3S по вертикали и S по горизонтали. Тогда скорость первого тела, относительно второго
равна
, а
ускорение равно нулю.
При этом угол наклона относительной скорости таков, что его тангенс равен 3 (потому что по
вертикали 3S, а по горизонтали S) Тангенс можно расписать как
II
способ
Найдем через основное тригонометрическое тождество
Перейдем в систему отсчета, которая движется с ускорение вниз.
Рассмотрим движение снежинки и снежинки
относительно горизонтальной оси
этой системы
и вертикальной .
Снежинка :
По горизонтально оси она пролетит расстояние с постоянной скоростью
Это
расстояние равно
По
вертикальной оси она также будет двигаться без ускорения (с учетом нашей системы отсчета).И ее
скорость при этом равна
Пусть она будет на расстоянии по вертикали от начала своего движения, с учетом формул
кинематики имеем
Теперь рассмотрим снежинку .
По горизонтальной оси она не будет двигаться, а по вертикальной будет двигаться с постоянной
скоростью и пройдет расстояние
. С учетом формул кинематики
Выразим из (1) время движения снежинок и объединим (2) и (3)
Поделим на и выразим
В безветренную погоду самолет затрачивает на перелет между городами 6 часов. Если во время полета
дует постоянный боковой ветер перпендикулярно линии полета, то самолет затрачивает на перелет на 9
минут больше. Найдите скорость ветра, если скорость самолета относительно воздуха постоянна и равна
328 км/ч. Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному
случаю.
Сборник А. И. Черноуцан
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. В условии данной задачи считаем движение тела равномерным, будем использовать законы
прямолинейного равномерного движения для описания движения тела.
Решение
В первой случае самолет пролетел расстояние
где – скорость самолета,
– 6 часов.
Во втором случае скорость самолета относительно земли будет складываться из скорости самолета и
скорости ветра, при этом сложение будет векторное. То есть
– скорость ветра. А расстояние, пройденное самолетом равно
Отсюда
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Указано, что движение тела равномерное.
3. Сказано, что тело является материальной точкой.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: формула кинематики прямолинейного
равномерного движения, формулы нахождения относительных скоростей).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Велосипедисты едут колонной со скоростью 5 м/с. Длина колонны равна 210 м. Навстречу им бежит
тренер со скоростью 2 м/с. Поравнявшись с тренером велосипедист резко разворачивается и едет в
обратном направлении с той же скоростью. Чему будет равна длина колонны после того, как все
велосипедисты развернутся?
Показать ответ и решение
Перейдем в систему отсчета, связанную с движением тренера.
Тогда скорость сближения колонны с тренером равна
где
– скорость колонны,
– скорость тренера.
Полный разворот колонна сделает за время
–
первоначальная длина колонны.
После разворота каждый участник колонны будет удаляться от тренера с постоянной скоростью
При
этом длина колонны после разворота будет равна
Тогда с учетом (1), (2), (3) формулу (4) можно переписать в виде
Показать ответ и решение
Сначала найдем время полета шарика до удара о потолок:
При
подстановке значений получаем квадратное уравнение, из которого c.
Теперь найдем скорость, которую шарик имел после 0,3 секунды полета:
После удара о потолок шарик абсолютно упруго отталкивается, то есть начинает лететь вниз с
начальной скоростью 2 м/с. Запишем уравнение его движения до приземления:
При
подстановке значений получаем квадратное уравнение:
Решив его, мы получим, что .
Осталось посчитать полное время полета шарика:
Показать ответ и решение
Обоснование
1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в
этой СО.
2. Движение тела поступательное, поэтому будем считать тело материальной точкой.
3. На учаскте разгона тело движется вертикально вверх с постоянным ускорением.
4. После окончания разгона тело будет двигаться в поле силы тяжести и именно эта сила сообщает
телу ускорение направленное вертикально вниз и равное м/с
.
5. Движение тела на обоих участках будем описывать законами прямолинейного равноускоренного
движения.
Решение
Сначала ракета двигалась равноускоренно вверх. Запишем формулу движения до момента
прекращения ускорения и формулу движения:
А скорость в конце разгона составит
После этого она находилась в свободном полете под действием силы тяжести, в ходе чего
остановилась в воздухе на высоте:
где — начальная скорость на этом участке.
Выразим (время от момента прекращения ускорения
до момента остановки ракеты) по формуле
конечной скорости:
Отсюда:
Подставим формулу для :
После этого ракета начнет падать вниз, пока не упадет:
Осталось выразить :
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Сказано, что тело можно считать материальной точкой.
3. Сказано, что после прекращения разгона тело движется в поле силы тяжести с ускореним свободного
падения.
4. Сказано, что описывать движение тела можно, используя законы прямолинейного равноускоренного
движения
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: записано уравнение координаты, записано
уравнение описывающее изменение скорости).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
В момент, когда опоздавший пассажир вышел на перрон вокзала, с ним поравнялось начало
предпоследнего вагона уходящего поезда. Желая определить, насколько он опоздал, пассажир измерил
время , за которое мимо него прошел предпоследний вагон, и время
, за которое мимо него
прошел последний вагон. Оказалось, что с, а
с. Считая, что поезд двигался
равноускоренно и длина вагонов одинакова, найти, на какое время пассажир опоздал к отходу
поезда.
Показать ответ и решение
Пусть — длина одного вагона,
— ускорение поезда.
В момент прихода пассажира поезд проехал путь, равный:
Когда проехал предпоследний вагон, путь стал равен:
Выразим отсюда длину вагона:
Когда проехал последний вагон, путь стал равен:
Отсюда также выразим :
Длины вагонов равны, значит:
Осталось выразить отсюда :
Показать ответ и решение
Запишем уравнение торможения, сразу отметив, что ускорение отрицательно, т.к. направлено против
движения автомобиля:
Конечная скорость . Отсюда:
Выразим ускорение:
Запишем формулу для скорости при равнозамедленном движении:
Отсюда:
Теперь запишем уравнение тормозного пути, при котором автомобиль прошел путь S/4 с тем же
ускорением:
Выразим :
- ЕГЭ по физике
Подборка заданий по кинематике для подготовки к ЕГЭ по физике в 11 классе.
→ Скачать задания
→ Скачать ответы
Данный тренинг соответствует разделу кодификатора 1. 1 — кинематика.
Этот раздел содержит 8 различных типов задач на разные темы. (1. 1. 1 — 1. 1. 
В тренинге задачи подобраны в соответствие с кодификатором.
Пример заданий:
Камень падает с высокого обрыва, двигаясь по вертикали. Сопротивление воздуха пренебрежимо мало. Модуль средней скорости камня с течением времени
1) увеличивается
2) уменьшается
3) не изменяется
4) сначала увеличивается, а затем начинает уменьшаться
Ответ: _____.
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Модуль скорости движения мотоцикла относительно автомобиля равен
1) 20 км/ч
2) 20 км/ч
3) 120 км/ч
4) 50 км/ч
Ответ: _____.
Связанные страницы:
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
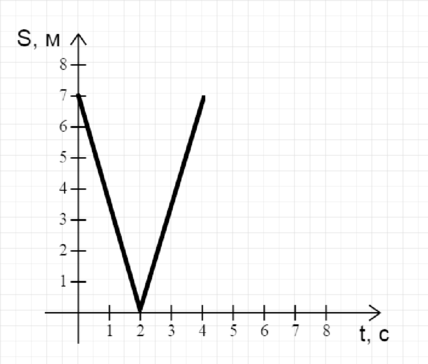
Из двух концов комнаты навстречу друг другу с постоянной скоростью движутся МО и Рыжий Боб. На графике показана зависимость расстояния между ними от времени. Скорость МО равна 3,14 м/с. С какой скоростью движется Рыжий Боб? (Ответ дайте в м/с)
По графику определяем, что расстояние между МО и Рыжим Бобом в начальный момент времени (S=7) м, а время, спустя которое они встретятся, (t=2) c. Перейдем в подвижную систему отсчета относительно МО. Тогда по закону сложения скоростей Рыжий Боб будет двигаться к нему со скоростью: [upsilon=upsilon_1+upsilon_2,] где (upsilon_1) и (upsilon_2) — скорости МО и Рыжего Боба соответственно (относительно неподвижной системы отсчета).
По закону равномерного прямолинейного движения: [S=upsilon t] Подставим сюда предыдущую формулу, и получим: [S=(upsilon_1+upsilon_2)t] Осталось выразить отсюда скорость Рыжего Боба: [upsilon_2=dfrac{S}{t}-upsilon_1=dfrac{7 text{ м}}{2~c}-3{,}14 text{ м/c} = 0{,}36 text{ м/c} .]
Ответ: 0,36
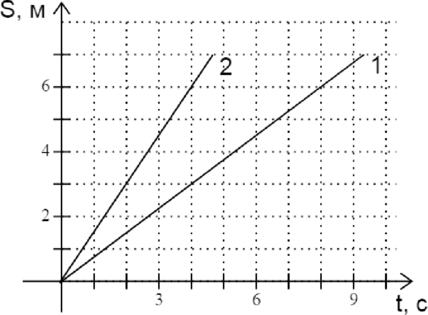
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Определите, во сколько раз скорость второго тела (upsilon_2) больше скорости первого тела (upsilon_1).
Т.к. пройденные пути тел линейно увеличиваются, тела движутся равномерно и прямолинейно.
По графику определяем, что первое тело за время (t_1=4) с проходит путь (S_1=3) м, а второе тело за время (t_2=2~c) проходит путь (S_2=3) м. По закону равномерного прямолинейного движения: [S_1=upsilon_1t_1
quad
S_2=upsilon_2t_2] Отсюда выразим (upsilon_1) и (upsilon_2): [upsilon_1=dfrac{S_1}{t_1}; quad
upsilon_2=dfrac{S_2}{t_2}.] Найдем (dfrac{upsilon_2}{upsilon_1}): [dfrac{upsilon_2}{upsilon_1}=dfrac{dfrac{S_2}{t_2}}{dfrac{S_1}{t_1}}=dfrac{dfrac{3 text{ м}}{2~c}}{dfrac{3 text{ м}}{4~c}}=2]
Ответ: 2
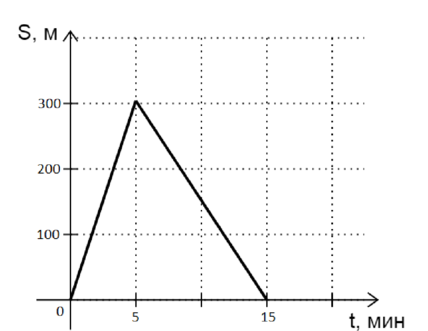
Дима каждый день ходит в школу. На рисунке представлен график движения Димы из дома в школу и обратно. Дом находится в точке (S=0), а школа — в точке (S=300) м. Чему равен модуль скорости Димы на пути из школы домой? (Ответ дайте в м/с)
Рассмотрим график: весь путь Дима двигался прямолинейно и равномерно (но в точке (S=300) м изменил свою скорость). Сначала он двигался из дома в школу со скоростью (upsilon_1) в течение времени (t_1=5) мин, после чего возвращался из школы домой cо скоростью (upsilon_2) в течение времени (t_2): [t_2=15text{ мин}-5text{ мин}=10text{ мин}=10cdot60text{ c}=600~text{ с}.] Чтобы найти (upsilon_2), нам необходимо рассмотреть участок движения Димы по пути из школы домой ((S_2)).
По закону равномерного прямолинейного движения: [S_2=upsilon_2t_2,] где (S_2=0text{ м}-300text{ м}=-300text{ м}).
Отсюда выражаем (upsilon_2): [upsilon_2=dfrac{S_2}{t_2}=dfrac{-300~text{м}}{600~text{c}}=-0,5~text{м/с}] Значит, (|upsilon_2|=|-0,5|text{ м/с}=0,5text{ м/с })
Ответ: 0,5
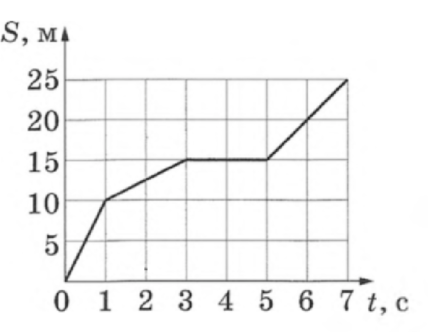
На рисунке представлен график зависимости пути (S), пройденного материальной точкой, от времени (t). Определите скорость (upsilon) точки на интервале времени от 5 с до 7 с. (Ответ дайте в м/с)
Т.к. пройденный путь материальной точки на интервале времени от 5 c до 7 c линейно увеличивается, материальная точка на этом интервале движется равномерно и прямолинейно. По закону равномерного прямолинейного движения:
[Delta S=upsilonDelta t,] где (Delta S=25 text{ м}-15text{ м}=10text{ м}), а (Delta t=7text{ c}-5text{ c}=2text{ c}). Выразим (upsilon): [upsilon=dfrac{Delta S}{Delta t}=dfrac{10text{ м}}{2text{ c}}=5text{ м/c}]
Ответ: 5
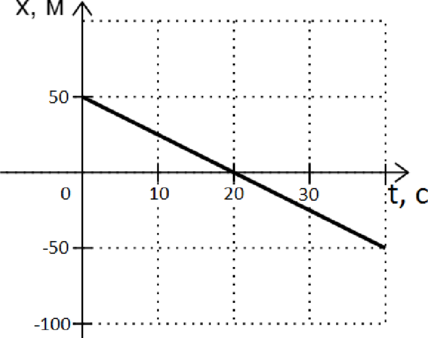
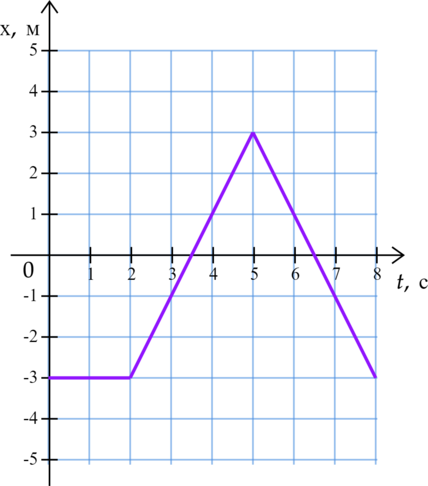
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении по оси Ox. Чему равна (upsilon_x) проекция скорости тела на ось Ох? (Ответ дайте в м/с)
Т.к. пройденный путь тела линейно уменьшается, тело движется равномерно и прямолинейно, и скорость тела постоянна: (upsilon_x=const). По закону прямолинейного равномерного движения тела: [Delta S=upsilon_xDelta t,] где (Delta S=-50text{ м}-50text{ м}=-100) — перемещение тела, а (Delta t=40 c) — время перемещения.
Отсюда выразим (upsilon_x): [upsilon_x=dfrac{Delta S}{Delta t}=dfrac{-100text{ м}}{40text{ c}}=-2,5~dfrac{text{м}}{text{c}}]
Ответ: -2,5
На рисунке приведен график зависимости координаты тела от времени при прямолинейном движении по оси (x). Какова проекция (upsilon_x) скорости тела в промежутке от 5 (c) до 8 (c)? (Ответ дайте в м/с)
Найдем изменение координаты тела в промежутке от 5 (c) до 8 (c). Для этого из конечной координаты вычтем начальную: [Delta x=x_text{к}-x_text{н}]
Подставим исходные данные: [Delta x=(-3)text{ м}-3text{ м}=-6text{ м}]
Найдем изменение времени в промежутке от 5 (c) до 8 (c): [Delta t=t_text{к}-t_text{н}]
Подставим исходные данные: [Delta t=8text{ с}-5text{ с}=3text{ c}]
Найдем проекцию скорости тела:
[upsilon_x=frac{Delta x}{Delta t}]
Подставим исходные данные: [upsilon_x=frac{-6text{ м}}{3text{ c}}=-2text{ м/c}]
Ответ: -2
Движение двух велосипедистов задано уравнениями (x_1=3t) (м) и (x_2=12-t) (м). Велосипедисты двигаются вдоль одной прямой. Найдите координату (x) места встречи велосипедистов. (Ответ дайте в метрах)
1 способ:
Велосипедисты встретятся, если совпадут их координаты, отсюда: [x_1=x_2]
Подставим уравнения: [3t=12-t] [4t=12]
Отсюда время, в которое встретятся велосипедисты: [t=3text{ c}]
Найдем координату (x) места встречи велосипедистов, для этого подставим время (t) в оба уравнения: [x_1=3cdot3=9text{ м}] [x_2=12-3=9text{ м}]
2 способ:
Изобразим движение велосипедистов: 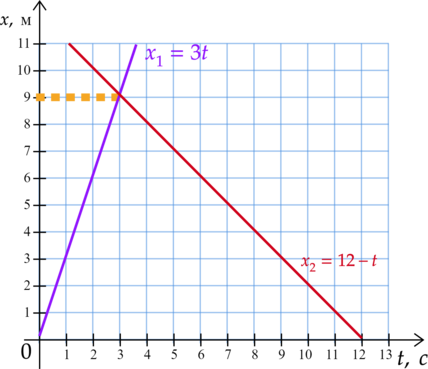
Ответ: 9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задания
с выбором ответа.
1. Координата тела меняется с течением времени
согласно закону x=5−2,5t, где все
величины выражены в СИ. Какой из графиков отражает зависимость проекции
скорости движения тела от времени?
2. На рисунке приведён график зависимости
координаты тела от времени при его прямолинейном движении по оси x.
Какой из графиков соответствует зависимости от
времени проекции υx скорости
тела в промежутке времени от 25 до 30 с?

На рисунке приведены графики зависимости проекций их скоростей υx от времени t. На
основании графиков выберите два верных утверждения о движении тел.
1)Проекция ax
ускорения тела 1 меньше проекции ax ускорения тела 2.
2)Проекция ax
ускорения тела 1 равна 0,3 м/с2.
3) Тело 2 в момент
времени 15 с находилось в начале отсчёта.
4) Первые 15 с тела
двигались в разные стороны.
5) Проекция ax
ускорения тела 2 равна 0,1 м/с2.

ее скорости на вертикальное направление меняется со временем согласно графику
на рисунке. В какой момент времени стрела достигла максимальной высоты?
|
1) |
1,5 с |
|
2) |
3 с |
|
3) |
4,5 с |
|
4) |
6 с |
5. Зависимость координаты от времени для
некоторого тела описывается уравнением x=8t−t2
, где все величины выражены в СИ. В какой момент времени скорость тела равна
нулю?
|
1) |
8 с |
|
2) |
4 с |
|
3) |
3 с |
|
4) |
0 с |
6. От высокой скалы откололся и стал свободно
падать камень. Какую скорость он будет иметь через 3 с от начала
падения?
|
1) |
30 м/с |
|
2) |
10 м/с |
|
3) |
3 м/с |
|
4) |
2 м/с |
7. Тело брошено вертикально вверх с начальной
скоростью 20 м/с. Каков модуль скорости тела через 0,5 с после начала
движения? Сопротивление воздуха не учитывать.
|
1) |
5 м/с |
|
2) |
10 м/с |
|
3) |
15 м/с |
|
4) |
20 м/с |
8. При прямолинейном равноускоренном движении
с нулевой начальной скоростью путь, пройденный телом за две секунды с начала
движения, больше пути, пройденного за первую секунду, в
|
1) |
2 раза |
|
2) |
3 раза |
|
3) |
4 раза |
|
4) |
5 раз |
9. Камень, брошенный вертикально вверх с поверхности
Земли со скоростью 20 м/с, упал обратно на Землю. Сопротивление воздуха мало.
Камень находился в полете примерно
|
1) |
1 с |
|
2) |
2 с |
|
3) |
4 с |
|
4) |
8 с |
10. Зависимость пути от времени прямолинейно
движущегося тела имеет вид: s(t) = 2t + 3t2, где все величины выражены в СИ. Ускорение тела равно
|
1) |
1 м/с2 |
|
2) |
2 м/с2 |
|
3) |
3 м/с2 |
|
4) |
6 м/с2 |
11 На рисунках изображены графики зависимости
модуля ускорения от времени для разных видов движения. Какой график
соответствует равномерному движению?
12. Скорость пули при вылете из ствола
пистолета равна 250 м/с. Длина ствола 0,1
м. Каково примерно ускорение пули внутри ствола, если считать ее движение
равноускоренным?
|
1) |
312 км/с2 |
|
2) |
114 км/с2 |
|
3) |
1248 км/с2 |
|
4) |
100 м/с2 |
13. Одной из характеристик автомобиля является
время t его разгона с места до скорости 100
км/ч. Два автомобиля имеют такие времена разгона, что
t1 = 2t2. Ускорение первого автомобиля по отношению
к ускорению второго автомобиля
|
1) |
меньше в 2 раза |
|
2) |
больше в 2√2 |
|
3) |
больше в 2 раза |
|
4) |
больше в 4 раза |
14. Мотоциклист и велосипедист одновременно
начинают равноускоренное движение из состояния покоя. Ускорение мотоциклиста в
3 раза больше, чем у велосипедиста. Во сколько раз больше времени понадобится
велосипедисту, чтобы достичь скорости 50
км/ч?
|
1) |
в 1/3 |
|
2) |
в 3√3 |
|
3) |
в 3 раза |
|
4) |
в 9 раз |
15. К.Э. Циолковский в книге «Вне
Земли», описывая полет ракеты, отмечал, что через 10 с после старта ракета находилась на расстоянии 5 км от поверхности Земли. С каким ускорением двигалась
ракета?
|
1) |
1000 м/с2 |
|
2) |
500 м/с2 |
|
3) |
100 м/с2 |
|
4) |
50 м/с2 |
16. Ускорение велосипедиста на одном из
спусков трассы равно 1,2 м/с2. На этом спуске его скорость
увеличивается на 18 м/с. Велосипедист заканчивает свой спуск после его
начала через
|
1) |
0,07 с |
|
2) |
7,5 с |
|
3) |
15 с |
|
4) |
21,6 с |
17. Тело, двигаясь вдоль оси ОХ прямолинейно и
равноускоренно, за некоторое время уменьшило свою скорость в 2 раза. Какой из
графиков зависимости проекции ускорения от времени соответствует такому
движению?
18. Автомобиль движется по прямой улице. На
графике представлена зависимость скорости автомобиля от времени. Модуль
ускорения максимален на интервале времени
|
1) |
от 0 с до 10 с |
|
2) |
от 10 с до 20 с |
|
3) |
от 20 с до 30 с |
|
4) |
от 30 с до 40 с |
19. На рисунке представлен график зависимости
пути S велосипедиста от времени t. В каком интервале времени после начала
движения велосипедист не двигался?
|
1) |
от 0 с до 1 с |
|
2) |
от 1 с до 3с |
|
3) |
от 3 с до 5с |
|
4) |
от 5 с и далее |

зависимости скорости u автомобиля от времени t. Определите
по графику путь, пройденный автомобилем в интервале времени от 0 до 3 с.
|
1) |
20 м |
|
2) |
10 м |
|
3) |
15 м |
|
4) |
25 м |

координат вдоль оси Ох, причем проекция скорости vx меняется
с течением времени по закону, приведенному на графике. Через 2 с ускорение
тела равно
|
1) |
0 м/с2 |
|
2) |
0,5 м/с2 |
|
3) |
1 м/с2 |
|
4) |
2 м/с2 |
22. Тело упало с некоторой высоты с нулевой
начальной скоростью и при ударе о землю имело скорость 40 м/с. Чему равно
время падения? Сопротивлением воздуха пренебречь.
|
1) |
0,25 с |
|
2) |
4 с |
|
3) |
40 с |
|
4) |
400 с |
23. Автомобиль движется по закруглению дороги
радиусом 20 м с центростремительным ускорением 5
м/с2. Скорость автомобиля равна
|
1) |
12,5 м/с |
|
2) |
10 м/с |
|
3) |
5 м/с |
|
4) |
4 м/с |
24. Две материальные точки движутся по
окружностям радиусами R1 и R2, причем R2 = 2R1.
При условии равенства линейных скоростей точек их центростремительные ускорения
связаны соотношением
|
1) |
a1 |
|
2) |
a1 |
|
3) |
a1 |
|
4) |
a1 |
25. Точка движется с постоянной по модулю
скоростью v по окружности радиуса R.
Как изменится центростремительное ускорение точки, если ее скорость увеличить
вдвое, а радиус окружности вдвое уменьшить?
|
1) |
уменьшится в 2 раза |
|
2) |
увеличится в 2 раза |
|
3) |
увеличится в 4 раза |
|
4) |
увеличится в 8 раза |
26. Точка движется по окружности радиуса R со скоростью v. Как изменится центростремительное
ускорение точки, если скорость уменьшить в 2 раза, а радиус окружности в 2 раза
увеличить?
|
1) |
уменьшится в 2 раза |
|
2) |
увеличится в 2 раза |
|
3) |
уменьшится в 8 раз |
|
4) |
не изменится |
27. Материальная точка равномерно движется со
скоростью u по окружности радиусом r. Если скорость
точки будет вдвое больше, то модуль ее центростремительного ускорения
|
1) |
не изменится |
|
2) |
уменьшится в 2 раза |
|
3) |
увеличится в 2 раза |
|
4) |
увеличится в 4 раза |
28. Шарик движется по окружности радиусом r со скоростью u. Как изменится его центростремительное
ускорение, если радиус окружности увеличить в 3 раза, оставив скорость шарика
прежней?
|
1) |
увеличится в 3 раза |
|
2) |
уменьшится в 3 раза |
|
3) |
увеличится в 9 раза |
|
4) |
уменьшится в 9 раза |
Задания
с кратким ответом.
1. Мимо остановки по прямой улице проезжает
грузовик со скоростью 10 м/с. Через 5 с от остановки вдогонку
грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с2.
На каком расстоянии от остановки мотоциклист догонит грузовик?
2. Материальная точка, двигаясь равноускоренно
по прямой, за время t увеличила скорость в 3 раза, пройдя путь 20
м. Найдите t, если ускорение точки равно 5 м/с2.
3. За 2 с прямолинейного равноускоренного
движения тело прошло 20 м, увеличив свою скорость в 3 раза. Определите
начальную скорость тела.
4. На последнем километре тормозного пути
скорость поезда уменьшилась на 10 м/с. Определите скорость в начале
торможения, если общий тормозной путь поезда составил 4 км,
а торможение было равнозамедленным.
5. Небольшой камень, брошенный с ровной
горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в
20 м от места броска. Сколько времени прошло от броска до того момента,
когда его скорость была направлена горизонтально и равна 10 м/с?

вращаются вокруг неподвижных осей (см. рисунок). Бóльшая шестерня радиусом 10 см
делает 20 оборотов за 10 с, а частота обращения меньшей шестерни равна 5 с–1.
Каков радиус меньшей шестерни? Ответ укажите в сантиметрах.
Задания
с развернутым ответом.
1. Тело, свободно падающее с некоторой высоты
без начальной скорости, за время t = 1 с после начала движения проходит путь в n = 5 раз меньший, чем за такой же
промежуток времени в конце движения. Найдите полное время движения.
2. Тело, свободно падающее с некоторой высоты,
первый участок пути проходит за время τ = 1 с,
а такой же последний – за время ½ τ.
Найдите полное время падения t, если начальная скорость равна нулю.
3. Маленький шарик падает сверху на наклонную
плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен
30°. На какое расстояние по горизонтали перемещается шарик между первым и
вторым ударами о плоскость? Скорость шарика в момент первого удара направлена
вертикально вниз и равна 1 м/с.
Кинематика часть А Стр. из
Кинематика 1 вар
ГРАФИКИ
Определение вида движения по графику
- Равноускоренному движению соответствует график зависимости модуля ускорения от времени, обозначенный на рисунке буквой
- А
- Б
- В
- Г
- Парашютист движется вертикально вниз с постоянной по значению скоростью. Какой график — 1, 2, 3 или 4 — правильно отражает зависимость его координаты Y от времени движения t относительно поверхности земли? Сопротивлением воздуха пренебречь.
1) 1 2) 2 3) 3 4) 4
Определение и сравнение характеристик движения по графику
- На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении. Определите проекцию ускорения тела.
- – 10 м/с2
- – 8 м/с2
- 8 м/с2
- 10 м/с2
4.По графику зависимости проекции скорости от времени, представленному па рисунке, определите модуль ускорения прямолинейно движущегося тела в момент времени t = 2 с.
- 2 м/с2
- 3 м/с2
- 10 м/с2
- 27 м/с2
5. Четыре тела движутся вдоль оси Оx.На рисунке изображены графики зависимости проекций скоростей υx от времени t для этих тел. Какое из тел движется с наименьшим по модулю ускорением?
1) 1 2) 2 3) 3 4) 4
6.На рисунке приведен график зависимости проекции скорости тела от времени.
Проекция ускорения тела в интервале времени от 5 до 10 с представлена графиком
1) 1 2) 2 3) 3 4) 4
7.Материальная точка движется прямолинейно с ускорением, зависимость от времени которого приведена на рисунке. Начальная скорость точки равна 0. Какая точка на графике соответствует максимальной скорости материальной точки:
- 2
- 3
- 4
- 5
Составление кинематических зависимостей (функций зависимости кинематических величин от времени) по графику
8.На рис. изображен график зависимости координаты тела от времени. Определите кинематический закон движения этого тела
- x(t) = 2 + 2t
- x(t) = – 2 – 2t
- x(t) = 2 – 2t
- x(t) = – 2 + 2t
Определение перемещения и пути по графику
9.По графику зависимости скорости тела от времени определите путь, пройденный прямолинейно движущимся телом за 3 с.
- 2 м
- 4 м
- 18 м
- 36 м
10.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке. Чему равно перемещение камня за первые 3 с?
- 0 м
- 30 м
- 45 м
- 60 м
11.Камень брошен вертикально вверх. Проекция его скорости на вертикальное направление изменяется со временем согласно графику на рисунке к заданию 10. Чему равно перемещение камня за все время полета?
- 0 м
- 30 м
- 60 м
- 90 м
УРАВНЕНИЯ
12.Движение троллейбуса при аварийном торможении задано уравнением: x = – 2,5 t2 +15t +30 , м Чему равна начальная координата троллейбуса?
- 2,5 м
- 5 м
- 15 м
- 30 м
13.Уравнение зависимости проекции скорости движущегося тела от времени: vx = 2 +3t (м/с). Каково соответствующее уравнение проекции перемещения тела?
1) Sx = 2t + 3t2 2) Sx = 4t + 3t2 3) Sx = t + 6t2 4) Sx = 2t + 1,5t2
14.Зависимость координаты от времени для некоторого тела описывается уравнением х = 8t – t2 . В какой момент времени скорость тела равна нулю?
- 8 с
- 4 с
- 3 с
- 0 c
ТАБЛИЦЫ
15.В таблице представлена зависимость координаты х равномерного движения тела от времени t:
|
t, с |
0 |
1 |
2 |
3 |
4 |
|
х, м |
0 |
2 |
4 |
6 |
8 |
С какой скоростью двигалось тело от момента времени 0 с до момента времени 4 с?
- 0,5 м/с
- 1,5 м/с
- 2 м/с
- 3 м/с
Движение по окружности
- При равномерном движении точки по окружности со скоростьюv. Модуль изменения скорости |∆v|за половину периода равен
l) v/2 2) v 3) v 4) 2v
2.Вектор ускорения при равномерном движении точки по окружности
- постоянен по модулю и по направлению; 2) равен нулю
3)постоянен по модулю, но непрерывно изменяется по направлению
4)постоянен по направлению, но непрерывно изменяется по модулю
3.Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории его центростремительное ускорение максимально?
- 1
- 2
- 3
- Во всех точках одинаково
- Период обращения Земли вокруг Солнца равен одному году, радиус орбиты Земли равен 150 млн.км. Скорость движения Земли по орбите равна примерно
- 30 м/с
- 30 км/с
- 150 км/с
- 1800 км/с
- Диск радиусом 20 см равномерно вращается вокруг своей оси. Скорость точки, находящейся на расстоянии 15 см от центра диска, равна 1,5 м/с. Скорость крайних точек диска равна
1) 4 м/с 2) 0,2 м/с 3) 2 м/с 4) 1,5 м/с
- Точка движется по окружности радиуса R со скоростью v. Как изменится центростремительное ускорение точки, если скорость уменьшить в 2 раза, а радиус окружности в 2 раза увеличить?
- уменьшится в 2 раза
- увеличится в 2 раза
- уменьшится в 8 раз
- не изменится
- Два спутника движутся по разным круговым орбитам вокруг Земли. Скорость первого из них в 2 раза больше, а радиус орбиты в 4 раза меньше, чем второго. Центростремительное ускорение первого спутника а1, второго — а2? Чему равно отношение a1 / a2?
1) 1
2) 2
3) 4
4) 16
- Две материальные точки движутся по окружностям радиусами R1 и R2 = 2R1 с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
- Т1=0,5Т2
- Т1=Т2
- Т1=2Т2
- Т1=4Т
Задания части В
- Материальная точка движется по окружности радиуса R. Что произойдет с периодом, частотой обращения и центростремительным (нормальным) ускорением точки при увеличении линейной скорости движения?
Установите соответствие между физическими величинами и их изменением: к каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.
|
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ |
ИХ ИЗМЕНЕНИЕ |
||
|
А) |
Период обращения материальной точки |
1) |
Увеличится |
|
Б) |
Частота обращения материальной точки |
2) |
Уменьшится |
|
В) |
Центростремительное (нормальное) ускорение |
3) |
Не изменится |
Получившуюся последовательность цифр перенесите в бланк ответов (без пробелов и каких-либо символов).