Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На экране наблюдается спектр с помощью дифракционной решетки, имеющей 500 штрихов на миллиметр. Расстояние от решетки до экрана Спектральная линия в спектре первого порядка находится на расстоянии
от центра экрана. Определите длину волны наблюдаемой спектральной линии.
2
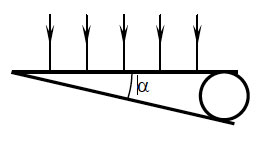
Масляная пленка на воде при наблюдении вертикально к поверхности кажется оранжевой. Каково минимальное возможное значение толщины пленки? Показатель преломления воды 1,33, масла — 1,47. Длина световой волны Учтите, что отражение света от оптически более плотной среды происходит с потерей полуволны, а от оптически менее плотной среды без потери полуволны.
3
Для наблюдения явления интерференции света используется точечный источник света и небольшой экран с двумя малыми отверстиями у глаза наблюдателя. Оцените максимальное расстояние d между малыми отверстиями в экране, при котором может наблюдаться явление интерференции света. Разрешающая способность глаза равна длина световой волны
4
Человек читает книгу, держа ее на расстоянии 50 см от глаз. Если это для него расстояние наилучшего видения, то какой оптической силы очки позволят ему читать книгу на расстоянии 25 см?
5
Бассейн глубиной 4 м заполнен водой, относительный показатель преломления на границе воздух-вода 1,33. Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?
Пройти тестирование по этим заданиям
Задачи из ДЕМОВАРИАНТОВ (с решениями)
1. В дно водоема глубиной 3 м вертикально
вбита свая, скрытая под водой. Высота сваи 2 м. Свая отбрасывает
на дне водоема тень длиной 0,75 м. Определите угол падения
солнечных лучей на поверхность воды. Показатель преломления
воды n = 4/3.
Образец возможного решения
2. На экране с помощью тонкой линзы получено
изображение предмета с пятикратным увеличением. Экран передвинули
на 30 см вдоль главной оптической оси линзы. Затем при неизменном
положении линзы передвинули предмет, чтобы изображение снова
стало резким. В этом случае получилось изображение с трехкратным
увеличением. На каком расстоянии от линзы находилось изображение
предмета в первом случае?
Образец возможного решения
3. На поверхности
воды плавает надувной плот шириной 4 м и длиной 6 м. Небо затянуто
сплошным облачным покровом, полностью рассеивающим солнечный
свет. Определите глубину тени под плотом. Глубиной погружения
плота и рассеиванием света водой пренебречь. Показатель преломления
воды относительно воздуха принять равным 4/3.
Образец возможного решения
4. Объектив проекционного аппарата имеет
оптическую силу 5,4 дптр. Экран расположен на расстоянии 4
м от объектива. Определите размеры экрана, на котором должно
уместиться изображение диапозитива размером 6×9 см.
Образец возможного решения
5. Небольшой
груз, подвешенный на нити длиной 2,5 м, совершает гармонические
колебания, при которых его максимальная скорость достигает 0,2
м/с. При помощи собирающей линзы с фокусным расстоянием 0,2
м изображение колеблющегося груза проецируется на экран, расположенный
на расстоянии 0,5 м от линзы. Главная оптическая ось линзы перпендикулярна
плоскости колебаний маятника и плоскости экрана. Определите
максимальное смещение изображения груза на экране от положения
равновесия.
Образец возможного решения
6. На дифракционную решетку с периодом d
= 0,01 мм нормально к поверхности решетки падает параллельный
пучок монохроматического света с длиной волны λ = 600
нм. За решеткой, параллельно ее плоскости, расположена тонкая
собирающая линза с фокусным расстоянием f = 5 см.
Чему равно расстояние между максимумами первого и второго
порядков на экране, расположенном в фокальной плоскости линзы?
Образец возможного решения
Избранные задачи прошлых лет (с ответами)
7. Под медленно
движущимся кораблем с вертикальными бортами плывет разведчик
в легком водолазном костюме. Ширина корабля 4 м, глубина погружения
его днища 1,5 м. Небо затянуто сплошным облачным покровом, полностью
рассеивающим солнечный свет. На каком максимальном расстоянии
от днища корабля должен держаться разведчик, чтобы его не могли
увидеть находящиеся вокруг другие водолазы? Рассеиванием света
водой и размерами разведчика пренебречь. Показатель преломления
воды относительно воздуха принять равным 4/3.
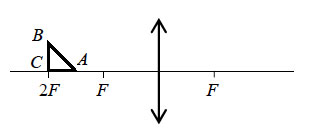
8. Равнобедренный
прямоугольный треугольник АВС площадью 50 см2 расположен
перед тонкой собирающей линзой так, что его катет АС лежит на
главной оптической оси линзы. Фокусное расстояние линзы 50 см.
Вершина прямого угла С лежит дальше от центра линзы, чем вершина
острого угла А. Расстояние от центра линзы до точки С равно
удвоенному фокусному расстоянию линзы (см. рисунок). Постройте
изображение треугольника АВС и найдите площадь получившейся
фигуры.
9. На оси
ОХ в точке x1 = 0 находится тонкая рассеивающая
линза с фокусным расстоянием f1 = — 20 см,
а в точке x2 = 20 см — тонкая собирающая
линза с фокусным расстоянием f2 = 30 см.
Главные оптические оси обеих линз лежат на оси ОХ. Свет от точечного
источника S, расположенного в точке x < 0, пройдя данную
оптическую систему, распространяется параллельным пучком. Найдите
координату x (в см) точечного источника S.
10. Условимся
считать изображение на пленке фотоаппарата резким, если вместо
идеального изображения в виде точки на пленке получается изображение
пятна диаметром не более некоторого предельного значения. Поэтому,
если объектив находится на фокусном расстоянии от пленки, то
резкими считаются не только бесконечно удаленные предметы, но
и все предметы, находящиеся дальше некоторого расстояния d.
Оцените предельный размер пятна, если при фокусном расстоянии
объектива 50 мм и диаметре входного отверстия 5 мм резкими оказались
все предметы далее 5 м.
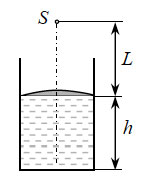
11. В сосуде на поверхности
воды плавает тонкая легкая плосковыпуклая линза выпуклой стороной
вверх (см. рисунок). Фокусное расстояние линзы в воздухе F.
Высота уровня воды в сосуде h. Изображение точечного
источника света S, расположенного на расстоянии L от
линзы на ее главной оптической оси, находится на дне сосуда.
Найти показатель преломления воды. Считать, что L >
F.
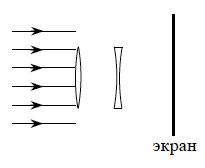
12. Параллельный световой
пучок падает нормально на тонкую собирающую линзу. На расстоянии
20 см от нее находится рассеивающая линза (см. рисунок). Оптическая
сила собирающей линзы 2,5 дптр, а у рассеивающей она равна -5
дптр. Диаметр линз равен 8 см. Экран расположен на расстоянии
L = 30 см от рассеивающей линзы. Каков диаметр светлого
пятна, создаваемого линзами на экране?
13. Дифракционная
решетка, имеющая 200 штрихов на 1 мм, расположена параллельно
экрану на расстоянии 1,25 м от него и освещается нормально падающим
пучком света длиной волны 500 нм. Определите расстояние между
вторыми дифракционными максимумами справа и слева от центрального
(нулевого). Считать, что tgα ≈ sinα.
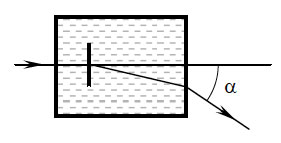
14. Дифракционная решетка
имеет расстояние между штрихами 1 мкм. Она находится в прямоугольной
кювете, заполненной водой, и располагается параллельно боковой
стенке кюветы. Луч света, длина волны которого 0,5 мкм, падает
перпендикулярно стенке кюветы, проходит через решетку и выходит
из кюветы. Под каким углом α выходит луч, образующий первый
дифракционный максимум?
15. Между краями двух
хорошо отшлифованных тонких плоских стеклянных пластинок помещена
тонкая проволочка, противоположные концы пластинок плотно прижаты
друг к другу (см. рисунок). На верхнюю пластинку нормально к
ее поверхности падает монохроматический пучок света длиной волны
600 нм. Определите угол α который образуют пластинки, если
расстояние между наблюдаемыми интерференционными полосами равно
0,6 мм. Считать tgα ≈ α.
16. Мыльная пленка представляет
собой тонкий слой воды, на поверхности которой находятся молекулы
мыла, обеспечивающие механическую устойчивость и не влияющие
на оптические свойства пленки. Мыльная пленка натянута на квадратную
рамку со стороной d = 2,5 см. Две стороны рамки расположены
горизонтально, а две другие — вертикально. Под действием силы
тяжести пленка приняла форму клина (см. рисунок), утолщенного
внизу, с углом при вершине α = 2•10-4
рад. При освещении квадрата параллельным пучком света лазера,
падающим перпендикулярно пленке, часть света отражается от нее,
образуя на ее поверхности интерференционную картину, состоящую
из 20 горизонтальных полос. Чему равна длина волны излучения
лазера в воздухе, если показатель преломления воды равен 4/3?
17. Вы светите
лазерной указкой на стену противоположного дома. Оцените расстояние
до дома, если диаметр пятна на стене D = 20 см (границы
пятна оцениваются из условия, что в области пятна лучи, идущие
от различных участков источника, не «гасят» друг друга), диаметр
выходного пучка лазера d = 3 мм, а длина волны λ
= 600 нм.
задачам прошлых лет
По теме: методические разработки, презентации и конспекты
тестовые задания по разделу «Экономическая сфера» для 9 класса
Данный тест предназначен для проверки и систематизации знаний учащихся 9 класса по экономической сфере. тест составлен в формате ГИА….
Тестовые задания по разделу «Лексика и грамматика» ГИА и ЕГЭ
Тестовые задания раздела «Лексика и грамматика» ГИА и ЕГЭ по теме «Technik «…
Тестовые задания по разделу учебной программы «Знания о физической культуре» для 9 классов
Тест включает в себя три части, соответствующих структуре экзаменационной работы.В заданиях с вариантами ответа (Часть 1 — 10 вопросов) предусмотрен один верный ответ.Часть 2 (5 вопросов) содержит зад…
ТЕСТОВЫЕ ЗАДАНИЯ ПО РАЗДЕЛУ МАТЕРИАЛОВЕДЕНИЕ 5 КЛАСС
Вашему вниманию представлены тестовые задания по разделу «материаловедение» для 5 класса….
Комплекс тестовых заданий для учащихся 7 класса по теме «Информация. Информационные процессы»
Приведены примеры тестов разного типа…
Комплекс тестовых заданий для учащихся 6 класса по теме «Морфемика. Словообразование».
Комплекс тестовых заданий для учащихся6 класса ПО ТЕМЕ «Морфемика. Словообразование». Класс: 6Предмет: русский языкУровень сложности: базовыйТип КОТЗ: при закреплении или проверке тек…
Пояснительная записка к заданиям по общей и органической химии. Тестовые задания по разделам.
Представлен тестовый материал по общей и органической химии….
32. Электродинамика. Квантовая физика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Геометрическая оптика
Бассейн глубиной (H = 3) м заполнен водой, показатель преломления которой (n = 4/3.) Каков радиус светового круга на поверхности воды от электрической лампы на дне бассейна?
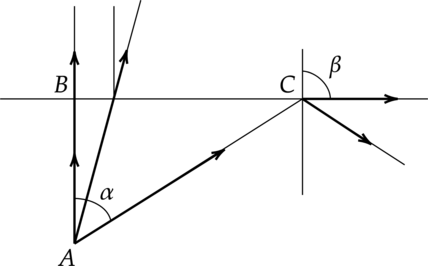
Рассмотрим ход лучей
Полное внутреннее отражение происходит начиная с такого значения угла падения (alpha), при котором (beta = 90^circ). По закону преломления [dfrac{sin beta}{sin alpha }= n Rightarrow sin alpha = dfrac{1}{n}] Искомая величина (BC) равна [BC= ABcdot tg alpha =dfrac{AB}{sqrt{n^2-1}}=dfrac{3text{ м}}{sqrt{dfrac{16}{9}-1}}approx 3,4 text{ м}]
Ответ: 3,4
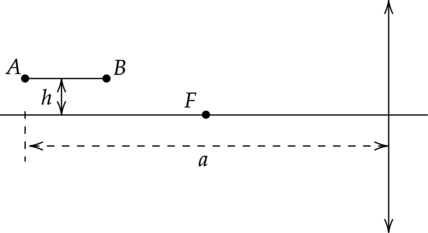
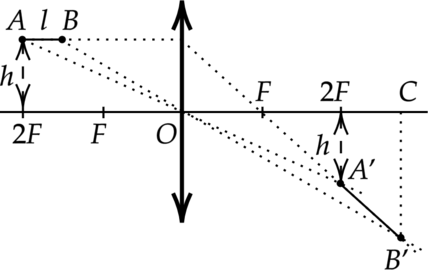
Тонкая палочка АВ длиной (l) = 10 см расположена параллельно главной оптической оси тонкой собирающей линзы на расстоянии (h) = 15 см от неё (см. рисунок). Конец А палочки располагается на расстоянии (a) = 40 см от линзы. Постройте изображение палочки в линзе и определите его длину (L). Фокусное расстояние линзы (F) = 20 cм.
“Демоверсия 2017”
1. Построение изображения (A’B’) предмета (AB) в линзе показано на рисунке.
2. Так как точка (A) находится на расстоянии (2F) от линзы, то её изображение (A’) также находится на расстоянии (2F) от линзы, и расстояние от точки (A’) до главной оптической оси равно (h).
3. Длина изображения (A’B’) [L=sqrt{(OC-2F)^2+(B’C-h)^2}] 4. Из формулы тонкой линзы [dfrac{1}{F}=dfrac{1}{2F-l}+dfrac{1}{OC}] следует [OC=dfrac{F(2F-l)}{F-l}=60text{ см}] 5. (dfrac{B’C}{h}=dfrac{OC}{2F-l}), откуда (B’C= hdfrac{OC}{2F-l}=30text{ см}) 6. Окончательные вычисления [L=sqrt{400+225}=25text{ см}]
Ответ: 25
Точечный источник находится на главной оптической оси собирающей линзы с фокусным расстоянием 8 см на расстоянии 6 см от линзы. Линзу начинают смещать со скоростью 3 мм/с в направлении, перпендикулярном оптической оси. С какой скоростью (в мм/с) движется изображение источника?
Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}+frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f=frac{Fd}{F-d}] [Gamma=frac{f}{d}=frac{F}{F-d}=frac{8}{2}=4]
(v) – скорость предмета относительно линзы
(u) – скорость изображения источника [u=vGamma=12 text{ мм/с}]
Ответ: 12
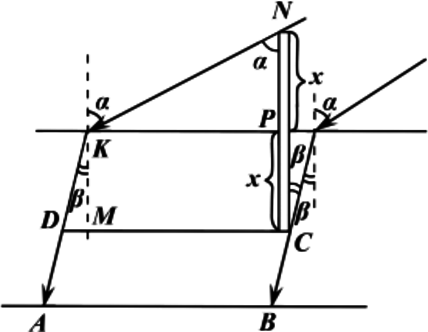
Палка, наполовину погружённая в вертикальном положении в воду, отбрасывает на дно бассейна тень длиной (l = 0, 5) м. Определите длину выступающей над водой части палки, если глубина воды равна (h = 3) м, а угол падения солнечных лучей равен (alpha = 30^circ ) (Показатель преломления воды – 4/3.) Ответ дайте в метрах и округлите до десятых
Построим ход лучей:
Закон преломления:
[sin alpha=n sin beta] (n=4 / 3) (по условию), тогда: [tg=frac{sin beta}{cos beta}=frac{sin beta}{sqrt{1-sin ^{2} beta}}=frac{frac{sin alpha}{n}}{sqrt{1-frac{sin ^{2} alpha}{n^{2}}}}=frac{sin alpha}{sqrt{n^{2}-sin ^{2} alpha}}=frac{1 / 2}{sqrt{(4 / 3)^{2}-(1 / 2)^{2}}}=frac{1 / 2}{sqrt{55 / 36}}=frac{3}{sqrt{55}}] Пусть (x) – длина надводной части палки. Палка погружена наполовину, следовательно, длина подводной части – (x .) Тогда [begin{array}{c}
l=|A B|=|C D|=|P K|+|K M| tg alpha=|P N| tg alpha+x tg beta=x tg alpha+x tg beta \
x=frac{l}{tg alpha+tg beta}=frac{0,5}{frac{3}{sqrt{55}}+frac{1}{sqrt{3}}} approx 0,51 text{ м}
end{array}]
Ответ: 0,5
Бассейн глубиной (H=4) м заполнен водой, относительный показатель преломления на границе воздух-вода (n=4/3). Какой кажется глубина бассейна наблюдателю, смотрящему в воду вертикально вниз?
Пусть (h) – кажущаяся высота.
По закону Снеллиуса [dfrac{sin beta}{sin alpha}= n] Рассмотрим ход лучей
Тогда [h=dfrac{tg alpha}{tg beta} H] Так как углы малые: [happrox dfrac{sin alpha}{sin beta} H approx dfrac{H}{n}=dfrac{4text{ м}}{4/3}approx 3 text{ м}]
Ответ: 3
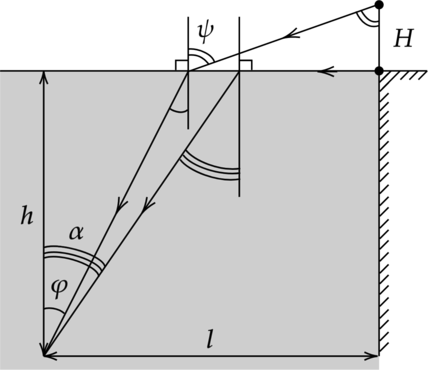
В горизонтальное дно водоема глубиной 3 м вертикально вбита свая, полностью скрытая под водой. При угле падения солнечных лучей на поверхность воды, равном 300, свая отбрасывает на дно водоёма тень длиной 0,8 м. Определите высоту сваи. Показатель преломления воды составляет (n = 4/3.) Ответ дайте в метрах и округлите до сотых.
Рассмотрим ход лучей
Из закона преломления, луч идущий горизонтально от ног тренера (угол падения равен 90(^circ)) следует по закону полного внутреннего отражения: [sin alpha = dfrac{1}{n} Rightarrow alpha = arcsin dfrac{3}{4}] Аналогично распишем закон преломления для луча идущего от головы тренера: [dfrac{sin psi}{sin varphi}= n Rightarrow sin psi = n sin varphi =dfrac{4}{3}cdot dfrac{1}{2}=dfrac{2}{3}] Из рисунка [H=(l-hcdot tg varphi)ctg psi =(l-h cdot tg varphi) dfrac{cos phi}{sin psi}= (l-h cdot tg varphi)=(l-h cdot tg varphi)dfrac{sqrt{1-sin^2 psi}}{sin psi}=dfrac{sqrt{1-n^2sin^2varphi^2}}{nsin varphi}] Подставляя числа из условий, получим [H= left(3-2,5cdot dfrac{sqrt{3}}{3}right)cdot dfrac{sqrt{5}}{2}approx 1,74text{ м}.]
Ответ: 1,74
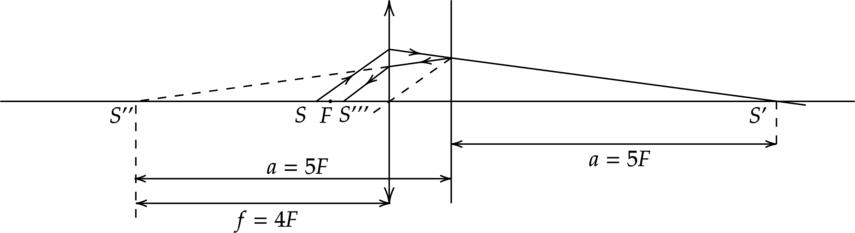
Точечный источник света находится на расстоянии 12 см от собирающей линзы с фокусным расстоянием 10 см. За линзой на расстоянии 10 см установлено плоское зеркало, перпендикулярное главной оптической оси линзы. На каком расстоянии (в см) от линзы находится изображение, образованное лучами, прошедшими через линзу после отражения от зеркала?
Формула тонкой линзы для собирающей линзы(без участия зеркала): [frac{1}{F}=frac{1}{d_1}+frac{1}{f_1}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f_1=frac{Fd_1}{d_1-F}=frac{10cdot12}{12-10}=60 text{ см}] Отразим лучи в зеркале после прохождения линзы один раз, получаем (S») – мнимый предмет, расстояние (d_2=40) см
Формула тонкой линзы для собирающей линзы (предмет S”, изображение S”’): [frac{1}{F}=-frac{1}{d_2}+frac{1}{f_2}] [f_2=frac{Fd_2}{F+d_2}=frac{10text{ см}cdot40text{ см}}{50text{ см}}=8 text{ см}]
Ответ: 8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Предлагаем разобрать три задачи, приведенные ниже. Это варианты задания №27 из ЕГЭ прошлых лет, рекомендованные как тренировочные.
Задача № 1
Коллекционер разглядывает при помощи лупы элемент марки, имеющий размер 0,2 мм, и видит его мнимое изображение, увеличенное до 1,2 мм. Рассматриваемый элемент расположен на расстоянии 7 мм от лупы. На каком расстоянии от лупы находится изображение? Ответ приведите в миллиметрах.
Решение
Составим чертеж, согласно условию задачи (Рис. 1):
Рис. 1
Лупа представляет собой собирающую линзу. Чтобы получать в ней неперевернутые увеличенные изображения, необходимо размещать предмет ближе фокусного расстояния. При этом изображение будет мнимым.
Из рисунка (Рис. 1) видно, что в силу подобия треугольников расстояние от предмета до лупы «d», расстояние от лупы до изображения «f», размер предмета «h» и размер изображения «H» связаны соотношением:
=
Выразим из этой формулы «f»:
f =
Подставим числовые значения:
f = = 42
Таким образом, изображение находится от лупы на расстоянии 42 мм.
Ответ: 42 мм.
Задача № 2
Линза с фокусным расстоянием F = 0,1 м даёт на экране изображение предмета, увеличенное в 6 раз. Каково расстояние от линзы до изображения? Ответ приведите в метрах.
Решение
Фокусное расстояние связано с расстоянием от предмета до линзы и расстоянием от линзы до изображения формулой линзы:
=
+
Увеличение линзы равно отношению высоты изображения к высоте объекта:
Г =
Из геометрического построения найдем, что:
Г =
Тогда получим:
= 6 =>
=
+
=
=> f = 7F = 7 · 0,1 = 0,7 м
Ответ: 0,7 м.
Задача № 3
Линза с фокусным расстоянием F = 0,3 м даёт на экране изображение предмета, увеличенное в 3 раза. Каково расстояние от линзы до изображения? Ответ приведите в метрах.
Решение
Фокусное расстояние связано с расстоянием от предмета до линзы и расстоянием от линзы до изображения формулой линзы:
=
+
Увеличение линзы равно отношению высоты изображения к высоте объекта:
Г =
Из геометрического построения найдем, что:
Г =
Тогда получим:
= 3 => f = 3d=>
=
+
=
=> f = 4F = 4 · 0,3 = 1,2 м
Ответ:1, 2 м.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Разделы сайта
Рекомендую
Геометрическая оптика
Преломление — подготовка к олимпиадам — 2

Решаем задачи на закон Снелла. Будут призмы и неровная поверхность воды…
Задача 1.
Поверхности воды касается равнобедренная стеклянная призма АВС (см. рисунок). Луч света, падающий из воздуха под углом на грань АС, после прохождения призмы…
Преломление — подготовка к олимпиадам

Решаем задачи по геометрической оптике — готовимся к олимпиадам. Здесь снова зеркало и закон Снелла.
Задача 1.
По столу катится шарик со скоростью . В противоположном направлении со скоростью перемещают…
14.09.2022 08:30:15 | Автор: Анна
|
|
Зеркала — олимпиадная подготовка

Продолжаем готовиться к Всероссу и решаем с ребятами сложные задачки по оптике. В этой статье — зеркала.
Задача 1.
Машина удаляется с постоянной скоростью от большой зеркальной витрины, двигаясь по прямой. На машине установлена лампа Л, которая светит равномерно во все стороны с мощностью
12.09.2022 08:08:07 | Автор: Анна
|
|
Задачи с двумя линзами

Предлагаю вашему вниманию несколько задач, в которых обязательно присутствуют две линзы. Линзы могут быть – обе — собирающими, и собирающей в комбинации с рассеивающей.
Задача 1.
Две собирающие линзы с фокусными расстояниями см и
22.09.2020 05:59:10 | Автор: Анна
|
|
Использование графиков при решении задач с линзами — 2

Тема этой и предыдущей статей – использование графиков при решении задач на оптику, а именно – задач с линзами. Конспект занятий Пенкина М.А.
Сначала давайте построим график, использование которого сильно облегчит решение задач.
Собирающая линза. Для нее известно, что если расстояние от предмета до линзы меньше, чем фокусное,…
30.07.2019 06:05:08 | Автор: Анна
|
|
Тонкие линзы: решение задач с помощью графика

Тема этой и следующей статей – использование графиков при решении задач на оптику, а именно – задач с линзами. Конспект занятий Пенкина М.А.
Сначала давайте построим график, использование которого сильно облегчит решение задач.
Собирающая линза. Для нее известно, что если расстояние от предмета до линзы меньше, чем…
28.07.2019 11:59:10 | Автор: Анна
|
|
Камень, брошенный под углом к горизонту, и его тень

Откуда задача – сказать не могу. Решение свое отыскала в куче неразобранных бумаг, текст воспроизвожу по памяти.
Задача. Камень бросили со скоростью под углом
16.07.2019 06:02:30 | Автор: Анна
|
|
Линзы: мнимый предмет

Этой статьей продолжается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. В статье собраны задачи со сходящимися пучками лучей, когда предмет — мнимый. Начало здесь, здесь и здесь.
Задача 1.
Предмет…
16.08.2017 18:46:07 | Автор: Анна
|
|
Линзы -3

Этой статьей продолжается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. Начало здесь и здесь.
Задача 1.
Высота пламени свечи 5 см. Линза дает на экране изображение этого пламени высотой 15 см. Не…
14.08.2017 10:43:14 | Автор: Анна
|
|
Линзы 2: оптическая сила
Этой статьей продолжается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. Начало здесь, более сложные — в следующих статьях.
Задача 1.
Предмет расположен на расстоянии 40 см от линзы с оптической силой 2 дптр. Как…
12.08.2017 10:53:06 | Автор: Анна
|
|
Линзы 1

Этой статьей начинается серия статей по геометрической оптике, связанных с построением в линзе и задачами на уравнение тонкой линзы. Начнем с простых задач, более сложные — в следующих статьях.
Задача 1.
На рисунке даны положение главной оптической оси линзы, источник света
10.08.2017 10:30:55 | Автор: Анна
|
|
Геометрическая оптика: глаз и очки

В этой статье решаем задачи про очки – несложные. Глаз – это тоже линза, и если фокусное расстояние этой линзы избыточное или недостаточное, то очки могут поправить дело.
У хорошо видящего человека лучи света, попадающие в глаз, преломляются хрусталиком так, что попадают прямо на сетчатку –…
08.08.2017 20:23:43 | Автор: Анна
|
|
Геометрическая оптика: призмы

В этой статье решаем задачи с призмами. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача 1.
Монохроматический луч падает нормально на боковую поверхность призмы, преломляющий угол которой равен . Показатель преломления материала призмы для этого луча равен 1,5….
06.08.2017 20:17:29 | Автор: Анна
|
|
Геометрическая оптика: пластинки

В этой статье решаем задачи с пластинками – средние по сложности. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача 1. Прямоугольная стеклянная пластинка толщиной 4 см имеет показатель преломления 1,6. На ее поверхность падает луч света под углом . Определите,…
04.08.2017 18:45:18 | Автор: Анна
|
|
Закон преломления Снеллиуса — 3
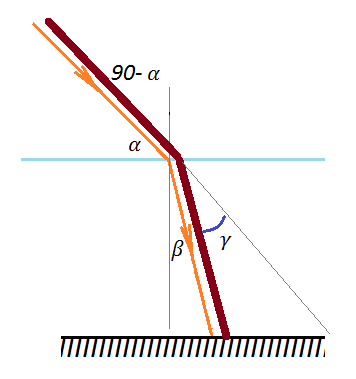
В этой статье будут представлены задачи на показатель преломления – средние по сложности. Здесь вы найдете простые задачи, здесь – задачи средние по сложности, но более простые, чем в этой статье. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача…
02.08.2017 18:21:55 | Автор: Анна
|
|
Геометрическая оптика: закон Снеллиуса — 2

В этой статье будут представлены задачи на показатель преломления – средние по сложности. Будем применять закон преломления Снеллиуса, а также геометрические знания. Начало здесь.
Задача 1.
Луч света падает на границу раздела двух сред под углом
30.07.2017 18:03:51 | Автор: Анна
|
|
Геометрическая оптика: закон Снеллиуса — 1
В этой статье я будут представлены задачи на показатель преломления – самые простые, стартовые задачи в одно действие. Будем применять закон преломления Снеллиуса.
Задача 1.
Определите показатель преломления скипидара и скорость распространения света в скипидаре, если известно, что при угле падения
28.07.2017 17:56:41 | Автор: Анна
|
|
Геометрическая оптика: зеркала

В этой статье собраны задачи на плоское зеркало. Угол падения равен углу отражения – это все, что нужно помнить для их решения.
Задача 1.
Почему мы не видим лица фехтовальщика, если оно закрыто частой сеткой, но она не мешает самому фехтовальщику хорошо видеть окружающие предметы?
Снаружи…
26.07.2017 17:50:43 | Автор: Анна
|
|
Геометрическая оптика: тень

Этой статьей я открываю серию статей по геометрической оптике. Все, что нам понадобится – это знания по элементарной тригонометрии: геометрические определения синуса, косинуса, тангенса угла и понятие о подобии треугольников.
Задача 1.
Ученик заметил, что палка длиной 1,2 м, поставленная вертикально, отбрасывает тень длиной 0,8…
24.07.2017 17:43:23 | Автор: Анна
|
|
Система из двух зеркал

В этой статье мы научимся строить изображения в системе из двух зеркал. Надо понимать, что предмет не обязательно должен находиться непосредственно перед зеркалом, чтобы можно было увидеть его изображение. Ведь часто мы видим, находясь в одной из комнат, что происходит в другой в зеркале, которое…
22.07.2017 17:34:21 | Автор: Анна
|
|
Задачи вступительного экзамена в Академическую гимназию СПбГУ по физике (прошлых лет)

В статье приведен типовой вариант задания вступительных испытаний по физике в Академическую гимназию СПбГУ, в класс физико-математического направления. Задачи разбиты по уровням сложности, есть очень непростые для среднего школьника.
Часть А.
Задача 1.
На рисунке приведен график зависимости скорости от времени для тела, движущегося прямолинейно. В…
06.06.2017 15:22:24 | Автор: Анна
|
|
Рыбак на льду

Задача о рыбаке на зимней рыбалке. Эх, оказаться бы на таком прозрачном льду, что сквозь него дно видно! И какими должны быть морозы, чтобы встал лед такой толщины, вы только представьте! Кстати, прозрачность льда зависит от наличия в нем пузырьков воздуха. Если лед замерзает медленно,…
10.05.2017 09:43:44 | Автор: Анна
|
|
Последние записи
Облако меток
Архивы
Данная подборка материала является методическим пособием для
учащихся: при подготовке к основному экзамену или при решении задач разного
типа по теме «Оптика». Так же можно использовать данные задачи для закрепления
темы и на зачетный урок.
Задачи по оптике
- Представлена тонкая линза, у которой указана
главная оптическая ось, и указано, что в плоскости, проходящей
через двойной фокус, располагается светящаяся точка. Необходимо
определить, какая из четырех точек на чертеже соответствует правильному
изображению этого предмета, то есть светящейся точке.
Задача может быть решена несколькими способами, рассмотрим
два из них.
Рис. 1.
На рис. 1 изображена собирающая линза с оптическим центом
(0), фокусы (),
линза разнофокусная и точки двойного фокуса ().
Светящаяся точка ()
лежит в плоскости, расположенной в двойном фокусе. Необходимо показать,
какая из четырех точек соответствует построению изображения или
изображению этой точки на схеме.
Решение задачи начнем с вопроса построения изображения.
Светящаяся точка ()
располагается на двойном расстоянии от линзы, то есть это расстояние
равно двойному фокусу, его можно построить следующим образом: взять
линию, которая соответствует лучу, движущемуся параллельно главной
оптической оси, преломленный луч пройдет через фокус (),
а второй луч пройдет через оптический центр (0). Пересечение окажется
на расстоянии двойного фокуса ()
от линзы, это не что иное, как изображение, и оно соответствует точке 2.
Правильный ответ: 2.
Одновременно с этим можно воспользоваться формулой тонкой
линзы и вместо подставить
,
ведь точка лежит на расстоянии двойного фокуса, при преобразовании
получим, что изображение тоже получается в точке, удаленной на двойном
фокусе, ответ будет соответствовать 2 (рис. 2).
Рис. 2.


Ответ: 2.
- Предмет высотой 3 сантиметра находится
на расстоянии 40 сантиметров от собирающей тонкой линзы. Определить
высоту изображения, если известно, что оптическая сила линзы составляет
4 диоптрии.
Записываем условие задачи и, поскольку величины указаны
в разных системах отсчета, переводим их в единую систему и запишем
уравнения, необходимые для решения задачи:
Мы
использовали формулу тонкой линзы для собирающей линзы с положительным
фокусом, формулу увеличения ()
через величину изображения и высоту самого предмета, а также через
расстояние от линзы до изображения и от линзы до самого предмета.
Вспомнив, что оптическая сила ()
– это и есть обратное значение фокусного расстояния, можем переписать
уравнение тонкой линзы. Из формулы увеличения запишем высоту изображения.
Далее запишем выражение для расстояния от линзы до изображения из
преобразования формулы тонкой линзы и запишем формулу, по которой
можно вычислить расстояние до изображения (.
Подставив значение в
формулу высоты изображения, мы получим необходимый результат ,
то есть высота изображения получилась больше, чем высота самого
предмета. Следовательно, изображение действительное и увеличение
больше единицы.
- Перед тонкой собирающей линзой поместили
предмет, в результате такого размещения увеличение получилось
равным 2. Когда предмет передвинули относительно линзы, то увеличение
стало равно 10. Определить на сколько передвинули предмет и в
каком направлении, если первоначальное расстояние от линзы до
предмета составляло 6 сантиметров.
Для решения задачи мы будем использовать формулу вычисления
увеличения и формулу собирающей тонкой линзы.
Из
этих двух уравнений мы и будем искать решение. Выразим расстояние от
линзы до изображения в первом случае, зная увеличение и расстояние.
Подставив значения в формулу тонкой линзы, мы получим значение фокуса .
Далее все повторяем для второго случая, когда увеличение составляет
10. Получим расстояние от линзы до предмета во втором случае, когда
предмет передвинули, .
Мы видим, что предмет был передвинут ближе к фокусу, так как фокус составляет
4 сантиметра, в этом случае увеличение составляет 10, то есть увеличивается
изображение в 10 раз. Окончательный ответ ,
сам предмет был передвинут ближе к фокусу линзы и таким образом увеличение
стало больше в 5 раз.
Далее прилагаются решения задач из методического пособия с подробным решением и
рисунками к самим задачам.
Далее рассмотрим задачи о плоских
зеркалах.
1. Два
плоских прямоугольных зеркала образуют двугранный угол φ=179°. На расстоянии
l=10 см от линии соприкосновения зеркал и на одинаковом расстоянии от каждого
зеркала находится точечный источник света. Определить расстояние d между
мнимыми изображениями источника в зеркалах.
2.
На сферическое зеркало падает
луч света. Найти построением ход луча после отражения в двух случаях:
а) от вогнутого зеркала;
б) от выпуклого зеркала.
На рисунке: P — полюс зеркала; O — оптический центр.
3.
Вогнутое сферическое зеркало
дает на экране изображение предмета, увеличенное в Г=4 раза. Расстояние a от
предмета до зеркала равно 25 см. Определить радиус R кривизны зеркала.
4.
Фокусное расстояние f
вогнутого зеркала равно 15 см. Зеркало дает действительное изображение
предмета, уменьшенное в три раза. Определить расстояние a от предмета до
зеркала.
5.
Радиус R кривизны выпуклого зеркала
равен 50 см. Предмет высотой h=15 см находится на расстоянии a, равном 1 м, от
зеркала. Определить расстояние b от зеркала до изображения и его высоту H.
6.
(28.45)Лупа дает увеличение
Г=2. Вплотную к ней приложили собирательную линзу с оптической силой Ф1=20
дптр. Какое увеличение Г2 будет давать такая составная лупа?
7.
Оптическая сила Ф объектива
телескопа равна 0,5 дптр. Окуляр действует как лупа, дающая увеличение Г1=10.
Какое увеличение Г2 дает телескоп?
8.
На собирающую линзу с фокусным расстоянием F1 = 40 см падает параллельный пучок
лучей. Где следует поместить рассеивающую линзу с фокусным расстоянием F2 = 15 см, чтобы пучок лучей после
прохождения двух линз остался параллельным?
Решение: По условию пучок падающих лучей ЕА параллелен главной оптической оси NN, после преломления в линзах
он должен таковым и остаться. Это возможно, если рассеивающая линза расположена
так, чтобы задние фокусы линз F1 и F2 совпали. Тогда продолжение луча АВ (рис. 7), падающего на рассеивающую
линзу, проходит через ее фокус F2,
и по правилу построения в рассеивающей линзе преломленный луч BD будет параллелен главной оптической
оси NN, следовательно,
параллелен лучу ЕА. Из
рис. 7 видно, что рассеивающую линзу следует поместить на расстоянии d=F1-F2=(40-15)(см)=25
см от собирающей линзы.
Ответ: на расстоянии 25 см
от собирающей линзы.