Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Каталог заданий.
Первообразная
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
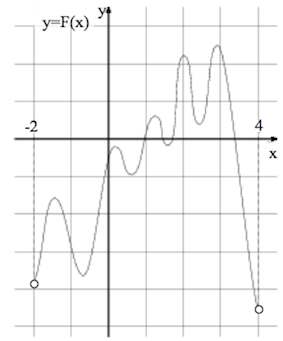
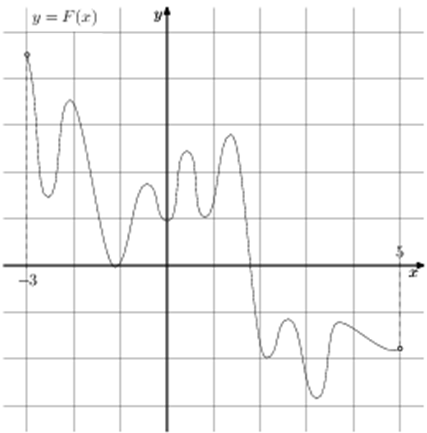
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 2.
2
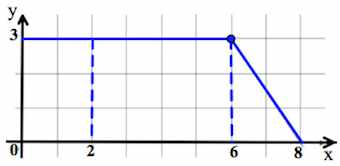
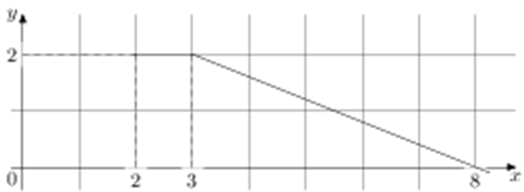
На рисунке изображён график некоторой функции
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.
3
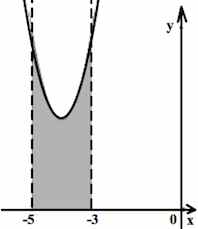
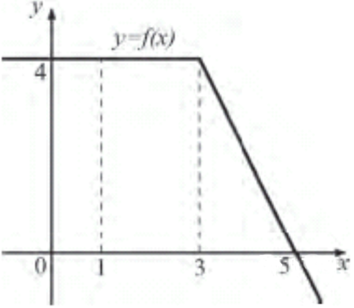
На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
4
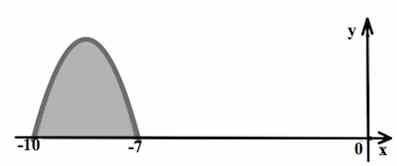
На рисунке изображён график некоторой функции y = f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Пройти тестирование по этим заданиям
Ресурс содержит презентацию и тест для самостоятельной работы. Тест составлен в 4 вариантах. Предназначен для подготовки к ЕГЭ. Цели ресурса: Образовательные: повторить и закрепить знания о первообразной функции и её свойствах, научиться применять знания при решении конкретных задач. Развивающие: развивать умение анализировать условие задачи. Воспитательные: воспитание аккуратности, внимательности, быстроты мышления.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
Подготовка к ЕГЭ Задание №7 (первообразная)
Слайд 2
1) На рисунке изображён график функции y = F( x ) — одной из первообразных функции f ( x ), определённой на интервале (−3; 5). Найдите количество решений уравнения f ( x ) = 0 на отрезке [−2; 4].
Слайд 3
2 ) На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F( x ) — одна из первообразных функции f ( x ).
Слайд 4
3 ) На рисунке изображён график функции y = f ( x ). Функция — одна из первообразных функции y = f ( x ). Найдите площадь закрашенной фигуры.
Слайд 5
4 ) На рисунке изображён график функции y = f ( x ). Функция — одна из первообразных функции y = f ( x ). Найдите площадь закрашенной фигуры.
Слайд 6
5 ) На рисунке изображен график некоторой функции Пользуясь рисунком, вычислите определенный интеграл .
Слайд 7
При подготовке презентации были использованы материалы с сайтов: https://www.uchportal.ru / https://ege.sdamgia.ru /
Предварительный просмотр:
|
ФИ_________________________________________________________В 1
Ответ:___________________
Ответ:___________________
Функция Ответ:___________________
Функция Ответ:___________________ |
ФИ_________________________________________________________В 2
Ответ________________________________
Ответ:___________________
Функция Ответ:___________________
Функция Ответ:___________________ |
|
ФИ__________________________________________________________В 3
Ответ_____________________
Ответ_____________________
Функция Ответ:___________________
Функция Ответ:___________________ |
ФИ_________________________________________________________В 4
Ответ____________________
Ответ_____________________
Функция Ответ:___________________
Функция Ответ:___________________ |
По теме: методические разработки, презентации и конспекты
Построение профиля задание С1 ЕГЭ по географии
При выполнении ЕГЭ по географии в задании С1 требуется выполнить профиль по топографической карте. Данный цикл занятий направленный на формирование у одинадцати классников умения выполнять этит тип за…
Варианты ЕГЭ математика (профиль), задания 1-12.
Варианты ЕГЭ математика (профиль), задания 1-12. Задания варианта соответствуют заданиям демоверсии ЕГЭ. При составлении вариантов использованы задания открытого банка заданий ЕГЭ. Ответы прилагаются….
- Мне нравится
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Первообразная функции»
Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1164
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.
Её площадь равна frac{4+3}{2}cdot 3=10,5.
Ответ
10,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1158
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1155
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.
Её площадь равна frac{5+3}{2}cdot 3=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1149
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 3], в которых производная функции F(x) равна нулю.
Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1146
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).
Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.
Ответ
10
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №907
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).
Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №307
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.
Показать решение
Решение
По формуле Ньютона-Лейбница S=F(-1)-F(-5).
F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.
F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.
F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.
Ответ
576
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №306
Тип задания: 7
Тема:
Первообразная функции
Условие
На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.
Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №104
Тип задания: 7
Тема:
Первообразная функции
Условие
На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.
Показать решение
Решение
На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:
intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)
Подставим значение первообразной из условия и получим площадь фигуры:
F(-1)-F(-4)=
=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=
=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5
Ответ
4,5
Задание №103
Тип задания: 7
Тема:
Первообразная функции
Условие
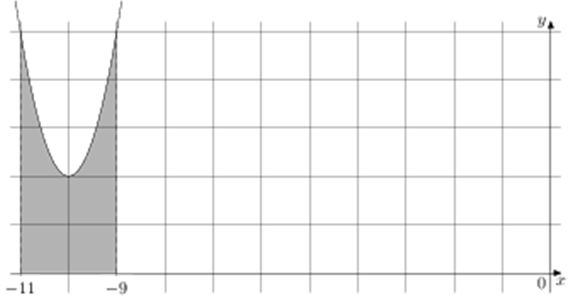
Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].
Показать решение
Решение
Формула первообразной имеет следующий вид:
f(x) = F'(x)
По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.
Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.
На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.
Ответ
3
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
ПЕРВООБРАЗНАЯ. ЗАДАНИЕ № 7. ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ
1.
На рисунке
изображён график функции y = F(x) — одной из
первообразных некоторой функции f(x), определённой на интервале
(−3; 5). Пользуясь рисунком, определите количество решений уравнения
f(x)=0 на отрезке [−2; 4].
2.
На рисунке
изображён график некоторой функции (два луча с общей начальной
точкой). Пользуясь рисунком, вычислите F(8) − F(2),
где F(x) — одна из первообразных функции f(x).
3.
На рисунке
изображён график функции y = f(x). Функция — одна из первообразных
функции y = f(x). Найдите площадь закрашенной
фигуры.
.
4.

функции y = f(x). Функция — одна из первообразных
функции f(x). Найдите площадь закрашенной фигуры.
5.

функции Пользуясь рисунком, вычислите
определенный интеграл
6.На
рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
. Найдите площадь закрашенной
фигуры.
7.На
рисунке изображён график некоторой функции . Функция
— одна из первообразных
функции .
Найдите площадь закрашенной фигуры.
8. На
рисунке изображён график функции (два луча с общей начальной точкой).
Пользуясь рисунком, вычислите , где
— одна из первообразных
функции .
6.На
рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
. Найдите площадь закрашенной
фигуры.
7.На
рисунке изображён график некоторой функции . Функция
— одна из первообразных
функции .
Найдите площадь закрашенной фигуры.
.
11.На
рисунке изображен график функции , определенной на интервале
. Найдите количество решений
уравнения на
отрезке .
10
Авг 2013
Категория: 07 Производная, ПО
07. Первообразная
2013-08-10
2022-09-11
Задача 1. На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
, где
— одна из первообразных функции
.
Решение: + показать
Задача 2. На рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
. Найдите площадь закрашенной фигуры.
Решение: + показать
Задача 3. На рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
. Найдите площадь закрашенной фигуры.
Решение: + показать
Задача 4. На рисунке изображён график функции – одной из первообразных некоторой функции
, определённой на интервале
. Пользуясь рисунком, определите количество решений уравнения
на отрезке
.
Решение: + показать

Вы можете пройти тест «Первообразная»
Автор: egeMax |
комментариев 7
ЕГЭ Профиль №6. Первообразная
Скачать файл в формате pdf.
ЕГЭ Профиль №6. Первообразная
| Задача 1. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)), определённой на интервале (left( { — 3;;5} right)). Пользуясь рисунком, определите количество решений уравнения (fleft( x right) = 0) на отрезке (left[ { — 2;;4} right]).
Ответ
ОТВЕТ: 10. |
 |
| Задача 2. На рисунке изображён график некоторой функции (y = fleft( x right)) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (Fleft( 8 right) — Fleft( 2 right)), где (Fleft( x right))— одна из первообразных функции (fleft( x right)).
Ответ
ОТВЕТ: 7. |
 |
| Задача 3. На рисунке изображен график некоторой функции (y = fleft( x right)). Пользуясь рисунком, вычислите определенный интеграл (intlimits_1^5 {fleft( x right)} ,dx)
Ответ
ОТВЕТ: 12. |
 |
| Задача 4. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = {x^3} + 30{x^2} + 302x — frac{{15}}{8}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 6. |
 |
Задача 5. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — {x^3} — 27{x^2} — 240x —  — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 4. |
 |
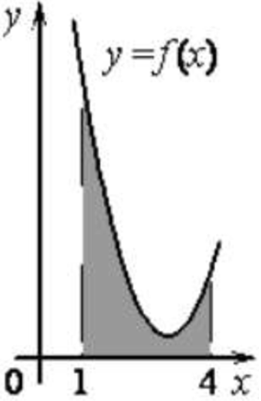
| Задача6 . На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = frac{1}{2}{x^3} — frac{9}{2}{x^2} + 14x — 12) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 6. |
 |
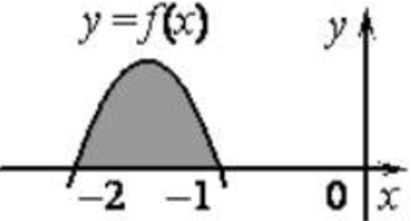
| Задача 7. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — {x^3} — frac{9}{2}{x^2} — 6x — frac{{123}}{7}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
Ответ
ОТВЕТ: 0,5. |
 |
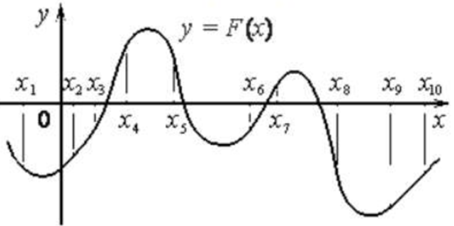
| Задача 8. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)) и отмечены десять точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольки из этих точек функция (fleft( x right)) положительна?
Ответ
ОТВЕТ: 7. |
 |
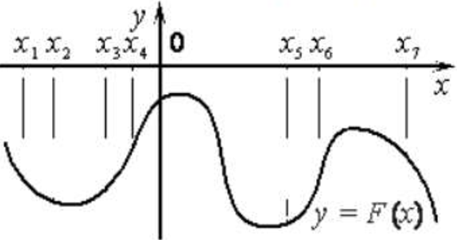
| Задача 9. На рисунке изображён график функции (y = Fleft( x right)) — одной из первообразных некоторой функции (fleft( x right)) и отмечены семь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7. В скольки из этих точек функция (fleft( x right)) отрицательна?
Ответ
ОТВЕТ: 3. |
 |






































.png)

.png)