Задания егэ с клеточками егэ - Помощь в подготовке к экзаменам и поступлению

Всего: 77 1–20 | 21–40 | 41–60 | 61–77

Добавить в вариант

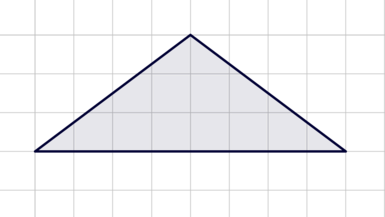
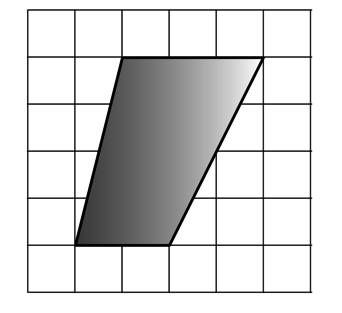
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

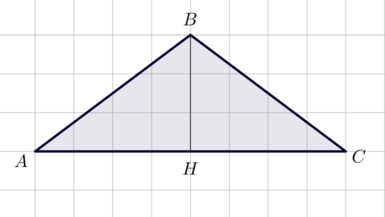
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.

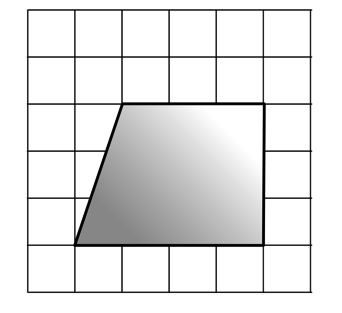
Найдите (в см²) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

1 см times 1 см (см. рис.). В ответе запишите

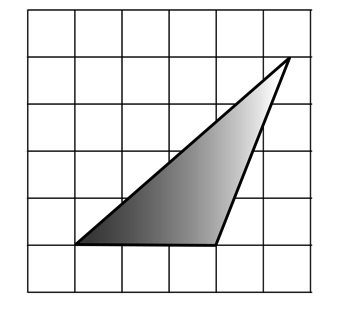
Найдите (в см²) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

1 см  times  1 см (см. рис.). В ответе запишите

На клетчатой бумаге с размером клетки изображён угол. Найдите его градусную величину.

На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.

Найдите (в см²) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). В ответе запишите

Найдите (в см²) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

1 см times 1 см (см. рис.). В ответе запишите

Всего: 77 1–20 | 21–40 | 41–60 | 61–77

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на клетчатой бумаге

(blacktriangleright) Помним, что каждая клетка представляет собой квадрат.

(blacktriangleright) В равных прямоугольниках равны диагонали.

(blacktriangleright) Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

(blacktriangleright) В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
И наоборот: катет, равный половине гипотенузы, лежит против угла (30^circ) (рис. 1).

(blacktriangleright) Медиана, проведенная к основанию в равнобедренном треугольнике, является высотой и биссектрисой (рис. 2).

Задание
1

#3089

Уровень задания: Равен ЕГЭ

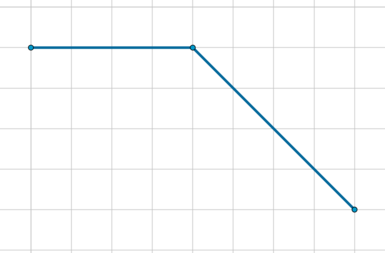
На клетчатой бумаге изображен угол. Найдите его градусную величину.

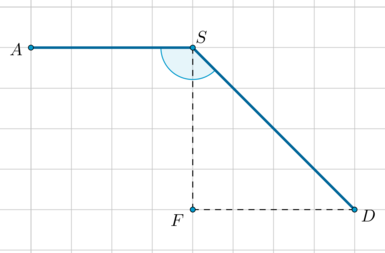
Обозначим этот угол (ASD). Отметим точку (F) так, чтобы получился прямоугольный (triangle SDF):

Тогда (angle ASD=angle ASF+angle FSD). Заметим, что (angle
ASF=90^circ). Заметим также, что (FS=FD), следовательно, (triangle
SDF) прямоугольный и равнобедренный, значит, его острые углы равны по (45^circ).
Следовательно, [angle ASD=90^circ+45^circ=135^circ.]

Ответ: 135

Задание
2

#3088

Уровень задания: Равен ЕГЭ

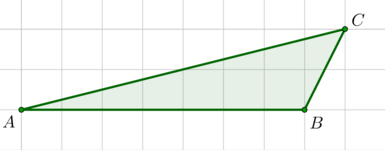
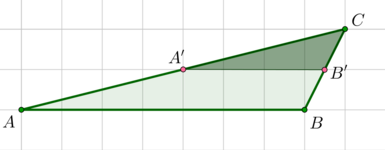
На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите площадь треугольника (A’B’C), где (A’B’) – средняя линия, параллельная стороне (AB).

Пусть (A’in AC, B’in BC).

По свойству средней линии (triangle ABCsim triangle A’B’C) с коэффициентом подобия, равным (2). Следовательно, их площади относятся как коэффициент подобия в квадрате, то есть [dfrac{S_{ABC}}{S_{A’B’C}}=4] Высота (triangle ABC), опущенная из (C), равна (2), (AB=7). Следовательно, (S_{ABC}=frac12cdot 2cdot 7=7). Тогда [S_{A’B’C}=dfrac74=1,75.]

Ответ: 1,75

Задание
3

#3087

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите длину средней линии, параллельной стороне (AB).

Длина средней линии треугольника, параллельной стороне (AB), равна (frac12AB). Так как (AB=7), то средняя линия равна (3,5).

Ответ: 3,5

Задание
4

#3086

Уровень задания: Равен ЕГЭ

На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна (3).

Будем искать радиус вписанной окружности по формуле (S=pcdot r), где (S) – площадь, (p) – полупериметр.
Заметим, что треугольник равнобедренный: (AB=BC.)

Так как длина стороны клетки равна (3), то (AH=12, BH=9), следовательно, (AB=sqrt{AH^2+BH^2}=15.) Тогда [dfrac12cdot BHcdot AC=dfrac{AB+BC+AC}2cdot r quadRightarrowquad
r=4.]

Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна (1), а затем умножать полученный ответ на (3). Если бы длина одной клетки была равна (1), то (AH=4, BH=3), (AB=5) и (r=frac43). Тогда после умножения на (3) также получили бы (r=4). При решении задачи таким способом вычисления будут легче.

Ответ: 4

Задание
5

#297

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисована трапеция. Найдите её площадь. Ответ дайте в квадратных миллиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции есть (0,5cdot (3 text{мм} + 4 text{мм})cdot 3 text{мм} = 10,5)мм(^2).

Ответ: 10,5

Задание
6

#298

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован треугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию, тогда площадь нарисованного треугольника есть (0,5cdot 3)мм (cdot 4)мм (= 6)мм(^2).

Ответ: 6

Задание
7

#299

Уровень задания: Равен ЕГЭ

На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован четырёхугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.

У данного четырёхугольника две стороны параллельны, а две другие не параллельны, следовательно, это трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции равна (0,5(2 text{мм} + 3 text{мм})cdot 4 text{мм} = 10) мм(^2).

Ответ: 10

Если выпускник готовится к сдаче ЕГЭ по математике и при этом рассчитывает на получение конкурентных баллов, ему непременно стоит освоить принцип решения задач на клетчатой бумаге. Подобные планиметрические задания каждый год включаются в программу аттестационного испытания. Таким образом, справляться с задачами ЕГЭ на клетчатой бумаге должны все учащиеся, независимо от уровня их подготовки.

Полезная информация

Задания ЕГЭ на клетчатой бумаге часто решаются гораздо проще, чем задачи, для выполнения которых требуется применение аналитических методов. Чаще всего в подобных упражнениях необходимо найти площадь фигуры. Решить такие задачи можно, вспомнив основные теоремы и свойства трапеции, треугольника, шестиугольника и т. д.

Как подготовиться к экзамену?

Если задания ЕГЭ на клетчатой бумаге вызывают у вас трудности, обратитесь к образовательному порталу «Школково». С нами вы сможете повторить материал по темам, которые являются для вас сложными, например, векторы на координатной плоскости и таким образом восполнить пробелы в знаниях. В разделе «Теоретическая справка» представлена вся базовая информация. Ее наши специалисты подготовили и изложили в максимально доступной форме на основе богатого практического опыта.

Освоить принцип решения задач на клетчатой бумаге помогут упражнения, представленные в разделе «Каталог». Мы подготовили простые и более сложные задания. Тренироваться в их выполнении учащиеся из Москвы и других российских городов могут в онлайн-режиме.

Справившись с заданием, выпускники имеют возможность сохранить его в разделе «Избранное». Это позволит в дальнейшем вернуться к нему и, к примеру, обсудить алгоритм его решения со школьным преподавателем. База заданий на сайте «Школково» регулярно обновляется.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

: ЕГЭ по биологии

Биология 11 класс. Тренировочные задания для подготовки к ЕГЭ по теме «Клетка».

→ Клеточная теория

→ Химический состав клетки

→ Цитология

→ Метаболизм клетки

→ ответы

Пример заданий:

1. Транскрипция представляет собой процесс

1) образования пептидных связей между аминокислотами

2) доставки аминокислот к рибосомам

3) синтеза ДНК в ядре на основе принципа комплементарности

4) синтеза иРНК на одной из полинуклеотидных цепей ДНК

Ответ:

2. В каком из перечисленных процессов участвуют ионы кальция?

1) транспорт газов

2) образование связей между аминокислотами

3) синтез белков

4) процесс свёртывания крови

Ответ:

Связанные страницы:

Источник

Задачи на клетчатой бумаге. Формула Пика.

Задачи на бумаге в клетку помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.

При решении задач на клетчатой бумаге ученикам не понадобится знание основ планиметрии, а будет нужна именно смекалка, геометрическое воображение и достаточно простые геометрические сведения, которые известны всем.

Формула Пика

Наш сюжет будет разворачиваться на обычном листке клетчатой бумаги.[1]

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах (рис. 1) и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить.

Но тут нас ждёт много хлопот (попробуйте!). Давайте «схитрим»:

вычислим площадь заштрихованной фигуры, которая «дополняет» наш

Рис. 1

многоугольник до прямоугольника АВСD, и вычтем её из площади прямоугольника. Заштрихованная фигура легко разбивается на прямоугольники и прямоугольные треугольники, и её площадь вычисляется без усилий.

Итак, хотя многоугольник и выглядел достаточно просто, для вычисления его площади нам пришлось потрудиться. А если бы многоугольник выглядел более причудливо?

Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис. 2).

Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую

Рис. 2

клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

S = В + + 4 · = В + — 1 .

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S = В + — 1 .

Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки!

Это и есть формула Пика.

Задача 1. Проверить формулу Пика для многоугольника на рисунке 1.

Решение.

В = 14, Г = 8. По формуле Пика: S = В + — 1 .

S = 14 + 8/2 – 1 = 17

Ответ: 17 кв. ед.

Можно убедиться в том, что формула Пика верна для всех рассмотренных примеров.

Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Попробуйте вычислить площади многоугольников с рисунка 3, используя формулу Пика. Правда ведь, легко получается!

Рис. 3

Рассмотрим ещё некоторые задачи на клетчатой бумаге с клетками размером 1 см times 1 см

Задача 2.[3]

Найдите площадь прямоугольника АВСD (рис.4).

Решение. По формуле Пика: S = В + — 1 .

В = 8, Г = 6

S = 8 + 6/2 – 1 = 10 (см²)

Рис. 4 Ответ: 10 см².

Задача 3. Найдите площадь параллелограмма АВСD (рис.5)

Решение. По формуле Пика: S = В + — 1 .

В = 6, Г = 6

S = 6 + 6/2 – 1 = 8 (см²)

Ответ: 8 см².

Рис. 5

Задача 4. Найдите площадь треугольника АВС (рис.6)

Решение. По формуле Пика: S = В + — 1 .

В = 6, Г = 5

S = 6 + 5/2 – 1 = 7,5 (см²)

Ответ: 7,5 см².

Рис. 6

Задача 5. Найдите площадь четырёхугольника АВСD (рис. 7)

Решение. По формуле Пика: S = В + — 1 .

В = 5, Г = 7

S = 5 + 7/2 – 1 = 7,5 (см²)

Ответ: 7,5 см².

Рис. 7

Согласитесь, рассмотренные задания аналогичны заданию В из вариантов контрольно-измерительных материалов ЕГЭ по математике.

Например:

Задача 6.[2] В. На клетчатой бумаге с клетками размером 1 см times 1 см изображен треугольник (рис. 8). Найдите его площадь в квадратных сантиметрах. pic.105

Решение. По формуле Пика: S = В + — 1 .

В = 12, Г = 6

S = 12 + 6/2 – 1 = 14 (см²)

Ответ: 14

Рис. 8

Задача 7. В. На клетчатой бумаге с клетками размером 1 см times 1 см изображена трапеция (рис. 9). Найдите ее площадь в квадратных сантиметрах. pic.148

Решение. Воспользуемся формулой Пика:

В = 12, Г = 17

S = 12 + 17/2 – 1 = 19,5 (см²)

Ответ: 19,5

Рис. 9

Поможет нам формула Пика и для решения геометрических задач с практическим содержанием.

Задача 8.[4] Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 10)

Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + — 1

В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 (см²)

1 см² — 200² м²; S = 40000 · 10,5 = 420 000 (м²)

Ответ: м²

Рис. 10

Задача 9. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м. (рис. 11)

Решение. Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + — 1

В = 7, Г = 4. S = 7 + 4/2 – 1 = 8 (см²)

1 см² — 200² м²; S = 40000 · 8 = 320 000 (м²)

Ответ: м²

Рис. 11

Получить полный текс

Источник

За это задание ты можешь получить 2 балла. Уровень сложности: базовый.
Средний процент выполнения: 71%
Ответом к заданию 7 по биологии может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

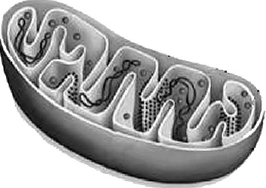
Все перечисленные ниже признаки, кроме двух, можно использовать для описания органоида, изображённого на рисунке. Определите два признака, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

имеются собственные рибосомы и ДНК
имеются во всех эукариотических клетках
являются энергетической станцией клетки
имеют одну мембрану
содержат фотосинтезирующий пигмент

Решение

На рисунке изображена митохондрия, это понятно по кристам, которые расположены в полости органоида. Одну мембрану имеют лизосомы, ЭПС, аппарат Гольджи, вакуоли. Пластиды содержат хлорофилл- основной пигмент участвующий в фотосинтезе.

Митохондрии (полуавтономный органоид) – есть кольцевая ДНК – способны делиться, но существовать без клетки не могут.
Способны размножаться бинарным делением, синтезировать собственные белки

Внешняя мембрана – гладкая

Внутренняя – складчатая, складки – кристы (для увеличения поверхности)

Матрикс – внутреннее содержимое митохондрии (рибосомы 70-S, РНК, кольцевая ДНК + много ферментов).

Митохондрия способна синтезировать примерно 30 видов белков, этого недостаточно для построения тела митохондрии, а значит белки поставляются и из цитоплазмы).
1. Окисление органических веществ с помощью кислорода – клеточное дыхание

2. Синтез АТФ в результате энергии, выделяющейся при клеточном дыхании

3. Синтез собственных белков

Ответ: 45

Задача 2

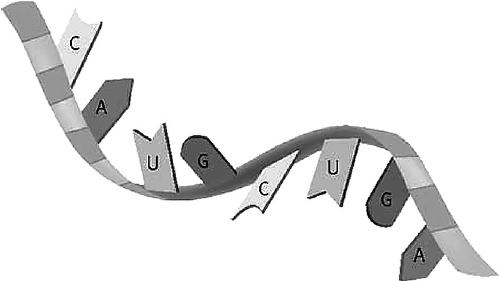
На рисунке изображена нуклеиновая кислота. Все перечисленные ниже характеристики, кроме двух, относятся к изображённой на рисунке нуклеиновой кислоте. Определите две характеристики, «выпадающие» из общего списка, и запишите цифры, под которыми они указаны.

содержит четыре типа нуклеотидов
способна к репликации
в качестве углевода содержит дезоксирибозу
находится в рибосомах, ядрышках, цитоплазме
одинарная цепочка

Решение

На рисунке одно из оснований урацил – а он содержится в РНК. Значит на рисунке изображена РНК. Способность к репликации есть у ДНК, также ДНК состоит из азотистых оснований и дезоксирибозы.

Ответ: 23

Задача 3

Все приведённые ниже характеристики, кроме двух, относятся к описанию сперматогенеза. Определите две характеристики, «выпадающие» из общего списка, и запишите цифры, под которыми они указаны.

начинается с наступлением половой зрелости
образовавшиеся гаметы подвижны
стадия размножения проходит в период эмбрионального развития
образуются одна гамета и три направительных тельца
включает период формирования

Решение

Для овогенеза характерно размножение в период эмбрионального развития девочки. Результатом овогенеза является образование одной гаметы и трех телец.

Ответ: 34

Задача 4

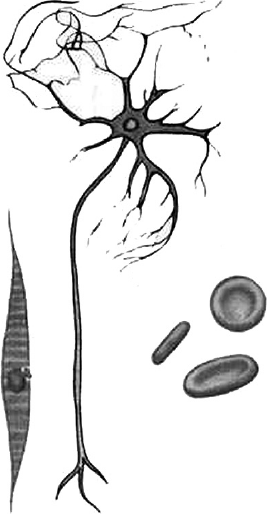
Рассмотрите рисунок различных форм клеток животных. Все перечисленные ниже клетки, кроме двух, изображены на рисунке. Определите два вида клеток, отсутствующих на рисунке, и запишите цифры, под которыми они указаны.

мышечная клетка
эпителиальная клетка
яйцеклетка
эритроцит
нервная клетка

Решение

На рисунке нет эпителиальных клеток, т.к. они имеют округлую или вытянутую форму. Яйцеклеток – они большого размера округлые.

Ответ: 23

Задача 5

Все перечисленные ниже структуры, кроме двух, характерны для прокариотических клеток. Определите две структуры, «выпадающие» из общего списка, и запишите цифры, под которыми они указаны.

рибосомы
клеточная стенка
цитоплазма
митохондрии
ядро

Решение

Эукариоты:
• Размер 10 – 100 мкм (большие)
• Есть ядро
• Есть мембранные органоиды
• Рибосомы большие 80-S
• Линейная ДНК с белками
• Есть митоз и мейоз, амитоз (амитоз характерен ТОЛЬКО для эукариот)
• Поглощение веществ путём фаго- и пиноцитоза
• Клеточная стенка есть не у всех организмов

Прокариоты:
• Размер 1-10 мкм (маленькие)
• Нет ядра, нуклеоид не отделен от цитоплазмы
• Нет мембранных органоидов
• Есть маленькие рибосомы 70-S
• Одна кольцевая ДНК — нуклеоид
• Деление надвое/простое (бинарное)
• Поглощение веществ специальными молекулами на мембране
• Есть клеточная стенка

Ответ: 45

Задача 6

Все приведённые ниже характеристики, кроме двух, относятся к описанию одного из этапов эмбрионального периода — дробления. Определите две характеристики, «выпадающие» из общего списка, и запишите цифры, под которыми они указаны.

первый период эмбрионального развития
ряд последовательных митотических делений зиготы
рост клеток не происходит
заканчивается образованием двухслойного зародыша
эмбриональные клетки расходятся из центра к периферии

Решение

Эмбриональные клетки расходятся из центра к периферии в процессе бластулы. Процесс образования двухслойного зародыша называется гаструляцией.

Ответ: 45

Задача 7

Все перечисленные ниже процессы, кроме двух, происходят во время изображённой на рисунке фазы митоза. Определите два процесса, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

хромосомы спирализуются
центромеры делятся, и хроматиды расходятся
ядерная мембрана и ядрышко разрушаются
хромосомы располагаются по экватору клетки
каждая хромосома состоит из двух хроматид

Решение

На рисунке изображена профаза митоза, когда хромосомы спирализуются. В метафазе хромосомы располагаются в плоскости экватора клетки, в анафазе хромосомы делятся на хроматиды.

Ответ: 24

Задача 8

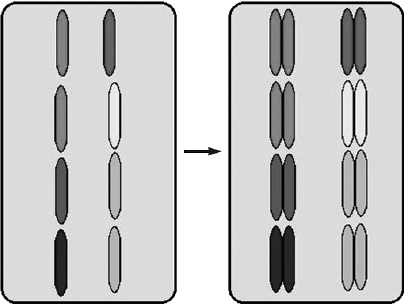
Все приведённые ниже термины, кроме двух, используются при описании изображённого на схеме процесса. Определите два термина, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

репликация
дупликация
репарация
самоудвоение
сплайсинг

Решение

на рисунке изображен процесс удвоения хромосом, он также называется репликация, дукликация. Репарация — особая функция клеток, заключающаяся в способности исправлять химические повреждения и разрывы в молекулах ДНК. Сплайсинг – это процесс вырезания из транскрипционной РНК некодирующих участков (интронов) с последующим сшиванием экзонов, что приводит к формированию непрерывной смысловой последовательности, содержащей информацию о первичной структуре белка.

Ответ: 35

Задача 9

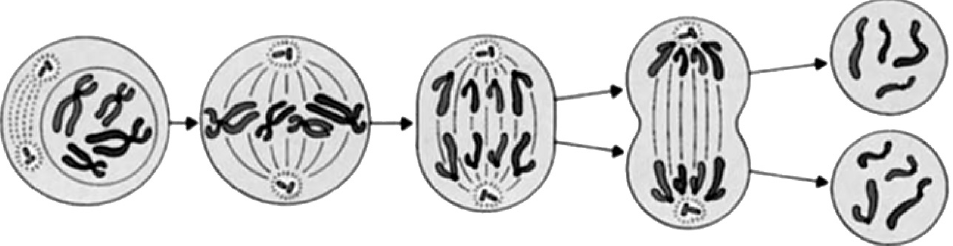
Все перечисленные ниже признаки, кроме двух, можно использовать для описания процесса, изображённого на рисунке. Определите два признака, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

в профазе происходит конъюгация и кроссинговер
дочерние клетки имеют одинаковый набор хромосом, такой же, как родительская клетка
обеспечивает рост, регенерацию, возобновление клеток при старении
образуются клетки с гаплоидным набором хромосом
непрямое деление эукариотической клетки

Решение

На рисунке изображен процесс митоза, т.к. из одной клетки образуется 2. Если бы это был мейоз, тогда бы было два этапа деления и образовалось 4 клетки. Мейоз отличается от митоза тем, что в первом в процессе профазы 1 происходит конъюгация (сближение) и кроссинговер (обмен участками) хромосом. Также в результате мейоза образуется 4 гаплоидные клетки, а в результате митоза 2 диплоидные.

Ответ: 14

Задача 10

Все перечисленные ниже признаки, кроме двух, можно использовать для описания клеточного центра. Определите два признака, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

компонент животных и грибных клеток
органоид округлой или грибовидной формы, состоящий из двух субъединиц — большой и малой
представлен двумя центриолями, расположенными перпендикулярно друг другу
расположен вблизи ядра
способны образовывать группы — полисомы

Решение

Клеточный центр присутствует у всех животных клеток и у высших грибов. Он лежит вблизи ядра и состоит из двух центриолей.
Клеточный центр/центросома =
2 центриоли (цилиндрический органоид, образованный 9-ю триплетами микротрубочек)
+ центросфера (ореол белков)
+ микротрубочки цитоскелета

Функции:

1. Во время подготовки к делению на базе центриолей строится веретено деления клетки: для расхождения хромосом к полюсам клетки во время митоза или мейоза

2. Центр организации цитоскелета

3. Участвует в развитии жгутиков или ресничек

Все остальные пункты характерны для рибосомы: рибосомы относятся к немембранным органоидам. Они очень мелкие (около 20 нм), но многочисленные (тысячи и даже миллионы на клетку), состоят из двух частей – субъединиц. Одну из субъединиц называют «малой», вторую – «большой». Скопление рибосом образуют полисомы.

Ответ: 25

Задача 11

Все приведённые ниже характеристики, кроме двух, используются при описании хромосомных мутаций. Определите две характеристики, «выпадающие» из общего списка, и запишите цифры, под которыми они указаны.

кратное увеличение числа хромосом
удвоение участка хромосомы
обмен участками негомологичных хромосом
поворот участка хромосомы на 180°
нерасхождение гомологичных хромосом в процессе мейоза

Решение

Полиплоидия — это кратное увеличение гаплоидного набора хромосом. Клетки с разным числом гаплоидных наборов хромосом называют триплоидными (Зn), тетраплоидными (4n), гексаплоидными (6n), октаплоидными (8n). Иногда в клеточном делении возникают проблемы, которые приводят к неправильному делению клетки. Отказ хромосом от правильного разделение в митозе или мейозе называется нерасхождением. Если на первом этапе мейотического деления происходит нерасхождение, то гомологичные хромосомы остаются парными, что приводит к двум дочерним клеткам с дополнительным набором хромосом и двум дочерним клеткам без хромосом. Нерасхождение также может происходить в мейозе II, когда сестринские хроматиды не могут отделиться до деления клеток. Нерасхождение часто является фатальным или может вызвать хромосомные аномалии, приводящие к врожденным дефектам. Трисомические клетки содержат дополнительную хромосому. У людей это приводит к образованию 47 хромосом вместо 46. Трисомия наблюдается в синдроме Дауна, где хромосома 21 имеет дополнительную или частичную хромосому. Также нарушения могут наблюдаться в половых хромосомах.

Ответ: 15

Задача 12

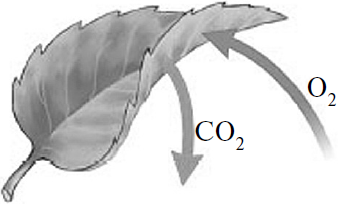
Все перечисленные ниже признаки, кроме двух, используются для описания изображённого на рисунке процесса. Определите два признака, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

исходные вещества — органические соединения и кислород
конечные продукты — углекислый газ и вода
синтез органических веществ из неорганических за счёт энергии окисления неорганических веществ
состоит из двух фаз: световой и темновой
энергия высвобождается

Решение

На рисунке показан процесс дыхания растений, т.к. происходит поглощение кислорода и выделение углекислого газа. Процесс фотосинтеза идет с поглощением углекислого газа и выделением кислорода. Фотосинтез – это синтез органических веществ из неорганических за счёт энергии окисления неорганических веществ, происходит в два этапа: световая и темновая фаза.

Ответ: 34

Задача 13

Все перечисленные ниже признаки, кроме двух, можно использовать для описания световой фазы фотосинтеза. Определите два признака, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

продуктами являются АТФ, атомы водорода и молекулярный кислород
продуктами являются глюкоза и крахмал
происходит в строме хлоропласта
происходит в тилакоидах гран
происходит фотолиз воды

Решение

Темновая фаза фотосинтеза происходит в строме хлоропласта, и конечными продуктами её реакции является крахмал и глюкоза.

Ответ: 23

Задача 14

Все приведённые ниже термины, кроме двух, используются при описании полового размножения. Определите два термина, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

гетерогамия
спорообразование
фрагментация
копуляция
андрогенез

Решение

Спорообразование — бесполое размножение с помощью спор у растений, грибов. Фрагментация — способ бесполого размножения, при котором особь делится на две или несколько частей (фрагментов), каждая из которых растет и образует новый организм.

Ответ: 23

Задача 15

Все перечисленные ниже признаки, кроме двух, используются для описания транскрипции. Определите два признака, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

перенос генетической информации из ядра к рибосоме
происходит в цитоплазме
происходит в ядре
синтез молекулы РНК
синтез полипептида

Решение

Биосинтез включает в себя два этапа:
1) Транскрипция — создание РНК цепи на транскрибируемой матрице ДНК (фермент РНК-полимераза):

1. В определенном участке ДНК разрываются водородные связи, получается две одинарных цепочки.

2. На одной из них по принципу комплементарности, начиная с определенного стартового участка (промотора) строится иРНК.

3. Затем иРНК отсоединяется, а цепочки ДНК снова соединяются между собой

4. Молекула иРНК через ядерную пору попадает в цитоплазму клетки

2) Трансляция — синтез полипептида на матрице РНК. Происходит на рибосоме в цитоплазме, с участием молекул тРНК, которые отвечают за доставку аинокислот к месту синтеза белка. Синтез белка начинается с АУГ-кодона, кодирующего метионин (стартовый кодон). Процесс биосинтеза белка происходит на полисоме (она же полирибосома)— несколько рибосом, одновременно транслирующих одну молекулу иРНК. Завершается трансляция на стоп-кодоне УАГ/ УАА/УГА.

Ответ: 25

Задача 16

Все приведённые ниже положения, кроме двух, относятся к хромосомной теории наследственности. Определите два положения, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

размножение клеток происходит путём их деления
гены расположены линейно
гены могут изменяться (мутировать)
сходные мутации могут возникать повторно
число групп сцепления у каждого вида равно гаплоидному числу хромосом

Решение

Современная клеточная теория гласит, что размножение клеток происходит путем их деления. Мутационная изменчивость говорить о том, что сходные мутации могут возникать повторно.

Ответ: 14

Задача 17

Все перечисленные ниже признаки, кроме двух, используются для описания ферментов. Определите два признака, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

играют роль биологических катализаторов
обеспечивают гомеостаз
обладают высокой специфичностью
регулируют рост и размножение
являются белка́ми

Решение

Поддерживают гомеостаз (постоянство внутренней среды) и участвуют в росте и развитии – гормоны.

Ответ: 24

Задача 18

Все приведённые ниже методы, кроме двух, используются при описании клеточной инженерии. Определите два метода, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

выращивание вне организма в искусственных условиях кусочков органов, тканей или отдельных клеток
создание искусственных гибридов антител
пересадка природных генов в ДНК бактерий или грибов
получение микробной массы, богатой белками и витаминами
получение межвидовых гибридов клеток — гибридо́м

Решение

Генная инженерия: пересадка гена в организм другого вида, например, пересадка человеческого гена в бактерию. Микробный биосинтез — получение микробной массы, богатой белками и витаминами.

Ответ: 34

Задача 19

Все приведённые ниже приёмы, кроме двух, используются при описании селекции животных. Определите два приёма, «выпадающих» из общего списка, и запишите цифры, под которыми они указаны.

проводят жёсткий индивидуальный отбор
применяют полиплоидию и искусственный мутагенез
проводят испытание производителей по потомству
полиэмбрионию и искусственное осеменение не применяют
подбор родительских пар осуществляют по экстерьеру

Решение

Полиплоидию (увеличение количества хромосомных наборов в клетках растений или животных, которое кратно одинарному числу хромосом) и искусственный мутагенез применяют при селекции растений. Полиэмбрионию (развитие более одного зародыша из одной зиготы у животных) и искусственное осеменение применяют в селекции животных.

Ответ: 24

Задача 20

Все приведённые ниже системы органов, кроме двух, у хордовых образуются из эктодермы. Определите две системы органов, «выпадающие» из общего списка, и запишите цифры, под которыми они указаны.

кожа
половая
кровеносная
органы чувств
нервная

Решение

Из разных зародышевых листков образуются разные системы органов. Из эктодермы – нервная система, покровы тела, железы. Из эндодермы – органы пищеварения, дыхания. Из мезодермы – органы кровообращения, выделения, половые органы, мышечная система.

Ответ: 23

Задачи на клетчатой бумаге

Полезная информация

Как подготовиться к экзамену?

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Задача 10

Решение

Задача 11

Решение

Задача 12

Решение

Задача 13

Решение

Задача 14

Решение

Задача 15

Решение

Задача 16

Решение

Задача 17

Решение

Задача 18

Решение

Задача 19

Решение

Задача 20

Решение

Рекомендуемые курсы подготовки