Всего: 101 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 12% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 1
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: ЕГЭ — 2016. Основная волна по математике 06.06.2016. Вариант 437. Юг
Имеется два сплава. Первый сплав содержит 5% меди, второй — 40% меди. Масса первого сплава больше массы второго на 50 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 2
Имеется два сплава. Первый сплав содержит 40% меди, второй — 25% меди. Масса первого сплава больше массы второго на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего
сплава. Ответ дайте в килограммах.
Источник: ЕГЭ по математике 27.03.2020. Досрочная волна. Вариант 1
Имеется два сплава. Первый сплав содержит 45% меди, второй — 20% меди. Масса первого сплава больше массы второго на 30 кг. Из этих двух сплавов получили третий сплав, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: ЕГЭ по математике 27.03.2020. Досрочная волна. Вариант 2
Имеется два сплава. Первый сплав содержит 35% меди, второй — 5% меди. Масса первого сплава больше массы второго на 80 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Источник: ЕГЭ по математике 28.03.2022. Досрочная волна. Москва. Вариант 1
Имеется два сплава. Первый сплав содержит 5% меди, второй — 12% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 10% никеля, второй − 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 1.
Имеется два сплава. Первый содержит 15% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 4
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Смешав 11-процентный и 72-процентный растворы кислоты и добавив 10 кг чистой воды, получили 31-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 51-процентный раствор кислоты. Сколько килограммов 11-процентного раствора использовали для получения смеси?
Всего: 101 1–20 | 21–40 | 41–60 | 61–80 …
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 — x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 — x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 — x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 — x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
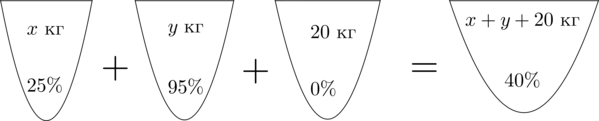
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
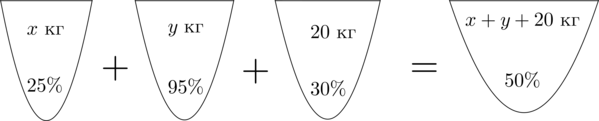
Аналогично составим схему, описывающую получение (50)-процентного раствора:
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Возможно, вам нужно заглянут сюда – “Простейшие задачи на проценты”
Задача 1. В сосуд, содержащий литров
-процентного водного раствора некоторого вещества, добавили
литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение: + показать
Задача 2. Смешали некоторое количество -процентного раствора некоторого вещества с таким же количеством
-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение: + показать
Задача 3. Имеется два сплава. Первый сплав содержит % никеля, второй —
% никеля. Из этих двух сплавов получили третий сплав массой
кг, содержащий
% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение: + показать
Задача 4. Смешав 54-процентный и 61-процентный растворы кислоты и добавив 10 кг чистой воды, получили 46-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 56-процентный раствор кислоты. Сколько килограммов 54-процентного раствора использовали для получения смеси?
Решение: + показать
Задача 5. Имеются два сосуда. Первый содержит кг, а второй —
кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий
% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий
% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Решение: + показать
Задача 6. Виноград содержит % влаги, а изюм —
%. Сколько килограммов винограда требуется для получения
килограммов изюма?
Решение: + показать
Задача 7. В 2008 году в городском квартале проживало человек. В 2009 году, в результате строительства новых домов, число жителей выросло на
%, а в 2010 году — на
% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
Решение: + показать
Задача 8. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за рублей, через два года был продан за
рублей.
Решение: + показать
Задача 9. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение: + показать
Задача 10. Шесть рубашек дешевле куртки на %. На сколько процентов девять рубашек дороже куртки? Видео*
Решение: + показать
Задача 11. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на %. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на
%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Решение: + показать
Задача 12. Дима, Андрей, Гриша и Коля учредили компанию с уставным капиталом рублей. Дима внес
% уставного капитала, Андрей —
рублей, Гриша —
уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли
рублей причитается Коле? Ответ дайте в рублях.
Решение: + показать
Задача 13. Клиент А. сделал вклад в банке в размере рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на
рубля больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Решение: + показать
Вы можете пройти Тест по задачам на проценты, сплавы, смеси
Муниципальное
общеобразовательное автономное учреждение
средняя
общеобразовательная школа №5
Методическая
разработка
элективного занятия по математике для учащихся 11
класса по теме
«Задачи на концентрацию, смеси и сплавы в материалах ЕГЭ»
Работу
выполнила учитель I квалификационной
категории Байлова Татьяна Викторовна
Пояснительная
записка
Решение задач
занимает в математическом образовании огромное место. Умение решать задачи
является одним из основных показателей уровня математического развития
школьников, глубины освоения учебного материала. Умение решать задачи
необходимо и экономисту, и врачу, и юристу, и военачальнику, и многим другим. А
для успешного решения, как говорил Декарт, необходим метод. Поэтому обучению
решения задач уделяется много внимания, но почему-то единственным методом такого
обучения были показ способов решения определенных видов задач и значительная
практика по овладению ими.
Решение
текстовых задач вообще, а задач на смеси и сплавы в частности, часто вызывает
трудности у учащихся школ. Тем более, что знакомство с ними происходит в 8-9
классах, а сами задачи включены в тексты ГИА-9 и ЕГЭ-11. В школьном курсе
математики предлагается очень мало задач на «смеси и
сплавы».
Задачи на
концентрацию, смеси и сплавы часто не решают учащиеся на экзамене, связано
это с нечетким пониманием химических процессов. Необходимо иметь в виду, что
в задачах такого рода предлагаемых на ЕГЭ по математике, никаких химических
процессов нет, влияющих на количественные соотношения
задачи.
Положение
текстовых задач в общей структуре КИМ в настоящее время абсолютно четко
зафиксировано. Во все годы проведения ЕГЭ количество текстовых задач менялось.
Сейчас их три. Выполнение или невыполнение этого задания не повлияет на
аттестационную оценку за курс «Алгебра и начала анализа» средней школы. Верно
решенная текстовая задача повысит лишь итоговую сертификационную оценку за ЕГЭ
в стобалльной шкале.
Поэтому тема
занятия выбрана для того, чтобы проанализировать теоретические источники,
отражающие глубину проблемы, выявить методы обучения решению текстовых задач на
смеси и сплавы.
Занятие по теме
«Задачи на концентрацию, смеси и сплавы»
Цели:
Образовательные:
Создание условий
для систематизации, обобщения и углубления знаний учащихся при решении
текстовых задач.
Повышение практической
направленности предмета через решение практических задач.
Воспитательные:
Формирование
математической грамотности учащихся.
Развивающие:
Развитие навыков
логического, творческого мышления, сообразительности и наблюдательности.
Оборудование:
Раздаточный
материал;
компьютерная
презентация в программе Power Point;
мультимедиапроектор;
ПК;
экран.
План занятия
1. Организационный
момент.
2. Сообщение
темы занятия.
3. Разминка.
4. Методы
решения задач.
5. Практическая
часть занятия.
6. Самостоятельное
решение задач.
7. Подведение
итогов занятия.
Основная часть.
I. Человеку часто
приходится смешивать различные жидкости, порошки, газообразные или твердые
вещества, или разбавлять что-либо водой. Текстовые задачи на смеси, сплавы и
растворы входят в различные сборники заданий по математике ГИА и ЕГЭ.
Если хотите
научиться плавать,
то смело входите в
воду, а если хотите
научиться решать
задачи, то решайте их. Дьёрдь
Пойа II.
Итак, ребята, сегодня на уроке мы с вами рассмотрим задачи, решение которых
связано с понятиями «концентрация», «процентное
содержание». Начнем
наше занятие с повторения понятий, необходимых нам для решения задач.
III.
Разминка.
1. Сотая часть
числа называется …(процент)
2. Соотнести
проценты и соответствующие им дроби: 5% — 0,05; 17% — 0,17; 123% — 1,23; 0,3% —
0,003; 25% — 0,25
3. Частное двух
чисел называют …(отношение)
4. Верное
равенство двух отношений называют …(пропорция)
5. В химии
определение этого понятия звучало бы так: гомогенная смесь, образованная не
менее чем двумя компонентами … (раствор). Один из которых называется растворителем,
а другой растворимым веществом.
6. Отношение массы
растворимого вещества к массе раствора называют массовой долей вещества в
растворе или …(концентрация)
IV.
Методы решения задач.
Ребята, какие
задачи называют текстовыми? Верно, это задачи, условия которых записаны
текстом.
На какие основные группы условно можно разбить задачи? Конечно,
это:
Текстовые задачи
Задачи на части и
проценты;
Задачи, связанные
с десятичной формой записи числа;
Задачи с целочисленными
данными;
Задачи на
равномерное движение по прямой;
Задачи на сплавы и
смеси;
Задачи на работу;
Задачи на бассейны
и трубы.
Рассмотрим
решение текстовых задач на смеси и сплавы
При решении
текстовых задач на смеси и сплавы постоянно приходится работать со следующими
понятиями:
Абсолютное
содержание вещества в смеси;
Относительное
содержание вещества в смеси.
Абсолютное
содержание вещества в смеси- это количества вещества,
выраженное в обычных единицах измерения(грамм, литр и т.д.).
Относительное
содержание вещества в смеси- это отношение абсолютного
содержания к общей массе(объему) смеси:
относительное содержание
=
Часто
относительное содержание называют концентрацией или процентным содержанием.
При этом используются различные формы записи относительного содержания
вещества: в долях и в процентах. Например, относительное содержание
0,05= =5%.
Используются
следующие допущения:
1.Всегда
выполняется «закон сохранения объема или массы» :
если два сплава (
раствора) соединяют в один «новый» сплав(раствор), то выполняются равенства:
V =V1+V2
— сохраняется объем;
m =m1
+m2 — сохраняется масса.
2.Точно такой же
«закон сохранения» выполняется для отдельных составляющих частей (компонент)
сплава (раствора): если первый сплав состоит из нескольких компонент, например
из А,В,С, а второй из компонент В,С,Д, то «новый» сплав, полученный при
соединении этих двух сплавов, будет содержать компоненты А,В,С,Д. Причем массы
этих компонент в «новом» сплаве равны сумме масс каждой из компонент, входящих
в первый и второй сплавы.
3.При соединении
растворов и сплавов не учитываются химические взаимодействия их отдельных
компонент.
4. Очень часто в
задачах на смеси и сплавы используется понятие объемной концентрации или
массовой концентрации компонент, составляющих раствор или сплав.
Объемная или
массовая концентрация есть число, показывающее, какую долю всего объема или
массы составляет данная компонента.
V.Примеры
решения задач
Имеется два
слитка, содержащие медь. Медь второго слитка на 3 кг больше, чем масса первого
слитка. Процентное содержание меди в первом слитке -10%, во втором- 40%. После
сплавливания этих двух слитков получился слиток, процентное содержание меди в
котором 30%. Определить массу полученного слитка.
|
1 |
2 |
общая |
|
Х Медь 0,1 |
Х+ Медь 0,4(х |
2Х Медь 0,3(2х |
0,1х +0,4(х+3) =
0,3(2х +3)
0,1х +0,4х+1,2
=0,6х +0,9
х=3 масса
сплава 2•3 +3 =9. Ответ: 9кг
Пример.
Два сплава массами m1 и m2 кг содержат медь и серебро
в отношениях 12 : 1 и 16 : 3 соответственно. Эти два сплава сплавили с m3
кг чистого серебра и m4 кг чистой меди. Определите процент серебра
в образовавшемся сплаве.
Решение. Полезно
для наглядности сделать поясняющий чертеж.
|
1 |
2 |
серебро |
медь |
Найдем
массу «нового» сплава по закону сохранения : m1
+ m2 + m3 + m4
Найдем теперь
массу серебра в каждом сплаве. В первом сплаве отношение количества меди к
количеству серебра равно 12 : 1. Значит, в первом сплаве содержится часть серебра, масса которого
составит m1 кг. Найдем
массу серебра во втором сплаве: m2 кг. По
закону сохранения массы получаем массу серебра в «новом» сплаве:
m1
+ m2 + m3
кг.
Следовательно,
процентное содержание серебра в «новом» сплаве равно
∙ 100%.
Пример.
Имеется два слитка, содержащие медь. Медь второго слитка на 3 кг больше, чем
масса первого слитка. Процентное содержание меди в первом слитке -10%, во
втором- 40%. После сплавливания этих двух слитков получился слиток, процентное
содержание меди в котором 30%. Определить массу полученного слитка.
Решение.
|
|
2 |
общая |
|
Медь |
Медь |
Медь |
0,1х +0,4(х+3) =
0,3(2х +3)
0,1х +0,4х+1,2
=0,6х +0,9
х=3 масса
сплава 2•3 +3 =9. Ответ: 9кг
Пример.
Смешали 500г 10%-го раствора соли и 400г 55% раствора соли. Определите
концентрацию соли в смеси.
Решение. Условие
задачи представим в виде рисунка:
500г 400г
|
Соль |
Соль |
|
Вода |
Вода |
500·0,1=50 (г), 500 -50
=450 (г), 400· 0,55= 220(г) , 400-220=180 (г) 400+500=900
|
Соль 50г |
Соль55% 220г |
|
Вода 450г |
Вода 180г |
|
Соль |
|
Вода |
Пример.
Руда содержит 40%
примесей, а выплавленный из нее металл содержит 4% примесей. Сколько получится
металла из 24 тонн руды?
Решение
|
Руда |
Металл |
|
Чистый Примеси |
Чистый Примеси |
Руда:
m=0,4·24=9,6(т) –
примеси
m=24 – 9,6=
14,4(т) чистый металл
Металл:
m=0,04х — примеси
m= х – 0,04х=0,96х
(т) чистый металл
|
Чистый |
Чистый |
|
Примеси |
Примеси |
0,96х =14,4
х=15. Ответ: 15т
VI.
Задачи для самостоятельного решения.
1. Сплав
меди и алюминия массой 10 кг содержит 35% меди. Сколько килограммов в этом
сплаве составляет алюминий?
Решение.
Так как меди в сплаве 355, то 65% составляет алюминий. Значит, вес алюминия в
сплаве 0,65 ∙ 10 =6,5
кг.
Ответ: 6,6 кг.
2. Сплав
меди и цинка весом 20кг содержит 30% меди. Добавили 22кг цинка. Сколько нужно
добавить меди, чтобы в сплаве стало 60% цинка.
Решение:
30%
70%
20кг = 6кг + 20кг
Добавили
цинка — +22кг
42кг
= 6кг + 36кг
100%
= 40% + 60%
36кг
составляет 60%.
36:0.6=60кг
– новый сплав.
60(кг) = 6(кг) +
36(кг) + x(кг)
x=18
(кг)
Итог
занятия. Что нового узнали на занятии? Был ли предложенный материал понятен?
Домашнее
задание. Карточки.
Литература.
1. Денищева
Л.О., Глазков Ю.А. и др. Единый
Государственный
экзамен 2008. Математика.
Учебно-тренировочные
материалы для подготовки
учащихся
/ ФИПИ – М.: Интеллект-Центр, 2007.
2.
Шевкин А.В. Текстовые задачи в школьном курсе
Математики.
М.: Педагогический университет
«Первое
сентября», 2006.
3.
Открытый банк заданий ЕГЭ 2015
http://www.nado5.ru/materials/novoe-v-yege-po-matematike
20 января 2023
В закладки
Обсудить
Жалоба
Задачи на смеси, сплавы, концентрацию
Один из прототипов задания №9 профильного ЕГЭ по математике.
По материалам открытого банка ФИПИ.
sm-sp-k.pdf
Задача 1
В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Задача 2
Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Задача 3
Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Задача 4
Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма
Задача 5
Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Задача 6
Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Задача 7
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Задача 8
Имеются два сосуда с растворами кислоты различной концентрации. Первый содержит 30 кг раствора, а второй — 20 кг раствора. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Задача 9
Имеется два сплава. Первый содержит 15% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Ответы
1. 5;
2. 17;
3. 21;
4. 190;
5. 100;
6. 9;
7. 60;
8. 18;
9. 70.
Источник: vk.com/profimatika
ЕГЭ Профиль №9. Задачи на проценты, смеси и сплавы
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Задачи на проценты, смеси и сплавы
|
Задача 1. В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году — на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году? В 2009 году число жителей стало равно (40000 + 40000 cdot frac{8}{{100}} = 43200), а в 2010 году: (43200 + 43200 cdot frac{9}{{100}} = 47088.) Ответ: 47088. |
| Задача 2. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Обозначим первоначальную стоимость акций за А. Пусть в понедельник акции подорожали на х %, поэтому они стали стоить (100 + х)% от А, то есть (A cdot frac{{100 + x}}{{100}}). Во вторник они подешевели на х %, поэтому они стали стоить (100 – х) % от (A cdot frac{{100 + x}}{{100}}), то есть (A cdot frac{{100 + x}}{{100}} cdot frac{{100 — x}}{{100}}.) В результате акции стали стоить 96% от А: (A cdot frac{{96}}{{100}}). Таким образом, получаем уравнение: (A cdot frac{{100 + x}}{{100}} cdot frac{{100 — x}}{{100}} = A cdot frac{{96}}{{100}},left| {,:,} right.A,,,, Leftrightarrow ,,,,frac{{{{100}^2} — {x^2}}}{{100}} = 96,,,, Leftrightarrow ,,,,10000 — {x^2} = 9600,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} = 400,,,, Leftrightarrow ,,,,{x_1} = 20;,,,,,{x_2} = — 20.) Так как (x > 0), то акции подорожали в понедельник на 20%. Ответ: 20. |
| Задача 3. Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки?
Стоимость четырех рубашек составляет 100 – 8 = 92 % от куртки. Следовательно, стоимость одной рубашки составляет (frac{{92}}{4} = 23)% от стоимости куртки. Тогда стоимость пяти рубашек составляет (5 cdot 23 = 115)%, что на 115 – 100 = 15 % превышает стоимость куртки. Ответ: 15. |
| Задача 4. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Пусть доход мужа, жены и дочери составляет x, y и z % соответственно. Тогда первое уравнение: (x + y + z = 100.) Если зарплату мужа увеличить вдвое (зарплата станет 2х), то общий доход увеличиться на 67 %, то есть второе уравнение будет: (2x + y + z = 167.) Если стипендию дочери уменьшить втрое (стипендия станет (frac{z}{3})), то общий доход уменьшиться на 4 %, то есть третье уравнение будет иметь вид: (x + y + frac{z}{3} = 96.) Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {x + y + z = 100;} \ {2x + y + z = 167;} \ {x + y + frac{z}{3} = 96.} end{array}} right.) Вычтем из второго уравнения первое: (2x — x + y — y + z — z = 167 — 100,,,, Leftrightarrow ,,,,,x = 67.) Вычтем из первого уравнения третье: (x — x + y — y + z — frac{z}{3} = 100 — 96,,,,, Leftrightarrow ,,,,frac{{2z}}{3} = 4,,,, Leftrightarrow ,,,,z = 6.) Подставляя найденные x и z в первое уравнение, получим: (67 + y + 6 = 100,,,, Leftrightarrow ,,,,y = 27.) Ответ: 27. |
| Задача 5. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рубля.
Пусть цена холодильника ежегодно уменьшалась на х%, тогда после первого понижения цена составила (100 – х) % от 20000 рублей, то есть: (20000 cdot frac{{100 — x}}{{100}} = 200 cdot left( {100 — x} right)), а после второго (100 – х) % от (200left( {100 — x} right)), то есть: (200left( {100 — x} right) cdot frac{{100 — x}}{{100}} = 2 cdot {left( {100 — x} right)^2}), что составило 15842 рубля. (2{left( {100 — x} right)^2} = 15842,,{left| {,:,2,,,, Leftrightarrow ,,,,left( {100 — x} right)} right.^2} = 7921.) (100 — x = 89;,,,,,,,,100 — x = — 89.) ({x_1} = 11,,,,,,,,,,,,,,,,,,,,,{x_2} = 189) Так как (0 < x < 100), то холодильник ежегодно дешевел на 11 %. Ответ: 11. |
| Задача 6. Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200000 рублей. Митя внес 14% уставного капитала, Антон — 42000 рублей, Гоша — 0,12 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1000000 рублей причитается Борису? Ответ дайте в рублях.
Митя внес 14 % уставного капитала. Антон (frac{{42000}}{{200000}} cdot 100 = 21)% уставного капитала. Гоша 0,12 уставного капитала, то есть 12%. Следовательно, Борис внес (100 — 14 — 21 — 12 = 53)% уставного капитала. Таким образом, от прибыли 1000000 рублей Борису причитается: (1000000 cdot frac{{53}}{{100}} = 530000) рублей. Ответ: 530000. |
| Задача 7. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Будем считать, что первый сосуд содержит 5 литров 12-процентного раствора вещества, а второй 7 литров воды (0-процентного раствора) и их содержимое перелили в третий сосуд. Пусть третий сосуд содержит x-процентный раствор вещества. Тогда количество вещества в первом сосуде (frac{{5 cdot 12}}{{100}}) литров, во втором (frac{{7 cdot 0}}{{100}}) литров, а в третьем (frac{{12 cdot x}}{{100}}) литров. При этом количество вещества в третьем сосуде равно количеству вещества в первых двух сосудах. (frac{{5 cdot 12}}{{100}} + frac{{7 cdot 0}}{{100}} = frac{{12 cdot x}}{{100}},left| {, cdot 100,,,,} right. Leftrightarrow ,,,,,,5 cdot 12 = 12 cdot x,,,,, Leftrightarrow ,,,,,,x = 5.) Ответ: 5. |
| Задача 8. Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Будем считать, что первый сосуд содержит А литров 15-процентного раствора вещества, а второй А литров 19-процентного раствора вещества и их содержимое перелили в третий сосуд. Пусть третий сосуд содержит x-процентный раствор вещества. Тогда количество вещества в первом сосуде (frac{{A cdot 15}}{{100}}) литров, во втором (frac{{A cdot 19}}{{100}}) литров, а в третьем (frac{{2A cdot x}}{{100}}) литров. При этом количество вещества в третьем сосуде равно количеству вещества в первых двух сосудах. (frac{{A cdot 15}}{{100}} + frac{{A cdot 19}}{{100}} = frac{{2A cdot x}}{{100}},,,left| {, cdot 100,,,,} right. Leftrightarrow ,,,,,,15 cdot A + 19 cdot A = 2A cdot x,,left| {,:A} right.,,,,, Leftrightarrow ,,,,,,2x = 34,,,,, Leftrightarrow ,,,,,x = 17.) Ответ: 17. |
| Задача 9. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Будем считать, что первый сосуд содержит 4 литра 15-процентного раствора вещества, а второй 6 литров 25-процентного раствора вещества и их содержимое перелили в третий сосуд. Пусть третий сосуд содержит x-процентный раствор вещества. Тогда количество вещества в первом сосуде (frac{{4 cdot 15}}{{100}}) литров, во втором (frac{{6 cdot 25}}{{100}}) литров, а в третьем (frac{{10 cdot x}}{{100}}) литров. При этом количество вещества в третьем сосуде равно количеству вещества в первых двух сосудах. (frac{{4 cdot 15}}{{100}} + frac{{6 cdot 25}}{{100}} = frac{{10 cdot x}}{{100}},left| {, cdot 100,,,,} right. Leftrightarrow ,,,,,,60 + 150 = 10 cdot x,,,,, Leftrightarrow ,,,,,,x = 21.) Ответ: 21. |
| Задача 10. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Виноград содержит 10% «сухого» вещества, а изюм 95% соответственно. При этом масса «сухого» вещества винограда и изюма равны. Пусть для получения 20 килограммов изюма требуется x килограммов винограда. Тогда масса «сухого» вещества в винограде (frac{{10 cdot x}}{{100}}) кг, а масса «сухого» вещества в изюме (frac{{20 cdot 95}}{{100}}) кг. Следовательно: (frac{{10 cdot x}}{{100}} = frac{{20 cdot 95}}{{100}},left| {, cdot 100,,,,,, Leftrightarrow ,,,,,10x = 20} right. cdot 95,,,,, Leftrightarrow ,,,,x = 190) кг. Ответ: 190. |
| Задача 11. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго.
Пусть x кг масса первого сплава. Так как масса третьего сплава 200 кг, то масса второго сплава (200 — x) кг. Тогда масса никеля в первом сплаве (frac{{x cdot 10}}{{100}}) кг, во втором (frac{{left( {200 — x} right) cdot 30}}{{100}}) кг, а в третьем (frac{{200 cdot 25}}{{100}}) кг. При этом масса никеля в третьем сплаве равна массе никеля в первых двух сплавах. (frac{{x cdot 10}}{{100}} + frac{{left( {200 — x} right) cdot 30}}{{100}} = frac{{200 cdot 25}}{{100}},left| {, cdot 100,,,,} right. Leftrightarrow ,,,,,,10x + 6000 — 30x = 5000,,,,, Leftrightarrow ,,,,,,20x = 1000,,,,, Leftrightarrow ,,,,,x = 50.) Значит масса первого сплава 50 кг, а масса второго сплава равна 150 кг. Следовательно, масса первого сплава на 100 кг меньше массы второго. Ответ: 100. |
| Задача 12. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Тогда масса меди в первом сплаве (frac{{x cdot 10}}{{100}}) кг, во втором (frac{{left( {x + 3} right) cdot 40}}{{100}}) кг, а в третьем (frac{{left( {2x + 3} right) cdot 30}}{{100}}) кг. При этом масса меди в третьем сплаве равна массе меди в первых двух сплавах. (frac{{x cdot 10}}{{100}} + frac{{left( {x + 3} right) cdot 40}}{{100}} = frac{{left( {2x + 3} right) cdot 30}}{{100}},left| {, cdot 100,,,,} right. Leftrightarrow ,,,,,,10x + 40x + 120 = 60x + 90,,,,, Leftrightarrow ,,,,,,10x = 30,,,,, Leftrightarrow ,,,,,x = 30.) Значит масса первого сплава 3 кг, а масса третьего сплава равна (2x + 3 = 2 cdot 3 + 3 = 9) кг. Ответ: 9. |
| Задача 13. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Пусть x кг масса 30-процентного раствора, а y кг масса 60-процентрого раствора кислоты. Тогда масса кислоты в 30-процентном растворе (frac{{x cdot 30}}{{100}}) кг, в 60-процентном (frac{{y cdot 60}}{{100}}) кг, в воде (frac{{10 cdot 0}}{{100}}) кг, а в 36-процентном (frac{{left( {x + y + 10} right) cdot 36}}{{100}}). При этом масса кислоты в 36-процентноом растворе равна массе кислоты 30-процентного, 60-процентного и воды. Таким образом, первое уравнение будет иметь вид: (frac{{x cdot 30}}{{100}} + frac{{y cdot 60}}{{100}} + frac{{10 cdot 0}}{{100}} = frac{{left( {x + y + 10} right) cdot 36}}{{100}},,left| { cdot 100} right.,,,,, Leftrightarrow ,,,,,30x + 60y = 36left( {x + y + 10} right).) Рассмотрим случай, когда вместо 10 кг воды добавили 10 кг 50-процентного раствора кислоты. Рассуждая аналогично, как и в первом случае, получим второе уравнение: (frac{{x cdot 30}}{{100}} + frac{{y cdot 60}}{{100}} + frac{{10 cdot 50}}{{100}} = frac{{left( {x + y + 10} right) cdot 41}}{{100}},,left| { cdot 100} right.,,,,, Leftrightarrow ,,,,,30x + 60y + 500 = 41left( {x + y + 10} right).) Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {30x + 60y = 36left( {x + y + 10} right);} \ {30x + 60y + 500 = 41left( {x + y + 10} right).} end{array}} right.) Вычтем из второго уравнения первое: (500 = 5left( {x + y + 10} right),left| {:5} right.,,,,, Leftrightarrow ,,,,,100 = x + y + 10,,,,, Leftrightarrow ,,,,,y = 90 — x.) Подставим выраженный y в первое уравнение: (30x + 60left( {90 — x} right) = 3600,,,,, Leftrightarrow ,,,,30x — 60x = 3600 — 5400,,,,, Leftrightarrow ,,,,,30x = 1800,,,,, Leftrightarrow ,,,,,x = 60.) Следовательно, для получения смеси использовали 60 кг 30-процентного раствора. Ответ: 60. |
| Задача 14. Имеются два сосуда. Первый содержит 30 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Будем считать, что первый сосуд содержит 30 кг x-процентного раствора кислоты, а второй 20 кг y-процентного раствора кислоты и их содержимое перелили в третий сосуд, в котором получилось 50 кг 68-процентного раствора кислоты. Тогда масса кислоты в первом сосуде (frac{{30 cdot x}}{{100}}) кг, во втором (frac{{20 cdot y}}{{100}}) кг, а в третьем (frac{{50 cdot 68}}{{100}}) кг. При этом масса кислоты в третьем сосуде равна массе кислоты в первых двух сосудах. Таким образом, первое уравнение будет иметь вид: (frac{{30 cdot x}}{{100}} + frac{{20 cdot y}}{{100}} = frac{{50 cdot 68}}{{100}},,left| { cdot 10} right.,,,,, Leftrightarrow ,,,,,3x + 2y = 340.) Смешаем равные массы по m кг. Рассуждая аналогично, как и в первом случае, получим второе уравнение: (frac{{m cdot x}}{{100}} + frac{{m cdot y}}{{100}} = frac{{2m cdot 70}}{{100}},,left| {, cdot 100} right.,,,,, Leftrightarrow ,,,,,m cdot x + m cdot y = 140m,left| {,:m} right.,,,,,, Leftrightarrow ,,,,,,x + y = 140.) Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {3x + 2y = 340} \ {x + y = 140} end{array},,,,,, Leftrightarrow ,,,,,left{ {begin{array}{*{20}{c}} {3x + 2y = 340} \ {y = 140 — x} end{array}} right.} right.) (3x + 2left( {140 — x} right) = 340,,,,,, Leftrightarrow ,,,,,3x — 2x = 340 — 280,,,,, Leftrightarrow ,,,,,x = 60.) Следовательно, в первом сосуде содержится 60% кислоты, а масса этой кислоты равна (frac{{30 cdot 60}}{{100}} = 18) кг. Ответ: 18. |
| Задача 15. Клиент А. сделал вклад в банке в размере 7700 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Еще ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 847 рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
Пусть банк начисляет x% годовых. Тогда через год вклад клиента А составит (left( {100 + x} right)) процентов от 7700 рублей, то есть (7700 cdot frac{{100 + x}}{{100}}) рублей. Через год банк начислит ещё x% и его вклад станет равен (left( {100 + x} right)) процентов от (7700 cdot frac{{100 + x}}{{100}}) рублей, то есть (7700 cdot {left( {frac{{100 + x}}{{100}}} right)^2}) рублей. Клиент Б открыл такой же вклад сроком на один год. Следовательно, через год на его вкладе будет сумма равная (7700 cdot frac{{100 + x}}{{100}}) рублей. Так как клиент А получил на 847 рублей больше, то: (7700 cdot {left( {frac{{100 + x}}{{100}}} right)^2} — 7700 cdot frac{{100 + x}}{{100}} = 847.) Пусть (frac{{100 + x}}{{100}} = t), тогда: (7700,{t^2} — 7700,t = 847,left| {,:,77,,,,, Leftrightarrow ,,,,,100,{t^2} — 100,t — 11 = 0;} right.) (D = {100^2} + 4 cdot 100 cdot 11 = 14400;,,,,,sqrt D = 120;,,,,,{t_1} = frac{{100 + 120}}{{200}} = 1,1;,,,,,{t_2} = frac{{100 — 120}}{{200}} = — frac{1}{{10}}.)Так как (x > 0), то (t > 1). Следовательно, (t = 1,1) и тогда (frac{{100 + x}}{{100}} = 1,1,,,,,, Leftrightarrow ,,,,,,x = 10.) Ответ: 10. |