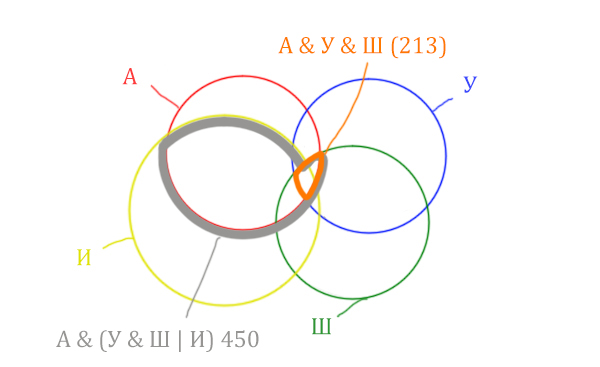Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
Задача (Простая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.
Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.
Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.
Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».
В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
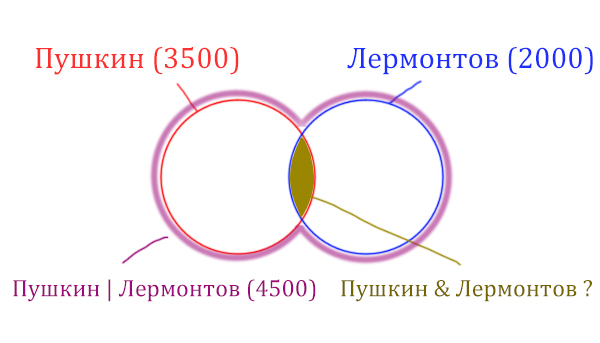
У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
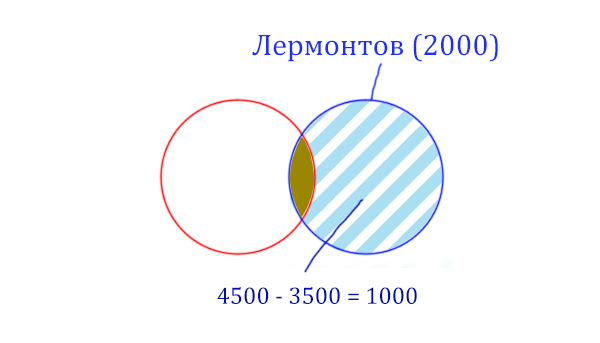
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
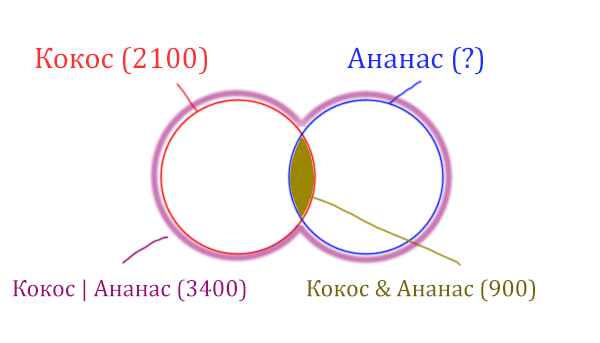
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
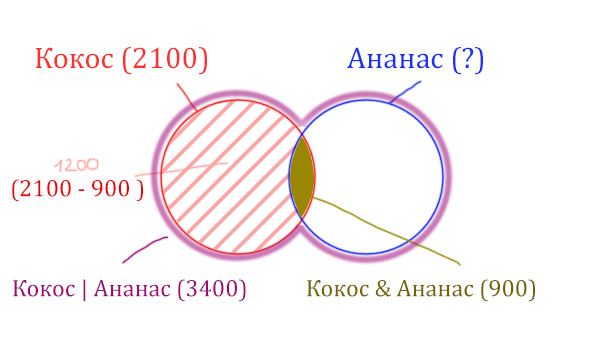
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
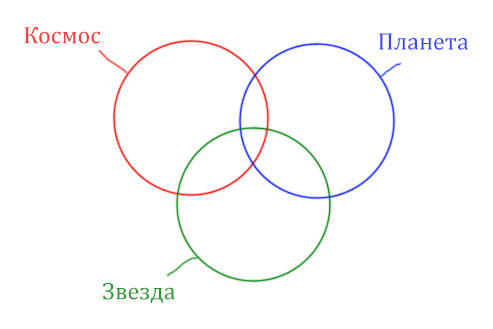
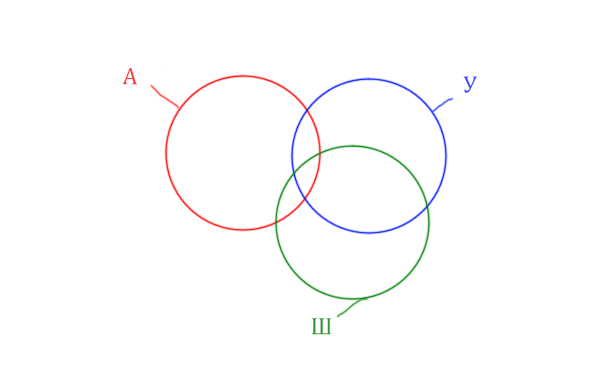
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».
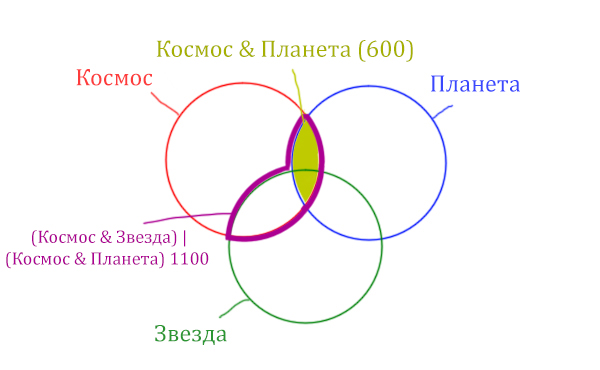
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
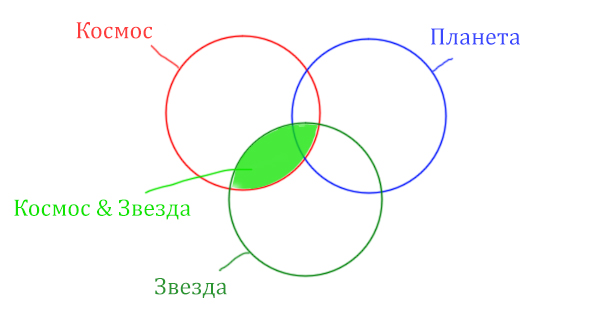
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
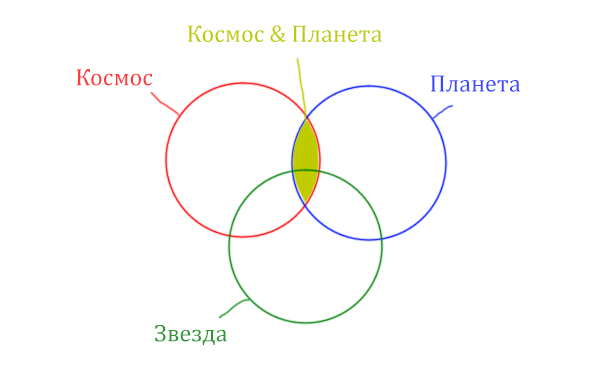
Теперь отметим вторую скобку Космос & Планета.
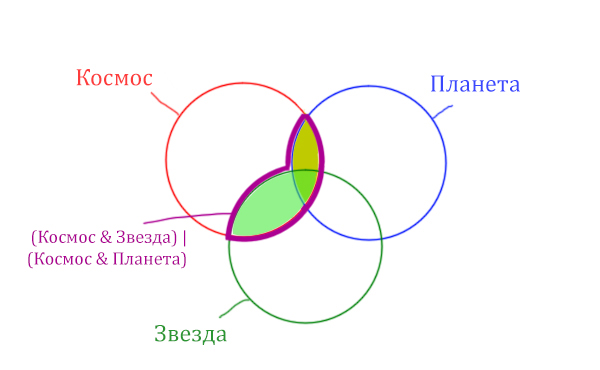
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
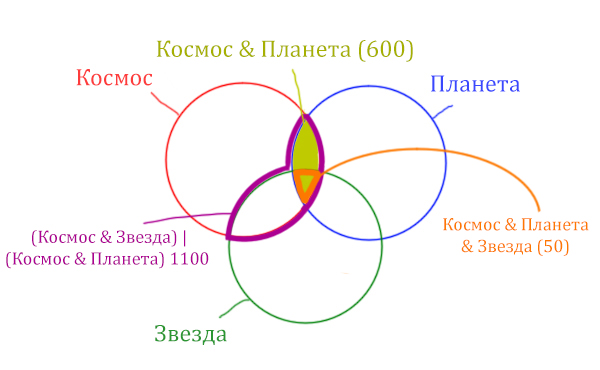
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
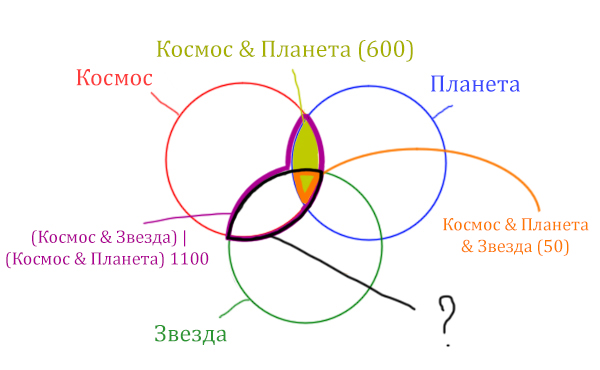
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
Теперь у нас есть все компоненты, чтобы решить эту задачу.
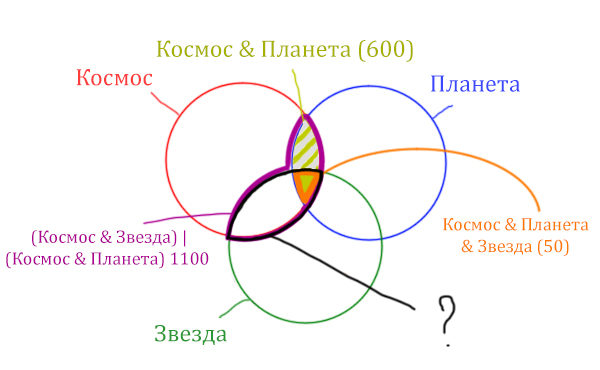
Найдём заштрихованную область.
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 — 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
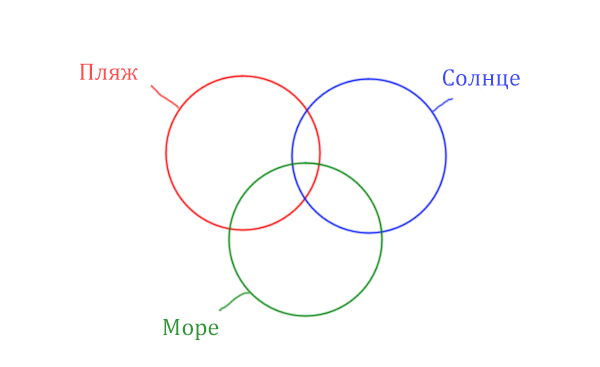
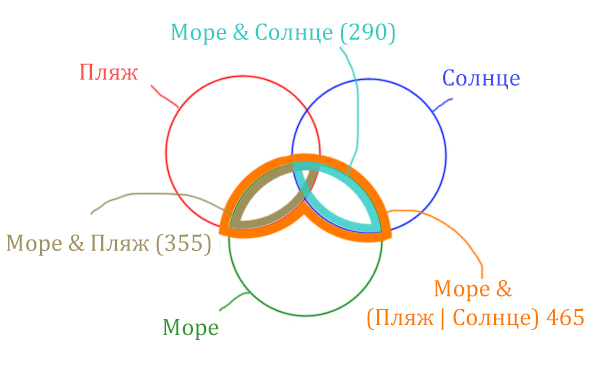
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
Отметим все области для которых нам даны количество страниц.
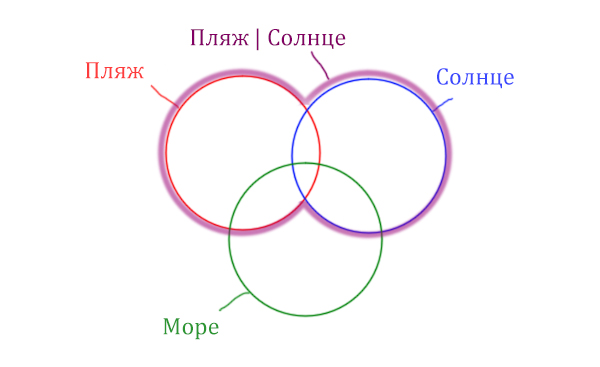
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
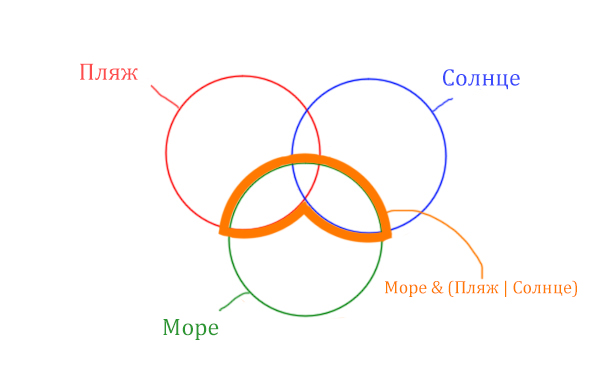
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
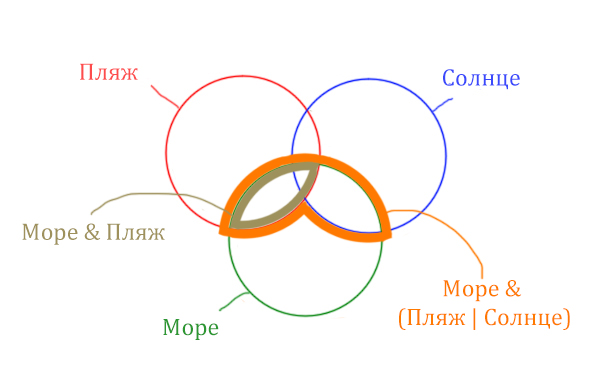
Теперь отметим Море & Пляж.
Теперь отметим Море & Солнце.
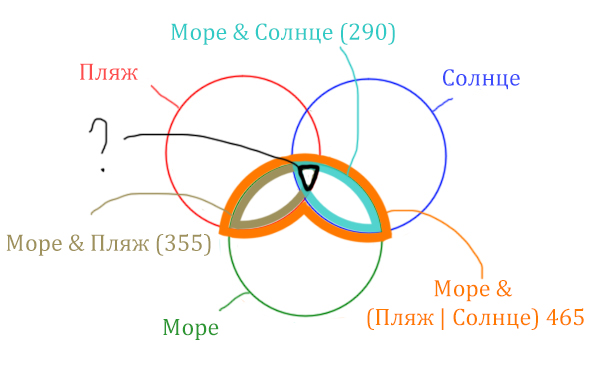
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
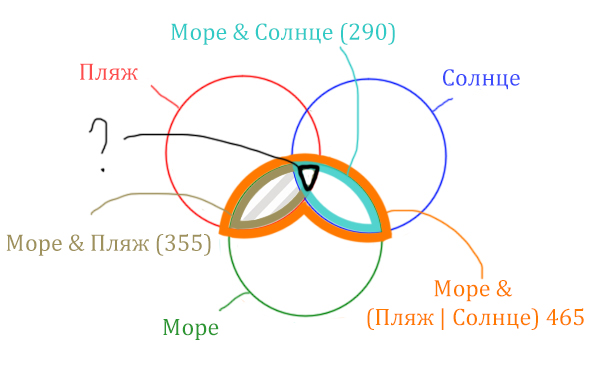
Найдём заштрихованную область!
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
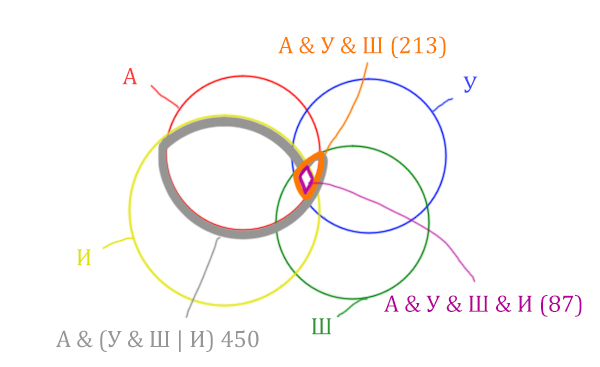
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
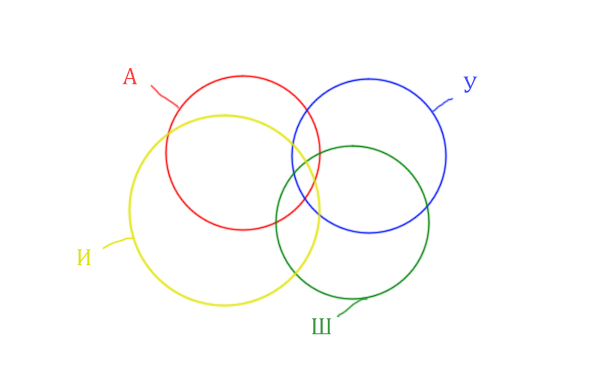
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
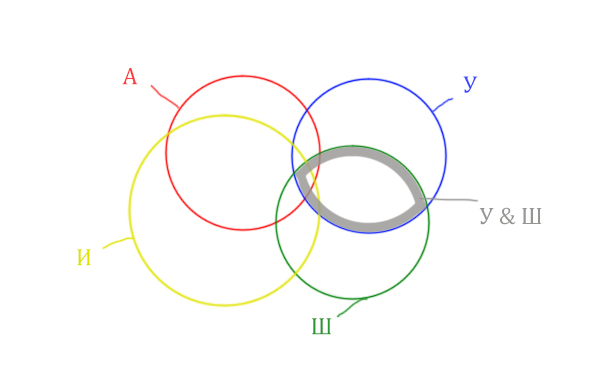
Область Уэльс & Шотландия выглядит так:
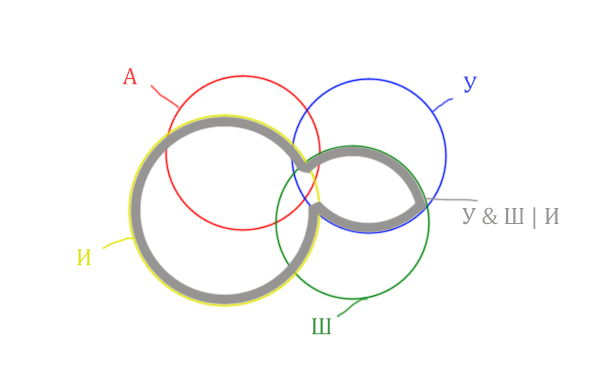
Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
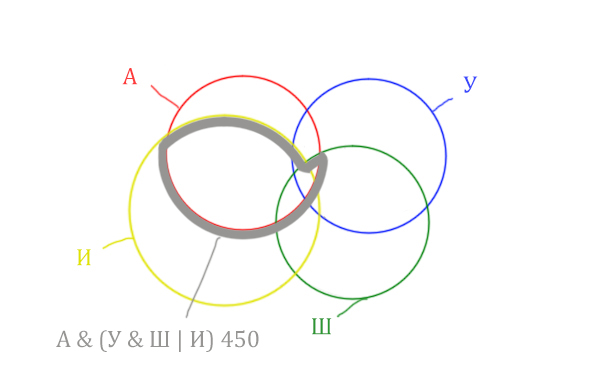
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
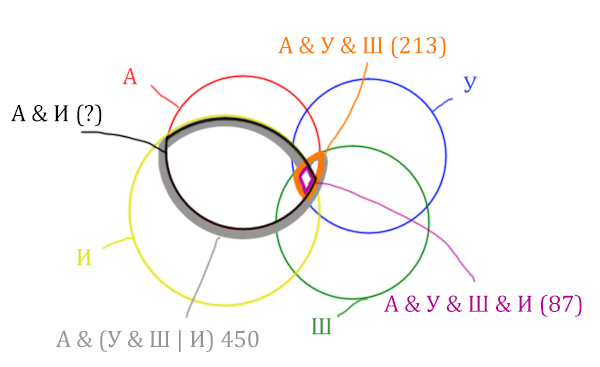
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
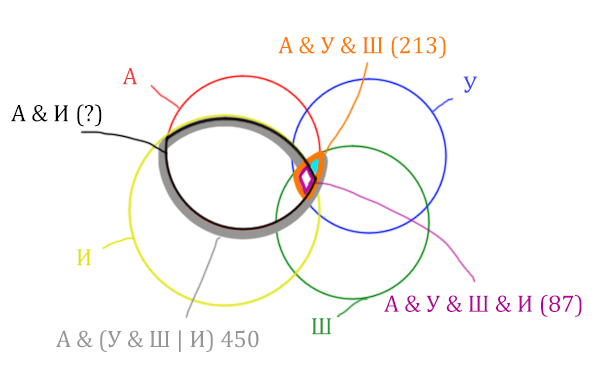
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324
Это и будет ответ!
Ответ: 324.
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
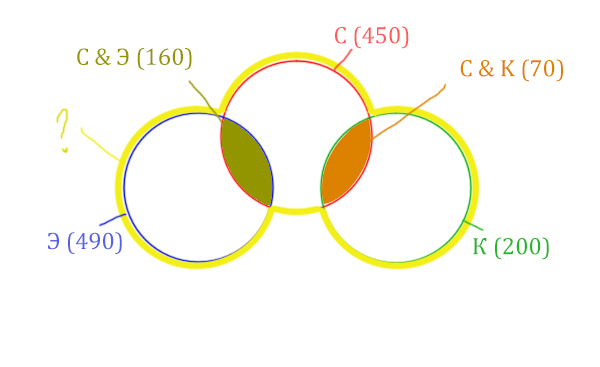
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
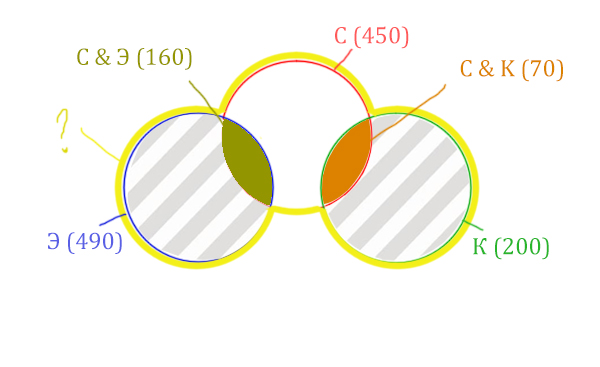
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
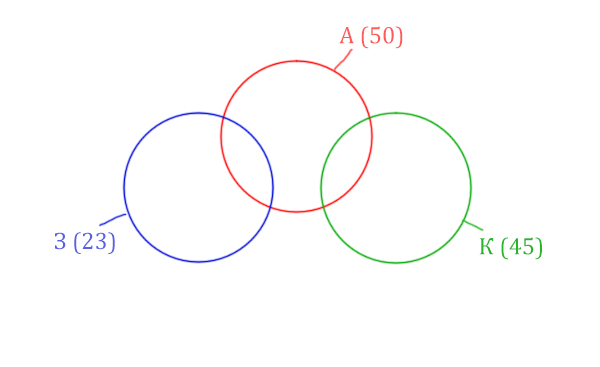
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
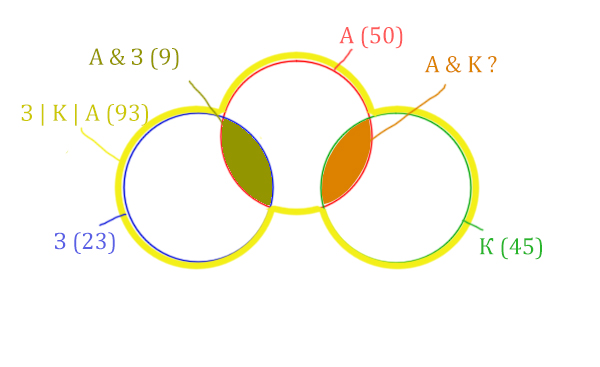
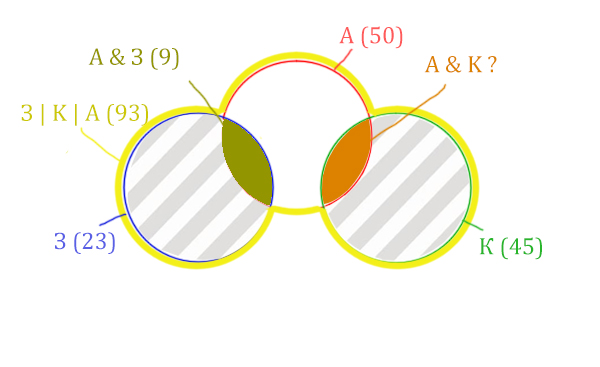
Нарисуем все данные на рисунке.
Нужно найти для начала заштрихованную правую часть.
Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Интересно…
как быть , когда идет произведение3 предметов + произведниее 3 педметов..
ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
| Ключевое слово | Найдено страниц |
|---|---|
| сканер | 200 |
| принтер | 250 |
| монитор | 450 |
Сколько сайтов будет найдено по запросу «(принтер | сканер) & монитор», если по запросу «принтер | сканер» было найдено 450 сайтов, по запросу «принтер & монитор» — 40, а по запросу «сканер & монитор» — 50.
2
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
|---|---|
| торты | пироги | 12000 |
| торты & пироги | 6500 |
| пироги | 7700 |
Сколько страниц (в тысячах) будет найдено по запросу торты
3
Некоторый сегмент сети Интернет состоит из 5000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
| Ключевое слово | Количество сайтов,для которых данное слово является ключевым |
|---|---|
| принтеры | 400 |
| сканеры | 300 |
| мониторы | 500 |
Сколько сайтов будет найдено по запросу (принтеры | мониторы) & сканеры
если по запросу принтеры | сканеры было найдено 600 сайтов,
по запросу принтеры | мониторы – 900,
а по запросу сканеры | мониторы – 750.
4
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Лебедь & (Рак | Щука) | 320 |
| Лебедь & Рак | 200 |
| Лебедь & Рак & Щука | 50 |
Какое количество страниц (в тысячах) будет найдено по запросу
Лебедь & Щука
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
5
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Пекин & (Москва | Токио) | 338 |
| Пекин & Москва | 204 |
| Пекин & Москва & Токио | 50 |
Какое количество страниц (в тысячах) будет найдено по запросу Пекин & Токио?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Пройти тестирование по этим заданиям
Автор — Лада Борисовна Есакова.
Для быстрого поиска информации в Интернете используют поисковые запросы. Поисковый запрос – это набор ключевых слов, соединенных знаками логических операций И, ИЛИ, НЕ.
Приоритет выполнения операций, если нет специально поставленных скобок, следующий: сначала НЕ, затем И, затем ИЛИ.
Нужно понимать, что операция И (одновременное выполнение условий) сокращает объем получаемого результата, а операция ИЛИ (выполнение хотя бы одного из условий) наоборот увеличивает объем.
Если в запросе стоит фраза в кавычках, система будет искать точно такую фразу целиком.
1. Расположение запросов по возрастанию (убыванию)
Операция «И» (&) обозначает одновременное присутствие ключевых слов в искомых документах, а потому уменьшает количество найденной информации. Чем больше ключевых слов соединены операцией «И», тем меньше количество найденной информации. И наоборот, операция «ИЛИ» (|) обозначает присутствие хотя бы одного ключевого слова в искомых документах, а потому увеличивает количество найденной информации.
Пример 1.
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
А) реферат | математика | Гаусс
Б) реферат | математика | Гаусс | метод
В) реферат | математика
Г) реферат & математика & Гаусс
Решение:
Самое маленькое количество страниц будет отобрано по запросу с наибольшим количеством операций «И» (запрос Г), Самое большое количество страниц будет отобрано по запросу с наибольшим количеством операций «ИЛИ» (запрос Б). По запросу А будет отобрано больше страниц, чем по запросу В, т.к. запрос А содержит больше ключевых слов, связанных операцией «ИЛИ».
Ответ: ГВАБ
2. Подсчет найденных по запросу страниц
Такой тип задач обычно решают системой уравнений. Предложу более наглядный и простой способ.
Принцип отбора информации по поисковым запросам хорошо иллюстрирует диаграмма Эйлера-Венна (круги Эйлера). На диаграмме множества изображаются пересекающимися кругами. Операция «И» (&) — это пересечение кругов, а операция «ИЛИ» (|) – это объединение кругов.
Например, обозначим кругами множества Яблоки, Груши, Бананы. По запросу Яблоки & Груши & Бананы будет отобрано пересечение (общая часть) всех трех кругов:
По запросу Яблоки | Груши будет отобрано объединение двух кругов:
Пример 2.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько страниц (в тысячах) будет найдено по запросу шахматы?
Решение:
Нарисуем диаграмму Эйлера-Венна. Прием решения задачи состоит в подсчете количества страниц, соответствующего каждой области, ограниченной линиями:
Запросу шахматы & теннис соответствует средняя область (1000 тыс. страниц), а запросу теннис – весь правый круг (5500 тыс. страниц).
Тогда правый «обрезанный круг» — это 5500-1000=4500:
Запросу шахматы | теннис соответствуют оба круга (7770), тогда левый «обрезанный круг» — это 7770-5500=2270

Итак, мы посчитали количества страниц для каждой ограниченной линиями области:
Несложно увидеть, что по запросу шахматы будет найдено 2270+1000=3270 тыс. страниц.
Ответ: 3270
Пример 3.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько страниц (в тысячах) будет найдено по запросу
Москва & (Париж | Лондон)
Решение:
Как и в предыдущей задаче, нарисуем диаграмму Эйлера-Венна и посчитаем количество страниц, соответствующее каждой известной области, ограниченной линиями:
Несложно увидеть, что запросу Москва & (Париж | Лондон) соответствует область:
Ответ: 427
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №17. Построение запросов для поисковых систем. Расположение запросов по возрастанию (убыванию). Подсчет количества страниц.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
(Старый формат ЕГЭ) 17. Запросы в поисковых системах
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Диаграммы Эйлера
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{ноутбук}&100\
hline
text{монитор}&200\
hline
text{стол}&350\
hline
text{ноутбук | стол}&450\
hline
text{ноутбук} & text{монитор}&50\
hline
text{стол} & text{монитор}&40\
hline
end{array}]
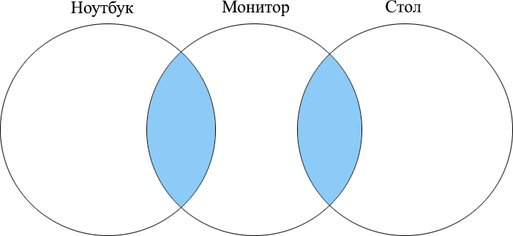
Сколько страниц будет найдено по запросу (ноутбук | стол) & монитор?
Если сложить количество страниц, найденных отдельно по запросам ”ноутбук” и ”монитор”, получим 450. Можно заметить, что (ноутбук | стол) так же равно 450. Это значит, что эти два множества не пересекаются, то есть (text{(ноутбук} & text{монитор)}=0).
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Исходя из рисунка, нам нужно найти сумму (text{(ноутбук} & text{монитор)}+text{(стол} & text{монитор)}). Все данные приведены в таблице, значит, наш ответ (50+40=90).
Ответ: 90
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{чайка}&200\
hline
text{утка}&150\
hline
text{курица}&120\
hline
text{чайка} & text{утка}&80\
hline
text{утка} & text{курица}&70\
hline
text{чайка} & text{курица}&60\
hline
text{чайка} & text{курица} & text{утка}&10\
hline
end{array}]
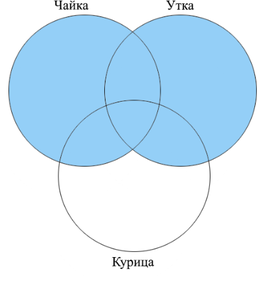
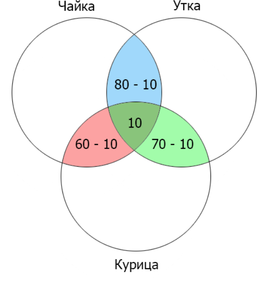
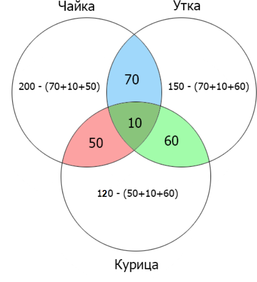
Сколько страниц будет найдено по запросу (чайка | утка)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Посчитаем количество найденных страниц для каждого пересечения:
Посчитаем оставшиеся данные:
Затем складываем все данные, входящие в круги ”чайка” и ”утка”: (70+70+50+10+60+10=270)
Второй способ решения
Чтобы найти объединение (операция «ИЛИ») множеств, необходимо сложить отдельно количество страниц, найденных по каждому запросу, а затем вычесть их пересечение (операция «И»): (200+150-80=270)
Ответ: 270
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{карандаш}&300\
hline
text{линейка}&200\
hline
text{ручка}&280\
hline
text{ручка} & text{линейка}&80\
hline
text{ручка} & text{карандаш}&70\
hline
text{линейка} & text{карандаш}&0\
hline
end{array}]
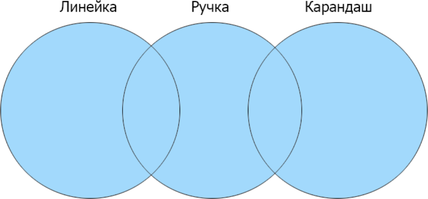
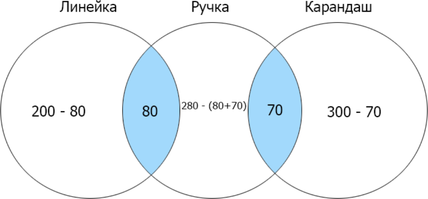
Сколько страниц будет найдено по запросу (линейка | ручка | карандаш)?
Первый способ решения
Отметим на кругах Эйлера то, что нам необходимо найти по условию задачи:
Отметим известные данные и посчитаем недостающее:
Затем складываем все данные, входящие в искомую область: (120+130+230+80+70=630).
Второй способ решения
Заметим, что по условию нам необходимо найти сумму всех найденных страниц по введенным запросам. Если мы сложим все отдельные значения найденных страниц, мы учтем по 2 раза каждое из двух пересечений. Таким образом, можем посчитать искомое по формуле: (линейка) + (ручка) + (карандаш) — (ручка & линейка) — (ручка & карандаш) (=300+200+280-80-70=630).
Ответ: 630
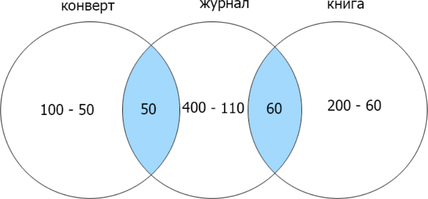
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{конверт}&100\
hline
text{книга}&200\
hline
text{журнал}&400\
hline
text{конверт | книга}&300\
hline
text{конверт} & text{журнал}&50\
hline
text{журнал} & text{книга}&60\
hline
end{array}]
Сколько страниц будет найдено по запросу (конверт | книга | журнал)?
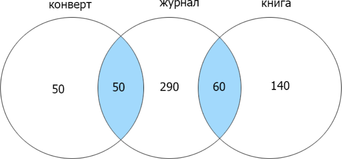
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к. сумма количества страниц, найденных по запросам конверт и книга = 300, а (конверт | книга) = 300, (конверт & книга) = 0. Теперь отобразим известные данные:
Отметим найденные данные и сложим каждую отдельную область для нахождения объедиения трех множеств:
(50+50+290+60+140=590).
Ответ: 590
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{шкаф} & text{стул}&50\
hline
text{стул} & text{стол}&60\
hline
text{стол} & text{шкаф}&70\
hline
text{(шкаф} & text{стул) | (стул} & text{стол) | (стол} & text{шкаф)}&120\
hline
end{array}]
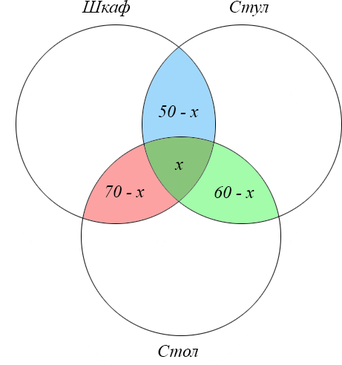
Сколько страниц будет найдено по запросу (шкаф & стул & стол)?
Обозначим искомую область за (x) и выразим данные через (x):
Из последней строки таблицы нам известно, что сумма всех отмеченных элементов равна 120. Значит, можем найти (x) через следующее уравнение:
((50-x)+(70-x)+(60-x)+x=120)
(180-2x=120)
(2x=60)
(x=30)
Ответ: 30
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
text{Запрос} & text{Найдено страниц (в тысячах)}\
hline
text{злодеи}&150\
hline
text{мягкие пушистики}&210\
hline
text{злодеи | мягкие пушистики}&300\
hline
end{array}]
Сколько страниц будет найдено по запросу кот, если известно, что коты находятся на пересечении множеств злодеев и мягких пушистиков?
Отметим искомую область:
Заметим, что кот = (злодеи & мягкие пушистики) = злодеи + пушистики — (злодеи | мягкие пушистики) = (150+210-300=60).
Ответ: 60
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
[begin{array}{| c | c |}
hline
textbf{Запрос} & textbf{Найдено страниц (в тысячах)}\
hline
text{сок}&100\
hline
text{фрукты}&100\
hline
text{сахар | фрукты | сок}&300\
hline
text{сок | фрукты}&200\
hline
text{сок} ; & ; text{сахар}&20\
hline
text{сахар} ; & ; text{фрукты}&30\
hline
end{array}]
Сколько страниц будет найдено по запросу сахар?
Заметим, что если сумма найденных страниц по каждому отдельному запросу равна их объедиению (операция «ИЛИ»), то их пересечение (операция «И») равно нулю. Т.к.сумма количества страниц, найденных по запросам сок и фрукты = 200, а (сок | фрукты) = 200, (сок & фрукты) = 0. Теперь отобразим известные данные: 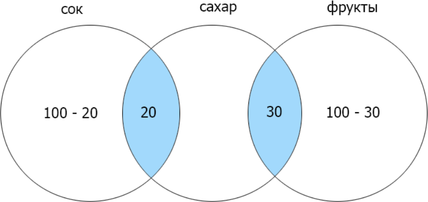
Ответ: 150

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
За это задание ты можешь получить 1 балл. На решение дается около 2 минут. Уровень сложности: повышенный.
Средний процент выполнения: 70.9%
Ответом к заданию 17 по информатике может быть цифра (число) или слово.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых одно число кратно 5, а другое кратно 7. В ответе запишите подряд два числа без разделителей: максимальную сумму внутри пары, а затем количество чисел в найденных парах (если одно число встречается в нескольких парах, учитываем его несколько раз). В данной задаче под парой подразумевается два числа стоящие на разных позициях элемента последовательности. Порядок расположения чисел в паре неважен.
Решение
a = []
f = open('17.txt', 'r')
for line in f:
a.append(int(line))
k = 0
max_sum = -20001
for i in range(len(a)):
for j in range(i, len(a)):
if i != j:
if (a[i] % 5 == 0 and a[j] % 7 == 0) or (a[j] % 5 == 0 and a[i] % 7 == 0):
k += 1
max_sum = max(max_sum, a[i] + a[j])
print(max_sum, k * 2, sep='')
Ответ: 199521142604
Задача 2
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых хотя бы одно число делится на 4, а сумма элементов пары не более максимального элемента последовательности, кратного 5. В ответе запишите подряд два числа без разделителей: количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
Решение
Нам тут тоже необходимо выполнить 2 прохода, поэтому при первом проходе сохраним всё в список и найдём максимальное число
a = []
max_5 = -10000
f = open('17_1.txt', 'r')
for line in f:
x = int(line)
a.append(x)
if x % 5 == 0:
max_5 = max(max_5, x)
sum_max = -20000
k = 0
for i in range(len(a) - 1):
if (a[i] % 4 == 0 or a[i + 1] % 4 == 0) and a[i] + a[i + 1] <= max_5:
k += 1
sum_max = max(sum_max, a[i] + a[i + 1])
print(k, sum_max)
Ответ: 18809983
Задача 3
В файле содержится последовательность целых чисел. Элементы принимают целые значения от -10000 до 10000 включительно. Определите и запишите в ответе два значения:
1) Количество пар элементов последовательности, в которых сумма чисел делится на 10
2)Максимальную сумму двух элементов в паре среди всех таких пар.
В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
В качестве ответа запишите сначала количество, а потом максимальное число без пробелов и разделителей. Если один из ответов отрицательный, записать его по модулю. Например, если количество чисел 99, а максимум -1234, то ответ 991234.
Решение
f = open(«fileotr7.txt»)
kol = 0
Max = -20000
pred = -10001
for x in f:
x = int(x)
if pred != -10001:
if (pred + x) % 10 == 0:
kol += 1
if pred+x > Max:
Max = pred+x
pred = x
print(kol, Max)
Количество: 648, сумма: 18780.
Ответ: 64818780
Задача 4
В файле содержится последовательность целых чисел. Элементы принимают целые значения от -10000 до 10000 включительно. Определите и запишите в ответе два значения:
1) Количество пар элементов последовательности, в которых оба числа делятся на 3
2) Минимальную сумму двух элементов в паре среди всех таких пар.
В данной задаче под парой подразумеваются два числа, расположенных на разных местах в наборе, порядок в паре неважен.
В качестве ответа запишите сначала количество, а потом минимальное число без пробелов и разделителей. Если один из ответов отрицательный, записать его по модулю. Например, если количество чисел 99, а минимум -1234, то ответ 991234.
Решение
f = open(«fileotr4.txt»)
kol = 0
Min = 20000
pred = -10001
a = []
for x in f:
x = int(x)
a.append(x)
for i in range(len(a)):
for j in range(i+1, len(a)):
if a[i] % 3 == 0 and a[j] % 3 == 0:
kol += 1
if a[i]+a[j]<Min:
Min = a[i]+a[j]
print(kol, Min)
Количество: 306936, сумма: -19971.
Ответ: 30693619971
Задача 5
В файле содержится последовательность целых чисел. Элементы принимают целые значения от -10000 до 10000 включительно. Определите и запишите в ответе два значения:
1) Количество пар элементов последовательности, в которых хотя бы одно число делится на 10
2) Минимальную сумму двух элементов в паре среди всех таких пар.
В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
В качестве ответа запишите сначала количество, а потом минимальное число без пробелов и разделителей. Если один из ответов отрицательный, записать его по модулю. Например, если количество чисел 99, а минимум -1234, то ответ 991234.
Решение
f = open(«fileotr2.txt»)
kol = 0
Min = 20000
pred = -10001
for x in f:
x = int(x)
if pred != -10001:
if pred % 10 == 0 or x % 10 == 0:
kol += 1
if pred+x < Min:
Min = pred+x
pred = x
print(kol, Min)
Количество: 1145, сумма: -19583.
Ответ: 114519583
Задача 6
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите количество и сумму чисел, которые делятся на 59, но не делятся на 2, 3 и 5.
В качестве ответа запишите сначала количество, а потом сумму без пробелов и разделителей. Например, если количество чисел 99, а сумма 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
count = 0
Sum = 0
f = open(«file.txt»)
for x in f:
x = int(x)
if (x % 59 == 0 and x % 2 != 0 and
x % 3 != 0 and x % 5 != 0):
count += 1
Sum += x
print(count, Sum)
Ответ: 427140
Задача 7
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите количество и сумму чисел, которые делятся на 29, но не делятся на 13, 17 и 31.
В качестве ответа запишите сначала количество, а потом сумму без пробелов и разделителей. Например, если количество чисел 99, а сумма 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
count = 0
Sum = 0
f = open(«file.txt»)
for x in f:
x = int(x)
if (x % 29 == 0 and x % 13 != 0 and
x % 17 != 0 and x % 31 != 0):
count += 1
Sum += x
print(count, Sum)
Ответ: 31169969
Задача 8
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите количество и сумму чисел, которые делятся на 29, но не делятся на 13, 17 и 31.
В качестве ответа запишите сначала количество, а потом сумму без пробелов и разделителей. Например, если количество чисел 99, а сумма 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
count = 0
Sum = 0
f = open(«file.txt»)
for x in f:
x = int(x)
if (x % 29 == 0 and x % 13 != 0 and
x % 17 != 0 and x % 31 != 0):
count += 1
Sum += x
print(count, Sum)
Ответ: 31168577
Задача 9
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите количество и сумму чисел, в составе которых есть ровно 3 девятки.
В качестве ответа запишите сначала количество, а потом сумму без пробелов и разделителей. Например, если количество чисел 99, а сумма 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
count = 0
summa = 0
f = open(«file1.txt»)
for x in f:
x = int(x)
copy = x
kol = 0
while copy > 0:
if copy % 10 == 9:
kol += 1
copy //= 10
if kol == 3:
count += 1
summa += x
print(count, summa)
Ответ: 219628
Задача 10
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите количество простых чисел и максимальное простое число. Простое число — число, которое делится только на единицу и само себя.
В качестве ответа запишите сначала количество, а потом максимум без пробелов и разделителей. Например, если количество чисел 99, а максимум 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
count = 0
Max = 0
f = open(«file1.txt»)
for x in f:
x = int(x)
kol_del = 0
for i in range(1, x + 1):
if x % i == 0:
kol_del += 1
if kol_del == 2:
count += 1
if x > Max:
Max = x
print(count, Max)
Ответ: 1049931
Задача 11
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите минимум и максимум среди чисел, которые оканчиваются на 3 и делятся на 7.
В качестве ответа запишите сначала минимум, а потом максимум без пробелов и разделителей. Например, если минимум равен 99, а максимум — 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
Max = 0
Min = 10000
f = open(«file.txt»)
for x in f:
x = int(x)
if x % 10 == 3 and x % 7 == 0:
if x > Max:
Max = x
if x < Min:
Min = x
print(Min, Max)
Ответ: 4839723
Задача 12
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите количество и сумму чисел, которые делятся на 2 и 13, но не делятся на 5 и 7.
В качестве ответа запишите сначала количество, а потом сумму без пробелов и разделителей. Например, если количество чисел 99, а сумма 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
count = 0
summa = 0
f = open(«file.txt»)
for x in f:
x = int(x)
if (x % 2 == 0 and x % 13 == 0 and
x % 5 != 0 and x % 7 != 0):
count += 1
summa += x
print(count, summa)
Ответ: 27137098
Задача 13
В файле содержится последовательность целых чисел. Элементы принимают целые значения от 1 до 10000 включительно. Определите количество и сумму чисел, которые делятся на 7 и 11, но не делятся на 3 и 5.
В качестве ответа запишите сначала количество, а потом сумму без пробелов и разделителей. Например, если количество чисел 99, а сумма 1234, то ответ 991234.
Для выполнения задания рекомендуется написать программу или воспользоваться редактором электронных таблиц.
Решение
Пример решения задачи на Python:
count = 0
summa = 0
f = open(«file.txt»)
for x in f:
x = int(x)
if (x % 7 == 0 and x % 11 == 0 and
x % 3 != 0 and x % 5 != 0):
count += 1
summa += x
print(count, summa)
Ответ: 419404
Рекомендуемые курсы подготовки
Круги Эйлера —
геометрическая схема, с помощью которой можно изобразить отношения между
подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других
прикладных направлениях.
Задача №1
В
языке запросов поискового сервера для обозначения логической операции
«ИЛИ» используется символ «|», а
для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц
некоторого сегмента сети Интернет.
|
Запрос |
Найдено |
|
Торты | |
12000 |
|
Торты |
6500 |
|
Пироги |
7700 |
Какое количество страниц (в тысячах) будет найдено по запросу Торты?Считается,
что все запросы выполнялись практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение задачи №1
Для решения задачи отобразим множества Тортов и Пирогов в виде
кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Торты │Пироги = А+Б+В =
12000
Торты & Пироги = Б = 6500
Пироги = Б+В =
7700
Чтобы найти количество Тортов (Торты = А+Б),
надо найти сектор А, для этого из общего множества
(Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В)
= А = 1200 – 7700 = 4300
Сектор А равен 4300,
следовательно
Торты = А+Б =
4300+6500 = 10800
Задача №2
В
языке запросов поискового сервера для обозначения логической операции
«ИЛИ» используется символ «|», а
для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц
некоторого сегмента сети Интернет.
|
Запрос |
Найдено |
|
Пироженое |
5100 |
|
Пироженое |
9700 |
|
Пироженое |
14200 |
Какое количество страниц (в тысячах) будет найдено по
запросу Выпечка?
Считается,
что все запросы выполнялись практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за время выполнения запросов.Решение
задачи №2
Для решения задачи отобразим множества Пироженых и
Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Пироженое & Выпечка = Б =
5100
Пироженое = А+Б =
9700
Пироженое │ Выпечка = А+Б+В =
14200
Чтобы
найти количество Выпечки (Выпечка = Б+В),
надо найти сектор В, для этого из общего множества
(Пироженое │ Выпечка ) отнимем множество Пироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500
Сектор В равен 4500,
следовательно Выпечка = Б + В =
4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому
серверу. Расположите номера запросов в порядке убывания количества
страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ
«|», а для логической операции «И» — символ
«&».
|
1 |
спаниели |
|
2 |
спаниели |
|
3 |
спаниели |
|
4 |
терьеры |
Решение задачи №3
Представим множества овчарок, терьеров и спаниелей в виде кругов
Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества
страниц.
Расположим номера запросов в порядке убывания количества
страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите
номера запросов в порядке возврастанияколичества страниц, которые
найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ
«|», а для логической операции «И» — символ
«&».
|
1 |
барокко |
|
2 |
барокко |
|
3 |
классицизм |
|
4 |
барокко |
Решение задачи №4

множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим
сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества
страниц.
Расположим номера запросов в порядке возрастания количества
страниц: 3 2 4 1
На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 17 задания. Объясняется тема о программной обработке числовой информации.
Содержание:
- ЕГЭ по информатике 17 задания объяснение
- Выполнение 17 задания ЕГЭ
- Работа с цифрами числа в n-й системе счисления
17-е задание: «Программная обработка целочисленной информации»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 1,
Примерное время выполнения
— 15 минут.
Проверяемые элементы содержания: Умение создавать собственные программы (20–40 строк) для обработки целочисленной информации
Выполнение 17 задания ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
17_1: Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Рассматривается множество целых чисел, принадлежащих числовому отрезку [1016; 7937], которые делятся на 3 и не делятся на 7, 17, 19, 27. Найдите количество таких чисел и максимальное из них.
В ответе запишите два целых числа: сначала количество, затем максимальное число.
! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц
Типовые задания для тренировки
Ответ: 1568 | 7935
Видео
✍ Решение:
-
✎ Решение с использованием программирования:
- Первое значение диапазона введем в ячейку A1:
- Используем прогрессию для заполнения всего диапазона числами. Для это выберите вкладку Главная и щелкните по кнопке Прогрессия:
- Столбец B будем использовать для поиска чисел, которые делятся на 3. Для этого в ячейку B1 введите формулу с рисунка:
- Двойным щелчком по маркеру заполнения скопируйте формулу на весь столбец:
- Столбец С будем использовать для поиска чисел, которые НЕ делятся на 7. Для этого в ячейку С1 введите формулу с рисунка:
- Заполните весь столбец двойным щелчком по маркеру заполнения.
- Cтолбцы D, E, F таким же образом будем использовать для поиска чисел столбца А, которые не делятся на 17, 19 и 27
- Для поиска всех истинных значений используем столбец G. В ячейку G1 введите функцию
ЕСЛИ: если все значения ячеек в столбцах B-F в этой строке истинны, выводим число из А1, иначе – пустую строку: - Ячейку H1 будем использовать для подсчета таких чисел, которые удовлетворяют всем условиям, т.е. для подсчета непустых ячеек столбца G:
- Ячейку H2 будем использовать для подсчета такого наибольшего числа:
Паскаль:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
var i, k, max: integer; begin k := 0; max := 0; for i := 1016 to 7937 do begin if (i mod 3 = 0) and (i mod 7 > 0) and (i mod 17 > 0) and (i mod 19 > 0) and (i mod 27 > 0) then begin max:= i; inc(k); end; end; writeln(k, ' ', max) end. |
PascalABC.NET:
1 2 3 4 |
begin var s := Range( 1017, 7937, 3).Where( i -> not i.DivsAny(7, 17, 19, 27) ); print( s.Count, s.Max ); end. |
Python:
1 2 3 |
a = [n for n in range(1016,7937+1) if (n%3==0 and n%7!=0 and n%17!=0 and n%19!=0 and n%27!=0)] print(len(a),max(a)) |
Список a формируем, используя генератор списка: то есть в список попадут только не числа из диапазона [1016,7937], которые удовлетворяют всем перечисленным условиям: n%3==0 (число делится на 3), n%7!=0 (число не делится на 7) и т.п.
C++:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#include <iostream> int main() { int count = 0; int maxGood = 0; for(int n=1016; n<=7937; n++) if( (n % 3 == 0) and (n % 7 != 0) and (n % 17 != 0) and (n % 19 != 0) and (n % 27 != 0) ) { maxGood = n; count += 1; } std::cout << count << " " << maxGood; } |
✎ Решение с помощью Excel:

Заполните весь столбце, используя маркер автозаполнения.

Видеоразбор 17 задания ЕГЭ:
📹 YouTube здесь
Видеорешение на RuTube здесь
Работа с цифрами числа в n-й системе счисления
17_2:
Рассматривается множество целых чисел, принадлежащих числовому отрезку [3712; 8432], которые удовлетворяют следующим условиям:
− запись в двоичной и четверичной системах счисления заканчивается одинаковой цифрой;
− кратны 13, 14 или 15.
Найдите количество таких чисел и минимальное из них.
! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц
Типовые задания для тренировки
Ответ: 471 3720
✍ Решение:
✎ Решение с использованием программирования:
Паскаль:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
var var k, n, min:integer; begin k:=0; min:=8433; for n:= 3712 to 8432 do if (n mod 2 = n mod 4) and ((n mod 13=0) or (n mod 14=0) or (n mod 15=0)) then begin if min>n then min:=n; k:=k+1; end; Writeln (k,' ',min); End. |
PascalABC.NET:
1 2 3 4 5 6 7 |
begin var s := Range( 3712, 8432) .Where(i -> ((i mod 13=0) or (i mod 14=0) or (i mod 15=0)) and (i mod 2 = i mod 4)); // или: .Where( i -> (i.DivsAny(13,14,15)) and (i mod 2 = i mod 4)); s.Count.Print; s.Min.Print; end. |
Python:
1 2 |
L = [x for x in range(3712, 8432+1) if (x % 13 == 0 or x % 14 == 0 or x % 15 == 0) and ( x % 2 == x % 4)] print(len(L),' ',L[0]) |
Формируем список (массив) L только из подходящих элементов, то есть удовлетворяющих всем, перечисленным в задании, условиям. Затем выводим длину списка (len(L)), т.е. найденное количество таких чисел, и нулевой элемент, он же минимальный, поскольку числа упорядочены по возрастанию (L[0])
C++:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#include <iostream> int main() { int count = 0; int min = 8433; for (int n = 3712; n <= 8432; n++) if (((n % 2 == n % 4) && ((n % 13 == 0) || (n % 14 == 0) || (n % 15 == 0))) ) { if (n < min) min = n; count += 1; } std::cout << count << " " << min; } |
✎ Решение с помощью Excel:
ЕСЛИ: если все значения ячеек в столбцах B, C в этой строке истинны, выводим число из А1, иначе – пустую строку:D визуально и найдите первое значение):17_3:
Рассматривается множество целых чисел, принадлежащих числовому отрезку [1000; 9999], запись которых в пятеричной системе имеет не менее 6 цифр и заканчивается на 21 или 23.
Найдите количество таких чисел и минимальное из них.
! Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц
Ответ: 550 3136
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.NET:
1 2 3 4 5 6 |
### uses school; var s := Range(1000, 9999) .Where(i -> (i.ToString.ToBase(5).Length=6) and (i div 5 mod 5 = 2) and((i mod 5 = 1) or (i mod 5 = 3))); s.Count.Print; s.Min.Print; |
Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
numb='' result=list() for i in range(1000, 9999+1): if ((i // 5) % 5 ==2) and (( i % 5 == 1) or ( i % 5 == 3)): while i>=5: #Цикл перевода числа из 10-й в 5-ю сс s=i%5 numb=str(s)+numb i=i//5 if i<5: numb=str(i)+numb n=len(numb) if n>5: result.append(numb) # список из чисел в 5-й с.с numb="" kolvo=len(result) minNumb=int(min(result),5) # перевод в десятичную с.с и поиск min print(kolvo,minNumb) |