Задания на спектры егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д11 B20 № 2007

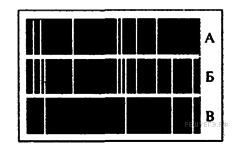
На рисунках А, Б и В приведены спектры излучения атомарных газов А и В и газовой смеси Б.

На основании анализа этих участков спектров можно сказать, что смесь газа содержит

1)  только газы А и В

2)  газы А, В и другие

3)  газ А и другой неизвестный газ

4)  газ В и другой неизвестный газ

Задания Д11 B20 № 2011

На рисунке изображена схема возможных значений энергии атомов разреженного газа.

В начальный момент времени атомы находятся в состоянии с энергией Возможно испускание газом фотонов с энергией

1)  только  Дж

2)  только и  Дж

3)  только и  Дж

4)  любой от до  Дж

Задания Д11 B20 № 2027

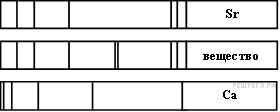
На рисунке приведены спектр поглощения разреженных атомарных паров неизвестного вещества (в середине) и спектры поглощения паров известных элементов (вверху и внизу).

По анализу спектров можно утверждать, что неизвестное вещество содержит

1)  только кальций (Са)

2)  только стронций (Sr)

3)  кальций и еще какое-то неизвестное вещество

4)  стронций и еще какое-то неизвестное вещество

Задания Д11 B20 № 2115

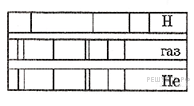
На рисунке приведены фрагмент спектра поглощения неизвестного разреженного атомарного газа (в середине), спектры поглощения атомов водорода (вверху) и гелия (внизу).

В химический состав газа входят атомы

1)  только водорода

2)  только гелия

3)  водорода и гелия

4)  водорода, гелия и еще какого-то вещества

Задания Д11 B20 № 2122

На рисунках А, Б, В приведены спектры излучения паров стронция, неизвестного образца и кальция.

Можно утверждать, что в образце

1)  не содержится ни стронция, ни кальция

2)  содержится кальций, но нет стронция

3)  содержатся и стронций, и кальций

4)  содержится стронций, но нет кальция

Пройти тестирование по этим заданиям

Источник

Задание 19 № 2007. На рисунках А, Б и В приведены спектры излучения атомарных газов А и В и газовой смеси Б.

На основании анализа этих участков спектров можно сказать, что смесь газа содержит

1) только газы А и В

2) газы А, В и другие

3) газ А и другой неизвестный газ

4) газ В и другой неизвестный газ

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре зависят только от свойств атомов этого вещества, но совершенно не зависят от способа возбуждения свечения атомов. Из рисунка видно, что на спектре газовой смеси Б присутствуют те и только те линии, которые есть либо на спектре газа А, либо на спектре газа В. Этот факт говорит в пользу того, что смесь газа Б содержит только газы А и В.

Правильный ответ: 1.

Задание 19 № 2027. На рисунке приведены спектр поглощения разреженных атомарных паров неизвестного вещества (в середине) и спектры поглощения паров известных элементов (вверху и внизу).

По анализу спектров можно утверждать, что неизвестное вещество содержит

1) только кальций (Са)

2) только стронций (Sr)

3) кальций и еще какое-то неизвестное вещество

4) стронций и еще какое-то неизвестное вещество

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре поглощения зависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре поглощения разреженных атомарных паров неизвестного вещества присутствуют все линии, которые есть на спектре стронция, нет линий, свойственных кальцию, но в тоже время есть дополнительные неизвестные линии. Этот факт говорит в пользу того, что в химический состав неизвестного вещества входит стронций и еще какое-то неизвестное вещество.

Правильный ответ: 4.

Задание 19 № 2115. На рисунке приведены фрагмент спектра поглощения неизвестного разреженного атомарного газа (в середине), спектры поглощения атомов водорода (вверху) и гелия (внизу).

В химический состав газа входят атомы

1) только водорода

2) только гелия

3) водорода и гелия

4) водорода, геля и еще какого-то вещества

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре поглощения зависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре поглощения неизвестного разреженного атомарного газа присутствуют те и только те линии, которые есть на спектре гелия. Этот факт говорит в пользу того, что в химический состав неизвестного газа входит только гелий (то есть это и есть гелий).

Правильный ответ: 2.

Задание 19 № 2122. На рисунках А, Б, В приведены спектры излучения паров стронция, неизвестного образца и кальция.

Можно утверждать, что в образце

1) не содержится ни стронция, ни кальция

2) содержится кальций, но нет стронция

3) содержатся и стронций, и кальций

4) содержится стронций, но нет кальция

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре pзависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре излучения паров неизвестного образца присутствуют все линии, которые есть на спектре стронция, нет линий, свойственных кальцию, но в тоже время есть дополнительные неизвестные линии. Этот факт говорит в пользу того, что в образце содержится стронций, но нет кальция.

Правильный ответ: 4.

Задание 19 № 2123. Длина волны фотона, излучаемого атомом при переходе из возбужденного состояния с энергией в основное состояние с энергией , равна (c — скорость света, h — постоянная Планка)

Решение.

Частота фотона, излучаемого атомом при переходе в состояние с более низкой энергией, связана с изменением энергии атома соотношением . Принимая во внимание связь , получаем, что длина волны фотона равна .

Правильный ответ: 3.

Задание 19 № 2135. Каков спектр энергетических состояний атомного ядра и какие частицы испускает ядро при переходе из возбужденного состояния в нормальное?

1) cпектр линейчатый, испускает гамма-кванты

2) cпектр сплошной, испускает гамма-кванты

3) cпектр сплошной, испускает бета-частицы

4) cпектр линейчатый, испускает альфа-частицы

Решение.

Атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определенная энергия. Таким образом, спектр энергетических состояний атомного ядра линейчатый. При переходе атома из возбужденного состояния в нормальное испускаются гамма-кванты.

Правильный ответ: 1.

Задание 19 № 3243. 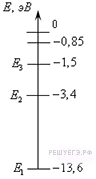На рисунке показаны энергетические уровни атома водорода. Если атом находится в основном состоянии, то для его перехода в ионизированное состояние необходимо

1) получить от атома энергию 3,4 эВ

2) сообщить атому энергию 3,4 эВ

3) получить от атома энергию 13,6 эВ

4) сообщить атому энергию 13,6 эВ

Решение.

Основным состоянием в атоме называется состояние с наименьшей энергии. Для водорода это уровень с энергией . Началом отсчета энергии является состояние, при котором ядро водорода и электрон перестают быть связанной системой. При этой энергии происходит ионизация. Таким образом, для того чтобы перевести атом водорода из основного состояния в ионизированное, необходимо сообщить ему энергию .

Задание 19 № 3342. Каков заряд ядра (в единицах элементарного заряда)?

1) 5

2) 11

3) 16

4) 6

Решение.

Числом протонов (заряд ядра в элементарных единицах заряда) записывается внизу перед наименованием элемента. Таким образом, заряд ядра равен 5.

Правильный ответ: 1.

Задание 19 № 3344. Атом бора содержит

1) 8 протонов, 5 нейтронов и 13 электронов

2) 8 протонов, 13 нейтронов и 8 электронов

3) 5 протонов, 3 нейтрона и 5 электронов

4) 5 протонов, 8 нейтронов и 13 электронов

Решение.

Число электронов в нейтральном атоме совпадает с числом протонов, которое записывается внизу перед наименованием элемента. Число вверху обозначает массовое число, то есть суммарное число протонов и нейтронов. Таким образом, атом бора содержит 5 протонов, 3 нейтронов и 5 электронов.

Правильный ответ: 3.

Задание 19 № 3387. На рисунке приведены спектры поглощения атомарных паров неизвестного вещества и трех известных элементов. По виду спектров можно утверждать, что неизвестное вещество содержит в заметном количестве атомы

1) только стронция (Sr) и кальция (Са)

2) только натрия (Na) и стронция (Sr)

3) только стронция (Sr), кальция (Са) и натрия (Na)

4) стронция (Sr), кальция (Са), натрия (Na) и других элементов

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре поглощения зависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре поглощения неизвестного вещества присутствуют все линии, которые есть на спектрах стронция, кальция и натрия. Помимо этого, на спектре есть линии, которых нет на других трех спектрах. Этот факт говорит в пользу того, что в химический состав неизвестного газа входят и стронций, и кальций, и натрий, а помимо их еще некоторые неизвестные элементы.

Задание 19 № 3750. Линейчатые спектры поглощения и испускания характерны для

1) любых тел

2) любых нагретых тел

3) для твердых нагретых тел

4) для нагретых атомарных газов

Решение.

Спектры излучения и поглощения связаны с энергетическими переходами в веществе. Чем «сложнее» система, тем запутаннее ее спектры. Для почти свободных атомов и молекул в разрежённых газах спектры поглощения и испускания состоят из отдельных спектральных линий и потому называются линейчатым. Таким образом, линейчатые спектры поглощения и испускания характерны для атомарных газов.

Правильный ответ: 4.

Задание 19 № 3884. На рисунке схематически изображена фотография спектральных линий атомов некоторого химического элемента в ультрафиолетовой части спектра. Из этого рисунка следует, что

1) атом данного химического элемента имеет шесть электронов

2) электроны в атоме этого химического элемента могут находиться только на шести энергетических уровнях

3) электроны в атоме этого химического элемента могут находиться только на четырёх энергетических уровнях

4) только при шести переходах электронов с одного энергетического уровня на другой атом этого химического элемента испускает фотон с длиной волны, лежащей в ультрафиолетовой области спектра

Решение.

Согласно постулатам Бора, энергия излучается или поглощается атомом только при переходе электрона из одного стационарного состояния в другое, при этом частота излучения пропорциональна разности энергий стационарных состояний. Спектр изображает наблюдаемые на эксперименте частоты излучений. Поэтому из приведенного здесь схематического рисунка ультрафиолетовой части спектра можно лишь заключить, что только при шести переходах электронов с одного энергетического уровня на другой атом химического элемента испускает фотон с частотой (длиной волны), лежащей в ультрафиолетовой области спектра.

Правильный ответ: 4.

Задание 19 № 4129. 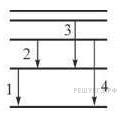На рисунке изображена схема электронных переходов между энергетическими уровнями атома, происходящих с излучением фотона. Минимальный импульс имеет фотон, излучаемый при переходе

1) 1

2) 2

3) 3

4) 4

Решение.

Квант энергии излучается при переходе на более низкий уровень энергии. При этом расстояние между уровнями пропорционально импульсу излучаемого фотона: . Из диаграммы видно, что среди предложенных вариантов ответа минимальному расстоянию между уровнями, а значит, и минимальному импульсу фотона соответствует переход 2.

Правильный ответ: 2.

Задание 19 № 4741. Схема низших энергетических уровней атомов разреженного атомарного газа имеет вид, изображённый на рисунке. В начальный момент времени атомы находятся в состоянии с энергией Согласно постулатам Бора данный газ может излучать фотоны с энергией

1) 0,3 эВ, 0,5эВ и1,5 эВ

2) только 1,5 эВ

3) любой в пределах от 0 до 0,5 эВ

4) только 0,3 эВ

Решение.

Согласно постулатам Бора, свет излучается при переходе атома на более низкие уровни энергии, при этом фотоны несут энергию, равную разности энергий начального и конечного состояний. Из приведенной здесь схемы видно, что фотон может излучиться только при переходе атома в состояние , при этом его энергия будет равна .

Правильный ответ: 2

Задание 19 № 4811. На рисунке указаны три низших значения энергии атома натрия. Атомы находятся в состоянии . При освещении атомарных паров натрия светом с энергией фотонов Дж

1) произойдёт переход атомов в состояние

2) произойдёт переход атомов в состояние

3) произойдёт ионизация атомов

4) атомы не будут поглощать свет

Решение.

Согласно постулатам Бора, свет поглощается при переходе атома на более высокие уровни энергии, при этом фотоны должны иметь энергию, равную разности энергий конечного и начального состояний.

Если атом в состоянии поглотит фотон, то его энергия станет равной

Из приведенной здесь схемы видно, что уровень с данной энергией действительно существует. Следовательно атомарные пары натрия будут поглощать фотоны переходить из состояния в состояние .

Правильный ответ: 2

Задание 19 № 4916. На рисунке показана схема низших энергетических уровней атома. В начальный момент времени атом находится в состоянии с энергией . Фотоны какой энергии может излучать атом?

1) только 2 эВ

2) только 2,5 эВ

3) любой, но меньшей 2,5 эВ

4) любой в пределах от 2,5 до 4,5 эВ

Решение.

Правильный ответ: 1

Задание 19 № 4951. На рисунке приведён спектр поглощения неизвестного газа и спектры поглощения атомарных паров известных элементов. По виду спектров можно утверждать, что неизвестный газ содержит атомы

1) азота (N), магния (Mg) и других элементов, но не калия (К)

2) только азота (N) и калия (К)

3) только магния (Mg) и азота (N)

4) магния (Mg), калия (К) и азота (N)

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре поглощения зависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре поглощения паров неизвестного газа присутствуют все линии, которые есть на спектрах магния, калия и азота. Этот факт говорит в пользу того, что в химический состав неизвестного газа входят магний (Mg), калий (К) и азот (N).

Правильный ответ: 4

Задание 19 № 5161. На рисунках А, Б и В приведены спектры излучения паров кальция Са, стронция Sr и неизвестного образца. Можно утверждать, что в неизвестном образце

1) не содержится стронция

2) содержатся кальций и ещё какие-то элементы

3) не содержится кальция

4) содержится только кальций

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре излучения зависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре излучения паров неизвестного газа присутствуют все линии, которые есть на спектре стронция. Этот факт говорит в пользу того, что в химический состав неизвестного газа входит стронций. С другой стороны, линий, характерных для кальция, в неизвестном спектре не наблюдается. Следовательно, неизвестный образец не содержит кальция. Таким образом, верно утверждение 3.

Правильный ответ: 3

Примечание. Можно утверждать, что в неизвестном веществе находится, например, кальций, только в том случае, если все линии кальция содержатся в спектре этого неизвестного вещества.

Задание 19 № 5196. На рисунке приведены спектры поглощения паров натрия, атомарного водорода и атмосферы Солнца.

Об атмосфере Солнца можно утверждать, что в ней

1) не содержится натрия

2) не содержится водорода

3) содержится только натрий и водород

4) содержится и натрий, и водород

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре зависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре атмосферы Солнца присутствуют все линии, которые есть на спектрах натрия водорода. Но помимо этих линий есть еще много других. Этот факт говорит в пользу того, что в химический состав атмосферы Солнца входят натрий, водород и что-то еще. Таким образом, верно утверждение 4.

Правильный ответ: 4

Задание 19 № 5231. На рисунке приведены спектр поглощения разреженных атомарных паров неизвестного вещества и спектры поглощения атомарных паров известных элементов. Проанализировав спектры, можно утверждать, что неизвестное вещество содержит

1) только водород (Н) и гелий (Не)

2) водород (Н), гелий (Не) и натрий (Na)

3) только натрий (Na) и водород (Н)

4) натрий (Na), водород (Н) и другие элементы, но не гелий (Не)

Решение.

На рисунке представлены линейчатые спектры. Главное свойство линейчатого спектра состоит в том, линии какого-либо вещества на спектре зависят только от свойств атомов этого вещества. Из рисунка видно, что на спектре поглощения паров неизвестного газа присутствуют все линии, которые есть на спектре водорода и натрия. Линии, характерные для гелия, отсутствуют. Однако присутствуют линии, соответствующие каким-то другим элементам. Все это говорит в пользу того, что в химический состав неизвестного газа входят натрий (Na), водород (Н) и другие элементы, но не гелий (Не)

Правильный ответ: 4

Задание 19 № 5616.

Схема низших энергетических уровней атома имеет вид, изображённый на рисунке. В начальный момент времени атом находится в состоянии с энергией . Согласно постулатам Бора атом может излучать фотоны с энергией

1) только 0,5 эВ

2) только 1,5 эВ

3) любой, меньшей 0,5 эВ

4) любой в пределах от 0,5 до 2 эВ

Решение.

Согласно постулатам Бора, свет излучается при переходе атома на более низкие уровни энергии, при этом фотоны несут энергию, равную разности энергий начального и конечного состояний. Единственный переход с излучением фотонов возможен на уровень с энергией равной

Правильный ответ указан под номером 2.

Задание 19 № 6090. Бета-частица представляет собой

1) нейтрон

2) электрон

3) ядро гелия

4) ион гелия

Решение.

Бета-частица — это частица с малой массой и зарядом, равным заряду электрона. Такая частица и есть электрон.

Правильный ответ указан под номером: 2.

Задание 19 № 6125. Спектр какого типа наблюдается у излучения атомарного водорода?

1) линейчатый

2) полосатый

3) сплошной

4) ответ зависит от разрешающей силы используемого спектроскопа

Решение.

Атом водорода излучает, когда его электроны переходят с более высоких энергетических уровней на более низкие, в результате чего возникают кванты света с определённой длиной волны, то есть спектр водорода — линейчатый.

Задание 19 № 6160. Спектр какого типа наблюдается у излучения атомарного гелия?

1) линейчатый

2) полосатый

3) сплошной

4) ответ зависит от разрешающей силы используемого спектроскопа

Решение.

Атом гелия излучает, когда его электроны переходят с более высоких энергетических уровней на более низкие, в результате чего возникают кванты света с определённой длиной волны, то есть спектр гелия — линейчатый.

Задание 19 № 6204. В таблице приведены значения энергии для второго и четвёртого энергетических уровней атома водорода.

Номер уровня	Энергия, 10^–19 Дж
2	–5,45
4	–1,36

Какой должна быть энергия фотона, при поглощении которого атом переходит со второго уровня на четвёртый?

1) 4,09·10⁻¹⁹ Дж

2) 1,36·10⁻¹⁹ Дж

3) 5,45·10⁻¹⁹ Дж

4) 6,81·10⁻¹⁹ Дж

Решение.

Для того, чтобы электрон перешёл со второго уровня на четвёртый под действием фотона, энергия фотона должна быть равна разности энергий четвёртого и второго энергетических уровней: −1,36 − (−5,45) = 4,09·10⁻¹⁹ Дж.

Правильный ответ указан под номером: 1.

Задание 19 № 6239. В таблице приведены значения энергии для третьего и четвёртого энергетических уровней атома водорода.

Номер уровня	Энергия, 10^–19 Дж
3	–2,42
4	–1,36

Какой должна быть энергия фотона, при поглощении которого атом переходит с третьего уровня на четвёртый?

1) 2,42·10^–19 Дж

2) 1,06·10^–19 Дж

3) 1,36·10^–19 Дж

4) 3,78·10^–19 Дж

Решение.

Для того, чтобы электрон перешёл с третьего уровня на четвёртый под действием фотона, энергия фотона должна быть равна разности энергий четвёртого и третьего энергетических уровней: −1,36 − (−2,42) = 1,06·10⁻¹⁹ Дж.

Правильный ответ указан под номером: 2.

Задание 19 № 6276. На рисунке приведены спектр поглощения неизвестного газа и спектры поглощения атомарных паров известных элементов. По виду спектров можно утверждать, что неизвестный газ содержит атомы

1) только азота ()

2) азота (), магния () и другого неизвестного вещества

3) только магния ()

4) только магния () и азота ()

Решение.

Сравним спектры атомов и спектры неизвестного газа. Из рисунка видно, что все линии, присутствующие в спектре магния есть и в спектре неизвестного газа. Аналогично для азота. Это означает, что газ содержит, как минимум, атомы магния и азота. Кроме линий магния и азота в спектре неизвестного газа содержатся линии, не принадлежащие ни магнию, ни азоту. Следовательно, присутствуют также атомы неизвестного вещества.

Правильный ответ указан под номером: 2.

Задание 19 № 6312. На рисунке приведены спектр поглощения неизвестного газа и спектры поглощения атомарных паров известных металлов. По виду спектров можно утверждать, что неизвестный газ содержит атомы

1) только стронция ()

2) стронция (), кальция () и другого вещества

3) только стронция () и кальция ()

4) только кальция ()

Решение.

Сравним спектры атомов и спектры неизвестного газа. Из рисунка видно, что все линии, присутствующие в спектре стронция есть и в спектре неизвестного газа. Аналогично для кальция. Это означает, что газ содержит, как минимум, стронция и кальция. Кроме линий стронция и кальция в спектре неизвестного газа содержатся линии, не принадлежащие ни стронцию, ни кальцию. Следовательно, присутствуют также атомы неизвестного вещества.

Правильный ответ указан под номером: 2.

Источник

Тема 29.

Электродинамика. Квантовая физика (Расчетная задача высокого уровня сложности)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

электродинамика. квантовая физика (расчетная задача высокого уровня сложности)

29.01Отражение и преломление

29.02Формула тонкой линзы

29.03Оптические системы

29.04Скорость изображения в различных оптических системах

29.05Волновая оптика

29.06Фотоэффект

29.07Ядерные реакции. Энергия связи

29.08Энергетические уровни в атоме

29.09Квантовая физика

Решаем задачи

Критерии оценки

3 балла ставится за задачу если:

_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: условие наблюдения
максимумов (или минимумов) в интерференционной картине от двух когерентных источников
)

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)

III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).

При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.

В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

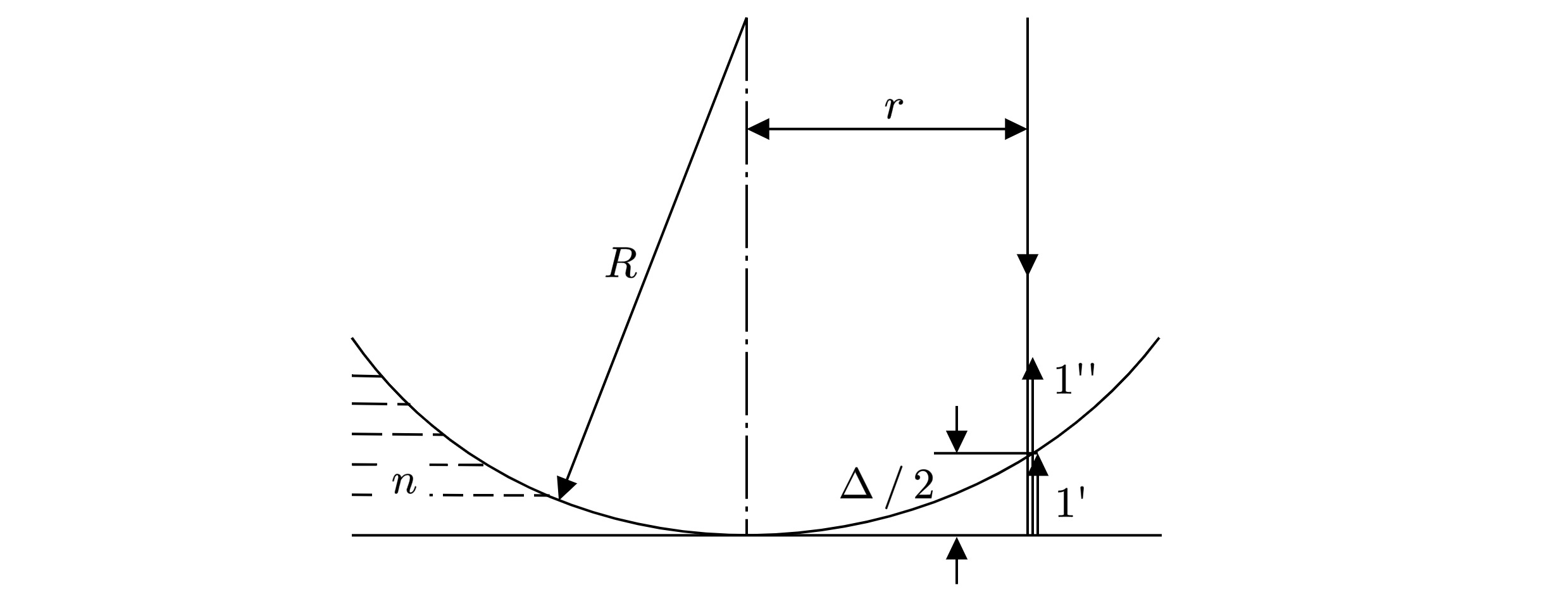
Пусть геометрическая разность хода лучей, идущих на расстоянии от главной оптической оси
линзы (1’ и 1”). 1’ – отражен от верхней поверхности пластины, 1” – отражен от нижней поверхности
пластины (см. рис.).

По теореме Пифагора имеем

Так как разность ходу мала, то 2 2
Δ ∕4 << r и приближенно получаем r2
Δ ≈ R . Поскольку волны 1
и 1’ распространяются в бензоле, заполняющем зазор между линзой и пластинкой, оптическая разность
хода между волнами 1’ и 1” равна

2
Δ опт = n Δ = nr-.
R

Дополнительный фазовый набег, равный , волна 1’ приобретает при отражении волны 1 от
оптически более плотной среды. Таким образом, условие первого интерференционного минимума имеет
вид Δопт + λ-= 3λ
2 2 . Объединяя записанные выражения, получаем

∘ ---- ∘ ----------------
r = λR--= 0,63-мк-м-⋅ 10-м-≈ 2 м м
n 1,5

Критерии оценки

3 балла ставится за задачу если:

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

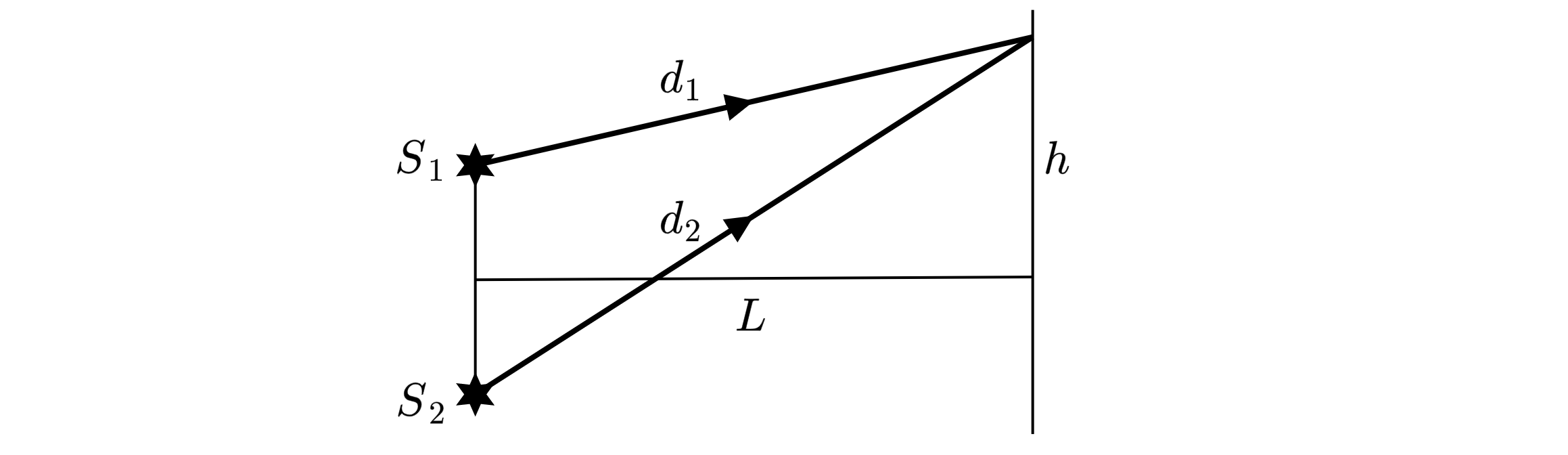
Запишем условие максимума:

где и – расстояния от источников до данной точки на экране (см. рисунок), – целое
число (порядок интерференционного максимума). Для волн первого максимума найдем из
рисунка:

( )2 ( )2
d2= L2 + h − l- , d2 = L2 + h + l- .
1 2 2 2

Вычтем второе из первого

Разложим разность квадратов:

Учитывая, что l < < L , h < < L , можно приближенно положить . Тогда
. Объединяя это равенство с записанным выше условием максимума первого порядка,
получаем

L 3 м
h ≈ λ--= 0,6 ⋅ 10−6 м-------≈ 3,6 мм
l 0,5 мм

Критерии оценки

3 балла ставится за задачу если:

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

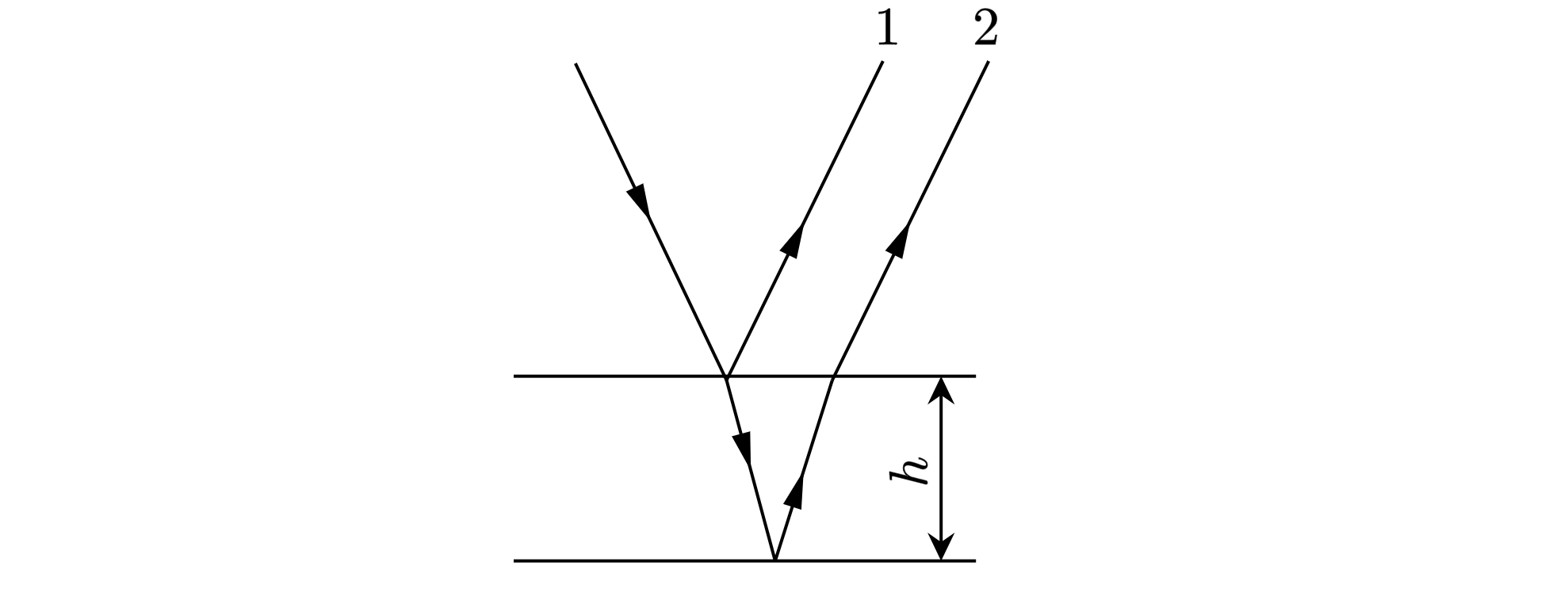
НПокрытие в отраженном свете будет казаться зеленым, если в направлении, в котором проводится
наблюдение, в результате интерференции будут усиливаться волны с длиной , соответствующей
зеленому цвету. Ход двух интерферирующих лучей изображен на рисунке. Луч 1 преломляется в
верхней грани пластины, затем отражается от нижней и вновь, преломившись в верхней пластине
выходит на воздух. Луч 2, падая в точке выхода из пластины луча 1, сразу отражается от верхней части
пластины (см .рис.).

Найдём длину пути первого луча, она составляет 2d1 . При этом из прямоугольного треугольника с
углом :

d d
d1 = ----- = ∘-------2--.
cos β 1 − sin β

По закону Снеллиуса:

sinα- sin-α-
sinβ = n ⇒ sin β = n ,

тогда

2dn
d1 = ∘------------.
n2 − sin2α

Откуда оптическая длина пути:

2dn2
δ1 = 2d1n = ∘------------
n2 − sin2α

Разность хода первого и второго луча до падения на покрытие (см. рисунок) составляет
величину

δ = x sin α.
2

определим из рисунка через tgβ :

x
--= dtgβ ⇒ x = 2dtg β.
2

Отсюда

2
δ = 2dtgβ sin α = 2d-sinβ-⋅ sinα = ∘--2dsin-α----
2 cosβ n2 − sin2 α

Разность хода между интерферирующими лучаи равна:

2 2 ∘ -----------
δ = δ1 − δ2 ∘--2dn------− ∘-2d-sin--α---= 2d n2 − sin2α.
n2 − sin2 α n2 − sin2 α

Амплитуды волн будут складываться, если наблюдается максимум , при этом минимальность
толщины соответствует минимальности , то есть k = 1 и δ = λ . Отсюда получаем, что минимальная
толщина покрытия

λ 0,53 м км
dmin = -∘------------= -∘------------------= 0,2 мкм
2 n2 − sin2α 2 (1,41 )2 − (1∕2 )2

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: сказано в каком случае
наблюдается зеленый цвет, сделан поясняющий рисунок, записан закон Снеллиуса, расписана разность
хода )

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

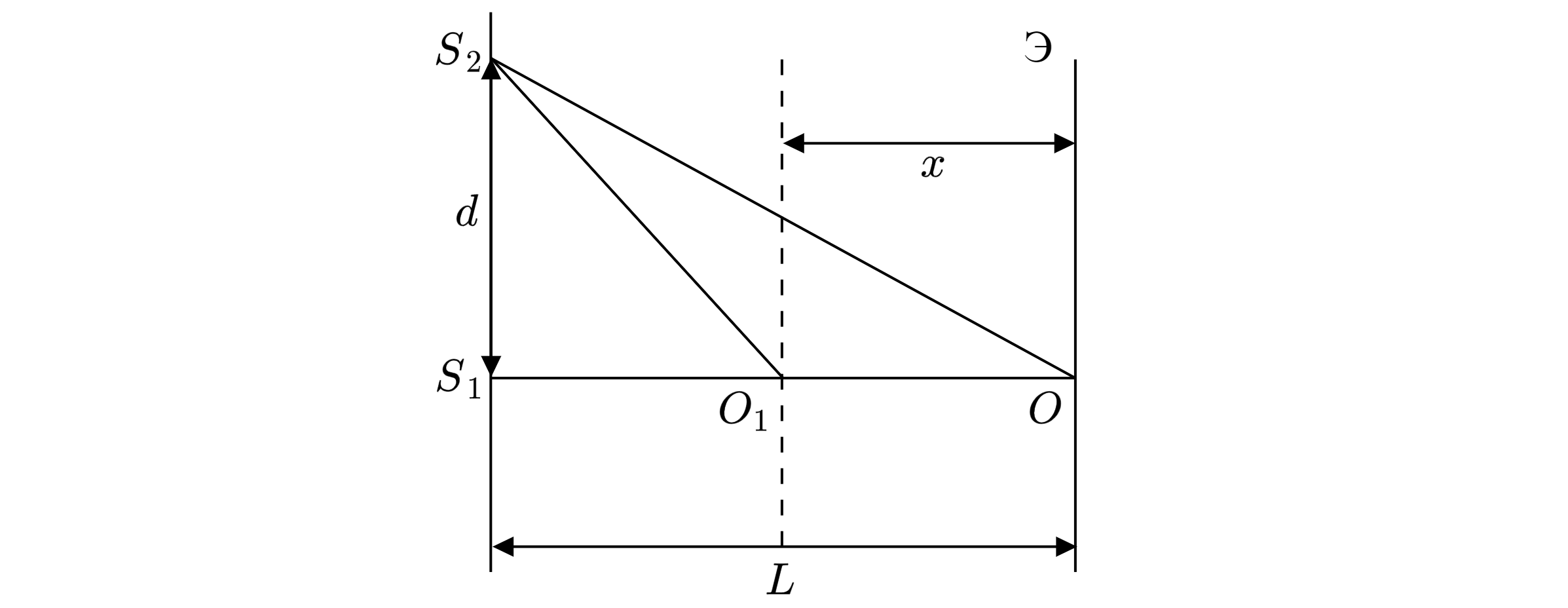
При удалении источника потемнение возникает в точке при условии первого минимума, то
есть при условии:

λ
S2O − S1O = --,
2

где – длина волн.
Из прямоугольного треугольника:

( ∘ ----------- )
√ -------- ( )2
L2 + d2 − L = λ-⇒ L ( 1 + -d − 1) = λ-
2 L 2

Так как d < < L , то можно считать малой величиной и

2 2
-d- = λ--⇒ d2 = L λ. (1)
2L 2

При приближении экрана на , то второй минимум в точке будет соответствовать разности
хода

3-
S2O1 − S1O1 = 2 λ,

или

( ∘ ----(-------)2- )
∘ -------2----2- 3- ( --d--- ) 3-
(L − x) + d − (L − x) = 2 λ ⇒ (L − x) 1 + L − x − 1 = 2λ

Аналогично

---d2---- 3- 2
2(L − x) = 2λ ⇒ d = 3(L − x )λ. (2 )

Приравнивая (1) и (2), получаем:

2 2
Lλ = 3(L − x)λ ⇒ x = --L = -⋅ 9 м = 6 м
3 3

Критерии оценки

3 балла ставится за задачу если:

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

Ослабление отраженного света достигается за счет взаимного ослабления при интерференции двух
световых волн (см. рисунок): отраженной от внешней границы пленки и от границы пленка-стекло.

при отражении от более оптически плотной среды происходит потеря полуволны, а с
учетом того, что 1 < n < n
п с , где n
п – показатель преломления пленки, n
с – показатель
преломления стекла, то каждый луч при отражении теряет пол полны, и условие минимума не
меняется.
Запишем условие минимума для лучей, отраженный от поверхности плёнки и поверхности
стекла:

2k + 1
2hn п = -------λ
2

Отсюда:

h = 2k-+-1-λ.
4n п

Так как необходимо погасить обе волны, то

2k1 +-1λ1 = 2k2-+-1-λ2,
2 2

Отсюда

k1 +-0,5- λ2-
k2 + 0,5 = λ1 = 0,6.

Для минимальности толщины плёнки необходима минимальность , найдем минимальные значения
и

Отсюда k1 = 1 , k2 = 2 и остается найти :

Два когерентных световых пучка падают на экран: один пучок по нормали, а другой – под углом
рад. Найти период интерференционной картины, т.е. расстояние между соседними
светлыми полосами на экране, если длина световой волны в обоих пучках равна
мкм.

ВМК МГУ

Показать ответ и решение

На рисунке изображены волновые фронты двух пучков – падающего на экран нормально (AB) и
падающего на экран наклонно (AC).

Пусть в некоторой точке A наблюдается один из максимумов интерференционной картины. Это
означает, что фазы обеих световых волн в этой точке совпадают. Соседний максимум интенсивности
находится в точке B, для которой также выполняется условие равенства фаз обеих волн. Это
имеет место, если расстояние между точками B и C равно длине световой волны . Из
треугольника ABC имеем Учитывая, что () получаем λ
d = --= 50
α
мкм

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: рассмотрен ход лучей и сказано
что расстояние между двумя точками равно длине волны )

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

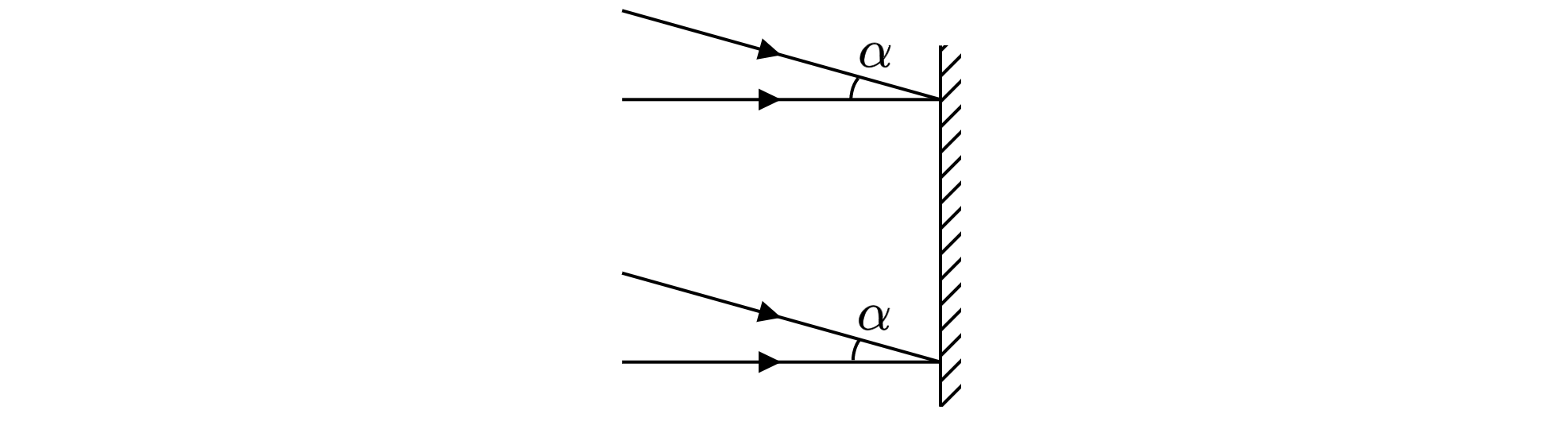
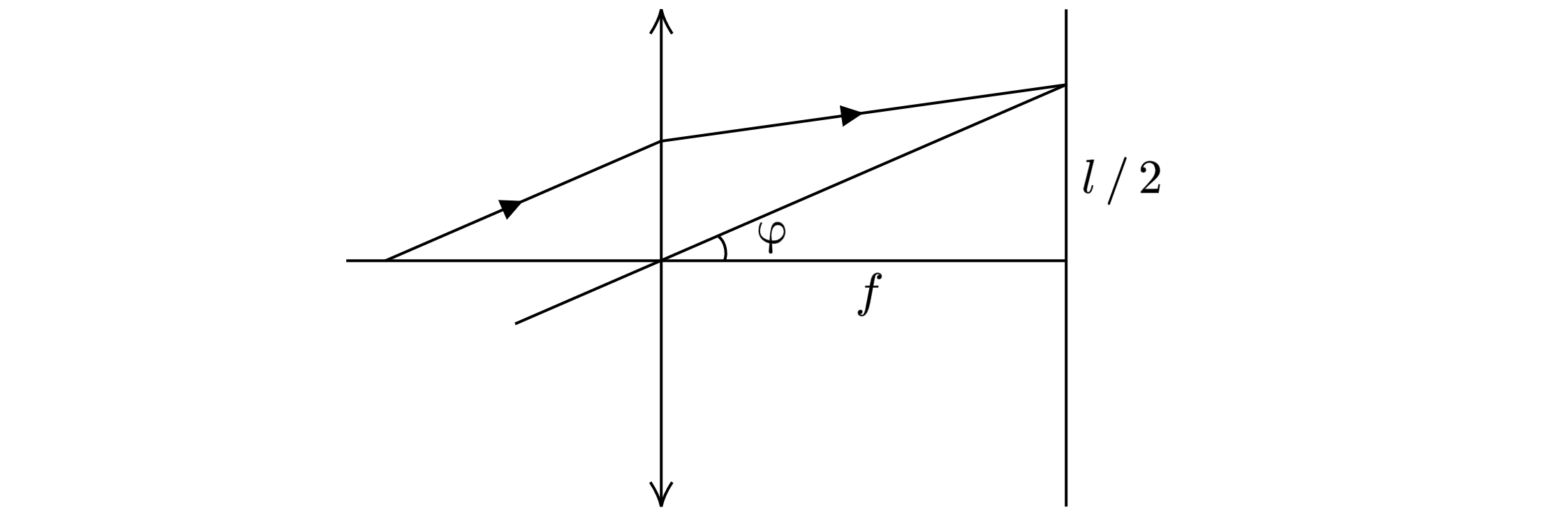
С помощью установки, схема которой показана на рисунке, наблюдают дифракцию параллельного пучка
белого света на дифракционной решетке Д, расположенной перпендикулярно оси пучка. При этом на
экране Э, установленном в фокальной плоскости тонкой собирающей линзы Л, видны две светлые
полосы, вызванные наложением спектральных компонент с длинами волн нм и
нм. Эти полосы расположены симметрично относительно главной оптической
оси линзы на расстоянии l = 30 см друг от друга. Найдите минимальный период решетки
dmin , при котором наблюдается эта картина, если фокусное расстояние линзы f = 20
см

ВМК МГУ

Показать ответ и решение

Введем величины: — период дифракционной решетки, — длина волны лучей, — угол
отклонения лучей, – порядок спектра. Запишем уравнение дифракционной решётки:

Чтобы волны наложились друг на друга должно выполняться условие:

Значит

λ2-= k1-= 1,25.
λ1 k2

Найдём минимальные значения k
1 и k
2 . Это k = 5
1 , k = 4
2 . Следовательно,

k λ k λ
d = --1-1 = -2-2.
sin φ sin φ

Из рисунка видно, что

l- -l-
2 = ftgφ ⇒ tgφ = 2f .

Используя формулу ---tgφ----
sin φ = √1--+-tgφ- , получаем, что

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записано уравнение
дифркционной решётки )

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

На рисунке представлена схема получения интерференции света с помощью плоского зеркала.
Центральный интерференционный максимум наблюдается в точке О экрана. Расстояние от источника S
до зеркала равно А, длина волны источника нм. Луч 1 идет параллельно зеркалу и попадает в
точку А экрана, где наблюдается второй интерференционный минимум. Чему равно расстояние А в этом
опыте?

Показать ответ и решение

Для наблюдения второго минимума необходима разность хода, равная

3-
Δl = 2 λ.

Первый луч проходит:

l1 = l.

Второй луч проходит две гипотенузы прямоугольного треугольника:

∘ --------
l2
L1 = 2 h2 + --
4

При этом при отражении от более оптически плотной среды происходит потеря полуволны,
значит:

∘ ------2-
l2 = 2 h2 + l-− λ.
4 2

Отсюда:

∘ --------
3 l2 λ
Δl = l2 − l1 = -λ = 2 h2 + -- − --− l.
2 4 2

Отсюда:

∘ ------2-
2 h2 + l-= 2λ + l
4

Возводим в квадрат

При этом 2
λ < < λ ⋅ l , значит, при вычислении можем пренебречь 2
λ и окончательно
получим:

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: сказано чему равна разность
хода, учтена потеря полуволны)

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

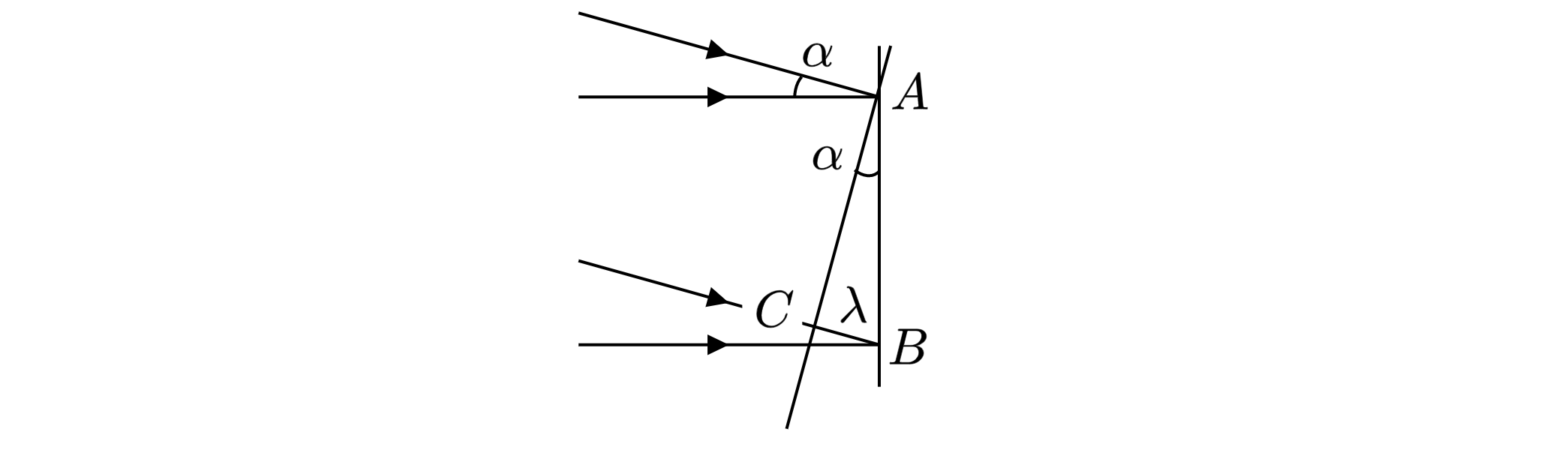
Показать ответ и решение

Углы, определяющие направления на дифракционные максимумы, при нормальном падении пучка на
решетку удовлетворяют условию где — длина волны света, m = 3 .

Импульс фотона связан с его длиной волны соотношением p = h-
λ где — постоянная Планка.
Из записанных соотношений находим:

m λ mh dpsinφ
sin φ = ----= ---- ⇒ m = --------
d pd h

Или

−6 −27
2 ⋅ 10--м-⋅ 1,32-⋅ 10--кг ⋅-м/c-⋅ 0,5
m = 6,6 ⋅ 10−34 Д ж⋅ с = 2

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула дифракционной
решётки, форула импульса фотона )

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записано условие дифракции
первого максимума )

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Волна красного света проходит через тонкую прозрачную пленку с показателем преломления 1,8.
Толщина пленки − 5
3,8 ⋅ 10 м. Определите, сколько раз длина волны света в пленке укладывается на ее
толщине, если длина волны в вакууме 720 нм. Волна падает на пленку перпендикулярно ее
плоскости.
Черноуцан

Показать ответ и решение

По закону преломления:

c-
v = n,

где – скорость света в среде, – показатель преломления среды.
Частота волны при переходе из одной среды в другую не изменяется, следовательно

где – длина волны в вакууме, – длина волны в среде.
Тогда

ν λ1 λ1
---- = n ⇒ λ2 = ---
ν λ2 n

На толщине будет укладываться

dn
N = ---= 95
λ1

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записан закон преломления
)

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

На дифракционную решетку перпендикулярно ее плоскости падает свет с длиной волны 500 нм. Сколько
штрихов на 1 мм должна иметь решетка, чтобы пятый главный максимум в дифракционной картине
находился под углом 90∘ по отношению к падающему свету?
Черонуцан

Показать ответ и решение

По формуле дифракционной решетки:

где – порядок максимума, – постоянная решетки, – длина волны решётки, –
направление на й максимум.
По условию k = 5 , , откуда:

Тогда количество штрихов на l = 1 мм:

N = l-= -1-м-м--= 400
d 2500 нм

Критерии оценки

Критерии проверки

3 балла ставится за задачу если:

_________________________________________________________________________________________________________________
Приведено полное решение включающее следующие элементы: I) Записаны положения теории и
физические законы, закономерности, применение которых необходимо для решения задачи выбранным
способом (в данном случае: формула условия наблюдения главных максимумов при нормальном падении
света на дифракционную решетку, формула расчета числа штрихов, приходящихся на единицу длины
решетки)

II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

_________________________________________________________________________________________________________________

Верно записаны все положения теории, физические законы, закономерности, и проведены
необходимые преобразования, но имеются один или несколько из следующих недостатков:

I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.

II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)

III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.

IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Монохроматический свет с частотой Гц распространяется в пластинке,прозрачной для
этого света и имеющей показатель преломления 1,6. Чему равна длина волны этого света в
пластинке?
Черноуцан

Показать ответ и решение

Показатель преломления данной среды относительно вакуума называется абсолютным показателем
преломления данной среды , его можно определить как отношение скорости света в вакууме , к
скорости света в данной среде

c
n = --
v

Откуда:

c
v = -- (1)
n

По формуле скорость света в среде равна

где – длина волны, – частота света.
Приравняв (1) и (2), получим

c c
--= λν ⇒ λ = ---
n n ν

Подставим числа из условий:

8
λ = ---3-⋅ 10-м/с-----= 125 нм
1,6 ⋅ 1,5 ⋅ 1015 Г ц

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула
нахождения показателя преломления, записана формула нахождения скорости волны в среде
)

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Показать ответ и решение

m λ mh 3 ⋅ 6,6 ⋅ 10− 34
sin φ = ---- = ----= -----−6----------−27-= 0,75
d pd 2 ⋅ 10 ⋅ 1,32 ⋅ 10

Следовательно,

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана формула
дифракционной решётки, записана формула импульса фотона )

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Определите постоянную дифракционной решетки, если при нормальном падении света на решетку
зеленая линия спектра лампы (длина волны 550 нм) наблюдается в пятом порядке под углом
30∘ .

Показать ответ и решение

Формула для дифракционной решетки:

– постоянная дифракционной решетки, – порядок дифракционного максимума, –
длина волны, – угол наблюдения данного максимума. Максимальный синус равен 1,
следовательно:

− 9
d = -m-λ- = 5-⋅ 550-⋅ 10-м- = 5500 н м
sin α 1∕2

Критерии оценки

3 балла ставится за задачу если:

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

При исследовании спектра ртути с помощью дифракционной решётки и гониометра (прибора для
точного измерения углов дифракции света) было обнаружено, что в спектре 3-го порядка вблизи
двойной жёлтой линии ртути со средней длиной волны λ = 578
1 нм видна сине-фиолетовая линия 4-го
порядка. Оцените её длину волны .

Показать ответ и решение

Формула для дифракционной решетки:

– период дифракционной решетки, – порядок дифракционного максимума, –
длина волны, – угол наблюдения данного максимума. Максимальный синус равен 1,
следовательно:

m3λ1-- 3-⋅ 578-нм
λ2 = m4 = 4 = 434 нм

Критерии оценки

3 балла ставится за задачу если:

I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записана фомрула
дифракционной решётки )

IV) Представлен правильный ответ с указанием единиц измерения искомой величины.

2 балла ставится за задачу если:

Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.

При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Источник

За это задание ты можешь получить 2 балла.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.

1) В осях P(V) работу газа можно найти, если умножить давление на объем

2) Реостат — прибор переменного сопротивления

3) При равномерном движении тела его вес всегда равен силе тяжести

4) Работа тепловой машины А=Qн-Qх

5) Если энергия фотона меньше работы выхода электрона из вещества, то фотоэффект ПРОИСХОДИТ

Решение

1) Неверно, как площадь под графиком

2) Верно

3) Верно

4) Верно

5) Неверно

Ответ: 234

Задача 2

1) Закон электромагнитной индукции Фарадея E=I*R

2) Если сломать полосовой магнит пополам, то он потеряет свои свойства

3) 1 Ват = 1 Дж/1 c

4) Пробой конденсатора — это разрыв всей цепи

5) Скалярная величина не имеет направления

Решение

1) Неверно, E=dФ/dt

2) Неверно

3) Верно

4) Неверно, если случился пробой конденсатора, значит ток может идти через него, как по обычному проводнику

5) Верно

Ответ: 35

Задача 3

1) Электрический ток создает магнитное поле

2) Гигрометр — прибор для измерения давления

3) Электрон не может выбиваться под воздействием падающего света

4) Сила Лоренца не действует на заряженные частицы

5) Атомная масса — есть число нуклонов

Решение

1) Электрический ток создает магнитное поле — верно

2) Гигрометр — прибор для измерения давления — неверно, он измеряет влажность

3) Электрон не может выбиваться под воздействием падающего света — неверно, такое может происходить при фотоэффекте

4) Сила Лоренца не действует на заряженные частицы — неверно, она не действует не нейтральные частицы, а на заряженные действует

5) Атомная масса — есть число нуклонов — верно, нуклоны — это протоны и нейтроны вместе

Ответ: 15

Задача 4

1) При движении по окружности линейная скорость направлена по касательной к траектории

2) Внутренняя энергия идеального газа – есть среднее значение кинетических энергий всех его молекул

3) Проводник с током создаёт вокруг себя однородное магнитное поле

4) Красной границей фотоэффекта называется минимальная частота (или максимальная длина волны) излучения, фотоны которого способны выбивать электроны.

5) Частота света определяется источником и не зависит от того, в какой среде свет распространяется.

Решение

1) Верно

2) Неверно. Внутренняя энергия идеального газа – есть сумма кинетических энергий всех его молекул

3) Неверно, магнитное поле вокруг прямого проводника представляется линиями в виде колец, густота которых уменьшается по мере удаления от проводника

4) Верно

5) Верно

Ответ: 145

Задача 5

1) По 3 закону Ньютона вес бруска, лежащего на столе, и сила реакции опоры стола равны по модулю и противоположны по направлению

2) Адиабатный процесс – процесс, происходящий при постоянной температуре

3) Электроны и протоны являются свободными носителями электрического заряда, их упорядоченное движение образует электрический ток

4) При помещении проводника в электрическое поле, напряженность электрического поля внутри него равна нулю

5) Отраженный от границы раздела двух сред луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела в точке падения

Решение

1) Верно

2) Неверно

3) Неверно, протоны не могут быть носителями тока, так как они находятся в составе ядра и не могут покидать его пределы.

4) Верно, под действием внешнего электрического поля в проводнике происходит перераспределение зарядов, что вызывает внутреннее электрическое поле, которое компенсирует внешнее

5) Верно, согласно закону отражения

Ответ: 145

Задача 6

1) На заряженную частицу в магнитном поле действует сила Лоренца

2) При переходе из воздуха в стекло скорость света уменьшается

3) Жёсткость пружины зависит от силы, с которой растягивают пружину

4) Сила Архимеда, действующая на тело в жидкости, не зависит от плотности жидкости

5) Согласно первому закону термодинамики, количество теплоты, полученное газом, всегда полностью идёт на изменение его внутренней энергии

Решение

1) На заряженную частицу в магнитном поле действует сила Лоренца — верно (не путать с силой Кулона!)

2) При переходе из воздуха в стекло скорость света уменьшается — верно. Оптическая плотность стекла отличается от оптической плотности воздуха, поэтому скорость света уменьшается (увеличиться она не может, так как не может быть скорости большей, чем скорость света в вакууме или в воздухе)

3) Жёсткость пружины зависит от силы, с которой растягивают пружину — неверно. Жесткость является постоянной характеристикой пружины и не меняется при её растяжении или сжатии.

4) Сила Архимеда, действующая на тело в жидкости, не зависит от плотности жидкости — неверно. $F_A=ρ_жgV$, где $ρ_ж$ — плотность жидкости, V — объём погружённой в жидкость части тела

5) Согласно первому закону термодинамики, количество теплоты, полученное газом, всегда полностью идёт на изменение его внутренней энергии — неверно, по первому закону термодинамики часть полученной теплоты может уходить ещё и на совершение работы. (Количество теплоты полностью переходит во внутреннюю энергию только в изохорных процессах, когда работа равна нулю)

Ответ: 12

Задача 7

1) Электроёмкость плоского конденсатора не зависит от вещества, которым заполнено пространство между его обкладками

2) При свободном полёте под углом к горизонту тело движется с ускорением свободного падения

3) Заряженная частица, влетевшая в магнитное поле перпендикулярно линиям поля движется по окружности

4) Согласно первому закону термодинамики, количество теплоты, полученное газом, идёт на изменение его внутренней энергии и совершение газом работы

5) Удлинение пружины обратно пропорционально силе, с которой растягивают пружину

Решение

1) Электроёмкость плоского конденсатора не зависит от вещества, которым заполнено пространство между его обкладками — неверно: $C={εε_0S}/d$, где $ε$ — относительная диэлектрическая проницаемость вещества, которым заполнено пространство между обкладками конденсатора.

2) При свободном полёте под углом к горизонту тело движется с ускорением свободного падения — верно, так как на тело в свободном полёте действует только сила тяжести, она задаёт телу ускорение: $F_{тяж}=ma$, $ $ $mg=ma$, $ $ $a=g$.

3) Заряженная частица, влетевшая в магнитное поле перпендикулярно линиям поля движется по дуге окружности — верно. Сила Лоренца меняет направление скорости заряженной частицы, задаёт ей центростремительное ускорение, и частица движется по дуге окружности (или просто по окружности, если места хватает)

4) Согласно первому закону термодинамики, количество теплоты, полученное газом, идёт на изменение его внутренней энергии и совершение газом работы — это первый закон термодинамики — верно.

5) Согласно закону Гука проекция силы упругости $F_x=-kx$, где x — деформация пружины. Значит удлинение пружины прямо пропорционально силе, с которой растягивают пружину, а не обратно пропорционально — 5 — неверно.

Ответ: 234

Задача 8

1) При полёте под углом к горизонту проекция скорости на горизонтальную ось пропорциональна времени полёта

2) Расширяясь, газ совершает положительную работу.

3) Системы отсчёта, в которых тело движется равномерно и прямолинейно, если на него не действуют никакие силы или их действие скомпенсировано, называются инерциальными

4) Скорость распространения радиоволн равна скорости света

5) Фокусное расстояние линзы — это точка на главной оптической оси линзы, в которой всегда располагается изображение предмета

Решение

1) При полёте под углом к горизонту проекция скорости на горизонтальную ось пропорциональна времени полёта — неверно. Горизонтальная проекция скорости не зависит от времени: $v_x=v_0cosα$, где α — угол между начальной скоростью и горизонтальной осью

2) Расширяясь, газ совершает положительную работу — верно

3) Системы отсчёта, в которых тело движется равномерно и прямолинейно, если на него не действуют никакие силы или их действие скомпенсировано, называются инерциальными — это первый закон Ньютона, верно

4) Скорость распространения радиоволн равна скорости света — верно. Радиоволны и свет — это электромагнитные волны, все они распространяются с одинаковой скоростью, значение которой в вакууме: $c=3·10^8$ м/с

5) Фокусное расстояние линзы — это точка на главной оптической оси линзы, в которой всегда располагается изображение предмета — неверно. Расположение изображения предмета зависит от расположения самого предмета и не обязательно будет находиться в фокусе. Фокус — это точка, в которой после преломления пересекаются лучи, которые до преломления в линзе были параллельны главной оптической оси.

Ответ: 234

Задача 9

1) Потенциальная энергия тела зависит только от его массы

2) Среднеквадратичная скорость теплового движения молекул газа пропорциональна квадратному корню из температуры

3) При параллельном подключении резисторов, напряжение на каждом резисторе пропорционально его сопротивлению

4) При протекании фотэффекта сила фототока насыщения пропорциональна интенсивности света, падающего на фотокатод.

5) При электронном бета-распаде ядра количество нуклонов в ядре не меняется.

Решение

1) Потенциальная энергия тела зависит НЕ только от его массы. (1 — неверно)

2) Среднеквадратичная скорость теплового движения молекул газа пропорциональна квадратному корню из температуры:

$E=3/2kT$, ${mv^2}/2=3/2kT$, $v=√{{3kT}/m}$. (2 — верно)

3) При параллельном подключении резисторов, напряжение на них одинаковое. (3 — неверно)

4) Согласно закону фотоэффекта, сила фототока насыщения пропорциональна интенсивности света, падающего на фотокатод. Увеличение интенсивности означает увеличение числа фотонов, а значит будет больше и число выбиваемых из катода фотоэлектронов, поэтому сила тока возрастает. (4 — верно)

5) При электронном бета-распаде ядра количество нуклонов в ядре не меняется, так как не меняется массовое число. Меняется лишь заряд ядра, что вызвано превращением нейтрона в протон. (5 — верно)

Ответ: 245

Предисловие

В 2017 году астрономия вернулась в общеобразовательные школы в качестве
обязательного предмета в 10-11 классах, и в программу ЕГЭ по физике с 2018 года
ввели одно задание (№24) по тематике астрономии и астрофизики, которое
оценивается в 2 балла. Суть заданий заключается в том, что используя информацию
из таблицы, необходимо выбрать из пяти предложенных вариантов ответов два
верных.

Условно все задания по астрономии можно разделить на 4-е типа:

• о звездах.

• о планетах Солнечной системы

• о спутниках планет Солнечной системы.

• о различных объектах Солнечной системы: астероид, комета и т.д.

В данном методическом пособии мною проведён разбор всех типов задач, с
подробными комментариями по поводу правильного выбора варианта ответов. Кроме
того, для восстановления в памяти основной сути вопроса перед каждым типом
заданий, в мини формате излагается теоретический материал.

Далее предлагаются аналогичные задания для самостоятельного решения,
выполнение этих заданий играет ведущую роль при подготовке к экзамену.

Все задания в пособии взяты из сборника: « ЕГЭ. Физика», под редакцией
М.Ю. Демидовой, которые соответствуют проекту демоверсии ЕГЭ 2020 года.

Настоящее пособие рекомендую для учеников 10 и 11 классов и их
педагогов, желающих качественно подготовиться к решению задач астрофизической
тематики в ЕГЭ по физике.

Методические рекомендации при работе с пособием:

Все задания №24 из ЕГЭ по физике разбиты на основные типы, по каждому
из которых изложен теоретический материал, проведен анализ таблицы или
диаграммы, сопровождающей задание. После этого приводится выполнение задания с
пояснениями и комментариями.

Для закрепления материала предлагается выполнить несколько заданий
самостоятельно. Ответы к заданиям, для самопроверки прилагаются в пособии.

Тема 1.
Звезды. Диаграмма Герцшпрунга-Рассела

Теоретический
материал.

Звезда – массивный газовый шар,
излучающий свет и удерживаемый в состоянии равновесия силами собственной
гравитации и внутренним давлением, в недрах которого происходят (или
происходили ранее) реакции термоядерного синтеза. Диаграмма Герцшпрунга –
Рассела показывает зависимость между абсолютной звёздной
величиной, светимостью, спектральным классом и температурой поверхности звезды.
Звёзды на этой диаграмме образуют хорошо различимые участки, 4 особые зоны (
см.рис.): главная последовательность, белые карлики, гиганты и сверхгиганты. Это
классы звезд по их размерам.

Основная часть звезд Вселенной, более 90%, относятся к главной
последовательности.

Мы можем увидеть, что большинство таких звезд имеют размеры большие,
чем 0,1 диаметра Солнца и не превышают 10 солнечных диаметров (условное
обозначение Солнца — ʘ):

0,1𝐷ʘ < 𝑫г.п. < 10𝐷ʘ.

Следующая область – звезды гиганты.

Их размеры больше звезд главной последовательности. Из диаграммы мы
видим, что диаметр гигантов может быть от 10 до 100 солнечных диаметров:

10𝐷ʘ < 𝑫г. < 100𝐷ʘ

Самые
большие звезды нашей Вселенной – это сверхгиганты. Их размеры превышают
100 солнечных диаметров:

𝑫𝒄.г. > 100𝐷ʘ.

В нижней части диаграммы располагается область белых
карликов. Они имеют достаточно малые размеры:

0,001𝐷ʘ < 𝑫б.к. < 0,1𝐷ʘ.

Поэтому, чтобы определить принадлежность звезды к тому
или иному классу, необходимо ее размеры сравнить с размерами Солнца.

В нижней части диаграммы указаны основные спектральные классы звезд
– классы звёзд по спектру излучения, в первую очередь, по температуре их
поверхности: O, B, A, F, G, K, M. О том, к какому спектральному
классу относится та или иная звезда, будем судить о температуре ее поверхности:

Класс O – самый
высокий класс в иерархии, а класс M – самый низкий. Чем выше класс,
иерархии, тем звезды горячее, больше, ярче. А чем ниже класс, тем,
соответственно они холоднее,

Вопрос, про
плотность: чем больше звезда, тем более она разряжена.

Название
спектральных классов можно запомнить, если выучить простую считалку: «Один(O)
бритый(B) англичанин(A) финики(F) жевал(G) как(K) морковь(M)». Кратко о
Солнце, звезде нашей Солнечной системы. Оно относится к звездам G – класса, так
как имеет температуру 5800 градусов Кельвина. Это соответствует желтому цвету.
Все звезды, которые будут иметь температуру выше, будут относиться к классам F,
A, B, O, а те, что ниже – к классам K, M.

Размеры белых
карликов
невелики, однако это достаточно массивные звезды, значит, они имеют большую
плотность. Это наибольшая плотность среди всех классов звезд. Сверхгиганты
при таких же или еще меньших массах очень большие звезды. Таким образом, их
плотность будет наименьшей. 𝜌с.г. ≪ 𝜌г.п. ≪ 𝜌б.к.

Из диаграммы
Герцшрунга-Рассела также можно сделать вывод о длительности «жизненного цикла»
звезды. Чем выше ее температура, тем меньше времени «проживет» звезда. И
наоборот, «жизненный цикл» звезды тем больше, чем ее температура ниже.

Слева на
диаграмме отображается светимость звезд. Светимость – это физическая
величина, равная энергии, излучаемой с поверхности звезды за 1 с.

Справа указана абсолютная
звездная величина. Это еще одна энергетическая характеристика звезды.

Анализ диаграммы, показывает, что

Ø
большая
часть звёзд, в том числе и Солнце, лежит на диаграмме так называемой Главной
последовательности.

Ø
отдельно
выделяются группы звёзд, образующие области красных гигантов и сверхгигантов
(правый верхний угол)

Ø
белых
карликов (внизу).

Ø
звёзды
правой нижней части Главной последовательности обычно называются красными
карликами

Ø
звёзды
левой верхней части – голубыми гигантами.

В течение своего жизненного
цикла звезда перемещается по диаграмме Герцшпрунга – Рессела по сложным
траекториям.

Для звёзд главной
последовательности также работает правило – чем горячее звезда, тем быстрее она
эволюционирует (поскольку горячие звёзды главной последовательности более
массивны, чем холодные).

На земном небе
звёзды образуют созвездия – характерные фигуры, известные астрономам ещё с
древних времён. Созвездия – исключительно видимые объединения звёзд – звёзды
одного созвездия обычно никак не связаны друг с другом и могут находиться на
колоссальных расстояниях одна от другой. Исключения составляют так называемые
двойные и кратные системы из нескольких звёзд, связанных между собой
гравитационными силами (например, система альфа Центавра состоит из трёх
звёзд).

Практические задания. Звезды. Диаграмма
Герцшпрунга-Рассела (ч.1)

Рассмотрим утверждения по порядку и
проанализируем их на правильность.

1.
«Жизненный цикл» звезды
спектрального класса G главной последовательности более длительный, чем звезды
спектрального класса В главной последовательности.

Решение: Чем холоднее звезда главной
последовательности, тем больше у неё продолжительность жизненного цикла.

Утверждение верно.

2.
Звезда Денеб, радиус
которой в 210 раз превышает радиус Солнца, относится к звездам главной
последовательности.

Решение: Денеб является сверхгигантом, так
как его радиус превышает радиус Солнца в 210 раз

Утверждение неверно.

3.
Средняя плотность гигантов
существенно больше средней плотности белых карликов.

Решение Характерный диаметр звезды гиганта
примерно в 1000 раз больше, чем характерный диаметр белого карлика (см.
диаграмму), то есть их объёмы отличаются в 1012 раз. А их массы не могут
отличаться более чем в несколько тысяч раз. Соответственно, средняя плотность
гигантов во много раз меньше средней плотности белых карликов.

Утверждение неверно.

4.
Чем выше светимость
звезды, тем больше абсолютная звездная величина. Решение: согласно
диаграмме спектр –светимости, зависимость обратная, т.е чем выше светимость
звезды, тем меньше ее абсолютная звездная величина.

Утверждение неверно.

5.
Для главной
последовательности светимость звезд спектрального класса О выше светимости
спектрального класса G.

Утверждение верное, видно из анализа
диаграммы.

Ответ: 15

1.
«Жизненный цикл» звезды
спектрального класса В главной последовательности более длительный, чем звезды
спектрального класса М главной последовательности.

Решение: Чем холоднее звезда главной
последовательности, тем больше у неё продолжительность жизненного цикла. В
данном случае более холодная звезда класса М, поэтому у нее более длительный
«жизненный цикл»

Утверждение неверно.

2.
Звезда Денеб относится к
сверхгигантам, спектрального
класса А, так как имеет температуру поверхности 8550 К, а ее радиус превышает
радиус Солнца в 210 раз.

Решение: так как к спектральному
классу А, согласно диаграмме соответствуют звезды с температурой от
7000 до 9000К.

Утверждение верно.

3.
Средняя плотность гигантов
существенно меньше средней плотности белых карликов.

Решение Характерный диаметр звезды гиганта
примерно в 1000 раз больше, чем характерный диаметр белого карлика (см.
диаграмму), то есть их объёмы отличаются. А вот массы отличаются
незначительно.. Соответственно, средняя плотность гигантов во много раз меньше
средней плотности белых карликов.

Утверждение верно.

4.
Чем больше абсолютная
звездная величина, тем выше светимость звезды.

Решение: согласно диаграмме спектр –
светимость, зависимость обратная, т.е чем выше светимость звезды, тем меньше ее
абсолютная звездная величина.

Утверждение неверно.

5.
Для главной последовательности светимость звезд, спектрального класса В
меньше светимости звезд спектрального класса К.

Решение:. Чем выше класс, то есть
в данном случае В, тем звезды горячее, больше и ярче.

Утверждение неверно.

Ответ: 23

1.
Радиус Звезды Бетельгейзе
почти в 1000 раз превышает радиус Солнца, а значит она относится к звездам
главной последовательности.

Решение: Звезда будет относиться к классу
звезд главной последовательности, если ее диаметр 0,1𝐷ʘ < 𝑫г.п. < 10𝐷ʘ, в данном случае условие не выполняется. Радиус
звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, значит она
сверхгигант.

Утверждение неверно.

2.
Плотность белых карликов
существенно выше средней плотности гигантов. Решение: Мы установили, что 𝜌с.г. ≪ 𝜌г.п. ≪
𝜌б.к.. Значит, плотность белых карликов,
существенно больше средней плотности гигантов.

Утверждение верно.

3.
«Жизненный цикл» звезды
спектрального класса О главной последовательности более длительный, чем звезды
спектрального класса F главной последовательности.

Решение: Для того чтобы сравнить длительности
жизненных циклов двух звезд, требуется сравнить их температуры. Звезды
спектрального класса O имеют среднюю температуру поверхности 𝑇 ≈ 40 000 К, а спектрального класса F – 𝑇 ≈ 7 000 К. <,
значит, «жизненный цикл» звезд спектрального класса O более
короткий.

Утверждение неверно.

4.
Температура поверхности
звёзд спектрального класса А выше температуры поверхности звёзд спектрального
класса G.

Решение: Запишем и сравним средние температуры
поверхности звезд, соответствующие спектральным классам G и A: ≈
9000К, ≈
5500 К. Видим, что <.

Утверждение верно.

5.
Звёзды спектрального
класса А имеют температуру поверхности не выше 5000К.

Решение: Запишем температуру поверхности
звезды соответствующие спектральным классам A: ≈
9000К,т.е она выше 5000К.

Утверждение неверно.

Ответ: 24

Задания для самостоятельного решения.

Задача№1

Тема 2. Звезды.
Диаграмма Герцшпрунга-Рассела (часть 2)

Теоретический
материал.

Отличие этого
задания от предыдущего состоит в том, что теперь диаграмма Герцшпрунга-Рассела
отсутствует перед вашими глазами. Однако чтобы его выполнить, нужно помнить все
те же соотношения и выводы.

Еще раз коротко
опишем основной теоретический материал.

1.
Температура
поверхности звезды позволяет нам судить о ее принадлежности к тому или иному
спектральному классу. Основные спектральные классы и соответствующие им
температуры и цвета представлены в таблице ( см.выше)

2.
Зная
радиус звезды (он представлен в радиусах Солнца), можно определить к какому
классу по размеру на диаграмме Герцшпрунга-Рассела эта звезда относится:
звездам главной последовательности, гигантам, сверхгигантам или белым карликам.
Напомню эти соотношения:

а) звезды главной последовательности 0,1𝑅ʘ < 𝑹г.п. < 10𝑅ʘ;

б) гиганты 10𝑅ʘ < 𝑹г. < 100𝑅ʘ;

в) сверхгиганты 𝑹𝒄.г. > 100𝑅ʘ;

г) белые карлики 0,001𝑅ʘ < 𝑹б.к. < 0,1𝑅ʘ.

3. Плотность по отношению к плотности воды – величина, равная
отношению средней плотности звезды к плотности воды. Например, для звезды ε
Возничего

= 0,33. Вспомним или узнаем
из справочных данных, что 𝜌воды = 1000 кг/ , тогда средняя плотность ε
Возничего 𝜌 = 0,33𝜌воды = 0,33 ∙ 1000 кг/= 330 кг/

Практические задания:

1.
Звезды Ригель является
сверхгигантом.

Решение: Определяем из таблицы радиус Ригеля 𝑅 = 138𝑅ʘ. Звезда относится к классу сверхгигантов, если 𝑹𝒄.г. > 100𝑅ʘ , то есть условие выполняется.

Утверждение верно.

2.
Звезда Альдебаран является
белым карликом.

Решение: Определяем из таблицы радиус
Альдебарана 𝑅 = 45𝑅ʘ. Звезда относится к классу белых карликов, если 0,001𝑅ʘ < 𝑹б.к. < 0,1𝑅ʘ. В нашем случае условие не выполняется.

Утверждение неверно.

3.
Так как звёзды Антарес А и
ан-Ният имеют примерно одинаковые массы, они относятся к одному
спектральному классу.

Решение: Чтобы судить о принадлежности звезды
к определенному спектральному классу, нужно знать температуру ее поверхности,
но не массу.

Утверждение неверно.

4.
Температура поверхности
звезды Ригель выше, температуры поверхности Солнца.

Решение: Температура поверхности Солнца ≈ 5500 К, а температура поверхности Т
Ригель=11200 К.

Утверждение верно.

5.
Так как звезда
Альдебаран и Меропа относятся к одному созвездию, значит, находятся на
одинаковом расстоянии от Земли.

Решение:То, что звёзды Альдебаран и Меропа
относятся к одному созвездию, вовсе не значит, что они находятся на одинаковом
расстоянии от Земли.

Утверждение неверно.

Ответ: 14

1.
Так как звёзды Антарес А
и ан-Ният имеют примерно одинаковые массы,они относятся к одному спектральному
классу.

Утверждение неверно.

2.
Звезда Альдебаран является
красным гигантом.

Решение: Определяем из таблицы радиус
Альдебарана 𝑅 = 45𝑅ʘ. Звезда относится к классу гигантов, если 10𝑅ʘ < 𝑹г. < 100𝑅ʘ. В нашем случае условие выполняется.

Утверждение верно.

3.
Звезда Ригель относится к
звездам главной последовательности

Решение: звезды главной последовательности 0,1𝑅ʘ < 𝑹г.п. < 10𝑅ʘ. Радиус Ригеля=138 𝑅ʘ, условие не выполняется.

Утверждение неверно.

4.
Так как звезды Ригель и Бетельгейзе
относятся к одному созвездию, значит, находятся на одинаковом расстоянии от
Земли.

Решение: То, что звёзды Ригель и Бетельгейзе
относятся к одному созвездию, вовсе не значит, что они находятся на одинаковом
расстоянии от Земли.

Утверждение неверно.

5.
Температура звёзды Антарес
А ниже, чем температура поверхности Солнца.

Решение: Температура поверхности Солнца ≈ 5500 К, а температура поверхности Т Антарес
А =3400 К.

Утверждение верно.

Ответ: 25

Задания для самостоятельного решения.

Задача № 2

Задача № 3

Задача №4

Задача № 5

Задача №6

Задача № 7

Задача № 8

Задача № 9

Задача № 10

Тема 3.
Планеты Солнечной системы

Теоретический материал .

Центром Солнечной системы является звезда Солнце, вокруг которой
обращается 8 планет: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран и
Нептун

Первые четыре планеты – Меркурий, Венера, Земля и Марс – изза близкого
расположения к Земле и схожести по своим свойствам называют планетами Земной
группы. Оставшиеся четыре планеты — Юпитер, Сатурн, Уран и Нептун – планеты-гиганты
(или газовые гиганты).

1.
Диаметр в районе экватора
позволяет определить объем данной планеты. Если форму планеты принять за
шар, то 𝑉 = ∗π∗ Если учесть, что радиус есть половина
диаметра, тогда 𝑉 = .

2.
Период обращения вокруг
Солнца – это время, за которое планета совершает один полный оборот вокруг
Солнца, т.е. это длительность года на данной планете.

3.
Следует также принимать во
внимание, что период можно рассчитать по формуле 𝑇 = 2𝜋𝑅/𝑣 , где 𝑅 − радиус траектории, а 𝑣 − линейная скорость планеты.

4.
Период вращения вокруг оси
– это время, за которое планета совершает один полный оборот вокруг своей оси.
Это время называют сутками на данной планете.

5.
Вторая космическая
скорость – это скорость,
которую необходимо сообщить телу у поверхности планеты, чтобы оно стало
искусственным спутником Солнца. Чтобы найти вторую космическую скорость, надо
знать радиус данной планеты и ускорение свободного падения: =     или = Отсюда можно найти ускорение свободного
падения:   𝑔 = . Вторая космическая скорость связана с первой. Первая космическая
скорость – это скорость, которую необходимо сообщить телу у поверхности
планеты, чтобы оно стало искусственным спутником этой планеты:

=
или =

Тогда установим связь между
первой и второй космическими скоростями:

= √ 2

6.
Средняя
плотность – это физическая величина, равная отношению массы планеты к ее
объему, т.е.

𝜌 = . Тогда 𝑚 = 𝜌𝑉 или 𝑚 = 𝜌 ∙ ∗π∗= 𝜌 ∙

7.
Информация
о наклоне оси позволяет нам сделать вывод о смене времен года на
данной планете. Она не наблюдается лишь в том случае, когда этот угол очень
мал, т.е. близок к 0, как, например, у Меркурия и Юпитера, или велик, т.е.
близок к 180° – у Венеры. На остальных планетах Солнечной системы согласно
данной таблице смена времён года наблюдается, и за один оборот вокруг Солнца,
т.е. за год на планете, смена сезонов происходит, как и на Земле, 4 раза.

Практическая часть.

1.
Среднее
расстояние от Солнца до Марса составляет 228 млн.км.

Решение: Среднее расстояние
от Солнца до Марса=1,52а.е.Учитывая, что 1а.е= 150млн.км, получим
1,52*150млн.км=228млн.км

Утверждение верно.

2.
Ускорение свободного падения на Венере составляет около 18,1
м/ .

Решение: Ускорение свободного
падения найдем как 𝑔 =

𝑔 =(2*7330*7330)/12104000=8,9
м/.

Утверждение неверно.

3.
Вторая космическая скорость для тела на Уране составляет 21,3
км/с.

Решение: связь между первой и второй
космическими скоростями:

= √ 2 =√ 2*15.1=21,3км/с.

Утверждение верно.

4.
Объем Юпитера почти в 3
раза больше объема Нептуна.

Решение: 𝑉 = , диаметр Юпитера d=142984км, а диаметр Нептуна d=49528км

===24раза

Утверждение неверно

5.
На Меркурии наблюдается
смена времен года.

Решение: Информация о наклоне оси позволяет
нам сделать вывод о смене времен года на данной планете. Она не наблюдается
лишь в том случае, когда этот угол очень мал, т.е. близок к 0, так как у
Меркурия он равен , то есть условие выполняется, у Меркурия не
наблюдается смена времен года.

Утверждение неверно.

Ответ:13

1.
Среднее расстояние от
Солнца до Юпитера составляет 300 млн.км.

Решение: Среднее расстояние от Солнца до Юпитера =5,2а.е.Учитывая, что
1а.е= 150млн.км, получим 5,2*150млн.км=780млн.км

Утверждение неверно.

2.
Вторая космическая
скорость для тела на Нептуне составляет 23,8 км/с.

Решение: связь между первой и второй космическими
скоростями:

= √ 2 =√ 2*16.8=23,8км/с.

Утверждение верно

3.
Ускорение свободного
падения на Марсе составляет около 15,1 м/ .

Решение: Ускорение свободного падения найдем как 𝑔 =

𝑔 =(2*3550*3550)/6794000=3,7 м/.

Утверждение неверно

4.
Объем Юпитера почти в
3 раза больше объема Нептуна.

Решение: 𝑉 = , диаметр Юпитера d=142984км, а диаметр Нептуна d=49528км

===24раза

Утверждение неверно

5.
На Меркурии
наблюдается смена времен года.

Решение: Информация о наклоне оси позволяет нам сделать вывод о смене
времен года на данной планете. Она не наблюдается лишь в том случае, когда этот
угол очень мал, т.е. близок к 0, так как у Меркурия он равен , то есть условие выполняется, у Меркурия не
наблюдается смена времен года.

Утверждение верно

Ответ:25

1.
Меркурианский год равен
меркурианским суткам

Решение: Меркурианский год
– период обращения вокруг Солнца, составляет 87,97 суток, а меркурианские сутки
– период вращения вокруг своей оси, составляет 58,6 суток.

Утверждение неверно.

2.
Планеты гиганты быстрее
вращаются вокруг своей оси, чем планеты земной группы.

Решение: угловая скорость вращения
планет-гигантов намного больше, чем у планет земной группы (согласно таблице
периоды вращения вокруг оси у планет-гигантов меньше).

Утверждение верно

3.
Первая космическая
скорость вблизи Урана составляет 15,1 км/с.

Решение: = √ 2 =1,4, тогда==21.29/1.4=15,1 км/с.

Утверждение верно

4.
Ускорение свободного
падения на Марсе составляет около 5,02 м/

Решение: Ускорение свободного падения найдем
как 𝑔 ==

Утверждение неверно

5.
Объем Венеры в 1,5 раза
больше объема Земли.

Решение: 𝑉 = , диаметр Венеры d=12104км, а диаметр Земли d=12756км

==≤ 1

Утверждение неверно

Ответ:23

Задания для
самостоятельного решения.

Задача № 11

Задача № 12.

Задача № 13

Задача № 14

Задача № 15

Тема 4.
Спутники планет Солнечной системы

Теоретический
материал.

1.
Радиус
спутника, если его форму условно принять за шар, позволяет определить объем
𝑉 = ∗π∗

2.
Радиус
орбиты есть не что иное, как расстояние от самого спутника до центра его
планеты (или ее поверхности, т.к. размеры планеты во много раз меньше радиуса
орбиты, эти расстояния можно считать одинаковыми).

Практические задания с решением.

1.
Первая космическая
скорость для Оберона составляет примерно 11км/с.

Решение: Запишем формулу устанавливающую связь между
первой и второй космическими скоростями:

= √ 2 ,тогда ==513м/с=0,5 км/с

Утверждение неверно.

2.
Ускорение свободного
падения на Луне примерно равно 1,6 м/с2

Решение: Ускорение свободного падения найдем как 𝑔 = = =1,6м/с2

Утверждение верно.

3.
Объем Титана почти в 2
раза больше объема Тритона.

Решение: В наших допущениях планеты, а также их
спутники имеют форму шара. Тогда объем можно рассчитать по следующей формуле: 𝑉 = ∗π∗

Объем Титана: 𝑉ти = ∗π∗. Объем Тритона: 𝑉тр = ∗π∗ . Найдем отношение их объемов: = = = = ≈ 6,88 Следовательно, объем Титана больше
объема Тритона почти в 7 раз.

Утверждение не верно.

4.
Орбита Каллисто
располагается дальше от поверхности Юпитера, чем орбита Ио

Решение: Сравним радиусы орбит этих спутников Юпитера:
у Ио – 𝑅ор и = 421,6 тыс км, а у Каллисто – 𝑅ор к = 1 883 тыс км. Очевидно, что Ио
находится гораздо ближе к поверхности Юпитера, чем Каллисто: 𝑅ор и < 𝑅ор к. Утверждение верно.

5.
Чем дальше от Солнца
располагается спутник планеты, тем меньше его размеры.

Решение: Нет, размеры спутников не зависят от
дальности от Солнца.

Утверждение неверно.

Ответ: 24

1.
Первая космическая
скорость для искусственного спутника Каллисто составляет примерно 3,45 км/с.

Решение: Запишем формулу устанавливающую связь между первой и второй
космическими скоростями: = √ 2 ,тогда ==1729м/с=1,7 км/с

Утверждение неверно.

2.
Ускорение свободного
падения на Титане примерно равно 1,35 м/с2

Решение: Ускорение свободного падения найдем как 𝑔 = == 1,35 м/с2

Утверждение верно.

3.
Объем Ио в 3 раза больше
объема Обертона.

Объем Ио: 𝑉ио = ∗π∗. Объем Тритона: 𝑉об = ∗π∗ . Найдем отношение их объемов: = = = = ≈ 14 раз Следовательно, объем Ио больше
объема Обертона почти в 14 раз.

Утверждение неверно.

4.
Объем Титана меньше объема Луны.

Решение: В наших допущениях планеты, а также
их спутники имеют форму шара. Тогда объем можно рассчитать последующей формуле:
𝑉 = ∗π∗

𝑉л = ∗π∗ ˃ 𝑉т = ∗π∗, если ˃, так как =1737 км ˂ Rт=2575км, то
значит 𝑉л ˂ 𝑉т.

Утверждение неверно.

5.
Европа находится
дальше от поверхности Юпитера, чем Ио.

Решение: Для того, чтобы ответить на вопрос
надо сравнить радиусы орбит этих спутников.=421,6тыс.км, радиус орбиты Европы ,то есть ˃.

Утверждение верно.

Ответ: 25

Задания для самостоятельного
решения.

Задача № 16

Задача № 17

Тема 5.
Астероиды Солнечной системы Астероиды

Теоретический
материал.

1. Напоминаем,
что если известен радиус, можно определить объем астероида (считаем, что
астероиды тоже имеют форму шара): 𝑉 = ∗π∗.

2. Астрономическая единица
равна среднему расстоянию от Земли до Солнца (1 а.е. = 150 млн км).

3. 1 ый закон
Кеплера: все небесные тела Солнечной системы обращаются по эллиптическим
орбитам, в одном из фокусов которых находится Солнце.

Центр эллипса
обозначим буквой 𝑂. У эллипса есть две характерные
точки, называемые фокусами, в одном из которых находится Солнце, обозначим их
как 𝐹1 и 𝐹2. Расстояние от центра
эллипса до крайней левой или правой точек называют большой полуосью,
обозначают буквой 𝑎. Расстояние от точки 𝑂 до крайних верхней или
нижней точек называют малой полуосью и обозначают как 𝑏.

4.
Характеристикой
эллипса является эксцентриситет. Эта величина равна:

𝑒 = =

Эксцентриситет влияет на внешний вид
эллипса, на его вытянутость. В справочных данных к этому заданию
указано, что если

·
𝑒 = 0, то эллипс представляет собой окружность,
так как это значит 𝑎 = 𝑏, и это радиус окружности. Точно
также, если 𝑒 = = 0, то 𝑂𝐹 = 0, значит, фокус и точка 𝑂 совпадают, т.е. Солнце в
этом случае находится в центре окружности.

·
0
< 𝑒 < 1,будет более вытянутой. Этот факт необходимо запомнить!

На рисунке изображены три
эллипса: у красного 𝑒 = 0, это окружность; у
синего 𝑒 ≈0,66; а у зеленого 𝑒 = 0,8, этот эллипс самый
вытянутый.

5.
Эксцентриситеты
эллиптических орбит астероидов не такие большие, это значит, что большая и
малая полуоси почти не отличаются друг от друга 𝑎 ≈ 𝑏. Тогда мы приблизительно
можем считать, что астероиды движутся по окружностям, в центрах которых
находится Солнце. Т.е. большая полуось — это среднее расстояние от астероида
до Солнца.

6.
Также
выделим на орбите две точки, самую близкую к Солнцу и самую далекую – это
перигелий и афелий (на рисунке – П и А).

7.
Большинство
астероидов Солнечной системы находятся между орбитами Марса и Юпитера и
образуют т.н. пояс астероидов. Важно помнить средние расстояния
от Солнца до Марса и Юпитера, т.е. большие полуоси их орбит:

𝑎м = 1,5 а. е. … Пояс астероидов … 𝑎ю = 5,2 а. е.

Если большая полуось
астероида больше чем у Марса и не превышает этого значения для Юпитера, это значит,
что астероид находится в поясе астероидов. В Солнечной системе есть еще один
пояс астероидов – пояс Койпера, он находится за орбитой Нептуна (30 − 55 а. е).

8.
Период
обращения вокруг Солнца – это время, за которое астероид совершает один полный
оборот вокруг Солнца, т.е. это длительность года на данном астероиде.

9.
Если
известны масса и размеры астероида, можно рассчитать его среднюю плотность: 𝜌 = = =

Практические задания.

1.
Астероид
Аквитания вращается по более « вытянутой» орбите, чем астероид Церера.

Решение: Более «вытянутая» орбита (более
эллипсоидальная) будет у того тела, у которого выше эксцентриситет орбиты. Из
таблицы видно, что эксцентриситет астероида Аквитания составляет 0,238, а
астероида Церера 0,077, то есть орбита у астероида Аквитания более «вытянутая».

Утверждение верно.

2.
Орбита астероида
Паллада находится между орбитами Марса и Юпитера.

Решение:
Орбита астероида Паллада =2,77 а.е, Она больше орбиты
Марса, но меньше орбиты Юпитера, то есть находится между орбитами этих
планет. (𝑎м = 1,5 а. е. Пояс астероидов … 𝑎ю = 5,2 а. е.)

Утверждение верно.

3.
Большие
полуоси орбит астероидов Эвномия и Юнона примерно одинаковы, следовательно они
движутся друг за другом по одной орбите. Решение: Большие полуоси это
вытянутость орбиты по одной из пространственных координат. Существует еще малая
полуось для описания эллипсоидальной орбиты. Кроме того, эти орбиты (эллипсы)
могут быть повернуты в пространстве по-разному, поэтому астероиды Эвномия и
Юнона не обязательно будут следовать друг за другом.

Утверждение неверно.

4.
Средняя плотность
астероида Веста составляет примерно 300кг/

Решение: Если известны масса и размеры астероида, можно рассчитать его
среднюю плотность:

𝜌 = = = ==3850

Утверждение неверно.

5.
Первая космическая
скорость для спутника астероида Геба составляет более 8

Первую космическую скорость можно вычислить
по формуле:

где M – масса астероида; R – радиус астероида.

Утверждение не верно.

Ответ:12

Задание для самостоятельного решения.

Задача № 18

Ответы к
заданиям для самостоятельного решения

Номер задания	ответ
1	35
2	45
3	135
4	4
5	125
6	35
7	23
8	15
9	24
10	13
11	13
12	13
13	24
14	35
15	13
16	14
17	13
18	34

Литература

1. Бакулин П.И.,
Кононович Э.В., Мороз В.И.. Курс общей

астрономии: учебник.
– М.: Наука. Главная редакция физикоматематической литературы, 1983. – 560 с.

2. Безуглова Г.С.
Физика. ЕГЭ-2018. Раздел «Элементы

астрофизики»: учебное
пособие. Под ред. Л.М. Монастырского. –

Ростов-на-Дону:
Легион, 2017. – (ЕГЭ).

3. ЕГЭ. Физика:
типовые экзаменационные варианты: 30

вариантов / под ред.
М.Ю. Демидовой. – М.: Издательство

«Национальное
образование», 2020. – 400 с. – (ЕГЭ. ФИПИ – школе).

4. http://fipi.ru –
официальный сайт Федерального института

педагогических
измерений

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Атомные спектры. Энергетические уровни

Электрон в атоме водорода перешёл с энергетического уровня с номером m в основное энергетическое состояние с номером (n = 1). При этом был испущен фотон с импульсом (6,45cdot10^{-27}) кг(cdot)м/с. Чему равен номер (m)?

Найдем энергию испущенного фотона: [E=pc=6,45cdot 10^{-27}text{ кг·м/с}cdot 3cdot 10^{8}text{кг·м/с}=19,5cdot 10^{-19}approx 12,09text{ эВ}]
Энергетические уровни водорода находятся по формуле: [E_n=-dfrac{13,6text{ эВ}}{n^2}]
Второй постулат Бора: [E=E_M-E_n]
Подставим значения: [12,09text{ эВ}=-13,6cdot text{ эВ}left(dfrac{1}{m^2}-dfrac{1}{n^2}right)] [12,09=-13,6cdotleft(dfrac{1}{m^2}-dfrac{1}{4}right)] [12,09=-13,6cdotleft(dfrac{1}{m^2}-dfrac{1}{4}right)]
Таким образом, (m=3).

Ответ: 3

Электрон в атоме водорода переходит с энергетического уровня с номером (n = 2) на энергетический уровень с (n = 1). Чему равен модуль импульса испущенного при этом фотона? Ответ выразите в кг(cdot)м/с, умножив на (10^{-27}).

Энергетические уровни водорода находятся по формуле: [E_n=-dfrac{13,6text{ эВ}}{n^2}]
Второй постулат Бора: [E=E_2-E_1]
Получим: [E=-13,6cdotleft(1-dfrac{1}{4}right)=10,2text{ эВ}]
Импульс энергии фотона: [p=dfrac{E}{c}=dfrac{10,2cdot1,6cdot10^{-19}}{3cdot10^{8}}=5,44cdot10^{27} text{ кг $cdot$ м/с}]

Ответ: 5,44

Атомные ядра с одинаковым массовым числом, но разным количеством протонов и нейтронов, принято называть изобарами. Примером изобар могут служить ядро аргона (_{18}^{40}Ar) и ядро одного из изотопов калия (_{19}K). Сколько нейтронов содержится в указанном ядре калия? ?

Количество нейтронов равно разности атомной массы и зарядового числа, тогда в указанном ядре калия: [40-19=21]

Ответ: 21

Атомные ядра с одинаковым массовым числом, но разным количеством протонов и нейтронов, принято называть изобарами. Примером изобар могут служить ядро кадмия (_{48}^{122}Cd) и ядро одного из изотопов олова (_{50}Sn). Сколько нейтронов содержится в указанном ядре олова? ?

Количество нейтронов равно разности атомной массы и зарядового числа, тогда в указанном ядре олова: [122-50=72]

Ответ: 72

Электрон в атоме водорода находится в основном (самом низком, с номером n = 1) энергетическом состоянии. Атом поглощает фотон с импульсом 6,8(cdot)10(^{-27}) кг(cdot)м/с. Найдите номер энергетического уровня, на который в результате этого перейдёт электрон.

Энергия фотона: [E_text{фот}=hnu=pc=12,75text{ эВ}] Второй постулат Бора: [hnu=E_m-E_n Rightarrow pc = dfrac{-13,6}{n^2}+13,6 Rightarrow n=4]

Ответ: 4

В таблице приведены значения энергии для второго и четвёртого энергетических уровней атома водорода. [begin{array}{|c|c|} hline text{Номер уровня
} & text{Энергия 10$^{-19}$ Дж}\ hline text{2} & text{-
5,45} \ hline text{4} & text{-1,36} \ hline end{array}]

Какой должна быть энергия фотона, при поглощении которого атом переходит со второго уровня на четвёртый? (Ответ дать в 10(^{-19}) Дж.)

Ответ: 4,09

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задачи для практики

Задача 1

Решение

Задача 2

Решение

Задача 3

Решение

Задача 4

Решение

Задача 5

Решение

Задача 6

Решение

Задача 7

Решение

Задача 8

Решение

Задача 9

Решение

Рекомендуемые курсы подготовки

Предисловие

Тема 1. Звезды. Диаграмма Герцшпрунга-Рассела

Тема 2. Звезды. Диаграмма Герцшпрунга-Рассела (часть 2)

Тема 3. Планеты Солнечной системы

Тема 4. Спутники планет Солнечной системы

Тема 5. Астероиды Солнечной системы Астероиды

Ответы к заданиям для самостоятельного решения

Литература

Атомные спектры. Энергетические уровни

Тема 1.
Звезды. Диаграмма Герцшпрунга-Рассела

Тема 2. Звезды.
Диаграмма Герцшпрунга-Рассела (часть 2)

Тема 3.
Планеты Солнечной системы

Тема 4.
Спутники планет Солнечной системы

Тема 5.
Астероиды Солнечной системы Астероиды

Ответы к
заданиям для самостоятельного решения