Задания номер 3 профильного егэ по математике прямоугольный треугольник

Каталог заданий.
Решение прямоугольного треугольника


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 1 № 27238

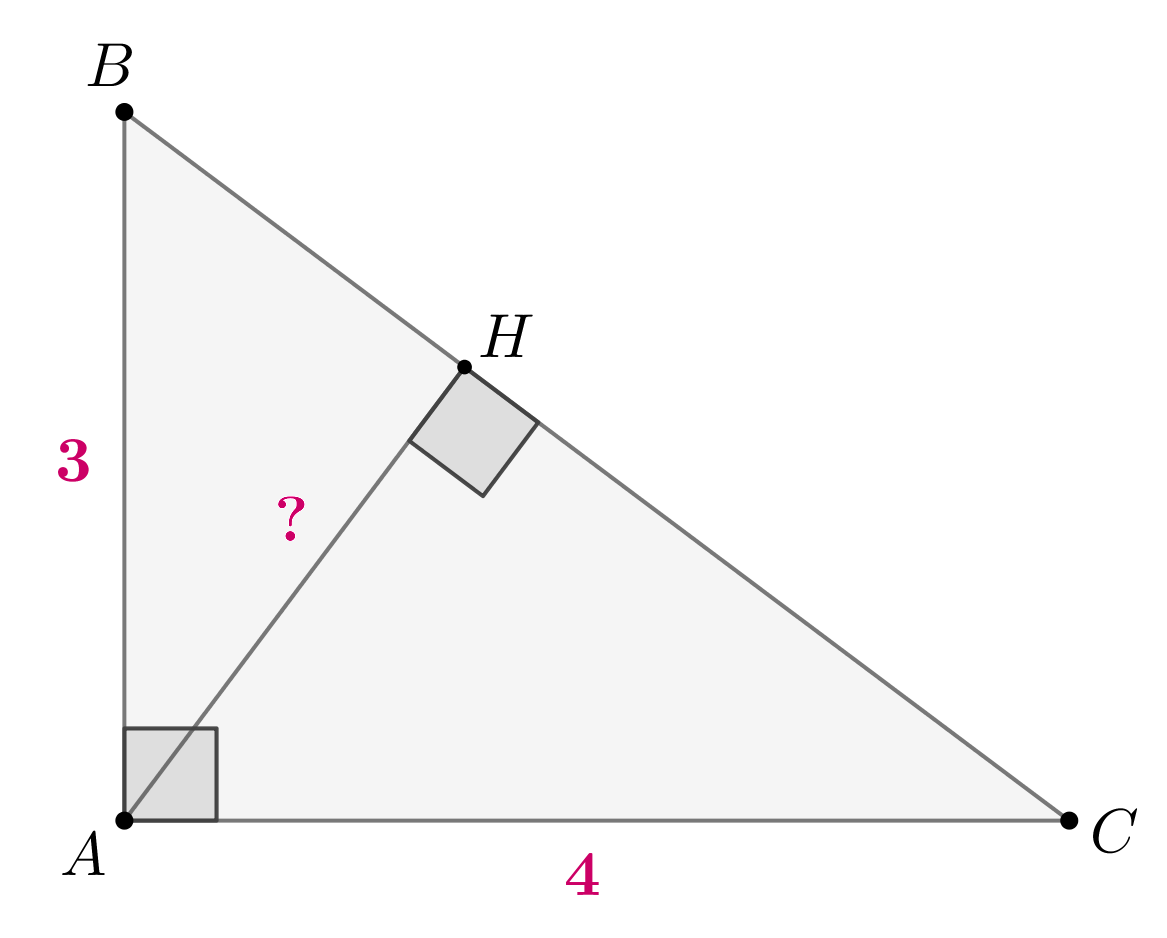
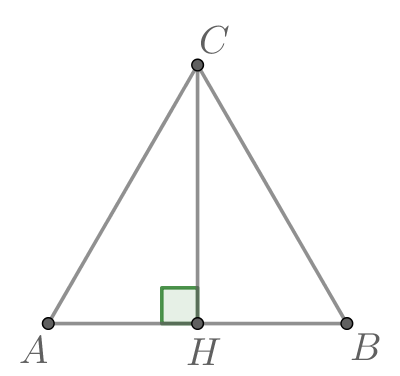
В треугольнике ABC угол C равен 90°, AC = 4,8, синус A = дробь: числитель: 7, знаменатель: 25 конец дроби . Найдите AB.

Аналоги к заданию № 27238: 4583 19737 635953 4584 4585 4586 4587 4588 4589 4590 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

2

Тип 1 № 27239

В треугольнике ABC угол C равен 90°, AC = 2, синус A = дробь: числитель: корень из 17, знаменатель: 17 конец дроби . Найдите  BC.

Аналоги к заданию № 27239: 4651 4787 4653 4655 4657 4659 4661 4663 4665 Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

3

Тип 1 № 27240

В треугольнике ABC угол C равен 90°, АС  =  4, косинус A = 0,5. Найдите АВ.

Аналоги к заданию № 27240: 26095 29575 29579 500952 29538 29539 29540 29541 29542 29543 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

4

Тип 1 № 27242

В треугольнике ABC угол C равен 90°, тангенс A = дробь: числитель: 33, знаменатель: 4 корень из 33 конец дроби , АС  =  4. Найдите АВ.

Аналоги к заданию № 27242: 29651 29747 530665 530685 29650 29652 29653 29654 29655 29656 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

5

Тип 1 № 27243

В треугольнике ABC угол C равен 90°, АС  =  8, тангенс A = 0,5. Найдите BC.

Аналоги к заданию № 27243: 29749 29791 29750 29751 29752 29753 29754 29755 29756 29757 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.2.1 Синус, косинус, тангенс, котангенс произвольного угла, 5.1.1 Треугольник

Решение

·

·

Курс Д. Д. Гущина

·

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник
Skip to content

ЕГЭ Профиль №3. Прямоугольный треугольник

ЕГЭ Профиль №3. Прямоугольный треугольникadmin2022-07-27T12:25:28+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №3. Прямоугольный треугольник

Задача 1. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (sin A = frac{7}{{25}}). Найдите АС.

Ответ

ОТВЕТ: 4,8.
Задача 2. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8) , (sin A = 0,5). Найдите ВС.

Ответ

ОТВЕТ: 4.
Задача 3. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8) , (cos A = 0,5). Найдите AС.

Ответ

ОТВЕТ: 4.
Задача 4. В треугольнике ABC угол C равен ({90^ circ }), (AB = 5), (cos A = frac{7}{{25}}). Найдите ВС.

Ответ

ОТВЕТ: 4,8.
Задача 5. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{33}}{{4sqrt {33} }}). Найдите AС.

Ответ

ОТВЕТ: 4.
Задача 6. В треугольнике ABC угол C равен ({90^ circ }), (AB = 7), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите BС.

Ответ

ОТВЕТ: 4.
Задача 7. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4,8), (sin A = frac{7}{{25}}). Найдите АB.

Ответ

ОТВЕТ: 5.
Задача 8. В треугольнике ABC угол C равен ({90^ circ }), (AC = 2), (sin A = frac{{sqrt {17} }}{{17}}). Найдите BC.

Ответ

ОТВЕТ: 0,5.
Задача 9. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (cos A = 0,5). Найдите АB.

Ответ

ОТВЕТ: 8.
Задача 10. В треугольнике ABC угол C равен ({90^ circ }), (AC = 0,5), (cos A = frac{{sqrt {17} }}{{17}}). Найдите BC.

Ответ

ОТВЕТ: 2.
Задача 11. В треугольнике ABC угол C равен ({90^ circ }), (AC = 4), (tgA = frac{{33}}{{4sqrt {33} }}). Найдите АB.

Ответ

ОТВЕТ: 7.
Задача 12. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8) , ({text{tg}},A = 0,5). Найдите BC.

Ответ

ОТВЕТ: 4.
Задача 13. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), (sin A = 0,5). Найдите АB.

Ответ

ОТВЕТ: 8.
Задача 14. В треугольнике ABC угол C равен ({90^ circ }), (BC = 0,5), (sin A = frac{{sqrt {17} }}{{17}}). Найдите AC.

Ответ

ОТВЕТ: 2.
Задача 15. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4,8), (cos A = frac{7}{{25}}). Найдите AB.

Ответ

ОТВЕТ: 5.
Задача 16. В треугольнике ABC угол C равен ({90^ circ }), (BC = 2), (cos A = frac{{sqrt {17} }}{{17}}). Найдите AC.

Ответ

ОТВЕТ: 0,5.
Задача 17. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = frac{{4sqrt {33} }}{{33}}). Найдите AB.

Ответ

ОТВЕТ: 7.
Задача 18. В треугольнике ABC угол C равен ({90^ circ }), (BC = 4), ({text{tg}},A = 0,5). Найдите AC.

Ответ

ОТВЕТ: 8.
Задача 19. В треугольнике ABC угол C равен ({90^ circ }), (AC = 24,;;BC = 7.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,28.
Задача 20. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;;BC = 24.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,28.
Задача 21. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;;BC = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 22. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;BC = 4.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,5.
Задача 23. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;BC = 20.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,6.
Задача 24. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;BC = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 25. В треугольнике ABC угол C равен ({90^ circ }), (AB = 25,;;AC = 20.) Найдите (sinA.)

Ответ

ОТВЕТ: 0,6.
Задача 26. В треугольнике ABC угол C равен ({90^ circ }), (AB = 8,;;AC = 4.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,5.
Задача 27. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt 5 ,;;AC = 8.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 28. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 15.
Задача 29. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;sin A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 12.
Задача 30. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;sin A = 0,25.) Найдите высоту СH.

Ответ

ОТВЕТ: 3,75.
Задача 31. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 12.
Задача 32. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 27,;;cos A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 15.
Задача 33. В треугольнике ABC угол C равен ({90^ circ }), (AB = 4sqrt {15} ,;;cos A = 0,25.) Найдите высоту СH.

Ответ

ОТВЕТ: 3,75.
Задача 34. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите AH.

Ответ

ОТВЕТ: 12,5.
Задача 35. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AB = 13,;;{text{tg}},A = 5). Найдите BH.

Ответ

ОТВЕТ: 12,5.
Задача 36. В треугольнике ABC угол C равен ({90^ circ }), (AB = 13,;;{text{tg}},A = frac{1}{5}). Найдите высоту CH.

Ответ

ОТВЕТ: 2,5.
Задача 37. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (BC = 3,;;sin ,A = frac{1}{6}). Найдите AH.

Ответ

ОТВЕТ: 17,5.
Задача 38. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;sin ,A = 0,5.) Найдите BH.

Ответ

ОТВЕТ: 4.
Задача 39. В треугольнике ABC угол C равен ({90^ circ }), (BC = 5,;;sin ,A = frac{7}{{25}}.) Найдите высоту CH.

Ответ

ОТВЕТ: 4,8.
Задача 40. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,      (BC = 3,;;cos ,A = frac{{sqrt {35} }}{6}.) Найдите AH.

Ответ

ОТВЕТ: 17,5.
Задача 41. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,       (BC = 5,;;cos ,A = frac{7}{{25}}.) Найдите BH.

Ответ

ОТВЕТ: 4,8.
Задача 42. В треугольнике ABC угол C равен ({90^ circ }), (BC = 8,;;cos ,A = 0,5.) Найдите высоту CH.

Ответ

ОТВЕТ: 4.
Задача 43. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите BH.

Ответ

ОТВЕТ: 4.
Задача 44. В треугольнике ABC угол C равен ({90^ circ }), (BC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.
Задача 45. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;sin ,A = frac{{sqrt {35} }}{6}.) Найдите BH.

Ответ

ОТВЕТ: 17,5.
Задача 46. В треугольнике ABC угол C равен ({90^ circ }), (AC = 8,;sin A = 0,5.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.
Задача 47. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 8,;;cos ,A = 0,5.) Найдите AH.

Ответ

ОТВЕТ: 4.
Задача 48. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 3,;;cos ,A = frac{1}{6}.) Найдите BH.

Ответ

ОТВЕТ: 17,5.
Задача 49. В треугольнике ABC угол C равен ({90^ circ }), (AC = 5,;cos A = frac{7}{{25}}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4,8.
Задача 50. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AC = 7,;{text{tg}},A = frac{{33}}{{4sqrt {33} }}.) Найдите AH.

Ответ

ОТВЕТ: 4.
Задача 51. В треугольнике ABC угол C равен ({90^ circ }), (AC = 7,;{text{tg}},A = frac{{4sqrt {33} }}{{33}}.) Найдите высоту СH.

Ответ

ОТВЕТ: 4.
Задача 52. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 8,;;BH = 4.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,5.
Задача 53. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 25,;;BH = 20.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,6.
Задача 54. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BC = 4sqrt 5 ,;;BH = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 55. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 20, (BC = 25.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,6.
Задача 56. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = 8.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,5.
Задача 57. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 4, (BC = sqrt {17} .) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,25.
Задача 58. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 24, (BH = 7.) Найдите (sin A.)

Ответ

ОТВЕТ: 0,28.
Задача 59. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 7, (BH = 24.) Найдите (cos A.)

Ответ

ОТВЕТ: 0,28.
Задача 60. В треугольнике ABC угол C равен ({90^ circ }), высота CH равна 8, (BH = 4.) Найдите ({text{tg}},A.)

Ответ

ОТВЕТ: 0,5.
Задача 61. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (AH = 27,;;{text{tg}},A = frac{2}{3}.) Найдите BH.

Ответ

ОТВЕТ: 12.
Задача 62. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (BH = 12,;;{text{tg}},A = frac{2}{3}.) Найдите AH.

Ответ

ОТВЕТ: 27.
Задача 63. В треугольнике ABC угол C равен ({90^ circ }), CH — высота,  (BH = 12,;;sin A = frac{2}{3}.) Найдите AB.

Ответ

ОТВЕТ: 27.
Задача 64. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, (AH = 12,;;cos A = frac{2}{3}.) Найдите AB.

Ответ

ОТВЕТ: 27.
Задача 65. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

Ответ

ОТВЕТ: 24.
Задача 66. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Ответ

ОТВЕТ: 6.
Задача 67. В треугольнике ABC угол C равен ({90^ circ }), угол В равен ({58^ circ }), CD медиана. Найдите угол ACD. Ответ дайте в градусах.

Ответ

ОТВЕТ: 32.
Задача 68. Острый угол прямоугольного треугольника равен ({32^ circ }). Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Ответ

ОТВЕТ: 61.
Задача 69. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

Ответ

ОТВЕТ: 45.
Задача 70. Один из углов прямоугольного треугольника равен ({29^ circ }). Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Ответ

ОТВЕТ: 16.
Задача 71. В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах.
Задача 72. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Задача 73. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
Задача 74. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Задача 75. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
Задача 76. В треугольнике ABC угол C равен 90°, угол A равен 30°, (AB = 2sqrt 3 ). Найдите высоту CH.
Задача 77. В треугольнике ABC угол C равен ({90^ circ }), CH — высота, угол A равен 30°, (AB = 2). Найдите AH.
Задача 78. В треугольнике ABC угол C равен 90°, CH — высота, угол A равен 30°, (AB = 4). Найдите BH.

Источник

Задание №3 ЕГЭ 2023 по математике для 11 класса профильный уровень все возможные  тренировочные задачи с ответами из банка заданий ФИПИ, новые прототипы заданий ЕГЭ 2023 для подготовки.

  • Прямоугольный треугольник задачи с ответами
  • Вписанные окружности задачи с ответами
  • Описанные окружности задачи с ответами
  • Равнобедренный треугольник задачи с ответами
  • Треугольник общего вида задачи с ответами
  • Квадрат, прямоугольник, ромб задачи с ответами
  • Трапеция задачи с ответами
  • Центральный и вписанные углы задачи с ответами
  • Окружность, касательная, хорда задачи с ответами

Прямоугольный треугольник задание №3 ЕГЭ профиль математика задачи с ответами:

Вписанные окружности задание №3 ЕГЭ профиль математика задачи с ответами:

Описанные окружности задание №3 ЕГЭ профиль математика задачи с ответами:

Равнобедренный треугольник задание №3 ЕГЭ профиль математика задачи с ответами:

Треугольник общего вида задание №3 ЕГЭ профиль математика задачи с ответами:

Квадрат, ромб, прямоугольник задание №3 ЕГЭ профиль математика задачи с ответами:

Трапеция задание №3 ЕГЭ профиль математика задачи с ответами:

Центральный и вписанные углы задание №3 ЕГЭ профиль математика задачи с ответами:

Окружность, касательная хорда задание №3 ЕГЭ профиль математика задачи с ответами:

1)Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

Правильный ответ: 24

2)Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Правильный ответ: 6

3)В треугольнике ABC угол C равен 90 , угол В равен 58 , CD медиана. Найдите угол ACD. Ответ дайте в градусах.

Правильный ответ: 32

4)Острый угол прямоугольного треугольника равен 32 . Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Правильный ответ: 61

5)Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

Правильный ответ: 45

6)Один из углов прямоугольного треугольника равен 29 . Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Правильный ответ: 16

7)В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21°. Найдите меньший угол данного треугольника. Ответ дайте в градусах.

Правильный ответ: 24

8)Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Правильный ответ: 42

9)В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Правильный ответ: 65

10)Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах

Правильный ответ: 21

11)Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

Правильный ответ: 21

12)В треугольнике ABC угол C равен 90 , CH — высота, угол A равен 30°, AB 2 . Найдите AH.

Правильный ответ: 1,5

13)В треугольнике ABC угол C равен 90°, CH — высота, угол A равен 30°, AB 4 . Найдите BH.

Правильный ответ: 1

14)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

Правильный ответ: 25

15)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.

Правильный ответ: 100

16)Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.

Правильный ответ: 12

17)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 25.

Правильный ответ: 10

18)Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 100.

Правильный ответ: 20

19)В треугольнике ABC угол A равен 38°, AC = BC. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 104

20)В треугольнике ABC угол C равен 118°, AC = BC. Найдите угол A. Ответ дайте в градусах.

Правильный ответ: 31

21)В треугольнике ABC AC = BC, угол C равен 52°. Найдите внешний угол CBD. Ответ дайте в градусах.

Правильный ответ: 116

22)В треугольнике ABC AC = BC. Внешний угол при вершине B равен 122°. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 64

23)В треугольнике ABC AB = BC. Внешний угол при вершине B равен 138°. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 69

24)Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

Правильный ответ: 41

25)Один угол равнобедренного треугольника на 90° больше другого. Найдите меньший угол. Ответ дайте в градусах.

Правильный ответ: 30

26)В треугольнике ABC AC=BC, угол С равен 120 градусов, AB= 2√3. Найдите AC.

Правильный ответ: 2

27)Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.

Правильный ответ: 24

28)Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.

Правильный ответ: 1

29)У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Правильный ответ: 6

30)В треугольнике ABC угол A равен 40°, внешний угол при вершине B равен 102°. Найдите угол C. Ответ дайте в градусах.

Правильный ответ: 62

31)Углы треугольника относятся как 2: 3: 4. Найдите меньший из них.

Правильный ответ: 40

32)В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах.

Правильный ответ: 38

33)В треугольнике ABC AD — биссектриса, угол C равен 50°, угол CAD равен 28°. Найдите угол B. Ответ дайте в градусах.

Правильный ответ: 74

34)В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Правильный ответ: 52

35)В треугольнике ABC угол A равен 72°, а углы B и C — острые. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

Правильный ответ: 108

36)Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

Правильный ответ: 130

37)В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.

Правильный ответ: 119

38)В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения CH и AD, угол BAD равен 26°. Найдите угол AOC. Ответ дайте в градусах.

Правильный ответ: 116

39)В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

Правильный ответ: 36

40)В треугольнике ABC угол A равен 44°, угол C равен 62°. На продолжении стороны AB отложен отрезок BD = BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.

Правильный ответ: 37

41)В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах.

Правильный ответ: 40

42)В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах.

Правильный ответ: 56

43)В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Правильный ответ: 49

44)В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Правильный ответ: 82

45)Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Правильный ответ: 9

46)Найдите площадь квадрата, если его диагональ равна 1

Правильный ответ: 0,5

47)Найдите диагональ квадрата, если его площадь равна 2.

Правильный ответ: 2

48)Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.

Правильный ответ: 18

49)Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.

Правильный ответ: 6

50)Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.

Правильный ответ: 18

51)Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.

Правильный ответ: 18

52)Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.

Правильный ответ: 14

53)Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.

Правильный ответ: 48

54)Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.

Правильный ответ: 13 

56)Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.

Правильный ответ: 48

57)Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

Правильный ответ: 2

58)Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Правильный ответ: 30

59)Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Правильный ответ: 6

60)Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Правильный ответ: 8

61)Найдите площадь ромба, если его высота равна 2, а острый угол 30 .

Правильный ответ: 8

62)Найдите площадь ромба, если его диагонали равны 4 и 12.

Правильный ответ: 24

63)Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

Правильный ответ: 3

64)Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Правильный ответ: 2

65)Сумма двух углов параллелограмма равна 100°. Найдите один из оставшихся углов. Ответ дайте в градусах.

Правильный ответ: 130

66)Один угол параллелограмма больше другого на 70°. Найдите больший угол. Ответ дайте в градусах.

Правильный ответ: 125

67)Диагональ параллелограмма образует с двумя его сторонами углы 26° и 34°. Найдите больший угол параллелограмма. Ответ дайте в градусах.

Правильный ответ: 120

68)Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.

Правильный ответ: 10

69)Диагональ прямоугольника вдвое больше одной из его сторон. Найдите больший из углов, который образует диагональ со сторонами прямоугольника? Ответ выразите в градусах.

Правильный ответ: 60

70)Найдите высоту ромба, сторона которого равна √3, а острый угол равен 60°. 

Правильный ответ:

71)Найдите больший угол параллелограмма, если два его угла относятся как 3:7. Ответ дайте в градусах.

Правильный ответ: 1,5

72)Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Правильный ответ: 126

73)Две стороны параллелограмма относятся как 3:4, а периметр его равен 70. Найдите большую сторону параллелограмма.

Правильный ответ: 90

74)Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

Правильный ответ: 20

75)Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Правильный ответ: 28

76)Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Правильный ответ: 10

77)Найдите большую диагональ ромба, сторона которого равна √3, а острый угол равен 60°.

Правильный ответ: 3

78)Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.

Правильный ответ: 48

79)В ромбе ABCD угол ABC равен 122°. Найдите угол ACD. Ответ дайте в градусах.

Правильный ответ: 29

80)В ромбе ABCD угол ACD равен 43°. Найдите угол ABC. Ответ дайте в градусах.

Правильный ответ: 94

81)Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

Правильный ответ: 141,75

82)Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.

Правильный ответ: 76,5

83)Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.

Правильный ответ: 44

84)Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Правильный ответ: 9

85)Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.

Правильный ответ: 0,96

86)Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7 . Найдите боковую сторону.

Правильный ответ: 21

87)Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11 . Найдите высоту трапеции.

Правильный ответ: 10

88)Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8 . Найдите большее основание.

Правильный ответ: 71

89)Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

Правильный ответ: 0,4

90)Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.

Правильный ответ: 8

91)Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.

Правильный ответ: 7

92)Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.

Правильный ответ: 15

93)Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.

Правильный ответ: 8

94)Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Правильный ответ: 160

95)Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Правильный ответ: 30

96)Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45°.

Правильный ответ: 16

97)Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Правильный ответ: 45

98)Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Правильный ответ: 160

99)Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

Правильный ответ: 5

99)Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 . Найдите площадь трапеции.

Правильный ответ: 42

100)Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Правильный ответ: 30

101)Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50 ? Ответ дайте в градусах.

Правильный ответ: 115

102)Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Правильный ответ: 38

103)Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Правильный ответ: 5

104)В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60°. Найдите меньшее основание.

Правильный ответ: 15

105)В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60°. Найдите ее периметр.

Правильный ответ: 69

106)Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Правильный ответ: 23

107)Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Правильный ответ: 10

108)Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45 . Найдите высоту трапеции.

Правильный ответ: 3

109)Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Правильный ответ: 0,5

110)В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Правильный ответ: 12

111)Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.

Правильный ответ: 5

112)Найдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.

Правильный ответ: 30

113)Найдите хорду, на которую опирается угол 30 , вписанный в окружность радиуса 3.

Правильный ответ: 3

114)Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Правильный ответ: 150

115)Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса √3.

Правильный ответ: 3

116)Дуга окружности AC, не содержащая точки B, имеет градусную меру 200°, а дуга окружности BC, не содержащая точки A, имеет градусную меру 80 . Найдите вписанный угол ACB. Ответ дайте в градусах.

Правильный ответ: 40

117)Хорда AB делит окружность на две дуги, градусные меры которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Правильный ответ: 105

118)Точки A, B, C расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

Правильный ответ: 100

119)AC и BD — диаметры окружности с центром O. Угол ACB равен 38 . Найдите угол AOD. Ответ дайте в градусах.

Правильный ответ: 104

120)В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 110°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Правильный ответ: 35

121)Найдите угол ABC. Ответ дайте в градусах.

Правильный ответ: 45

122)Найдите градусную меру дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.

Правильный ответ: 45

123)Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах

Правильный ответ: 46

124)Угол между хордой AB и касательной BC к окружности равен 32°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Правильный ответ: 64

125)Через концы A, B дуги окружности в 62° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Правильный ответ: 118

126)Касательные CA и CB к окружности образуют угол ACB, равный 122°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Правильный ответ: 58

127)Найдите угол ACO, если его сторона CA касается окружности, О- центр окружности, сторона CO пересекает окружность в точке B, а дуга AB окружности, заключенная внутри этого угла равна 64°. Ответ дайте в градусах.

Правильный ответ: 26

128)Угол ACO равен 28°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Правильный ответ: 62

129)Найдите угол ACO, если его сторона CA касается окружности, O— центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

Правильный ответ: 26

130)Угол ACO равен 24°. Его сторона CA касается окружности с центром в точке O. Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Правильный ответ: 114

131)Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 118° и 38°. Ответ дайте в градусах.

Правильный ответ: 40

132)Угол ACB равен 42°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

Правильный ответ: 20

Задание 3 ЕГЭ математика 11 класс рабочая тетрадь И.В. Ященко

Тренировочные варианты ЕГЭ по математике 11 класс с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на прямоугольный треугольник, использование тригонометрических функций. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.

Использование тригонометрических функций

Прямоугольный треугольник

27238. В треугольнике ABC угол C равен 90º, AC = 4,8, . Найдите AB.

27244. В треугольнике ABC угол C равен 90º, BC = 4, sin A = 0,5. Найдите AB.

27242. В треугольнике ABC угол C равен 90º, AC = 4,  Найдите AB.

27240. В треугольнике ABC угол C равен 90º, AC = 4, cos A = 0,5. Найдите AB.

27249. В треугольнике ABC угол C равен 90º, BC = 4, tg A = 0,5. Найдите AC.

27247. В треугольнике ABC угол C равен 90º, BC = 2,   Найдите AC.

27243. В треугольнике ABC угол C равен 90º, AC = 8, tg A = 0,5. Найдите BC.

27250. В треугольнике ABC угол C равен 90º, AC = 24, BC = 7. Найдите sin A.

27268. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, Найдите AH.

27269. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, sin A = 0,5. Найдите BH.

27270. В треугольнике ABC угол C равен 90º, BC = 5, . Найдите высоту CH.

27277. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, Найдите BH.

27336. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, BH = 4. Найдите sin A.

27339. В треугольнике ABC угол C равен 90º, высота CH равна 20, BC = 25. Найдите sin A.

27342. В треугольнике ABC угол C равен 90º, высота CH равна 24, BH = 7. Найдите sin A.

27431. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, sin A = 2/3. Найдите AB.

27271. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, . Найдите AH.

27272. В треугольнике ABC угол C равен 90º, CH — высота, BC = 5, cos A = 7/25. Найдите BH.

27273. В треугольнике ABC угол C равен 90º, BC = 8, cos A = 0,5. Найдите высоту CH.

27280. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, cos A =1/6. Найдите BH.

27337. В треугольнике ABC угол C равен 90º, CH — высота, BC = 25, BH = 20. Найдите cos A.

27340. В треугольнике ABC угол C равен 90º, высота CH равна 4, BC = 8. Найдите cos A.

27343. В треугольнике ABC угол C равен 90º, высота CH равна 7, BH = 24. Найдите cos A.

27432. В треугольнике ABC угол C равен 90º, CH — высота, AH = 12, cos A = 2/3. Найдите AB.

27265. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A =1/5. Найдите AH.

27266. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A = 5. Найдите BH.

27267. В треугольнике ABC угол C равен 90º, AB = 13, tg A = 1/5. Найдите высоту CH.

27341. В треугольнике ABC угол C равен 90º, высота CH равна 4, Найдите tg A.

27344. В треугольнике ABC угол C равен 90º, высота CH равна 8, BH = 4. Найдите tg A.

27357. В треугольнике ABC угол C равен 90º, CH — высота, AH = 27, tg A = 2/3. Найдите BH.

27358. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, tg A = 2/3. Найдите AH.

27789. В треугольнике ABC угол C равен 90º, угол A равен 30º, Найдите высоту CH.

27790. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 2. Найдите AH.

27791. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 4. Найдите BH.

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Прямоугольный треугольник»

Открытый банк заданий по теме прямоугольный треугольник. Задания B6 из ЕГЭ по математике (профильный уровень)

Производная и первообразная функции

Задание №893

Тип задания: 6
Тема:
Прямоугольный треугольник

Условие

В треугольнике ABC угол C равен 90^{circ}, BC=8, tg A=0,4. Найдите AC.

Показать решение

Решение

tg A=frac{BC}{AC},

frac{8}{AC}=0,4,

AC=8:0,4=20.

Прямоугольный треугольник ABC

Ответ

20

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №296

Тип задания: 6
Тема:
Прямоугольный треугольник

Условие

В треугольнике ABC угол C равен 90^{circ}, CH — высота, BH=7, sin A=frac13. Найдите AB.

Прямоугольный треугольник с высотой

Показать решение

Решение

По условию sin A=frac13. angle A=angle BCH, значит, sinangle BCH=frac13 и frac{BH}{BC}=frac13.

BC=3BH=3cdot7=21.

Высота CH проведена из вершины прямого угла triangle ABC, поэтому она делит его на два подобных треугольника CBH и ABC.

Из подобия frac{BH}{BC}=frac{BC}{BA}, BA=frac{BC^2}{BH}=frac{21^2}{7}=63.

Ответ

63

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №290

Тип задания: 6
Тема:
Прямоугольный треугольник

Условие

В треугольнике ABC:angle C=90^{circ}, CH — высота, BC=14,, sin A=0,7. Найдите BH.

Прямоугольный треугольник ABC с высотой CH

Показать решение

Решение

В прямоугольном треугольнике ABC:angle A=90^{circ}-angle B,, sin A=sin(90^{circ}-angle B)=cos angle B=0,7.

В triangle BHC:cosangle B=frac{BH}{BC}, BH=BCcdotcos angle B=14cdot0,7=9,8.

Ответ

9,8

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №70

Тип задания: 6
Тема:
Прямоугольный треугольник

Условие

Треугольник ABC имеет прямой угол C = 90^{circ}, AC = 12, cos A=frac{sqrt{51}}{10}. Найдите высоту CH.

Треугольник ABC

Показать решение

Решение

Рассмотрим треугольник ACH. Мы знаем, что косинус угла равен отношению прилежащего катета к гипотенузе, значит:

cos A = frac{AH}{AC}

AH=ACcdot cos A=12cdotfrac{sqrt{51}}{10}

Используя теорему Пифагора, найдем высоту CH:

CH^2=AC^2-AH^2=144-frac{144 cdot 51}{100}=frac{7056}{100}

CH=sqrt{frac{7056}{100}}=frac{84}{10}=8,4

Ответ

8,4

Задание №67

Тип задания: 6
Тема:
Прямоугольный треугольник

Условие

Треугольник ABC имеет прямой угол C = 90^{circ}, cos A = 0,41. Найдите sin B.

Треугольник ABC

Показать решение

Решение

Косинус угла равен отношению прилежащего катета к гипотенузе, т.е. cos A=frac{AC}{AB}.

Синус угла равен отношению противолежащего катета к гипотенузе, т.е. sin B=frac{AC}{AB}.

В силу данных утверждений, получаем, что sin B = cos A = 0,41

Ответ

0,41

Задание №65

Тип задания: 6
Тема:
Прямоугольный треугольник

Условие

Треугольник ABC имеет прямой угол C = 90^{circ}, AC = 5, cos A = frac45. Найдите высоту CH.

Треугольник ABC

Показать решение

Решение

Рассмотрим треугольник ACH. Мы знаем, что косинус угла равен отношениею прилежащего катета к гипотенузе, значит:

cos A = frac{AH}{AC}

AH=ACcdot cos A=5cdotfrac{4}{5}=4

Используя теорему Пифагора, найдем высоту CH:

CH^2=AC^2-AH^2=25-16=9

CH=sqrt{9}=3

Ответ

3

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

1

.

04

Прямоугольный треугольник и теорема Пифагора

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

1.01Треугольник: внутренние и внешние углы

1.02Треугольник: высота, биссектриса, медиана

1.03Треугольник: задачи на подобие

1.04Прямоугольный треугольник и теорема Пифагора

1.05Треугольник: площадь и периметр

1.06Параллелограмм и его свойства

1.07Параллелограмм и свойство его биссектрисы

1.08Прямоугольник и его свойства

1.09Ромб и его свойства

1.10Квадрат и его свойства

1.11Трапеция и ее свойства

1.12Равнобедренная трапеция

1.13Окружность: центральный и вписанный углы

1.14Окружность: углы, образованные хордами, секущими, касательными

1.15Окружность: отрезки хорд, секущих, касательных

1.16Окружность: описанная около многоугольника

1.17Окружность: вписанная в многоугольник или угол

1.18Длина окружности или дуги и площадь круга или сектора

1.19Правильный шестиугольник и его свойства

1.20Площадь многоугольника: различные формулы

1.21Внешние углы многоугольника и тригонометрия

1.22Решение треугольника и других фигур с помощью тригонометрии

1.23Теорема синусов и теорема косинусов

1.24Координатная плоскость

1.25Векторы: сложение, вычитание, координаты

1.26Задачи на клетчатой бумаге

Решаем задачи

Найдите высоту прямоугольного треугольника с катетами 3 и 4, проведенную к
гипотенузе.

Показать ответ и решение

Пусть дан △ABC с ∠A = 90∘ и проведена AH ⊥ BC.

PIC

Тогда

AH-⋅BC- = S△ABC = AB-⋅AC- ⇔ 2 2 AB-⋅AC- AH = BC

По теореме Пифагора BC =5. Следовательно,

AH = 3⋅4= 12 = 2,4 5 5

Тем самым мы вывели формулу: высота прямоугольного треугольника с
катетами a и b, проведенная к гипотенузе c, равна

ab h = c

Показать ответ и решение

Рассмотрим прямоугольный треугольник AHB.

PIC

Так как ∠C = 120∘ и AC = CB, то

180∘-− 120∘ ∘ ∠A = ∠B = 2 =30

Катет, лежащий против угла ∘ 30 , равен половине гипотенузы, следовательно, в прямоугольном треугольнике
AHB

√- HA = 1AB = 3 2

Рассмотрим прямоугольный треугольник ACH. Так как ∠ACB =120∘, то

∠ACH = 180∘ − 120∘ = 60∘

Так как в прямоугольном треугольнике сумма острых углов равна 90∘, то

∠HAC = 90∘ − 60∘ = 30∘

Следовательно, HC = 0,5AC. Тогда по теореме Пифагора

2 2 2 2 AC2 AC = HC + HA ⇒ AC = --4-+ 3 ⇒ AC =2

В треугольнике ABC AC =BC = 4, ∠C = 30∘. Найдите высоту AH.

PIC

Показать ответ и решение

Рассмотрим прямоугольный треугольник ACH. Катет, лежащий против угла 30∘, равен половине гипотенузы,
следовательно,

AH = 0,5AC = 2

Заметим, что условие BC = 4 в данной задаче является лишним.

Показать ответ и решение

Так как катет, лежащий против угла 30∘, равен половине гипотенузы, то

BC = 1AB = 2 2

По свойству прямоугольного треугольника ∠BCH = ∠A = 30∘, следовательно, в треугольнике BCH :

1 HB = 2BC = 1

Показать ответ и решение

Так как катет, лежащий против угла 30∘, равен половине гипотенузы, то

BC = 1AB = 1 2

Тогда по теореме Пифагора в треугольнике ABC :

AC = ∘AB2-−-BC2-= √3

В прямоугольном треугольнике AHC :

1 √3 HC = 2AC = 2--

Тогда по теореме Пифагора

∘ ----- ∘ ---2-----2 3 AH = AC − HC = 3− 4 = 1,5

Показать ответ и решение

По теореме Пифагора в треугольнике из BCH :

∘---------- √ ------ BH = BC2 − HC2 = 17− 16 = 1

Следовательно,

tg∠BCH = BH--= 0,25 CH

По свойству прямоугольного треугольника ∠BCH = ∠BAC, следовательно,

tg∠A = tg ∠BAC = 0,25

Найдите основание равнобедренного треугольника, если угол при основании равен 30∘, а взятая внутри треугольника точка
находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии 2√3- от основания.

В равнобедренном треугольнике ABC, в котором AB = BC = 30, AC = 48, найти расстояние между точкой пересечения медиан и
точкой пересечения биссектрис.

PIC

Показать ответ и решение

PIC

Т.к. треугольник ABC равнобедренный, то BK — медиана, высота и биссектриса. Значит, 1 AK = 2 AC = 24.

По теореме Пифагора в треугольнике ABK :

∘ ---------- √-------- BK = AB2 − AK2 = 900− 576= 18

Пусть точка M — точка пересечения медиан AF и BK. По свойству медиан точка M делит медианы в отношении 2:1,
считая от вершины, тогда BM = 12, MK = 6.

Пусть точка T — точка пересечения биссектрис AE и BK. В треугольнике ABK по свойству биссектрис AT делит отрезок
BM на части, пропорциональные прилежащим сторонам, то есть:

TK-= TB- ⇒ TK- = 18−-TK- ⇒ TK = 8 AK AB 24 30

Найдем TM :

TM =T K − KM = 8 − 6 = 2.

В прямоугольном треугольнике CAT из вершины C прямого угла опущена высота CH. Известно, что T H = 12, CH = 5.
Найдите 13sin∠A.

PIC

Показать ответ и решение

PIC

По свойству прямоугольного треугольника и высоты, опущенной из его прямого угла, △CHT ∼ △CAT. Значит, ∠HCT = ∠A.
Поэтому будем искать sin∠HCT.

В треугольнике HCT :

TH sin ∠HCT = TC-

По теореме Пифагора из этого же треугольника мы можем найти TC :

∘ ---------- ∘ ------- T C = TH2 + CH2 = 122+ 52 = 13

Следовательно,

sin∠A = sin∠HCT = 12 ⇒ 13sin ∠A = 12. 13

Показать ответ и решение

Проведем CK ⊥ AB :

PIC

Так как треугольник ABC равнобедренный, то CK также является медианой и биссектрисой, следовательно, AK = 0,5AB и
∘ ∠ACK = 120- =60∘. 2

Так как сумма острых углов прямоугольного треугольника равна 90∘, то

∘ ∘ ∘ ∠CAK = 90 − 60 =30

Катет, лежащий против угла 30∘, равен половине гипотенузы, то есть CK = 0,5AC = √3. Тогда по теореме
Пифагора:

∘ ---2-----2 AK = AC − CK = 3 ⇒ AB = 2AK = 6

В треугольнике ABC AC =BC = 2√3, ∠C = 120∘. Найдите высоту AH.

PIC

Показать ответ и решение

Рассмотрим прямоугольный треугольник ACH. Так как ∠ACB = 120∘, то

∘ ∘ ∘ ∠ACH = 180 − 120 = 60

Так как сумма острых углов прямоугольного треугольника равна 90∘, то

∘ ∘ ∘ ∠HAC = 90 − 60 = 30

Катет, лежащий против угла 30∘, равен половине гипотенузы, следовательно, HC = 0,5AC = √3. Тогда по теореме
Пифагора

∘ ---2-----2 AH = AC − HC = 3

Показать ответ и решение

Рассмотрим прямоугольный треугольник ACH. Катет, лежащий против угла 30∘, равен половине гипотенузы, следовательно,
4 =AH = 0,5AC, откуда

AC =BC = 8

В равностороннем треугольнике ABC высота CH равна 2√3. Найдите AB.

PIC

В треугольнике ABC AB =BC = AC = 2√3. Найдите высоту CH.

PIC

Показать ответ и решение

Так как катет, лежащий против угла 30∘, равен половине гипотенузы, то

√ - BC =0,5AB = 3

По свойству прямоугольного треугольника ∠BCH = ∠A = 30∘, следовательно, в треугольнике BCH :

√ - HB = 0,5BC = --3 2

Тогда по теореме Пифагора в треугольнике BCH :

∘---------- ∘ -- CH = BC2 − BH2 = 9 = 1,5 4

Показать ответ и решение

В треугольнике BCH :

sin∠BCH = BH--= 0,5 BC

По свойству прямоугольного треугольника ∠BCH = ∠BAC, следовательно,

sin∠A = sin ∠BAC =0,5

В треугольнике ABC угол C = 90∘, AC = 24, BC = 7. Найдите sin ∠A.

PIC

Показать ответ и решение

Так как по определению BC- sin ∠A = AB , то нужно найти AB. По теореме Пифагора

∘ ---------- ∘------- √ --- AB = AC2 + BC2 = 242+ 72 = 625 = 25

Значит,

sin ∠A = 7-= 0,28 25

Показать ответ и решение

В прямоугольном треугольнике катет, лежащий против угла в 30∘, равен половине гипотенузы. В данном случае известно, что в
треугольнике ABC сторона, лежащая против угла в 30∘, равна половине другой стороны. Значит ли это, что треугольник ABC
обязательно прямоугольный? Подобного рода умозаключения в общем случае очень опасны, так как часто попросту
неверны.

Но в данном конкретном случае нам повезло: докажем, что треугольник ABC — прямоугольный. В самом деле, если
опустить перпендикуляр BH из точки B на прямую, содержащую AC, то окажется, что BH =0,5AB = BC.

PIC

Но если при этом BH и BC не совпадают, то HBC — прямоугольный треугольник, у которого гипотенуза BC равна катету
BH, чего быть не может, следовательно, BH и BC совпадают и треугольник ABC — прямоугольный.

По теореме Пифагора в треугольнике ABC :

2 AB2 = BC2 + AC2 ⇔ 4BC2 = BC2 + AC2 ⇔ AC2 = 3BC2 ⇔ AC2-= 3 BC

Две вершины квадрата расположены на гипотенузе равнобедренного прямоугольного треугольника, а две другие — на катетах.
Найдите сторону квадрата, если гипотенуза равна 9.

Показать ответ и решение

PIC

В прямоугольном треугольнике сумма острых углов равна 90∘. Так как треугольник равнобедренный, то

∘ ∠CBA = ∠BCA = 90-= 45∘ 2

Квадрат образует с гипотенузой углы ∠GF C = 90∘, ∠DEF = 90∘.

В прямоугольных треугольниках DBE и GF C

∠BDE = 90∘− ∠DBE = 45∘ ∘ ∘ ∠F GC = 90 − ∠F CG = 45

Значит, треугольники DBE и GFC — равнобедренные, то есть BE = ED, FG = F C. Так как ED =F G = EF по свойству
квадрата, то

BE = FC = EF

Пусть сторона квадрата равна a, тогда длину гипотенузы можно выразить через сторону квадрата:

BC = 3⋅a= 9 ⇒ a= 3

Катеты прямоугольного треугольника относятся как 5:4, а площадь равна 4,1. Найдите гипотенузу этого треугольника.

PIC

Показать ответ и решение

Т.к. катеты относятся как 5:4, то их можно обозначить за 4x и 5x. Тогда необходимо найти гипотенузу, по теореме Пифагора
равную

∘---------- √ ---- 25x2+ 16x2 = 41x2

Т.к. площадь прямоугольного треугольника равна полупроизведению катетов, то

2 S = 0,5 ⋅5x⋅4x= 10x = 4,1

Следовательно, x2 = 0,41.

Значит, гипотенуза равна

∘ ------- ∘ ---------- 41⋅0,41= 41⋅41⋅0,01 =41 ⋅0,1 =4,1.

Источник

Задание 790

В тре­уголь­ни­ке ABC угол C равен 90°, AC=4,8, $$sin A=frac{7}{25}$$. Най­ди­те AB.

Ответ: 5

Задание 791

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 2,  $$sin A=frac{sqrt{17}}{17}$$ . Най­ди­те BC.

Ответ: 0,5

Задание 793

В тре­уголь­ни­ке ABC угол C равен 90°,   $$tan A=frac{33}{4sqrt{33}}$$, АС = 4. Най­ди­те АВ.

Ответ: 7

Задание 795

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 24, BC = 7. Най­ди­те  sin A.

Ответ: 0,28

Задание 796

В тре­уголь­ни­ке ABC угол C равен 90°, CH – вы­со­та, AB = 13,  $$tan A=frac{1}{5}$$. Най­ди­те AH

Ответ: 12,5

Задание 797

В тре­уголь­ни­ке АВС угол С равен 90°, СН — вы­со­та, AB = 13,  $$tan A=5$$. Най­ди­те ВН.

Ответ: 12,5

Задание 798

В тре­уголь­ни­ке ABC угол C равен 90°, AB = 13,  $$tan A=frac{1}{5}$$. Най­ди­те вы­со­ту CH.

Ответ: 2,5

Задание 799

В тре­уголь­ни­ке АВС угол С равен 90°, CH — вы­со­та, BC = 3,  $$sin A=frac{1}{6}$$. Най­ди­те АН.

Ответ: 17,5

Задание 800

В тре­уголь­ни­ке ABC угол C равен 90°, CH — вы­со­та, BC  = 8,  $$sin A=0,5$$. Най­ди­те BH.

Ответ: 4

Задание 801

В тре­уголь­ни­ке АВС угол С равен 90°, BC = 5,  $$sin A=frac{7}{25}$$. Най­ди­те вы­со­ту СН.

Ответ: 4,8

Задание 802

В тре­уголь­ни­ке ABC угол C равен 90°, СН — вы­со­та, BC = 3,  $$cos A=frac{sqrt{35}}{6}$$. Най­ди­те АН.

Ответ: 17,5

Задание 803

В тре­уголь­ни­ке АВС угол С равен 90°, СН — вы­со­та, BC = 5 ,  $$cos A=frac{7}{25}$$. Най­ди­те ВН.

Ответ: 4.8

Задание 804

В тре­уголь­ни­ке АВС угол С равен 90°, BC = 8,  $$cos A=0,5$$ . Най­ди­те СН.

Ответ: 4

Задание 805

В тре­уголь­ни­ке ABC угол C равен 90°, CH  — вы­со­та, BC = 8, BH = 4. Най­ди­те  sin A .

Ответ: 0,5

Задание 806

В тре­уголь­ни­ке ABC угол C равен 90°, CH – вы­со­та, AC = 3,  $$cos A=frac{1}{6}$$. Най­ди­те BH.

Ответ: 17,5

Источник

Понравилась статья? Поделить с друзьями:
  • Задания не с разными частями речи егэ 11 класс
  • Задания не входящие в егэ этого года
  • Задания на электролиз егэ химия 2022
  • Задания на электричество егэ физика
  • Задания на эксперимент биология егэ