в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
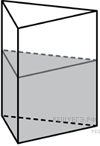
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 114.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 138.
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Цилиндр описан около шара. Объем шара равен 38. Найдите объем цилиндра.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 116. Найдите объем конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 42. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 156. Найдите объём конуса.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 36. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 63. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: Основная волна ЕГЭ по математике 29.05.2019. Центр
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 2. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
Источник: ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 3
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
1)Аквариум имеет форму прямоугольного параллелепипеда с размерами 80 см × 30 см × 40 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров.
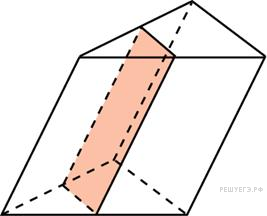
2)Через точку, делящую высоту конуса в отношении 1:3, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 5.
3)Два ребра прямоугольного параллелепипеда равны 8 и 5,
а объём параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
4)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка
в четыре раза ниже второй, а вторая
в полтора раза шире первой. Во сколько раз объём второй коробки больше объёма первой?
5)Сторона основания правильной треугольной призмы ABCA1B1C1 равна 2, а высота этой призмы равна 4. Найдите объём призмы АВСА1В1С1
6)Объём конуса равен 24π, а его высота равна 8. Найдите радиус основания конуса.
7)Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
8)В бак, имеющий форму прямой призмы, налито 12 л воды. После полного погружения в воду детали уровень воды
в баке увеличился в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
9)Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6,
а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
10)Даны два конуса. Радиус основания и высота первого конуса равны соответственно 3 и 2, а второго — 2 и 3. Во сколько раз объём первого конуса больше объёма второго?
11)В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды
в баке поднялся в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре
1000 кубических сантиметров.
12)Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5,
а второго — 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого
13)Даны два шара с радиусами 5 и 1. Во сколько раз объём большего шара больше объёма меньшего?
14)В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 120 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
15)
15)Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Числа на рисунке обозначают длины рёбер в сантиметрах. Найдите объём этой детали. Ответ дайте в кубических сантиметрах.
16)Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса

изображенного на рисунке (все двугранные углы прямые).
Ответ: 46
2) Найдите объем V части конуса, изображенной
на рисунке. В ответе укажите . Ответ: 168

изображенной на рисунке. В ответе укажите .
Ответ: 13.5

высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Ответ: 13

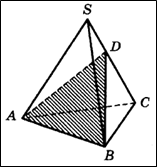
Найдите площадь поверхности многогранника, вершинами которого являются середины
сторон данного тетраэдра.
Ответ: 0.6
6) Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132.
Найдите высоту призмы.


призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым
ребром, равным 10.
Ответ: 248

четырехугольной пирамиды, основанием которой является грань куба, а вершиной —
центр куба.
Ответ: 2
9) Во сколько раз уменьшится объем конуса,
если его высоту уменьшить в 12,5 раза?
Ответ: 12.5
10) Цилиндр и конус имеют общие основание и
высоту. Найдите объем конуса, если объем цилиндра равен 159. Ответ: 53

изображенной на рисунке. В ответе укажите .
Ответ: 4
12) Найдите объем V части цилиндра,
изображенной на рисунке. В ответе укажите . Ответ:93,75

изображенного на рисунке и составленного из единичных кубов. Ответ:7
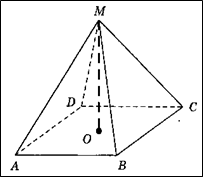
14) Объем правильной четырехугольной пирамиды
SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды
EABC. Ответ:3

4. Найдите площадь боковой поверхности цилиндра, деленную на . Ответ:4
16) Сосуд, имеющий форму правильной
треугольной призмы, налили 1100 см3 воды и погрузили в воду деталь.
При этом уровень воды поднялся с отметки 25 см до отметки 29 см. Найдите объем
детали. Ответ выразите в см3. Ответ:176
17) Найдите высоту правильной треугольной
пирамиды, стороны основания которой равны 4, а объем равен .
Ответ: 1.5
11 февраля 2016
В закладки
Обсудить
Жалоба
Задачи на нахождение объёмов тел
Задание №8 профильного уровня ЕГЭ по математике (бывшее B11).
В данной разработке представлены задачи от самых простых до более сложных. К задачам представлено подробное решение.
Задание 8. Из спецификации к демоверсии:
Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
Автор: Тихончук Людмила Юрьевна, учитель математики.
8obemi.docx
Решение
Построим сначала сечение пирамиды плоскостью gamma.
а) Плоскость gamma пересекает плоскость SAD по прямой AD, а плоскость SBC — по прямой MN, проходящей через точку K, параллельной BC (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает её, то линия пересечения параллельна этой прямой). ADNM — сечение пирамиды плоскостью gamma. ADNM — равнобедренная трапеция.
BC parallel gamma, следовательно, все точки, принадлежащие прямой BC, равноудалены от плоскости gamma. Значит, расстояние от точки B до плоскости gamma равно расстоянию от точки C до плоскости gamma. Что и требовалось доказать.
б) Так как расстояние от любой точки прямой BC до плоскости gamma одно и то же, будем искать расстояние от точки T до плоскости gamma, то есть нужно из точки T провести отрезок TH, перпендикулярный плоскости ADN, который равен высоте пирамиды BADNM. Тогда V_{BADNM}=frac{1}{3}S_{ADNM} cdot TH.
K — середина отрезка MN, так как принадлежит апофеме ST. Обозначим через P середину отрезка AD, тогда KP perp AD как высота равнобедренной трапеции ADNM. S_{BADNM}=frac{AD+MN}{2} cdot PK.
AD perp PST, действительно, KP perp AD и PT perp AD, следовательно, достаточно построить отрезок TH perp PK, так как тогда TH перпендикулярна двум пересекающимся прямым плоскости gamma (AD и PK).
S_{bigtriangleup PKT} выразим двумя способами:
frac{1}{2} TH cdot PK=frac{1}{2} PT cdot KL, откуда TH=frac{PT cdot KL}{PK}.
Из прямоугольного треугольника SOT с катетами OT=8, SO=6 и гипотенузой ST по теореме Пифагора ST=10, находим KL из подобия прямоугольных треугольников SOT и KLT с общим острым углом STO:
frac{SO}{KL}=frac{ST}{KT}=frac{OT}{LT}, frac{6}{KL}=frac{10}{2}, KL=frac{6}{5}. Далее frac{8}{LT}=frac{10}{2}, LT=frac{8}{5}, OL=OT-LT=8-frac{8}{5}=frac{32}{5}.
PK найдем по теореме Пифагора из прямоугольного треугольника PKL:
PK^{2}= PL^{2}+LK^{2}= (PO+OL)^{2}+LK^{2},
PK^{2}= left ( 8+frac{32}{5} right )^{2}+left ( frac{6}{5}right )^{2}= frac{5220}{25} cdot PK= frac{6sqrt{145}}{5}.
TH=frac{PT cdot KL}{PK}=frac{16 cdot dfrac{6}{5}}{dfrac{6sqrt{145}}{5}}=frac{16}{sqrt{145}}.
Основание MN равнобедренной трапеции найдем из подобия треугольников SMN и SBC, высоты которых SK=8, ST=10.
frac{MN}{BC}=frac{SK}{ST}, frac{MN}{16}=frac{8}{10}, откуда MN=frac{64}{5}.
V_{BADNM}= frac{1}{3} cdot frac {AD+MN}{2} cdot PK cdot TH= frac{1}{3} cdot frac{16+dfrac{64}{5}}{2} cdot frac{6sqrt{145}}{5} cdot frac{16}{sqrt{145}}= 92,16.
Ответ
92,16
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Прямоугольный параллелепипед
1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Задание 13 № 27079 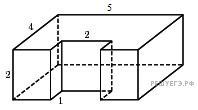
Пояснение.
Объем прямоугольного параллелепипеда равен произведению его измерений. Поэтому, если x — искомое ребро, то 2 

Ответ: 4.
Ответ: 4
27079
4
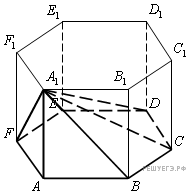
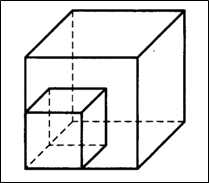
2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Задание 13 № 27191 
Пояснение.
Объем данного многогранника равен разности объемов параллелепипедов со сторонами 5, 2, 4 и 1, 2, 2:

Ответ: 36.
Ответ: 36
27191
36
3. Объем параллелепипеда 

Задание 13 № 27209 
Пояснение.
Искомый объем равен разности объемов параллелепипеда со сторонами 


Ответ: 1,5.
Ответ: 1,5
27209
1,5
Задание 13 № 245339
Пояснение.
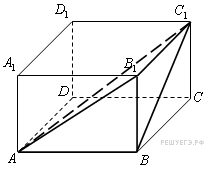

Ответ: 10.
Ответ: 10
245339
10
9. В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
Задание 13 № 506456 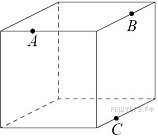
Пояснение.
Объем вытесненной жидкости равен объему детали (закон Архимеда). Уровень жидкости поднялся на h=20 см, сторона основания a=20 см, значит вытесненный объем будет равен 
Ответ: 8000.
Ответ: 8000
506456
8000
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166084.
10. Плоскость, проходящая через три точки A, B и C, разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше граней?
Задание 13 № 506659 
Пояснение.
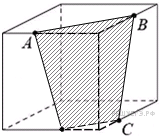
Ответ: 7.
Ответ: 7
506659
7
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 152742.
11. В бак, имеющий форму прямой призмы, налито 12 л воды. После полного погружения в воду детали, уровень воды в баке поднялся в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
6
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
10. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
11
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
12. От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
17. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
Задание 13 № 27183
18. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы, площадь основания которой равна 2, а боковое ребро равно 3.
21. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3.
22. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 3.
23. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы, площадь основания которой равна 6, а боковое ребро равно 2.
24. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы, площадь основания которой равна 6, а боковое ребро равно 2.
1.
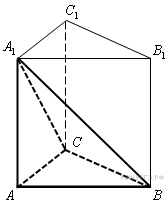
В правильной треугольной пирамиде SABC с вершиной S биссектрисы треугольника ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 6. Найдите длину отрезка OS.
16. Объем параллелепипеда 
17
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
19. Объем треугольной пирамиды , являющейся частью правильной шестиугольной пирамиды , равен 1. Найдите объем шестиугольной пирамиды.
20. Объем правильной четырехугольной пирамиды равен 12. Точка D – середина ребра . Найдите объем треугольной пирамиды .
21. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию
Помощь по заданию Сообщить об ошибке
26
Объем параллелепипеда равен 12. Найдите объем треугольной пирамиды .
27. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
28. Найдите объем параллелепипеда , если объем треугольной пирамиды равен 3.
36. Пирамида Снофру имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 220 м, а высота — 104 м. Сторона основания точной музейной копии этой пирамиды равна 44 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
7. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. 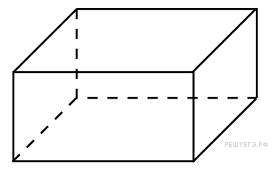
8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
9. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
30. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна 5. Найдите объём призмы, если её высота равна 3.
31. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна 6. Найдите объём призмы, если её высота равна 6.
32. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 5, а гипотенуза равна 5√2. Найдите объём призмы, если её высота равна 4.
33. В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 2, а гипотенуза равна √15. Найдите объём призмы, если её высота равна 3.
Данное занятие может быть проведено после изучения формул объемов многогранников на уроках геометрии в 11-м классе или в рамках элективного курса по подготовке к ЕГЭ. Материал также доступен и учащимся 10-го класса (во 2-м полугодии).
Цели занятия:
- показать примеры задач, аналогичных заданиям ЕГЭ по математике базового уровня и первой части профильного уровня;
- повторить теоретический материал, связанный с площадями фигур, со свойствами многогранников;
- отработка навыков самоконтроля;
- отработка навыков сотрудничества между учащимися.
Оборудование:
- оборудование для демонстрации презентации Microsoft PowerPoint (компьютер, проектор, экран или доска);
- раздаточный материал (тексты задач с чертежами);
- таблица квадратов натуральных чисел.
План занятия
- Организационный момент
- Устная работа
- Решение задач
- Работа в группах
- Подведение итогов
Ход занятия
Занятие сопровождается демонстрацией презентации.
1. Организационный момент
Cообщение целей занятия, деление класса на группы по 4 человека (можно объединить учащихся, сидящих за соседними партами).
2. Устная работа
Условия задач и правильные ответы демонстрируются на слайдах. Задачи решаются устно, ответы можно спросить у нескольких учащихся, один из них коротко рассказывает путь решения.
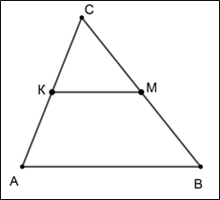
Задача 1. (Слайд №4) Площадь треугольника АВС равна 120. КМ – средняя линия, параллельная стороне АВ. Найти площадь четырехугольника АКМВ. (Ответ: 90)
Рисунок 1
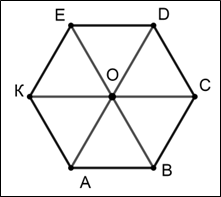
Задача 2. (Слайды №5,6) Площадь правильного шестиугольника АВСДЕК равна 60, О – центр шестиугольника. Найти площади треугольника АОВ, треугольника АВС, треугольника АВЕ, четырехугольника ВСДЕ. (Ответ: 10; 10; 20; 30)
Рисунок 2
Задача 3. (Слайд №7) Площадь грани прямоугольного параллелепипеда равна 15. Ребро, перпендикулярное этой грани, равно 6. Найти объем параллелепипеда. (Ответ: 90)
Рисунок 3
Задача 4. (Слайд №8) Во сколько раз увеличится объем куба, если его ребро увеличить в 5 раз? (Ответ: 125)
Рисунок 4
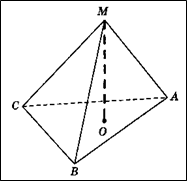
Задача 5. (Слайд №9) В правильной треугольной пирамиде МАВС О – точка пересечения медиан основания. Площадь треугольника АВС равна 5, а объем пирамиды – 35. Найти длину отрезка МО. (Ответ: 21)
Рисунок 5
Задача 6. (Слайд №10) Как изменится объем пятиугольной пирамиды, если её высоту увеличить в 4 раза? (Ответ: увеличится в 4 раза)
Рисунок 6
Задача 7. (Слайд №11) В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды составил 20 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? (Ответ: 5 см)
Рисунок 7
При подведении итогов устной работы необходимо обратить внимание на формулы для вычисления объемов призмы и пирамиды.
3. Решение задач
Чертежи заранее сделаны на доске, каждый ученик получает заготовку с чертежами (Приложение 1). Учащиеся у доски записывают краткие решения, сопровождая их устными пояснениями. Также можно использовать слайды №13, 14, 15.
Задача 8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 3. Объем параллелепипеда равен 108. Найти его диагональ.
Рисунок 8
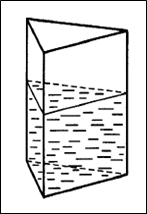
Задача 9. В сосуд, имеющий форму правильной треугольной призмы, налили 1000 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найти объем детали. Ответ выразить в см3.
Рисунок 9
Задача 10. Объем треугольной пирамиды SABC равен 15. Плоскость проходит через сторону АВ основания этой пирамиды и пересекает противоположное боковое ребро в точке D, делящей ребро SC в отношении 1 : 2, считая от вершины S. Найти объем пирамиды DABC.
Рисунок 10
4. Работа в группах
Каждая группа получает набор задач (Приложение 2), к которым надо записать краткие решения. После истечения отведенного времени проверяются ответы, представители групп могут прокомментировать ход решения задач. В это время чертежи демонстрируются на слайдах №17, 18, 19. Для быстрой проверки можно использовать слайд №20. После этого листы с решениями сдаются учителю.
5. Подведение итогов
При подведении итогов следует обратить внимание на две основные формулы объемов и их частные случаи, а также на отношение объемов подобных тел (слайд 22).
Задача. (Слайд №23) Боковые ребра правильной треугольной пирамиды взаимно перпендикулярны и равны 6. Найти объем пирамиды. (Ответ: 36)
При решении этой задачи очень важно обратить внимание на метод решения. Если тетраэдр перевернуть, то задачу можно решить устно.
Задача. (Слайды №24, 25) Объем тетраэдра равен 12. Найти объем многогранника, вершинами которого являются середины сторон данного тетраэдра. (Ответ: 6)
6. Домашнее задание (Приложение 3)
Литература
- Ященко И. В. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни. – М: Издательство «Экзамен», 2020.
- Балаян Э. Н. Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10-11 классы. – Ростов н/Д: Феникс, 2018.
- Материалы сайта: https://math-ege.sdamgia.ru/
Список приложений
- Приложение 1 – задачи для работы в классе
- Приложение 2 – задачи для работы в группах
- Приложение 3 – домашнее задание
- Приложение 4 – ПРЕЗЕНТАЦИЯ