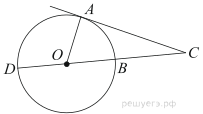
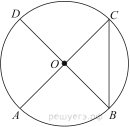
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
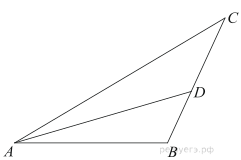
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
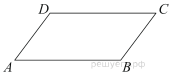
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
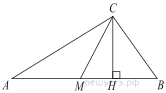
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
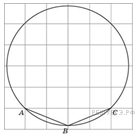
1. Найдите площадь квадрата, изображённого
на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ
дайте в квадратных сантиметрах.
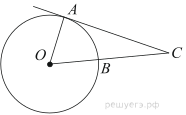
2. Найдите вписанный угол, опирающийся на дугу, равную 15 окружности.
Ответ дайте в градусах.

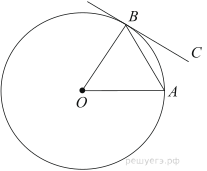
пирамиде О центр основания, SO=35, Найдите длину отрезка ВД
4. Найдите объём многогранника, изображённого на рисунке (все
двугранные углы прямые).

Найдите высоту цилиндра.
6. Найдите площадь поверхности многогранника, изображённого на
рисунке
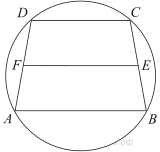
7. Найдите площадь трапеции, изображённой на рисунке.
8.В треугольнике АВС
угол С=58,биссектрисы АD и ВЕ пересекаются в точке О.Найти угол АОВ.
9. Диаметр основания конуса равен
40, а длина образующей — 25. Найдите высоту конуса.
10. В цилиндрическом сосуде уровень
жидкости достигает 98 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр
которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
11. В треугольнике
АВС высоты СЕ и ВД пересекаются в точке О.Угол А равен 56 градусов.Найдите угол
ДОЕ .Ответ дайте в градусах.
12. В прямоугольном параллелепипеде ВВ1=16,А1В1=2,А1Д1=8,Найти АС1.
13. В цилиндрическом сосуде уровень
жидкости достигает 64 см. На какой высоте будет находиться уровень
жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого
в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
14. В треугольнике АВС АС=ВС, АВ=20,
высота АН=8. Найти синус ВАС.
15. Около конуса описана сфера (сфера
содержит окружность основания конуса и его вершину). Центр сферы совпадает с
центром основания конуса.
Радиус сферы равен Найдите
образующую конуса.
16. Найдите объём многогранника, вершинами
которого являются точки D ,A1,B1,C1,D1,E1,F1, правильной шестиугольной призмы
площадь основания которой равна 12, 
17. Найдите
площадь параллелограмма, изображённого на рисунке.
18.В треугольнике
АВС АD биссектриса ,угол С 104 градуса, угол САD равен 6 градусов.Нацйти угол В
19. Найдите объём многогранника,
вершинами которого являются точки С, А1,В1,С1 правильной треугольной
призмы АВСА1В1С1 площадь основания которой равна 4, а боковое ребро равно 9.
20. Два угла вписанного в окружность
четырёхугольника равны 56 и 77 градусов.
Найдите меньший из оставшихся
углов. Ответ дайте в градусах.
21. Дано два шара. Радиус первого шара в 2
раза больше радиуса второго. Во сколько раз площадь поверхности первого шара
больше площади поверхности второго?
22. Диагональ куба равна .Найдите его объём.
23.
В
прямоугольном параллелепипеде АВ-7, АД=3, ААВ1=4.Найти площадь сечения,
проходящего через точки А,В,С1
24. Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
25. Площадь основания конуса равна 36π, высота =10 см . Найдите площадь осевого сечения
этого конуса.
26. Через
среднюю линию основания треугольной призмы, объём которой равен 52, проведена
плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной
призмы.
27. Площадь основания конуса равна
48. Плоскость, параллельная плоскости основания конуса, делит его высоту на
отрезки длиной 4 и 12, считая от вершины. Найдите площадь сечения конуса этой
плоскостью.
28. Объём треугольной призмы, отсекаемой
от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной
вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен
1,5. Найдите объём куба
29. Куб описан около сферы радиуса 2.
Найдите объём куба.
30. В правильной четырёхугольной
пирамиде все рёбра равны 2. Найдите площадь сечения пирамиды плоскостью,
проходящей через середины боковых рёбер.
Вариант 1 6. Планиметрия
1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2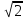
4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.
7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.
8. Найдите величину угла АВС. Ответ дайте в градусах.
9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Вариант 2 6. Планиметрия
В 1. Сторона правильного треугольника равна 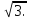
2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.
4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.
6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.
Вариант 3 6. Планиметрия
1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.
2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25. Найдите высоту АН.
4. В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.
5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А = . Найдите ВН.
6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите
8. Найдите площадь ромба, если его диагонали равны 4 и 12.
9. В треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН.
10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах
Вариант 4 6. Планиметрия
1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = . Найдите BH.
2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.
3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.
6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.
7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41
Найдите радиус окружности, вписанной в этот треугольник.
8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4, ВН = 4. Найдите
10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.
Вариант 5 6. Планиметрия
1. Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2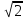
2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А = . Найдите АН.
4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.
5. Катеты равнобедренного прямоугольного треугольника равны 2+ Найдите радиус окружности, вписанной в этот треугольник.
6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.
7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.
9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.
Вариант 6 6. Планиметрия
1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.
2. Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС= . Найдите
4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.
6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.
7. В треугольнике ABC угол C равен 90°, АС = 8, cos А = Найдите АВ.
8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
10. В треугольнике ABC угол ACB равен °, угол B равен
°, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Вариант 7 6. Планиметрия
1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.
3. В треугольнике ABC AC = BC, AB = 22, tg А = . Найдите AC.
4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
5. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.
7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.
9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.
10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.
Вариант 8 6. Планиметрия
1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.
3. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
4. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.
5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.
6. В треугольнике ABC AC = BC, AB = 8, tg А = . Найдите AC.
7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.
8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.
9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47.
10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2
Вариант 9 6. Планиметрия
1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на
4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.
5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.
6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту
7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.
8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.
10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.
Вариант 10 6. Планиметрия
1. Найдите величину угла АВС. Ответ дайте в градусах.
2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.
3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.
4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А = . Найдите АВ.
5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.
6. Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.
7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
9. В треугольнике известно, что , , угол
равен 90°. Найдите радиус вписанной окружности.
10. В треугольнике АВС АС = ВС = 27 , — высота, sin ВАС =
. Найдите
|
6. Планиметрия |
||||
|
Вариант 1
|
Вариант 2
|
Вариант 3
|
Вариант 4
|
Вариант 5
|
|
Вариант 6
|
Вариант 7
|
Вариант 8
|
Вариант 9
|
Вариант 10
|
По теме: методические разработки, презентации и конспекты
Решение стереометрической задачи тремя различными способами
Здесь представлено на трех файлах моё решение решение задачи С2 (вариант 13) из пособия «МАТЕМАТИКА. Подготовка к ЕГЭ-2011» под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова. Эта-же задача встречается в пос…
Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».
ВЫЧИСЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Рассмотрим несколько геометрических задач, для решения которых необходимо вычислить те или иные расстояния или углы в пространст…
Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э…
Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …
Программа внеурочной деятельности «Практикум решения стереометрических задач». Пропедевтика стереометрических знаний на примере качественных стереометрических задач.
Всем известная трудность в изучении стереометрии, возникающая у учащихся 10 классов, в значительной степени объясняется низким уровнем развитием их пространственных представлений. Ученики теряю…
Геометрия на плоскости (планиметрия)
Задание
1
#199
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 81^{circ}), (angle C = 25^{circ}). Найдите внешний угол при вершине (A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle B + angle C =) внешнему углу при вершине (A), следовательно (A_{text{внеш}}) ( = 81^{circ} + 25^{circ} = 106^{circ}).
Ответ: 106
Задание
2
#200
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 22^{circ}), внешний угол при вершине (C) равен (130^{circ}). Найдите (angle B). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle A + angle B = C_{text{внеш}}), тогда (22^{circ} + angle B = 130^{circ}), откуда находим (angle B = 130^{circ} — 22^{circ} = 108^{circ}).
Ответ: 108
Задание
3
#201
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 35^{circ}), внешний угол при вершине (B) равен (91^{circ}). Найдите (angle A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle C + angle A = B_{text{внеш}}), тогда (35^{circ} + angle A = 91^{circ}), откуда находим (angle A = 91^{circ} — 35^{circ} = 56^{circ}).
Ответ: 56
Задание
4
#202
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 70^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 70^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 70^{circ} — 70^{circ} = 40^{circ}).
Ответ: 40
Задание
5
#203
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 47^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle C = angle A = 47^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 47^{circ} — 47^{circ} = 86^{circ}).
Ответ: 86
Задание
6
#204
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 36^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 36^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 36^{circ} — 36^{circ} = 108^{circ}).
Ответ: 108
Задание
7
#205
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 38^{circ}), (AB = BC). Найдите (angle C). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C). Так как у любого треугольника сумма углов равна (180^{circ}), то (180^{circ} = 38^{circ} + angle A + angle C = 38^{circ} + 2cdot angle A), откуда (2cdot angle A = 142^{circ}), тогда (angle A = 71^{circ}).
Ответ: 71
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.