Каталог заданий.
Применение производной к исследованию функций
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
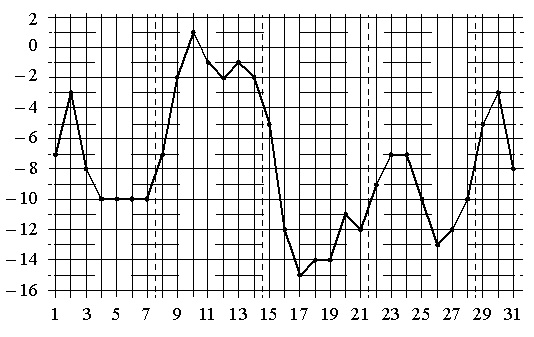
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите сумму целых точек, входящих в эти промежутки.
2
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
3
На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402
4
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье
5
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург
Пройти тестирование по этим заданиям
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке
равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции
в точке
Производная функции в точке
равна тангенсу угла наклона касательной, проведенной в точке
.
Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0,25.
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке
образует тупой угол
с положительным направлением оси
. Поэтому из прямоугольного треугольника мы найдём тангенс угла
, смежного с углом
.
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку
, имеем:
Ответ: −0, 25.
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой
в точке
При значения выражений
и
равны.
При этом производная функции равна угловому коэффициенту касательной, то есть
.
Из второго уравнения находим или
Первому уравнению удовлетворяет только
.
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где
— расстояние от точки отсчета в метрах,
— время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени
с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени
получим:
.
Ответ: 3.
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция
возрастает.
Если , то функция
убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| 0 | 0 |
5. На рисунке изображен график функции , определенной на интервале
Найдите количество точек, в которых производная функции
равна 0.
Производная функции в точках максимума и минимума функции
Таких точек на графике 5.
Ответ: 5.
6. На рисунке изображён график — производной функции
, определённой на интервале
. В какой точке отрезка
функция
принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке производная функции
положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение
Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
7. На рисунке изображён график функции , определённой на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции
точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале
Найдите количество точек максимума функции
на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
Ответ: 1.
9. На рисунке изображен график производной функции , определенной на интервале
Найдите точку экстремума функции
на отрезке
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке
В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.
Первообразная и формула Ньютона-Лейбница
Функция , для которой
является производной, называется первообразной функции
Функции вида
образуют множество первообразных функции
10. На рисунке изображён график — одной из первообразных некоторой функции
, определённой на интервале
Пользуясь рисунком, определите количество решений уравнения
на отрезке
Функция для которой
является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции
равна нулю. Это точки максимума и минимума функции
На отрезке
таких точек 4.
Ответ: 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье
Первообразная функции. Формула Ньютона-Лейбница.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Графики функций
В задании №13 ЕГЭ по математике базового уровня придется продемонстрировать умения и знания одного из понятий поведения функции: производных в точке или скоростей возрастания или убывания. Теория к этому заданию будет добавлена чуть позже, но это не помешает нам подробно разобрать несколько типовых вариантов.
Разбор типовых вариантов заданий №14 ЕГЭ по математике базового уровня
Вариант 14МБ1
[su_note note_color=”#defae6″]
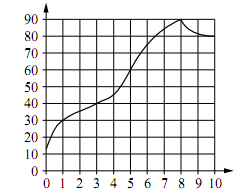
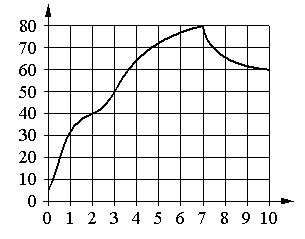
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ:
А) 0 – 1 мин. Б) 1 – 3 мин. В) 3 – 6 мин. Г) 8 – 10 мин. |
ХАРАКТЕРИСТИКИ:
|
В таблице под каждой буквой укажите соответствующий номер.
[/su_note]
Алгоритм выполнения:
- Выбрать интервал времени, на котором температура падала.
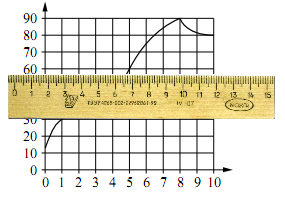
- Приложить линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.
- С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.
- Методом исключения выберем недостающий вариант ответа.
Решение:
Выберем интервал времени, на котором температура падала. Этот участок видно не вооруженным глазом, он начинается в 8 мин от момента запуска двигателя.
Г – 2
Приложим линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.
Ниже линейки окажется участок, соответствующий интервалу времени 0 – 1 мин.
А – 4
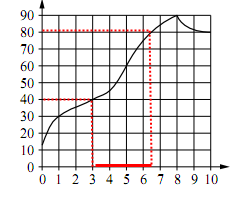
С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.
Опустим из точек, соответствующих 40°С и 80°С перпендикуляры на график, а из полученных точек опустим перпендикуляры на ось времени.
Видим, что этому температурному интервалу соответствует интервал времени 3 – 6,5 мин. То есть из приведенных в условии 3 – 6 мин.
В – 3
Методом исключения выберем недостающий вариант ответа.
Б – 1
Ответ:
А – 4
Б – 1
В – 3
Г – 2
Вариант 14МБ2
[su_note note_color=”#defae6″]
Установите соответствие между графиками функций и графиками их производных.
[/su_note]
Алгоритм выполнения для каждой из функций:
- Определить промежутки возрастания и убывания функций.
- Определить точки максимума и точки минимума функций.
- Сделать выводы, поставить в соответствие предложенные графики.
Решение:
Проанализируем график функции А. Если Функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. В точке максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 3.
А – 3
Проанализируем график функции Б.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 4. Точка максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
Б – 4
Проанализируем график функции В.
Сначала функция В возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. Точка максимума функции x = 1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
В – 2
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 1.
Г – 1
А – 3
Б – 4
В – 2
Г – 1
Ответ: 3421.
Вариант 14МБ3
[su_note note_color=”#defae6″]
Установите соответствие между графиками функций и графиками их производных.
[/su_note]
Алгоритм выполнения для каждой из функций:
- Определить промежутки возрастания и убывания функций.
- Определить точки максимума и точки минимума функций.
- Сделать выводы, поставить в соответствие предложенные графики.
Решение:
Проанализируем график функции А.
Если функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 3 и 4. В точке максимума функции x=0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
А – 4
Проанализируем график функции Б.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x=-1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
Б – 2
Проанализируем график функции В.
Сначала функция В убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x = 0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 1.
В – 1
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 3.
Г – 3
А – 4
Б – 2
В – 1
Г – 3
Ответ: 4213.
Вариант 14МБ4
[su_note note_color=”#defae6″]
На рисунке изображен график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. В правом столбце указаны значения производной в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
ТОЧКИ
А
В
С
D
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) –4
2) 3
3) 2/3
4) -1/2
[/su_note]
Вспомним, что означает производная, а именно ее значение в точке – значение функции производной в точке равно тангенсу угла наклона (коэффициенту) касательной.
В ответах у нас есть два положительных, и два отрицательных варианта. Как мы помним, если коэффициент прямой (графика y = kx+ b) положительный – то прямая возрастает, если же он отрицательный – то прямая убывает.
Возрастающих прямых у нас две – в точке A и D. Теперь вспомним, что же означает значение коэффициента k?
Коэффициент k показывает, насколько быстро возрастает или убывает функция (на самом деле коэффициент k сам является производной функции y = kx+ b).
Поэтому k = 2/3 соответствует более пологой прямой – D, а k = 3 – A.
Аналогично и в случае с отрицательными значениями: точке B соответствует более крутая прямая с k = – 4, а точке С – -1/2.
Вариант 14МБ5
[su_note note_color=”#defae6″]
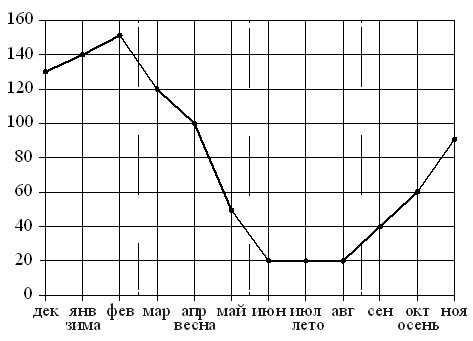
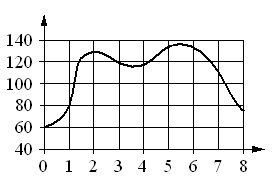
На рисунке точками показаны объемы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных обогревателей. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.
[/su_note]
Алгоритм выполнения
Анализируем части графика, соответствующие разным временам года. Формулируем ситуации, отображенные на графике. Находим для них наиболее подходящие варианты ответов.
Решение:
Зимой кол-во продаж превысило 120 шт./мес., причем оно все время увеличивалось. Эта ситуация соответствует варианту ответа №3. Т.е. получаем: А–3.
Весной продажи постепенно упали со 120 обогревателей за месяц до 50. Наиболее приближенным к этой формулировке является вариант №2. Имеем: Б–2.
Летом кол-во продаж не менялась и была минимальной. 2-я часть этой формулировки не отражена в ответах, а для первой подходит только №4. Отсюда имеем: В–4.
Осенью продажи росли, однако их кол-во ни в одном из месяцев не превысило 100 штук. Эта ситуация описана в варианте №1. Получаем: Г–1.
Вариант 14МБ6
[su_note note_color=”#defae6″]
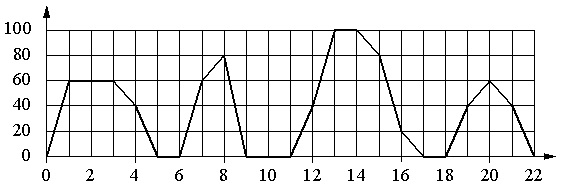
На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной – время в минутах, прошедшее с начала движения автобуса.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.
[/su_note]
Алгоритм выполнения
- Определяем цену деления на горизонтальной и на вертикальной шкале.
- Анализируем по очереди предложенные утверждения 1–4 из правой колонки («Характеристики»). Сопоставляем их с временными интервалами из левой колонки таблицы, находим пары «буква–число» для ответа.
Решение:
Цена деления горизонтальной шкалы составляет 1 с, вертикальной – 20 км/ч.
Далее анализируем характеристики, данные в правой колонке таблицы.
- Когда автобус делает остановку, его скорость равна 0. Нулевую скорость в течение 2 минут подряд автобус имел только с 9-й по 11-ю минуту. Это время попадает в интервал 8–12 мин. Значит, имеем пару для ответа: Б–1.
- Скорость 20 км/ч и больше автобус имел в течение нескольких временных промежутков. Причем вариант А здесь не подходит, т.к., к примеру, на 7-й минуте скорость составляла 60 км/ч, вариант Б – потому что он уже применен, вариант Г – потому что в начале и конце промежутка автобус имел нулевую скорость. В данном случае подходит вариант В (12–16 мин); на этом промежутке автобус начинает движение со скоростью 40 км/ч, далее ускоряется до 100 км/м и потом постепенно снижает скорость до 20 км/ч. Итак, имеем: В–2.
- Здесь установлено ограничение для скорости. При этом варианты Б и В мы не рассматриваем. Оставшиеся же интервалы А и Г подходят оба. Поэтому правильно будет рассмотреть сначала 4-й вариант, а потом снова вернуться в 3-му.
- Из двух оставшихся интервалов для характеристики №4 подходит только 4–8 мин, поскольку на этом промежутке остановка была (на 6-й минуте). На промежутке 18–22 мин остановок не было. Получаем: А–4. Отсюда следует, что для характеристики №3 нужно взять интервал Г, т.е. получается пара Г–3.
Вариант 14МБ7
[su_note note_color=”#defae6″]
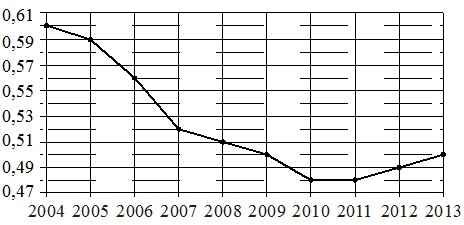
На рисунке точками показан прирост населения Китая в период с 2004 по 2013 год. По горизонтали указывается год, по вертикали – прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику прироста населения Китая в этот период.
[/su_note]
Алгоритм выполнения
- Определяем цену деления вертикальной шкалы рисунка. Находится она как разница пары соседних значений шкалы, деленная на 2 (т.к. между двумя соседними значениями имеется 2 деления).
- Анализируем последовательно приведенные в условии характеристики 1–4 (левая табличная колонка). Сопоставляем каждую из них с конкретным периодом времени (правая табличная колонка).
Решение:
Цена деления вертикальной шкалы составляет 0,01%.
- Падение прироста непрерывно продолжалось с 2004 по 2010 год. В 2010–2011 годах прирост был стабильно минимальным, и начиная с 2012 года оно начал увеличиваться. Т.е. остановка прироста произошла в 2010 году. Этот год находится в периоде 2009–2011 гг. Соответственно, имеем: В–1.
- Наибольшим падением прироста следует считать самую «круто» падающую линию графика на рисунке. Она приходится на период 2006–2007 гг. и составляет 0,04%, за год (0,59–0,56=0,04% в 2006 г. и 0,56–0,52=0,04% в 2007 г.). Отсюда получаем: А–2.
- Указанный в характеристике №3 прирост начался с 2007 года, продолжился в 2008 г. и завершился в 2009 году. Это соответствует периоду времени Б, т.е. имеем: Б–3.
- Прирост населения начал увеличиваться после 2011 г., т.е. в 2012–2013 гг. Поэтому получаем: Г–4.
Вариант 14МБ8
[su_note note_color=”#defae6″]
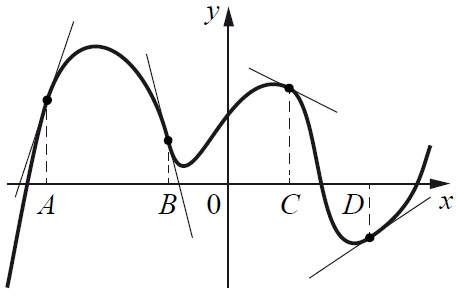
На рисунке изображены график функции и касательные, проведенные к нему в точках с абсциссами А,В,С и D.
В правом столбце указаны значения производной функции в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
[/su_note]
Алгоритм выполнения
- Рассматриваем пару касательных, имеющих острый угол с положит.направлением оси абсцисс. Сравниваем их, находим соответствие среди пары соответствующих значений производных.
- Рассматриваем пару касательных, образующих с положит.направлением оси абсцисс тупой угол. Сравниваем их по модулю, определяем соответствие их значениям производных среди двух оставшихся в правой колонке.
Решение:
Острый угол с положит.направлением оси абсцисс образуют производные в т.В и т.С. Эти производные имеют положит.значения. Поэтому выбирать тут следует между значениями №№1 и 3. Применяя правило о том, что если угол меньше 450, то производная меньше 1, а если больше, то больше 1, делаем вывод: в т.В производная по модулю больше 1, в т.С – меньше 1. Это означает, что можно составить пары для ответа: В–3 и С–1.
Производные в т.А и т.D образуют с положит.направлением оси абсцисс тупой угол. И тут применяем то же правило, немного перефразировав его: чем больше касательная в точке «прижата» к линии оси абсцисс (к отрицат. ее направлению), тем больше она по модулю. Тогда получаем: производная в т.А по модулю меньше, чем производная в т.D. Отсюда имеем пары для ответа: А–2 и D–4.
Вариант 14МБ9
[su_note note_color=”#defae6″]
На рисунке точками показана среднесуточная температура воздуха в Москве в январе 2011 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры.
[/su_note]
Алгоритм выполнения
Анализируем последовательно характеристики 1–4 (правая колонка), используя график на рисунке. Ставим каждой из них в соответствие конкретный временной период (левая колонка).
Решение:
- Рост температуры наблюдался только в конце периода 22–28 января. Здесь 27 и 28 числа она повышалась соответственно на 1 и на 2 градуса. В конце периода 1–7 января температура была стабильной (–10 градусов), в конце 8–14 и 15–21 января понижалась (с –1 до –2 и с –11 до –12 градусов соответственно). Поэтому получаем: Г–1.
- Поскольку каждый временной период охватывает 7 дней, то анализировать нужно температуру, начиная с 4-го дня каждого периода. Неизменной в течение 3–4 дней температура была только с 4 по 7 января. Поэтому получаем ответ: А–2.
- Месячный минимум температуры наблюдался 17 января. Это число входит в период 15–21 января. Отсюда имеем пару: В–3.
- Температурный максимум пришелся 10 января и составил +1 градус. Эта дата попадает в период 8–14 января. Значит, имеем: Б–4.
Вариант 14МБ10
[su_note note_color=”#defae6″]
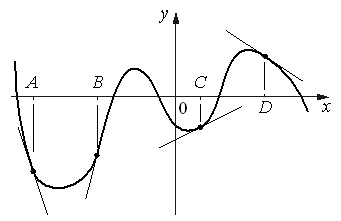
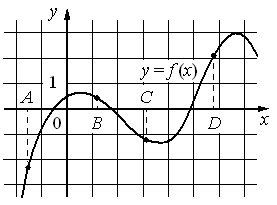
На рисунке изображен график функции y=f(x) и отмечены точки А, В, С и D на оси Ох..
Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и ее производной
[/su_note]
Алгоритм выполнения
- Значение функции в точке положительно, если эта точка расположена выше оси Ох.
- Производная в точке больше нуля, если касательная к этой точке образует острый угол с положительным направлением оси Ох.
Решение:
Точка А. Она находится ниже оси Ох, значит значение функции в ней отрицательно. Если провести в ней касательную, то угол между нею и положит.направлением Ох составит около 900, т.е. образует острый угол. Значит, в данном случае подходит характеристика №3. Т.е. имеем: А–3.
Точка Б. Она находится над осью Ох, т.е. точка имеет положит.значение функции. Касательная в этой точке будет довольно близко «прилегать» к оси абсцисс, образуя тупой угол (немногим меньше 1800) с положительным ее направлением. Соответственно, производная в этой точке отрицательна. Т.о., здесь подходит характеристика 1. Получаем ответ: В–1.
Точка С. Точка расположена ниже оси Ох, касательная в ней образует большой тупой угол с положит.направлением оси абсцисс. Т.е. в т.С значение и функции, и производной отрицательно, что соответствует характеристике №2. Ответ: С–2.
Точка D. Точка находится выше оси Ох, а касательная в ней образует с положит.направлением оси острый угол. Это говорит о том, что как значение функции, так и значение производной здесь больше нуля. Ответ: D–4.
Вариант 14МБ11
[su_note note_color=”#defae6″]
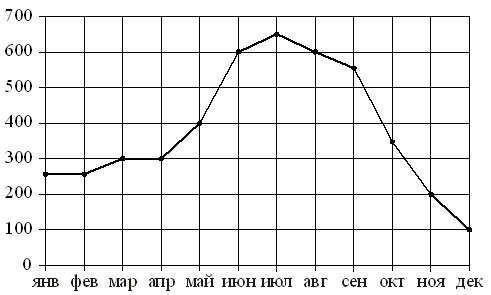
На рисунке точками показаны объемы месячных продаж холодильников в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных холодильников. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников.
[/su_note]
Алгоритм выполнения
- При необходимости найти кол-во холодильников за тот или иной период нужно определять их сумму за три месяца.
- Анализировать следует характеристики 1–4 (правая колонка), находя для каждой из них соответствие в виде временного периода (левая колонка).
Решение:
Анализируем характеристики:
- Меньше всего холодильников продано в начале и в конце года. Поэтому рассмотрим периоды январь–март и октябрь–декабрь. В январе–марте было продано примерно 250+250+300=800 холодильников, в октябре–декабре – примерно 350+200+100=650. Значит, здесь подходит все-таки последний период. Ответ: Г–1.
- Длительный рост продаж наблюдался с апреля по июль. Это время охватывает полностью период апрель–июнь и захватывает начало следующего. Поэтому получаем: Б–2.
- Тут тоже требуется найти сумму проданных единиц за целые периоды. Для 1-го и последнего периода она уже найдена (см.п.1). Считаем для 2-го и 3-го, получаем: 300+400+600=1300 – в апреле–июне, примерно 650+600+550=1800 – в июле–сентябре. К требуемым 800 холодильникам максимально приближен объем продаж в январе–марте. Поэтому имеем: А–3.
- Одинаковое падение объема продаж означает, что разница между кол-вом проданных холодильников должна быть одинаковой. Падение продаж наблюдалось, начиная с конца июля. В августе падение составило 650–600=50 штук, в сентябре – 600–550=50 штук. Далее, в октябре, разница составила уже 550–350=200 холодильников, в ноябре 350–200=150, в декабре 200–100=100. Т.о., подходит в данном случаем период июль–сентябрь. Ответ: В–4.
Вариант 14МБ12
[su_note note_color=”#defae6″]
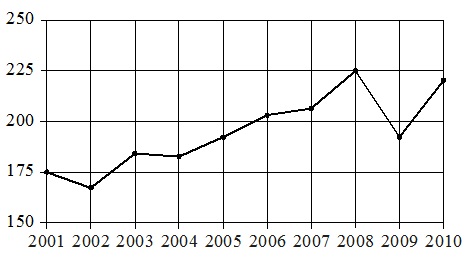
На рисунке точками показан годовой объем добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указывается год, по вертикали – объем добычи угля в миллионах тонн. Для наглядности точки соединены линиями.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов характеристику добычи угля в этот период.
[/su_note]
Алгоритм выполнения
- Точки, которые не приходятся на точные значения шкалы вертикальной оси, определяем приблизительно.
- Анализируем по очереди приведенные (в правом столбце) характеристики, используя данный график. Определяем соответствие каждой из них конкретного временного периода.
Решение:
Анализируем характеристики:
- Объем добычи меньше 190 млн т приходился на период с 2001 года по 2005 год. Затем спад добычи зафиксирован в 2009 году, но один год не составляет периода. 2001–2005 годы полностью попадают в период А (2002–2004 гг.). Поэтому получаем ответ: А–1.
- Такая формулировка «объем… сначала уменьшался, а затем начал расти» соответствует 2 периодам – 2002–2003 гг. и 2009–2010 гг. Но т.к. первый из этих периодов уже взят в качестве ответа, то правильно здесь использовать пару Г–2.
- Ситуация, описанная в 3-й характеристике, наиболее точно отображена в периоде 2006–2008 гг. Именно в это время добыча сначала понемногу увеличивалась (примерно с 190 млн т до 210), а потом резко возросла до 250 млн т. Т.е. подходящий ответ здесь: 2006–2008 гг. и, соответственно, имеем: В–3.
- Медленный рост следует искать в период, когда линия графика имеет наиболее пологий вид. Это: 2004–2006 год, что соответствует периоду Б, т.е. получаем: Б–4.
Вариант 14МБ13
[su_note note_color=”#defae6″]
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси – температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику температуры.
[/su_note]
Алгоритм выполнения
Анализируем сначала очередную характеристику, а затем сопоставляем ее с конкретным временным интервалом.
Решение:
- Выше 600 температура была с 4-й по 7-ю минуту. Поэтому здесь нужно взять интервал 4–6 мин. Получаем: В–1.
- Температура падала только после 7-й минуты. Соответственно, тут подходит интервал 7–9 мин. Ответ: Г–2.
- Самый быстрый рост температуры происходил там, где график имеет наиболее «крутой» вертикальный подъем. Это имеет место только в 1-ю минуту нагревания. Т.е. подходящим интервалом является 0–1 мин. Ответ: А–3.
- В пределах 40–50 0С температура имела место, начиная со 2-й по 3-ю минуту. Значит, нужно выбрать интервал 2–3мин. Ответ: Б–4.
Вариант 14МБ14
[su_note note_color=”#defae6″]
На графике изображена зависимость частоты пульса гимнаста от времени в течение и после его выступления в вольных упражнениях. На горизонтальной оси отмечено время (в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси – частота пульса (в ударах в минуту).
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику пульса гимнаста на этом интервале.
[/su_note]
Алгоритм выполнения
- Для анализа характеристики нужно использовать только 1-ю половину графика.
- Для точек графика, которые не попадают в «узлы» сетки рисунка (т.е. для которых невозможно определить точные значения), нужно определять значения приблизительно.
- Величина роста пульса связана с пологостью (или, напротив, крутизной) линии графика. Это означает, что чем большее изменение значения функции происходит за тот или иной (но обязательно одинаковый) промежуток времени, тем больше величина роста.
Решение:
Анализируем предложенные характеристики:
- Если частота пульса сначала падала, а затем росла, то на графике это должно выразиться в «прогибе» линии графика вниз. Такая кривизна наблюдается только в течение 3–4 минуты. Значит, получаем ответ: Г–1.
- Самый большой «подъем» линии на 1-й половине графика имеет место с 1-й по 2-ю минуту. Отсюда получаем: Б–2.
- Частота пульса падала, начиная со 2-й минуты. В течение 3–4 минут тоже наблюдалось падение, однако оно потом перешло в рост. Поэтому правильным здесь следует считать интервал В. Т.о., ответ: В–3.
- Единственный интервал, на котором частота не превысила 100 ударов, – 0–1 мин. Отсюда имеем ответ: А–4.
Даниил Романович | Просмотров: 21.2k
В данном блоке представлен тренажер заданий «Производная и графики»
Скачать:
Предварительный просмотр:
- На рисунке изображен график функции y=f(x), определенной на интервале (−2;12). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−7;5). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−7;5). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−7;5). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−4;8). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−9;5). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−5;9). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−1;13). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−8;5). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−8;3). Найдите сумму точек экстремума функции f(x).
- На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Найдите сумму точек экстремума функции f(x).
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
- Прямая y=3x+1 является касательной к графику функции ax2+2x+3. Найдите a.
- Прямая y=−5x+8 является касательной к графику функции 28x2+bx+15. Найдите b, учитывая, что абсцисса точки касания больше 0.
- Прямая y=3x+4 является касательной к графику функции 3x2−3x+c. Найдите c.
- Прямая y = 7x−5 параллельна касательной к графику функции y = x2+6x−8. Найдите абсциссу точки касания.
- Прямая y = 6x+8 параллельна касательной к графику функции y = x2−3x+5. Найдите абсциссу точки касания.
- рямая y = 3x+6 параллельна касательной к графику функции y = x2−5x+8. Найдите абсциссу точки касания.
- Прямая y = 8x+11 параллельна касательной к графику функции y = x2+5x+7. Найдите абсциссу точки касания
- Прямая y = −4x−11 является касательной к графику функции y = x3+7x2+7x−6. Найдите абсциссу точки касания.
- Прямая y = −2x+6 является касательной к графику функции y = x3−3x2+x+5. Найдите абсциссу точки касания.
- Прямая y = −x+14 является касательной к графику функции y = x3−4x2+3x+14. Найдите абсциссу точки касания.
- Прямая y = x+9 является касательной к графику функции y = x3−3x2+4x+8. Найдите абсциссу точки касания.
- Прямая y = −6x−10 является касательной к графику функции y = x3+4x2−6x−10. Найдите абсциссу точки касания.
- Материальная точка движется прямолинейно по закону x(t)=6t2−48t+17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9 с.
- Материальная точка движется прямолинейно по закону x(t)=
t3−3t2+2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=6 с.
- Материальная точка движется прямолинейно по закону x(t)=−t4+6t3+5t+23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=3 с.
- Материальная точка движется прямолинейно по закону x(t)=t2−13t+23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
- Материальная точка движется прямолинейно по закону x(t)=
t3−3t2−5t+3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
- На рисунке изображён график функции y=f(x), определённой на интервале (− 9; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
- На рисунке изображён график функции y=f(x), определённой на интервале (− 5; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
- На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Определите количество целых точек, в которых производная функции положительна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−5;6). Определите количество целых точек, в которых производная функции положительна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−9;8). Определите количество целых точек, в которых производная функции f(x) положительна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−2;11). Определите количество целых точек, в которых производная функции положительна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Определите количество целых точек, в которых производная функции положительна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Определите количество целых точек, в которых производная функции положительна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−1;12). Определите количество целых точек, в которых производная функции отрицательна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−7;7). Определите количество целых точек, в которых производная функции отрицательна.
- На рисунке изображен график функции y=f(x), определенной на интервале (−4;9). Определите количество целых точек, в которых производная функции отрицательна.
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−8;3). В какой точке отрезка [−3;2] функция f(x) принимает наибольшее значение?
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−6;6). В какой точке отрезка [−5;−1] функция f(x) принимает наибольшее значение?
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−6;6). В какой точке отрезка [3;5] функция f(x) принимает наибольшее значение?
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−2;9). В какой точке отрезка [2;6] функция f(x) принимает наибольшее значение?
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−8;3). В какой точке отрезка [−3;2] функция f(x) принимает наибольшее значение?
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−8;5). В какой точке отрезка [−1;4] функция f(x) принимает наибольшее значение?
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−7;5). В какой точке отрезка [−1;3] функция f(x) принимает наибольшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−2;9). В какой точке отрезка [−1;3] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−2;9). В какой точке отрезка [2;6] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) — производной функции f(x), определенной на интервале (−8;4). В какой точке отрезка [−7;−3] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−7;5). В какой точке отрезка [−6;−1] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−4;9). В какой точке отрезка [−2;2] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−9;8). В какой точке отрезка [−8;−4] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−9;8). В какой точке отрезка [1;7] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−9;8). В какой точке отрезка [−5;3] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−5;5). В какой точке отрезка [−4;−1] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
- На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наименьшее значение?
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−7;14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−6;9].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−4;16). Найдите количество точек максимума функции f(x), принадлежащих отрезку [0;13].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−13;8). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−8;6].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−21;2). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−19;1].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−17;5). Найдите количество точек максимума функции f(x), принадлежащих отрезку [−15;0].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−1;16). Найдите количество точек максимума функции f(x), принадлежащих отрезку [0;15].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−18;6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [−13;1].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−2;21). Найдите количество точек минимума функции f(x), принадлежащих отрезку [2;19].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−17;2). Найдите количество точек минимума функции f(x), принадлежащих отрезку [−12;1].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−22;2). Найдите количество точек минимума функции f(x), принадлежащих отрезку [−17;0].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−10;12). Найдите количество точек минимума функции f(x), принадлежащих отрезку [−9;10].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−14;4). Найдите количество точек минимума функции f(x), принадлежащих отрезку [−13;3].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−11;11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−10;10].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−5;5). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−4;4].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−12;5). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−10;0].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−8;16). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−4;15].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−4;20). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [0;18].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−2;15). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [2;10].
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−7;4). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−6;6). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−5;5). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−1;13). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−6;10). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−3;8). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−2;10). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−2;9). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−3;9). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−2;12). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−5;7). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−5;7). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−4;7). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−6;7). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−4;9). В ответе укажите сумму целых точек, входящих в эти промежутки.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−11;3). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−16;2). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−6;8). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−4;10). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−5;10). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки возрастания функции (−6;8). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−1;14). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−14;3). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−2;12). В ответе укажите длину наибольшего из них.
На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−3;14). В ответе укажите длину наибольшего из них.
На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−2;16). В ответе укажите длину наибольшего из них.
- На рисунке изображен график y=f(x) — производной функции y=f′(x), определенной на интервале f(x). Найдите промежутки убывания функции (−12;2). В ответе укажите длину наибольшего из них.
- На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
- На рисунке изображен график y=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2x−2 или
совпадает с ней.
- На рисунке изображен график y=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−9;8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=x−7 или совпадает с ней.
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−9;8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=−x+8 или совпадает с ней.
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−6;6). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=−3x−11 или совпадает с ней.
- На рисунке изображен график функции y=f(x), определенной на интервале (−5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6.
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−5;5). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=−0,5x+9 или совпадает с ней.
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−5;5). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=−2x+2 или совпадает с ней.
- На рисунке изображен график функции y=f(x), определенной на интервале (−1;10). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=−3.
- На рисунке изображен график функции y=f(x), определенной на интервале (−3;8). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=−20.
- На рисунке изображен график функции y=f(x), определенной на интервале (−2;12). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=7.
- На рисунке изображен график функции y=f(x), определенной на интервале (−9;3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=14.
- На рисунке изображен график функции y=f(x), определенной на интервале (−4;10). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=−10.
- На рисунке изображен график функции y=f(x), определенной на интервале (−5;9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=−10.
- На рисунке изображен график функции y=f(x), определенной на интервале (−1;13). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=11.
- На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9;
. Найдите точку экстремума функции f(x) на отрезке [−3; 3].
- На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (−6;6). Найдите точку экстремума функции f(x) на интервале (−4;5).
- На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ;
. Найдите точку минимума функции f(x).
- На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: x1, x2,x3, …, x8. В скольких из этих точек производная функции f(x) положительна?
- На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7. В скольких из этих точек производная функции f(x) положительна?
- На рисунке изображён график функции y=f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, …, x12. В скольких из этих точек производная функции f(x) отрицательна?
- На рисунке изображён график y=f′(x) — производной функции f(x). На оси абсцисс отмечено восемь точек: x1, x2, x3, …, x8. Сколько из этих точек лежит на промежутках возрастания функции f(x)?
- На рисунке изображён график y=f′(x) — производной функции f(x). На оси абсцисс отмечено восемь точек: x1, x2, x3, …, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
- На рисунке изображен график функции y=f(x) и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
- На рисунке изображен график функции y=f(x) и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
- На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (−3;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−2;4].
- На рисунке изображён график функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)−F(2), где F(x) — одна из первообразных функции f(x).
- На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x3+30x2+302x−158 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
- На рисунке изображён график некоторой функции y=f(x). Функция F(x)=−x3−27x2−240x−8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
- На рисунке изображен график функции y=f(x), определенной на интервале (−9;8). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=10.
По теме: методические разработки, презентации и конспекты
Каталог заданий В1,В2
Материал взят с сайта www.rechuege.ru Дмитрия Гущина и предназначен для отработки заданий на вычисление В1 и В2…
- Мне нравится
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Производная и первообразная функции»
Открытый банк заданий по теме производная и первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1165
Условие
Прямая y=3x+2 является касательной к графику функции y=-12x^2+bx-10. Найдите b, учитывая, что абсцисса точки касания меньше нуля.
Показать решение
Решение
Пусть x_0 — абсцисса точки на графике функции y=-12x^2+bx-10, через которую проходит касательная к этому графику.
Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=-24x_0+b=3. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть -12x_0^2+bx_0-10=3x_0+2. Получаем систему уравнений begin{cases} -24x_0+b=3,\-12x_0^2+bx_0-10=3x_0+2. end{cases}
Решая эту систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания меньше нуля, поэтому x_0=-1, тогда b=3+24x_0=-21.
Ответ
-21
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1164
Условие
На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).
Показать решение
Решение
По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.
Её площадь равна frac{4+3}{2}cdot 3=10,5.
Ответ
10,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1163
Условие
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-4; 10). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Показать решение
Решение
Как известно, функция f(x) убывает на тех промежутках, в каждой точке которых производная f'(x) меньше нуля. Учитывая, что надо находить длину наибольшего из них естественно по рисунку выделяются три таких промежутка: (-4; -2); (0; 3); (5; 9).
Длина наибольшего из них — (5; 9) равна 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1162
Условие
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-8; 7). Найдите количество точек максимума функции f(x), принадлежащих промежутку [-6; -2].
Показать решение
Решение
Из графика видно, что производная f'(x) функции f(x) меняет знак с плюса на минус (именно в таких точках будет максимум) ровно в одной точке (между -5 и -4) из промежутка [-6; -2]. Поэтому на промежутке [-6; -2] ровно одна точка максимума.
Ответ
1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1161
Условие
На рисунке изображён график функции y=f(x), определённой на интервале (-2; 8). Определите количество точек, в которых производная функции f(x) равна 0.
Показать решение
Решение
Равенство нулю производной в точке означает, что касательная к графику функции, проведённая в этой точке, параллельна оси Ox. Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 5.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1160
Условие
Прямая y=-3x+4 параллельна касательной к графику функции y=-x^2+5x-7. Найдите абсциссу точки касания.
Показать решение
Решение
Угловой коэффициент прямой к графику функции y=-x^2+5x-7 в произвольной точке x_0 равен y'(x_0). Но y’=-2x+5, значит, y'(x_0)=-2x_0+5. Угловой коэффициент прямой y=-3x+4, указанной в условии, равен -3. Параллельные прямые имеют одинаковые угловые коэффициенты. Поэтому находим такое значение x_0, что =-2x_0 +5=-3.
Получаем: x_0 = 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1159
Условие
На рисунке изображён график функции y=f(x) и отмечены точки -6, -1, 1, 4 на оси абсцисс. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Показать решение
Решение
Проводим касательные к графику функции в точках с указанными абсциссами. Определяем, под каким углом они наклонены к положительному направлению оси Ox. Как известно, значение тангенса указанного угла это и есть значение производной в указанных точках.
В точках -1 и 4 касательные наклонены под острым углом, поэтому в этих точках значение производной отрицательно. Учитывая, что в точке x=-6 касательная наклонена под меньшим тупым углом (ближе к вертикальной прямой), значение производной в этой точке наименьшее.
Ответ
-6
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1158
Условие
На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].
Показать решение
Решение
Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).
Ответ
7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1157
Условие
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x_0. Найдите значение производной функции f(x) в точке x_0.
Показать решение
Решение
По рисунку определяем, что касательная проходит через точки A(-6; 2) и B(-1; 1). Обозначим через C(-6; 1) точку пересечения прямых x=-6 и y=1, а через alpha угол ABC (на рисунке видно, что он острый). Тогда прямая AB образует с положительным направлением оси Ox угол pi -alpha, который является тупым.
Как известно, tg(pi -alpha) и будет значением производной функции f(x) в точке x_0. Заметим, что tg alpha =frac{AC}{CB}=frac{2-1}{-1-(-6)}=frac15. Отсюда по формулам приведения получаем: tg(pi -alpha ) =-tg alpha =-frac15=-0,2.
Ответ
-0,2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1156
Условие
Прямая y=-2x-4 является касательной к графику функции y=16x^2+bx+12. Найдите b, учитывая, что абсцисса точки касания больше нуля.
Показать решение
Решение
Пусть x_0 — абсцисса точки на графике функции y=16x^2+bx+12, через которую
проходит касательная к этому графику.
Значение производной в точке x_0 равно угловому коэффициенту касательной, то есть y'(x_0)=32x_0+b=-2. С другой стороны, точка касания принадлежит одновременно и графику функции и касательной, то есть 16x_0^2+bx_0+12=-2x_0-4. Получаем систему уравнений begin{cases} 32x_0+b=-2,\16x_0^2+bx_0+12=-2x_0-4. end{cases}
Решая систему, получим x_0^2=1, значит либо x_0=-1, либо x_0=1. Согласно условию абсцисса точки касания больше нуля, поэтому x_0=1, тогда b=-2-32x_0=-34.
Ответ
-34
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
















































































































































.png)



.png)
