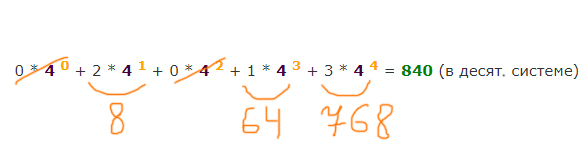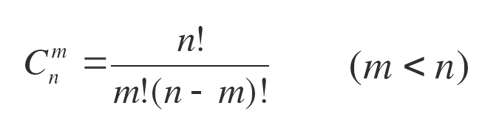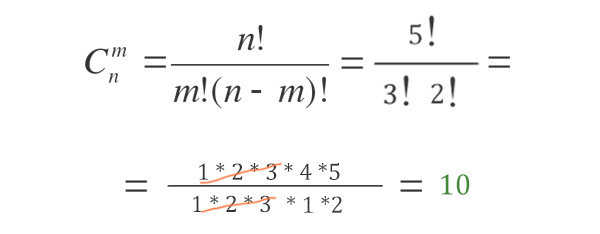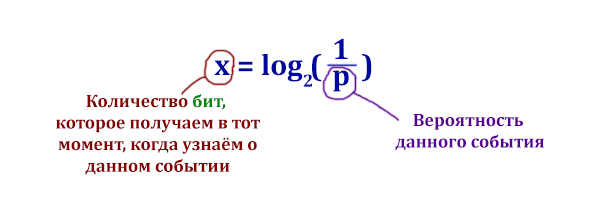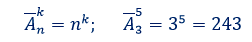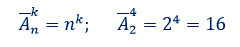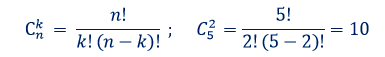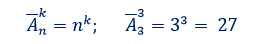Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
2
Сколько слов длины 6, начинающихся с согласной буквы, можно составить из букв Г, О, Д? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
3
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
4
Вася составляет 5-буквенные слова, в которых есть только буквы С, Л, О, Н, причём буква С используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Источник: ЕГЭ 05.05.2015. Досрочная волна.
5
Сколько слов длины 6, начинающихся и заканчивающихся согласной буквой, можно составить из букв Г, О, Д? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Пройти тестирование по этим заданиям
Сегодня на повестке дня 8 задание из ЕГЭ по информатике 2021. Данный тип заданий включает в себя нахождение количества вариантов, элементы комбинаторики и другие математические понятия.
Перейдём к практике решения задач задания 8 ЕГЭ по информатике 2021.
Задача (Классика)
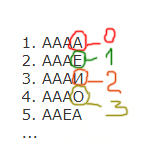
Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…
Запишите слово, стоящее на 248-м месте от начала списка.
Решение:
Обозначим условно А — 0, Е — 1, И — 2, О — 3.
Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.
Теперь запишем список с помощью цифр.
1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…
Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.
Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.
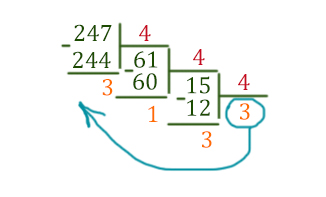
Переведём число 247 в четверичную систему!
Получилось число 33134 в четверичной системе. Сделаем обратное декодирование в буквы. Таким образом, ответ будет ООЕО.
Ответы: ООЕО
Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике, но другой вариации.
Задача (Классика, Другая вариация)
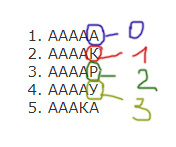
Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА
Решение:
Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.
У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.
1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……
Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!
Получили число в четверичной системе 310204. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 310204 из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.
Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу 840 нужно прибавить 1, и в ответе будет 841
Ответ: 841
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)
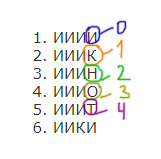
Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И,
записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…
Под каким номером в списке идёт первое слово, которое начинается
с буквы О?
Решение:
Закодируем буквы цифрами.
Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.
Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 30005. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.
Теперь, как в предыдущей задаче, переведём число 30005 из пятеричной системы в десятичную.
0 * 5 0 + 0 * 5 1 + 0 * 5 2 +
3 * 5 3 = 375 (в десят. системе)
Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.
Ответ: 376
Задача (Досрочная волна 2020 ЕГЭ по информатике, вариант 1)
Вася составляет 5-буквенные слова, в которых есть только буквы В, О, Л, К,
причём буква В используется в каждом слове ровно 1 раз. Каждая из других
допустимых букв может встречаться в слове любое количество раз или
не встречаться совсем. Словом считается любая допустимая
последовательность букв, не обязательно осмысленная. Сколько существует
таких слов, которые может написать Вася?
Решение:
Для начала решим вводную подзадачу.
Пусть у нас есть те же буквы В, О, Л, К, каждая из букв может встречаться в слове любое количество раз или
не встречаться совсем. Сколько можно составить 5-буквенных слов ?
Т.е буквы могут повторяться!
Например
Такая конструкция сильно напоминает перебор чисел, где вместо цифр используются буквы.
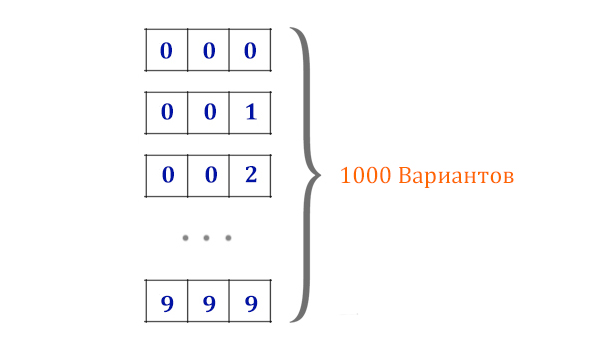
Рассмотрим перебор трёхразрядных чисел. Вместо 5 букв теперь можно использовать 10 цифр ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). Цифры так же могут повторяться. Сколько получится вариантов ?
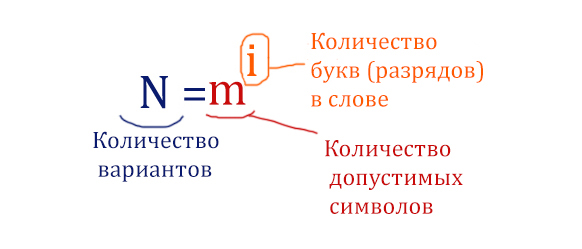
Выведем общую формулу для количества вариантов, когда символы могут повторяться!
Для трёхразрядных чисел от 000 до 999:
N = 103 = 1000 вариантов.
Вернёмся к пятибуквенным словам и нашей подзадаче. Здесь количество букв (разрядов) в слове равно 5, количество допустимых символов равно 4 ( В, О, Л, К ).
N = 45 = 1024 вариантов.
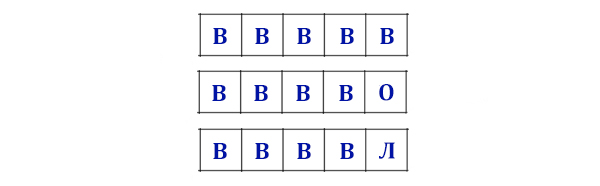
Вернёмся к изначальной задаче. Сначала найдём количество вариантов, когда буква В находится в самой левой ячейке!
Применим формулу! Здесь слово сократилось до четырёхразрядного. А количество букв для использования 3 (О, Л, К).
N = 34 = 81 комбинация.
Но буква В так же может стоять во второй ячейке слева. Этот случай тоже даст 81 других комбинаций. Буква В может стоять в каждой из 5-ти ячеек, и везде будет получатся 81 комбинация.
Таким образом, окончательный ответ будет:
N = 81 * 5 = 405 различных вариантов.
Ответ: 405
Разобравшись с этой задачей, больше половины тренировочных задач десятого задания из различных книг и сайтов по подготовке к ЕГЭ по информатике будут решаться, как по маслу!
Задача(Закрепление формулы)
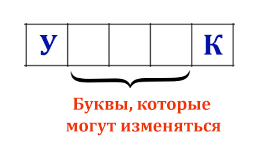
Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?
Решение:
Применим главную формулу 8 задания из ЕГЭ по информатике
N = mi = 63 = 216
Здесь буквы могут изменяться на 3 ячейках! Значит, в формуле i=3. Количество допустимых символов, которые можно поставить в каждую ячейку равно 6. Значит, в формуле m=6.
В ответе будет 216.
Примечание: Здесь можно использовать все буквы в каждой ячейке, включая У и К. В некоторых задачах их уже использовать нельзя, т.е. сказано, что буквы У и К используются один раз в слове. Тогда в формуле m, будет на 2 единицы меньше. Нужно внимательно читать задачу!
Ответ: 216
Задача (Демонстрационный вариант ЕГЭ по информатике, 2019)
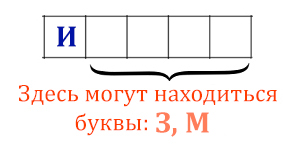
Вася составляет 5-буквенные слова, в которых есть только буквы З, И, М, А,
причём в каждом слове есть ровно одна гласная буква и она встречается
ровно 1 раз. Каждая из допустимых согласных букв может встречаться
в слове любое количество раз или не встречаться совсем. Словом считается
любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Вася?
Решение:
Рассмотрим количество вариантов, когда гласная И стоит в первом месте!
Подсчитаем количество слов с помощью супер-формулы
N = mi = 24 = 16
Длина изменяющихся ячеек равна 4, а количество допустимых букв равно 2.
Но буква И может стоять не только на первом месте. Она так же может стоять и на 2, и на 3, и на 4, и на 5 месте. Каждый такое случай добавляет столько же новых слов.
Значит, при использовании только буквы И будет количество слов 16 * 5 = 80. Ещё столько же слов добавится, если в словах вместо буквы И будет использоваться буква А. Поэтому окончательный ответ будет 80 * 2 = 160
Ответ: 160
Отработаем главную формулу 8 задания из ЕГЭ по информатике.
Задача (Развиваем понимание формулы!)
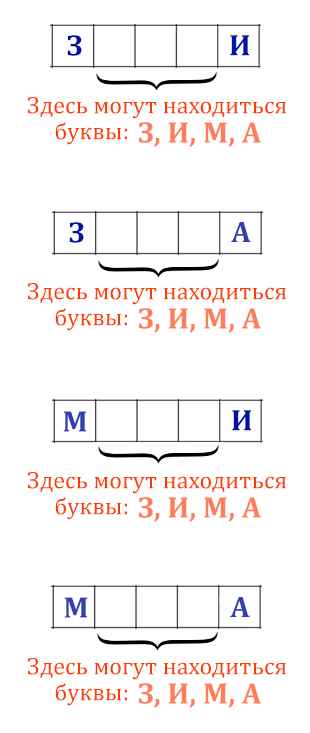
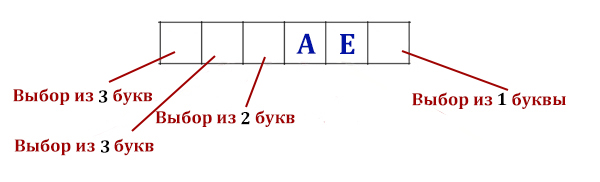
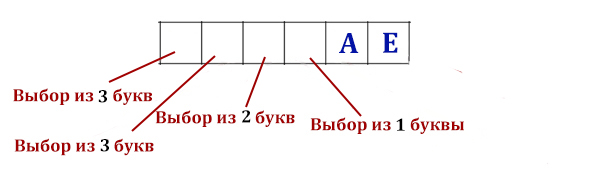
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Решение:
Рассмотрим, какие варианты могут быть, если у нас на первом месте стоит согласная, а на последнем месте гласная
Получилось 4 разных случая. Подсчитаем, сколько слов можно составить при одном случае.
N = mi = 43 = 64
Длина изменяющихся ячеек равна 3, а количество возможных букв 4.
Но т.к. таких случая у нас четыре, то ответ будет 4 * 64 = 256
Ответ: 256
Рассмотрим важнейший «метод умножения» при решении 8 задания из ЕГЭ по информатике.
Задача (Другой метод решения!!)
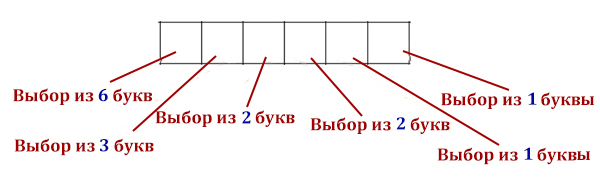
Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз , при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?
Решение:
Эта задача отличается от уже разобранных тем, что каждую букву можно использовать один раз. В этой задаче удобнее воспользоваться немного другим методом решения! «Методом умножения»!
Решим вводную подзадачу (без дополнительных ограничений).
Сколькими способами можно составить 6-x буквенное слово из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз .
Чтобы найти возможные варианты, перемножаем для каждой ячейки количество букв из которых у нас есть выбор!
N = 6 * 5 * 4 * 3 * 2 * 1 = 720
Вернёмся к изначальной задаче!
В начале подсчитаем «методом умножения» количество слов, не обращая внимание, на условие, в котором сказано, что слово не может содержать сочетание АЕ.
N = 5 * 5 * 4 * 3 * 2 * 1 = 600
В формуле стоят почти все те же самые числа, как и в вводном примере, только первый множитель не 6, а 5. Это произошло из-за того, что у нас в задаче слово не может начинаться на букву Й. Значит, выбор на первую позицию будет не из 6 букв, а из 5.
Но в 600 комбинаций входят и те случаи, когда в слове присутствует сочетание АЕ. Теперь найдём сколько таких слов, где присутствует сочетание АЕ
Узнаем количество вариантов в каждом таком случае.
N1 = 4 * 3 * 2 * 1 = 24
На первом месте мы не можем использовать букву Й, поэтому мы на первом месте выбираем из 3 букв.
N2 = 3 * 3 * 2 * 1 = 18
Аналогично предыдущему случаю.
N3 = 3 * 3 * 2 * 1 = 18
N4 = 3 * 3 * 2 * 1 = 18
N5 = 3 * 3 * 2 * 1 = 18
Всего слов с сочетанием АЕ будет
24 + 18 + 18 + 18 + 18 = 96
Значит, всего слов, которые удовлетворяют условию задаче будет
N = 600 — 96 = 504
Примечание: Метод умножения можно было использовать и в задачах, которые мы рассмотрели ранее. Например, в задаче «Закрепление формулы» в первой свободной ячейке выбираем из 6 букв, во второй свободной ячейке тоже из 6 букв, и в третий свободной ячейке тоже можно использовать 6 букв. Значит, по методу умножения получается N = 6 * 6 * 6 = 63 = 216
Ответ: 504
Задача (Закрепления «метода умножения»)
Полина составляет 6-буквенные коды из букв П, О, Л, И, Н, А. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Полина?
Решение:
Опять сказано, что каждая буква используется 1 раз, следовательно, нужно применять «метод умножения».
На первое место можно выбрать из 6 букв, предположим, мы выберем согласную. Тогда на второе место нужно выбирать из 3 гласных. Потом опять должна идти согласная, но их у нас осталось только 2. Далее, на следующее место выбираем из 2 гласных букв. И на предпоследнее место выбирается 1 согласная, а на последнее место остаётся 1 гласная.
Т.к. количество гласных букв и согласных одинаковое, и равно трём, то если мы бы начали делать «метод умножения» с гласной буквы, количество вариантов бы не поменялось.
N = 6 * 3 * 2 * 2 * 1 * 1 = 72
Ответ: 72
Задача (Азбука Морзе)
Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее трёх и не более четырёх сигналов (точек и тире) ?
Решение:
Зная формулу, без проблем решим данную примерную задачу из ЕГЭ по информатике.
У нас есть 2 символа, которые можно использовать: точка и тире. Фраза, что сообщение может иметь «не менее трёх и не более четырёх сигналов», означает, что сообщения могут быть длиною 3 символа и длиною 4 символа.
Подсчитаем общее количество вариантов.
N = 23 + 24 = 8 + 16 = 24 комбинаций.
Значит, для 24 различных символов (цифр, букв, знаков пунктуации и т.д.) мы найдём различные комбинации, чтобы их закодировать
Ответ: 24
Задача (Обратная предыдущей)
Световое табло состоит из цветных индикаторов. Каждый индикатор может окрашиваться в четыре цвета: белый, черный, желтый и красный. Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 300 различных сигналов?
Решение:
Нам нужно закодировать 300 различных вариантов! Имеются 4 различных лампочки! (Они имеют смысл, как количество допустимых символов!) На этот раз нужно узнать количество лампочек (количество разрядов, «длину слова»). Применяем формулу.
N = 4x = 300
Не найдётся такое целое x, чтобы равенство стало верным. Поэтому берём целое минимальное x такое, чтобы 4x больше 300.
45 = 1024
Пять лампочек на табло хватит, чтобы закодировать 300 сигналов, но, к сожалению, много комбинаций просто не пригодится!
Ответ: 5
Задача (Важная!)
Нужно выбрать в подарок 3 книги из 5. Сколькими способами можно выбрать ?
Решение:
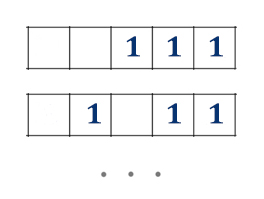
На рисунке показано две комбинации, как можно выбрать в подарок 3 книги из 5.
Данную задачку нужно решать используя формулу сочетаний из раздела комбинаторика.
n — количество книг, из которых мы выбираем подарок, m — количество книг, которое мы хотим выбрать, C — количество вариантов (способов).
Восклицательный знак — это факториал!
Факториалом числа «n» (условное обозначение n!- читается как «эн» — факториал) называется произведение чисел от 1 до «n»
Примечание: При использовании формулы сочетаний, не важен порядок, в котором мы выбираем одни и те же книги. Это будет один и тот же вариант.
Ответ: 10
Следующая задача часто встречается в книгах по подготовке к ЕГЭ по информатике.
Задача (Главная формула + сочетания)
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно три раза, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Решение:
В начале нужно посчитать, сколькими способами на 5-ти ячейках можно расположить 3 единицы!
Обратите внимание, как будто мы выбираем 3 книги в подарок из 5 возможных! Значит, опять применяем формулу сочетаний из комбинаторики. Мы вычисляли уже её точно с такими же числами в прошлой задаче, количество вариантов равно 10.
Подсчитаем, сколько вариантов кодового замка можно составить при одном определённом расположении трёх единиц.
Применим формулу, есть две ячейки, в которых изменяются цифры, а в каждой ячейке может быть одна из 4 цифр.
N = mi = 42 = 16
Т.к. различных вариантов, как расположить единицы на 5 ячейках равно 10, то ответ будет 16 * 10 = 160
Ответ: 160
Ещё одна задача из примерных вариантов по подготовке к ЕГЭ по информатике.
Задача (Таблица соревнований)
Для записи результатов соревнований используется таблица, в которой для каждой из 20-ти команд по каждому из 10-ти видов состязаний записано 1, 2 или 3 (если команда заняла соответствующее место в этом состязании) или прочерк (если не заняла призовое место или не участвовала). Какое количество информации (бит) содержит таблица ?
Решение:
Есть таблица с 20 командами и для каждой команды есть результат по 10-ти видам состязаний.
| 1 команда | 2 команда | 3 команда | … | 20 команда | |
| 1 дисциплина | 1 | — | 1 | … | 3 |
| 2 дисциплина | — | 2 | 1 | … | 2 |
| … | … | … | … | … | … |
| 10 дисциплина | 1 | 1 | 2 | … | — |
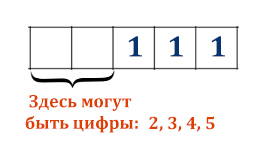
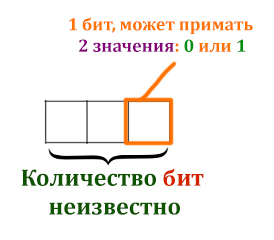
В каждой ячейке может быть 4 различных значения ( 1, 2, 3, — ). Нужно узнать, сколько бит занимает одна ячейка таблицы. Один бит может быть либо единицей, либо нулём.
Сделав рисунок, задача обрела привычные очертания.
Как будто мы решаем задачу с перебором слов. Но здесь длина слова неизвестна, а количество вариантов, которое должно получится уже дано и равно 4 (четырём). Применим главную формулу из 10 задания из ЕГЭ по информатике.
N = mi = 2i = 4
i=2 бита (длина равна «2 буквам», если воспринимать задачу, как со словами.)
Одна ячейка таблицы весит 2 бита. Найдём количество ячеек во всей таблице соревнований.
Всего ячеек = 20 * 10 = 200
Тогда вся таблица будет весит:
V = 2 бита * 200 = 400 бит.
Ответ: 400
Формула Шеннона
Задача (Формула Шеннона)
В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?
Решение:
Данную задачу нужно решать по формуле Шеннона
Найдём вероятность p того, что вытащили чёрный шарик.
p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + 
p = 1 / 4
Применим формулу Шеннона.
x = log2(4)
2x = 4
x = 2 бита
Ответ: 2
Доброго времени суток ! Помогите пожалуйста решить задачу .) Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?
В закрытом ящике находится 32 карандаша, некоторые из них синего цвета. Наугад вынимается один карандаш. Сообщение «этот карандаш – НЕ синий» несёт 4 бита информации. Сколько синих карандашей в ящике?
Был бы очень рад , если вы разберете и эту задачку
Добрый день. Полностью разобрал этот номер, но наткнулся на один интересный пример. Объясните доступным языком, пожалуйста. На решу егэ вообще не понял их решение:
Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Т должна входить в код не менее одного раза, а буква Й — не более одного раза. Сколько различных кодов может составить Тимофей? (ответ: 8006)
Добрый день! Подскажите пожалуйста, как решить следующую задачу: Сколько существует чисел, шестнадцатеричная запись которых содержит 3 цифры, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.
Петя составляет семибуквенные слова перестановкой букв слова АССАСИН. Сколько всего различных слов может составить Петя? Мое решение: 21 вариант с буквой А, 35- с буквой С, и 4 на буквы И и Н. Всего 60 и умножаем на 7. Получается 420. Не уверена, что применила верный алгоритм. Прокомментируйте, пожалуйста, решение
Можете заказать решение задачи через раздел «связь».
В Задаче (Другой метод решения!!) допущена ошибка в решении, ведь 24 + 18 + 18 + 18 + 18 = 114,значит N = 600 — 114 = 486!
Добрый день! Помогите пожалуйста решить задачку
Сколько чисел длиной 6 можно составить, если известно, что цифры идут в порядке убывания, при этом четные и нечетные цифры чередуются?
У меня только один вопрос. Почему в школах на уроках информатики вместо действительно полезного изучения какого нибудь языка программирования, заставляют заниматься вот этой вот ересью и решать какое по счету слово напишет Вася? Я могу только составить в ответ на это только слова которые нельзя здесь писать. От таких знаний и занятий ни один ребенок не захочет стать программистом, потому что это непонятно, и неизвестно зачем уметь решать такие задачи. Я сам программист с 10 летним стажем не смог объяснить ребенку как решать некоторые задачи и самое главное, я не знаю зачем дети должны уметь это решать.
Дмитрий, согласен с Вами. Особенно 11 задание и формула Шеннона. Надо либо излагать задание корректно, либо исключить вообще: «В корзине лежат черные и белые шары. Среди них 18 черных шаров. Сообщение о том, что достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?» — для двух состояний достаточно одного бита.
marvell special for u
c = 0
from itertools import*
for i in permutations(‘МАТВЕЙ’, r=6):
i = ».join(i)
if i[0] != ‘Й’ and i.count(‘АЕ’) == 0:
print(i)
c += 1
print(c)
Комбинаторные задачи в ЕГЭ
Комбинаторные методы в ЕГЭ по информатике применяются для решения задачи №10 (бывшая В4). Рассмотрим решение типичных задач, с использованием комбинаторных приемов.
Решим задачу под номером В4 из демонстрационной версии ЕГЭ по информатике 2014 года.
Задача. Для передачи аварийных сигналов договорились использовать специальные цветные сигнальные ракеты, запускаемые последовательно. Одна последовательность ракет – один сигнал; в каком порядке идут цвета – существенно. Какое количество различных сигналов можно передать при помощи запуска ровно пяти таких сигнальных ракет, если в запасе имеются ракеты трёх различных цветов (ракет каждого вида неограниченное количество, цвет ракет в последовательности может повторяться)?
Решение.
Ракеты могут быть трех различных цветов, при этом в одной последовательности пять ракет. Значит, рассматривается выборка объема пять из трех элементов (n = 3, k = 5).
Определим комбинаторную схему. Два положения в условие задачи:
- «в каком порядке идут цвета – существенно»;
- «цвет ракет в последовательности может повторяться»;
указывают на то, что – это размещения с повторениями.
Ответ. 243
Решим задачу №10 из демоверсии ЕГЭ по информатике 2016 года.
Игорь составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Игорь использует 5-буквенные слова, в которых есть только буквы П, И, Р, причём буква П появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Игорь?
Решение.
1) буква «П» появляется ровно 1 раз, значит она может находиться на одной из 5 позиций в слове.
2) буквы «И» и «Р» заполнят остальные 4 позиции. Рассмотрим выборки объема 4 из 2 элементов (k = 4, n = 2). Кодовые слова могут отличаться как порядком следования букв, так и составом, значит, комбинаторная схема – размещения с повторениями. Найдем число таких размещений:
3) применим правило произведения: 5 * 16 = 80
Ответ. 80
Типичная тренировочная задача №10 для подготовки к ЕГЭ по информатике.
Задача. Вася составляет 5-буквенные слова из четырехбуквенного алфавита {A, C, R, T}, причём буква А используется в каждом слове ровно 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом, считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Решение.
1) пронумеруем позиции в слове, тогда варианты расположений букв «А» можно представить в качестве неупорядоченного выбора двух цифр из пяти. Значит, комбинаторная схема — сочетания без повторений
2) остальные допустимые символы будут занимать 3 позиции. Эти выборки объемом 3 из 3 элементов будут отличаться как порядком следования, так и набором символов. Очевидно, комбинаторная схема – размещения с повторениями.
3) применим правило произведения: 27 * 10 = 270
Ответ. 270
Скачать материал

Скачать материал




- Сейчас обучается 629 человек из 77 регионов


- Сейчас обучается 84 человека из 29 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Элементы комбинаторики
Введение в теорию вероятностей
Применение комбинаторики -
2 слайд
Комбинато́рика — это область математики, прежде всего связанная с подсчетом, как средство и цель получения результатов, так и с определением свойств конечных структур. Она тесно связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Полный охват комбинаторики не является общепризнанным. Согласно Х. Дж. Райзеру, определение предмета трудно, потому что она пересекает много математических разделов. -
3 слайд
Поскольку область может быть описана типами задач, которые она решает, комбинаторика связана с:
перечислением (подсчет) определенных структур, иногда упоминаемых аранжировками или конфигурациями в самом общем смысле, связанными с конечными системами;
существованием таких структур, которые удовлетворяют определенным заданным критериям;
построением таких структур; возможно, несколькими способами;
оптимизацией, поиском «наилучшей» структуры или решения из нескольких возможных, будь то «наибольшая», «наименьшая» или удовлетворяющая какому-либо другому критерию оптимальности. -
4 слайд
Правило сложения (правило «или») — одно из основных правил комбинаторики, утверждающее, что,
если элемент A можно выбрать n способами,
а элемент B можно выбрать m способами,то выбрать A или B можно n + m способами.
-
5 слайд
Правило умножения (правило «и») — одно из основных правил комбинаторных принципов. Согласно ему, если элемент A можно выбрать n способами,
и при любом выборе A элемент B можно выбрать m способами,
то пару (A, B) можно выбрать n·m способами Естественным образом обобщается на произвольное количество независимо выбираемых элементов.
Данное правило обычно принимается за аксиому, как и правило суммы. -
6 слайд
В комбинаторике
размеще́нием (из n по k) называется упорядоченный набор из k различных элементов
из некоторого множества различных n элементов. -
7 слайд
Правило умножения. Простой
Выбрать книгу и диск из 10 книг и 12 дисков можно 10*12=120 способами.Количество размещений с повторениями
Если есть множество из n типов элементов, и нужно на каждом из m мест расположить элемент какого-либо типа (типы элементов могут совпадать на разных местах), то количество вариантов этого будет nm.
k k
An =n
Порядок важен
Есть повтор -
8 слайд
Правило умножения. Составной
Пусть требуется найти количество слов, составленных не более, чем из 3-x букв алфавита {a, b, c}. Количество n-буквенных слов равно количеству размещений из 4 букв на n мест с повторениями — оно равно 4n . Количество всех слов (так как нужно учитывать любое из слов) будет складываться из количеств одно-, двух- и трёхбуквенных слов.
Тогда ответ на первоначальный вопрос будет
41+42+43 = 84 . -
9 слайд
Размеще́ние без повторений (из n по k) называется упорядоченный набор из k различных элементов
из некоторого множества различных n элементов.
Пример 1:
<1,3,2,5>— это 4-элементное размещение
из 6-элементного множества {1,2,3,4,5,6}
k
An =n!/(n-k)!
Порядок важен
Нет повтора -
10 слайд
СОЧЕТАНИЯ
В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данного множества, содержащего n различных элементов.
Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.Так, например, наборы (3-элементные сочетания, подмножества, k=3 ) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} ( n=6 ) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
-
11 слайд
Число сочетаний из n по k равно
k
Cn =n!/k!(n-k)!
n – множество, из которого выбираем
k – количество выборок -
12 слайд
При решении задач лучше всего начинать с построения схем.
Потому что задачи всегда разные -
13 слайд
Задача 1
Сколько различных слов длины 6 можно составить из букв С,О.К, которые содержат ровно одну букву С. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая последовательность букв. -
14 слайд
Рисуем схему
2 2 2 2 2 2*2*2*2*2=32
С * * * * *
* С * * * *
* * С * * * Всего вариантов 6,
* * * С * * тогда 32*6=192
* * * * С *
* * * * * С -
15 слайд
Задача 2
Сколько различных слов длины 6 можно составить из букв С,О,К, которые содержат ровно две буквы С. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая последовательность букв. -
16 слайд
Расписывать схему сложно, так как буквы С может быть где угодно в слове. Поэтому здесь лучше использовать формулу сочетаний из 6 по 2. То есть , сколько вариантов размещения двух букв С существует в слове длиной 6. При этом не играет роль перестановок
То есть это будет равно количеству сочетаний из 6 по 22
С6=n!/k!(n-k)!=6*5*4*3*2/2*4*3*2=15
Где n – число элементов, из которых выбираем
k – число элементов, которое выбираем -
17 слайд
Рассмотрим одну из схем размещения. Допустим
С С * * * * (не важно, где находятся С)
Получается С С 2 2 2 2
перемножаем, получаем 16 вариантов
С учётом того, что количество размещений равно 15, получаем, что всего вариантов различных слов длины 6 можно составить из букв С,О,К, которые содержат ровно две буквы С будет
15*16=240
15 вариантов -
18 слайд
Задача 3
Сколько различных слов длины 5 можно составить из букв М, Ы, Ш, Ь, которые содержат ровно одну букву М и одну букву Ш. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая последовательность букв. -
19 слайд
Слово пятибуквенное
* * * * *
В предыдущей задаче было не важно какие места занимают С С. Здесь буквы разные. Поэтому здесь применяя формулу размещений из 5 по 2, получим количество вариантов для размещений букв М и Ш
k
A n=n!/(n-1)!=5!/3!=20
А для остальных букв (их осталось 2) применяем схему
20 * 2 * 2* 2
Всё перемножаем, получаем 160. Ответ 160 вариантов -
20 слайд
Задача 3
Сколько различных слов длины 5 можно составить из букв М, Ы, Ш, Ь, которые содержат ровно одну букву М и одну букву Ш. Причём, эти буквы должны стоять рядом. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая последовательность букв -
21 слайд
Рисуем схему
2 2 2 2*2*2=8
М Ш * * *
* М Ш * *
* * М Ш * Всего вариантов 4,
* * * М Ш тогда 8*4=32Но может быть и вариант
Ш М * * *
* Ш М * *
* * Ш М *
* * * Ш МИх тоже 32 варианта. Таким образом,
Ответ: 32*2=64 -
22 слайд
Задача 4
Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой И. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Тимофей? -
23 слайд
Задача 5
Для передачи сообщений, составленных из заглавных букв русского алфавита, используется неравномерный двоичный код, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известны кодовые слова, назначенные для некоторых букв: Б – 01, В – 001, Е – 0001, Ш – 111. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово КУКУШКА?
КУКУШКА
Задание по условию Фано
«с ловушкой»!!!
У- 2 раза (110)
К- 3 раза (10)
А — 1 раз – но не 0000!!! (поскольку надо иметь возможность закодировать остальные буквы русского алфавита)
2*3+3*2+3+5=20Итог: 20
-
24 слайд
Задача 6
При регистрации на сервере каждый пользователь получает уникальный персональный код, состоящий из двух частей. Первая часть кода содержит 12 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 5 символов, каждый из которых может быть одной из 9 цифр (цифра 0 не используется). При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Для хранения данных о 30 пользователях потребовалось 2100 байт. Сколько байтов выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
25>26 5 бит/символ, 24>9 4 бита/цифра
12*5+4*5=80 бит=10 байт
2100 / 30 = 70 байт/пользователь
70 – 10 = 60 байт на допол. сведенияИтог: 60
-
25 слайд
Задача 6
На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт К?
-
26 слайд
Перерисуем граф с учетом проезда через К
С=П+М+Р=16+16+16=48
П=М=16
Р=М=16
М=К+Л=8+8=16
Л=К=8
К=Д=Б+Е=5+3=8
Б=А+В+Е=1+1+3=5
Е=В+А+Г=3
Итог: 48
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 784 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Информатика. Углубленный уровень (в 2-ух частях) », Поляков К.Ю., Еремин Е.А.
Тема
Глава 3. Логические основы компьютеров
Больше материалов по этой теме
-
«Информатика. Углубленный уровень (в2 частях)», Поляков К.Ю., Еремин Е.А.
Тема
Глава 1. Информация и информационные процессы
Больше материалов по этой теме
Другие материалы
- 07.03.2023
- 46
- 1
- 07.03.2023
- 26
- 1
- 07.03.2023
- 23
- 1



- 06.03.2023
- 397
- 15
- 06.03.2023
- 99
- 9
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
ЕГЭ – 2021, задание 8. Кодирование данных, комбинаторика
Для решения данного задания необходимо помнить, что:
-
Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки.
-
В русском языке 33 буквы: 10 гласных букв (а, у, о, ы, и, э, я, ю, ё, е), 21 согласная буква (б, в, г, д, ж, з, й, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ) и два знака (ь, ъ).
-
Алфавит – набор символов, используемых при кодировании.
-
Мощность алфавита – количество символов в алфавите.
-
Число возможных слов Q длиной в L букв, когда есть m1 вариантов выбора первой буквы, m2 вариантов выбора второй буквы и т.д., вычисляется как произведение
Q = m1 * m2 * … * mL
-
Тогда количество сообщений Q длиной в L букв, которое можно получить из алфавита мощностью М, при равном количестве вариантов выбора для всех букв равно
Q=МL
Рассмотрим примеры решения различных задач по данной теме.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1 (демо-2021). Демоверсия 2020
Игорь составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Игорь использует трёхбуквенные слова, в которых могут быть только буквы Ш, К, О, Л, А, причём буква К появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Игорь?
Решение:
Для составления трехбуквенных слов (то есть слов длиной 3 буквы) используется алфавит мощностью пять букв. Здесь отдельное условие выбора указано только для буквы К, для остальных четырех букв алфавита (обозначим их символами х) – выбор одинаковый и равен 42 = 16.
При этом буква К может стоять на любом из трех мест в слове, тогда возможны три варианта слов: Кхх, хKх, ххК. Тогда общее количество вариантов слов будет
Q = 3 * 16 = 48
Ответ: 48
Задача 2.
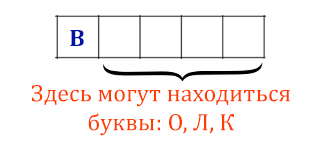
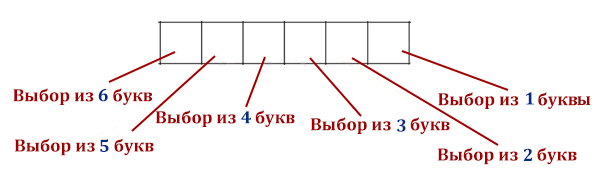
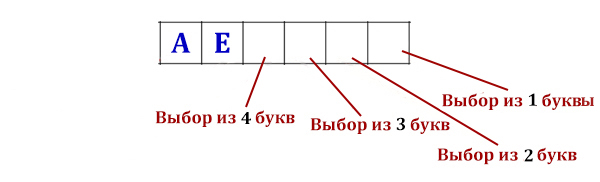
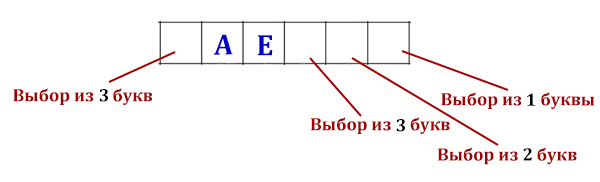
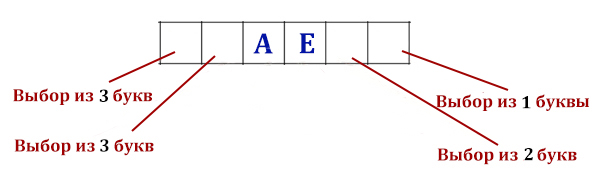
Сколько слов длины 4, начинающихся с согласной буквы, можно составить из букв Л, Е, Г, О? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Решение.
Всего из 4 различных букв можно составить 44 = 256 вариантов различных слов длиной четыре.
Но так как слова должны начинаться только с согласной буквы (здесь их 2 из четырех), полученных слов будет 256 / 2 = 128 вариантов.
Ответ: 128
Задача 3.
Сколько существует различных символьных последовательностей длины 5 в трёхбуквенном алфавите {Т, О, К}, которые содержат ровно две буквы О?
Решение.
Общее количество слов, которое можно составить из 3 букв длиной 5, равно
35 = 243 варианта.
Рассмотрим варианты пятибуквенных слов, в которых буква О стоит в разных позициях:
-
ОО*** О*О** О**О* О***О — 4 шаблона, где звездочками обозначены 23 = 8 вариантов слов, которые можно составить из двух оставшихся букв (Т и К). Тогда получаем здесь всего 4 * 8 = 32 варианта;
-
*ОО** *О*О* *О**О — 3 шаблона, которые дают 3 * 8 = 24 варианта слов;
-
**ОО* **О*О — 2 шаблона, которые дают 2 * 8 = 16 вариантов;
-
***ОО = 1 шаблон, который дает 8 вариантов слов.
Тогда всего получаем 32 + 24 + 16 + 8 = 80 вариантов слов с двумя буквами О.
Ответ: 80
Задача 4.
Коля составляет 5-буквенные слова, в которых есть только буквы К, Л, О, У, Н, причём буква У используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Коля?
Решение.
Так как по условию буква У встречается в слове хотя бы один раз, то
-
рассчитаем количество слов, в которых буква У встречается все пять раз
-
и вычтем случаи, когда буква У не встречается ни разу.
В первом случае, когда буква У используется на всех 5 позициях, получаем
5 * 5 * 5 * 5 *5 = 3125 вариантов.
Во втором случае буква У не используется совсем, то есть используются только 4 буквы:
4 * 4 * 4 * 4 * 4 = 1024
Тогда разница между ними и даст нам требуемый результат: 3125 – 1024 = 2101
Ответ: 2101
Задача 5.
Коля составляет 5-буквенные слова, в которых есть только буквы П, О, Л, Е, причём буква Е может использоваться не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Коля?
Решение.
Всего здесь возможно получить 45 = 1024 слова, но есть ограничение – одна из букв не может использоваться более 3 раз. При этом, буква использоваться 5 раз может только в единственном случае.
Когда же буква используется 4 раза, то возможны варианты:
Е Е Е Е *, Е Е Е * Е, Е Е * Е Е , Е * Е Е Е и * Е Е Е Е – всего 5 шаблонов, где на месте звездочки может быть любая из трех оставшихся букв, то есть всего 15 вариантов. Значит, всего не может быть использовано 15 + 1 = 16 вариантов.
Тогда возможное количество слов при заданном условии будет 1024 – 16 = 1008 слов.
Ответ: 1008
Задача 6. Илья составляет 3-буквенные слова из букв К, Л, М, Н, О, Я. Буква Я в слове может быть только одна (или ни одной) и только на первой или последней позициях. Сколько различных кодовых слов может составить Илья?
Решение.
Максимальное число различных слов, которое можно получить в этой задаче, равно 63 = 216 вариантов.
При этом возможны только следующие шаблоны:
* * *, Я * * и * * Я — всего 3 шаблона,
где на месте звезд могут быть в первом случае — 5 букв (без Я), то есть 53 = 125 вариантов,
во втором и третьем случае – 52 = 25 * 2 = 50 вариантов. Итого возможно получить
125+50 = 175 вариантов различных слов.
Ответ: 175
Задача 7. Палиндром – это символьная строка, которая читается одинаково в обоих направлениях. Сколько различных 4-символьных палиндромов можно составить из строчных латинских букв? (В латинском алфавите 26 букв).
Решение.
4-символьный палиндром состоит из пары двух одинаковых букв, тогда общее количество таких возможных палиндромов будет 262 = 676 вариантов.
Ответ: 676
Задача 8. Все 6-буквенные слова, составленные из букв М, А, К записаны в алфавитном порядке. Вот начало списка:
1. АААААА
2. АААААК
3. АААААМ
4. ААААКА
5. ААААКК
……
Запишите номер первого слова, которое начинается на букву М.
Решение.
Данный список будет состоять из трех равных частей, каждая из которых будет содержать 36 / 3 = 243. Тогда третья часть начнется со строки под номером 243 * 2 + 1 = 487.
Ответ: 487
Задача 9.
Иннокентий составляет семибуквенные слова из букв Е, И, Й, К, Н, О,
Т. Сколько слов может составить Иннокентий, если известно, что в каждом из них есть комбинация КОТ?
Решение:
Подвох в условии этой задачи в том, что не сказано, что комбинация КОТ встречается только один раз!
Тогда сначала посчитаем общее число возможных комбинаций, в которых слово кот встречается только один раз, и вычтем из этого количества те, где комбинация повторяется дважды.
Всего возможны варианты:
КОТхххх, хКОТххх, ххКОТхх, хххКОТх, ххххКОТ, где х – одна из четырех оставшихся букв, то есть 5 * 74 = 12005
Второй раз комбинация КОТ может встретиться в четвертом и пятом варианте, причем в пятом варианте – дважды:
КОТКОТх , КОТхКОТ и хКОТКОТ.
В каждом случае остается свободной одна позиция из семи различных букв, то есть три раза по 7 вариантов букв – итого 21.
Итого получаем: 12005 – 21 = 11984.
Ответ: 11984
Задача 10
Василий составляет 4-буквенные коды из букв Г, А, Ф, Н, И, Й. Каждую букву можно использовать любое количество раз, при этом код не может начинаться с буквы Й и должен содержать хотя бы одну гласную. Сколько различных кодов может составить Василий?
Решение:
Решим задачу с конца, так как решение с начала – на много длиннее. Для этого мы сосчитаем, сколько вариантов кодов может быть всего (без учета заданных ограничений) и вычтем количество кодов, которых быть не может.
В данном задании мощность алфавита М = 6, длина получаемых кодов L = 4 то есть общее возможное количество вариантов слов (без учета ограничений на использование букв) равно Q = 64 = 1296. Напомним, что буква Й – согласная, т.е. в используемом в задаче алфавите четыре согласных и две гласных буквы.
Не может быть кодов, которые начинаются на Й, их количество
Q = 1(Й) *6 *6 *6 =216
Также не может быть кодов, в которых нет ни одной гласной буквы, их количество Q = 3 *4 *4 *4 =192.
Тогда остается возможных кодов 1296-216-192 = 888.
Ответ: 888
Задача 11. Все 4-буквенные слова, составленные из букв С, Л, О, Н, записаны в алфавитном порядке. Вот начало списка:
1. ЛЛЛЛ
2. ЛЛЛН
3. ЛЛЛО
4. ЛЛЛС
……
Запишите слово, которое стоит на 250-м месте от начала списка.
Решение.
Пронумеруем буквы в порядке их следования в алфавите цифрами от 0 до 3:
Л = 0, Н = 1, О = 2, С = 3
и запишем заданное нам начало списка этими цифрами:
1. 0000
2. 0001
3. 0002
4. 0003
……
Очевидно, что получили числа в четверичной системе счисления, записанные в порядке возрастания. Очень важно, что число ноль стоит на первом месте. Тогда далее на каждом месте будет стоять число, на 1 меньшее номера слова. Значит, на 250-м месте от начала списка будет находиться число 249, но записанное в четверичной системе счисления:
249 = 33214
Заменив обратно цифры на буквы, получаем: ССОН
Проверка решения.
При желании можно получить ответ, решив задачу с конца списка.
Всего в данной задаче возможно получить 44 = 256 вариантов различных слов. Запишем полученные слова с конца: 255 = СССС, 254 = СССО, 253 = СССН, 252 = СССЛ, 251 =ССОС, 250 =ССОН – что и требовалось доказать. Или же для проверки выполните обратный перевод числа в десятичную систему счисления.
Ответ: ССОН
Задача 2. Все 5-буквенные слова, составленные из букв А, Л, С, У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААЛ
3. ААААС
4. ААААУ
5. АААЛА
……
Укажите номер слова УЛАСА.
Решение. Нумеруем буквы в порядке их следования в алфавите цифрами от 0 до 3, получаем: А = 0, Л = 1, С = 2, У = 3, тогда получаем число 31020 в четверичной системе счисления. После перевода его в десятичную систему счисления получаем
310204 = 840.
Значит, искомое нами число занимает 840 +1 = 841 место.
Ответ: 841
Комбинаторика, перечисления
Сколько существует различных двоичных кодов длиной 8 символов, содержащих 5 единиц? Двоичный код обязательно начинается и заканчивается единицей.
Первым и последним символом в двоичном коде является единица. Необходимо найти количество вариантов поставить k = 3 недостающие единицы на n = 6 оставшихся мест в коде. Сделать это можно (C^3_6 = frac{6!}{(6-3)! cdot 3!} = frac{4 cdot 5 cdot 6}{6} = 20) способами. Значит всего существует 20 различных искомых кодов.
Ответ: 20
Максим составляет пары слов. Первое 6-буквенное слово состоит из букв М, О, Щ, Н, а второе 2-буквенное из букв В, Е, Б. Каждая из букв в словах может встречаться любое количество раз или не встречаться совсем, причём в первом слове должно быть 5 подряд идущих согласных. Сколько различных пар слов может составить Максим?
В первом слове Максим должен получить 5 подряд идущих согласных, а значит либо на 1, 2, 3, 4 и 5 местах должны стоять согласные, а на 6 любая из 4 букв, либо на 2, 3, 4, 5, 6 местах должны стоять согласные, а на 1 любая из 4 букв. Всего согласных 3. Значит первое слово можно составить (2 cdot (3 cdot 3 cdot 3 cdot 3 cdot 3 cdot 4) = 1944) способами. Во втором слове на каждое из 2 мест можно поставить любую из 3 букв. Значит второе слово можно составить (3 cdot 3 = 9) способами.
Представим, что первые слова — чашки, а вторые слова — блюдца. Сколько различных вариаций кружка+чашка можно составить?
Можно составить (1944 cdot 9 = 17496) различных пар слов (блюдец с чашкой).
Ответ: 17496
Сколько существует различных двоичных кодов длиной 5 символов, содержащих 3 единицы? Двоичный код обязательно начинается с единицы.
Первой в двоичном коде стоит единица. Необходимо найти количество вариантов поставить k = 2 недостающие единицы на n = 4 оставшихся места в коде. Сделать это можно (C^2_4 = frac{4!}{(4-2)! cdot 2!} = frac{3 cdot 4}{2} = 6) способами. Значит всего существует 6 различных искомых кодов.
Ответ: 6
Сколько существует различных двоичных кодов длиной 6 символов, содержащих 4 единицы? Двоичный код обязательно начинается с единицы.
Первой в двоичном коде стоит единица. Необходимо найти количество вариантов поставить k = 3 недостающие единицы на n = 5 оставшихся мест в коде. Сделать это можно (C^3_5 = frac{5!}{(5-3)! cdot 3!} = frac{4 cdot 5}{2} = 10) способами. Значит всего существует 10 различных искомых кодов.
Ответ: 10
Сколько существует различных двоичных кодов длиной 7 символов, содержащих 3 единицы? Двоичный код обязательно начинается с единицы.
Первой в двоичном коде стоит единица. Необходимо найти количество вариантов поставить k = 2 недостающие единицы на n = 6 оставшихся мест в коде. Сделать это можно (C^2_6 = frac{6!}{(6-2)! cdot 2!} = frac{5 cdot 6}{2} = 15) способами. Значит всего существует 15 различных искомых кодов.
Ответ: 15
Сколько существует различных двоичных кодов длиной 10 символов, содержащих 5 единиц? Двоичный код обязательно начинается и заканчивается единицей.
Первым и последним символом в двоичном коде является единица. Необходимо найти количество вариантов поставить k = 3 недостающие единицы на n = 8 оставшихся мест в коде. Сделать это можно (C^3_8 = frac{8!}{(8-3)! cdot 3!} = frac{6 cdot 7 cdot 8}{6} = 56) способами. Значит всего существует 56 различных искомых кодов.
Ответ: 56
Сколько существует различных троичных кодов длиной 5 символов, содержащих 1 единицу и 2 двойки? Троичный код обязательно начинается с единицы.
Первым символом в троичном коде является единица. Необходимо найти количество вариантов поставить k = 2 недостающие цифры на n = 4 оставшихся места в коде. Сделать это можно (C^2_4 = frac{4!}{(4-2)! cdot 2!} = frac{3 cdot 4}{2} = 6) способами. Значит всего существует 6 различных искомых кодов.
Ответ: 6
Задача 8 по информатике ЕГЭ относится к комбинаторике и системе счисления. Её можно решить путем написания кода. Но для этого нужно будет потратить довольно много времени. Если не понимать как это решается вручную, то код писать опасно.
Задача № 8 (первый вариант) по системе счисления и комбинаторика
Данную задачу лучше решать вручную, так как это не занимает много времени. И так первое возможное условие задачи:

Эта задача относится к задаче с системой счисления.
Для того, чтобы решить эту задачу, нужно использовать систему счисления.
Буква Е – 0, буква Л – 1, буква М – 2, буква Р – 3, буква У-4.
В результате мы видим пятиричную систему счисления.
ЕЕЕЕ – 0000 0
ЕЕЕЛ – 0001 1
ЕЕЕМ- 0002 2
ЕЕЕР – 0003 3
ЕЕЕУ – 0004 4
ЕЕЛЕ – 0010 5

Несмотря на то, что нумерация букв начинается с нуля, а список набора букв начинается с единицы.
Раз нумерация строк начинается с 1, то набор букв ЛЕЕЕ будет на 126 месте.
Задача № 8 ЕГЭ (второй вариант) на системы счисления и комбинаторика
Решение
АААА 00000 0
ААААО 00001 1
ААААУ 00002 2
АААОА 00010 3
Опять помним, что список начинается с единицы, поэтому 210-1 = 209
Мы работаем с числом 209, но оно дается в десятичной системе счисления.
Для того, чтобы восстановить слово, надо перевести полученное место в троичную систему счисления:

2 меньше трех, поэтому читаем число в обратном порядке: 21202
Теперь составляем из чисел буквы: УОУАУ
Ответ: УОУАУ
Задача № 8 ЕГЭ (третий вариант) системы счисления и комбинаторика

Здесь пятибуквенные слова. Опять определяем действительный номер с учетом, что нумерация идет с 1.
150-1 = 149
Присваиваем каждой букве цифры, начиная с нуля по порядку. Нумерация слов в списке начинается с единицы. А вот нумерация цифр в числе с нуля.
ЛЛЛЛЛ 00000 0
ЛЛЛЛН 00001 1
ЛЛЛЛР 00002 2
ЛЛЛЛТ 00003 3
ЛЛЛНЛ 00010 4
В результате 149 в десятичной системе счисления переводим в четверичную путем деления 149 на четыре. Затем собираем остатки с конца в начало.

Получаем РННН, но у нас по условию нужно пятибуквенное слово. Для этого необходимо в начало слова добавить ничего не значащий ноль: 02111
Теперь ответ будет ЛРННН
Задача № 8 ЕГЭ (четвертый вариант) на системы счисления и комбинаторика

Числа начинаются с нуля, поэтому говорим о пятиричной системе счисления:
ААААА 00000 0
ААААК 00001 1
ААААЛ 00002 2
ААААО 00003 3
ААААШ 00004 4
АААКА 00010 5
Мы сначала найдем число, а затем добавим 1.
ШКОЛА – пишем в пятиричной системе счисления – 41320

ШКОЛА в пятиричной системе счисления 41320, в десятичной системе счисления 2710
Ответ: 2710+1 = 2711
Задача № 8 (пятый вариант) системы счисления и комбинаторика

АААА 0000 0
АААВ 0001 1
АААД 0002 2
АААП 0003 3
АААР 0004 4
ААВА 0010 5
В условии сказано, что слово не содержит гласных и не содержит одинаковых букв. Поэтому нас интересует слово: ВДПР = 1234 (система счисления пятиричная).
Буквы ставим по алфавиту.
Необходимо преобразовать в десятичную систему счисления:

ВДПР в пятиричной системе 1234 , в десятичной системе 194. Это число. А нужно номер, номер будет на 1 больше.
194+1 = 195
Задача № 8 ЕГЭ (шестой вариант) система счисления и комбинаторика

АААА 0000 0
АААВ 0001 1
АААД 0002 2
АААП 0003 3
АААР 0004 4
ААВА 0010 5
В условии сказано, что слово не содержит гласных и не содержит одинаковых букв. Поэтому нас интересует слово: ВДПР = 1234 (система счисления пятиричная). Буквы ставим по алфавиту.
Необходимо преобразовать в десятичную систему счисления:

ВДПР в пятиричной системе 1234 , в десятичной системе 194. Это число. А нужно номер, номер будет на 1 больше.
194+1 = 195
Ответ: 195
Задача № 8 ЕГЭ (седьмой вариант) система счисления и комбинаторика

Дано 4 буквы, система счисления четверичная. Расписываем:
ООООО 00000
ООООП 00001
ООООР 00002
ООООТ 00003
ОООПО 00010
В четверичной системе счисления указанные в условии слова представляют собой следующие числа:

Переведем эти числа в десятичную систему счисления:

Чтобы найти количество между ними, то мы должны найти разницу:
786-531 = 255
Но по условию задания надо найти количество слов, включая эти слова, то надо прибавить 1.
255+1 = 256
Ответ: 256
Задача № 8 ЕГЭ (восьмой вариант) система счисления и комбинаторика

Обозначим позиции букв в словах.
У нас всего 3 буквы.
Первую букву можно выбрать только 3 способами, вторую – тоже тремя способами, третью тоже тремя.

Задача № 8 ЕГЭ (девятый вариант) система счисления и комбинаторика

Здесь вводится ограничение, буква К встречается только один раз.
Трехбуквенные слова.
Соответственно схематически строим схему слова:
____ _____ ______
Представьте, буква К окажется только на первом месте. Больше мы не можем использовать. Соответственно, на второе место можно поставить любую букву из оставшихся, т.е. 4 варианта.
К*4*4 = 16 (К = 1)
Но буква К может находиться и на втором месте, и на третьем месте.
4*К*4 = 16
4*4*К = 16
Далее используем комбинаторные правила сложения: 16+16+16 = 48
Ответ: 48
Решение задач по теме «Информационные модели» можно посмотреть по ссылке.
Задача № 8 ЕГЭ (десятый вариант) система счисления и комбинаторика

Всего есть 4 буквы. Слова составляем пятибуквенные.
Ограничение: в каждом слове одна гласная буква. У нас гласные буквы: И,А.
Согласные буквы встречаются любое количество раз или не встречаются совсем.
Нам необходимо рассмотреть два случая, когда мы составляем слова с буквой А, и слова с буквой И.

Итого 16*5 = 80
По аналогии составляем также слова с буквой И, получим те же самые 80 слов.
В результате: 80+80 =160
Ответ: 160 слов с этими ограничениями.
Задача № 8 ЕГЭ (одиннадцатый вариант) система счисления и комбинаторика
Условие: Василий составляет четырех буквенные коды из букв Г,Е,Р,О,Й. Каждую букву можно использовать любое количество раз, при этом код не может начинаться с буквы Й т должен содержать хотя бы одну гласную.
Сколько различных кодов может составить Василий.
Букв 5, слова 4-х буквенные.
Есть ограничения: не должно начинаться с Й и содержать хотя бы одну гласную букву.
В этой задаче надо использовать не только комбинаторику, но и теорию множества.
Принцип
Для того, чтобы определить количество слов, которое содержит хотя бы одну гласную букву, то можно схематически раскрыть вопрос:
А – это множество кодов или слов, которые могут быть составлены по правилу задачи.
Теперь среди этого набора вычленим только те, которые вообще не содержат гласных букв (множество В)
Из А вычтем В, то получим множество С, которое содержит слова, которые содержат хотя бы одну гласную.

Теперь определим сколько же будет слов в множестве А.
Слова четырехбуквенные. Кроме Й на первом месте может стоять 4 возможных буквы.
На втором месте может стоять все 5 букв по очереди.
А: 4*5*5*5 = 4*125 = 500
Помним, что Й – согласная буква
В: 2*3*3*3 = 2*27=54
Количество слов, в которых нет гласных 54
Количество слов, которые содержат хотя бы одну гласную: 500-54 = 446
Ответ: 446.
Задача № 8 ЕГЭ (двенадцатый вариант) система счисления и комбинаторика
Условие задачи: Вася составляет трехбуквенные слова, в которых есть только буквы В,Е,С,Н,А. Причем буква А используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Вася?
Задача содержит условие, при котором нужно применять при решении комбинаторику и теорию множеств.
Условия: слова трехбуквенные, количество букв – 4, слова содержат хотя бы 1 раз букву А.
Опять берем множество А в которое входят все слова с буквой А
В – множество в котором вообще нет буквы А
__ __ ___
Мощность множества А определяем следующим образом:
На первую позицию букву А можно поставить 5 способами, на вторую – 5 способами и на третью – 5 способами:
А: 5*5*5 =125
В: 4*4*4 = 64
Множество С в котором есть хотя бы одна буква А: АВ (разность)
125-64 = 61
Ответ: 61
Мы рассмотрели двенадцать видов задач по теме системы счисления и комбинаторики, которые в ЕГЭ по информатике размещаются как задание № 8. Однако, ежегодно вносятся изменения и возможно возникновение других типов задач.