Демонстрационная версия ЕГЭ—2015 по математике. Профильный уровень.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
Ответ:
2
На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией. Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия.
Ответ:
3
Строительный подрядчик планирует купить 20 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.
| Поставщик | Цена кирпича
(руб.за 1 шт.) |
Стоимость
доставки (рублей) |
Специальные условия |
|---|---|---|---|
| А | 19 | 3000 | Нет |
| Б | 18 | 5000 | Доставка бесплатная, если сумма
заказа превышает 50 000 рублей |
| В | 16 | 6500 | При заказе товара на сумму свыше
50 000 рублей скидка на доставку 50% |
Во сколько рублей обойдётся наиболее дешёвый вариант покупки с учётом доставки?
Ответ:
4
В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете не будет вопроса о грибах.
Ответ:
5
Найдите корень уравнения 3x − 5 = 81.
Ответ:
6
Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32°.
Ответ:
7
На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.
Ответ:
8
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.
Ответ:
9
10
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен
Найдите образующую конуса.
Ответ:
11
Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Ответ:
12
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
13
В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCD со стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1, причём BE = 1.
а) Постройте сечение призмы плоскостью A1C1E.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
Найдите все значения параметра a, при каждом из которых наименьшее значение функции больше 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно −8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
2014-08-30
2018-08-30
2015
ЕГЭ 2015
Демоверсия ЕГЭ 2015
Демоверсия базового ЕГЭ по математике 2015
Демоверсия профильного ЕГЭ по математике 2015
Апробация КИМ ЕГЭ, базовый уровень (октябрь 2014)
1, 2, 3, 4, 5, 6, 7
Диагностическая работа по математике (январь 2015)
профильный уровень
базовый уровень
Диагностическая работа по математике (февраль 2015)
базовый уровень
Диагностическая работа по математике (5 марта 2015)
профильный уровень
Досрочный ЕГЭ по математике (26 марта 2015)
профильный уровень (с критериями)
Тренировочная работа по математике апрель 2015
профильный уровень
Досрочный ЕГЭ по математике (резервный день)
профильный уровень (задания 15-21)
Диагностическая работа по математике апрель 2015
профильный уровень, разбор на сайте 1-20, 15-21 (критерии)
базовый уровень
Реальный ЕГЭ по математике (4 июня 2015)
Образец варианта
ОГЭ 2015
Демонстрационный вариант ОГЭ 2015
Демо версия ОГЭ 2015
ОГЭ от 27 мая 2015 г.
ОГЭ по математике
Реальные варианты ЕГЭ 2015
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Миша живёт в доме, в котором всего один подъезд. При этом на каждом этаже по (5) квартир. Миша живет в квартире номер (29). На каком этаже живёт Миша?
Количество полных этажей, которые расположены ниже Мишиного, есть округлённый в меньшую сторону результат деления (29) на (5), следовательно, (5) этажей ниже, чем Мишин, тогда Миша живёт на (6) этаже.
Ответ: 6
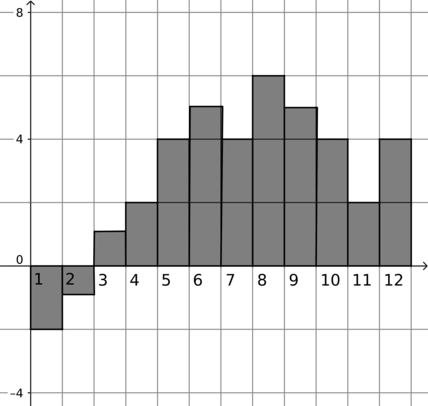
На диаграмме показана температура воздуха в Москве за первые (12) дней марта 2010 года. По горизонтали указываются дни месяца, по вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько из указанных дней температура не превышала (3) градуса Цельсия.
Температура не превышала (3) градуса Цельсия (1), (2), (3), (4) и (11) марта, то есть (5) дней.
Ответ: 5
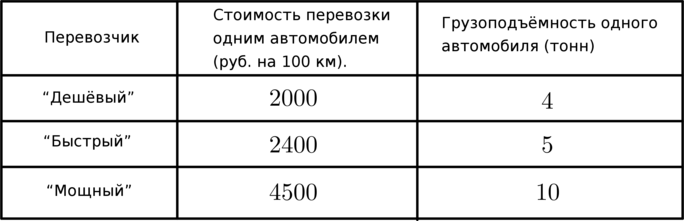
Для транспортировки (38 тонн) груза на (1000 км) можно комбинировать услуги трёх фирм-перевозчиков. Стоимость перевозки и грузоподъёмность автомобилей каждого перевозчика указаны в таблице.
Во сколько рублей обойдется наиболее дешёвый вариант перевозки?
Наиболее дешёвый способ: снарядить 3 машины перевозчика “Мощный” на (1000 км) (то есть по 10 раз) и ещё 2 машины перевозчика “Дешёвый” на (1000 км), что обойдётся в (3cdot 4500cdot 10 +
2cdot 2000cdot 10 = 175,000 руб).
Ответ:
175000
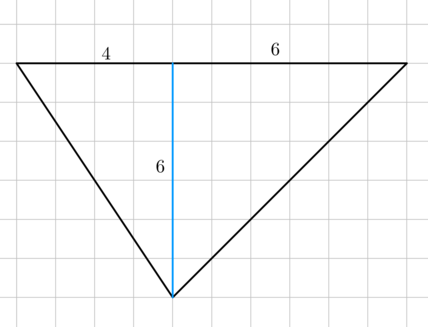
На клетчатой бумаге с размером клетки (1times 1) изображён треугольник. Найдите его площадь.
Данный треугольник можно разрезать на два прямоугольных треугольника, как показано на рисунке. Площади полученных при этом треугольников будут равны (0,5cdot 4cdot 6 = 12) и (0,5cdot
6cdot 6 = 18), следовательно, площадь исходного треугольника равна (12 + 18 = 30).
Ответ: 30
На чемпионате по стрельбе из лука выступают (40) спортсменов, среди них по (8) стрелков из Дании и Туниса. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что пятым будет выступать стрелок из Дании.
Искомая вероятность есть отношение количества спортсменов из Дании к общему количеству спортсменов и равна [dfrac{8}{40} = 0,2,.]
Ответ: 0,2
Найдите корень уравнения [(3x + 4)^2 = (8 + 3x)^2]
Сделаем преобразования:
[(3x + 4)^2 = (8 + 3x)^2quadLeftrightarrowquad 9x^2 + 24x + 16 =
9x^2 + 48x + 64quadLeftrightarrowquad x = -2,.]
Ответ: -2
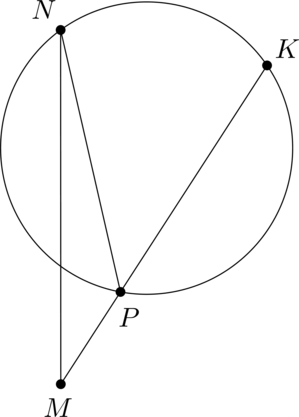
Угол (NMK) равен (35^circ), градусная мера дуги (NK), не содержащей точку (P), равна (88^circ). Найдите угол (MNP). Ответ дайте в градусах.
Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, то (angle NPK = 88^circ : 2 = 44^circ).
(angle NPK) – внешний угол треугольника (NMP), тогда (angle NPK =
angle NMK + angle MNP), откуда [angle MNP = 44^circ — 35^circ
= 9^circ,.]
Ответ: 9
На рисунке изображён график (y = f'(x)) – производной функции (f(x)), определённой на интервале ((-3; 19)). Найдите количество точек максимума функции (f(x)), принадлежащих отрезку ([-1; 18]).
В точке максимума производная равна (0), причём в некоторой окрестности точки максимума слева от неё производная должна быть положительна, а справа от неё – отрицательна. Таким образом, функция (f(x)) имеет единственную точку максимума на указанном отрезке ((x = 15)).
Ответ: 1
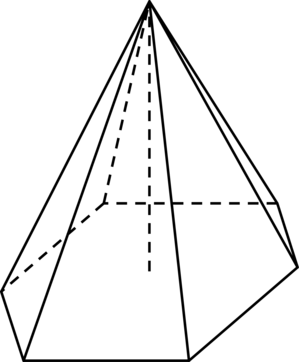
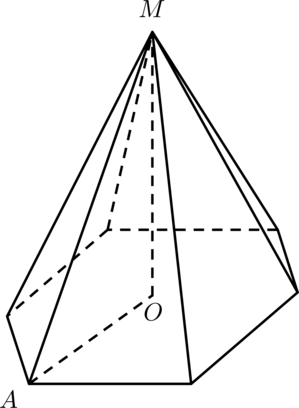
В правильной шестиугольной пирамиде боковое ребро равно (13), а сторона основания равна (5). Найдите высоту пирамиды.
В правильной пирамиде проекция (O) вершины (M) на плоскость основания есть центр описанной около основания окружности.
В правильном шестиугольнике расстояние от центра до вершины равно стороне, следовательно, (AO = 5). Заметим, что (triangle MOA) — прямоугольный, т.к. (MO) перпендикулярно плоскости основания. По теореме Пифагора [MO^2 = MA^2 — AO^2qquadRightarrowqquad MO = sqrt{13^2 — 5^2} =
12,.]
Ответ: 12
Найдите значение выражения [sqrt{8}sin^2dfrac{3pi}{8} —
sqrt{2}]
Используя формулу косинуса двойного угла (cos 2x = 1 — 2sin^2 x), получаем (sin^2 x = dfrac{1 — cos 2x}{2}), тогда [sqrt{8}sin^2dfrac{3pi}{8} — sqrt{2} = 2sqrt{2}cdot dfrac{1 — cos dfrac{3pi}{4}}{2} — sqrt{2} =
2sqrt{2}cdot dfrac{1 + dfrac{sqrt2}{2}}{2} — sqrt{2} =
sqrt{2} + 1 — sqrt{2} = 1,.]
Ответ: 1
Известно, что при некотором физическом процессе, в котором участвует газ, выполнено соотношение (p_1V_1^{1,5} = p_2V_2^{1,5}), где (p_1), (p_2) – давление газа в паскалях в начальный и конечный моменты времени, а (V_1), (V_2) – объём газа в литрах в начальный и конечный моменты времени. В начальный момент времени объём газа равен (3 л), а его давление равно (16 атмосферам). Каким должен стать конечный объём газа, чтобы его конечное давление стало (2
атмосферы)? Ответ дайте в литрах.
Подставляя имеющиеся данные, получим [16cdot 3^{1,5} = 2cdot V_2^{1,5}qquadRightarrowqquad 2^3cdot 3^{1,5} = V_2^{1,5}qquadRightarrowqquad V_2 = 12,.]
Ответ: 12
В сосуд налили (1500 куб. см) воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в (1,4) раза. Найдите объем детали. Ответ выразите в куб. см.
Объём жидкости с погружённой деталью стал (1500cdot 1,4 = 2100
куб.см), следовательно, объём детали равен (2100 — 1500 = 600
куб.см).
Ответ: 600
Расстояние между городами (M) и (N) равно (490 км). Из города (M) в город (N) выехал первый автомобиль, а через час после этого навстречу ему из города (N) выехал второй автомобиль со скоростью (80 км/ч). Найдите скорость первого автомобиля, если автомобили встретились на расстоянии (330 км) от города (M). Ответ дайте в км/ч.
Расстояние, которое до места встречи проехал второй автомобиль, равно (490 — 330 = 160 км), следовательно, он ехал в течение (160 :
80 = 2 ч). Тогда первый автомобиль ехал до места встречи в течение (2 + 1 = 3 ч), следовательно, его скорость равна (330 : 3 = 110
км/ч).
Ответ: 110
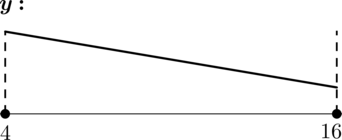
Найдите наименьшее значение функции (y = dfrac{2}{3}xsqrt{x} — 4x
+ dfrac{1}{3}) на отрезке ([4; 16])
ОДЗ: (x geqslant 0).
1) [y’ = dfrac{2}{3}left(sqrt{x} + dfrac{x}{2sqrt{x}}right) —
4 = sqrt{x} — 4] Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [y’ = 0qquadLeftrightarrowqquad sqrt{x} = 4qquadLeftrightarrowqquad x = 16,.]
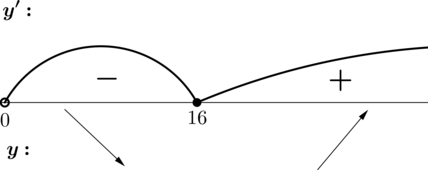
2) Найдём промежутки знакопостоянства (y’):
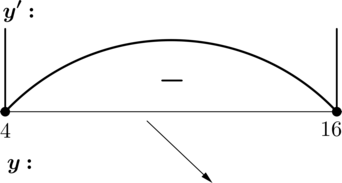
3) Найдём промежутки знакопостоянства (y’) на отрезке ([4; 16]):
4) Эскиз графика (y) на отрезке ([4; 16]):
Таким образом, наименьшего значения на отрезке ([4; 16]) функция (y) достигает в (x = 16): [y(16) = dfrac{2}{3}cdot 64 — 64 + dfrac{1}{3} = -21,.]
Ответ: -21
а) Решите уравнение [cos 2x + sin left(dfrac{pi}{2} — xright) = 0]
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-2pi; dfrac{pi}{2}right]).
а) ОДЗ: (x) – произвольный.
По формулам приведения и формуле косинуса двойного угла (cos 2x=2cos^2x-1): [2cos^2 x — 1 + cos x = 0]
Сделаем замену (cos x = t): [2t^2 — 1 + t = 0qquadLeftrightarrowqquad 2(t — 0,5)(t + 1) = 0
qquadLeftrightarrowqquad left[
begin{gathered}
begin{aligned}
&t = -1\
&t = 0,5
end{aligned}
end{gathered}
right.]
Сделаем обратную замену:
1) (cos x = -1) равносильно (x = pi+2pi n), (ninmathbb{Z}).
2) (cos x = 0,5) равносильно (x = pm dfrac{pi}{3} + 2pi k), (kinmathbb{Z}).
б) (-2pi leqslant pi+2pi n leqslant dfrac{pi}{2}) равносильно (-dfrac32leqslant nleqslant -dfrac{1}{4}), но (ninmathbb{Z}), следовательно, среди этих решений подходит только решение при (n =
-1): (x = -pi).
(-2pi leqslant dfrac{pi}{3} + 2pi k_1 leqslant dfrac{pi}{2}) равносильно (-dfrac{7}{6} leqslant k_1 leqslant dfrac{1}{12}), но (k_1inmathbb{Z}), следовательно, среди этих решений подходят только решения при (k_1 = -1) и (k_1=0): (x = -dfrac{5pi}{3}) и (x=dfrac{pi}3).
(-2pi leqslant -dfrac{pi}{3} + 2pi k_2 leqslant
dfrac{pi}{2}) равносильно (-dfrac{5}{6} leqslant k_2 leqslant
dfrac{5}{12}), но (k_2inmathbb{Z}), следовательно, среди этих решений подходит только решение при (k_2 = 0): (x =
-dfrac{pi}{3}).
Ответ:
а) (pi+2pi n, ninmathbb{Z}), (pm dfrac{pi}{3} + 2pi k,
kinmathbb{Z})
б) (-dfrac{5pi}{3}), (-pi), (-dfrac{pi}{3}), (dfrac{pi}{3})
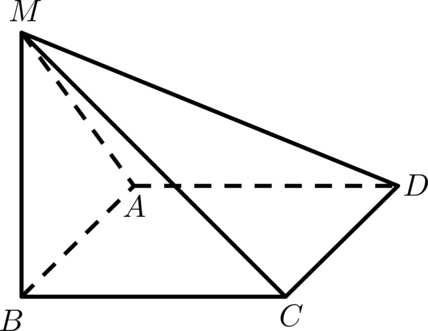
В основании четырёхугольной пирамиды (MABCD) лежит прямоугольник (ABCD) со сторонами (AB = 4), (AD = 15). При этом известны длины некоторых боковых рёбер: (MA = sqrt{26}), (MB = sqrt{10}), (MC =
sqrt{235}).
а) Докажите, что (MB) – высота пирамиды (MABCD).
б) Найдите угол между (MD) и плоскостью ((ABM)).
а) Рассмотрим треугольник (MBA): [MA^2 = 26 = 10 + 16 = (sqrt{10})^2 + 4^2 = MB^2 + BA^2,,] следовательно, треугольник (MBA) прямоугольный и (MBperp AB).
Рассмотрим треугольник (MBC): [MC^2 = 235 = 10 + 225 = (sqrt{10})^2 + 15^2 = MB^2 + BC^2,,] следовательно, треугольник (MBC) прямоугольный и (MBperp BC).
Таким образом, (AB perp MBperp BC), то есть (MB) перпендикулярна двум пересекающимся прямым в плоскости ((ABCD)), следовательно, (MB) – высота пирамиды (MABCD).
б) [MBperp (ABCD)qquadRightarrowqquad MBperp AD;qquad ABperp
AD,,] то есть (ADperp (MBA)), следовательно, (AM) – проекция (MD) на плоскость ((MAB)) и угол между (MD) и ((MAB)) равен углу (AMD).
По теореме Пифагора в треугольнике (MAD): [MD^2 = MA^2 + AD^2 = 26 + 225 = 251qquadRightarrowqquad MD = sqrt{251},.] Тогда [sin AMD = dfrac{AD}{MD} =
dfrac{15}{sqrt{251}}qquadRightarrowqquad angle AMD = arcsin
dfrac{15}{sqrt{251}},.]
Ответ:
б) (arcsin dfrac{15}{sqrt{251}})
Решите неравенство [1 -dfrac{10}{3^{x^2-1} — 1} + dfrac{16}{(3^{x^2-1} — 1)^2}geqslant 0]
ОДЗ: [3^{x^2 — 1}neq 1qquadLeftrightarrowqquad x^2 — 1neq
0qquadLeftrightarrowqquad xneq pm 1]
Решим на ОДЗ. Сделаем замену (t = 3^{x^2 — 1} —
1): [1 — dfrac{10}{t} + dfrac{16}{t^2}geqslant 0qquadLeftrightarrowqquad dfrac{t^2 — 10t + 16}{t^2}geqslant 0qquadLeftrightarrowqquad dfrac{(t — 2)(t — 8)}{t^2}geqslant 0]
По методу интервалов
откуда (tin (-infty; 0)cup(0; 2]cup[8; +infty)). Таким образом, [left[
begin{gathered}
3^{x^2-1} — 1 < 0\
0 < 3^{x^2-1} — 1leqslant 2\
3^{x^2-1} — 1geqslant 8
end{gathered}
right. qquadLeftrightarrowqquad left[
begin{gathered}
3^{x^2-1} < 1\
1 < 3^{x^2-1} leqslant 3\
3^{x^2-1} geqslant 9
end{gathered}
right. qquadLeftrightarrowqquad left[
begin{gathered}
x^2 — 1 < 0\
0 < x^2 — 1 leqslant 1\
x^2 — 1 geqslant 2
end{gathered}
right.] что равносильно [left[
begin{gathered}
x^2 < 1\
1 < x^2 leqslant 2\
x^2 geqslant 3
end{gathered}
right. qquadLeftrightarrowqquad left[
begin{gathered}
xin(-1; 1)\
xin[-sqrt{2}; -1)cup(1; sqrt{2}]\
xin(-infty; -sqrt{3}]cup[sqrt{3}; +infty)
end{gathered}
right.] Тогда с учётом ОДЗ ответ: [xin (-infty; -sqrt{3}]cup[-sqrt{2}; -1)cup(-1; 1)cup(1; sqrt{2}]cup[sqrt{3}; +infty),.]
Ответ:
((-infty; -sqrt{3}]cup[-sqrt{2}; -1)cup(-1; 1)cup(1;
sqrt{2}]cup[sqrt{3}; +infty))
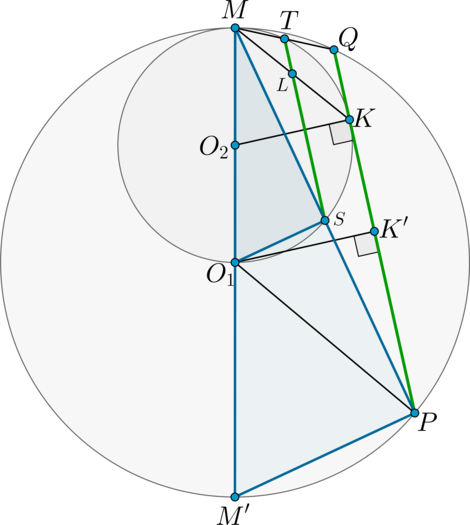
Две окружности касаются внутренним образом в точке (M), причём меньшая из окружностей проходит через центр большей окружности. Хорда (PQ) большей окружности касается меньшей в точке (K); (S) и (T) – точки пересечения меньшей окружности с (MP) и (MQ) соответственно.
а) Докажите, что прямые (ST) и (PQ) параллельны.
б) Пусть (L) – точка пересечения (MK) и (ST). Найдите (ML), если радиус большей окружности равен (5), а (PQ = 6).
а) Пусть (O_1) и (O_2) центры большей и меньшей окружностей соответственно. Так как (O_1M) и (O_2M) перпендикулярны касательной, проходящей через точку (M), то точки (O_1), (O_2) и (M) лежат на одной прямой. Пусть (M’) – точка пересечения этой прямой с большей окружностью, отличная от (M).
Докажем, что хорды данных окружностей, лежащие на одной прямой, проходящей через точку (M), относятся как их диаметры. Рассмотрим доказательство на примере хорд (MS) и (MP).
Рассмотрим треугольники (MM’P) и (MO_1S). Эти треугольники прямоугольные, так как (MO_1) – диаметр меньшей окружности (описанной около треугольника (MO_1S)), а (MM’) – диаметр большей окружности (описанной около треугольника (MM’P)). При этом острый угол (O_1MS) у них общий, следовательно, эти треугольники подобны.
Из подобия получаем требуемое: [dfrac{MS}{MP} = dfrac{MO_1}{MM’}]
Для других хорд, лежащих на прямой, проходящей через точку (M), утверждение доказывается аналогично.
Из доказанного следует, что [dfrac{MS}{MP} = dfrac{MT}{MQ},.]
Рассмотрим треугольники (MST) и (MPQ): (angle SMQ) – общий, (dfrac{MS}{MP} = dfrac{MT}{MQ}), следовательно, эти треугольники подобны, откуда (angle MST = angle MPQ), следовательно, (STparallel PQ).
б) Опустим перпендикуляры (O_1K’) и (O_2K) на (PQ).
По теореме Пифагора [K’O_1^2 = O_1P^2 — K’P^2]
Так как (O_1P = O_1Q), то (O_1K’) – медиана в треугольнике (PO_1Q), следовательно, (K’P = 3), тогда (K’O_1 = sqrt{25 — 9} = 4).
Так как (MO_1) – радиус большей окружности и диаметр меньшей, то радиус меньшей окружности равен (0,5cdot 5 = 2,5)
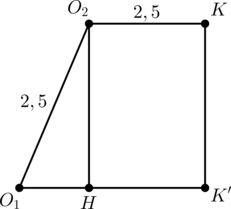
Рассмотрим прямоугольную трапецию (O_2O_1K’K).
Пусть (O_2H) перпендикуляр к (O_1K’), тогда (O_1H = O_1K’ — O_2K =
4-2,5=1,5), следовательно, по теореме Пифагора (2 = O_2H = KK’). Тогда [PK = PK’+K’K=3+2=5,qquad KQ = PK’-K’K=3-2=1.]
Так как хорды данных окружностей, лежащие на одной прямой, проходящей через точку (M), относятся как их диаметры, то (ST) – средняя линия в треугольнике (MPQ), тогда (SL) – средняя линия в треугольнике (MPK) и (LT) – средняя линия в треугольнике (MKQ), следовательно, [SL = 0,5PK=2,5,qquad LT = 0,5KQ=0,5,.]
По теореме о произведении отрезков хорд [MLcdot LK = SLcdot LT = 1,25=dfrac54,,] откуда, с учётом равенства (ML = LK), получим [ML =
dfrac{sqrt{5}}{2},.]
Ответ:
б) (dfrac{sqrt{5}}{2})
15 января планируется взять кредит в банке на 11 месяцев. Условия его возврата таковы:
(bullet) 1-ого числа каждого месяца долг возрастает на (y%) по сравнению с долгом на конец предыдущего месяца;
(bullet) со 2-ого по 14-ое числа каждого месяца необходимо выплатить часть долга в виде платежа банку;
(bullet) 15-ого числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-ое число предыдущего месяца.
Известно, что общая сумма выплат по кредиту превысила сумму кредита на (30%) процентов. Найдите (y).
Фраза “долг должен быть на одну и ту же сумму меньше” означает, что кредит выплачивается дифференцированными платежами. Следовательно, т.к. кредит взят на 11 месяцев, то эта “одна и та же сумма”, на которую уменьшается долг каждый месяц, равна (frac1{11}) части от суммы кредита. Обозначим сумму кредита за (A) и составим таблицу.
Т.к. каждый месяц долг увеличивается на (y%), то в первый месяц долг увеличиться на (0,01ycdot A) рублей, то есть составит (A+0,01yA) рублей.
После выплаты долг должен уменьшиться на (frac1{11}A) рублей, то есть должен составить (frac{10}{11}A) рублей. Значит, выплата в первый месяц будет равна (A+0,01yA-frac{10}{11}A=0,01yA+frac1{11}A)
[begin{array}{|l|c|c|c|}
hline text{Номер месяца}&text{Долг после начисления }%&
text{Долг после выплаты}&text{Выплата}\
hline 1& A+0,01ycdot A&
frac{10}{11}A& 0,01ycdot A+frac1{11}A\
hline 2& frac{10}{11}A+0,01ycdot frac{10}{11}A&
frac{9}{11}A& 0,01ycdot frac{10}{11}A+frac1{11}A\
hline 3& frac9{11}A+0,01ycdot frac9{11}A&
frac8{11}A& 0,01ycdot frac9{11}A+frac1{11}A\
hline dots&dots&dots&dots\
hline 10& frac2{11}A+0,01ycdot frac2{11}A&
frac1{11}A& 0,01ycdot frac2{11}A+frac1{11}A\
hline 11& frac1{11}A+0,01ycdot frac1{11}A&
0& 0,01ycdot frac1{11}A+frac1{11}A\
hline end{array}]
Заметим, что все выплаты состоят из двух частей, причем одна часть (left(frac1{11}Aright)) фиксирована.
По условию общая сумма выплат (R) превысила на (30%) сумму кредита (A). Это значит, что переплата по кредиту (R-A) составляет (30%) от (A). Найдем общую сумму выплат:
(R=left(0,01ycdot A+frac1{11}Aright)+left(0,01ycdot
frac{10}{11}A+frac1{11}Aright)+ left(0,01ycdot
frac9{11}A+frac1{11}Aright)+dots+)
(+left(0,01ycdot frac2{11}A+frac1{11}Aright)+left(0,01ycdot
frac1{11}A+frac1{11}Aright)=)
(=0,01ycdot
Aleft(1+frac{10}{11}+frac9{11}+dots+frac2{11}+frac1{11}right)+11cdot
frac1{11}A=)
В скобке — сумма 11 членов арифметической прогрессии, где (a_1=frac1{11}, a_{11}=1). По формуле (S_{11}=dfrac{a_1+a_{11}}2cdot 11), значит
(=0,01ycdot Acdot frac12left(frac1{11}+1right)cdot
11+A=0,06yA+A)
Тогда переплата составила (R-A=0,06yA). Т.к. переплата составила (30%) от (A), то
[dfrac{R-A}{A}cdot 100%=30% quad Rightarrow quad dfrac{0,06yA}A=0,3 quad
Rightarrow quad y=5]
Ответ:
(5)
Найдите все значения параметра (a), при каждом из которых система уравнений
[begin{cases}
x^2 — 4x + y^2 + 2y + 3,75 = |4x — 2y — 10|\
2x + 4y = a
end{cases}]
имеет более двух решений.
Рассмотрим два случая:
1) (4x — 2y — 10geqslant 0)
Первое уравнение системы в этом случае приводится к виду [x^2 — 8x + y^2 + 4y + 13,75 = 0qquadLeftrightarrowqquad (x — 4)^2 + (y + 2)^2 = 2,5^2,.]
Отдельно рассматриваемое данное уравнение задаёт на плоскости ((x; y)) окружность с центром в точке (O_1(4; -2)) и радиусом (2,5), но с учётом условия (4x — 2y — 10geqslant 0) нам подходит только часть этой окружности, лежащая в полуплоскости (y leqslant 2x — 5).
2) (4x — 2y — 10 < 0)
Первое уравнение системы в этом случае приводится к виду [x^2 + y^2 = 6,25qquadLeftrightarrowqquad x^2 + y^2 = 2,5^2,.]
Отдельно рассматриваемое данное уравнение задаёт на плоскости ((x; y)) окружность с центром в точке (O(0; 0)) и радиусом (2,5), но с учётом условия (4x — 2y — 10 < 0) нам подходит только часть этой окружности, лежащая в полуплоскости (y > 2x — 5).
Решая системы уравнений [begin{cases}
(x — 4)^2 + (y + 2)^2 = 2,5^2\
y = 2x — 5
end{cases}
qquad text{и}qquad
begin{cases}
x^2 + y^2 = 2,5^2\
y = 2x — 5
end{cases},,] находим, что окружности из пунктов 1) и 2) пересекаются с прямой (y
= 2x — 5) в точках (C(2,5; 0)) и (D(1,5; -2)).
При каждом фиксированном значении (a) второе уравнение исходной системы задаёт прямую, параллельную (OO_1) (при (a = 0) оно задаёт прямую (OO_1), а при (aneq 0) прямую, полученную из (OO_1) параллельным переносом).
Найдём значение (a), при котором прямая (y = 0,25a — 0,5x) имеет с окружностью (x^2 + y^2 = 2,5^2) одну общую точку: [x^2 + (0,25a — 0,5x)^2 = 2,5^2qquadLeftrightarrowqquad 5(x^2 -0,2ax + 0,01a^2) + dfrac{a^2}{4} — dfrac{a^2}{20} = 25,.]
Чтобы данное уравнение имело единственное решение, необходимо и достаточно, чтобы левая часть представляла собой полный квадрат, откуда получим (a^2 = 125), то есть (a = pm 5sqrt{5}).
Проводя вычисления, можно показать, что при (a = pm 5sqrt{5}) окружность из пункта 2) также имеет с прямой (y = 0,25a — 0,5x) одну общую точку, то есть случаям (mathbf{1}) и (mathbf{4}) на рисунке отвечают прямые (y = 0,25a — 0,5x) при (a = 5sqrt{5}) и (a =
-5sqrt{5}) соответственно.
Также легко показать, что случаям (mathbf{2}) и (mathbf{3}) отвечают прямые (y = 0,25a — 0,5x) при (a = 5) и (a = -5) соответственно.
Прямая (y = 0,25a — 0,5x) при (a > 5sqrt{5}) не имеет общих точек с нарисованными дугами окружностей.
При (a = 5sqrt{5}) эта прямая имеет две общие точки с этими дугами окружностей.
При (5 < a < 5sqrt{5}) эта прямая имеет четыре общие точки с этими дугами окружностей.
При (a = 5) эта прямая имеет три общие точки с этими дугами окружностей.
При (-5 < a < 5) эта прямая имеет две общие точки с этими дугами окружностей.
При (a = -5) эта прямая имеет три общие точки с этими дугами окружностей.
При (-5sqrt{5} < a < -5) эта прямая имеет четыре общие точки с этими дугами окружностей.
При (a = -5sqrt{5}) эта прямая имеет две общие точки с этими дугами окружностей.
При (a < -5sqrt{5}) эта прямая не имеет общих точек с этими дугами окружностей.
Таким образом, ответ: [ain (-5sqrt{5}; -5]cup[5; 5sqrt{5}),.]
Ответ:
((-5sqrt{5}; -5]cup[5; 5sqrt{5}))
Среди посетителей одного из магазинов был проведён опрос. Известно, что каждому опрошенному целое число лет. Участник опроса попадает в возрастную категорию А, если ему более (40) лет, иначе он попадает в категорию Б. Спустя (4) года опрос был проведён повторно, причём среди тех же людей, что и в первый раз.
а) Могло ли оказаться так, что во время повторного опроса средний возраст опрашиваемых, попавших в категорию Б, понизился?
б) Могло ли оказаться так, что при повторном опросе средний возраст опрашиваемых, попавших в категорию А, понизился, и средний возраст опрашиваемых, попавших в категорию Б, тоже понизился?
в) Известно, что первоначально средний возраст опрашиваемых составил (40) лет, средний возраст опрашиваемых, попавших в категорию Б, составил (28) лет, а средний возраст опрашиваемых, попавших в категорию А, составил (55) лет. При повторном опросе средний возраст опрашиваемых, попавших в категорию Б, стал равен (31) году, а попавших в категорию А – (57) годам. При каком наименьшем числе участников опроса возможна такая ситуация?
а) Это могло быть, например, в случае, когда в категорию Б попадали изначально три человека, одному из которых было (40) лет, а двум другим по (10) лет. Тогда их средний возраст при первом опросе был (20) лет, а при втором опросе в категории Б остались только двое, которым исполнилось по (14) лет, то есть их средний возраст стал (14) лет.
б) Это могло быть, например, в случае, когда в категорию Б попадали те же трое, что в пункте а), а в категорию А изначально попадали два человека, которым было по (70) лет.
в) Пусть количество опрошенных, которые попадали в категорию А при первом опросе, было равно (n), а количество опрошенных, попадавших в категорию Б, было равно (m), тогда суммарный возраст участников при первом опросе составлял (40(n + m)), причём [40(n + m) = 55n +
28mqquadLeftrightarrowqquad 5n = 4m,,] откуда, в частности, следует, что (n) делится на (4), а (m) делится на (5).
Так как средний возраст в категории А вырос не на 4 года, то в категорию А должны были перейти опрошенные, которые ранее относились к категории Б. Пусть их ровно (k) человек. Так как при повторном опросе им могло быть не более (44) лет, то суммарный возраст участников категории А за счёт появления этих (k) человек не мог увеличиться более, чем на (44k), тогда [57(n + k)leqslant 59n + 44kqquadRightarrowqquad 2ngeqslant 13k,.]
Так как (k geqslant 1), то (ngeqslant 7), но (n) делится на (4), следовательно, (ngeqslant 

Проверим, подходит ли нам этот случай. Пусть возраст перешедшего в категорию А из категории Б стал (41leqslant xleqslant 44), тогда [begin{cases}
57(n + 1) = 59n + x\
31(m — 1) = 32m — x,,
end{cases}] откуда (x = 41) – подходит по условию.
Таким образом, менее (18) человек быть не могло, а (18) человек могло быть, например, так:
в первый раз опросили (8) человек, каждому из которых было по (55) лет, одного человека в возрасте (37) лет и (9) человек, каждому из которых было по (27) лет.
Ответ:
а) Да
б) Да
в) (18)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
В настоящем разделе представлены тренировочные варианты выпускных экзаменационных работ по математике в 2015 году.
Тесты ЕГЭ — 2015 по математике представлены несколькими вариантами. Их структура, количество и уровень сложности заданий соответствуют уровню будущих реальных вариантов ЕГЭ. Практическая ценность данных тестов очень высока, т.к. они полностью моделируют работу выпускника на ЕГЭ по математике в 2015 году.
Подготовка к ЕГЭ по математике актуальна для всех выпускников, так как экзамен по данному предмету является обязательным. Качественная подготовка же, в свою очередь, предусматривает постоянные практические тренировки по решению примерных вариантов будущей экзаменационной работы. Именно для таких тренировок и разработаны тесты ЕГЭ — 2015 по математике. С помощью этих тестов учащийся может реально оценить свои возможности, выяснить свои «слабые» места в подготовке, научиться рационально расходовать «выделяемое» для экзамена время при решении теста.
Тесты ЕГЭ — 2015 по математике помогут будущим участникам экзамена и в психологическом плане: решая разные варианты данных тестов, учащиеся уясняют для себя как устроен основной каркас экзаменационной работы, какими знаниями нужно обладать, чтобы уверенно и правильно выполнять задания. ЕГЭ по математике перестанет быть для них чем то страшным и малопонятным и обретет вполне реальные очертания.
Так что, не теряйте драгоценное время и приступайте к подготовке!
И помните проверенное жизнью правило: «Тяжело в учении — легко в бою!»
Удачи всем при написании ЕГЭ по математике в 2015 году!