Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
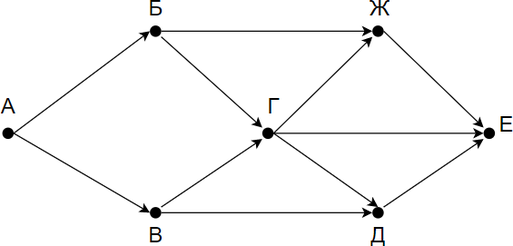
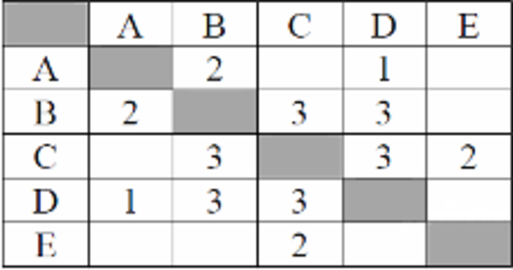
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
Источник: Демонстрационная версия ЕГЭ—2016 по информатике.
2
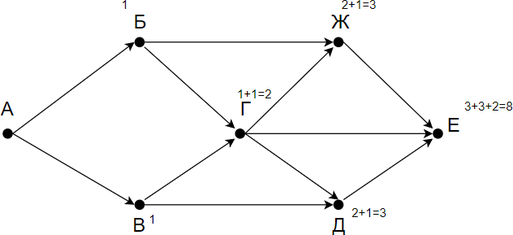
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта Г в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
3
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.
4
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 40 | 15 | |||||
| П2 | 40 | 35 | 50 | ||||
| П3 | 10 | 65 | 8 | ||||
| П4 | 15 | 35 | 22 | 33 | |||
| П5 | 10 | 50 | |||||
| П6 | 50 | 65 | 22 | 50 | 40 | ||
| П7 | 8 | 33 | 40 |
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.
5
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 40 | 15 | |||||
| П2 | 40 | 35 | 48 | ||||
| П3 | 10 | 65 | 11 | ||||
| П4 | 15 | 35 | 22 | 33 | |||
| П5 | 10 | 50 | |||||
| П6 | 48 | 65 | 22 | 50 | 40 | ||
| П7 | 11 | 33 | 40 |
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.
Пройти тестирование по этим заданиям
На уроке рассматривается решение 13 задания ЕГЭ по информатике
Содержание:
- Объяснение заданий 13 ЕГЭ по информатике
- Графы. Поиск количества путей
- Решение заданий 13 ЕГЭ по информатике
13-е задание: «Информационные модели»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)
До ЕГЭ 2021 года — это было задание № 15 и № _ ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование указаний в условии задания, что путь должен включать (или не включать) заданные промежуточные вершины»
ФГБНУ «Федеральный институт педагогических измерений»
Графы. Поиск количества путей
- Если в город
Rиз городаAможно добраться только из городовX,YиZ, то количество различных путей из городаAв городRравно сумме числа различных путей проезда изAвX, изAвYи изAвZ, то есть: - где NR — это количество путей из вершины
Aв вершинуR - Число путей не бесконечно, исключением является только граф, в котором есть циклы – замкнутые пути.
- Часто задачи с графами целесообразней решать с конца.
NR = NX + NY + NZ
Решение заданий 13 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
13_1:
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей, ведущих из города А в город М и проходящих через город Г?

✍ Решение:
- Удалим ребра, которые проходят «мимо» вершины Г или до которых от пункта А можно дойти, минуя вершину Г:
- Вершина В удалена, т.к. возможны только следующие траектории движения через этот пункт (которые НЕ проходят через пункт Г):
- 1. А — Б — В — И — М
- 2. А — Б — В — Е — И — М
- 3. А — Б — В — Е — М
- 4. А — Б — В — Е — К — М
- Теперь посчитаем результаты по оставшимся вершинам:
М = И + Е + К
-----
И = Е
Е = Г + Ж
Г = Б + А + Д = 1 + 1 + 1 = 3
Ж = Г = 3
К = Е + Ж
Теперь возвращаемся, подставляя найденные значения: ↑
Е = Г + Ж = 3 + 3 = 6
Ж = Г = 3
И = Е = 6 (получили из последующих шагов)
К = Е + Ж = 6 + 3 = 9
М = И + Е + К = 6 + 6 + 9 = 21
Результат: 21
Видео ЕГЭ по информатике (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13_2:
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей, ведущих из города А в город М и не проходящих через город Г?

✍ Решение:
- Удалим ребра, которые проходят через вершину Г:
- Теперь посчитаем результаты по оставшимся вершинам:
М = И + Е + К
-----
И = В + Е
В = 1
Е = В + Ж
Ж = 1
Теперь возвращаемся, подставляя найденные значения: ↑
Е = В + Ж = 1 + 1 = 2
И = В + Е = 1 + 2 = 3
К = Е = 2
М = И + Е + К = 3 + 2 + 2 = 7
Результат: 7
Подробное решение данного 13 задания в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13 задание. Демоверсия ЕГЭ 2018 информатика:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих через город Ж?

✍ Решение:
Результат: 20
Подробное решение 13 задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13_4:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Какова длина самого длинного пути из города А в город М?
Длиной пути считать количество дорог, составляющих этот путь.

✍ Решение:
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Простейшие задачи на графы
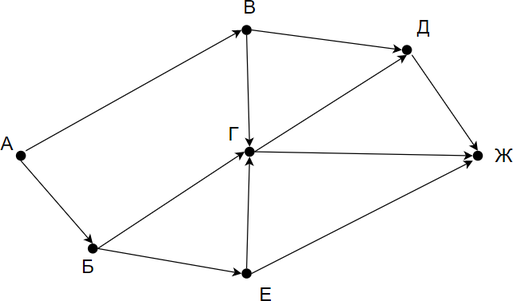
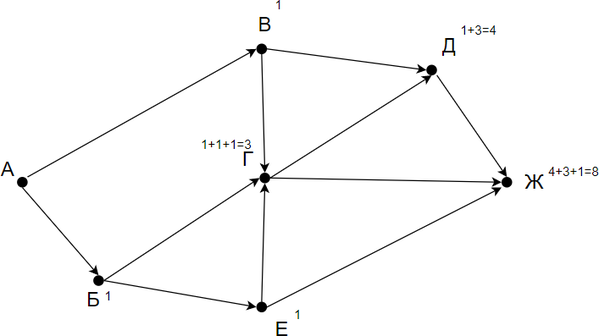
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?
Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем:
Г = Б + В
Д = Г + В
Ж = Б + Г
Е = Ж + Г + Д
Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Заметим, что количество путей в город Ж является суммой путей в города Д, Г и Е. Количество путей в город Г — сумма путей в город В, Б и Е. Таким образом получаем:
Г = Б + В + Е
Д = В + Г
Ж = Д + Г + Е
Заметим, что в пункты Б, В и Е можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8
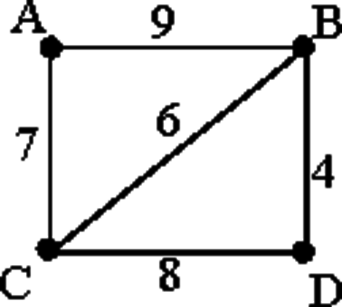
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, D.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 7 км.
A—D—B—C—E: длина маршрута 9 км.
A—D—C—E: длина маршрута 6 км.
Самый короткий путь: A—D—C—E. Длина маршрута 6 км.
Ответ: 6
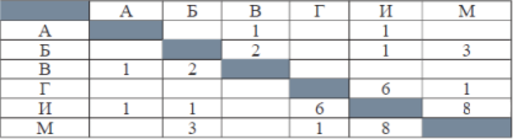
Геральт спешит выручить Цири из плена Кагыра. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого короткого участка кратчайшего пути от Геральта до Цири (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:
Найдём все варианты маршрутов из И в М и выберем самый короткий.
Из пункта И можно попасть в пункты А, Б, Г, М.
Из пункта Г можно попасть в пункты И, М.
Из пункта В можно попасть в пункты А, Б.
Из пункта Б можно попасть в пункты В, И, М.
И—А—В—Б—М: длина маршрута 7 км.
И—Б—М: длина маршрута 4 км.
И—Г—М: длина маршрута 7 км.
И—М: длина маршрута 8 км.
Самый короткий путь: И—Б—М. Длина маршрута 4 км. Самый короткий участок этого пути равен 1 км.
Ответ: 1
На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог.
Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами.
Заметим, что наиболее удалены друг от друга пункты A и D. Найдём все варианты маршрутов из A в D и выберем самый короткий.
A—B—D: длина маршрута 13 км.
A—C—D: длина маршрута 15 км.
A—B—C—D: длина маршрута 23 км.
A—C—B—D: длина маршрута 17 км.
Заметим, что кратчайшее расстояние между пунктами A и D равняется 13.
Ответ: 13
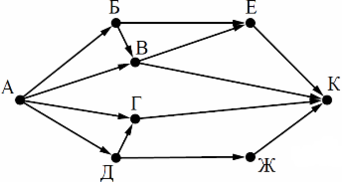
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + N Г + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 2 = 3;
NЖ = NД = 1;
NВ = NА + NБ = 1 + 1 = 2;
NГ = NА + NД = 1 + 1 = 2;
NД = NА = 1;
NБ = NА = 1.
Подставим в формулу (*): N = 3 + 2 + 2 + 1 = 8.
Ответ: 8
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами B и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Проанализируем некоторые возможные маршруты.
Маршрут B—D—E, длина 11 км.
Маршрут B—C—D—E, длина 10 км.
Маршрут B—С—D—A—E, длина 9 км.
Любые другие маршруты будут длиннее маршрута B—С—D—A—E. Самый короткий путь: B—С—D—A—E. Длина маршрута 9 км.
Ответ: 9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Поиск путей в
графе
Разбор заданий № 15 ЕГЭ (11 кл)
Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных
моделей (схемы, карты, таблицы, графики и формулы). (повышенный уровень, время – 3
мин)
Что
нужно знать:
|
Теория |
|
Граф представляется как |
|
Теория графов находит применение, например, в |
|
(ГИС). Существующие или вновь проектируемые |
|
рассматриваются как вершины, а соединяющие |
|
электропередачи и т. п. — как рёбра. |
|
производимых на таком графе, позволяет, например, |
|
путь или ближайший |
|
Графы[2] используют во всех отраслях нашей |
|
необходимо в управлении |
|
транспортировки и |
|
Графы используют в связи с развитием теории вероятности, |
|
и информационных |
|
Граф3 |
|
вершин; обозначается граф через G(V, Е). Неупорядоченная |
|
ребром, упорядоченная пара — дугой. |
|
неориентированным; |
|
вершин может соединяться двумя или более |
|
такие рёбра (дуги) называются кратными. |
|
кончаться в одной и той же вершине, такая |
|
соединённые ребром или дугой, называются смежными. |
|
вершину, также называются смежными. Ребро |
|
называется инцидентными. Говорят, что ребро |
|
(u, v) |
|
Маршрут на графике — это последовательность ребер 𝑎1,𝑎2,…, 𝑎𝑛 |
|
одного ребра служит |
Информационные
ресурсы:
1.
Теория: Способы представления графов,
2.
Задания для тренировки: https://inf-ege.sdamgia.ru/test?a=catlistwstat
a.
Графы, содержащие
более или менее десяти вершин просмотреть
b.
Графы, содержащие
десять вершин просмотреть
3.
Онлайн-тесты Константина Полякова для подготовки к ЕГЭ: http://kpolyakov.spb.ru/school/egetest/b15.htm
Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2020)
|
На рисунке представлена схема дорог, связывающих города А, |
|
И, К, Л, М. По каждой |
|
указанном стрелкой. Сколько существует различных |
|
проходящих через |

Решение:
1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город М,
позволяют обойти город Ж:

2. Посчитаем
последовательно количество путей до каждого из городов:
a. Начало
маршрута А = 1;
b. последовательно
будем рассматривать соседние (связанные) вершины и подсчитывать количество
проходящих через них путей:
Д = А = 1; Г =А + Д = 2; В = А
+ Г = 3; Б = А + В = 4; Е = Б
= 4;
З = Д + Г + В = 6; Ж = З + В + Б + Е = 17; И
= Ж =17; К = И =17; Л = И
= 17; М = Л + И + К = 51.
c. Подсчет
количества путей можно отобразить на графе:

Ответ: 51.
Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2019)
|
На рисунке представлена схема дорог, связывающих города А, |
||
|
И, К, Л, М. По каждой |
||
|
указанном стрелкой. Сколько существует различных путей |
||
|
проходящих через |
||
|
|
Решение:
1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город М,
позволяют обойти город Л:

2. Посчитаем
последовательно количество путей до каждого из городов и отобразим это на
графе:

Ответ: 28.
Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2018)
|
На рисунке представлена схема дорог, связывающих города А, |
|
|
И, К, Л, М. По каждой |
|
|
указанном стрелкой. Сколько существует различных путей |
|
|
проходящих через |
|
|
|
|
|
Решение: |
1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город М,
позволяют обойти город Ж:

2. Посчитаем
последовательно количество путей до каждого из городов и отобразим это на
графе:

Ответ: 20.
Разбор заданий № 1. СтатГрад. Подготовка к ЕГЭ 2019[3]
Вариант №1
|
На рисунке – схема |
||
|
Т. По каждой дороге |
||
|
стрелкой. |
||
|
Сколько существует |
||
|
|
Решение:
Посчитаем последовательно количество
путей до каждого из городов: 1. Начало маршрута А
= 1;
2. последовательно
будем рассматривать соседние (связанные) вершины и подсчитывать количество
проходящих через них путей:
Д = А = 1; Г =А + Д = 2; Б = А
= 1; В = А + Б = 2; Е = А
+ Б + В + Г + Д = 7; Л =
Е = 7; К = Е = 7; М = К + Е + Л = 21; Н
= К + Л + М = 35; П = М = 35; Р = М + П = 70; Т = П
+ Р = 105.
3. Подсчет
количества путей можно отобразить на графе:

Ответ: 105.
Вариант №2
|
На рисунке – схема |
||
|
Т. По каждой дороге |
||
|
стрелкой. |
||
|
Сколько существует |
||
|
|
Решение:
Посчитаем последовательно количество путей до каждого
из городов: 1. Начало маршрута А
= 1;
2. последовательно
будем рассматривать соседние (связанные) вершины и подсчитывать количество
проходящих через них путей:
Д = А = 1; Б = А = 1; Г =А + Б = 2; В = А + Б = 2; Е = А
+ Б + В + Г + Д = 7; К =
Е = 7; Л = Е = 7; М = Е + К + Л = 21; Н
= К + М + Л = 35; П = Н =
35; Р = Н = 35; Т = П
+ Р = 70.
3. Подсчет
количества путей можно отобразить на графе:

Ответ: 70.
Вариант №3
|
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, |
||
|
С, Т. По каждой дороге |
||
|
стрелкой. Сколько существует различных путей |
||
|
через город Л? |
||
|
|
Решение:
1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город Л:

4. Рассматривая
соседние (связанные) вершины, посчитаем последовательно количество путей до
каждого из городов, результат отобразим на графе (А = 1):

Ответ: 64.
Вариант №4
|
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, |
||
|
С, Т. По каждой дороге |
||
|
стрелкой. Сколько существует различных путей |
||
|
через город Н? |
||
|
|
Решение:
1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город Н:

2. Рассматривая соседние (связанные) вершины,
посчитаем последовательно количество путей до каждого из городов, результат
отобразим на графе (А = 1):

Ответ: 32.
Вариант №5
|
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, |
||
|
С, Т. По каждой дороге |
||
|
стрелкой. Сколько существует различных путей |
||
|
через город Е? |
||
|
|
Решение:
1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город Е:

2. Рассматривая соседние (связанные) вершины,
посчитаем последовательно количество путей до каждого из городов, результат
отобразим на графе (А = 1):

Ответ: 63.
Вариант №6
|
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, |
||
|
С, Т. По каждой дороге |
||
|
стрелкой. Сколько существует различных путей |
||
|
через город В? |
||
|
|
Решение:
1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город В:

2. Рассматривая соседние (связанные) вершины,
посчитаем последовательно количество путей до каждого из городов, результат
отобразим на графе (А = 1):

Ответ: 42.
Разбор заданий № 18. ЕГЭ 2020. Ушаков Д.М. 10 тренировочных
вариантов[4]
Вариант 1
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 30. Вариант 2
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 41.
Вариант 3
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 25
Вариант 4
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 32
Вариант 5
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

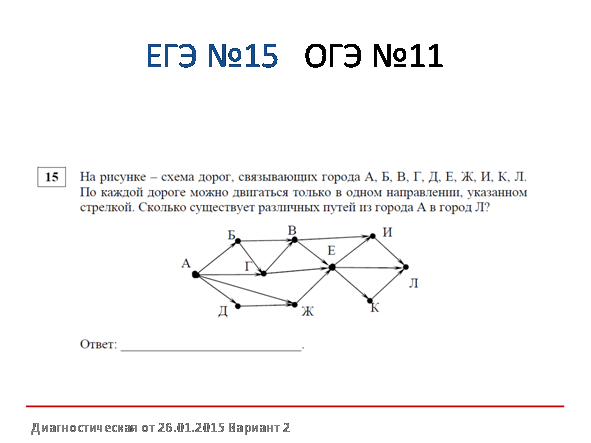
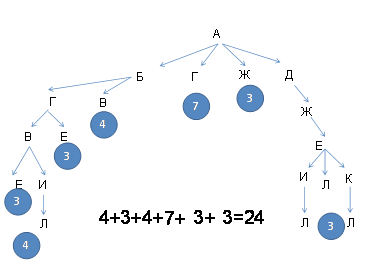
Ответ: 24
Вариант 6
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 12
Вариант 7
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 18
Вариант 8
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 30
Вариант 9
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует |
||
|
|
Решение:
Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 19
Вариант 10
|
На рисунке – схема |
||
|
По каждой дороге можно двигаться только в |
||
|
Сколько существует различных путей из |
||
|
Е? |
||
|
|
Использование теории графов для решения заданий ЕГЭ
|
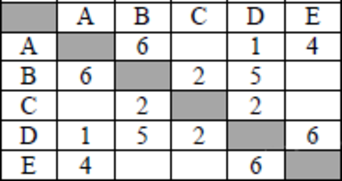
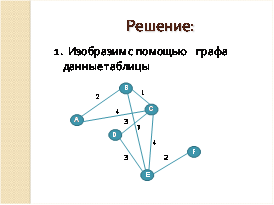
1. Между населенными пунктами A,B,C,D,E,Fпостроены дороги, протяженность которых приведена в таблице(отсутствие числа означает, что прямой дороги нет). Определить длину кратчайшего пути между пунктами E и F. (Передвигаться можно только по построенным дорогам).
Решение: |
Сначала изобразим конечный пункт F. В этот пункт можно попасть только из пункта Е. Соединяем пункты Е и F дугой и указываем вес этой дуги. Он равен двум, то есть расстоянию между пунктами Е и F. Соответственно по графу можно увидеть, что в пункт Е можно попасть из пунктов B, C и D. В пункт В можно попасть из А. В пункт С – из В и А. В пункт D – из С. В пункт В попадаем из А. В пункт С – из В и А. И в пункт В из А.
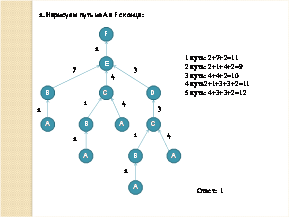
Данную схему можно рассматривать как ориентированный взвешенный граф, который наглядно показывает, что есть 5 путей из пункта А в пункт F. Подсчитываем длину каждого пути
1 путь: 2+7+2=11;
2 путь: 2+1+4+2=9;
3 путь: 4+4+2=10;
4 путь2+1+3+3+2=11;
5 путь: 4+3+3+2=12.
Так как нам надо определить длину кратчайшего пути, то выбираем второй путь, длина которого равна 9. Данный ответ находится под цифрой 1. Поэтому в ответе надо поставить крестик в клеточке, соответствующей первому ответу.
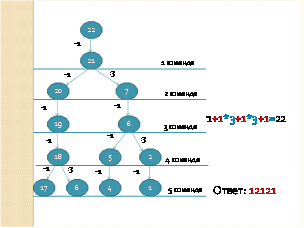
2. У исполнителя Утроитель две команды, которым присвоены номера
1. Прибавь 1;
2. Умножь на 3.
Запишите порядок команд в программе преобразования числа 1 в число 22, содержащей не более 5 команд.
Решение:
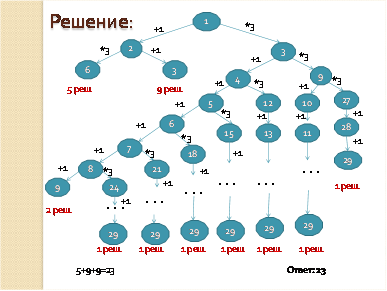
Для решения данного задания используем метод от обратного, то есть будем преобразовывать число 22 в 1. Соответственно команды исполнителя заменим командами антагонистами, то есть команду «Прибавь 1» заменим командой «Вычти 1», а «Умножь на 3» заменим командой «Раздели на 3». Ход выполнения команд можно изобразить в виде дерева, каждая вершина которого имеет две ветки, соответствующие командам 1 и 2. Корнем этого дерева является число 22. Это дерево будет иметь 5 ярусов, так как программа должна содержать не более 5 команд. Но здесь нужно учесть один момент. Если число делится на 3, то вершина будет иметь 2 потомка, а если нет, то одного (то есть делить на 3 мы не можем, а можем только вычитать 1). Получаем следующее дерево.
Инвертируем теперь команды и преобразуем число 1 в 22.
1+1*3+1*3+1=22.
Учитывая номера команд, записываем программу решения данной задачи в виде последовательности соответствующих команд. Ответ: 12121
Решение: (1 способ)
Условие данного задания представлено в виде ориентированного графа, вершинами которого являются названия городов, а дороги, соединяющие эти города, являются дугами графа. Для того, чтобы решить данную задачу, построим еще один ориентированный граф, но с учетом того, по каким дорогам можно будет попасть в пункт Л.
По графу легко подсчитать количество дорог, ведущих из города А в город Л.
3.У Исполнителя Кузнечик 2 команды:
1. Прибавь 3;
2. Вычти 2.
Сколько различных чисел можно получить из числа 1 с помощью программы, которая содержит ровно 5 команд.
Решение:
Оформим решение данной задачи в виде дерева, вершинами которого будут являться числа, соответствующие промежуточным значениям. Данное дерево будет иметь корень, равный 1 и 5 ярусов, так как у нас должно быть ровно 5 команд.

4. У исполнителя Устроитель две команды, которым присвоены номера:
1. Прибавь 1;
2. Умножь на 3.
Программа для Устроителя – это последовательность команд.
Сколько есть программ, которые преобразуют 1 в число 29?
При решении данной задачи следует учитывать, что если число больше 9, то умножать на 3 мы не можем, так как получится число, большее 29, следовательно, вершины с числами большими 9 будут иметь только одну ветвь, соответствующую команде +1.

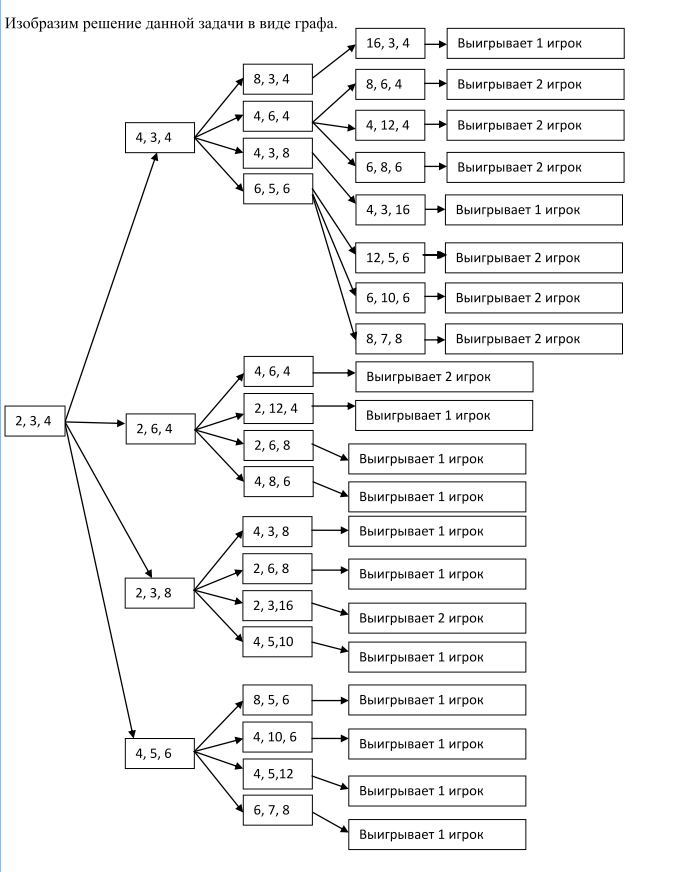
5.Даны три кучи камней, содержащих соответственно 2, 3, 4 камня. За один ход разрешается или удвоить количество камней в какой-нибудь куче, или добавить по 2 камня в каждую из всех трех куч. Выигрывает тот, после чьего хода в какой-нибудь куче становится больше или равно 15 камней или во всех трех кучах суммарно становится больше либо равно 25 камней. Игроки ходят по очереди. Выяснить, кто выигрывает при правильной игре – первый или второй игрок?
Решение: В разумной партии каждый игрок должен стараться следовать общему правилу – всегда оставлять противнику проигрышную позицию. В ходе решения задач можно заметить, что в одной партии в Камешки только один из игроков может следовать этому правилу – тот, кто первым может занять выигрышную позицию (имеет выигрышную стратегию). Если он будет ей следовать, а, значит, делать только разумные ходы и оставлять противнику только проигрышные позиции, то выиграет при любой игре противника. Если начальная позиция выигрышная, то выигрышную стратегию имеет Первый, если проигрышная – Второй.
Изобразим решение данной задачи в виде графа.
Ответ: при правильной стратегии игры выигрывает первый игрок. При этом первый его ход должен быть 2, 3, 4 4, 5, 6.
Литература:
ФИПИ (открытый банк данных)
Материалы демонстрационных вариантов ЕГЭ по информатике 2016, 2015 года
Материалы диагностической работы 2015 года.