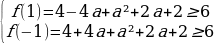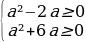Задание № 18 варианта КИМ ЕГЭ по математике профильного уровня
Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.
Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.
«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.
Чему нужно научиться, решая задачи с параметром
В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.
Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т.д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.
Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.
Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме:
Следующая тема курса – графические методы решения задач с параметром
Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости (x; y) или в плоскости (x; a). Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т.д.), эти свойства и приемы их использования тоже нужно знать.
На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.
В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.
Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.

Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
Купить доступ к этой задаче в составе
экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Разбор задач с параметрами из ЕГЭ по математике, по теме задачи с параметром ЕГЭ, как решать задание 18 в экзамене ЕГЭ, задачи с параметром ЕГЭ, задания с параметром ЕГЭ, задача 18 ЕГЭ, модуль и окружности, решение параметров ЕГЭ, решение задачи 18, система уравнений с параметром, научиться решать задачи с параметрами, сложных задач варианта КИМ ЕГЭ, начертить графики функций, ЕГЭ по математике профильного уровня, методы решения уравнений и неравенств, выпускникам 11 класса в 2018 году, поступающим в технический вуз.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с параметром
Задание
1
#1220
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+3=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-3). Рассмотрим два случая:
1) (a=0). В этом случае левая часть равна (0), а правая – нет, следовательно, уравнение не имеет корней.
2) (ane 0). Тогда (x=-dfrac{3}{a}).
Ответ:
(a=0 Rightarrow xin varnothing; \
ane 0 Rightarrow
x=-dfrac{3}{a}).
Задание
2
#1221
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+a^2=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-a^2). Рассмотрим два случая:
1) (a=0). В этом случае левая и правая части равны (0), следовательно, уравнение верно при любых значениях переменной (x).
2) (ane 0). Тогда (x=-a).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
ane 0 Rightarrow x=-a).
Задание
3
#1222
Уровень задания: Легче ЕГЭ
Решите неравенство (2ax+5cosdfrac{pi}{3}geqslant 0) при всех значениях параметра (a).
Неравенство можно переписать в виде (axgeqslant -dfrac{5}{4}). Рассмотрим три случая:
1) (a=0). Тогда неравенство принимает вид (0geqslant
-dfrac{5}{4}), что верно при любых значениях переменной (x).
2) (a>0). Тогда при делении на (a) обеих частей неравенства знак неравенства не изменится, следовательно, (xgeqslant
-dfrac{5}{4a}).
3) (a<0). Тогда при делении на (a) обеих частей неравенства знак неравенства изменится, следовательно, (xleqslant -dfrac{5}{4a}).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
a>0 Rightarrow xgeqslant -dfrac{5}{4a}; \
a<0 Rightarrow xleqslant -dfrac{5}{4a}).
Задание
4
#1223
Уровень задания: Легче ЕГЭ
Решите неравенство (a(x^2-6) geqslant (2-3a^2)x) при всех значениях параметра (a).
Преобразуем неравенство к виду: (ax^2+(3a^2-2)x-6a geqslant 0). Рассмотрим два случая:
1) (a=0). В этом случае неравенство становится линейным и принимает вид: (-2x geqslant 0 Rightarrow xleqslant 0).
2) (ane 0). Тогда неравенство является квадратичным. Найдем дискриминант:
(D=9a^4-12a^2+4+24a^2=(3a^2+2)^2).
Т.к. (a^2 geqslant 0 Rightarrow D>0) при любых значениях параметра.
Следовательно, уравнение (ax^2+(3a^2-2)x-6a = 0) всегда имеет два корня (x_1=-3a, x_2=dfrac{2}{a}). Таким образом, неравенство примет вид:
[(ax-2)(x+3a) geqslant 0]
Если (a>0), то (x_1<x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вверх, значит, решением являются (xin (-infty; -3a]cup
big[dfrac{2}{a}; +infty)).
Если (a<0), то (x_1>x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вниз, значит, решением являются (xin big[dfrac{2}{a};
-3a]).
Ответ:
(a=0 Rightarrow xleqslant 0; \
a>0 Rightarrow xin (-infty; -3a]cup big[dfrac{2}{a}; +infty);
\
a<0 Rightarrow xin big[dfrac{2}{a}; -3abig]).
Задание
5
#1851
Уровень задания: Легче ЕГЭ
При каких (a) множество решений неравенства ((a^2-3a+2)x
-a+2geqslant 0) содержит полуинтервал ([2;3)) ?
Преобразуем неравенство: ((a-1)(a-2)x geqslant a-2). Получили линейное неравенство. Рассмотрим случаи:
1) (a=2). Тогда неравенство примет вид (0 geqslant 0), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
2) (a=1). Тогда неравенство примет вид (0 geqslant -1), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
3) ((a-1)(a-2)>0 Leftrightarrow ain (-infty;1)cup (2;+infty)). Тогда:
(xgeqslant dfrac{1}{a-1}). Для того, чтобы множество решений содержало полуинтервал ([2;3)), необходимо, чтобы
(dfrac{1}{a-1} leqslant 2 Leftrightarrow dfrac{3-2a}{a-1}
leqslant 0
Rightarrow ain (-infty; 1)cup [1,5; +infty)).
Учитывая условие (ain (-infty;1)cup (2;+infty)), получаем (ain
(-infty;1)cup (2;+infty)).
4) ((a-1)(a-2)<0 Leftrightarrow ain (1;2)). Тогда:
(xleqslant dfrac{1}{a-1} Rightarrow dfrac{1}{a-1} geqslant 3).
Действуя аналогично случаю 3), получаем (ain (1;
dfrac{4}{3}big]).
Ответ:
(ain (-infty;dfrac{4}{3}big]cup [2;+infty)).
Задание
6
#1361
Уровень задания: Легче ЕГЭ
Определить количество корней уравнения (ax^2+(3a+1)x+2=0) при всех значениях параметра (a).
Рассмотрим два случая:
1) (a=0). Тогда уравнение является линейным: (x+2=0 Rightarrow
x=-2). То есть уравнение имеет один корень.
2) (ane 0). Тогда уравнение является квадратным. Найдем дискриминант: (D=9a^2-2a+1).
Рассмотрим уравнение (9a^2-2a+1=0): (D’=4-36<0), следовательно, уравнение (9a^2-2a+1=0) не имеет корней. Значит, выражение ((9a^2-2a+1)) принимает значения строго одного знака: либо всегда положительно, либо отрицательно. В данном случае оно положительно при любых (a) (в этом можно убедиться, подставив вместо (a) любое число).
Таким образом, (D=9a^2-2a+1>0) при всех (ane 0). Значит, уравнение (ax^2+(3a+1)x+2=0) всегда имеет два корня: (x_{1,2}=dfrac{-3a-1pm
sqrt D}{2a})
Ответ:
(a=0Rightarrow) один корень
(ane 0 Rightarrow) два корня.
Задание
7
#1363
Уровень задания: Легче ЕГЭ
Решить уравнение (sqrt{x+2a}cdot (3-ax-x)=0) при всех значениях параметра (a).
Данное уравнение равносильно системе:
[begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x=-2a \
&3-(a+1)x=0 qquad (*)
end{aligned} end{gathered} right.
end{cases}]
Рассмотрим два случая:
1) (a+1=0 Rightarrow a=-1). В этом случае уравнение ((*)) равносильно (3=0), то есть не имеет решений.
Тогда вся система равносильна (
begin{cases}
xgeqslant 2\
x=2
end{cases} Leftrightarrow x=2)
2) (a+1ne 0 Rightarrow ane -1). В этом случае система равносильна: [begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x_1=-2a \
&x_2=dfrac3{a+1}
end{aligned} end{gathered} right.
end{cases}]
Данная система будет иметь одно решение, если (x_2leqslant -2a), и два решения, если (x_2>-2a):
2.1) (dfrac3{a+1}leqslant -2a Rightarrow a<-1 Rightarrow ) имеем один корень (x=-2a).
2.2) (dfrac3{a+1}>-2a Rightarrow a>-1 Rightarrow ) имеем два корня (x_1=-2a, x_2=dfrac3{a+1}).
Ответ:
(ain(-infty;-1) Rightarrow x=-2a\
a=-1 Rightarrow x=2\
ain(-1;+infty) Rightarrow xin{-2a;frac3{a+1}})

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
23 апреля 2017
В закладки
Обсудить
Жалоба
Параметры. От простого к сложному. Практикум по решению задач
Решение задач с параметрами является одним из самых трудных разделов школьной математики и требует большого количества времени на их изучение.
Теоретическое изучение физических процессов, решение экономических задач часто приводит к различным уравнениям или неравенствам, содержащим параметры, и необходимой частью их решения является исследование характера процесса в зависимости от значений параметров. Таким образом, задачи с параметрами представляют собой небольшие исследовательские задачи.
Автор: Агашкова Надежда Анатольевна.
pr-sl-p.pdf
Сразу оговорюсь — для того, чтобы научиться решать задачи с параметром, не выйдет просто прочитать краткую инструкцию с указаниями, что вам делать. Нужно потратить некоторое время, чтобы научиться решать такие задачи. Здесь необходимо развитое аналитическое мышление (задачи бывают совершенно разные и нужно уметь анализировать разные функции), отличное умение решать все типы уравнений и неравенств (если вы не можете решить любое задание С1 или С3, то для вас будет очень сложно решить и С6), знание, как ведут себя различные функции и умение строить их графики. Как видите, все не так уж просто, но и 4 первичных балла дают не просто так. Тем не менее, решить С6 более чем реально, нужно набраться терпения. На самом деле, не так уж и много материала, да и раз вы задумались о С6, скорее всего, большинство необходимых знаний у вас есть, в основном придется потратить время на отработку практических навыков и разбор различных методов решения. Материал разбит на несколько частей, и я рекомендую внимательно их изучить, разбирая представленные примеры.
Решение уравнения или неравенства с параметром обычно предполагает несколько случаев, и ни один из них нельзя потерять.
Для того, чтобы решить задачу с параметром, необходимо для начала преобразовать заданное выражение к более простому виду, если это, конечно, возможно. При этом необходимо понимать, какие преобразования являются равносильными, а какие нет. В противном случае могут появиться посторонние корни, которые будет нужно проверить (это не всегда просто, поэтому рекомендую стараться использовать равносильные преобразования).
Рекомендации к выполнению задания 18 ЕГЭ:
- Надо избавиться от логарифмов, модулей, показательных степеней и т.д.
- Еще раз внимательно прочитать задание. Понять, что от вас требуется.
- Попытаться проанализировать получившееся после преобразований выражение на наличие каких-либо специальных свойств функции (периодичность, возрастание/убывание, четность/нечетность и т.д.)
- Часто решить задачу с параметром можно и удобно при помощи графиков. Иногда удобно выполнять построения на обычной координатной плоскости (Х, У), а иногда удобно построить графики в плоскости (Х, а), где а – параметр. Данный способ решения возможен, если вы видите знакомые функции (параболы, прямые, гиперболы, окружности и т.д.). Разумеется, бывает несколько способов решения поставленной задачи, но графический, как правило, наименее громоздок и прост для понимания. Ведь графики показывают поведение функций, и весь необходимый анализ появится у вас перед глазами.
- Важно помнить, что методы решения уравнения или неравенства зависят от степени многочлена. Для этого необходимо рассматривать те значения параметра, при которых (если это возможно) обращается в нуль коэффициент при старшей степени. Пример: (a*x^2-3*x+1=0), при (a=0) выражение принимает вид (-3*x+1=0), т.е. превращается в линейную функцию, а способы решения квадратного и линейного уравнений различны.
Глава 5.
Ответы на задачи для самостоятельного решения
-
a≤
;
≤a≤3; a3.
-
aЄ(
;-1)U(0;
).
-
aЄ{
;-2]U[0;
].
-
aЄ(-∞;0)U(0;2].
-
aЄ(-
;-
)U[-
;
)
-
aЄ(-∞;-
)U(-
;0).
-
a=-1.
-
aЄ(1.5;+∞).
-
aЄ[-2;
].
10) aЄ(-4;-3).
11) (-2;-6), (6;2).
12) aЄ[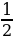
Методическое пособие по решению задач с параметром из ЕГЭ.
Тамбов
2018 год
Оглавление
|
Глава 1.Кратко о параметре |
|
|
Глава 2.Простые примеры задач с параметром |
|
|
Глава 3.Методы решения задач среднего уровня сложности |
|
|
Глава 4.Параметр в ЕГЭ 2018 года |
|
|
Глава 4.1.Функции, зависящие от параметра |
|
|
Глава 4.2.Уравнения с параметром |
|
|
Глава 4.3.Неравенства с параметром |
|
|
Глава 4.4.Системы с параметром |
|
|
Глава 5.Ответы на задачи для самостоятельного решения |
Ответ: a=1/4.
Задачи для самостоятельного решения:
10)Определите все значения параметра a, при каждом из которых система 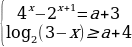
11)При каких значениях параметров a и b система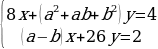
12)Найдите все значения a, при каждом из которых система неравенств 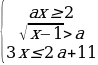
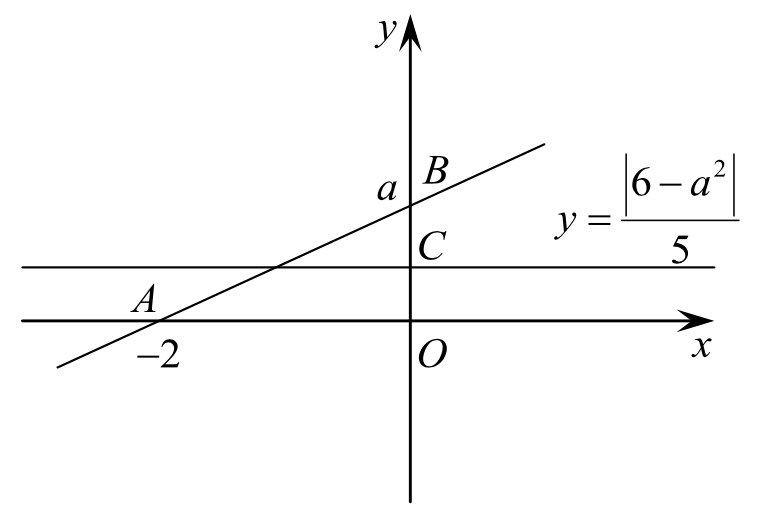
или с точкой В, то условие задачи выполнено.
Решим неравенство 0≤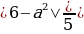
Ответ: aЄ[1;6].
3 задача: Найдите все значения параметра a, при каждом из которых система уравнений 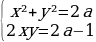
Решение: Заменим первое уравнение разностью, а второе – суммой исходных уравнений: 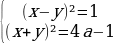
При a система решений не имеет. При a≥1/4 получаем:
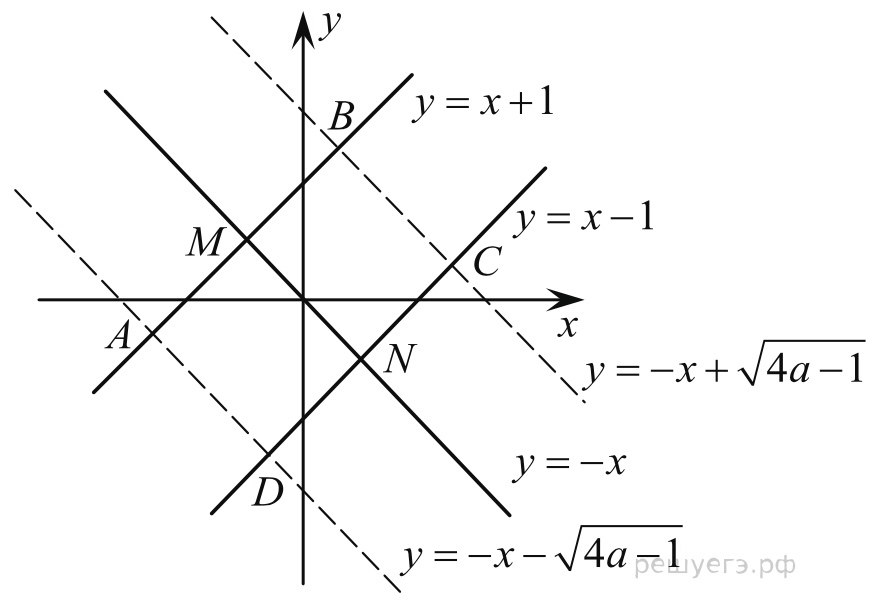
y=x-1 или y=x+1
y=- x-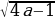
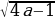
Ясно (см. рисунок), что при a1/4 система имеет четыре решения (координаты точек A, B, C и D), а при a=1/4 — два решения (координаты точек M и N).
Глава 1.
Коротко о параметре
Если в уравнении, помимо переменной x, есть переменная a и требуется решить это уравнение относительно x, считая переменную a постоянной, то данное уравнение будет называться уравнением с одной переменной x и параметром a.
Определение: параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Особенность уравнений с параметрами:
с одной стороны, параметр в уравнении следует считать величиной известной, а с другой — конкретное значение параметра не дано. С одной стороны, параметр является величиной постоянной, а с другой — может принимать различные значения. Получается, что параметр в уравнении — это «неизвестная величина», «переменная постоянная». Этот «каламбур» довольно точно отражает суть тех сложностей, которые встают перед теми, кто решает уравнения с параметром.
Глава 2.
Простые примеры задач с параметром
Чаще всего в задачах содержится один параметр, хотя бывают случаи, когда параметров больше одного. Решить уравнение с параметром – значит указать для каждого значения параметра множество решений уравнения.
Самые простые задачи с параметром и их решения:
-
x/2=a = x=2a при любом a
-
ax=10 = x=10/a = x=10/a при a≠0
-
x=√a = x=√a при a≥0
-
2ax–4=0 = 2ax=4 = x=2/a = x=2/a при a≠0
-
|x|=a–1 = a–1≥0 = x=a–1 или x=1–a при a≥1
Как можно увидеть, простейшие задачи с параметром чем-то напоминают обычные задачи, в которых нужно посчитать значение x. Разница лишь в том, что в данном случае x выражается через переменную a.
Глава 3.
Методы решения задач среднего уровня сложности
ординаты точки А, но не большие 4. Имеем:
a=-(-12+8√2)-4=8-8√2.
Тогда система будет иметь решения при 8-8√2≤a≤4.
Ответ: aЄ[8-8√2;4].
2 задача: Найдите все неотрицательные значения a , при каждом из которых система уравнений 
Решение: Первому уравнению системы удовлетворяют те и только те точки (x;y), которые лежат на отрезке AB прямой, соединяющей точки A(-2;0) и B(0;a), где a≥0, поскольку уравнение задаёт множество точек (x;y), сумма расстояний от каждой из которых до точек А и В равна 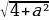
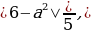
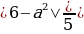
Отсюда следует, что условие задачи выполнено тогда и только тогда, когда точка С лежит между точками О и В, причём если точка С совпадает с точкой А
Решение: Преобразуем систему:
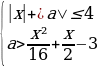
Первое неравенство задает на плоскости xOa квадрат, ограниченный отрезками прямых a=x+4, a=x-4, a=-x-4, a=- x+4, а неравенство 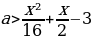
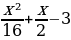
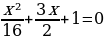
x=-12±8√2
М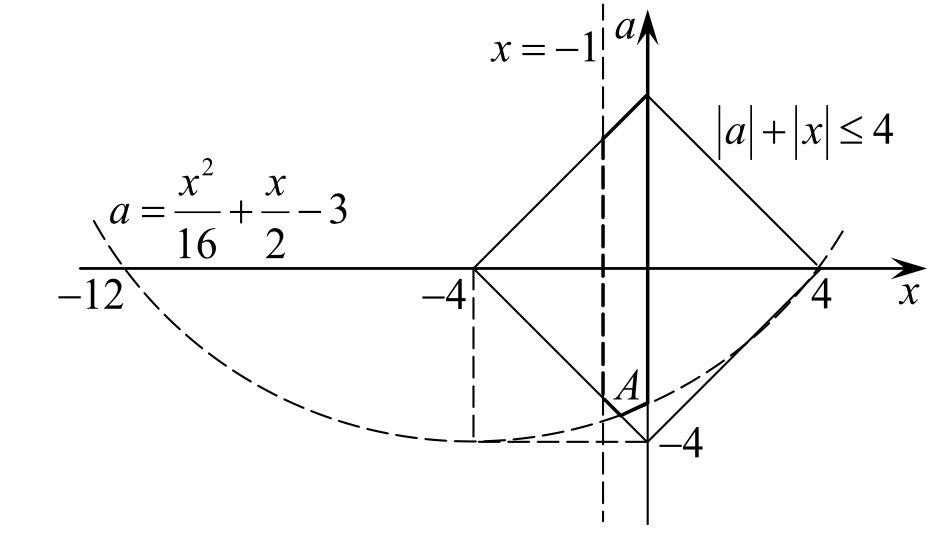
Всего существует 3 основных способа решения задач, содержащих параметр. Рассмотрим каждый из них:
1 способ: аналитический. Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Аналитический способ решения задач с параметром бывает довольно трудным, он требует высокой грамотности и наибольших усилий по овладению им.
Пример задачи с аналитическим способом решения: При каких значениях параметра a уравнение 52x-3*5x+a— -1=0 имеет единственный корень?
Решение: Сделаем замену 5x=t, t0. Тогда наше уравнение примет вид: t2-3*t+a-1=0. У этого уравнения 1 корень будет в двух случаях:
-
Если дискриминант будет равен нулю
-
Если дискриминант будет больше нуля, но один из корней будет отрицательный
Рассмотрим эти два случая:
-
D=9-4a+4=13-4a=0
Отсюда получаем a=13/4 – первый подходящий корень.
2) D=13-4a
Тогда корни будут такие:
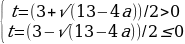
Возьмем первый корень положительным, а второй наоборот. В таком случае условие единственного ответа будет выполнено.
Решая неравенство t=(3+√(13-4a))/20 получаем, что,
a≤1.
Значит в ответ нужно записать, что aЄ(-∞;1)U{13/4}.
2 способ: графический. В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Пример задачи с графическим способом решения: При каких a уравнение |x2+2x–3|–2a=|x–a|+3 имеет ровно три корня?
Решение: Используем графический метод решения. График функции y=|x2+2x–3| отличается от параболы y=x2+2x–3 только тем, что отрицательная ее область зеркально отражается вверх относительно
Задачи для самостоятельного решения:
7)Найдите все целые отрицательные значения параметра a, при каждом из которых существует такое действительное число ba, что неравенство 20b≥6|2a+b|+2|b-2|-|2a—b|-5|4a²-b+2| не выполнено.

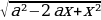
9)Найдите все значения a, при каждом из которых неравенство |x²-4x+a|≤10 выполняется для всех xЄ[a;a+5].
Глава 4.4.
Системы с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения параметра a, при каждом из которых система неравенств 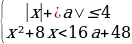
-1/5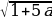
0≤a≤3: (1;2)
3a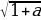
a≥8: пустое множество
Ответ: aЄ(-∞;-1/5]U[8;+∞).
3 задача: Найдите все значения a , при каждом из которых неравенство |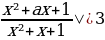
Решение: Поскольку знаменатель левой части больше нуля при любом x, получаем: |x²+ax+1|x²+3x+3.
Решим полученное неравенство:
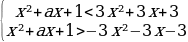
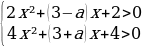
Чтобы любое значение x удовлетворяло этой системе неравенств, дискриминанты левых частей должны быть отрицательными:
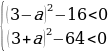
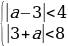
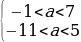
Ответ:aЄ(-1;5).
оси OX (ведь модуль не может принимать отрицательных значений).
График функции y=|x–a|+2a+3 представляет собой всем известную «галочку», вершина которой смещена в точку (a;2a+3). В зависимости от значений параметра возможны следующие варианты взаимного расположения этих графиков на координатной плоскости:
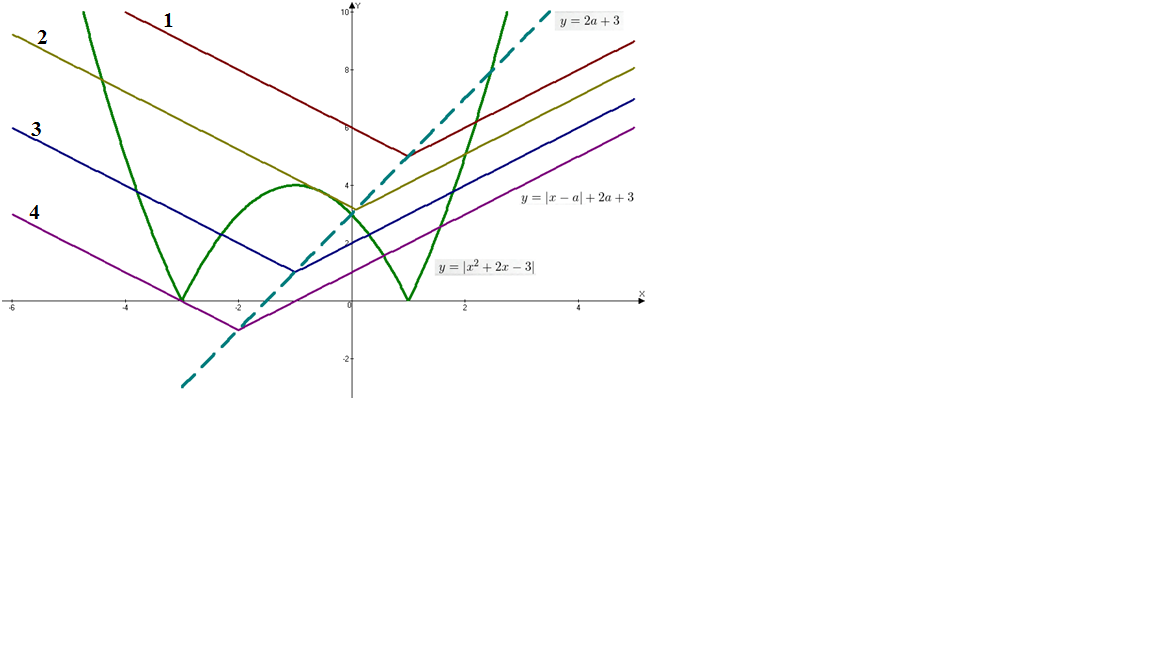
Видно, что три решения уравнение будет в случаях 2 и
4.
Первый случай выполняется при условии выполнении равенства 0=|-3-a|+2a+3. В этом случае модуль раскрывается в минусом, поэтому a=-2.
Во втором случае оба модуля раскрываются с минусом, получается квадратное уравнение x2+x+3a=0.Для выполнения условия, дискриминант этого уравнения должен быть равен 0. Это выполняется при a=1/12.
Значит в ответ нужно записать, что a={-2;1/12}.
3 способ: решение относительно параметра. При таком решении x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
Пример задачи с этим способом решения: Для всех действительных значений параметра a решите уравнение x3–-(2–a)x2–ax–a(a–2)=0.
Решение: Для начала давайте раскроем скобки и посмотрим, что у нас получится. После раскрытия скобок уравнение примет вид: x3–a2+ax2–ax+2a–2x2 = 0. Можно заметить, что, являясь кубическим относительно x, это уравнение квадратное относительно переменной a.
достаточно, чтобы одновременно выполнялись 2 условия: f(0)
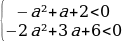
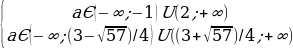
Пересечение этих промежутков и будет ответом.
Ответ: aЄ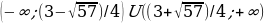
2 задача: Найдите все значения параметра а, при каждом из которых неравенство |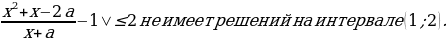
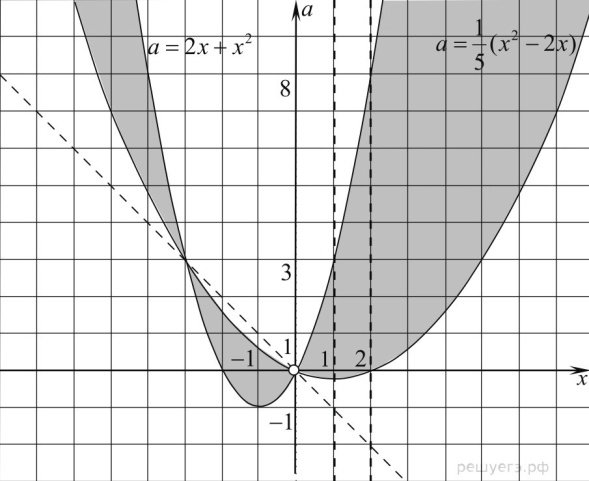
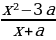
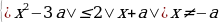
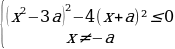
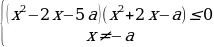
Решим неравенство на интервале (1;2):
a≤-1/5:пустое множество
Неравенства с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения параметра а, при каждом из которых множество решений неравенства 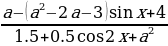
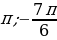
Решение: Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
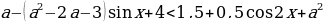
Для того, чтобы множество решений неравенства содержало отрезок [-2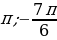
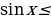
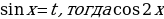
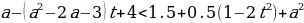
-a²+a+2
Введем функцию: f(t)= t²-(a²-2a-3)t-a²+a+2
Для того, чтобы выполнялось наше условие, необходимо и
Поэтому, считая переменную x параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно a: –a2+(x2–x+2)a+x3–-2x2 = 0.
Преобразуем: a2–(x2–x+2)a –x3 + 2x2 = 0.
x2–x+2=x2+(2–x)
–x3+2x2 =x2(2–x)
Легко заметить, что в первом случае можно увидеть сумму квадратов, а во втором их произведение. Поэтому по теореме, обратной теореме Виета получаем, что a1=x2, a2=2–x. Исходное уравнение преобразуется в совокупность из двух: a=x2 и a=2–x.
Из того, что x2=a следует, что:
1)при a решений нет
2)при a=0 решение будет всего одно, x=0
3)при a0 решений два, x=√a и x=–√a
Второе уравнение совокупности будет иметь 1 корень при любом a.
Мы смогли найти все решения исходного уравнения для любого действительного значения параметра: x=2–a
при a; x=0 или x=2 при a=0; x=√a или x=-√a или x=2-a при a0.
Легко заметить, что при a=1 равенства x=2–a и x=√a принимают одинаковое значение x=1. Можно легко найти второй такой корень, приравняв x=2–a и x=–√a. Это будет x=–2 при a=4.
Значит ответ нужно записать в таком виде: x=2-a при a1=0, x2=2 при a=0; x=√a, x=-√a и x=2–x при 0aaa4; x=1, x=–1 при a=1; x=2, x=–2 при a=4.
Глава 4.
Параметр в ЕГЭ 2018 года
Чтобы решить задание 18 по математике профильного уровня нужно знать:
-
Задание 18 в ЕГЭ подразделяется на несколько видов:
-
1) функции, зависящие от параметра;
-
2) уравнения с параметрами;
-
3) неравенства с параметрами;
-
4) системы и неравенства с параметрами.
-
-
Пусть задано уравнение f(x; a) = 0, которое следует решить относительно переменной х, а произвольное действительное число обозначено буквой а, то f(x; a) = 0 – это уравнение с параметром а.
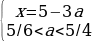
Число x=5-3a лежит на отрезке [0;2], если 1≤a≤5/3. Тогда для второго случая получаем: 1≤a≤5/4.
Корень x=5-3a равен x=3a-1, если a=1.
Значит исходное уравнение имеет ровно один корень на отрезке [0;2] при 7/8.
Ответ: aЄ(7/8;5/4).
Задачи для самостоятельного решения:
4)Найдите все значения а, при каждом из которых уравнение x²+(x-1)*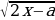
5)Найдите все значения а, при каждом из которых уравнение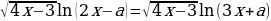
6)Найдите все значения параметра a, при каждом из которых уравнение 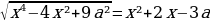
Глава 4.3.
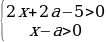
Имеем такую систему:
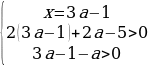
Упрощая эти неравенства, получаем:
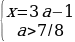
Число 3a-1 лежит на отрезке [0;2], если 1/3≤a≤1. Тогда для первого случая получаем: 7/8
Второй случай:
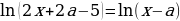
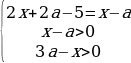
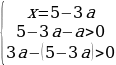
-
Решить неравенство с параметром — это значит исследовать каким будет решение неравенства для всех возможных значений параметра.
-
Решить уравнение с параметром – это значит найти все значения параметров, при которых данное уравнение имеет решение.
Линейные уравнения с параметрами — общий вид ax = b ,где a, b – параметры.
Обратите внимание: для данного вида уравнения контрольным значением параметра является то значение, при котором обращается в нуль коэффициент при неизвестном.
При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.
Особым значением параметра а является значение а=0.
-
1)Если а≠0, то при любой паре параметров а и b оно
-
имеет единственное решение .
-
2)Если а=0, то уравнение принимает вид 0х=b. В этом случает значение b=0 является особым значением параметра b.
-
3)При b≠0 уравнение решений не имеет.
-
4)При b=0 уравнение примет вид:0х=0. Решением данного уравнения является любое действительное число.
Дробно-рациональные уравнения с параметрами, сводящиеся к линейным.
При решении данного типа уравнений следует дробное уравнение заменить целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. Далее следует решать уравнение по известному алгоритму, исключив посторонние корни, т. е. те числа, которые обращают общий знаменатель в ноль (решить уравнения относительно параметра).
Показательные уравнения с параметрами
Многие показательные уравнения с параметрами сводятся к элементарным показательным уравнениям вида аf (x) = bφ(х)
(1), где а 0, b 0.
ОДЗ такого уравнения находится как пересечение
областей допустимых значений функций f(x) и φ(х).
Для решения уравнения (1) нужно рассмотреть
следующие случаи:
-
1)При a=b=1 решением уравнения (1) является область его допустимых значений D.
-
2)При а=1, b≠1 решением уравнения (1) служит решение уравнения φ(х)=0 на области допустимых значений D.
-
3)При а≠1, b=1 решением уравнения (1) служит решение уравнения f(х)=0 на области допустимых значений D.
-
4)При a=b (a0, a≠1, b0, b≠1) уравнение (1) равносильно уравнению f(x)=φ(х) на области D.
-
5)При a≠b (a0, a≠1, b0, b≠1) уравнение (1) тождественно уравнению на области D.
Ответ: a-9/16.
2 задача: Найдите все значения a, при каждом из которых модуль разности корней уравнения x²-6x+12+a²-
-4a=0 принимает наибольшее значение.(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
Решение: По теореме Виета получаем, что 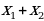
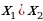
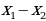
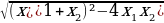
=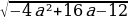
Следовательно, нужно только найти наибольшее значение выражения 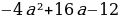
Ответ: a=2. При этом модуль разности корней равен 2.
3 задача: Найдите все значения а, при каждом из которых уравнение 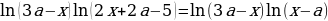
Решение: Имеем уравнение вида ab=ac, откуда на ОДЗ либо a=0, либо b=c. Рассмотрим эти 2 случая:
Первый случай:
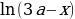
Ответ: a=0, a≥2.
Задачи для самостоятельного решения:
1)Найдите все значения параметра а, при каждом из которых множество значений функции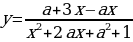
2)Найдите все такие значения параметра a, при каждом из которых наименьшее значение функции y=3|x+a|+|x²-x—
—2| меньше 2.
3)Найдите все такие значения параметра a, при каждом из которых наименьшее значение функции f(x)=|x²+2x-3|+4|x—
-a| не больше 3.
Глава 4.2.
Уравнения с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения a, при каждом из которых уравнение 64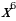
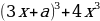
Решение: Преобразуем уравнение 64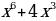
=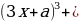
Рассмотрим функцию f(x)=t³+t. Она монотонно возрастает как сумма двух возрастающих функций. Поэтому уравнение f(4x²)=f(3x+a) равносильно уравнению 4x²=3x+a. Оно имеет более одного корня в тех случаях, когда дискриминант уравнения 4x²-3x—a=0 положителен. То есть когда 9+16a0, a-9/16.
Глава 4.1.
Функции, зависящие от параметра
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения a, при каждом из которых наибольшее значение функции f(x)=|x—a|-x² не меньше 1. (Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
Решение: Чтобы наибольшее значение данной функции было не меньше 1, необходимо и достаточно, чтобы она в какой-то точке приняла значение 1. Поэтому можно сказать, что |x—a|-x²≥1. В зависимости от переменной a это неравенство равносильно системе неравенств:
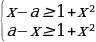
Решая эти неравенства получаем 2 дискриминанта:
D=-3-4a и D=-3+4a. Неравенства будут иметь решения, если эти дискриминанты неотрицательны. Решая -3-4a≥0 и -3+4a≥0 получаем, что a≤-3/4 и a≥3/4.
Ответ: aЄ(-∞;-3/4]U[3/4;+∞).
:
2 задача: Найти все значения параметра a, при каждом из которых среди значений функции y=(x²-2x+a)/(6+x²) есть ровно одно целое число.(Источник: МИОО: Тренировочная работа по математике 2010 год вариант 501. (Часть С))
Решение: Функция определена и непрерывна на всей числовой прямой. Уравнение (x²-2x+a)/(6+x²)=1 при любом a имеет решение x=(a-6)/2. Значит, при любом a одно из значений функции равно 1.
Поскольку функция непрерывна, множество её значений образует промежуток, включающий число 1. Других целых значений функции нет, если для всех x:
0(x²-2x+a)/(6+x²).
Это равносильно системе неравенств:
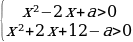
Чтобы неравенства выполнялись для всех x дискриминанты обоих трёхчленов должны быть отрицательны, следовательно: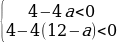
Ответ: aЄ(1;11).
3 задача: Найдите все значения a, при каждом из которых наименьшее значение f(x)=4x²-4ax+a²+2a+2 на множестве |x|≥1 не меньше 6.(Источник: Портал РешуЕГЭ задание 500471)
Решение: Графиком функции f(x)=4x²-4ax+a²+2a+
+2 является парабола, ветви которой направлены вверх, а вершина имеет координаты (a/2;2a+2).
-
Значит, минимум функции f(x) на всей числовой оси достигается при x=a/2.
-
На множестве |x|≥1 эта функция достигает наименьшего значения либо в точке x=a/2, если эта точка принадлежит множеству, либо в одной из граничных точек x=±1.
-
Если наименьшее значение функции не меньше 6, то и всякое значение функции не меньше 6. В частности,
-
-
Упрощая, получаем систему неравенств:
-
-
Решая эту систему, получаем значения a:
-
a€(-∞;-6]U{0}U[2;+∞).
-
Но нам подходят не все данные корни. Сделаем отбор корней.
-
1) Если a≤-6, то a/2≤-3 значит, наименьшее значение функции достигается в точке a/2 и f(a/2)=2a+2=
-
=-10, что не удовлетворяет условию задачи.
-
2) Если a=0, то a/2=0, значит, наименьшее значение функции достигается в одной из граничных точек x=±1, в которых значение функции не меньше 6.
-
3)Если a≥2, то a/2≥1, значит, наименьшее значение функции достигается в точке x=a/2 и f(a/2)=2a+2≥6, что удовлетворяет условию задачи.
Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»
М
Тамбов
2018 год

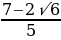 ;
; 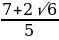 ≤a≤3; a3.
≤a≤3; a3.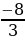 ;-1)U(0;
;-1)U(0;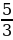 ).
).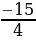 ;-2]U[0;
;-2]U[0;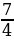 ].
].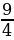 ;-
;-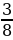 ;
;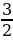 )
)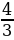 )U(-
)U(-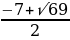 ].
].