Задания второй части по физике егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На T—p диаграмме показан процесс изменения состояния некоторой массы идеального одноатомного газа.

Внутренняя энергия газа уменьшилась на 30 кДж. Чему равно количество теплоты, отданное газом? Ответ приведите в килоджоулях..

Одноатомный идеальный газ в количестве 4 молей поглощает количество теплоты 2 кДж. При этом температура газа повышается на 20 К. Чему равна работа, совершенная газом в этом процессе? Ответ приведите в килоджоулях., округлите до целого числа.

На рисунке показан график зависимости температуры от давления для неизменной массы идеального одноатомного газа.

Газ совершил работу, равную 5 кДж. Чему равно количество теплоты, полученное газом? Ответ приведите в килоджоулях..

В калориметре находится вода, масса которой 100 г и температура 0 °C. В него добавляют кусок льда, масса которого 20 г и температура –5 °C. Какой будет температура содержимого калориметра после установления в нём теплового равновесия? Ответ приведите в градусах Цельсия.

Чему равен КПД цикла, проводимого с идеальным одноатомным газом? Ответ приведите в процентах, округлить до целых.

Пройти тестирование по этим заданиям

Источник

Задача 1

К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.

Решение

1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:

Изменение полной энергии системы равно работе силы трения

где — модуль силы реакции опоры.

2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.

Запишем закон Ньютона для горизонтальной и вертикальной осей:

3. Подставим полученное выражение для в равенство из пункта 1:

После подстановки получим

Ответ:

Задача 2

Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?

Решение

Согласно закону сохранения механической энергии, имеем два равенства:

где и — скорости летящей пули соответственно на высоте и непосредственно перед мишенью. Вся энергия подлетевшей к мишени пули потрачена на механическую работу, так что

Решая полученную систему уравнений, находим массу пули:

Задача 3

Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закрепленного кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?

Решение

Согласно закону сохранения энергии:

, (1)

где — скорость шайбы в момент отрыва от кольца на высоте .

В точке отрыва сила нормальной реакции опоры равна 0; . Центростремительное ускорение шайбы найдём из второго закона Ньютона (см. рис.):

. (2)

. (3)

Объединяя (1), (2) и (3), получим:

м.

Ответ: 0,18.

Задача 4

Грузы массами M = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту а = 30°, коэффициент трения = 0,3). Чему равно минимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?

Решение

Если масса m достаточно мала, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой М, направлена вверх вдоль наклонной плоскости. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат. На первое тело действуют сила тяжести, сила нормальной реакции опоры, сила натяжения нити и сила трения:

(ось направлена вниз вдоль наклонной плоскости);

(ось направлена вверх перпендикулярно наклонной плоскости).

На второе тело действуют сила тяжести и сила натяжения нити:

(ось направлена вертикально вниз).

Учитывая, что (нить легкая, между блоком и нитью трения нет), то (сила трения покоя). Получим:

кг.

Ответ: 0,24.

Задача 5

Тело, брошено с поверхности земли со скоростью v под углом a к горизонту. Сопротивление воздуха пренебрежимо мало.

Установите соответствие между физическими величинами, характеризующими движение тела, и формулами, по которым их можно определить.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

Решение

Рассмотрим динамику движения тела, брошенного под углом к горизонту с начальной скоростью . В задаче нас интересует вертикальное движение тела.

Из рисунка видно, что проекция начальной скорости на ось Oy равна

Проекция ускорения равна

где м/с2 – ускорение свободного падения. Таким образом, скорость тела вдоль оси Oy будет меняться по закону

Можно заметить, что в точке максимального подъема скорость , получаем уравнение

То есть для буквы «А» соответствует формула под номером 4.

Для определения максимальной высоты , запишем формулу движения тела, подброшенного вертикально вверх:

и, учитывая, что , , а время для достижения максимальной высоты составляет , получаем выражение:

То есть для буквы «Б» соответствует формула под номером 1.

Ответ: А4, Б1.

Задача 6

Воздушный шар объемом V = 2500 м3 с массой оболочки = 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры t1 нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой = 200 кг? Температура окружающего воздуха t = 7 °С, его плотность = 1,2 кг/м3. Оболочку шара считать нерастяжимой.

Решение

Шар взлетает, когда сила тяжести, действующая на него, равна силе Архимеда

, (1)

где m — масса воздуха в шаре. Из уравнения Менделеева-Клапейрона

, , (2)

где , , — молярная масса воздуха. Объединяя (1) и (2), получим:

соответственно °С.

Ответ: 350.

Задача 7

Брусок массой m₁ = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m₂ = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.

Решение

Кинетическая энергия брусков после столкновения где v — скорость системы после удара, определяемая из закона сохранения импульса на горизонтальном участке: m₁v₁ = (m₁ + m₂)v.

Исключая из системы уравнений скорость v, получим:

Кинетическая энергия первого бруска перед столкновением определяется из закона сохранения механической энергии при скольжении по наклонной плоскости: что даёт выражение

Подставляя значения масс и энергии из условия, получим численное значение h = 0,8 м

Ответ: h = 0,8 м.

Задача 8

Небольшой груз, прикрепленный к нити длиной l = 15 см, вращается вокруг вертикальной оси так, что нить отклоняется от вертикали на угол a = 60°. С какой скоростью движется груз?

Решение

На груз действуют сила натяжения нити и сила тяжести , как указано на рисунке.

В инерциальной системе отсчёта, связанной с Землёй, ускорение тела определяется вторым законом Ньютона:

Здесь — центростремительное ускорение. Решая полученную систему, получим:

м/с.

Ответ: 1,5.

Задача 9

Камень массой m = 4 кг падает под углом a = 30° к вертикали со скоростью 10 м/с в тележку с песком общей массой M = 16 кг, покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в нее камня.

Решение

Общая инерция камня, падающего в тележку, равна . Величина инерции, в горизонтальном направлении от падения камня составит . Тогда из закона сохранения инерции, учитывая, что тележка вначале была неподвижной, а после падения в нее камня увеличила свою массу на массу камня, получаем

откуда

м/с

Ответ: 1.

Задача 10

Два груза одинаковой массы М, связанные нерастяжимой и невесомой нитью, движутся прямолинейно по гладкой горизонтальной поверхности под действием горизонтальной силы F, приложенной к одному из грузов (см. рис.). Минимальная сила F, при которой нить обрывается, равна 12 Н. При какой силе натяжения обрывается нить?

Решение

Сила, под действием которой движутся грузы массой M – это равнодействующая, то есть учитывающая силу трения. Следовательно, из второго закона Ньютона можно записать , где — ускорение, с которым движутся грузы. Сила натяжения нити T создается последним грузом, который перемещается с тем же ускорением , но имеет массу M, т.е. . Выражая ускорение как , получаем силу натяжения, равную Н.

Ответ: 6.

Задача 11

Груз, лежащий на столе, связан легкой нерастяжимой нитью, переброшенной через идеальный блок, с грузом массой 0,25 кг. На первый груз действует горизонтальная постоянная сила F, равная 9 Н (см. рис.). Второй груз движется с ускорением 2 м/с2, направленным вверх. Трением между грузом и поверхностью стола пренебречь. Какова масса первого груза?

Решение

На второй груз действует сила тяжести и противоположная сила тяги первого груза Н (трение здесь не учитывается). Таким образом, для системы из двух грузов массами и можем записать

где — масса первого груза. Отсюда получаем:

Подставляем числовые значения, находим

кг.

Ответ: 3.

Задача 12

Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.

Решение

Выберем следующую систему координат: ось направим вдоль плоскости, а ось — перпендикулярно ей. Тогда кинематические уравнения движения шарика имеют вид:

В момент второго соударения шарика с плоскостью

Решая систему уравнений, получаем:

Из рисунка видно, что

Ответ:

Задача 13

На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 5/2*h (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.

Решение

На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), направленные по вертикали, поэтому проекция импульса системы на горизонтальную ось Ох системы отсчёта, связанной со столом, сохраняется.

В начальный момент , а в момент . Из закона сохранения импульса получим: , где m — масса шайбы, М — масса горки.

Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение

Решение системы дает отношение масс

Ответ: .

Задача 14

Снаряд, движущийся со скоростью v0 разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆E. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна v1. Найдите массу m осколка.

Решение

Введём обозначение: v2 — модуль скорости летящего назад осколка снаряда. Система уравнений для решения задачи:

Выразим v2 из первого уравнения: — и подставим во второе уравнение. Получим: . Отсюда следует:

Ответ: .

Задача 15

Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆Е. Модуль скорости осколка, движущегося по направлению движения снаряда, равен v1, а модуль скорости второго осколка равен v2. Найдите ∆Е.

Решение

Введём обозначение: v0 — модуль скорости снаряда до разрыва. Система уравнений для решения задачи:

Выразим v0 из первого уравнения: и подставим во второе уравнение. Получим:

Отсюда следует:

Ответ: .

Задача 16

При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с некоторой высоты (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземляется на горизонтальный стол, поднявшись в полёте на высоту h над краем трамплина. С какой высоты H начинал движение гонщик?

Решение

Применим закон сохранения энергии и найдём скорость велосипедиста при отрыве от трамплина.

Рассмотрим проекции скорости на горизонтальную и вертикальную оси:

В тот момент, когда велосипедист достигнет наивысшей точки полёта вертикальная проекция его скорости станет равной нулю, при этом в горизонтальном направлении он пролетит половину пути. Найдём время, за которое велосипедист достигнет наивысшей точки.

Координата зависит от времени по закону Значит, максимальная высота полёта велоспедиста

Откуда

Ответ:

Задача 17

После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме.

В некоторый момент времени льдинка находилась в точке А с координатой и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.

Решение

1) Льдинка сможет выскользнуть из ямы через ее правый край.

2) Трения при движении льдинки нет, поэтому ее механическая энергия сохраняется. Запас кинетической энергии льдинки в точке A позволяет ей подняться до уровня, где ее потенциальная энергия составит 4 Дж.

3) Левый край ямы поднят до большей высоты. Следовательно, этого края льдинка не достигнет и заскользит вправо. Правый же край ямы ниже: на верху этого края потенциальная энергия льдинки меньше 4 Дж. Поэтому льдинка выскользнет из ямы через правый край.

Задача 18

Гладкий клин массой M с углом при основании стоит на горизонтальной плоскости, часть которой под ним и левее — гладкая, а часть — справа от него — шероховатая (см. рис.). На вершине клина, на высоте H над плоскостью находится маленький брусок массой m, коэффициент трения которого о шероховатую часть плоскости равен Брусок отпускают без начальной скорости, он скатывается по клину и далее скользит по шероховатой плоскости и останавливается на некотором расстоянии L по горизонтали от своего начального положения. Найдите это расстояние L, если в точке перехода с клина на плоскость есть гладкое закругление, так что скорость бруска при переходе с клина на плоскость не уменьшается.

Решение

При соскальзывании бруска с клина выполняются законы сохранения горизонтальной проекции импульса и механической энергии данной системы тел: где v и V — скорости бруска и клина, соответственно, после соскальзывания бруска с клина. Из этих уравнений следует, что скорость бруска перед его попаданием на шероховатый участок плоскости равна:

До попадания на этот участок брусок сдвинется из начального положения по горизонтали без трения на расстояние равное, очевидно, длине основания клина, а затем пройдёт по шероховатой плоскости расстояние на котором его кинетическая энергия будет израсходована на работу против силы сухого трения скольжения. По закону Амонтона — Кулона эта сила равна так как сила N давления бруска на неподвижную горизонтальную плоскость равна mg. Таким образом, и Искомое расстояние L в результате равно сумме l₁ и l₂:

Ответ:

Задача 19

В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, m₁ = 2 кг, m₂ = 4 кг, m₃ = 1 кг. Найдите модуль и направление ускорения груза массой m₃.

Решение

1. Введём на рисунке неподвижную систему координат, у которой ось x горизонтальна и направлена вправо, а ось y направлена вертикально вниз. Обозначим также силы, определяющие ускорения тел вдоль направлений их движения: силу T натяжения нити, которая, как следует из условия задачи, постоянна по модулю вдоль всей нити, и силу тяжести

2. Записывая второй закон Ньютона в проекциях на оси x и y для трёх грузов, имеем:

3. Поскольку нить нерастяжима, из постоянства её длины получаем следующее соотношение для координат грузов:

Отсюда следует связь между ускорениями грузов:

4. Решая полученную систему уравнений, находим модуль искомого ускорения:

вектор направлен вниз.

Ответ: вектор направлен вниз.

Задача 20

К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.

Решение

1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:

Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:

2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:

3. Найдем массу стержня:

Ответ:

Задача 21

Найдите модуль ускорения a груза массой m в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза M, ускорение свободного падения равно g.

Решение

Введём координатную ось Х, направленную вниз, и отметим на ней координаты грузов М и m: x_M и x_m (см. рис.). Пронумеруем блоки цифрами 1, 2, 3 и укажем на рисунке силы натяжения нитей и силы тяжести, действующие на грузы. Согласно условию, в силу невесомости нитей и блоков, а также отсутствия сил трения, первая нить, охватывающая блоки 1 и 2, натянута с силой T, а вторая — с силой 2T, так что на груз m действует направленная вверх сила 4T. Если сместить груз М вдоль оси Х вниз на расстояние Δx_M, то в силу нерастяжимости нитей блок 2 сместится, как следует из рисунка, на −Δx_M/2, а блок 3 и груз m — на Δx_m = −Δx_M/4. Таким образом, Δx_M + 4Δx_m = 0.

Отсюда получаем уравнение кинематической связи: A + 4a = 0, где A и a — проекции ускорений грузов М и m на ось Х. Уравнения движения грузов (второй закон Ньютона) в проекциях на ось Х имеют вид: МA = Мg – T, ma = mg – 4T. Решая полученную систему из трех уравнений, находим, что модуль ускорения груза М равен:

Ответ:

Задача 22

Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.

Решение

1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.

Здесь — сила натяжения нити, — сила тяжести, и — вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.

2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:

где — длина стержня; (1)

(2)

(3)

3. Модуль силы реакции шарнира

Из (1) получим Окончательно

Ответ:

Задача 23

Из двух ровных досок сделан желоб, представляющий собой двугранный угол с раствором Желоб закреплен так, что его ребро горизонтально, а доски симметричны относительно вертикали. В желобе на боковой поверхности лежит цилиндр массой Коэффициент трения между досками и цилиндром равен К торцу цилиндра приложена горизонтально направленная сила Найдите модуль ускорения цилиндра.

Решение

Изобразим вид на желоб со стороны торца цилиндра. На цилиндр в плоскости чертежа действуют направленная вниз сила тяжести и две равные по модулю силы реакции досок, направленные перпендикулярно стенкам желоба. Так как цилиндр не движется в вертикальном направлении, то, в соответствии со вторым законом Ньютона, сумма проекций этих трех сил на вертикаль равна нулю:

где

Отсюда В горизонтальном направлении (вдоль желоба) на цилиндр действуют сила а также, в противоположном направлении, две силы сухого трения Предположим, что цилиндр будет двигаться по желобу. Тогда по закону Амонтона — Кулона для силы сухого трения скольжения можно записать:

Записывая второй закон Ньютона в проекции на горизонтальную ось, направленную вдоль ребра желоба, получим:

где — модуль искомого ускорения цилиндра. Заметим, что Это означает, что приложенная к торцу цилиндра сила превышает силу трения покоя, то есть цилиндр и в самом деле будет скользить вдоль желоба.

Следовательно, Подставляя числовые данные и проверяя размерность, окончательно получим:

Ответ:

Задача 24

Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?

Решение

Обозначим расстояние от оси вращения треугольника до грузика через Тогда период колебаний при горизонтальном положении оси равен, очевидно,

После наклона оси на угол возвращающая сила при отклонении треугольника от положения равновесия уменьшится: составляющая силы тяжести вдоль оси, равная (здесь — масса грузика), будет компенсироваться силами реакции со стороны подшипников, в которых закреплена эта ось, а в направлении, перпендикулярном оси, будет действовать эффективная «сила тяжести», равна Поэтому период малых колебаний грузика при наклоненной оси будет равен

Таким образом, период колебаний увеличится в раз.

Ответ: период колебаний увеличится в раз.

Задача 25

На гладкой горизонтальной плоскости лежат два груза массами и соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.

Решение

Нарисуем силы Т натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок О (см. рисунок). Введём систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось X:

В силу невесомости блока О имеем или

В силу нерастяжимости нити (длиной L) и неподвижности блоков А и В (их координаты и постоянны) имеется следующая кинематическая связь между координатами и грузов и координатой блока О (здесь — радиус блоков А и В, R — радиус блока О):

или

и значит

Решаем записанную систему уравнений и получаем ответ:

Ответ:

Задача 26

Два вращающихся вала соединены замкнутым ремнём, который не проскальзывает относительно валов. Радиус первого вала равен R, радиус второго вала равен 2R. Чему равно отношение угловой скорости точки A к угловой скорости вращения первого вала

Решение

Скорость движения точек первого вала, находящихся на расстоянии от его центра, даётся формулой Угловая скорость вращения точки А равна угловой скорости вращения второго вала. Валы связаны ремнём, поэтому скорости ободов у валов одинаковы, а их угловые скорости

В итоге получаем

Ответ: 0,5.

Задача 28

Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?

Решение

При движении по окружности угловая и линейная скорости тела связаны с радиусом окружности соотношением: Центростремительное ускорение равно Поскольку велосипедисты едут с одинаковым угловыми скоростями, для отношения центростремительных ускорения велосипедистов имеем:

Ответ: 2.

Задача 29

Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.

Первое решение

Найдём горизонтальную скорость снаряда:

Найдём вертикальную проекцию скорости снаряда в момент обнаружения:

Определим, за какое время снаряд долетел из верхней точки траектории в точку, в которой был зафиксирован:

Таким образом, время опускания снаряда составляет

Таким образом, максимальная высота снаряда:

Второе решение

Найдём горизонтальную скорость снаряда: эта скорость остается постоянной на протяжении всего полета. Определим величину вертикальной проекции скорости в начальный момент: Используя формулу для максимальной высоты брошенного под углом к горизонту тела, получаем:

Ответ: около 16 км.

Задача 30

К концу вертикального стержня привязана лёгкая нерастяжимая нить с маленьким грузиком на конце. Грузик раскрутили на нити так, что она отклонилась от вертикали на угол α = 30º (см. рисунок). Как и во сколько раз надо изменить угловую скорость ω вращения грузика вокруг стержня для того, чтобы этот угол стал равным β = 60º?

Решение

1. Обозначим силу натяжения нити T, массу грузика m, длину нити l, радиус окружности, по которой вращается грузик, R, и изобразим систему на рисунке (см. рисунок).

2. Запишем уравнение движения грузика по окружности вокруг стержня в проекциях на вертикальную ось и на радиус окружности с учётом выражения для центростремительного ускорения грузика: , .

3. Из написанных соотношений следует, что , а .

4. Для того, чтобы угол отклонения нити стал равным β, угловая скорость вращения грузика должна увеличиться в

раза.

Ответ: 1,3 раза.

Задача 31

В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1 600 Н? Ускорение свободного падения равно

Задача 32

На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с².

Решение

Из графика видно, что скорость в интервале времени от 40 с до 50 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 45 с. Найдём это ускорение:

Ответ: 2.

Задача 32

Два небольших тела с массами 2 кг и 3 кг висят на разных концах невесомой нерастяжимой нити, перекинутой через гладкий неподвижный блок. Первое тело находится на высоте 40 см ниже второго. Тела пришли в движение без начальной скорости. Через какое время они окажутся на одной высоте? Сделайте схематический рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.

Решение

Задача 33

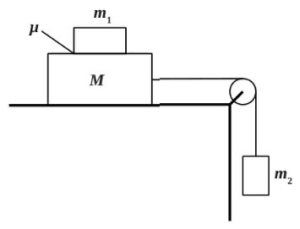
Система грузов M, m₁ и m₂, показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m₁ равен μ = 0,3. Грузы M и m₂ связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 2,4 кг, m₁ = m₂ = m. При каких значениях m грузы M и m₁ движутся как одно целое? Сделайте рисунок с указанием сил, действующих на грузы.

Решение

Задача 34

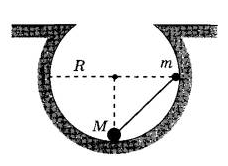
Небольшие шарики, массы которых m и M, соединены лёгким стержнем и помещены в гладкую сферическую выемку радиусом R = 20 см. В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Минимальная высота, на которой оказался шарик m в процессе движения, равна 4 см от нижней точки выемки. Определите отношение масс M и m.

Решение

Задача 35

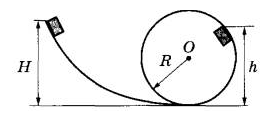
Небольшой брусок массой m начинает соскальзывать с высоты H по гладкой горке, переходящей в мёртвую петлю (см. рисунок). Определите высоту отрыва бруска, если высота горки H. Радиус окружности R. Сделайте рисунок с указанием сил, поясняющий решение.

Решение

Направим ось Ох вдоль ускорения и пусть сила тяжести образует с этой осью угол α Запишем второй закон Ньютона для бруска на высоте h:

Выразим отсюда скорость бруска, учитывая, что и по третьему закону Ньютона N=F :

На высоте h брусок обладает как кинетической, так и потенциальной энергией. Из закона сохранения энергии найдём искомую высоту H:

откуда

Задача 36

В маленький шар массой M=100г, висящий на нити длиной l=50 см, попадает и застревает в нем пулька массой m=20г, летящая под углом 30 град к горизонту (см рисунок). Какую скорость v имела пуля перед попаданием в шар, если после соударения шар с застрявшей в нем пулей отклонился по вертикали на угол 60 град? Сопротивлением воздуха пренебречь. Какие законы вы использовали для описания взаимодействия пульки с шаром и подьема тел? Обоснуйте их применимость к данному случаю.

Решение

Задача 37

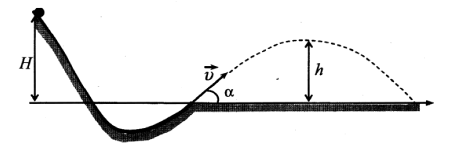
При выполнение трюка летающий велосипедист гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты H. На краю трамплина скорость гонщика направлена под таим углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящейся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

Решение

Источник

Реальные варианты ЕГЭ 2019

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Тренировочные варианты «Школково». Основная волна. (Вторая часть)

В закрытой комнате нагревается воздух. Как изменятся относительная влажность и плотность водяных паров в комнате? Считайте, что парциальное давление паров не изменяется.

Относительная влажность вычисляется по формуле: [phi=dfrac{p}{p_text{ н}}] где (p) – парциальное давление паров, (p_text{н}) – парциальное давление насыщенных паров. При увеличении температуры давление насыщенных паров возрастает, следовательно, относительная влажность уменьшается.
Из уравнения Менделеева – Клапейрона получаем: [pV=dfrac{m}{mu}RT Rightarrow rho =dfrac{pmu}{RT}] При увеличении температуры плотность водяных паров в комнате уменьшается.

Ответ:

Дан невесомый стержень, к концам которого подвешены шары массами (m_1) и (m_2) (см. рис.). Стержень опирается на две опоры в точках C и D. Длина стержня L равна 1 м, (m_2) = 0,3 кг. Сила реакции опоры в точке D в два раза больше, чем в точке С. Также известно, что расстояния (CD = 0,6) м, (AC = 0,2) м. Найдите массу левого шарика (m_1).

На твердое тело, образованное двумя шарами и стержнем действует силы тяжести первого и второго шаров (m_1 g)и (m_2g), а также силы реакции опоры (N_1) и (N_2). По условию (2N_1=N_2) Запишем второй закон Ньютона и правило моментов относительно точки А. [begin{cases}
N_1 +N_2 -m_1g -m_2 g=0\
N_1 x +N_2 (l+x)-m_2 g L=0\
end{cases}] где (x) – AC и плечо силы (N_1). Так как (N_2=2N_1), то систему уравнений можно переписать в виде [begin{cases}
3N_1 =g(m_1 +m_2)\
N_1 x +2N_1 (l+x)=m_2 g L\
end{cases}] Поделим второе уравнение на первое [x+dfrac{2l}{3}=Ldfrac{m_2}{m_1+m_2}] Преобразуем уравнение [dfrac{m_2L}{x+dfrac{2}{3}l}-m_2=m_1] Подставим числа из условия [m_1=m_2left(dfrac{L}{x+dfrac{2}{3}l}-1right)dfrac{1text{ м}cdot 0,3text{ кг}}{0,2text{ м}+0,4text{ м}}-0,3text{ кг}=0,2text{ кг}]

Ответ: 0,2

Постоянную массу идеального одноатомного газа изобарно сжали так, что (T_2=dfrac{T_1}{k}) Затем этот же газ адиабатически расширяется так, что (T_3=dfrac{T_2}{2}) Отношение модулей работ в изобарном и адиабатическом процессах (n=4) Найдите (k).

При изобарном сжатии над гахов совершается работа, модуль которой (A_1=|pDelta V|) где (p) – давление гелия в этом процессе, (Delta V) – изменение его объёма.
В соответствии с уравнением Менделеева—Клапейрона для этого процесса можно записать: [pDelta V =nu R (T_1-T_2)=A_1] В адиабатном процессе (процессе без теплообмена) в соответствии с первым законом термодинамики сумма изменения внутренней энергии газа и его работы равна нулю: [dfrac{3}{2}nu R (T_3-T_2)+A_2=0] При записи последнего соотношения учтено выражение для изменения внутренней энергии идеального одноатомного газа: [Delta U =dfrac{3}{2}nu R (T_3-T_2)] Преобразуя записанные уравнения с учётом соотношений температур, заданных в условии задачи, получаем: [A_1=nu RT_2(k-1)hspace{5 mm}A_2=dfrac{3}{4}nu RT_2] По условию (dfrac{A_1}{A_2}=n=4) Следовательно [dfrac{4nu RT_2(k-1)}{3nu R T_2}=4 Rightarrow 4k-4=12 Rightarrow 4k=16 Rightarrow k=4]

Ответ: 4

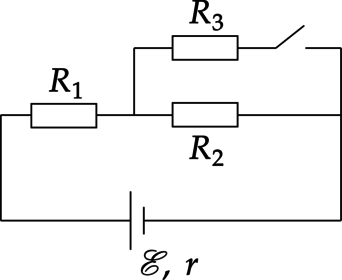
В цепи изображённой на рисунке (R_1=R_2=R_3=3) Ом, (r=0,5 ) Ом В начальный момент ключ K замкнут. Во сколько раз уменьшится мощность, выделяемая на (R_1) после размыкания ключа?

Сила тока по закону Ома для полной цепи равна: [I=dfrac{xi}{R_0+r}] Общее сопротивление в первом и во втором случаях равно: [R_{01}=R_1+dfrac{R_2cdot R_3}{R_3}=4,5text{ Ом}] [R_{02}=R_1+R_2=6text{ Ом}] Мощность, выделяемая на резисторе определяется формулой: [P=I^2R] То есть отношение мощностей: [dfrac{P_1}{P_2}=dfrac{I_1^2}{I_2^2}=left(dfrac{R_{02}+r}{R_{01}+r}right)^2=left(dfrac{6text{ Ом}+0,5 text{ Ом}}{4,5text{ Ом}+0,5text{ Ом}}right)^2=1,69]

Ответ: 1,69

Вылетевший при фотоэффекте с катода электрон попадает в электромагнитное поле как показано на рисунке. Вектор напряжённости электрического поля направлен вертикально вверх. Вектор магнитного поля направлен от наблюдателя. Определите, при каких значениях напряжённости электроны, вылетевшие с максимально возможной скоростью, отклоняются вверх. Частота падающего на катод света (nu=6,2cdot 10^{14}text{ Гц}) Работа выхода (A_{text{ вых}}=2,39) эВ Магнитная индукция поля (B=0,5) Тл. Ответ дайте в кВ/м

Электроны заряжены отрицательно, следовательно, сила Кулона (F_k=qE), действуйющая на электроны направлена вниз, сила Лоренца (F_l=qvB) же наоборот направлена вверх, следовательно, чтобы электроны отклонялись вверх должно выполняться неравенство [F_l>F_k Rightarrow qvB>qE Rightarrow E < vB] Максимальную скорость найдем из уравнения Энштейна: [hnu=A_text{ вых}+dfrac{mv^2}{2} Rightarrow v=sqrt{dfrac{2(hnu — A_text{ вых})}{m}}] Откуда произведение (vB): [vB=Bsqrt{dfrac{2(hnu — A_text{ вых})}{m}}=0,5 text{ Тл}sqrt{dfrac{2(6,6cdot 10^{-34}text{ Дж$cdot$ с}cdot 6,2cdot 10^{14}text{ Гц}-2,39cdot 1,6cdot10^{-19}text{ Дж})}{9,1cdot 10^{-31}text{ кг}}}approx 1,2 cdot 10^{5}text{ В/м}] Откуда следует для того чтобы электроны отклонялись вверх, напряжённость должна быть меньше (120 text{ кВ/м})

Ответ: 120

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

25 апреля 2021

В закладки

Обсудить

Жалоба

Решение и оформление задач второй части ЕГЭ по физике

Задачи 27-32.

27) Механика – квантовая физика (качественная задача).
28) Механика, молекулярная физика (расчётная задача).
29) Механика (расчётная задача).
30) Молекулярная физика (расчётная задача).
31) Электродинамика (расчётная задача).
32) Электродинамика, квантовая физика (расчётная задача).

Презентация: 27-32f.pdf

Источник

Молекулярная физика, термодинамика, электродинамика. Расчётная задача

В. З. Шапиро

Задание № 25 открывает вторую часть экзаменационной работы по физике, которая посвящена решению задач. Оно представляет собой расчетную задачу с кратким ответом. Тематика этого задания – термодинамика и электродинамика. В этом номере не требуется подробного решения, в бланк ответа необходимо внести только численный результат. Но, в отличие от заданий части № 1, решение потребует более глубоких знаний по вышеуказанным темам.

1. Кусок льда опустили в термос с водой. Начальная температура льда 0 °С, начальная температура воды 30 °С. Теплоёмкостью термоса можно пренебречь. При переходе к тепловому равновесию часть льда массой 210г растаяла. Чему равна исходная масса воды в термосе?

Ответ: __________________________г.

Необходимая теория: Количество теплоты

Дано:

t₁ = 0 °С;

t₂ = 30 °С;

m₁ =210 г = 0,21 кг.

Найти: m₂ – ?

Решение:

Подобные задачи, в которых происходит теплообмен между телами, необходимо решать, составляя уравнение теплового баланса. Для этого рассмотрим, какие изменения происходят с каждым телом, вступающим в теплообмен.

Q₁ – количество теплоты, необходимое для плавления льда массой m₁.

Q₁ = ?m₁.

Q₂ – количество теплоты, отданное водой при охлаждении от 30 °С до 0 °С.

Q₂ = сm₂(t₁ – t₂).

Составим уравнение теплового баланса:

Q₁+ Q₂ = 0.

?m₁ + сm₂(t₁ – t₂) = 0.

сm₂(t₁ – t₂) = -?m₁.

$displaystyle m_2 = frac{- lambda m_1}{c(t_1 - t_2)},$ подставим численные значения и проведем расчет.

$displaystyle m_2 = frac{-330000 cdot 0,21}{4200(0-30)}$ = 0,55 (кг) = 550 (г).

Ответ: 550 г.

Секрет решения. В задачах на теплообмен трудности возникают с момента прочтения и краткой записи условия. Особенно это касается расставления индексов для различных температур. Рационально поступить следующим образом: присваивать индексы 1, 2, 3 и т.д. согласно порядку перечисления температур в условии задачи. Затем необходимо расписать процессы, происходящие с каждым телом, вступающим в теплообмен. Если тело нагревается или охлаждается, то при использовании формулы Q = сm (t_кон – t_нач) на первом месте пишется конечная температура, на втором – начальная. Причем индексы для этих температур могут быть любые. Тогда при составлении уравнения теплового баланса, в котором сумма количеств теплоты равна нулю, с «+» получатся количества теплоты, которые поглощаются телами, а с «-» – количества теплоты, которые выделяются телами.

В некоторых случаях уравнение теплового баланса в общем виде может иметь громоздкий вид. Его решение с буквенными обозначениями представляется трудоемким. Поэтому на этом этапе рациональнее подставить численные значения и решить его относительно неизвестной величины.

2. Прямоугольный контур, образованный двумя рельсами и двумя перемычками, находится в однородном магнитном поле, перпендикулярном плоскости контура. Правая перемычка скользит по рельсам, сохраняя надежный контакт с ними. Известны величины: индукция магнитного поля В = 0,1Tл, расстояние между рельсами l = 10 см, скорость движения перемычки u = 2 м/c, сопротивление контура R = 2 Ом. Какова сила индукционного тока в контуре?

Ответ: ___________________________ мА.

Необходимая теория: Электромагнитная индукция

Дано:

В = 0,1 Тл;

l = 10 cм = 0,1 м;

= 2 м/с;

R = 2 Ом.

Найти: I –?

Решение:

Согласно закону электромагнитной индукции, на концах проводника, движущегося в магнитном поле, возникает ЭДС индукции.

Формула для расчета ЭДС индукции для этого случая имеет вид:

Так как вектор магнитной индукции перпендикулярен вектору скорости (см. рис), то $alpha=90^circ , sin 90{}^circ =1.$ Формула для расчета ЭДС принимает вид:

E=vBl.

Согласно закону Ома для участка цепи, сила тока в проводнике равна:

$displaystyle I= frac{E}{R}= frac{vBl}{R} .$

Проведем расчет для силы тока:

$displaystyle I=frac{2cdot 0,1cdot 0,1}{2} = 0,01 (A) = 10$ (мА).

Ответ: 10 мА.

Секрет решения. Данная задача является комбинированной, т.е. в ней совмещены темы из разных разделов физики. Безусловно, электромагнитная индукция и постоянный электрический ток, темы близкие, но изучаются в школьном курсе физики в разное время. Здесь надо добиться понимания единой картины процессов, происходящих в электродинамике.

3. В двух идеальных колебательных контурах происходят незатухающие электромагнитные колебания. Максимальное значение заряда конденсатора во втором контуре равно 6 мкКл. Амплитуда колебаний силы тока в первом контуре в 2 раза меньше, а период его колебаний в 3 раза меньше, чем во втором контуре. Определите максимальное значение заряда конденсатора
в первом контуре.

Ответ: _________________________мкКл.

Необходимая теория: Электромагнитные колебания

Дано:

$q_{max2} = 6$ Кл $= 6 cdot 10^{-6}$ Кл;

$displaystyle frac{l_{max1}}{l_{max2}} = frac{1}{2};$

$displaystyle frac{T_1}{T_2} = frac{1}{3}.$

Найти: $q_{max1} - ?$

Решение:

Колебания электрического заряда в контуре можно представить в виде формулы:

$q=q_{max}cos wt.$

Силу тока необходимо выразить как производную от заряда.

i=q

Таким образом, колебания силы тока в контуре выражаются уравнением:

$i= -q_{max}w sin wt.$

Сравнивая с уравнением для тока в общем виде,

$i=I_{max} sin wt ,$ получим, что амплитуда силы тока равна:

$displaystyle I_{max}= q_{max}w=q_{max}cdot frac{2pi}{T}$ (1).

Запишем полученное уравнение для двух случаев:

$I_{max1}= q_{max1}w_1=q_{max1}cdot frac{pi}{T_1}$ (2).

$I_{max2}= q_{max2}w_2=q_{max2}cdot frac{2pi}{T_2}$ (3).

Разделим (3) на (2).

$displaystyle frac{I_{max2}}{I_{max1}}= frac{q_{max2}cdot frac{2pi}{T_2}}{q_{max1}cdot frac{2pi}{T_1}} =frac{q_{max2} T_1}{q_{max1 }T_2}.$

Отсюда выразим максимальное значение заряда конденсатора в первом контуре:

$displaystyle q_{max1 }=frac{q_{max2 }cdot T_1cdot I_{max1}}{I_{max2}cdot T_2}.$

Подставим численные значения и проведем расчет:

$displaystyle q_{max1 }= 6cdot {10}^{-6}cdot frac{1}{3}cdot frac{1}{2}=1cdot {10}^{-6}$ Кл=1 мкКл

Ответ: 1 мкКл.

Секрет решения. На первый взгляд, решение задачи выглядит очень сложным. Но здесь надо выделить ключевые моменты, которые не потребуют запоминания огромного числа формул.

Сила тока – это первая производная от заряда
Заряд может меняться c течением времени по законам: $q = q_{max} cos wt$ или $q = q_{max} sin wt$ В условии задачи об этом ничего не говорится, поэтому подойдет любая формула.

Надо уметь находить производную сложной функции.
Величина, стоящая перед функциями синус или косинус, является амплитудой физической величины.
Общие формулы для любых колебательных процессов и равномерного движения тела по окружности имеют вид:

$displaystyle T = frac{1}{vartheta}; , vartheta = frac{1}{T}; , w = 2 pi vartheta = frac{2 pi}{T}.$

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 25 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник

ЕГЭ по физике — скорее практический предмет. Преобладают не задания на термины и формулы, а задачи базового и высокого уровня сложности. Чтобы подготовиться и сдать экзамен на высокие баллы, нужно уделять внимание второй части. В ней оценивают ответ и процесс решения. Проверяющие снижают оценку даже за неправильное или непонятное оформление. В статье разбираемся в оформлении задач по физике и выводим основные правила решения заданий из второй части.

Правила

6 правил для получения максимального балла:

Пишите структурированное решение. Используйте схему, известную со средней школы. В левой части листа напишите «дано» — величины, указанные в условии. Используйте буквенные обозначения, принятые в физике, а числа переводите в систему СИ. Это делается тут же через знак = или в отдельном столбике. В правой части сделайте рисунок (он необходим в подавляющем большинстве задач). Он должен быть крупным и понятным. С ним работает проверяющий. После рисунка идет непосредственное решение;
Развернутость и последовательность — основные принципы заполнения бланка ответов. Не торопитесь писать задачу в бланк. Начните с черновика — напишите основные формулы, разберитесь в происходящих процессах. Переписывая решение в чистовик, старайтесь писать подробно. Описывайте вывод формул и указывайте их названия («Применим закон сохранения импульса»). В большинстве задач подсказки содержатся в условии. Прописывайте свои умозаключения («Тело движется равномерно и прямолинейно, поэтому используем формулу…»);
В длинных задачах заменяйте формулы цифрами. В номерах высокого уровня сложности встречается много выражений. Их нужно комбинировать, выводить одно из другого. В таком решении легко запутаться, вы сделаете текст непонятным для проверяющего. Обозначьте формулы цифрами и ссылайтесь на них («Сложив (1) и (2), получим уравнение адиабатного процесса для системы»);
Используйте формулы из кодификатора. В нем перечислены уравнения из школьного курса физики. Используя их, достаточно написать название и буквенное выражение («Применяем второй закон Ньютона: F=ma»). Для решения нужна формула, отсутствующая в перечне? Придется вывести ее с нуля. Просто напишете выражение — проверяющий вправе снять баллы;
Описывайте вводимые величины. Иногда величин из условия недостаточно, нужно дописать свои. Например, дан диаметр, а в выражении фигурирует радиус. Вы не просто делите число на 2, а пишете «Найдем радиус R=d/2». В противном случае проверяющие снимают баллы — решение непонятное;
Объединяйте формулы. В большинстве заданий используется несколько формул. Можно последовательно использовать их, находя и подставляя нужные числа. Но лучше объединять несколько формул, выводя финальную. Это показывает владение физикой и возможность свободно решать задачи. Букв слишком много и выражение получается громоздким? Правилом можно пренебречь. В вычислениях не должно быть одновременно букв и цифр. Из всей формулы не известна одна величина — оставляйте все в буквах.

Общие рекомендации для второй части

Несколько советов для решения номеров второй части:

решайте задачи с разными типами и оформлением. Например, вы работаете с темой «Термодинамика». Посмотрите классические задания с текстовым «дано». После этого сделайте номера с минимумом информации, где все нужно понимать из рисунка. Третий вариант — график, описывающий процессы. Четвертый — таблица значений. Вы рассматриваете одну задачу с нескольких углов, что способствует глубокому пониманию темы;
используйте задачники. ФИПИ и Решу.ЕГЭ подходят, когда вы хотите проработать непосредственно формат экзамена. Но при разборе конкретной темы обращайтесь к школьным и вузовским задачникам. Там есть номера разных типов и уровней сложности. Знания будут не поверхностными, а структурированными. Даже задачи с подвохом не станут проблемой;
развивайте логику. Номера из первой части типичны. Поняв принцип, вы научитесь выполнять конкретный вариант заданий. Со второй частью сложнее. Она основана на главных законах физики, но там они приведены в необычные условия, буквально вывернуты наизнанку. Рассуждайте логически, старайтесь не делать по образцу, а действительно понимать происходящие процессы. Тогда наберете высокий балл.

Мы разобрались в правилах выполнения второй части по физике и оформлении задач. Остается практиковаться и применять полученные знания. Конечно, это будет трудно: часть C рассчитана на высокий уровень владения предметом. Хотите получить максимальный балл? Нужно заниматься с преподавателем. Это можно сделать на курсах подготовки к ЕГЭ. На них разбираются сложные моменты, много внимания уделяется практике. Мы уверены — потратив достаточно времени на подготовку, вы добьетесь желаемых результатов.

Источник

Илья Шолин,

старший преподаватель факультета фундаментальной физико-химической инженерии МГУ,

м.н.с. лаборатории физики высоких давлений ИФТТ РАН,

ведущий специалист направления образовательных технологий группы компаний InEnergy

Задание № 25

Что требуется

Решить задачу по механике или молекулярной физике.

Особенности

В этом задании проверяется умение решать стандартные, типовые задачи. Речь идет о применении одного или двух законов и соответствующих им формул. Такие задачи часто встречаются в наиболее распространенных задачниках, в них практически нет подводных камней, и для решения не требуется нестандартных подходов.

Советы

Чтобы успешно справиться с этим заданием, нужно брать стандартные школьные задачники и решать задачи по соответствующим разделам.

Задание № 26

Что требуется

Решить задачу по молекулярной физике или термодинамике.

Особенности

На ЕГЭ представлены пять разделов физики: механика, молекулярная физика и термодинамика, электродинамика, основы специальной теории относительности и квантовая физика. Основы специальной теории относительности являются достаточно специфическим разделом. Его освоению в школе уделяется совсем немного времени, но на ЕГЭ по физике он чаще всего встречается лишь в одном задании (№ 18). Из года в год статистика результатов экзамена показывает, что чем дальше по темам, тем хуже решаемость задач. Так, задачи по механике успешно решает значительный процент выпускников, по молекулярной физике — чуть меньше, по электродинамике — еще меньше, а по квантовой физике процент самый низкий. Разница в количестве абитуриентов, верно решивших задачи в рамках того или иного раздела, не столь велика (около 10—15%), но тенденция сохраняется из года в год.

Распространенная ошибка, которая часто возникает в задаче № 26, связана с применением первого закона термодинамики к различным изопроцессам. Выпускники неправильно пишут знаки необходимых величин. Этот закон включает в себя теплоту, подводимую или отводимую из системы, изменение внутренней энергии и работу. В зависимости от того, расширяется газ или сжимается, нагревается или охлаждается, подводят теплоту в систему или, наоборот, отводят, у всех названных выше величин меняются знаки, и они входят в уравнение либо с плюсом, либо с минусом. Участники экзамена регулярно ошибаются при расстановке знаков. Здесь нужно вспомнить, что чему должно соответствовать, и подумать, с какими знаками величины подставить в уравнение, чтобы получить корректное решение и правильный ответ.

Успешнее всего ребята справляются с задачами на уравнение Менделеева — Клайперона и на формулу для внутренней энергии идеального газа. Если на ЕГЭ попадаются эти темы, большинство абитуриентов верно решает задачу.

Советы

Статистика успешного выполнения задания № 26 может меняться в три-четыре раза в зависимости от темы. Поэтому советую внимательно повторить то, как правильно пользоваться первым законом термодинамики, а также темы, которые находятся в разделе молекулярной физики и термодинамики и вызывают у вас наибольшие трудности.

Задание № 27

Что требуется

Решить задачу по электродинамике или квантовой физике.

Особенности

В спецификации ФИПИ под этим номером идет задача по электродинамике или квантовой физике. При этом в методических рекомендациях по результатам ЕГЭ-2017 указано: «В следующем году последней расчетной задачей с кратким ответом на позиции 27 будут преимущественно задания по квантовой физике (на уравнение Эйнштейна для фотоэффекта или на формулу для энергии или импульса фотонов)». Эта информация сильно сужает список тем, которые стоит повторять при подготовке к этому заданию.

Советы

Обратите внимание на темы, о которых идет речь выше, и прорешайте соответствующие типичные задачи.

Задание № 28

Что требуется

Решить качественную задачу из любого раздела, который есть в кодификаторе.

Особенности

Качественная задача не имеет числового ответа. Ответ здесь может звучать как «больше», «меньше», «увеличится», «уменьшится», «вырастет», «упадет». В этих задачах, как правило, важен не столько результат, сколько сам ход решения. Например, в условии может быть схема электрической цепи, а затем в цепи происходит какое-то изменение (переключили ключ или заменили какой-нибудь элемент). В качестве решения надо указать, что изменится в системе или что произойдет с показаниями тех или иных измерительных приборов, которые содержатся в цепи.

Задание проверяет знание законов физики, умение их применить, а также логику переходов в построении решения. Насколько выпускник понимает то или иное явление? Нет ли логических ошибок в его рассуждениях? Могу сказать, что, по статистике, эта задача имеет один из самых низких процентов решаемости за всю историю ЕГЭ по физике.

Советы

Если на экзамене вы претендуете на максимальный балл, вам стоит обратить особое внимание на это задание. Существуют отдельные сборники по качественным задачам (например, «Качественные задачи по физике в средней школе», М.Е. Тульчинский). Хочу отметить, в зависимости от года издания, список рассматриваемых в этих сборниках тем может оказаться шире, чем требуется на ЕГЭ. Например, в сборниках, изданных в советское время, часто встречаются задачи на тепловое расширение, а в ЕГЭ такой темы нет. Поэтому подберите соответствующие темы по кодификатору ЕГЭ и прорешайте задачи по ним из какого-нибудь сборника качественных задач.

В методических рекомендациях, на которые я уже ссылался выше, этому заданию уделяется особое внимание, методика его решения обсуждается на нескольких страницах (стр. 20—22). Там рассматривается несколько типичных ошибок участников ЕГЭ по физике 2018 года и подходы к решению такого рода заданий. Выпускникам будет полезно ознакомиться с этим документом. Его можно найти на сайте ФИПИ.

Задание № 29

Что требуется

Решить задачу по механике.

Особенности

Задачи № 25—28 относились к повышенному уровню сложности, а последние четыре, начиная с № 29, уже относятся к высокому. Здесь от участников экзамена требуется применить законы физики в необычных условиях, которые редко встречаются в типовых задачниках.

Есть еще и такой нюанс. В прошлом году в кодификатор ЕГЭ по физике были внесены изменения, расширился список рассматриваемых тем. Обратите внимание, что в раздел «Механика» добавилась вторая космическая скорость, которой раньше там не было. Теперь могут появиться задачи и по этой теме.

Советы

В первую очередь обратите внимание на такие разделы механики, как «Статика» и «Колебания и волны». Эти темы достаточно часто встречаются в этом задании и вызывают наибольшие затруднения у выпускников.

Задание № 30

Что требуется

Решить задачу по молекулярной физике или термодинамике.

Особенности

В спецификации ЕГЭ по физике есть противоречие. В одной части этого документа говорится, что под этим номером идет задача по молекулярной физике или термодинамике, а в другой части, где описываются уровни сложности заданий, указано, что успешное выполнение этого задания требует знаний из нескольких разделов физики. По своему опыту могу сказать, что правильным стоит считать второй вариант. Кстати, это замечание относится ко всем четырем последним заданиям (№ 29—32).

Если на экзамене вам досталась задача по молекулярной физике, то чаще всего для решения требуются знания из области механики. Например, здесь могут рассматриваться изопроцессы, происходящие с идеальным газом, и создаваемое газом давление приводит к движению поршня, которое тоже надо описать, используя соотношения, известные из механики.

Советы

Чаще всего эта задача посвящена изопроцессам, происходящим в газах, и применению к этим процессам первого начала термодинамики. Также под № 30 встречаются задачи на уравнение теплового баланса, которые обычно не вызывают серьезных затруднений.

Задание № 31

Что требуется

Решить задачу по электродинамике.

Особенности

Это задача по электродинамике, но здесь надо применить знания из разных разделов. Например, часто в условии возникающие электродинамические силы приводят к механическому движению. Таким образом всплывают элементы механики, в частности, в решении нередко приходится использовать закон сохранения энергии.

Советы

Обратите внимание на следующие темы: электромагнитная индукция, электромагнитные колебания и волны, элементы физической оптики (дифракция и интерференция света). Эти разделы достаточно сложные, и по ним необходимо отдельно готовиться.

Наименьшие же трудности у ребят вызывают задачи на геометрическую оптику и применение закона Ома.

Задание № 32

Что требуется

Решить задачу по электродинамике или квантовой физике.

Особенности

Чаще всего под № 32 на ЕГЭ дают задачу по электродинамике. Но попадаются и задачи из квантовой физики, в частности на уравнение Эйнштейна для фотоэффекта.

Советы

Повторите следующие темы: фотоэффект, геометрическая оптика, электромагнитные колебания.

Общие рекомендации по решению задач части 2

Чтобы подготовиться к последним четырем заданиям, нужно решать задачи, которые рассматривают одно и то же явление с разных сторон. Допустим, у нас есть задача, в которой условие дано в форме обычного текста или рисунка со схемой. Что-то дано, что-то надо найти. Это первый подход. Второй вариант — это когда то же самое условие может быть в виде графика, который, например, описывает колебания той или иной величины (напряжение, сила тока, заряд на конденсаторе). Третий вариант — это условие в виде таблицы значений или функции. В итоге одно и то же явление можно описывать самыми разными способами. При подготовке я рекомендую найти и прорешать по несколько задач по каждой теме, в которых используются различные подходы.
Не всегда полезно прорешивать задачи из открытого банка заданий и демоверсий ЕГЭ. Ведь они в большей степени предназначены для проверки знаний по определенным темам, а не для обучения. Если вам нужно разобрать конкретные темы, лучше использовать задачники по физике.
Последние четыре задачи ЕГЭ рассчитаны на выпускников с очень высоким уровнем знаний по предмету. Другим школьникам они могут показаться нерешаемыми. Конечно, все основные законы физики большинство участников экзамена знает. Но здесь их нужно использовать в таких необычных условиях, что порой бывает сложно догадаться, о каком законе или явлении идет речь и какие соотношения эти явления описывают. Часто главная проблема заключается именно в этом — трудно понять, про что эта задача и какие законы в ней можно использовать.

Источник