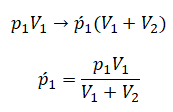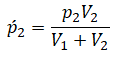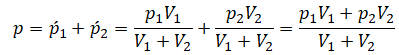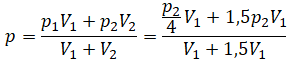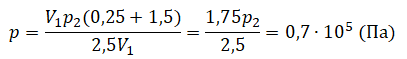Всего: 14 1–14
Добавить в вариант
В двух одинаковых баллонах при одинаковой температуре находятся аргон и неон. Давление аргона равно 140 кПа, а давление неона равно 180 кПа. Весь аргон из баллона перекачали в баллон с неоном. Чему стало равно давление смеси газов, если температуру поддерживают постоянной, а газы можно считать идеальными? Ответ запишите в килопаскалях.
В двух одинаковых баллонах при одинаковой температуре находятся кислород и азот. Давление кислорода равно 120 кПа, а давление азота равно 150 кПа. Весь азот из баллона перекачали в баллон с кислородом. Чему стало равно давление смеси газов, если температуру поддерживают постоянной, а газы можно считать идеальными? Ответ запишите в килопаскалях.
Сосуд объёмом 10 л содержит смесь водорода и гелия общей массой 2 г при температуре 27 °C и давлении 200 кПа. Каково отношение массы водорода к массе гелия в смеси?
Источник: Задания для школы экспертов. Физика. 2016 год.
Сосуд объёмом 10 л содержит смесь водорода и гелия общей массой 2 г и давлении 200 кПа. Соотношение массы водорода к массе гелия в смеси равно 1,5. Чему равна температура в сосуде?
Источник: ЕГЭ по физике 24.07.2020. Резервная волна. Вариант 1 (Часть С)
В сосуде неизменного объёма находилась при комнатной температуре смесь двух идеальных газов, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль первого газа. Температура в сосуде поддерживалась неизменной. Как изменились в результате парциальное давление первого газа и суммарное давление смеси газов?
Для каждой величины определите соответствующий характер изменения:
1) увеличилось
2) уменьшилось
3) не изменилось
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Парциальное давление
первого газа |
Суммарное давление
смеси газов |
Источник: Демонстрационная версия ЕГЭ—2023 по физике
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд — со вторым, второй — с третьим. Первоначально давление газа в сосудах было равно соответственно р, 3р и р. В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
В откачанный сосуд объёмом V = 30 л, имеющий жёсткие стенки, напустили ν1 = 0,4 моля аргона со среднеквадратичной скоростью движения атомов u1 = 250 м/с и ν2 = 0,6 моля неона со среднеквадратичной скоростью движения атомов u2 = 500 м/с. Какое равновесное давление установится в этом сосуде, если его теплоёмкостью и теплообменом с окружающей средой можно пренебречь?
В сосуде неизменного объема при комнатной температуре находилась смесь водорода и гелия, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль водорода. Считая газы идеальными, а их температуру постоянной, выберите из предложенного перечня все утверждения, которые соответствуют результатам проведенных экспериментальных исследований, и укажите их номера.
1) Парциальное давление водорода уменьшилось.
2) Давление смеси газов в сосуде не изменилось.
3) Концентрация гелия увеличилась.
4) В начале опыта концентрации газов были одинаковые.
5) В начале опыта массы газов были одинаковые.
В откачанный сосуд объёмом V = 20 л, имеющий жёсткие стенки, напустили ν1 = 0,5 моля аргона со среднеквадратичной скоростью движения атомов u1 = 300 м/с и ν2 = 0,3 моля неона со среднеквадратичной скоростью движения атомов u2 = 600 м/с. Какое равновесное давление установится в этом сосуде, если его теплоёмкостью и теплообменом с окружающей средой можно пренебречь?
В сосуде неизменного объема при комнатной температуре находилась смесь водорода и гелия, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль гелия. Считая газы идеальными, а их температуру постоянной, выберите из предложенного перечня все утверждения, которые соответствуют результатам проведенных экспериментальных исследований, и укажите их номера.
1) Парциальное давление водорода уменьшилось.
2) Давление смеси газов в сосуде уменьшилось.
3) Концентрация водорода увеличилась.
4) В начале опыта концентрации водорода была больше, чем концентрация гелия.
5) В начале опыта масса гелия была больше, чем масса водорода.
В сосуде с жёсткими стенками находится в равновесном состоянии смесь одного моля гелия и одного моля аргона. Температуру смеси повысили. Выберите все верные утверждения.
1) Среднеквадратичные скорости молекул гелия и молекул аргона в равновесном состоянии одинаковы.
2) Средние кинетические энергии поступательного теплового движения молекул гелия и молекул аргона в равновесном состоянии одинаковы.
3) В результате повышения температуры внутренняя энергия гелия увеличилась больше, чем внутренняя энергия аргона.
4) После повышения температуры парциальное давление гелия в сосуде увеличилось.
5) После повышения температуры давление в сосуде увеличилось.
В большом сосуде с жёсткими стенками, закрытом подвижным поршнем, находятся воздух и насыщенный водяной пар при температуре 100 °C. Давление в сосуде равно 300 кПа. Поршень переместили, поддерживая температуру содержимого сосуда постоянной. При этом половина водяного пара сконденсировалась. Какое давление установилось в сосуде? Ответ выразите в килопаскалях.
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. Перегородка может пропускать атомы гелия и является непроницаемой для атомов аргона. Вначале в левой части сосуда содержится 8 г гелия, а в правой — 1 моль аргона. Температура газов одинакова и остаётся постоянной. Выберите все верные утверждения, описывающие состояние газов после установления равновесия в системе. Запишите цифры, под которыми они указаны.
1) Внутренняя энергия гелия в сосуде больше, чем внутренняя энергия аргона.
2) Концентрация гелия и аргона в правой части сосуда одинакова.
3) В правой части сосуда общее число молекул газов в 2 раза меньше, чем в левой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии больше, чем в начальном.
5) Давление в обеих частях сосуда одинаково.
Источник: Демонстрационная версия ЕГЭ—2022 по физике
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой — 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите все верные утверждения, описывающие состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
Всего: 14 1–14
Уравнение Менделеева-Клапейрона и закон Дальтона
В этой статье предложены задачи на применение уравнения Менделеева-Клапейрона. Также вспомним и закон Дальтона: давление смеси газов складывается из парциальных давлений всех компонентов смеси.
Задача 1.
Сферическую оболочку воздушного шара делают из материала, квадратный метр которого имеет массу кг. Шар наполняют гелием. Атмосферное давление
Па равно давлению гелия в шаре. Определите минимальную массу оболочки, при которой шар оторвется от земли. Температура гелия и окружающего воздуха одинакова и равна
С.
Масса гелия в оболочке равна:
Масса оболочки:
Масса всего шара:
Чтобы шар оторвался, необходимо, чтобы сила тяжести была бы уравновешена силой Архимеда:
Приравняем силу тяжести и силу Архимеда:
Чтобы определить плотность гелия, запишем уравнение Менделеева-Клапейрона для гелия:
Для воздуха поступим аналогично, при этом объем можно принять равным 1 м (это неважно):
Тогда
А масса оболочки равна
Ответ: 93 кг
Задача 2.
Воздушный шар объемом м
с массой оболочки
кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры
нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой
кг? Температура окружающего воздуха
С, плотность
кг/м
. Оболочку шара считать нерастяжимой.
Масса всего шара:
Чтобы шар оторвался, необходимо, чтобы сила тяжести была бы уравновешена силой Архимеда:
Приравняем силу тяжести и силу Архимеда:
Из уравнения Менделеева-Клапейрона получим массу воздуха в шаре:
Теперь составим уравнение Менделеева-Клапейрона для наружного воздуха, чтобы определить давление:
Вернемся к силе тяжести и силе Архимеда:
Подставим давление:
Упрощаем:
Откуда :
Подставляем числа:
Ответ: K или
С.
Задача 3.
Теплоизолированный цилиндр, расположенный горизонтально, разделен подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент времени температура гелия равна 300 К, а аргона — 900 К, объемы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объем, занимаемый гелием, после установления теплового равновесия, если поршень перемещается без трения? Теплоемкостью цилиндра и поршня пренебречь.
Из уравнения Менделеева-Клапейрона
Так как давление одинаково, то
Общий объем сосуда равен , где
— объемы обоих газов.
После установления теплового равновесия объемы ,
.
Давления будут тоже другими (и равными!):
Тогда
Но , а с учетом отношения объемов
Таким образом, объем гелия изменится в 1,5 раза.
Задача 4.
Сосуд объемом 10 л содержит смесь водорода и гелия общей массой 2 г. При температуре С давление в сосуде равно 200 кПа. Каково отношение массы водорода к массе гелия в смеси?
Каждый газ создает свое парциальное давление, поэтому
Из уравнения Менделеева-Клапейрона
Тогда
Определив массу водорода, найдем массу гелия как .
Определяем отношение масс:
Ответ: .
Задача 5. В камере, заполненной азотом, при температуре К находится открытый цилиндрический сосуд. Высота сосуда
см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры
. В результате расстояние от дна сосуда до низа пробки становится равным
см. Затем сосуд нагревают до первоначальной температуры
. Расстояние от дна сосуда до низа пробки при этой температуре становится равным
см. Чему равна температура
? Величина силы трения между пробкой и стенками постоянна. Массой пробки пренебречь. Давление азота в камере во время эксперимента поддерживается постоянным.
Сначала состояние газа в сосуде описывается уравнением:
Когда сосуд охлаждают, его состояние изменится:
Затем сосуд снова нагрели:
Здесь ,
,
,
— атмосферное давление.
При охлаждении сосуда объем газа будет уменьшаться вследствие падения давления, и пробку будет затягивать в сосуд. При этом сила трения направлена против движения пробки, то есть вверх. Тогда
Откуда
Когда же сосуд вновь начнут нагревать, расширяющийся азот будет выталкивать пробку вверх, и сила трения будет направлена вниз, тогда:
Подставим силу трения, полученную ранее:
Из уравнений Менделеева-Клапейрона найдем
Или
Подставим объемы:
Также
Подставим объемы:
Приравняем давление , полученное двумя способами:
Подставим :
Ответ: К.
Давление смеси газов равно сумме их парциальных давлений.
p = p1’ + p2’ + … .
К примеру, давление воздуха складывается из давления азота, кислорода, углекислого газа, водяного пара и т. д.
Определение
Парциальное давление — давление, которое производил бы данный газ, если бы другие газы отсутствовали.
Применение закона Дальтона при решении задач
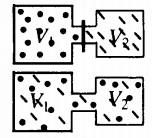
Самая популярная задача на закон Дальтона, это случай, когда газы находятся в сосудах, соединенных трубкой с краном. По условию этой задачи нужно найти давление, которое установится после того, как этот кран будет открыт.
После открытия крана первый и второй газы заполнят оба сосуда. Используем закон Бойля — Мариотта для первого газа (так как температура остается постоянной):
Этот же закон можем применить для второго газа. Тогда мы получим:
Применим закон Дальтона и получим:
Пример №1. Два сосуда соединены трубкой с краном. Определить давление, которое установится после того, как кран будет открыт. Считать, что объем второго сосуда в 1,5 раза больше первого. Давление во втором сосуде составляет половину от атмосферного давления. В первом сосуде оно меньше в 4 раза.
Проанализируем условия задачи и запишем:
V2 = 1,5V1
p2 = 4p1
p2 = 105 Па
Теперь можем применить выведенную ранее формулу:
Преобразуем выражение и найдем установившееся давление:
Задание EF17512
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд – со вторым, второй – с третьим. Первоначально давление газа в сосудах было равно соответственно р, 3р и р. В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
Алгоритм решения
1.Записать исходные данные.
2.Применить закон Дальтона для определения давления в первом сосуде.
3.Применить закон Менделеева — Клапейрона для установления характера изменения количества газа в первом сосуде в ходе эксперимента.
Решение
Запишем исходные данные:
• Объемы сосудов равны: V1 = V2 = V3 = V.
• Температуры равны: T1 = T2 = T3 = T.
• Давления распределены следующим образом: p1 = p, p2 = 3p, p3 = p.
После того, как открыли кран между 2 и 3 сосудом, объем возрос вдвое, и давление распределилось по нему равномерно. Согласно закону Дальтона, оно стало равным сумме давлений, оказываемых газами в количестве вещества ν2 и ν3. Так как объем после открытия крана увеличивается вдвое, то парциальное давление каждого из количества вещества равно половине исходного давления:
p23=p2+3p2=2p
Потом кран 2–3 закрыли, но открыли кран 1–2. Применим закон Дальтона, получим:
p12=2p2+p2=3p2
Теперь применим закон Менделеева — Клапейрона:
pV=νRT
Для начального состояния газа в 1 сосуде:
pV=ν1RT
Для конечного состояния газа в 1 сосуде:
3p2V=ν2RT
Так как температура и объем неизменны, но давление увеличилось в 1,5 раза, то и количество газа в первом сосуде увеличилось в 1,5 раза.
Ответ: Увеличилось
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18873

Для каждой величины определите соответствующий характер изменения:
- увеличилась
- уменьшилась
- не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Записать исходные данные.
2.Установить характер изменения парциального давления неона.
3.Применить закон Менделеева — Клапейрона, чтобы установить характер изменения общего давления смеси газов.
Решение
Исходные данные:
• Количество неона: ν1 = 1 моль.
• Количество аргона: ν2 = 1 моль.
• Количество впущенного аргона: ν4 = 1 моль.
Сначала парциальное давление неона и аргона равно. Это объясняется тем, что давление газов при неизменном количестве вещества зависит только от объема и температуры. Эти величины постоянны.
Когда из сосуда выпустили половину газовой смеси, в нем оказалось по половине моля каждого из газов. Затем в сосуд впустили 1 моль аргона. Следовательно, в сосуде стало содержаться 0,5 моль неона и 1,5 моль аргона. Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Из уравнения видно, что давление и количество вещества — прямо пропорциональные величины. Следовательно, если количество неона уменьшилось, то его парциальное давление тоже уменьшилось.
Общая сумма количества вещества равна сумме количеств вещества 1 (неона) и 2 (аргона): 0,5 + 1,5 = 2 (моль). Изначально в сосуде тоже содержалось 2 моль газа. Так как количество вещества, температура и объем сохранились, давление тоже осталось неизменным.
Ответ: 23
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 3.2k
1. Сосуд
объёмом 10 л содержит смесь водорода и гелия общей массой 2 г при температуре
27 °С и давлении 200 кПа. Каково отношение массы водорода к массе гелия в
смеси?
Решение.
Запишем уравнение
Менделеева-Клайперона для водорода и гелия в смеси:
Согласно закону
Дальтона давление смеси равно
,
а масса смеси равна
.
Объединяя полученные
выражения, имеем:

подставляя числовые
значения, получаем:

Ответ: 1,5.
2. Сосуд объёмом 15 л содержит смесь
водорода и гелия общей массой 2 г при температуре 27 °С. Отношение массы
водорода к массе гелия в смеси равно 1,5. Каково давление газовой смеси в
сосуде?
Решение.
1. Запишем уравнение
Клапейрона — Менделеева для водорода и гелия в смеси:
2. Согласно закону
Дальтона давление смеси: (3).
3. По условию задачи, (4).
Кроме того, масса смеси (5).
4. Решая систему
уравнений (4)-(5), получаем:
.
5. Из системы уравнений
(1)-(3) следует:
Ответ: Па = 130 кПа.
3. В школьном физическом кружке
изучали уравнение теплового баланса. В одном из опытов использовали два
калориметра. В первом калориметре находилось 300 г воды, во втором — 200 г льда
и 200 г воды при 0 °С. Какой была первоначальная температура воды в первом
калориметре, если после добавления в него всего содержимого второго в первом
калориметре установилась температура 2 °С? Теплоёмкостью калориметров
пренебречь.
Решение.
Количество теплоты,
полученное льдом при его таянии при 0 °С:
,
(1)
Количество теплоты,
полученное водой при её нагревании от 0 °С до температуры °С:
. (2)
Количество теплоты,
отданное водой при её охлаждении от температуры t до температуры :
.
(3)
Уравнение теплового
баланса:
.
(4)
Объединяя (1)-(4),
получаем:
Ответ: 57 °С.
4. В школьном физическом кружке
изучали уравнение теплового баланса. В одном из опытов использовали два
калориметра. В первом калориметре находилась вода при 50 °С, во втором — 200 г
льда и 200 г воды при 0 °С. Какая масса воды находилась первоначально в первом
калориметре, если после добавления в него всего содержимого второго в первом
калориметре установилась температура 2 °С? Теплоёмкостью калориметров
пренебречь.
Решение.
Количество теплоты,
полученное льдом при его таянии при 0 °С:
(1)
Количество теплоты,
полученное водой при её нагревании от 0 °С до температуры t0 = 2 °С:
. (2)
Количество теплоты,
отданное водой при её охлаждении от температуры t до температуры t0:
.
(3)
Уравнение теплового
баланса:
(4)
Объединяя (1)-(4),
получаем:
Ответ: 344 г.
5. Теплоизолированный горизонтальный
сосуд разделён пористой перегородкой на две равные части. В начальный момент в
левой части сосуда находится v=2 моль гелия, а в правой — такое же количество
моль аргона. Атомы гелия могут проникать через перегородку, а для атомов аргона
перегородка непроницаема. Температура гелия равна температуре аргона: Т = 300
К. Определите отношение внутренних энергий газов по разные стороны перегородки
после установления термодинамического равновесия.
Решение.
Так как сосуд
теплоизолирован и начальные температуры газов одинаковы, то после установления
равновесия температура в сосуде будет равна первоначальной, а гелий равномерно
распределится по всему сосуду. После установления равновесия в системе в каждой
части сосуда окажется по 1 моль гелия: . В
результате в сосуде с аргоном окажется 3 моль смеси: .
Внутренняя энергия
одноатомного идеального газа пропорциональна температуре и количеству молей:
,
откуда следует, что
Запишем условие
термодинамического равновесия: .
Тогда
.
Ответ: .
6. Теплоизолированный сосуд разделён
вертикальной пористой перегородкой на две равные части. В начальный момент в
левой части сосуда находится v = 2 моль гелия, а в правой — такое же количество
моль аргона. Атомы гелия могут проникать через перегородку, а для атомов аргона
перегородка непроницаема. Начальная температура гелия Т1 = 900 К, начальная
температура аргона Т2 = 300 К. Во сколько раз увеличилась внутренняя энергия
газа в правой части сосуда в результате установления термодинамического
равновесия?
Решение.
В результате установления
термодинамического равновесия в системе в каждой части сосуда окажется по 1
моль гелия =
1 моль, а аргон целиком останется в правой части сосуда. Поэтому в правой части
сосуда окажется 3 моль смеси: моль,
— а в левой части сосуда окажется =
1 моль гелия.
В системе с постоянным
числом частиц, согласно первому началу термодинамики, .
Так как сосуд теплоизолирован (Q = 0) и объём сосуда и его частей не меняется
(А = 0), то из первого начала следует, что .
Внутренняя энергия
одноатомного идеального газа пропорциональна температуре и количеству молей: .
Поэтому первоначально внутренняя энергия газа в левой части сосуда (т.е. гелия) ,
внутренняя энергия газа в правой части сосуда (т.е. аргона) , а
после установления термодинамического равновесия внутренняя энергия газа в
левой части сосуда (т.е. гелия) , а
внутренняя энергия газа в правой части сосуда (т.е. смеси гелия и аргона) ,
где T — равновесная температура в системе.
Условие означает,
что , т.
е.
.
Отсюда следует, что .
Искомое отношение
Ответ: 3.
7. Цикл тепловой машины, рабочим
веществом которой является один моль идеального одноатомного газа, состоит из
изотермического расширения, изохорного охлаждения и адиабатического сжатия. В
изохорном процессе температура газа понижается на ∆T, а работа, совершённая
газом в изотермическом процессе, равна A. Определите КПД тепловой машины.
Решение.
1. Коэффициент полезного
действия тепловой машины
где —
работа, совершённая за цикл; —
количество теплоты, полученное за цикл рабочим веществом тепловой машины от
нагревателя; —
количество теплоты, отданное за цикл холодильнику.
В рассматриваемом цикле
газ получает количество теплоты в изотермическом процессе и отдаёт в изохорном.
2. В изотермическом
процессе внутренняя энергия одноатомного идеального газа не изменяется,
следовательно, в соответствии с первым законом термодинамики количество
теплоты, полученное газом, равно работе газа: .
3. Поскольку в изохорном
процессе газ работу не совершает, количество теплоты, отданное газом (в
соответствии с первым законом термодинамики), равно изменению его внутренней
энергии:
.
Подставляя второе и
третье соотношения в первое, получаем значение КПД тепловой машины.
.
8. Цикл тепловой машины, рабочим
веществом которой является v молей идеального одноатомного газа, состоит из
изотермического расширения, изохорного охлаждения и адиабатического сжатия. В
изохорном процессе температура газа понижается на ∆T, а КПД тепловой машины
равен .
Определите работу, совершённую газом в изотермическом процессе.
Решение.
1. Коэффициент полезного
действия тепловой машины

где —
работа, совершённая за цикл; — количество теплоты, полученное за
цикл рабочим веществом тепловой машины от нагревателя; —
количество теплоты, отданное за цикл холодильнику.
В рассматриваемом цикле
газ получает количество теплоты в изотермическом процессе и отдаёт в изохорном.
2. В изотермическом
процессе внутренняя энергия одноатомного идеального газа не изменяется,
следовательно, в соответствии с первым законом термодинамики количество
теплоты, полученное газом, равно работе газа: .
3. Поскольку в изохорном
процессе газ работу не совершает, количество теплоты, отданное газом, равно
изменению его внутренней энергии:
.
Подставляя второе и
третье соотношения в первое, получаем искомую работу, совершённую газом в
изотермическом процессе.
.
Ответ: .
9. Тепловой двигатель использует в
качестве рабочего вещества 1 моль идеального одноатомного газа. Цикл работы
двигателя изображён на pV-диаграмме и состоит из двух адиабат, изохоры,
изобары. Зная, что КПД этого цикла =
15 %, а минимальная и максимальная температуры газа при изохорном процессе =
37 °С и =
302 °С, определите количество теплоты, получаемое газом за цикл.
Решение.
При изобарном расширении
на участке 1-2 газ получает от нагревателя количество теплоты Q12, а на участке
3-4 отдаёт холодильнику в изохорном процессе количество теплоты Q34. На других
участках теплообмен отсутствует, В соответствии с первым началом термодинамики
работа газа за цикл А равна разности количества теплоты, полученного от нагревателя,
и количества теплоты, отданного холодильнику: А = Ql2 — Q34.
По определению КПД
теплового двигателя ,
что позволяет найти количество теплоты, полученное от нагревателя: ,
если известно Q34.
Количество теплоты Q34,
отданное при изохорном охлаждении на участке 3-4, равно уменьшению внутренней
энергии газа этом участке: .
Внутренняя энергия идеального газа пропорциональна абсолютной температуре, и
для 1 моль одноатомного газа , а
модуль её изменения на участке 3-4
.
В итоге получим:
.
Подставляя значения
физических величин, получим:
Дж.
Ответ: 3886 Дж.
10. Тепловой двигатель использует в
качестве рабочего вещества 1 моль идеального одноатомного газа. Цикл работы
двигателя изображён на pV-диаграмме и состоит из двух адиабат, изохоры,
изобары. Зная, что КПД цикла равен 50%, определите модуль отношения изменения
температуры газа при изобарном процессе ∆T12 к изменению его температуры ∆T34
при изохорном процессе.
Решение.
При изобарном расширении
на участке 1-2 газ получает от нагревателя количество теплоты Q12, а на участке
3-4 отдаёт холодильнику в изохорном процессе количество теплоты Q34. На других
участках теплообмен отсутствует. В соответствии с первым началом термодинамики
работа газа за цикл A равна разности количества теплоты, полученного от
нагревателя, и количества теплоты, отданного холодильнику: , а
КПД теплового двигателя .
Количество теплоты Q12,
полученное при изобарном расширении на участке 1-2, равно сумме увеличения
внутренней энергии газа при увеличении его температуры и работы газа этом
участке: .
Внутренняя энергия идеального газа пропорциональна абсолютной температуре, и
для 1 моль одноатомного газа , а
её изменение
.
Работа газа при изобарном
расширении .
Выражая её через изменение температуры с помощью уравнения Клапейрона —
Менделеева ,
получим: .
Отсюда: .
Количество теплоты Q34,
отданное при изохорном охлаждении на участке 3-4, равно уменьшению внутренней
энергии газа на этом участке:
.
В итоге получим: .
Отсюда находим:
.
Ответ: 1,2.
11. Газонепроницаемая оболочка
воздушного шара имеет массу 400 кг. Шар заполнен гелием. Он может удерживать
груз массой 225 кг в воздухе на высоте, где температура воздуха 17 °С, а
давление Па.
Какова масса гелия в оболочке шара? Оболочка шара не оказывает сопротивления
изменению объёма шара, объём груза пренебрежимо мал по сравнению с объёмом
шара.
Решение.
Шар с грузом удерживается
в равновесии при условии, что сумма сил, действующих на него, равна нулю: ,
где M иm — массы оболочки шара и груза, —
масса гелия, a —
сила Архимеда, действующая на шар. Из условия равновесия следует: .
Давление гелия р и его
температура T равны давлению и температуре окружающего воздуха. Следовательно,
согласно уравнению Клапейрона — Менделеева ,
где —
молярная масса гелия, —
средняя молярная масса воздуха, V — объём шара. Отсюда:
;

Так как
,
то
кг.
Ответ: 100 кг.
12. Газонепроницаемая оболочка
воздушного шара заполнена гелием массой 100 кг. Он может удерживать груз массой
225 кг в воздухе на высоте, где температура воздуха 17 °С, а давление 10^5 Па.
Какова масса оболочки шара? Оболочка шара не оказывает сопротивления изменению
объёма шара, объём груза пренебрежимо мал по сравнению с объёмом шара.
Решение.
Шар с грузом удерживается
в равновесии при условии, что сумма сил, действующих на него, равна нулю: ,
где M и —
массы оболочки шара и груза, —
масса гелия, a —
сила Архимеда, действующая на шар. Из условия равновесия следует: .
Давление гелия p и его
температура T равны давлению и температуре окружающего воздуха. Следовательно,
согласно уравнению Клапейрона — Менделеева
,
где —
молярная масса гелия, —
средняя молярная масса воздуха, V — объём шара. Отсюда:
;

Ответ: M = 400 кг.
13. Над одноатомным идеальным газом
проводится циклический процесс, показанный на рисунке. На участке 1-2 газ
совершает работу А12 = 1000 Дж. На адиабате 3-1 внешние силы сжимают газ,
совершая работу |А31| = 370 Дж. Количество вещества газа в ходе процесса не
меняется. Найдите количество теплоты |Qхол|, отданное газом за цикл
холодильнику.
Решение.
1. В данном цикле рабочее
тело на участке 1-2 получает положительное количество теплоты от нагревателя:
.
На участке 2-3 (изохора)
рабочее тело отдаёт холодильнику количество теплоты
.
Наконец, на участке 3-1
(адиабата) внешние силы сжимают газ, совершая работу
.
Поэтому количество
теплоты ,
отданное газом за цикл холодильнику, можно представить в виде:
.
2. Модель одноатомного
идеального газа:
3. Судя по рисунку в
условии, ,
откуда .
Поэтому
откуда получаем: .
4. В результате
Дж.
Ответ: 3370 Дж.
14. Над одноатомным идеальным газом
проводится циклический процесс, показанный на рисунке. На участке 1-2 газ
совершает работу А12 = 1000 Дж. Участок 3-1 — адиабата. Количество теплоты,
отданное газом за цикл холодильнику, равно =
3370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите работу
|А31| внешних сил на адиабате.
Решение.
1. В данном цикле рабочее
тело на участке 1-2 получает положительное количество теплоты от нагревателя:
На участке 2-3 (изохора)
рабочее тело отдаёт холодильнику количество теплоты Наконец, на участке 3-1
(адиабата) внешние силы сжимают газ, совершая работу
.
Поэтому работу внешних
сил на адиабате |А31| можно представить в виде:
2. Модель одноатомного
идеального газа:
3. Судя по рисунку в условии, ,
откуда .
Поэтому
откуда получаем: .
4. В результате
Дж.
Ответ: 370.
15. Один моль аргона, находящийся в
цилиндре при температуре Т1 = 600К и давлении Па,
расширяется и одновременно охлаждается так, что его температура при расширении
обратно пропорциональна объёму. Конечное давление газа Па.
Какое количество теплоты газ отдал при расширении, если при этом он совершил
работу A = 2493 Дж?
Решение.
1. Аргон является
одноатомным газом, подчиняющимся уравнению Клапейрона-Менделеева: pV=vRT, внутренняя
энергия одноатомного идеального газа пропорциональна температуре:
,
так что
2. С помощью уравнения
Клапейрона-Менделеева и условия расширения определим
конечную температуру 
внутреннюю энергию 
3. Уменьшение внутренней
энергии при расширении
Дж.
4. В соответствии с
первым началом термодинамики уменьшение внутренней энергии равно сумме
совершённой работы и количества теплоты, отданного газом: ,
поэтому
Дж.
Ответ: 1247 Дж.
16. Один моль аргона, находящийся в
цилиндре при температуре Т1 = 600К и давлении р1 = Па,
расширяется и одновременно охлаждается так, что его температура при расширении
обратно пропорциональна объёму. Конечное давление газа р2 = 10^5 Па. На какую
величину изменилась внутренняя энергия аргона в результате расширения?
Решение.
1. Аргон является
одноатомным газом, подчиняющимся уравнению Клапейрона-Менделеева: pV=vRT,
внутренняя энергия одноатомного идеального газа пропорциональна температуре:
,
так что
2. С помощью уравнения
Клапейрона-Менделеева и условия расширения
определим конечную
температуру 
внутреннюю энергию 
3. Уменьшение внутренней
энергии при расширении

Ответ: 3740 Дж.
17. Один моль одноатомного идеального
газа совершает процесс 1-2-3, график которого показан на рисунке в координатах
р-Т. Известно, что давление газа р в процессе 1-2 увеличилось в 2 раза. Какое
количество теплоты было сообщено газу в процессе 1-2-3, если его температура Т
в состоянии 1 равна 300 К, а в состоянии 3 равна 900 К?
Решение.
Для определения
количества теплоты необходимо
сложить количества теплоты, сообщённые газу на участках 1-2 и 2-3: .
Исходя из приведённого
графика, можно сделать вывод, что процесс 1-2 является изохорным. Для него, как
следует из уравнения Клапейрона-Менделеева, ,
откуда .
Следовательно,
К.
Работа газа в процессе
1-2 равна нулю, и для него первый закон термодинамики с учётом выражения для
внутренней энергии одноатомного идеального газа принимает вид:
кДж.
Процесс 2-3 является
изобарным с давлением ,
для него первый закон термодинамики принимает вид:
,
где —
изменение внутренней энергии газа, —
совершённая газом работа. Из уравнения Клапейрона-Менделеева pV = vRT следует,
что
.
Таким образом, кДж.
В результате кДж.
Ответ: 10 кДж.
18. С одноатомным идеальном газом
происходит циклический процесс, показанный на рисунке. За цикл газ совершает
работу Ац = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя?
В ходе процесса масса газа не меняется.
Решение.
За цикл количество
теплоты, полученное от нагревателя:
Работа газа за цикл
.
Отсюда
кДж.
Ответ: 57,5 кДж.
19. В сосуде объёмом V = 0,02 м3 с
жёсткими стенками находится одноатомный газ при атмосферном давлении. В крышке
сосуда имеется отверстие площадью s, заткнутое пробкой. Максимальная сила
трения покоя F пробки о края отверстия равна 100 Н. Пробка выскакивает, если
газу передать количество теплоты не менее 15 кДж. Определите значение s, полагая
газ идеальным.
Решение.
Пробка выскочит, если
сила, с которой газ давит изнутри на пробку, превысит суммарную силу давления
атмосферного воздуха снаружи на пробку и трения пробки о края отверстия. А это
произойдёт, когда давление газа превысит атмосферное давление на величину ,
откуда: .
Поскольку изначально
давление газа в сосуде равно атмосферному, именно такое изменение давления газа
в сосуде определяет предельное количество теплоты, переданное газу.
Поскольку объём V газа не
меняется, изменение давления газа связано с изменением его температуры T.
Согласно уравнению Клапейрона-Менделеева ,
где v — количество газообразного вещества.
Чтобы найти изменение
температуры газа, обратимся к первому закону термодинамики: . В
нашем случае работа внешних сил A = 0, поскольку объём газа не меняется, и
изменение внутренней энергии газа равно количеству полученной им теплоты: .
Для идеального
одноатомного газа имеем: .
Соотнеся это равенство с уравнением Клапейрона-Менделеева и равенством ,
находим:
,
Па.
Следовательно,
м2.
Ответ: м2.
20. В калориметре находится 1 кг льда
при температуре -5 °С. Какую массу воды, имеющей температуру 20 °С, нужно
добавить в калориметр, чтобы температура его содержимого после установления
теплового равновесия оказалась -2 °С? Теплообменом с окружающей средой и
теплоёмкостью калориметра пренебречь.
Решение.
Количество теплоты,
необходимое для нагревания льда, находящегося в калориметре, до температуры t:
.
(1)
Количество теплоты,
выделяющееся при охлаждении воды до t0 = 0°С:
. (2)
Количество теплоты,
выделяющееся при отвердевании воды при 0 °С:
.
(3)
Количество теплоты,
выделяющееся при охлаждении льда, полученного из воды, до температуры t:
. (4)
Уравнение теплового
баланса:
. (5)
Объединяя (l)-(5),
получаем:
г.
Ответ: 15 г.
21. В
камере, заполненной азотом, при температуре Т0 = 300 К находится открытый
цилиндрический сосуд (рис. 1). Высота сосуда L = 50 см. Сосуд плотно закрывают
цилиндрической пробкой и охлаждают до температуры T1. В результате расстояние
от дна сосуда до низа пробки становится равным h = 40 см (рис. 2). Затем cocyд
нагревают до первоначальной температуры Т0. Расстояние от дна сосуда до низа
пробки при этой температуре становится равным Н = 46 см (рис. 3). Чему равна
температура Т1? Величину силы трения между пробкой и стенками сосуда считать
одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь. Давление
азота в камере во время эксперимента поддерживается постоянным.


Решение.
1. Пусть р0 — давление
азота в камере; р1 — давление в сосуде в ситуации на рис. 2; р2 — давление в
сосуде при температуре Т0 в конце опыта; S — площадь горизонтального сечения
сосуда.
2. Параметры азота в
сосуде в первоначальном состоянии и при температуре Т1 связаны равенством, следующим
из уравнения Клапейрона-Менделеева:
,
откуда
.
Условие равновесия
пробки при температуре Т1:
,
откуда
.
3. Параметры азота в
сосуде в первоначальном и конечном состояниях тоже связаны равенством,
следующим из уравнения Клапейрона-Менделеева:
,
откуда
.
Условие равновесия
пробки в конечном состоянии:
,
откуда
4. Приравнивая друг
другу два выражения для получаем равенство:
.
Отсюда: К.
Ответ: 219
К.
22. В камере, заполненной азотом, при
температуре Т0 = 300 К находится открытый цилиндрический сосуд (рис. 1). Высота
сосуда L = 50 см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до
температуры T1 = 220 К. В результате расстояние от дна сосуда до низа пробки
становится равным h = 40 см (рис. 2). Затем сосуд нагревают до первоначальной
температуры Т0. Расстояние от дна сосуда до низа пробки при этой температуре
становится равным Н (рис. 3). Чему равно НЧ Величину силы трения между пробкой
и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой
пробки пренебречь. Давление азота в камере во время эксперимента поддерживается
постоянным.


Решение.
1. Пусть р0 — давление
азота в камере; р1 — давление в сосуде в ситуации на рис. 2; р2 — давление в
сосуде при температуре T0 в конце опыта; S — площадь горизонтального сечения
сосуда.
2. Параметры азота в
сосуде в первоначальном состоянии и при температуре Т1 связаны равенством,
следующим из уравнения Клапейрона-Менделеева:
,
откуда
.
Условие равновесия пробки
при температуре T1:
,
откуда
.
3. Параметры азота в сосуде
в первоначальном и конечном состояниях тоже связаны равенством, следующим из
уравнения Клапейрона-Менделеева:
,
откуда
.
Условие равновесия пробки
в конечном состоянии:
,
откуда
.
4. Приравнивая друг другу
два выражения для р2, получаем равенство:
.
Отсюда:
Ответ: 46 см.
23. С разреженным газом, который
находится в сосуде с поршнем, провели два опыта. В первом опыте газу сообщили,
закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его
температура изменилась на некоторую величину ∆T. Во втором опыте, предоставив
газу возможность изобарно расширяться, сообщили ему количество теплоты Q2 =
1039 Дж, в результате чего его температура изменилась также на ∆T. Каким было
изменение температуры ∆T в опытах? Количество вещества газа v = 36 моль.
Решение.
Согласно первому началу
термодинамики
,
(1)
,
(2)
где —
приращение внутренней энергии газа (одинаковое в двух опытах), A — работа газа
во втором опыте. Работа A совершалась газом в ходе изобарного расширения, так что
,
(3)
( — изменение объёма газа).
С помощью уравнения
Клапейрона-Менделеева эту работу можно выразить через приращение температуры
газа:
.
(4)
Решая систему уравнений
(1)-(4), будем иметь:
К.
Ответ: 1 К.
24. С разреженным газом, который
находится в сосуде с поршнем, провели два опыта. В первом опыте газу сообщили,
закрепив поршень, количество теплоты Q1 = 742 Дж, в результате чего его
температура изменилась на ∆T = 1 К. Во втором опыте, предоставив газу
возможность изобарно расширяться, сообщили ему количество теплоты Q2 = 1039 Дж,
в результате чего его температура изменилась также на ∆T. Определите количество
вещества газа.
Решение.
Согласно первому началу
термодинамики (1),
(2),
где —
приращение внутренней энергии газа (одинаковое в двух опытах), А — работа газа
во втором опыте. Работа А совершалась газом в ходе изобарного расширения, так
что (3)
( — изменение объёма газа). С помощью
уравнения Клапейрона-Менделеева эту работу можно выразить через
приращение температуры газа: (4).
Решая систему уравнений (1)-(4), будем иметь:
моль.
Ответ: 36 моль.
25. Сферическую оболочку воздушного
шара делают из материала, квадратный метр которого имеет массу 2 кг. Шар
наполняют гелием при атмосферном давлении Па.
Определите минимальную массу оболочки, при которой шар начнёт поднимать сам
себя. Температура гелия и окружающего воздуха одинакова и равна 0 °С. (Площадь
сферы ,
объём шара .)
Решение.
Второй закон Ньютона в
проекциях на вертикаль: .
Силы выражены через радиус r:
,
откуда
,
откуда получаем радиус
оболочки:
,
где b = 2 кг/м2 —
отношение массы оболочки к её площади.
Плотности гелия и
воздуха:
Радиус оболочки:
м,
её масса:
кг.
Ответ: 745 кг.
26. Сферическую оболочку воздушного
шара наполняют гелием при атмосферном давлении Па.
Минимальная масса оболочки, при которой шар начинает поднимать сам себя, равна
m = 500 кг. Температура гелия и окружающего воздуха одинакова и равна 0 °С.
Чему равна масса одного квадратного метра материала оболочки шара? (Площадь
сферы , объём
шара .)
Решение.
Второй закон Ньютона в
проекциях на вертикаль: .
Силы выражены через радиус r:
,
откуда следует, что
,
откуда получаем радиус
оболочки:
,
где b — отношение массы
оболочки к её площади. Плотности гелия и воздуха:
,
следовательно,
.
Радиус оболочки:
,
ее масса:

Отсюда

Ответ: масса одного квадратного метра
материала оболочки шара примерно 1,75кг.
27. В цилиндр объёмом 0,5 м3 насосом
закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть
отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом
состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А
(см. рисунок). К свободному концу стержня длиной 0,5 м подвешен груз массой 2
кг. Клапан открывается через 580 с работы насоса, если в начальный момент
времени давление воздуха в цилиндре было равно атмосферному. Площадь закрытого
клапаном отверстия м2.
Температура воздуха в цилиндре и снаружи не меняется и равна 300 К. Определите
расстояние АВ, если стержень можно считать невесомым.
Решение.
Клапан откроется, когда
избыточная сила F давления воздуха на клапан изнутри цилиндра сравняется с
силой давления стержня на этот клапан. Если превышение давления воздуха в
цилиндре над атмосферным ∆p, а площадь клапана s, то F=s∙∆p. Сила действия
стержня на клапан равна ,
где —
соответственно масса груза, длина стержня и длина его участка АВ. Итак, должно
выполняться условие .
Дополнительное давление
воздуха определяется увеличением массы воздуха
в цилиндре. Согласно уравнению Клапейрона-Менделеева ,
где M — молярная масса воздуха. Поэтому условие открытия клапана имеет вид:
,
или в виде
.
Если насос закачивает
каждую секунду w кг воздуха, то массу он
закачает в цилиндр за время .
Следовательно, клапан откроется в момент, когда выполнится равенство
м.
Ответ: 0,1 м.
28. В цилиндр объёмом 0,5 м3 насосом
закачивается воздух со скоростью 0,002 кг/с. В верхнем торце цилиндра есть
отверстие, закрытое предохранительным клапаном. Клапан удерживается в закрытом
состоянии стержнем, который может свободно поворачиваться вокруг оси в точке А
(см. рисунок). К свободному концу стержня подвешен груз массой 2 кг. Клапан
открывается через 580 с работы насоса, если в начальный момент времени давление
воздуха в цилиндре было равно атмосферному. Площадь закрытого клапаном
отверстия м2,
расстояние АВ равно 0,1 м. Температура воздуха в цилиндре и снаружи не меняется
и равна 300 К. Определите длину стержня, если его считать невесомым.
Решение.
Клапан откроется, когда
избыточная сила F давления воздуха на клапан изнутри цилиндра сравняется с
силой давления стержня на этот клапан. Если превышение давления воздуха в
цилиндре над атмосферным ∆p, а площадь клапана s, то F=s∙∆p. Сила действия
стержня на клапан равна ,
где —
соответственно масса груза, длина стержня и длина его участка АВ. Итак, должно
выполняться условие .
Дополнительное давление
воздуха определяется увеличением массы воздуха
в цилиндре. Согласно уравнению Клапейрона-Менделеева ,
где M — молярная масса воздуха. Поэтому условие открытия клапана имеет вид:
,
или в виде
.
Если насос закачивает
каждую секунду w кг воздуха, то массу он
закачает в цилиндр за время .
Следовательно, клапан откроется в момент, когда выполнится равенство
м.
Ответ: 0,5 м.
29. В горизонтальном цилиндрическом
сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное
давление газа р1 = Па.
Расстояние от дна сосуда до поршня равно L. Площадь поперечного сечения поршня
S = 25 см2. В результате медленного нагревания газ получил количество теплоты Q
= 1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на
него со стороны стенок сосуда действует сила трения величиной Fтр = Н.
Найдите L. Считать, что сосуд находится в вакууме.
Решение.
1. Поршень будет медленно
двигаться, если сила давления газа на поршень и сила трения со стороны стенок
сосуда уравновесят друг друга: ,
откуда .
2. Поэтому при нагревании
газа поршень будет неподвижен, пока давление газа не достигнет значения р2. В
этом процессе газ получает количество теплоты Q12. Затем поршень будет
сдвигаться, увеличивая объём газа, при постоянном давлении. В этом процессе газ
получает количество теплоты Q23.
3. В процессе нагревания,
в соответствии с первым началом термодинамики, газ получит количество теплоты:
.
4. Внутренняя энергия
одноатомного идеального газа в начальном состоянии:
,
в конечном состоянии:
.
5. Из пп. 3, 4 получаем

Ответ: 0,3 м.
30. В горизонтальном цилиндрическом
сосуде, закрытом поршнем, находится одноатомный идеальный газ. Первоначальное
давление газа p1 = Па.
Расстояние от дна сосуда до поршня L = 0,3 м. Площадь поперечного сечения
поршня S. В результате медленного нагревания газ получил количество теплоты Q =
1,65 кДж, а поршень сдвинулся на расстояние х = 10 см. При движении поршня на
него со стороны стенок сосуда действует сила трения величиной Fтр = Н.
Найдите S. Считать, что сосуд находится в вакууме.
Решение.
1. Поршень будет медленно
двигаться, если сила давления газа на поршень и сила трения со стороны стенок
сосуда уравновесят друг друга: .
Предположим, что р2 > p1.
2. Тогда при нагревании
газа поршень будет неподвижен, пока давление газа не достигнет значения р2. В
этом процессе газ получает количество теплоты Ql2. Затем поршень будет
сдвигаться, увеличивая объём газа, при постоянном давлении. В этом процессе газ
получает количество теплоты Q23.
3. В процессе нагревания,
в соответствии с первым началом термодинамики, газ получит количество теплоты:
.
4. Внутренняя энергия
одноатомного идеального газа в начальном состоянии:
,
в конечном состоянии:
.
5. Из пп. 3, 4 получаем:
,
откуда
Тогда как
и предполагалось.
Ответ: 25 см2.
Газовые смеси, в которых компоненты не взаимодействуют друг с другом, могут быть описаны с помощью закона Дальтона. Он связывает парциальные давления компонентов и их мольные доли в одно равенство. Рассмотрим подробнее этот закон, а также покажем, как его можно использовать, на конкретных примерах.
Идеальные газы
Закон Дальтона в физике оказывается справедливым исключительно для идеальных газов. Под таковыми понимают газы, составляющие частицы которых (атомы, молекулы) не взаимодействуют между собой. Для идеального газа при неизменном числе молекул (атомов) в нем (n = const) справедливо равенство, связывающее три макроскопических параметра (давление P, объем V и температуру T):
P*V = n*R*T, R = 8,314 Дж/(К*моль) — постоянная величина.
Все реальные газы при давлениях в несколько атмосфер и температурах порядка комнатной и выше можно с хорошей точностью считать идеальными, то есть для них справедливо приведенное равенство.
Парциальное давление компонента
Чтобы понять суть закона Дальтона, необходимо разобраться с понятием «парциальное давление».
Поскольку молекулы разных газов не «чувствуют» друг друга, для каждого химического компонента i в газовой смеси будет справедливо равенство:
Pi*V = ni*R*T.
То есть можно считать каждый компонент независимым от других. Поскольку его молекулы занимают весь объем V и имеют температуру T, характерную для всей смеси, то отсюда и следует справедливость записанного выражения.
Давление Pi называется парциальным для i-го компонента. Иными словами, парциальное давление — это то давление, которое только i-й компонент создает на стенки сосуда. Парциальным оно называется потому, что является частью от общего давления, или его порцией.
Формулировка закона Дальтона
В первые годы XIX века, занимаясь изучением поведения различных газовых смесей, британский ученый Джон Дальтон установил следующий факт: если суммировать все парциальные давления компонентов газовой смеси, то получится общее давление, которое можно измерить барометром, манометром или другим предназначенным для этого прибором. Это и есть закон Дальтона. Запишем его в виде математического равенства:
Ptot = ∑i(Pi).
Понять, почему это равенство справедливо, можно, если вспомнить, что компоненты смеси создают давление независимо друг от друга.
Учитывая, что парциальное давление Pi прямо пропорционально количеству вещества ni компонента i, что справедливо всегда, когда T=const и V = const, тогда приходим к еще одному равенству:
Pi/Ptot = ni/n = xi.
Величина xi называется мольной долей. С атомными процентами ai компонента она связана простым соотношением:
ai = xi*100.
Выражение, которое позволяет определить мольную долю компонента через его парциальное давление и наоборот, также называется законом Дальтона.
Следует не забывать, что рассмотренный закон справедлив не только в случае идеальных газов, но и в случае отсутствия химических реакций в них. Последние приводят к изменениям компонентного и мольного состава, что нарушает закон для давления газовой смеси.
Примеры решения задач
В этом пункте рассмотрим примеры применения закона Дальтона для решения практических задач.
Задача 1. Необходимо определить парциальное давление трех основных компонентов в сухом воздухе.
Из литературных данных можно узнать, что поскольку воздух является сухим, то основными его компонентами будут азот (около 78 %), кислород (около 21 %) и благородный газ аргон (около 1 %). Учитывая, что общее давление воздуха на уровне моря равно 1 атмосфере, и переводя атомные проценты в мольные доли, получим значения парциальных давлений для каждого компонента:
Pi = Ptot*xi
PN2 = 1 *0,78 = 0,78 атм.
PO2 = 1*0,21 = 0,21 атм.
PAr = 1*0,01 = 0,01 атм.
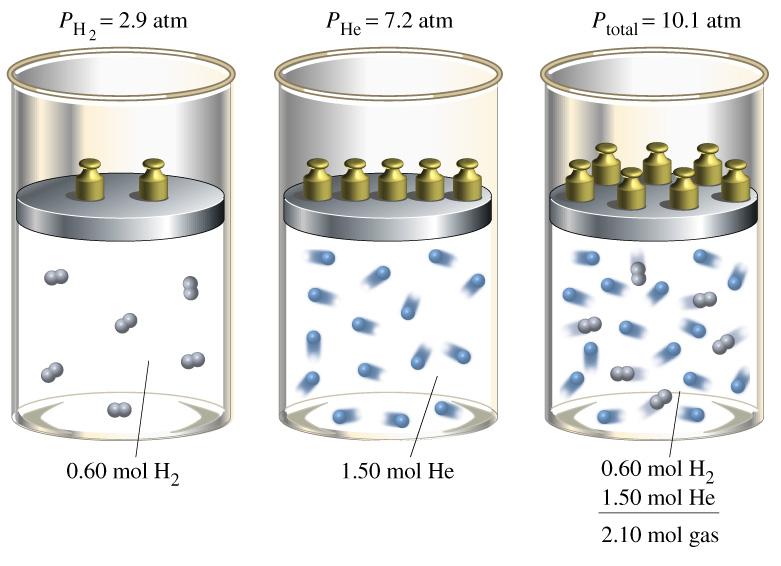
Задача 2. Есть два баллона с чистыми газами. Первый баллон содержит азот с температурой 300 К, объемом в 10 литров и давлением в 2 атмосферы. Второй баллон содержит кислород с температурой 300 К, но имеющий объем 15 литров и давление 1,5 атмосферы. Оба баллона соединили друг с другом. Необходимо рассчитать парциальное давление каждого компонента в полученной смеси.
Решать эту задачу начнем с вычисления количества вещества для азота и кислорода. Используя уравнение для идеального газа, получим:
PN2*VN2 = nN2*R*T =>
nN2 = PN2*VN2/R*T = 2*101325*10-2/(8,314*300) = 0,812 моль;
nO2 = PO2*VO2/R*T = 1,5*101325*1,5*10-2/(8,314*300) = 0,914 моль.
Когда два баллона соединят, произойдет перемешивание газов так, что каждый компонент займет весь объем двух баллонов. Общее давление, которое будет в системе, можно рассчитать, пользуясь также уравнением состояния идеального газа:
Vtot = VN2+VO2 = 2,5*10-2 м3;
n = nN2+nO2 = 0,812+0,914 = 1,726 моль.
Ptot = n*R*T/Vtot = 1,726*8,314*300/(2,5*10-2) = 172199,568 Па или 1,7 атм.
Теперь можно применить формулы закона Дальтона, чтобы рассчитать парциальные давления кислорода и азота:
PN2 = Ptot*nN2/n = 1,7*0,812/1,726 = 0,8 атм.;
PO2 = Ptot — PN2 = 1,7 — 0,8 = 0,9 атм.
Отношение полученных парциальных давлений газов равно отношению количеств вещества для них.
Задачи на закон или правило Генри-Дальтона
Суть закона Генри-Дальтона состоит в том, что концентрация растворённого в природной воде того или иного газа, помимо температуры (чем выше температура воды, тем растворимость газа уменьшается) и минерализации (чем выше минерализация воды, тем растворимость газа также уменьшается), зависит от природы самого газа и от его парциального давления в газовой смеси, например, в воздухе.
В атмосферном воздухе содержатся многие газы; помимо азота, кислорода и аргона, в ничтожно малых количествах, другие инертные газы, а также аммиак, метан и другие углеводороды, различные окислы азота, окислы углерода, серосодержащие газы и др.
Вместе с тем, мы не можем говорить о том, чем меньше содержится того или иного газа в воздухе, тем его концентрация в природных водах ниже.
Некоторые воздушные газы имеют весьма высокую растворимость, в первую очередь, аммиак, а также сероводород, сернистый газ, хлористый водород и нек. др. Существуют газы умеренной растворимости, например, углекислый газ, окисляя азота. Такие газы, как азот и кислород относят, обычно, к газам плохо растворимым.
Задача 252
Какова максимально возможная концентрация (мг/л) молекулярного азота (N2) в пресной воде при выбранном парциальном давлении (например, 760 мм.рт.ст.) и данной температуре? Содержание молекулярного азота в воздухе 976125 мг/м3. Растворимость азота в воде при нормальных условиях 15, 4 мл/л. Алгоритм решения подобных задач предложен еще во второй половине ХIХ в. Д.И. Менделеевым в своей книге «Основы химии».
Решение:
1). Найдём плотность азота или возьмём это значение из прилагаемой ниже таблицы.
Ρ = 28 г/моль (молярная масса азота): 22, 4 моль/л (молярный объём) = 1, 25 г/л.
Переведём эту величину в мг/л. 1, 25 г/л = 1250 мг/л.
2). По условию, содержание молекулярного азота в воздухе 976125 мг/м3, следовательно, если 1 л N2 имеет массу 1250 мг, то какой объём (л) будет иметь N2, содержащийся в 1 м3 воздуха?
1250 мг – 1 л.
976125 мг – Х л. Х = 976125: 1250 =780, 9 л, т.е. концентрация азота в воздухе, равная 976125 мг/м3 (по условию задачи) соответствует 780, 9 л/м3.
3). Переведём 780, 9 л/м3 в %
1 м3 = 1000 л, т.е. 1000 л есть 100%, следовательно, 780, 9 л – 78, 1%. Это и есть % содержание азота в воздухе. Если в условии концентрация газа уже даётся в %, то предыдущие три действия не нужны.
4). Рассуждаем следующим образом. Если бы в воздухе содержалось 100% молекулярного азота, тогаз растворялся бы при парциальном давлении 1 атм. или760 мм.рт.ст. (нормальное атмосферное давление).
100% — 1 атм.
78, 1% — Х атм. Х = 78, 1: 100 = 0, 781 атм, т.е. азот воздуха растворяется именно при этом парциальном давлении.
5). Растворимость N2 при 1 атм. 15, 4 мл/л, а при 0, 781 атм. – Х мл/л. Отсюда Х = 12, 03 мл/л.
6). Переведём концентрацию азота в воздухе из мл/л в мг/л, поскольку это требуется по условию задачи. Используем значение плотности азота.
1000 мл N2 «весит» 1250 мг, следовательно, 12, 03 мл «весят» (1250 ∙ 12, 3: 1000) 15, 375 мг/л Это и есть ответ.
Варианты задачи 252
Какова максимально возможная концентрация (в мг/л) газа (конкретный газ и его химическая формула указаны в таблице) в природной воде при её определенной температуре и минерализации, если его растворимость (в мл/л) при данных условиях и парциальном давлении 1 атм. указана в таблице. Содержание данного газа в воздухе (в мг/м3) также указано в прилагаемой таблице.
| № задачи |
Газ, его формула |
Содержание в воздухе, мг/м3 |
Растворимость газа при парциальном давлении 1 атм., мл/л |
| Водород, Н2 | 0, 0446 | 20, 6 | |
| Водород, Н2 | 0, 0446 | 16, 4 | |
| Гелий, Не | 0, 02 | 20, 4 | |
| Закись азота, N2O | 0, 45 | ||
| Закись азота, N2O | 0, 45 | ||
| Гелий, Не | 0, 02 | 9, 9 | |
| Оксид азота, (II), NO | 0, 07 | 51, 5 | |
| Сероводород, H2S | 0, 05 | ||
| Сероводород, H2S | 0, 05 | ||
| Сероводород, H2S | 0, 05 | ||
| Сероводород, H2S | 0, 05 | ||
| Сероводород, H2S | 0, 05 | ||
| Сернистый, SO2 | 0, 05 | ||
| Сернистый, SO2 | 0, 05 | ||
| Аммиак, NH3 | 0, 6 | ||
| Аммиак, NH3 | 0, 6 | ||
| Гелий, Не | 0, 92857 | 9, 9 | |
| Неон, Ne | 16, 0714 | 11, 6 | |
| Углекислый, СО2 | 589, 2857 | ||
| Азот, N2 | 976125 | 15, 4 | |
| Кислород, О2 | |||
| Аргон, Ar | 16607, 14 | ||
| Метан, СН4 | 1, 571 | 55, 6 | |
| Криптон, Kr | 3, 9286 | ||
| Закись азота, N2О | 1, 964 | ||
| Водород, Н2 | 0, 0446 | 18, 2 | |
| Ксенон, Хе | 0, 4679 | ||
| Озон, О3 | 0, 02143 | ||
| Окись углерода, СО | 0, 075 | ||
| Окись углерода, СО | 1, 25 | ||
| Сернистый, SO2 | 2, 857 | ||
| Закись азота, N2O | 0, 982 | ||
| Озон, О3 | 0, 214 | ||
| Диоксид азота, NO2 | 1, 027∙ 10-3 | 73, 8 | |
| Диоксид азота, NO2 | 2, 054∙ 10-3 | 73, 8 | |
| Диоксид азота, NO2 | 0, 0411 | 73, 8 |
Плотности некоторых газов
| Газ, название |
г/дм3, мг/см3, кг/м3 |
г/м3 |
| Углекислый, СО2 | 1, 96 | |
| Сернистый газ, оксид серы (IV), SO2 | 2, 86 | |
| Аммиак, NH3 | 0, 76 | |
| Водород, Н2 | 0, 09 | |
| Аргон, Ar | 1, 79 | |
| Кислород, О2 | 1, 43 | |
| Азот, N2 | 1, 25 | |
| Оксид азота (II), окись азота, NO | 1, 34 | |
| Оксид азота (I), закись азота, N2O | 1, 96 | |
| Двуокись азота, оксид азота (IV), NO2 | 2, 05 | |
| Окись углерода, оксид углерода (II), СО | 1, 25 | |
| Хлористый водород, HCl | 1, 63 | |
| Метан, СН4 | 0, 71 | |
| Гелий, Не | 0, 18 | |
| Сероводород, H2S | 1, 52 | |
| Неон, Ne | 0, 90 | |
| Криптон, Kr | 3, 74 | |
| Озон, O3 | 2, 14 | |
| Ксенон, Xe | 5, 86 |
|
Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений… |
Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета… |
Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где… |
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса… |
|
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно… ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ Кишечный шов (Ламбера, Альберта, Шмидена, Матешука) Кишечный шов– это способ соединения кишечной стенки. |