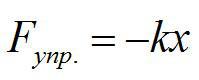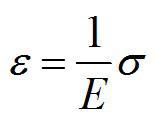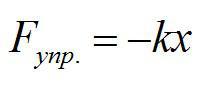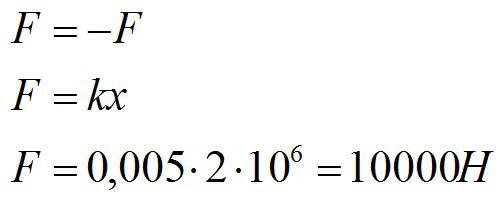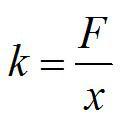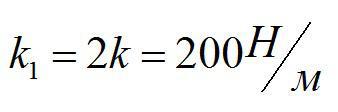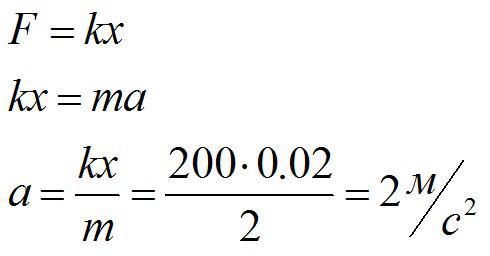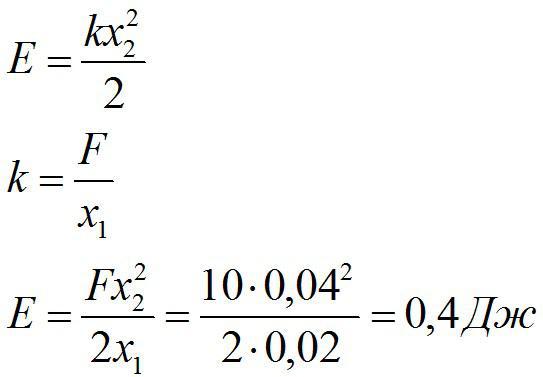Закон гука задачи егэ - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На сколько сантиметров растянется пружина, жёсткость которой под действием силы 100 H? Пружину считайте идеальной.

На рисунке изображен лабораторный динамометр.

Шкала проградуирована в ньютонах. Каким будет растяжение пружины динамометра, если к ней подвесить груз массой 200 г? (Ответ дайте в сантиметрах.) Ускорение свободного падения считать равным 10 м/с².

Под действием силы 4,5 Н пружина удлинилась на 6 см. Чему равен модуль силы, под действием которой удлинение этой пружины составит 4 см? (Ответ дайте в ньютонах.)

На сколько растянется пружина жесткостью под действием силы 1000 Н? (Ответ дайте в сантиметрах.)

Пройти тестирование по этим заданиям

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 79 1–20 | 21–40 | 41–60 | 61–79

Добавить в вариант

На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины? (Ответ дайте в ньютонах на метр.)

Источник: Демонстрационная версия ЕГЭ—2013 по физике.

На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?

Ответ запишите в ньютонах на метр.

На рисунке представлен график зависимости модуля силы упругости, возникающей при растяжении пружины, от ее деформации. Какова жесткость этой пружины? (Ответ дайте в ньютонах на метр.)

На рисунке представлен график зависимости модуля силы упругости пружины от величины её деформации. Определите жёсткость пружины. Ответ дайте в ньютонах на метр.

На гладкой горизонтальной поверхности находится пружина, прикреплённая одним концом к вертикальной стене. Если к свободному концу пружины приложить некоторую горизонтально направленную силу, то в равновесном состоянии её длина будет равна 7 см. При увеличении модуля силы на 0,4 Н длина пружины в равновесном состоянии увеличивается на 1 см. Какова жёсткость этой пружины?

В лёгкий сосуд наливают 500 г воды и подвешивают его к пружине, прикреплённой другим концом к потолку, Затем в дне сосуда открывают отверстие, через которое вода медленно вытекает. На рисунке изображён график зависимости длины l пружины от времени t. Используя этот график, определите жёсткость пружины. (Ответ выразите в ньютонах на метр и округлите до целого числа.)

Динамометр лежит на гладком столе (на рисунке показан вид сверху). Корпус динамометра привязан лёгкой нитью N к вбитому в стол гвоздю, а к крюку динамометра приложена постоянная сила. Чему равен модуль силы натяжения нити N? (Ответ дайте в ньютонах.)

Нерастянутая пружина имеет длину 20 см. Для того чтобы растянуть эту пружину на 2 см, потребовалось приложить к двум её концам равные по модулю силы, направленные противоположно друг другу вдоль оси пружины. Чему станет равна длина этой пружины, если увеличить модуль каждой из приложенных сил в 5 раз, не меняя их направления? Для пружины справедлив закон Гука. Ответ дайте в сантиметрах.

Пружину, соединенную с двух сторон пластинами массой m, поставили на горизонтальную площадку (см. рис.). Затем на верхнюю пластину положили груз массой M  =  500 г так, что ось пружины осталась вертикальной. После этого резким ударом в горизонтальном направлении груз сбросили с пластины. Пренебрегая трением груза о пластину, определите, какой может быть масса пластины m, чтобы нижняя пластина оторвалась от площадки?

Какие законы Вы используете для описания движения пружины и тел? Обоснуйте их применение к данному случаю.

Источник: ЕГЭ по физике 24.07.2020. Резервная волна. Вариант 1 (Часть С)

Сосуд разделён на две части подвижным поршнем, который движется без трения относительно стенок сосуда. В правой части сосуда есть отверстие. Поршень соединен с правым краем сосуда пружиной, в начальном положении она растянута. В левой части сосуда имеется отверстие, плотно закрытое пробкой. Объяснить, как изменится положение поршня, если вынуть пробку.

Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи, ЕГЭ по физике 06.06.2022. Основная волна. Центр

На графике приведена зависимость модуля силы упругости F растянутой пружины от величины ее растяжения Найти период свободных колебаний груза массой 0,5 кг, подвешенного на этой пружине. Ответ укажите в секундах с точностью до одного знака после запятой.

Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.

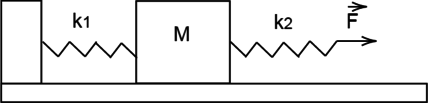
Кубик массой 2 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рис.). Левая пружина жёсткостью k₁ = 500 Н/м сжата на 3 см. С какой силой правая пружина действует на кубик? Ответ приведите в ньютонах.

Пружина жёсткостью 2·10⁴ Н/м одним концом закреплена в штативе. На какую величину она растянется под действием силы 400 Н? Ответ приведите в сантиметрах.

Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 3

Установите взаимосвязь между физическим явлением и фамилией физика, в честь которого назван закон, описывающей это явление.

ФИЗИЧЕСКОЕ ЯВЛЕНИЕ

А)  Электромагнитная индукция

Б)  Взаимосвязь между силой и деформацией

УЧЁНЫЙ

1)  Лоренц

2)  Фарадей

3)  Ньютон

4)  Гук

К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Нерастянутая пружина имеет длину 30 см. Для того чтобы сжать эту пружину на 1,5 см, потребовалось приложить к двум её концам равные по модулю силы, направленные противоположно друг другу вдоль оси пружины. Чему станет равна длина этой пружины, если увеличить модуль каждой из приложенных сил в 6 раз, не меняя их направления? Для пружины справедлив закон Гука. Ответ дайте в сантиметрах.

Определите силу, под действием которой пружина жёсткостью 200 Н/м удлинится на 5 см.

Источник: Демонстрационная версия ЕГЭ−2017 по физике

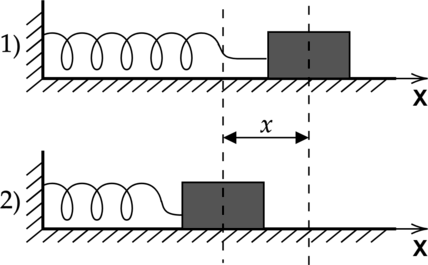
Невесомая пружинка находится на гладкой горизонтальной поверхности и одним концом прикреплена к стене (см. рис.). В некоторый момент времени пружинку начинают деформировать, прикладывая к её свободному концу А внешнюю силу и равномерно перемещая точку А.

Установите соответствие между графиками зависимостей физических величин от координаты точки А x и этими величинами. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ЗАВИСИМОСТЬ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ ОТ КООРДИНАТЫ ТОЧКИ А

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

1)  Потенциальная энергия пружины

2)  Модуль силы упругости

3)  Проекция силы упругости

4)  Проекция внешней силы

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

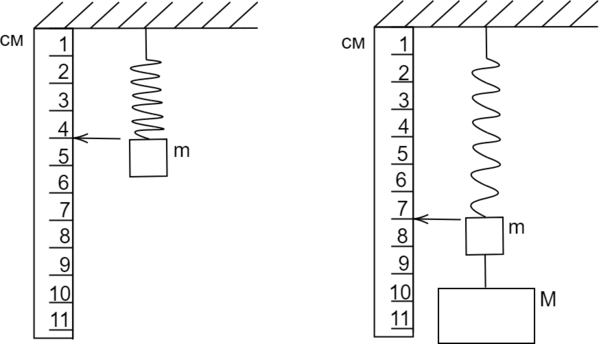
На рисунке 1 изображены две лёгкие пружины с различными коэффициентами жёсткости (k₁  =  200 Н/м и k₂  =  500 Н/м), соединённые с грузами различных масс. Пружины не деформированы. Затем свободный (левый) конец этой конструкции прикрепляют к потолку (см. рисунок 2).

Установите соответствие между физическими величинами и их значениями в СИ. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

А)  сумма масс грузов

Б)  отношение удлинений нижней и верхней пружин

ЗНАЧЕНИЕ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ В СИ

1)  0,8

2)  1,25

3)  2,125

4)  2,5

Всего: 79 1–20 | 21–40 | 41–60 | 61–79

Источник

Задачи на силу упругости с решениями

Формулы, используемые на уроке «ЗАДАЧИ на силу упругости с решениями»

Название величины	Обозначение	Единицы измерения	Формула

Сила упругости	F_упр	H	F_упр = –kx F_упр = k•Δl
Коэффициент упругости (жесткость)	k	H/м, кг/с²	k = ES/L
Модуль Юнга (модуль упругости)	E	Н/м²	E = σ/ε

Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Под действием груза в 200 Н пружина динамометра удлинилась на 0,5 см. Каково удлинение пружины под действием груза в 700 Н?

ОТВЕТ: 1,75 см.

Задача № 2.
Под действием силы давления вагона 50 кН буферные пружины между вагонами сжимаются на 1 см. С какой силой давит вагон, если пружины сжались на 4 см?

ОТВЕТ: 200 кН.

Задача № 3.
Резиновая лента удлинилась на 10 см под действием силы 10 Н. Какова ее жесткость?

ОТВЕТ: 100 Н/м.

Задача № 4.
Пружина без нагрузки длиной 20 см имеет коэффициент жесткости 20 Н/м. Какой станет длина пружины под действием силы 2 Н?

ОТВЕТ: на 0,1 м.

Задача № 5.
На сколько удлинится пружина под нагрузкой 12,5 Н, если под нагрузкой в 10 Н пружина удлинилась на 4 см?

ОТВЕТ: на 5 см.

Задачи на силу упругости

Задача № 6.
Какой груз нужно подвесить к пружине, жесткость которой 1000 Н/м, чтобы растянуть ее на 10 см?

ОТВЕТ: m ≈ 10 кг.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 7.
Грузовик взял на буксир легковой автомобиль «Волга» массой m = 2 т и, двигаясь равноускоренно, за 50 с проехал путь 400 м. На сколько удлинился при этом трос, соединяющий автомобили, если его жесткость 2 • 10⁶ Н/м? Трением пренебречь.

ОТВЕТ: на 0,32 мм.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 8.
На рисунке приведен график зависимости удлинения резинового жгута от модуля приложенной к нему силы. Найти жесткость жгута.

ОТВЕТ: 10 Н/м.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 9.
Две пружины равной длины, скрепленные одними концами, растягивают за свободные концы руками. Пружина жесткостью 200 Н/м удлинилась на 4 см. Какова жесткость второй пружины, если ее удлинение равно 2 мм?

ОТВЕТ: 4000 Н/м.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Краткая теория к теме
«Задачи на силу упругости»

В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации. Виды упругих деформаций: растяжение, сжатие, кручение, изгиб, сдвиг, срез.

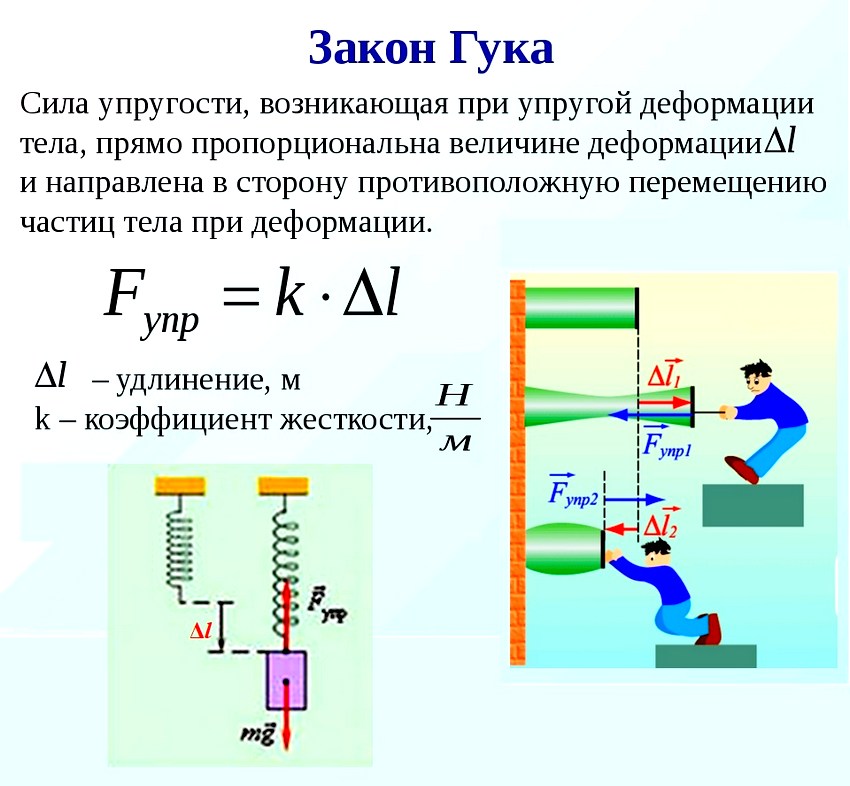
Силы упругости — силы, возникающие при деформации тела и направленные в сторону, противоположную деформации. При небольших деформациях растяжения или сжатия силу упругости можно определить по закону Гука: F_упр = –kx, где x — удлинение/сжатие тела (всегда положительное значение), k — коэффициент пропорциональности (коэффициент упругости), названный жесткостью тела Знак «минус» в законе означает, что сила упругости всегда направлена в сторону, противоположную деформации. Единицы измерения жесткости тела в СИ: 1 Н/м.

В некоторых учебниках и задачниках закон Гука выражают формулой F_упр = k • Δl. В этом случае: Δl — удлинение/сжатие тела (всегда отрицательное значение), k — коэффициент упругости (жесткость) тела.

Иногда, силу упругости, возникающую при деформации опоры, называют силой реакции опоры и обозначают буквой N. Силу упругости, возникающую при деформации нити или каната, называют силой натяжения нити (каната) и обозначают буквой Т.

Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела. Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным. Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.

Конспект урока по физике «ЗАДАЧИ на силу упругости». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:

Вернуться к Списку конспектов по физике для 7-11 классов
Найти конспект через Кодификатор ОГЭ по физике
Найти конспект через Кодификатор ЕГЭ по физике

Источник

Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.

Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.

Сила упругости и закон Гука: определения

Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.

Примеры действия силы упругости:

пружины сжимаются и разжимаются в матрасе;
мокрое белье колышется на натянутой веревке;
лучник натягивает тетиву, чтобы выпустить стрелу.

Простейшие деформации – деформации растяжения и сжатия.

Закон Гука:

Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.

Коэффициент k – жесткость материала.

Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:

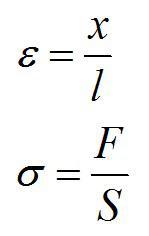
Сила упругости и закон Гука: определения

S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.

Здесь Е – модуль Юнга, зависящий от свойств материала.

Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.

Вопросы на силу упругости и закон Гука

Вопрос 1. Какие бывают деформации?

Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.

Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?

Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.

Вопрос 3. Как направлена сила упругости?

Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.

Вопрос 4. Какую природу имеет сила упругости?

Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.

Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?

Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.

Задачи на силу упругости и закон Гука с решениями

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задача №1. Расчет силы упругости

Условие

Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.

Решение

Запишем закон Гука:

По третьему закону Ньютона:

Ответ: 10 кН.

Задача №2. Нахождение жесткости пружины

Условие

Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?

Решение

По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.

Ответ: 200 Н/м

При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.

Задача №3. Нахождение ускорения тела

Условие

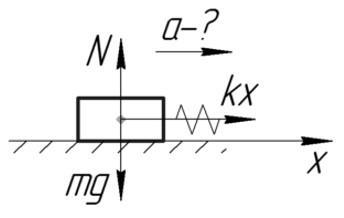
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.

Решение

За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:

Ответ: 2 м/с^2.

Задача №4. Нахождение жесткости пружины по графику

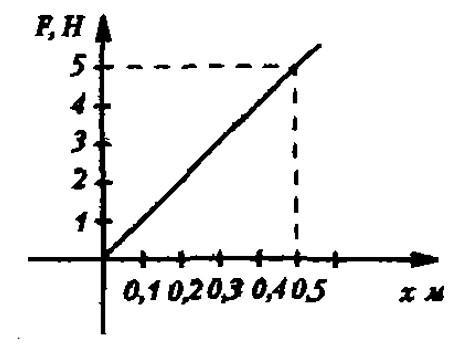
Условие

На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.

Решение

Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.

Ответ: k=10 Н/м.

Задача №5. Определение энергии деформации

Условие

Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.

Решение

Энергия сжатой пружины равна:

Ответ: 0,4 Дж.

Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Сила упругости

Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.

Понятие о деформациях

Деформация — это изменение формы и размеров тела.

К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.

Деформации бывают упругими и пластическими.

Закон Гука

Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.

Единицы измерения коэффициента жесткости: (k=)[Н/м].

Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.

На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)

Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]

Ответ: 7,5

К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)

Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]

Ответ: 5

Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.

Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]

Ответ: 100

Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.

После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]

Ответ: 7500

К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.

После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]

Ответ: 1

К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.

Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]

Ответ: 3,6

Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.

По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]

Ответ: 400

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Сила упругости. Закон Гука

Закон Гука: Ut tensio sic vis — каково растяжение, такова и сила. Закон выражает зависимость между размерами малых деформаций тел и силами или силой, вызывающей данные деформации. Его можно записать так: . Здесь — сила, воздействующая на тело, она может как сжимать тело, так и растягивать его, — жесткость материала — коэффициент, разный для разных материалов. Чем он больше, тем жестче материал и его труднее сжать или растянуть. — это удлинение. Вообще в формуле присутствует знак «минус»: F=-k*x . Он свидетельствует о том, что сила упругости всегда направлена в сторону, противоположную деформации.

Также закон Гука можно записать и в другой форме: . В этой форме закона Гука — нормальное напряжение в поперечном сечении (нормальное — значит, перпендикулярное срезу) — это, по сути, плотность силы: (S — площадь среза, или поперечного сечения). Е — коэффициент, называемый Модулем Юнга — его можно определить по справочнику для разных материалов, — относительное удлинение, .

Задачи.

1. На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен (не забываем массу представить в единицах СИ — килограммах): Н. Тогда по закону Гука определим модуль удлинения лески:

Выражаем модуль удлинения:

Подставим числа, жесткость лески при этом выражаем в Ньютонах: $delim{|}{x}{|}=3/{0,3*10^3}=10^{-2}=0,01$ м, или 1 см.

Ответ: 1 см.

2. На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной 1 и медной 2 проволок равной длины и диаметра. Сравнить жесткости проволок.

Задача 2

На рисунке видно, что при воздействии одной и той же силы F удлинение стальной проволоки вдвое меньше, чем медной. Значит, стальную растянуть вдвое труднее — или ее жесткость вдвое больше.

3. Найти удлинение буксирного троса жесткостью 100 кН/м при буксировке автомобиля массой 2 тонны с ускорением 0,5 м/с*с. Трением пренебречь.

В этой задаче также сначала определим силу. Силу, которая действует на конец троса со стороны буксируемого автомобиля, можно определить по второму закону Ньютона: ведь ускорение, с которым двигается тело, прямо пропорционально силе и обратно пропорционально массе тела, в данном случае выражение записано для модуля силы: F=ma . Выразив массу машины в килограммах, определим этот модуль силы: Н. Тогда модуль удлинения троса , вычисляем:

$delim{|}{x}{|}=10^3/{100*10^3}=1/100$ м, или 1 см.

Ответ: 1 см.

4. Подвешенное к тросу тело массой 10 кг поднимается вертикально. С каким ускорением движется тело, если трос жесткостью 59 кН/м удлинился на 2 мм?

Это обратная двум предыдущим задача. Здесь сначала мы определим модуль силы упругости:

, при подстановке важно не забывать применять в расчетах величины, представленные в единицах СИ: $F=59*10^3*2*10^{-3}=118$ .

Зная силу, можно определить и ускорение (модуль ускорения): для этого воспользуемся вторым законом Ньютона: F-mg=ma ,откуда

Таким образом, получили ответ: 2 м/c*c

5. С каким максимальным ускорением можно поднимать с помощью веревки тело массой 200 кг, если веревка выдерживает неподвижный груз массой 240 кг?

Веревка выдерживает висящее тело массой 240 кг — а на висящее тело действует сила тяжести, равная Н (если принять равным 10 ускорение свободного падения). Тогда по второму закону Ньютона F-mg=ma такая сила может заставить тело массой 200 кг двигаться с ускорением:.

Ответ: 2 м/c*c

6. Жесткость одной пружины равна k_1 , а другой — k_2 . Какова жесткость пружины, составленной из этих двух пружин, соединенных последовательно?

Запишем для каждой из пружин закон Гука. Для первой: $F=k_1*delim{|}{x_1}{|}$ .

Для второй: $F=k_2*delim{|}{x_2}{|}$ — иными словами, пружины с разной жесткостью можно растянуть по-разному при воздействии одной и той же силы. Первую можно удлинить так: $delim{|}{x_1}{|}=F/{k_1}$ , вторую же можно удлинить так: $delim{|}{x_2}{|}=F/{k_2}$ Наконец, соединим их и снова будем растягивать с той же силой: . Удлинение такой составной пружины сложится из удлинений первой и второй: $delim{|}{x_1}{|}+delim{|}{x_2}{|}=F/{k_1}+F/{k_2}=delim{|}{x}{|}$ .

Вынесем за скобку силу: $delim{|}{x}{|}=F(1/{k_1}+1/{k_2})$ и приведем к общему знаменателю сумму в скобках:

$delim{|}{x}{|}=F({k_1}+{k_2})/{k_1*k_2}$

Отсюда $F=delim{|}{x}{|}*{{k_1}*{k_2}}/{k_1+k_2}$ , а жесткость составной пружины $k={{k_1}*{k_2}}/{k_1+k_2}$

7. Жесткость данного куска проволоки равна k. Чему равна жесткость половины этого куска проволоки?

Эту задачу можно решить, воспользовавшись второй формой закона Гука. Тогда для целой проволоки имеем: ${sigma_1}=E{varepsilon_1}$ , а для половины ${sigma_2}=E{varepsilon_2}$ .

Так как это одна и та же проволока, то модуль Юнга у обоих кусков одинаков. Также одинаково у обоих кусков и нормальное напряжение: ведь на оба куска воздействуют с одной и той же силой, и сечение также одинаково. Поэтому из закона Гука заключаем, что относительное удлинение также одинаково: ${varepsilon_1}={varepsilon_2}$ . Для целого куска относительное удлинение равно: ${varepsilon_1}={Delta{x_1}}/x$ , а для второго куска ${varepsilon}={Delta{x_2}}/{{1/2}x}$ . Приравняем оба выражения, тогда:

${Delta{x_1}}/x={Delta{x_2}}/{{1/2}x}$ , или ${Delta{x_1}}=2{Delta{x_2}}$ .

Теперь вспомним первую форму закона: $F=k_1*delim{|}{x_1}{|}=k_2*delim{|}{x_2}{|}$ .
Подставив соотношение относительных удлинений, полученное выше, имеем: $k_1*2*delim{|}{x_2}{|}=k_2*delim{|}{x_2}{|}$ , или , то есть жесткость половинки вдвое больше, чем целой проволоки — действительно, чем короче кусок, тем труднее его растянуть.

8. Жесткость пружины равна 50 Н/м. Если с помощью этой пружины равномерно тянуть по полу коробку массой 2 кг, то длина пружины увеличивается с 10 до 15 см. Какова сила упругости в этом случае? Чему равна сила трения коробки о пол?

Удлинение пружины здесь равно 15-10=5 см. Выразим в метрах: 0,05 м. Тогда по закону Гука: $F=k*delim{|}{x_1}{|}=50*0,05=2,5$ Н — силу упругости нашли. Теперь определим силу трения о пол. Какие силы действуют на коробку? 1. Сила тяжести. 2. Сила реакции опоры. 3. Сила, с которой коробку тянут. 4. Сила трения. Так как сила тяжести уравновешена силой реакции опоры, то остались две силы, очевидно, что между ними также равновесие, тогда сила трения равна силе упругости, и равна 2,5Н.

Ответ: 2,5 Н.

Источник

Задачи на применение закон Гука с ответами

1.
Под действием силы 4,5 Н
пружина удлинилась на 6 см. Чему равен модуль силы, под действием которой
удлинение этой пружины составит 4 см? (Ответ дайте в ньютонах.)

Ответ: 3 Н.

2.
Две пружины растягиваются
одинаковыми силами F. Жёсткость первой пружины k ₁в 1,5 раза больше жесткости второй пружины k ₂.Чему равно отношение удлинений пружин

∆ l ₂/∆l ₁?

Ответ: 1,5

3.
На сколько растянется пружина
жесткостью 10 ⁴ Н/м под действием силы 1000 Н? (Ответ дайте
в сантиметрах.)

Ответ: 10 см

4.
При помощи пружинного динамометра
поднимают с ускорением a= 2,5 м/с²,
направленным вверх, груз массой 2 кг. Определите модуль удлинения пружины
динамометра, если жесткость пружины k
= 1000 Н/м.

Ответ 2,5 см.

5.
Груз массой 3 кг растягивает пружину на 5
см, каким должен быть груз, который растянет эту пружину на 8 см?

Ответ:
4,8 кг

6.
   Подвешенное к тросу тело массой 10 кг
поднимается вертикально. С каким ускорением движется тело, если трос жесткостью
59 кН/м удлинился на 2 мм?

Ответ:
1,8 м/с²

7.Какова
жесткость пружины, если груз массой 10 кг растягивает пружину на 0,1 м.
Определите, какой груз надо подвесить к пружине, чтобы растянуть её на 20 см?

Ответ:
1000 Н/м, 20 кг

8.
С каким ускорением движется тело массой 2 кг по горизонтальной поверхности с
помощью пружины жесткостью 100 Н/м, если пружина во время движения удлинилась
на 1 см. Трением пренебречь.

Ответ:
0,5 м/с²

9.
Груз массой 2 кг тянут за пружину вверх. Определите растяжение пружины, если
груз движется с ускорением 3 м/с². Коэффициент жесткости пружины
равен 1300 Н/м

Ответ:
0,02 м

10. На рисунке приведен график зависимости
модуля силы упругости от удлинения пружины. Чему равна жесткость пружины?

Ответ: 10 Н/м.

11. Пружину, жесткость которой 100 Н/м
разрезали на две части. Чему равна жесткость каждой пружины?

Ответ : 200 Н/м.

Источник

Задачи на силу упругости с решениями

Название величины

Обозначение

Единицы измерения

Формула

Сила упругости

Fупр

H

Fупр = –kx Fупр = k•Δl

Коэффициент упругости (жесткость)

k

H/м,

кг/с2

k = ES/L

Модуль Юнга (модуль упругости)

E

Н/м2

E = σ/ε

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория к теме «Задачи на силу упругости»

Сила упругости и закон Гука: определения

Вопросы на силу упругости и закон Гука

Задачи на силу упругости и закон Гука с решениями

Задача №1. Расчет силы упругости

Задача №2. Нахождение жесткости пружины

Задача №3. Нахождение ускорения тела

Задача №4. Нахождение жесткости пружины по графику

Задача №5. Определение энергии деформации

Сила упругости

Сила упругости. Закон Гука

F_упр

F_упр = –kx
F_упр = k•Δl

кг/с²

Н/м²

Краткая теория к теме
«Задачи на силу упругости»