Закон изменения скорости егэ математика

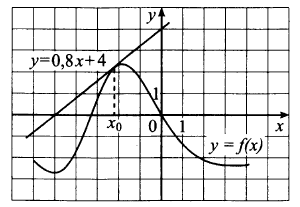
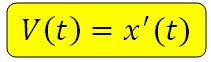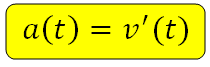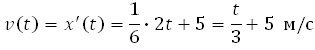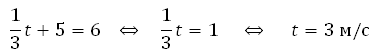15 мая 2014

Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.

На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.

Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.

Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:

[v={S}’={x}’left( t right)]

Точно так же мы можем посчитать и ускорение:

[a={v}’={{S}’}’={{x}’}’left( t right)]

Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.

Давайте посмотрим, как это работает при решении реальных задач.

Пример № 1

Материальная точка движется по закону:

[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.

Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.

[v={S}’={x}’left( 2 right)]

Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.

Давайте решать. В первую очередь, посчитаем производную:

[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]

Нам требуется найти производную в точке 2. Давайте подставим:

[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]

[=-16+32-12+5=9]

Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.

Пример № 2

Материальная точка движется по закону:

[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]

где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?

Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.

В первую очередь, вновь ищем производную:

[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]

[{x}’left( t right)={{t}^{2}}-8t+19]

От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:

[{{t}^{2}}-8t+19=3]

[{{t}^{2}}-8t+16=0]

[{{left( t-4 right)}^{2}}=0]

[t-4=0]

[t=4]

Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.

Ключевые моменты

В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.

Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.

Смотрите также:

1. Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
2. ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
3. Схема Бернулли. Примеры решения задач
4. Комбинаторика в задаче B6: средний тест
5. Как решать задачи про летающие камни?
6. B4: счетчики на электричество

    Физический смысл производной. В состав ЕГЭ по математике входит группа задач для решения которых необходимо знание и понимание физического смысла производной. В частности, есть задачи, где дан закон движения определённой точки (объекта), выраженный уравнением и требуется найти его скорость в определённый момент времени движения, либо время, через которое объект приобретёт определённую заданную скорость. Задачи очень простые, решаются  они  в одно действие. Итак:

Пусть задан закон движения материальной точки x (t) вдоль координатной оси, где x координата движущейся точки, t – время.

Скорость в определённый момент времени – это производная координаты по времени. В этом и состоит механический смысл производной.

Аналогично, ускорение – это производная скорости по времени: 

Таким образом, физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого-либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество).

Кроме того, необходимо знать таблицу производных (знать её нужно также, как таблицу умножения) и правила дифференцирования. Если конкретно, то для решения оговоренных задач необходимо знание первых шести производных (см. таблицу):

Рассмотрим задачи:

Материальная точка движется прямолинейно по закону  

x (t) = t² – 7t – 20

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.

Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.)

Найдем закон изменения скорости:  v (t) = x′(t) = 2t – 7 м/с.

При t = 5 имеем:

Ответ: 3

Решить самостоятельно:

Материальная точка движется прямолинейно по закону x (t) = 6t² – 48t + 17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 c.

Посмотреть решение

Материальная точка движется прямолинейно по закону  x (t) = 0,5t³ – 3t² + 2t, где x — расстояние от точки отсчета в метрах,  t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.

Посмотреть решение

Материальная точка движется прямолинейно по закону

x (t) = –t⁴ + 6t³ + 5t + 23

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.

Посмотреть решение

Материальная точка движется прямолинейно по закону

x (t) = (1/6) t² + 5t + 28

где x — расстояние от точки отсчета в метрах,  t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?

Найдем закон изменения скорости:

Для того, чтобы найти, в какой момент времени t скорость была равна 3 м/с,  необходимо решить уравнение:

Ответ: 3

Решите самостоятельно:

Материальная точка движется прямолинейно по закону  x (t) = t² – 13t + 23, где x — расстояние от точки отсчета в метрах,  t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?

Посмотреть решение

Материальная точка движется прямолинейно по закону

x (t) = (1/3) t³ – 3t² – 5t + 3 

где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?

Посмотреть решение

Отмечу, что ориентироваться только на такой тип задач на ЕГЭ не стоит. Могут совершенно неожиданно ввести задачи обратные представленным. Когда дан закон изменения скорости и будет стоять вопрос о нахождении закона движения.

Подсказка: в этом случае необходимо найти интеграл от функции скорости (это так же задачи в одно действие). Если потребуется найти пройденное расстояние за определённый момент времени, то необходимо подставить время в полученное уравнение и вычислить расстояние. Впрочем, мы такие задачи тоже будем разбирать, не пропустите! Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Поиск

Всего: 20    1–20

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 20    1–20

ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 6

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 6 ЕГЭ профиль проверяет умение применять производную для решения прикладных задач. Такие задачи часто встречаются в физике и технических областях науки.

Задание состоит из текстовой задачи на определение физического, геометрического смысла производной, промежутков возрастания и убывания функции по её графику и графику её производной или первообразной. Ответом является целое число или конечная десятичная дробь.

При подготовке необходимо повторить правила нахождения производной, физический и геометрический смысл производной, понятие возрастания и убывания функции, понятие первообразной.

План выполнения задания № 6:

1. Внимательно прочитайте задачу.
2. Рассмотрите график. Определите, какой из графиков вам дан: функции, производной функции или первообразной функции. От ответа на данный вопрос зависит ход решения задачи.
3. Определите по графику необходимые значения.
4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

1) Задачи на Физический смысл производной

Задачи на применение физического смысла производной состоят из текста и выражения, описывающего уравнение движения материальной точки или тела.

Производная перемещения по времени выражает скорость движения: v(t) = x'(t) = at + v₀.
Производная скорости по времени выражает ускорение движения: a(t) = v'(t).

Задача № 6 (1). Материальная точка движется прямолинейно по закону x(t) = 2t² – 8t – 9, где х — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в м/с) в момент времени t = 5с.
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 4t – 8.
При t = 5 имеем: v(5) = 4 • 5 – 8 = 12.
Ответ: 12.
Комментарий. Иногда в ответе получаются отрицательные числа, которые учащиеся рассматривают как ошибочный ответ.

Задача № 6 (2). Тело движется прямолинейно по закону: x(t) = 2t³ + t – 1. В какой момент времени (в секундах) его ускорение будет равно 12 м/с²?
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 6t² + 1.
Ускорение — это производная скорости по времени: a(t) = v'(t) = 12t.
Чтобы найти, в какой момент времени ускорение было 12 м/с², решим уравнение: 12t = 12. Отсюда t = 1 c.
Ответ: 1.
Комментарий. Обратите внимание: в задании нужно найти, в какой момент времени ускорение (не скорость!) будет равно 12 м/с².

2) Задачи на Геометрический смысл производной

Задание ориентировано на умение выпускников читать и анализировать графики, содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.

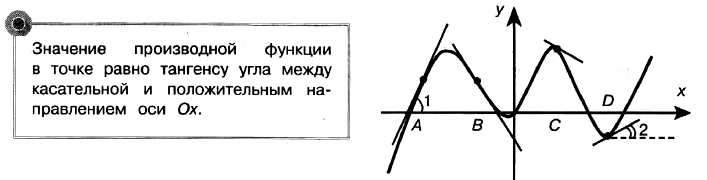
Геометрический смысл производной: угловой коэффициент касательной к графику функции в точке с абсциссой х₀ равен производной этой функции в точке х₀.
Геометрический смысл производной: k = tg a = f'(x)

Производная функции в точке с абсциссой х есть тангенс угла наклона касательной, проведённой к графику этой функции в точке (х₀; f(x₀)). При tg a > 0 производная функции положительна, при tg a < 0 производная отрицательна. При tg a = 0 производная равна нулю.

Точка х₀ называется точкой максимума (минимума) функции, если существует такая окрестность точки х₀, что для любого х из этой окрестности верно неравенство f(x) < f(x₀)  (f(x) > f(x₀)).

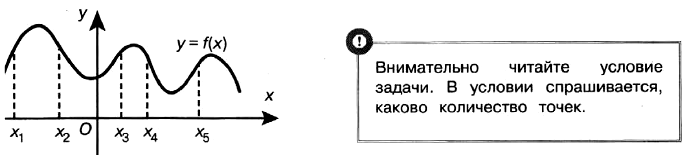
Задача № 6 (3). На рисунке изображён график функции y = f(x) и отмечены пять точек на оси абсцисс: х₁, х₂, х₃, х₄, х₅. В скольких из этих точек производная функции f(x) отрицательна?

Решение: Производная функции отрицательна в тех точках, которые принадлежат участкам убывания функции. Это точки х₂, х₄ — всего 2 точки.
Ответ: 2.

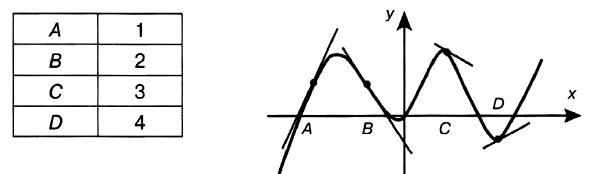
Задача № 6 (4). На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. Пользуясь графиком, определите, в какой из данных точек значение производной наибольшее. В ответе укажите число, которое ей соответствует по таблице.

Решение: Производная функции положительна в точках А и D, так как в данных точках функция возрастает.

Угол 1 больше угла 2, значит, тангенс первого угла больше тангенса второго угла, соответственно, значение производной в точке А больше значения производной в точке D.
Ответ: 1.

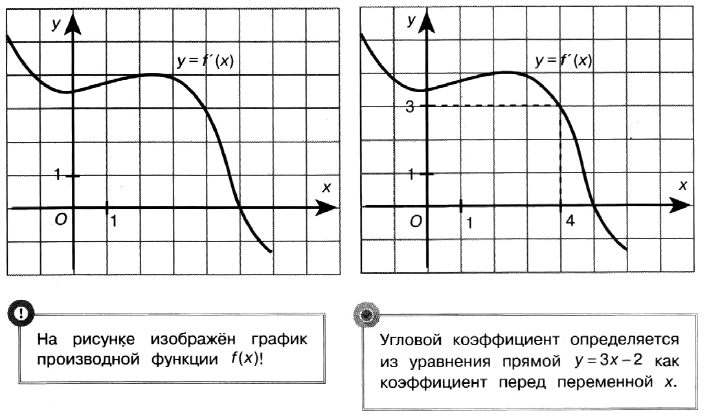
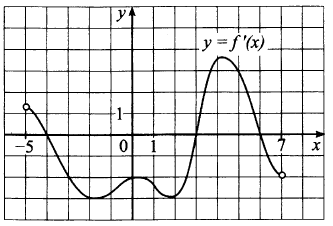
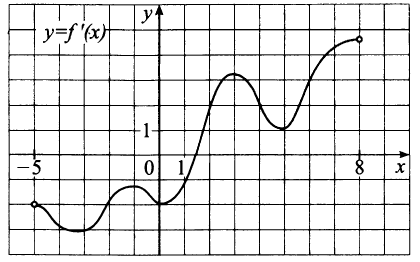
Задача № 6 (5). На рисунке изображён график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику параллельна прямой у = 3х–2 или совпадает с ней.

Решение: Поскольку касательная параллельна прямой у = 3х – 2 или совпадает с ней, она имеет угловой коэффициент, равный 3 (у’ = 3). Найдём, при каких х производная принимает значение 3. Из графика видно, что значению у = 3 соответствует точка х = 4.
Ответ: 4.

3) Задачи на Применение
производной к исследованию функций

Задание содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.

• Если функция y = f(x) имеет экстремум в точке х₀, то в этой точке производная равна нулю или не существует.
• Если f'(x) = 0 и при переходе через точку х₀ значения производной меняют знак с «+» на «–», то х₀ — точка максимума.
• Если f'(x) = 0 и при переходе через точку х₀ значения производной меняют знак с «–» на «+», то х₀ — точка минимума.
• Если f'(x) = 0 и при переходе через точку х₀ значения производной не меняют знак, то х₀ не является точкой экстремума.
• Если в каждой точке х некоторого промежутка f'(х) > 0, то функция f(x) возрастает на этом промежутке.
• Если в каждой точке х некоторого промежутка f'(х) < 0, то функция f{x) убывает на этом промежутке.

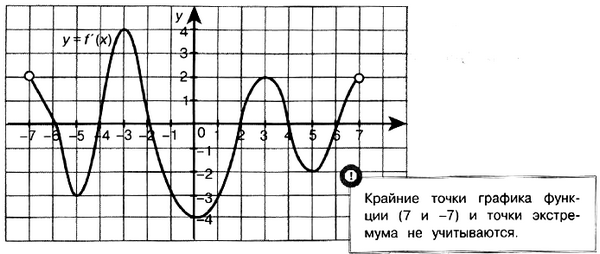
Задача № 6 (6). На рисунке изображён график производной функции f(x), определённой на интервале (–7; 7). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение: Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых её производная положительна, то есть промежуткам (–7; –6); (–4; –2); (2; 4); (6; 7). Данные промежутки содержат целые числа –3; 3. Их сумма равна 0.
Ответ: 0.
ПРИМЕЧАНИЕ: В ответе нужно указать сумму целых точек, входящих в промежутки возрастания.

4) Задачи на Первообразную

Функцию y = F(x) называют первообразной для функции y = f(x) на заданном промежутке х, если для всех х из этого промежутка верно равенство F'(x) = f(x).

Если функция y = F(x) является первообразной для функции y = f(x) на некотором промежутке, то и функция y = F(x) + C (С — постоянная) является первообразной для функции f на этом промежутке.

Пусть функция f(x) непрерывна на отрезке [а; b]. Тогда площадь трапеции, ограниченной линиями y = f(x); у = а; у = b и у = 0, равна F(b) – F(a), где F(x) — первообразная функции f(x).

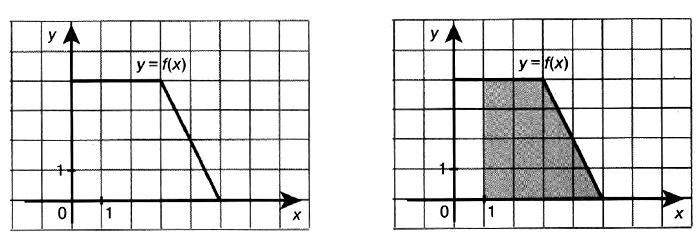
Задача № 6 (7). На рисунке изображён график некоторой функции y = f(x). Пользуясь рисунком, вычислите F(5) – F(1), где F(x) — одна из первообразных функции f(x).

Решение: Разность значений первообразной в точках 5 и 1 равна площади выделенной на рисунке трапеции.
Площадь трапеции ограничена точками 1 и 5.
Площадь трапеции вычисляется по формуле S = h • (a + b)/2.
Из рисунка видно, что а =2, b = 4, h = 4. Значит, F(5) – F(1) = 4 • (2 + 4)/2 = 12.
Ответ: 12.
ПРИМЕЧАНИЕ: Если результат отрицательный или равен нулю, значит, в вычислениях была допущена ошибка.

Тренировочные задания с самопроверкой

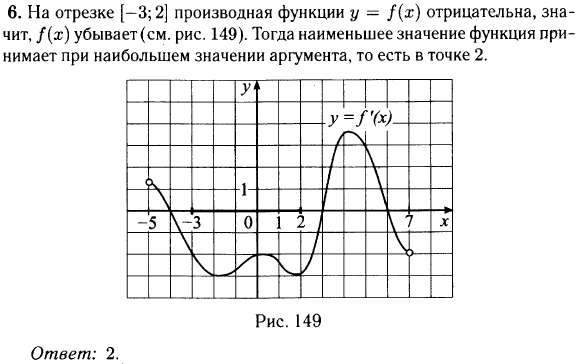
№ 6.1. На рисунке изображён график у = f’(x) – производной функции f(x), определённой на интервале (–5; 7). В какой точке отрезка [–3; 2] f(x) принимает наименьшее значение?

№ 6.2. Прямая у = 5х + 4 параллельна касательной к графику функции у = х² – 4х – 12. Найдите абсциссу точки касания.

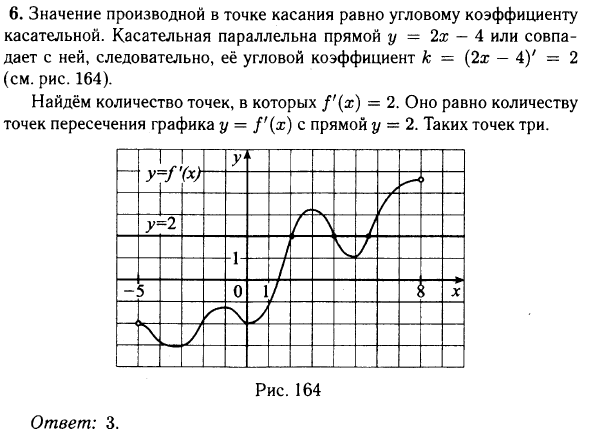
№ 6.3. На рисунке изображён график у = f‘(х) – производной функции f(х), определённой на интервале (–5; 8). Найдите количество точек, в которых касательная к графику функции f(х) параллельна прямой у = 2х – 4 или совпадает с ней.

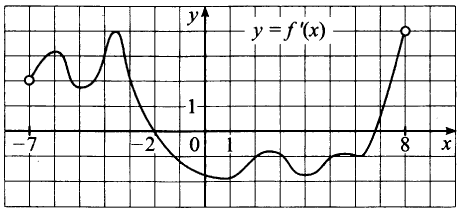
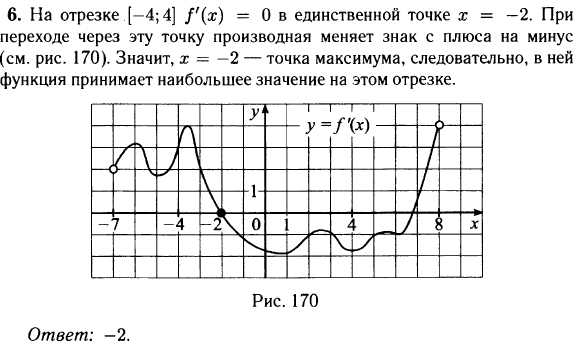
№ 6.4. На рисунке изображён график у = f‘(x) – производной функции f(x), определённой на интервале (–7; 8). Найдите, в какой точке отрезка [–4; 4] функция принимает наибольшее значение.

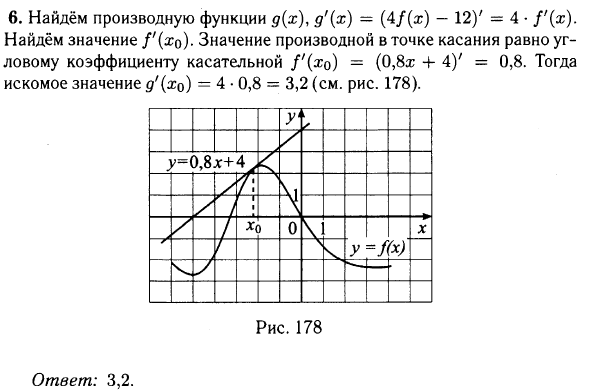
№ 6.5. На рисунке изображены график функции у = f(x) и касательная к этому графику, проведённая в точке x₀. Уравнение касательной показано на рисунке. Найдите значение производной функции g(х) = 4f(x) – 12 в точке x₀.

---

Вы смотрели: ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

Просмотров:
20 370

ЕГЭ Профиль №7. Физический смысл производнойadmin2023-02-16T22:47:46+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №7. Физический смысл производной

Если положение точки при ее движении по числовой прямой задается функцией (S = fleft( t right)), где t – время движения, то производная функции S – мгновенная скорость движения в момент времени t: (S’left( t right) = vleft( t right)). По аналогии с этой моделью вообще говорят о том, что производная функции (y = fleft( x right)) — это есть скорость изменения функции. Вторая производная функции S (или первая производная функции v) – мгновенное ускорение в момент времени t:   ({S^{//}}left( t right) = v’left( t right) = aleft( t right)).

Задача 1. Материальная точка движется прямолинейно по закону (xleft( t right) =  — frac{1}{3}{t^2} + 4t + 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени  (t = 3;{text{c}}). Ответ ОТВЕТ: 2. Решение Скорость движения – это производная от пути по времени, то есть, чтобы найти закон изменения скорости нужно вычислить производную от пути (xleft( t right)) по времени  t. Следовательно: (vleft( t right) = x’left( t right) =  — frac{2}{3}t + 4.) Тогда скорость материальной точки в момент (t = 3) с равна: (vleft( 3 right) =  — frac{2}{3} cdot 3 + 4 = 2) м/с. Ответ: 2.
Задача 2. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + 2{t^2} — 15), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 2;{text{c}}). Ответ ОТВЕТ: 12. Решение Скорость движения – это производная от пути по времени, то есть, чтобы найти закон изменения скорости нужно вычислить производную от пути (xleft( t right)) по времени  t. Следовательно: (vleft( t right) = x’left( t right) = {t^2} + 4t.) Тогда скорость материальной точки в момент (t = 2) с равна: (vleft( 2 right) = {2^2} + 4 cdot 2 = 12) м/с. Ответ: 12.
Задача 3. Материальная точка движется прямолинейно по закону (xleft( t right) = {t^4} + 9{t^2} — 3t + 23), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени (t = 1;{text{c}}{text{.}}) Ответ ОТВЕТ: 19. Решение Скорость движения – это производная от пути по времени, то есть, чтобы найти закон изменения скорости нужно вычислить производную от пути (xleft( t right)) по времени  t. Следовательно: (vleft( t right) = x’left( t right) = 4{t^3} + 18t — 3.) Тогда скорость материальной точки в момент (t = 1) с равна: (vleft( 1 right) = 4 cdot {1^3} + 18 cdot 1 — 3 = 19) м/с. Ответ: 19.
Задача 4. Материальная точка движется прямолинейно по закону (xleft( t right) =  — frac{1}{6}{t^2} + 5t — 19), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 4 м/с? Ответ ОТВЕТ: 3. Решение Скорость движения – это производная от пути по времени, то есть, чтобы найти закон изменения скорости нужно вычислить производную от пути (xleft( t right)) по времени  t. Следовательно: (vleft( t right) = x’left( t right) =  — frac{1}{3}t + 5.) Найдём момент времени t, когда скорость материальной точки будет равна 4 м/с: (4 =  — frac{1}{3}t + 5,,,,,, Leftrightarrow ,,,,,t = 3) с. Ответ: 3.
Задача 5. Материальная точка движется прямолинейно по закону (xleft( t right) = frac{1}{3}{t^3} + {t^2} — 9t + 12), где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 15 м/с? Ответ ОТВЕТ: 4. Решение Скорость движения – это производная от пути по времени, то есть, чтобы найти закон изменения скорости нужно вычислить производную от пути (xleft( t right)) по времени  t. Следовательно: (vleft( t right) = x’left( t right) = {t^2} + 2t — 9.) Найдём момент времени t, когда скорость материальной точки будет равна 15 м/с: (15 = {t^2} + 2t — 9,,,,,, Leftrightarrow ,,,,,{t^2} + 2t — 24 = 0,,,,,, Leftrightarrow ,,,,,{t_1} = 4,,,,,{t_2} =  — 6) с. По смыслу задачи  (t ge 0,)  поэтому (t = 4) с. Ответ: 4.
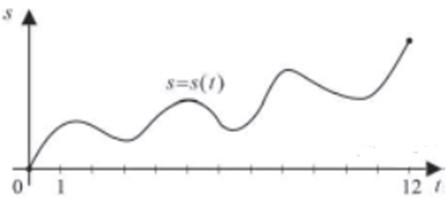
Задача 6. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние S. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте). Ответ ОТВЕТ: 6. Решение Скорость движения – это производная от пути по времени. Так как требуется определить, сколько раз за время движения скорость точки обращалась в ноль, то для этого необходимо определить количество точек экстремума (точек минимума и максимума) функции (Sleft( t right)), которых на графике 6. Ответ: 6.

Физический смысл производной

Определение

Физический смысл производной заключается в том, что мгновенная скорость материальной точки в определенный момент времени $ t_0 $ равна производной закона движения $ s(t_0) $ этой точки в момент времени $ t_0 $: $$ v(t_0) = s'(t_0) $$

Примеры решения

Пример 1

Найти мгновенную скорость движения материальной точки в момент времени $ t_0 = 2 c $, если точка движется по закону $ s(t) = 4t^2+2t+1 $

Решение

Скорость точки равна производной пути по времени: $$ v(t) = s'(t) = (4t^2+2t+1)’ = 8t + 2 $$ Мгновенная скорость в момент времени $ t_0 = 2 $: $$ v(t_0) = v(2) = 8 cdot 2 + 2 = 16 + 2 = 18 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ v = 18 text{м/с} $$

Пример 2

Пусть точка движется прямолинейно по закону $ s(t) = 3t^2-3t — 5 $. В какой момент времени скорость точки будет $ v = 3 $ м/с?

Решение

Используя физический смысл производной, находим закон изменения скорости материальной точки: $$ v(t) = s'(t) = (3t^2-3t-5)’ = 6t — 3 $$ Чтобы найти момент времени $ t_0 $, в который скорость будет равной трём, нужно составить и решить уравнение $ v(t_0) = 3 $: $$ 6t_0 — 3 = 3 $$ $$ 6t_0 = 6 $$ $$ t_0 = 1 $$

Ответ

$$ t_0 = 1 c $$