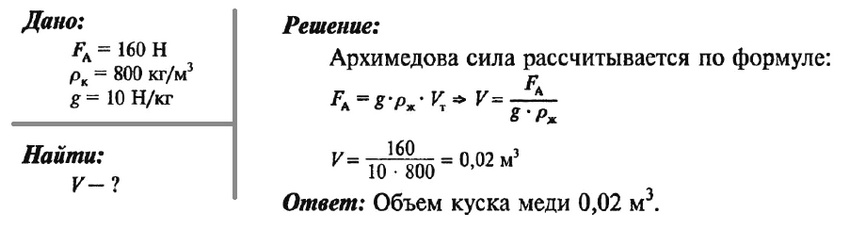Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ответ приведите в килограммах на кубический метр. Ускорение свободного падения принять равным 10 м/с2.
3
В четыре сосуда, вертикальные сечения которых показаны на рисунке, налита вода. Одна клеточка на рисунке соответствует 10 см.
В одном из этих сосудов гидростатическое давление на дно максимально. Чему оно равно? (Ответ дайте в паскалях.) Ускорение свободного падения принять равным 10 м/с2.
4
Кубик из пробки с ребром 10 см опускают в воду. Каково отношение объёма кубика, находящегося над водой, к объёму кубика, находящегося под водой? Плотность пробки 0,25 г/см3.
5
Пустой цилиндрический стеклянный стакан плавает в воде, погрузившись на половину своей высоты. Дно стакана при плавании горизонтально, плотность стекла 2500 кг/м3. Чему равно отношение внутреннего объёма стакана к его наружному объёму? Ответ представьте в виде десятичной дроби, округлив до десятых долей.
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 100 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
К концам лёгкого стержня длиной l, лежащего на клиновидной опоре, установленной на расстоянии от его левого конца, подвешены на невесомых нитях два тяжёлых груза 1 и 2 с плотностями
(слева) и
(справа). Стержень находится в равновесии в горизонтальном положении (см. рис.).
Затем, опустив точку опоры стержня, грузы полностью погрузили в стаканы с жидкостями — водой слева и керосином справа, и при этом равновесие стержня сохранилось. Чему равно отношение плотностей грузов Какие законы Вы использовали для решения этой задачи? Обоснуйте их применимость к данному случаю.
К концам лёгкого стержня длиной l, лежащего на клиновидной опоре, установленной на расстоянии от его левого конца, подвешены на невесомых нитях два тяжёлых груза 1 и 2 с плотностями
(слева) и
(справа). Стержень находится в равновесии в горизонтальном положении (см. рис.).
Затем, опустив точку опоры стержня, грузы полностью погрузили в стаканы с жидкостями — керосином слева и водой справа, опустив точку опоры стержня, и при этом его равновесие сохранилось. Чему равно отношение плотностей грузов Какие законы Вы использовали для решения этой задачи? Обоснуйте их применимость к данному случаю.
На кусок алюминия массой 0,54 кг при полном погружении в воду действует сила Архимеда, равная 2 Н. Чему равна при этом масса вытесненной воды? Ответ дайте в килограммах.
Источник: ЕГЭ по физике 2021. Досрочная волна. Вариант 1
Сейчас люди на праздники стали часто запускать в небо китайские фонарики, представляющие собой лёгкие бумажные мешки с отверстием внизу, в котором на проволочном каркасе крепится кусок пористого материала, пропитанного горючим. После его поджигания фонарик поднимается в небо на большую высоту, а потом может приземлиться вдали от точки старта. В городе, в лесу и при сильном ветре запускать фонарики опасно!
Опишите, основываясь на известных физических законах и закономерностях, процессы, происходящие в течение всех фаз полёта такого фонарика. В чём причина опасности, о которой говорилось выше?
В наше время на дни рождения часто дарят резиновые шарики, надутые гелием, — они не взрывоопасны и имеют довольно большую подъёмную силу. Объясните, основываясь на известных физических законах и закономерностях, происхождение этой подъёмной силы и определите, на сколько она изменится, если вместо гирлянды из 27 шаров, в каждый из которых накачали по 1 молю гелия, надуть тем же количеством гелия один большой шар? Толщина резиновой оболочки у всех шаров одинакова, давление и температура близки к нормальным, а подъёмная сила гирлянды равна 1,52 Н.
В наше время на дни рождения часто дарят резиновые шарики, надутые гелием, – они не взрывоопасны и имеют довольно большую подъёмную силу. Объясните, основываясь на известных физических законах и закономерностях, происхождение этой подъёмной силы и определите, на сколько она изменится, если вместо гирлянды из 8 шаров, в каждый из которых накачали по 1 молю гелия, надуть тем же количеством гелия один большой шар? Толщина резиновой оболочки у всех шаров одинакова, давление и температура близки к нормальным, а подъёмная сила гирлянды равна 0,45 Н.
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см3, плотность жидкости 800 кг/м3, объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите два верных утверждения.
1) Модуль силы Архимеда, действующей на тело, меньше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити равен модулю силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити меньше модуля силы Архимеда, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, равен модулю силы тяжести, действующей на тело.
5) Объём погружённой части тела равен четверти объёма этого тела.
К телу, имеющему внутреннюю герметичную полость, на невесомой нерастяжимой нити привязан сплошной шарик. Система «тело + шарик» плавает в сосуде с жидкостью, не касаясь стенок и дна сосуда. Плотность материала тела и шарика 1,6 г/см3, плотность жидкости 800 кг/м3, объём полости составляет 3/4 объёма тела, объём шарика равен 1/4 объёма тела. Исходя из условия задачи, выберите все верные утверждения.
1) Модуль силы Архимеда, действующей на тело, больше модуля силы Архимеда, действующей на шарик.
2) Модуль силы натяжения нити меньше модуля силы тяжести, действующей на шарик.
3) Модуль силы натяжения нити равен модулю силы тяжести, действующей на тело.
4) Модуль силы тяжести, действующей на шарик, меньше модуля силы тяжести, действующей на тело.
5) Объём погружённой части тела равен 3/4 объёма этого тела.
Тонкий однородный стержень, частично погружённый в воду, удерживается в состоянии равновесия с помощью невесомой нерастяжимой нити (см. рис.). Длина отрезка АВ в два раза меньше длины отрезка ОА.
Выберите все верные утверждения.
1) Модуль силы натяжения нити меньше модуля действующей на стержень силы тяжести.
2) Сумма модулей силы натяжения нити и силы Архимеда больше модуля действующей на стержень силы тяжести.
3) Относительно оси, проходящей через точку О, плечо действующей на стержень силы тяжести меньше плеча силы Архимеда.
4) Относительно оси, проходящей через точку О, отношение плеча действующей на стержень силы Архимеда к плечу силы натяжения нити равно 1,2.
5) Относительно оси, проходящей через точку О, момент силы Архимеда больше момента действующей на стержень силы тяжести.
Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними (см. рис.). Из приведённого ниже списка выберите все правильные утверждения.
1) Плотность материала, из которого изготовлены бруски, равна 500 кг/м3.
2) Если на верхний брусок положить груз массой 0,7 кг, то бруски утонут.
3) Если воду заменить на керосин, то глубина погружения брусков уменьшится.
4) Сила Архимеда, действующая на бруски, равна 20 Н.
5) Если в стопку добавить ещё два таких же бруска, то глубина её погружения увеличится на 10 см.
Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 1
Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают в воде так, что уровень воды приходится на границу между ними (см. рис.). Из приведённого ниже списка выберите все правильные утверждения.
1) Если воду заменить на подсолнечное масло, то глубина погружения брусков уменьшится.
2) Если на верхний брусок поставить гирю массой 1,5 кг, то бруски не утонут.
3) Если в стопку добавить ещё три таких же бруска, то глубина её погружения увеличится на 15 см.
4) Сила Архимеда, действующая на бруски, равна 10 Н.
5) Плотность материала, из которого изготовлены бруски, равна 500 кг/м3.
Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 2
На поверхности воды плавает сплошной деревянный брусок. Как изменятся глубина погружения бруска и сила Архимеда, действующая на брусок, если его заменить сплошным бруском той же плотности и высоты, но большей массы? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Глубина погружения бруска |
Сила Архимеда |
Источник: Демонстрационная версия ЕГЭ—2016 по физике.
Прямоугольный сплошной параллелепипед ABCDMFEK, длины рёбер которого относятся как 3 : 2 : 1, изготовлен из некоторого материала. Если аккуратно опустить параллелепипед в жидкость так, как показано на рисунке 1, то он будет плавать так, что его нижняя грань будет погружена на глубину
Как изменятся модуль силы Архимеда, действующей на параллелепипед, и глубина погружения нижней грани параллелепипеда, если его аккуратно опустить в эту же жидкость, повернув так, как показано на рисунке 2?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
| Модуль силы Архимеда,
действующей на параллелепипед |
Глубина погружения
нижней грани параллелепипеда |
|---|---|
Прямоугольный сплошной параллелепипед ABCDMFEK, длины рёбер которого относятся как 3 : 2 : 1, изготовлен из некоторого материала. Если аккуратно опустить параллелепипед в жидкость так, как показано на рисунке 1, то он будет плавать так, что его нижняя грань будет погружена на глубину h < 2a.
Как изменятся глубина погружения нижней грани параллелепипеда и модуль силы Архимеда, действующей на параллелепипед, если его аккуратно опустить в эту же жидкость, повернув на 90 градусов так, как показано на рисунке 2?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Глубина погружения
нижней грани параллелепипеда |
Модуль силы Архимеда,
действующей на параллелепипед |
|---|---|
Деревянный кубик с ребром 10 см плавает частично погруженный в воду. Его начинают медленно погружать, действуя силой, направленной вертикально вниз. В таблице приведены значения модуля силы, под действием которой кубик находится в равновесии частично или полностью погруженный в воду. Выберите все верные утверждения на основании данных, приведенных в таблице.
| № опыта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Модуль силы, F, H | 0,2 | 0,8 | 1,8 | 3,0 | 4,0 | 5,0 | 6,0 | 6,0 |
1) В опыте № 8 сила Архимеда, действующая на кубик, больше, чем в опыте № 7.
2) В опыте № 5 кубик погружен в воду полностью.
3) Масса кубика равна 0,5 кг.
4) При выполнении опытов № 1 — № 5 сила Архимеда, действующая на тело, увеличивалась.
5) Плотность кубика равна 400 кг/м3.
Тело массой 600 г плавает в очень глубоком сосуде на поверхности жидкости, погрузившись в неё на 3/4 своего объёма. К телу прикладывают направленную вертикально вниз силу, модуль которой равен 3 Н. Чему через достаточно большое время после этого станет равен модуль силы Архимеда, действующей на тело?
Тело массой 800 г плавает в очень глубоком сосуде на поверхности жидкости, погрузившись в неё на 2/3 своего объёма. К телу прикладывают направленную вертикально вниз силу, модуль которой равен 5 Н. Чему через достаточно большое время после этого станет равен модуль силы Архимеда, действующей на тело?
Наполненная газом сферическая резиновая оболочка полностью погружена в глубокий водоём и имеет радиус 75 см. Оболочку начинают погружать вглубь водоёма, и через некоторое время её радиус становится равным 25 см (а форма остаётся сферической). Во сколько раз в результате такого погружения изменяется модуль действующей на оболочку силы Архимеда? Считайте изменение плотности воды с увеличением глубины пренебрежимо малым.
Наполненная газом сферическая резиновая оболочка полностью погружена в глубокий водоём и имеет радиус 15 см. Оболочку начинают поднимать к поверхности водоёма, и через некоторое время её радиус становится равным 60 см (а форма остаётся сферической). При этом оболочка по-прежнему остаётся полностью погруженной в воду. Во сколько раз в результате такого подъёма изменяется модуль действующей на оболочку силы Архимеда? Считайте изменение плотности воды с уменьшением глубины пренебрежимо малым.
На поверхности воды плавает прямоугольный брусок из древесины плотностью 400 кг/м3. Брусок заменили на другой брусок той же массы и с той же площадью основания, но из древесины плотностью 600 кг/м3. Как при этом изменились глубина погружения бруска и действующая на него сила Архимеда?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Глубина погружения
бруска |
Сила Архимеда |
|---|---|
Источник: Демонстрационная версия ЕГЭ—2022 по физике
Всего: 100 1–20 | 21–40 | 41–60 | 61–80 …
Статика жидкостей и газов.
-
Гидростатическое давление.
-
Закон Паскаля.
-
Гидравлический пресс.
-
Закон Архимеда.
-
Плавание тел.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: давление жидкости, закон Паскаля, закон Архимеда, условия плавания тел.
В гидро- и аэростатике рассматриваются два вопроса: 1) равновесие жидкостей и газов под действием приложенных к ним сил; 2) равновесие твёрдых тел в жидкостях и газах.
Многие из обсуждаемых далее фактов относятся равным образом как к жидкостям, так и к газам. В таких случаях мы будем называть жидкость и газ средой.
При сжатии среды в ней возникают силы упругости, называемые силами давления. Силы давления действуют между соприкасающимися слоями среды, на погружённые в среду твёрдые тела, а также на дно и стенки сосуда.
Сила давления среды обладает двумя характерными свойствами.
1. Сила давления действует перпендикулярно поверхности выделенного элемента среды или твёрдого тела. Это объясняется текучестью среды: силы упругости не возникают в ней при относительном сдвиге слоёв, поэтому отсутствуют силы упругости, касательные к поверхности.
2. Cила давления равномерно распределена по той поверхности, на которую она действует.
Естественной величиной, возникающей в процессе изучения сил давления среды, является давление.
Пусть на поверхность площади действует сила
, которая перпендикулярна поверхности и равномерно распределена по ней. Давлением называется величина
.
Единицей измерения давления служит паскаль (Па). 1 Па — это давление, производимое силой 1 Н на поверхность площадью 1 м .
Полезно помнить приближённое значение нормального атмосферного давления: Па.
к оглавлению ▴
Гидростатическое давление.
Гидростатическим называется давление неподвижной жидкости, вызванное силой тяжести. Найдём формулу для гидростатического давления столба жидкости.
Предположим, что в сосуд с площадью дна налита жидкость до высоты
(рис. 1). Плотность жидкости равна
 |
| Рис. 1. Гидростатическое давление |
Объём жидкости равен , поэтому масса жидкости
. Сила
давления жидкости на дно сосуда — это вес жидкости. Так как жидкость неподвижна, её вес равен силе тяжести:
.
Разделив силу на площадь
, получим давление жидкости:
.
Это и есть формула гидростатического давления.
Так, на глубине 10 м вода оказывает давление Па, примерно равное атмосферному. Можно сказать, что атмосферное давление приблизительно равно 10 м водного столба.
Для практики столь большая высота столба жидкости неудобна, и реальные жидкостные манометры — ртутные. Посмотрим, какую высоту должен иметь столб ртути ( кг/м
), чтобы создать аналогичное давление:
м = 750 мм.
Вот почему для измерения атмосферного давления широко используется миллиметр ртутного столба (мм рт. ст.).
к оглавлению ▴
Закон Паскаля.
Если поставить гвоздь вертикально и ударить по нему молотком, то гвоздь передаст действие молотка по вертикали, но не вбок. Твёрдые тела из-за наличия кристаллической решётки передают производимое на них давление только в направлении действия силы.
Жидкости и газы (напомним, что мы называем их средами) ведут себя иначе. В средах справедлив закон Паскаля.
Закон Паскаля. Давление, оказываемое на жидкость или газ, передаётся в любую точку этой среды без изменения по всем направлениям.
(В частности, на площадку, помещённую внутри жидкости на фиксированной глубине, действует одна и та же сила давления, как эту площадку ни поворачивай.)
Например, ныряльщик на глубине испытывает давление
. Почему? Согласно закону Паскаля вода передаёт давление атмосферы
без изменения на глубину
, где оно прибавляется к гидростатическому давлению водяного столба
.
Отличной иллюстрацией закона Паскаля служит опыт с шаром Паскаля. Это шар с множеством отверстий, соединённый с цилиндрическим сосудом (рис. 2)
 |
| Рис. 2. Шар Паскаля |
Если налить в сосуд воду и двинуть поршень, то вода брызнет из всех отверстий. Это как раз и означает, что вода передаёт внешнее давление по всем направлениям.
То же самое наблюдается и для газа: если сосуд наполнить дымом, то при движении поршня струйки дыма пойдут опять-таки из всех отверстий сразу. Стало быть, газ также передаёт давление по всем направлениям.
Вы ежедневно пользуетесь законом Паскаля, когда выдавливаете зубную пасту из тюбика. А именно, вы сжимаете тюбик в поперечном направлении, а паста двигается перпендикулярно вашему усилию — в продольном направлении. Почему? Ваше давление передаётся внутри тюбика по всем направлениям, в частности — в сторону отверстия тюбика. Туда-то паста и выходит.
к оглавлению ▴
Гидравлический пресс.
Гидравлический пресс — это устройство, дающее выигрыш в силе. То есть, прикладывая сравнительно небольшую силу в одном месте устройства, оказывается возможным получить значительно большее усилие в другом его месте.
Гидравлический пресс изображён на рис. 3. Он состоит из двух сообщающихся сосудов, имеющих разную площадь поперечного сечения и закрытых поршнями. В сосудах между поршнями находится жидкость.
 |
| Рис. 3. Гидравлический пресс |
Принцип действия гидравлического пресса очень прост и основан на законе Паскаля.
Пусть — площадь малого поршня,
— площадь большого поршня. Надавим на малый
поршень с силой . Тогда под малым поршнем в жидкости возникнет давление:
.
Согласно закону Паскаля это давление будет передано без изменения по всем направлениям в любую точку жидкости, в частности — под большой поршень. Следовательно, на большой поршень со стороны жидкости будет действовать сила:
.
Полученное соотношение можно переписать и так:
.
Мы видим, что больше
во столько раз, во сколько
больше
. Например, если площадь большого поршня в 100 раз превышает площадь малого поршня, то усилие на большом поршне окажется в 100 раз больше усилия на малом поршне. Вот каким образом гидравлический пресс даёт выигрыш в силе.
к оглавлению ▴
Закон Архимеда.
Мы знаем, что дерево в воде не тонет. Следовательно, сила тяжести уравновешивается какой-то другой силой, действующей на кусок дерева со стороны воды вертикально вверх. Эта сила называется
выталкивающей или архимедовой силой. Она действует на всякое тело, погружённое в жидкость или газ.
Выясним причину возникновения архимедовой силы. Рассмотрим цилиндр площадью поперечного сечения и высотой
, погружённый в жидкость плотности
. Основания цилиндра горизонтальны. Верхнее основание находится на глубине
, нижнее — на глубине
(рис. 4).
На боковую поверхность цилиндра действуют силы давления, которые приводят лишь к сжатию цилиндра. Эти силы можно не принимать во внимание.
На уровне верхнего основания цилиндра давление жидкости равно . На верхнее основание действует сила давления
, направленная вертикально вниз.
На уровне нижнего основания цилиндра давление жидкости равно . На нижнее основание действует сила давления
, направленная вертикально вверх (закон Паскаля!).
Так как , то
, и поэтому возникает равнодействующая сил давления, направленная вверх. Это и есть архимедова сила
. Имеем:
.
Но произведение равно объёму цилиндра
. Получаем окончательно:
. (1)
Это и есть формула для архимедовой силы. Возникает архимедова сила вследствие того, что давление жидкости на нижнее основание цилиндра больше, чем на верхнее.
Формулу (1) можно интерпретировать следующим образом. Произведение — это масса
жидкости , объём которой равен
. Но тогда
, где
— вес жидкости, взятой в объёме
. Поэтому наряду с (1) имеем:
. (2)
Иными словами, архимедова сила, действующая на цилиндр, равна весу жидкости, объём которой совпадает с объёмом цилиндра.
Формулы (1) и (2) справедливы и в общем случае, когда погружённое в жидкость или газ тело объёма имеет любую форму, а не только форму цилиндра (конечно, в случае газа
— это плотность газа). Поясним, почему так получается.
Выделим мысленно в среде некоторый объём произвольной формы. Этот объём находится в равновесии: не тонет и не всплывает. Следовательно, сила тяжести, действующая на среду, находящуюся внутри выделенного нами объёма, уравновешена силами давления на поверхность нашего объёма со стороны остальной среды — ведь на нижние элементы поверхности приходится большее давление, чем на верхние.
Иными словами, равнодействующая сил гидростатического давления на поверхность выделенного объёма — архимедова сила — направлена вертикально вверх и равна весу среды в этом объёме.
Сила тяжести, действующая на наш объём, приложена к его центру тяжести. Значит, и архимедова сила должна быть приложена к центру тяжести выделенного объёма. В противном случае сила тяжести и архимедова сила образуют пару сил, которая вызовет вращение нашего объёма (а он находится в равновесии).
А теперь заменим выделенный объём среды твёрдым телом того же объёма и той же самой формы. Ясно, что силы давления среды на поверхность тела не изменятся, так как неизменной осталась конфигурация среды, окружающей тело. Поэтому архимедова сила попрежнему будет направлена вертикально вверх и равна весу среды, взятой в объёме
. Точкой приложения архимедовой силы будет центр тяжести тела.
Закон Архимеда. На погружённое в жидкость или газ тело действует выталкивающая сила, направленная вертикально вверх и равная весу среды, объём которой равен объёму тела.
Таким образом, архимедова сила всегда находится по формуле (1). Заметим, что в эту формулу не входят ни плотность тела, ни какие-либо его геометрические характеристики — при фиксированном объёме величина архимедовой силы не зависит от вещества и формы тела.
До сих пор мы рассматривали случай полного погружения тела. Чему равна архимедова сила при частичном погружении? На ту часть тела, которая находится над поверхностью жидкости, никакая выталкивающая сила не действует. Если эту часть мысленно срезать, то величина архимедовой силы не изменится. Но тогда мы получим целиком погружённое тело, объём которого равен объёму погружённой части исходного тела.
Значит, на частично погружённое в жидкость тело действует выталкивающая сила, равная весу жидкости, объём которой равен объёму погружённой части тела. Формула (1) справедлива и в этом случае, только объём всего тела нужно заменить на объём погружённой части
погр:
погр.
Архимед обнаружил, что целиком погружённое в воду тело вытесняет объём воды, равный собственному объёму. Тот же факт имеет место для других жидкостей и газов. Поэтому можно сказать, что на всякое тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом среды.
к оглавлению ▴
Плавание тел.
Рассмотрим тело плотности и жидкость плотности
. Допустим, что тело полностью погрузили в жидкость и отпустили.
С этого момента на тело действуют лишь сила тяжести и архимедова сила
. Если объём тела равен
, то
.
Имеются три возможности дальнейшего движения тела.
1. Сила тяжести больше архимедовой силы: , или
. В этом случае тело тонет.
2. Сила тяжести равна архимедовой силе: , или
. В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
3. Сила тяжести меньше архимедовой силы: , или
. В этом случае тело всплывает, достигая поверхности жидкости. При дальнейшем всплытии начнёт уменьшаться объём погружённой части тела, а вместе с ним и архимедова сила. В какой-то момент архимедова сила сравняется с силой тяжести (положение равновесия). Тело по инерции всплывёт дальше, остановится, снова начнёт погружаться. . . Возникнут затухающие колебания, после которых тело останется плавать в положении равновесия (
), частично погрузившись в жидкость.
Таким образом, условие плавания тела можно записать в виде неравенства: .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Статика жидкостей и газов.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.03.2023
Давление. Атмосферное давление. Закон Паскаля. Закон Архимеда
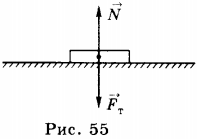
1. Твёрдые тела оказывают давление на опору. На тело, стоящее на опоре, действуют сила тяжести ( vec{F}_т=mvec{g} ) и сила реакции опоры ( vec{N} ) (рис. 55).
Если опора неподвижна, то это тело действует на неё с силой ( vec{F} ), называемой силой давления и равной в этом случае по модулю силе тяжести: ( F=mg ).
Физическая величина, равная отношению силы давления ( F ) к площади поверхности ( S ) называется давлением и обозначается буквой ( p ):
[ p=F/S ]
Единицей давления является 1 паскаль (1 Па):
[ [,p,]=1Н/1м^2=1,Н/м^2=1,Па ]
Более крупная единица давления — килопаскаль.
[ 1, кПа = 1000, Па ]
Как видно из формулы, давление на поверхность зависит от площади поверхности. Так, человек проваливается в снег при ходьбе по нему и спокойно перемещается на лыжах. В том случае, когда нужно увеличить давление на твёрдое тело, используют заострённые предметы, например, булавки, гвозди, ножи и т.п.
2. Жидкости и газы тоже оказывают давление на сосуд, в котором они находятся. Так, молекулы газа, находящегося в воздушном шаре, непрерывно движутся и при этом соударяются со стенками шара. Эти удары и вызывают давление газа на стенки шара и любого другого сосуда, в котором газ находится. Удар одной молекулы слаб, но внутри шара находится огромное число молекул, поэтому
их суммарное давление на стенки шара ощутимо.
Чем выше температура газа, чем с большей скоростью движутся молекулы и чем чаще и сильнее ударяются они о стенки сосуда, тем, следовательно, давление газа на стенки сосуда больше.
Если уменьшить объём газа в сосуде, не меняя его массу, то число молекул в единице объёма увеличится, увеличится и плотность газа. Число ударов молекул о стенки сосуда при этом возрастёт, следовательно, увеличится давление газа. При увеличении объёма газа при той же массе уменьшится его плотность и число ударов молекул о стенки сосуда. Давление уменьшится.
Таким образом, давление газа тем больше, чем выше его температура и меньше объём при неизменной массе. При повышении температуры и уменьшении объёма молекулы с большей силой и чаще ударяются о стенки сосуда.
3. Опыт показывает, что давление, производимое на жидкость или газ, передаётся по всем направлениям. Если шар с отверстиями, соединённый с трубкой, внутри которой находится поршень, наполнить водой, а затем нажать на поршень, то можно заметить, что вода брызнет из всех отверстий. При этом струйки вытекающей воды будут примерно одинаковыми. Это говорит о том, что давление, которое мы создаём, действуя на воду, передаётся водой по всем направлениям одинаково. Тот же эффект можно наблюдать, если шар заполнить дымом. Дым тоже будет передавать производимое на него давление по всем направлениям одинаково.
То, что газы и жидкости передают давление по всем направлениям, объясняется подвижностью их молекул. Она проявляется в том, что слои и частицы жидкостей и газов могут свободно перемещаться друг относительно друга но разным направлениям. Благодаря подвижности молекул давление, которое оказывает поршень на ближайший к нему слой, передаётся последующим слоям. Молекулы газа и жидкости движутся хаотически, поэтому и их действие распределяется равномерно по всему объёму шара. Таким образом, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения в каждую точку жидкости или газа. Это утверждение называется законом Паскаля.
4. Закон Паскаля находит применение в гидравлических машинах.
Основной частью любой гидравлической машины являются два соединенных между собой цилиндра разного диаметра. Цилиндры заполнены жидкостью, чаще всего маслом, и в них помещены поршни.
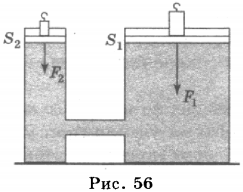
Пусть на большой поршень площадью ( S_1 ) действует сила ( F_1 ) (рис. 56). Эта сила будет оказывать на поршень давление ( p_1 ): ( p_1=F_1/S_1 ).
Это давление ( p_1 ) будет передаваться жидкости, находящейся под большим поршнем. Согласно закону Паскаля, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения. Следовательно, давление будет передаваться жидкости, находящейся под меньшим поршнем, и на меньший поршень со стороны жидкости будет действовать давление ( p_2=p_1 ). Соответственно, на меньший поршень со стороны жидкости будет действовать сила ( F_2=p_2S_2 ), направленная вверх. Откуда ( p_2=F_2/S_2 ).
Чтобы жидкость и поршни находились в равновесии, на меньший поршень следует подействовать силой, равной по модулю силе ( F_2 ), направленной вертикально вниз. Для этого можно, например, положить на поршень груз.
Так как ( p_1=p_2 ), то ( F_1/S_1=F_2/S_2 ) или ( F_1/F_2=S_1/S_2 ).
Таким образом, гидравлическая машина даёт выигрыш в силе во столько раз, во сколько раз площадь большего поршня больше площади меньшего поршня.
Это означает, что с помощью некоторой силы, приложенной к малому поршню гидравлической машины, можно уравновесить существенно большую силу, приложенную к большему поршню.
Гидравлическая машина, так же как и любой простой механизм, даёт выигрыш в силе, но не даёт выигрыша в работе.
5. Твёрдые тела производят давление на опору вследствие действия на них силы тяжести. Поскольку на жидкости тоже действует сила тяжести, то и жидкости оказывают давление на дно сосуда. Это можно доказать экспериментально.
Если в трубку, дно которой затянуто плёнкой, налить воду, то плёнка заметно прогнётся. Это происходит потому, что на воду действует сила тяжести, и каждый слой воды давит на слои воды, лежащие ниже, и соответственно на дно сосуда.
Давление производится жидкостью не только на дно сосуда, оно существует внутри жидкости на любой её глубине. При этом производимое давление передаётся по закону Паскаля по всем направлениям одинаково.
Если в трубку с дном, затянутым плёнкой, добавить воды, то плёнка прогнётся сильнее. Это происходит потому, что увеличивается вес воды и соответственно давление воды на дно трубки. Таким образом, давление жидкости на дно сосуда тем больше, чем больше высота столба жидкости.
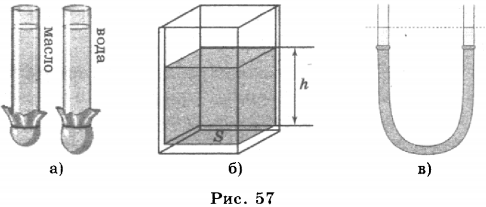
Если теперь в трубку до той же высоты налить масло, плотность которого меньше плотности воды, то плёнка прогнётся меньше, чем в том случае, когда в ней была вода (рис. 57 а). Это означает, что давление на дно сосуда тем больше, чем больше плотность жидкости.
Сила ( F ), с которой жидкость давит на дно, равна её весу ( P ). Вес жидкости ( P ) равен произведению её массы ( m ) и ускорения свободного падения ( g ): ( F=P=mg ).
Масса жидкости ( m ) равна произведению её плотности ( rho ) и объёма ( V ): ( m=rho V ), где ( V=Sh ) (рис. 57 б). Тогда ( F=mg=rho V!g=rho Shg ).
Разделив вес жидкости (силу, с которой она давит на дно сосуда) на площадь дна, получим давление жидкости ( p ): ( p=F/S ) или ( p=rho gSh/S ), т.е. ( p=rho gh )
Давление жидкости на дно и стенки сосуда равно произведению плотности жидкости, ускорения свободного падения и высоты столба жидкости.
6. Два или более сосудов, соединённых между собой у дна, называются сообщающимися сосудами. Примерами сообщающихся сосудов могут служить гидравлические машины и жидкостный манометр. Самым простым сообщающимся сосудом, которым вы пользуетесь каждый день, является чайник.
Если две стеклянные трубки соединить резиновой трубкой (рис. 57 в), то получатся сообщающиеся сосуды. Наливая в одну трубку воду, можно заметить, что она будет перетекать и в другую трубку. При этом уровни воды в трубках будут все время одинаковы.
Можно поднять одну из трубок или наклонить ее, в любом случае друг относительно друга уровни воды или любой другой жидкости останутся одинаковыми, т.е. будут лежать в одной и той же горизонтальной плоскости.
Можно сделать вывод: в сообщающихся сосудах поверхности однородной жидкости всегда устанавливаются на одном уровне.
Это верно при условии, что давление на поверхность жидкости одинаково. При использовании сообщающихся сосудов в качестве жидкостного манометра именно по разности уровней жидкости в трубках можно судить о значении давления.
Объяснить то, что в сообщающихся сосудах однородная жидкость устанавливается на одном уровне, можно следующим образом. Жидкость в сосудах не перемещается, следовательно, её давления в сосудах на одном уровне, в том числе и на дно, одинаковы. Она имеет одинаковую плотность, т.к. она однородная. Следовательно, в соответствии с формулой ( p=rho gh ) высоты жидкости тоже одинаковы.
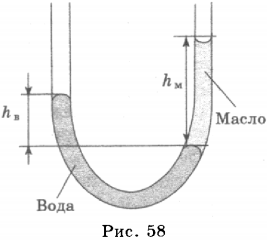
Если в одну трубку налить воду, а в другую масло, плотность которого меньше плотности воды, то уровень воды будет ниже, чем уровень масла в другой трубке (рис. 58).
Это объясняется тем, что давление жидкости на дно сосуда зависит от высоты столба жидкости и от её плотности. При одинаковом давлении, чем больше плотность жидкости, тем меньше высота её столба. Поскольку плотность масла меньше плотности воды, то столб масла выше столба воды. Жидкости, имеющие разную плотность, устанавливаются в сообщающихся сосудах на разных уровнях; во сколько раз плотность одной жидкости больше плотности другой, во столько раз меньше высота её столба.
7. Земля окружена воздушной оболочкой — атмосферой. Воздух, как и газы, входящие в состав атмосферы, имеет массу. Соответственно, на него действует сила тяжести, и он оказывает давление на поверхность Земли.
Давление воздушной оболочки на поверхность Земли и находящиеся на ней тела называется атмосферным давлением.
В существовании атмосферного давления легко убедиться на опытах. Если опустить в воду трубку с плотно прилегающим к её стенкам поршнем и поднимать поршень вверх, то вода будет подниматься по трубке вслед за поршнем.
Это происходит потому, что при подъёме поршня между ним и поверхностью воды образуется разреженное пространство. На поверхность воды в сосуде действует атмосферное давление, которое в соответствии с законом Паскаля передаётся по всем направлениям, в том числе и в направлении трубки. Оно и заставляет воду подниматься за поршнем.
Для расчёта атмосферного давления нельзя использовать формулу, по которой рассчитывается давление столба жидкости, так как для этого нужно знать высоту атмосферы и плотность воздуха. Но атмосфера не имеет определённой границы, а плотность воздуха изменяется с высотой. Однако атмосферное давление можно измерить.
Опыт по измерению атмосферного давления был предложен итальянским ученым Торричелли в XVII в. Стеклянную трубку длиной 1 м, запаянную с одного конца, заполнили ртутью. Закрыв другой конец трубки, её перевернули и опустили в сосуд с ртутью. Затем этот конец трубки открыли, и часть ртути вылилась из неё в сосуд, а часть осталась в трубке. Высота столба ртути, оставшейся в трубке, оказалась равной примерно 760 мм.
Объясняется это следующим образом: атмосферное давление действует на ртуть в сосуде, это давление передаётся по всем направлениям и действует на ртуть в основании трубки снизу вверх. Это давление уравновешивает давление столба ртути в трубке. Таким образом, атмосферное давление равно давлению, которое оказывает у основании трубки столб ртути высотой 760 мм. Это давление называют нормальным атмосферным давлением.
Если атмосферное давление выше нормального, то высота столба ртути больше, если — меньше нормального, то столб ртути опустится ниже.
Нормальное атмосферное давление равно 101 300 Па.
Атмосферное давление чаще выражают не в паскалях, а в миллиметрах ртутного столба (мм рт.ст.). 1 мм рт.ст. = 133,3 Па.
Если к трубке в опыте Торричелли прикрепить шкалу и проградуировать её в миллиметрах, то получим прибор — ртутный барометр, с помощью которого можно измерять атмосферное давление.
В быту и технике для измерения атмосферного давления применяют более удобный в обращении металлический барометр, называемый анероидом.
Атмосферное давление зависит от высоты. Это объясняется тем, что воздух хорошо сжимаем, так же как и все газы. Верхние слои воздуха давят на лежащие ниже и сжимают их, соответственно плотность слоёв воздуха, а следовательно и давление, у поверхности Земли больше, чем на некоторой высоте от неё.
Так, в местности, лежащей на уровне моря, давление равно примерно 760 мм рт. ст., т.е. нормальному атмосферному. В горах оно выше. Измерения показывают, что на каждые 12 м подъёма атмосферное давление уменьшается примерно на 1 мм рт.ст.
8. Если подвешенный к пружине динамометра шарик опустить в сосуд с водой, то можно заметить, что показание динамометра уменьшится.
Точно так же можно изменить показания динамометра, если подействовать на шарик рукой снизу вверх. Следовательно, когда шарик опустили в воду, на него, помимо силы тяжести и силы упругости пружины динамометра, стала действовать сила, направленная вверх. Эту силу называют выталкивающей или архимедовой силой.
Выталкивающая сила возникает за счёт разности давления воды на нижнюю поверхность шарика и давления на его верхнюю поверхность, поскольку давление жидкости зависит от высоты её столба.
Сила давления ( F_1 ), действующая на верхнюю поверхность шарика, направлена вниз, сила давления ( F_2 ), действующая на нижнюю поверхность шарика, направлена вверх. Так как ( F_2 ) больше ( F_1 ), то результирующая этих двух сил, являющаяся выталкивающей силой, будет направлена вверх.
Выталкивающая сила тем больше, чем больше плотность жидкости, в которую погружено тело, и чем больше объём тела, погружённого в жидкость.
Опыт показывает, что выталкивающая сила ( F ) может быть вычислена по формуле: ( F=rho gV ), где ( rho ) — плотность жидкости, в которую погружено тело, ( V ) — объём погружённой части тела.
Выталкивающая сила равна произведению плотности жидкости, ускорения свободного падения и объёма погружённой части тела.
Этот закон называют законом Архимеда.
В воздухе, так же как и в любом другом газе, на тело действует выталкивающая сила. Она имеет ту же природу, что и выталкивающая сила, действующая на тело в жидкости. Её происхождение обусловлено разностью давлений на нижнюю и верхнюю грани тела. Однако, поскольку плотность газа намного меньше плотности жидкости, выталкивающая сила, действующая на тело, в газе меньше, чем в жидкости. Часто при решении задач пренебрегают выталкивающей силой, действующей на тело в воздухе, и считают, что вес покоящегося тела в воздухе равен по модулю действующей на него силе тяжести.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Ребёнка везут на санках по свежевыпавшему снегу. Какие санки — с широкими или узкими полозьями — следует выбрать, чтобы не проваливаться в снег?
1) с широкими
2) с узкими
3) безразлично
4) ответ зависит от веса санок
2. Брусок в форме прямоугольного параллелепипеда положили на стол сначала узкой гранью (1), а затем — широкой (2). Сравните силы давления (( F_1 ) и ( F_2 )) и давления (( p_1 ) и ( p_2 )), производимые бруском на стол в этих случаях.
1) ( F_1=F_2; p_1>p_2 )
2) ( F_1=F_2; p_1<p_2 )
3) ( F_1<F_2; p_1<p_2 )
4) ( F_1=F_2; p_1=p_2 )
3. Сила ( F_1 ), действующая со стороны жидкости на один поршень гидравлической машины, в 16 раз меньше силы ( F_2 ), действующей на другой поршень. Как соотносятся модули работы ( (A_1) ) и ( (A_2) ) этих сил, совершаемой при перемещении поршней? Трением пренебречь.
1) ( A_1=A_2 )
2) ( A_1=16A_2 )
3) ( A_2=16A_1 )
4) ( A_1=4A_2 )
4. В сосуды различной формы налита одна и та же жидкость. Высота уровня жидкости во всех сосудах одинакова. В каком из сосудов давление на дно наименьшее?
1) в сосуде А
2) в сосуде Б
3) в сосуде В
4) во всех сосудах одинаковое
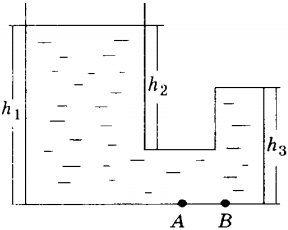
5. Стеклянный сосуд, правое колено которого запаяно, заполнен жидкостью плотностью с (см. рисунок). Давление, оказываемое жидкостью на дно сосуда в точке Б, равно
1) ( rho gh_3 )
2) ( rho gh_1 )
3) ( rho g(h_1-h_2) )
4) ( rho gh_2 )
6. Атмосферное давление на вершине горы Казбек
1) меньше, чем у её подножия
2) больше, чем у её подножия
3) равно давлению у её подножия
4) может быть больше или меньше, чем у её подножия, в зависимости от погоды
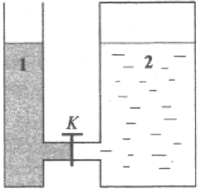
7. В открытых сосудах 1 и 2 находятся соответственно ртуть и вода. Если открыть кран К, то
1) ни вода, ни ртуть перетекать не будут
2) вода начнёт перетекать из сосуда 2 в сосуд 1
3) перемещение жидкостей будет зависеть от атмосферного давления
4) ртуть начнёт перетекать из сосуда 1 в сосуд 2
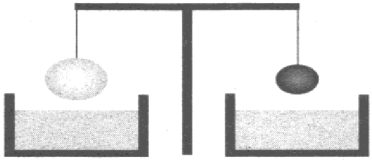
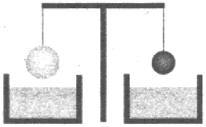
8. Два однородных шара, один из которых изготовлен из стали, а другой — из олова, уравновешены на рычажных весах (см. рисунок). Нарушится ли равновесие весов,
если шары опустить в воду?
1) Равновесие весов не нарушится, так как шары одинаковой массы.
2) Равновесие весов нарушится — перевесит шар из стали.
3) Равновесие весов нарушится — перевесит шар из олова.
4) Равновесие весов не нарушится, так как шары опускают в одну и ту же жидкость.
9. Алюминиевый шар, подвешенный на нити, опущен в крепкий раствор поваренной соли. Затем шар перенесли из раствора поваренной соли в дистиллированную воду. При этом сила натяжения нити
1) может остаться неизменной или измениться в зависимости от объёма шара
2) не изменится
3) увеличится
4) уменьшится
10. Теплоход переходит из устья реки в солёное море. При этом архимедова сила, действующая на теплоход,
1) увеличится
2) уменьшится или увеличится в зависимости от размера теплохода
3) не изменится
4) уменьшится
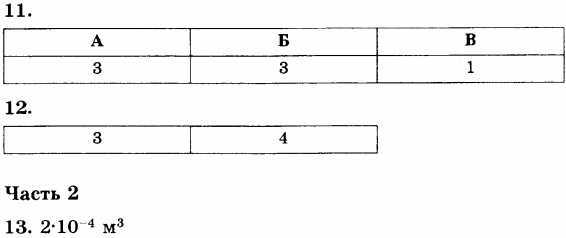
11. Шарик, опущенный в жидкость, начинает опускаться на дно. Как по мере движения шарика в жидкости изменяются выталкивающая сила, действующая на него, вес шарика, давление жидкости? Установите соответствие между физическими величинами и характером их изменения. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) выталкивающая сила
Б) вес
B) давление жидкости
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИН
1) увеличивается
2) уменьшается
3) не изменяется
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) атмосферное давление можно рассчитать так же, как давление жидкости на дно сосуда.
2) в опыте Торричелли можно ртуть заменить водой при той же длине трубки.
3) для того, чтобы столб воды производил на дно сосуда такое же давление, что и столб керосина, его высота должна составлять 0,8 от высоты столба керосина.
4) на вершине горы атмосферное давление меньше, чем у её подножия.
5) закон Паскаля справедлив для газов, жидкостей и твёрдых тел.
Часть 2
13. Камень весит в воздухе 6 Н, а в воде 4 Н. Чему равен объём этого камня?
Ответы
Давление. Атмосферное давление. Закон Паскаля. Закон Архимеда
2.9 (58.53%) 68 votes
Задачи на силу Архимеда с решениями
Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».
Название величины |
Обозначение |
Единица измерения |
Формула |
Объем тела |
V |
м3 |
Vт = FA / pg |
Плотность жидкости |
p |
кг/м3 |
pж = FA / (Vg) |
Сила Архимеда |
FA |
Н |
FA = pж Vт g |
Постоянная |
g ≈ 10 Н/кг |
Н/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Тело объемом 2 м3 погружено в воду. Найдите архимедову силу, действующую на тело.
Задача № 2. Определить выталкивающую силу, действующую на деревянный плот объемом 12 м3, погруженный в воду на половину своего объема.
Задача № 3. Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?
Задача № 4. Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?
Задача № 5. Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?
Задача № 6. Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?
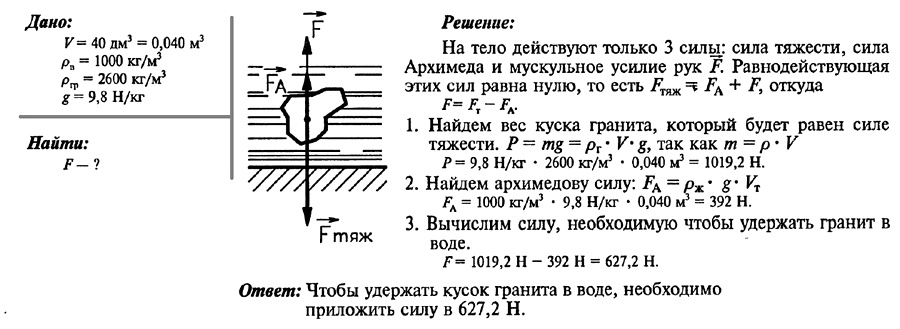
Задача № 7. Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?
Задача № 8. Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
Задача № 9 (повышенной сложности). Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?
Задача № 10 (повышенной сложности). Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)
Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.
Конспект урока «Задачи на силу Архимеда с решениями».
Следующая тема: «Задачи на механическую работу».
Посмотреть интерактивный материал
Конспект
В ходе урока необходимо рассмотреть решение типичных задач. Задача 1. Вес кирпича в воздухе равен 30 ньютонов, в воде – 10 ньютонов. Чему равна действующая на кирпич архимедова сила? Задача 2. На погружённый в воду кирпич действует выталкивающая сила, равная 20 ньютонам. Чему равен объём этого кирпича?
Ключевые слова
Архимедова (выталкивающая) сила, закон Архимеда, плавание тел.
Назад
Вперёд
Сообщить об ошибке в уроке