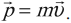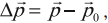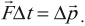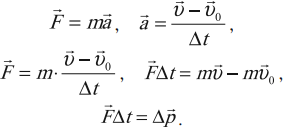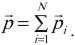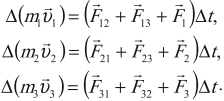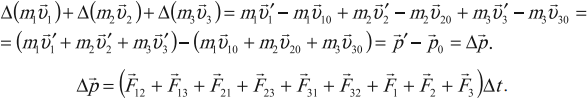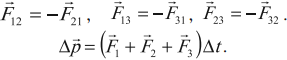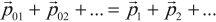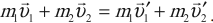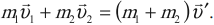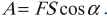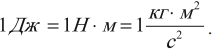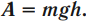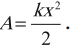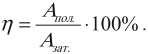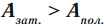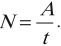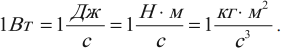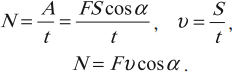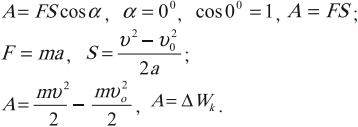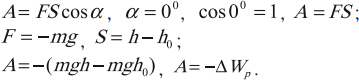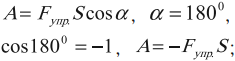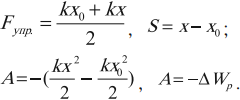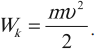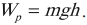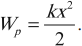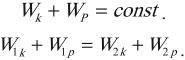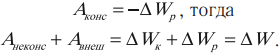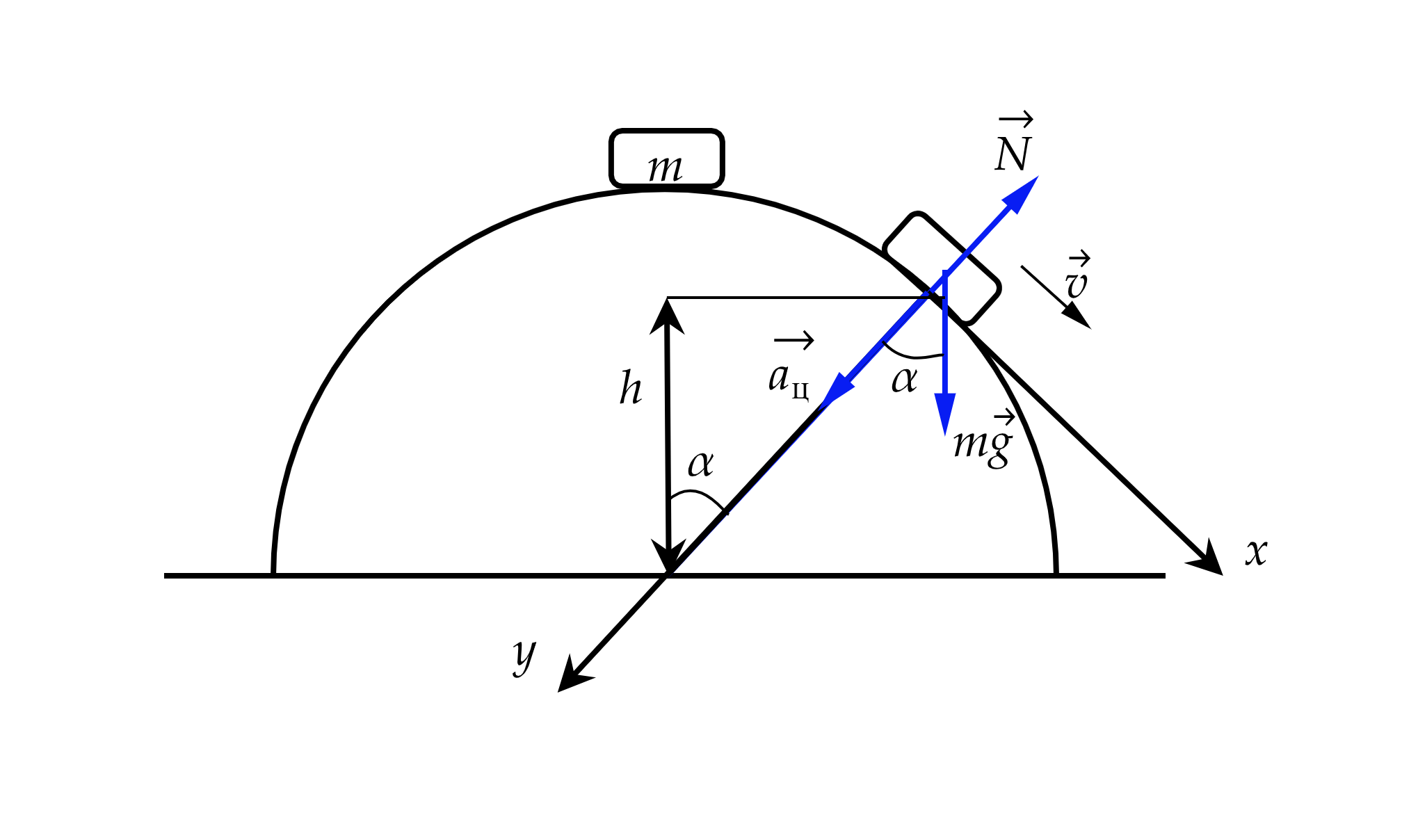Законы сохранения в механике
Содержание
- Импульс тела
- Импульс системы тел
- Закон сохранения импульса
- Работа силы
- Мощность
- Работа как мера изменения энергии
- Кинетическая энергия
- Потенциальная энергия
- Закон сохранения механической энергии
- Основные формулы по теме «Законы сохранения в механике»
Импульс тела
Импульс тела – это векторная физическая величина, равная произведению массы тела на его скорость:
Обозначение – ( p ), единицы измерения – (кг·м)/с.
Импульс тела – это количественная мера движения тела.
Направление импульса тела всегда совпадает с направлением скорости его движения.
Изменение импульса тела равно разности конечного и начального значений импульса тела:
где ( p_0 ) – начальный импульс тела,
( p ) – конечный импульс тела.
Если на тело действует нескомпенсированная сила, то его импульс изменяется. При этом изменение импульса тела равно импульсу подействовавшей на него силы.
Импульс силы – это количественная мера изменения импульса тела, на которое подействовала эта сила.
Обозначение – ( F!Delta t ), единицы измерения — Н·с.
Импульс силы равен изменению импульса тела:
Направление импульса силы совпадает по направлению с изменением импульса тела.
Второй закон Ньютона (силовая форма):
Важно!
Следует всегда помнить, что совпадают направления векторов:
• силы и ускорения: ( vec{F}uparrowuparrowvec{a} );
• импульса тела и скорости: ( vec{p}uparrowuparrowvec{v} );
• изменения импульса тела и силы: ( Deltavec{p}uparrowuparrowvec{F} );
• изменения импульса тела и ускорения: ( Deltavec{p}uparrowuparrowvec{a} ).
Импульс системы тел
Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которых мы изучаем, называется механической системой или просто системой.
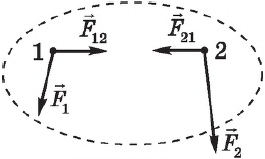
Рассмотрим систему, состоящую из трех тел. На тела системы действуют внешние силы, а между телами действуют внутренние силы.
( F_1,F_2,F_3 ) – внешние силы, действующие на тела;
( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} ) – внутренние силы, действующие между телами.
Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в виде уравнения:
В левой части каждого уравнения стоит изменение импульса тела за малое время ( Delta t ).
Обозначим: ( v_0 ) – начальные скорости тел, а ( v^{prime} ) – конечные скорости тел.
Сложим левые и правые части уравнений.
Но силы взаимодействия любой пары тел в сумме дают нуль.
Важно!
Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
Закон сохранения импульса
Закон сохранения импульса
Векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой:
Замкнутая система – это система, на которую не действуют внешние силы.
Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций.
При абсолютно упругом ударе взаимодействующие тела до и после взаимодействия движутся отдельно.
Закон сохранения импульса для абсолютно упругого удара:
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
Закон сохранения импульса для абсолютно неупругого удара:
Реактивное движение – это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-то его части.
Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.
Для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой, поэтому реактивное движение позволяет телу двигаться в безвоздушном пространстве.
Реактивные двигатели
Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Используются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-ракетными двигателями.
Реактивные двигатели делятся на два класса:
- ракетные;
- воздушно-реактивные.
В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.
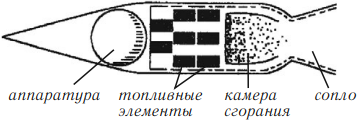
Ракетный двигатель на твердом топливе
При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где находится сопло. Выходящие через сопло газы не встречают на своем пути стенку, на которую могли бы оказать давление. В результате появляется сила, толкающая ракету вперед.
Сопло – суженная часть камеры, служит для увеличения скорости истечения продуктов сгорания, что, в свою очередь, повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.
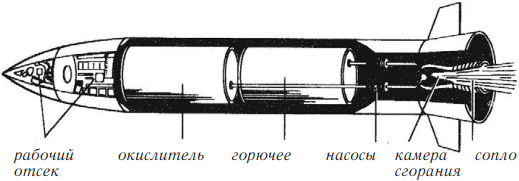
Ракетный двигатель на жидком топливе
В ракетных двигателях на жидком топливе в качестве горючего используют керосин, бензин, спирт, жидкий водород и др., а в качестве окислителя – азотную кислоту, жидкий кислород, перекись водорода и пр.
Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру сгорания, где температура достигает 3000 0С и давление до 50 атм. В остальном работает так же, как и двигатель на твердом топливе.
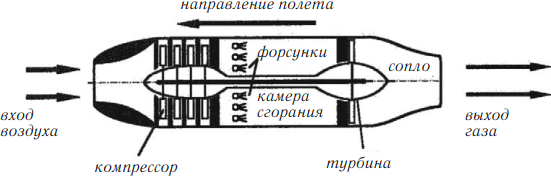
Воздушно-реактивный двигатель
В носовой части находится компрессор, засасывающий и сжижающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (керосин) попадает в камеру сгорания с помощью специальных форсунок. Раскаленные газы выходят через сопло, вращают газовую турбину, приводящую в движение компрессор.
Основное отличие воздушно-реактивных двигателей от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы.
Алгоритм применения закона сохранения импульса к решению задач:
- Запишите краткое условие задачи.
- Определите характер движения и взаимодействия тел.
- Сделайте рисунок, на котором укажите направление векторов скоростей тел до и после взаимодействия.
- Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.
- Запишите закон сохранения импульса в векторной форме.
- Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
- Решите полученную систему уравнений относительно неизвестных величин.
- Выполните действия единицами измерения величин.
- Запишите ответ.
Работа силы
Механическая работа – это скалярная векторная величина, равная произведению модулей вектора силы, действующей на тело, вектора перемещения и косинуса угла между этими векторами.
Обозначение – ( A ), единицы измерения – Дж (Джоуль).
1 Дж – это работа, которую совершает сила в 1 Н на пути в 1 м:
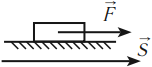
Механическая работа совершается, если под действием некоторой силы, направленной не перпендикулярно, тело перемещается на некоторое расстояние.
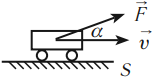
Зависимость механической работы от угла ( alpha )
- ( alpha=0^{circ},, cosalpha=1,, A=FS,,A>0; )
- ( 0^{circ}<alpha<90^{circ},, A=FScosalpha,,A>0; )
- ( alpha=90^{circ},, cosalpha=0,, A=0; )
- ( 90^{circ}<alpha<180^{circ},, A=FScosalpha,,A<0; )
( alpha=180^{circ},, cosalpha=-1,, A=-FS,,A<0; )
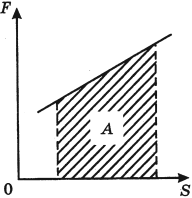
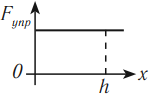
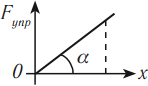
Геометрический смысл механической работы
На графике зависимости ( F=F(S) ) работа силы численно равна площади фигуры, ограниченной графиком, осью перемещения и прямыми, параллельными оси силы.
Формулы для вычисления работы различных сил
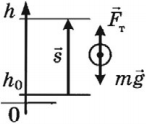
Работа силы тяжести:
Работа силы упругости:
Коэффициент полезного действия механизма (КПД) — это физическая величина, равная отношению полезной работы, совершенной механизмом, ко всей затраченной при этом работе.
Обозначение – ( eta ), единицы измерения – %.
( A_{mathit{пол.}} ) – полезная работа – это та работа, которую нужно сделать;
( A_{mathit{зат.}} ) – затраченная работа – это та работа, что приходится делать на самом деле.
Важно!
КПД любого механизма не может быть больше 100%.
Мощность
Мощность – это количественная мера быстроты совершения работы.
Обозначение – ( N ), единицы измерения – Вт (Ватт).
Мощность равна отношению работы к времени, за которое она была совершена: .
1 Вт – это мощность, при которой за 1 с совершается работа в 1 Дж:
1 л. с. (лошадиная сила) = 735 Вт.
Связь между мощностью и скоростью равномерного движения:
Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.
Важно!
Если интервал времени стремится к нулю, то выражение представляет собой мгновенную мощность, определяемую через мгновенную скорость.
Работа как мера изменения энергии
Если система тел может совершать работу, то она обладает энергией.
Работа и изменение кинетической энергии (теорема о кинетической энергии)
Если под действием силы тело совершило перемещение и вследствие этого его скорость изменилась, то работа силы равна изменению кинетической энергии.
Силы, работа которых не зависит от формы траектории, называются консервативными.
Работа и изменение потенциальной энергии тела, поднятого над землей
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
Работа и изменение потенциальной энергии упруго деформированного тела
Работа силы упругости равна изменению потенциальной энергии, взятому с противоположным знаком.
Кинетическая энергия
Кинетическая энергия – это энергия, которой обладает тело вследствие своего движения.
Обозначение – ( W_k (E_k) ), единицы измерения – Дж.
Кинетическая энергия равна половине произведения массы тела на квадрат его скорости:
Важно!
Так как кинетическая энергия отдельного тела определяется его массой и скоростью, то она не зависит от того, взаимодействует ли это тело с другими телами или нет. Значение кинетической энергии зависит от выбора системы отсчета, как и значение скорости. Кинетическая энергия системы тел равна сумме кинетических энергий отдельных тел, входящих в эту систему.
Потенциальная энергия
Потенциальная энергия – это энергия взаимодействия тел или частей одного и того же тела.
Обозначение – ( W_p (E_p) ), единицы измерения – Дж.
Потенциальная энергия тела, поднятого на некоторую высоту над землей, равна произведению массы тела, ускорения свободного падения и высоты, на которой он находится:
Потенциальная энергия упруго деформированного тела равна половине произведения жесткости на квадрат удлинения:
Важно!
Величина потенциальной энергии зависит от выбора нулевого уровня. Нулевым называется уровень, на котором потенциальная энергия равна нулю. Нулевой уровень выбирается произвольно, исходя из удобства решения задачи.
Закон сохранения механической энергии
Полная механическая энергия – это энергия, равная сумме кинетической и потенциальной энергий.
Обозначение – ( W (E) ), единицы измерения – Дж.
Закон сохранения механической энергии
В замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т. е. не изменяется с течением времени:
Если между телами системы действуют кроме сил тяготения и упругости другие силы, например сила трения или сопротивления, действие которых приводит к превращению механической энергии в тепловую, то в такой системе тел закон сохранения механической энергии не выполняется.
Важно!
В случае, если кроме консервативных сил (тяжести, упругости, тяготения) существуют еще и неконсервативные силы, например сила трения, а также внешние силы, то
Теорема о кинетической энергии справедлива для сил любой природы:
Если на систему тел действуют неконсервативные и внешние силы, то изменение полной энергии равно сумме работ неконсервативных и внешних сил.
Закон сохранения и превращения энергии
Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой или передается от одного тела к другому.
Основные формулы по теме «Законы сохранения в механике»
Законы сохранения в механике
3.1 (62.61%) 46 votes
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Мальчик столкнул санки с вершины горки. Сразу после толчка санки имели скорость 5 м/с. Высота горки 10 м. Трение санок о снег пренебрежимо мало. Какова скорость санок у подножия горки? (Ответ дайте в метрах в секунду.) Ускорение свободного падения считать равным 10 м/с2.
Мальчик столкнул санки с вершины горки. Сразу после толчка санки имели скорость а у подножия горки она равнялась
Трение санок о снег пренебрежимо мало. Какова высота горки? (Ответ дайте в метрах.) Ускорение свободного падения считать равным 10 м/с2.
Мальчик столкнул санки с вершины горки. Высота горки 10 м, у ее подножия скорость санок равнялась Трение санок о снег пренебрежимо мало. Какой была скорость санок сразу после толчка? (Ответ дайте в метрах в секунду.) Ускорение свободного падения считать равным 10 м/с2.
Задания Д28 C1 № 3279
Определите начальную скорость бруска, если известно, что после того, как он проехал 0,5 м вниз по наклонной плоскости с углом наклона 30° к горизонту, его скорость стала равна 3 м/с. Трением пренебречь. Ответ приведите в метрах в секунду.
На горизонтальной шероховатой плоскости (коэффициент трения равен μ) покоятся два одинаковых груза массой m на расстоянии L друг от друга, один из которых соединён со стенкой лёгкой нерастянутой горизонтальной пружиной жёсткостью k (см. рис.). Левому грузу сообщили в некоторый момент начальную скорость V0 в направлении правого, после чего грузы испытали абсолютно упругое лобовое столкновение. На какое расстояние l сместится после столкновения правый груз?
Какие законы Вы использовали для описания взаимодействия грузов? Обоснуйте их применение к данному случаю.
На горизонтальном гладком столе лежит длинная доска массой M = 10 кг, а на её левом конце — деревянный брусок массой m = 1 кг (см. рис.). В брусок попадает и прилипает к нему пластилиновый снаряд массой m0 = 200 г, летевший горизонтально по направлению вдоль доски со скоростью V0 = 10 м/с, после чего брусок скользит до остановки по шероховатой доске, не сваливаясь с неё. Какое количество теплоты Q выделится в этой системе в течение всего процесса?
Снаряд, движущийся со скоростью разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна
Найдите массу m осколка.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 2.
Снаряд в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Модуль скорости осколка, движущегося по направлению движения снаряда, равен а модуль скорости второго осколка равен
Найдите массу снаряда.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3.
Снаряд массой 2m, движущийся со скоростью разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося по направлению движения снаряда, равна
Найдите ΔЕ.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 4.
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Какие законы Вы используете для описания неупругого столкновения брусков? Обоснуйте их применение к данному случаю.
На горизонтальном гладком столе лежит длинная доска массой M = 10 кг, а на её левом конце — деревянный брусок массой m = 1 кг (см. рис.). В брусок попадает и прилипает к нему пластилиновый снаряд массой m0 = 200 г, летевший горизонтально по направлению вдоль доски со скоростью V0 = 10 м/с, после чего брусок скользит до остановки по шероховатой доске, не сваливаясь с неё. Какое количество теплоты Q выделится в этой системе в течение всего процесса?
Какие законы Вы используете для описания взаимодействия бруска, доски и пули? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 23.03.2018, вариант ФИ10401
Задания Д29 C2 № 4824
Снаряд в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Модуль скорости осколка, движущегося по направлению движения снаряда, равен а модуль скорости второго осколка равен
Найдите массу снаряда.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3.
Задания Д29 C2 № 7160
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Модуль скорости осколка, движущегося по направлению движения снаряда, равен а модуль скорости второго осколка равен
Найдите ΔЕ.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 4.
Снаряд массой 4 кг, летящий со скоростью 400 м/с в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ = 0,5 МДж. Найдите модуль скорости осколка, движущегося по направлению движения снаряда.
Какие законы Вы используете для описания взрыва снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 2018. Часть С (ДВ)
Брусок скользит по наклонной плоскости вниз без трения. Что происходит при этом с его скоростью, потенциальной энергией, силой реакции наклонной плоскости?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость бруска | Потенциальная энергия
бруска |
Сила реакции наклонной
плоскости |
Задания Д29 C2 № 4789
Снаряд, движущийся со скоростью разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна
Найдите массу m осколка.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 2.
Снаряд массой 4 кг, летящий со скоростью 400 м/с в полёте разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ΔЕ = 0,5 МДж. Найдите модуль скорости осколка, движущегося по направлению движения снаряда.
Источник: ЕГЭ по физике 2018. Часть С (ДВ)
На горизонтальной шероховатой плоскости (коэффициент трения равен μ) покоятся два одинаковых груза массой m на расстоянии L друг от друга, один из которых соединён со стенкой лёгкой нерастянутой горизонтальной пружиной жёсткостью k (см. рис.). Левому грузу сообщили в некоторый момент начальную скорость V0 в направлении правого, после чего грузы испытали абсолютно упругое лобовое столкновение. На какое расстояние l сместится после столкновения правый груз?
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?
Какие законы Вы используете для описания характера изменения энергии тела? Обоснуйте их применимость к данному случаю.
Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …
Полная теория по Законам сохранения в Механике, теория и практика ЕГЭ по физике
- 30.09.2013
Полный материал по физике на тему: Законы сохранения в механике.
Материал содержит в себе необходимую теорию по теме, а также множество различных практических заданий и тестов, ориентированных на ЕГЭ.
Вместе с этим материалом вы сможете максимально качественно изучить раздел физики «Законы сохранения в механике» для ЕГЭ.
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Импульс тела
Импульсом тела называется величина, равная произведению массы тела на его скорость.
Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:
$p↖{→}=mυ↖{→}$
Направление вектора импульса всегда совпадает с направлением скорости.
За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.
Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:
$a↖{→}={{υ_2}↖{→}-{υ_1}↖{→}}/{∆t}$
где, ${υ_1}↖{→}$ и ${υ_2}↖{→}$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:
${m({υ_2}↖{→}-{υ_1}↖{→})}/{∆t}=F↖{→}$
Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:
${p_2}↖{→}-{p_1}↖{→}=F↖{→}∆t$
Здесь ${p_2}↖{→}-{p_1}↖{→}=∆p↖{→}$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:
$∆p↖{→}=F↖{→}∆t$
Выражение $∆p↖{→}=F↖{→}∆t$ представляет собой математическую запись второго закона Ньютона.
Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.
Выражение $∆p↖{→}=F↖{→}∆t$ называется уравнением движения тела. Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.
Импульс системы тел. Закон изменения импульса
Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:
${p_{сист}}↖{→}={p_1}↖{→}+{p_2}↖{→}+…$
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
Рассмотрим систему, состоящую из двух тел. Силы ($F_{12}$ и $F_{21}$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.
Пусть кроме внутренних сил на систему действуют внешние силы ${F_1}↖{→}$ и ${F_2}↖{→}$. Для каждого тела можно записать уравнение $∆p↖{→}=F↖{→}∆t$. Сложив левые и правые части этих уравнений, получим:
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_{12}}↖{→}+{F_{21}}↖{→}+{F_1}↖{→}+{F_2}↖{→})∆t$
Согласно третьему закону Ньютона ${F_{12}}↖{→}=-{F_{21}}↖{→}$.
Следовательно,
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$
В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — ${∆p_{сист}}↖{→}$.С учетом этого равенство ${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$ можно записать:
${∆p_{сист}}↖{→}=F↖{→}∆t$
где $F↖{→}$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.
Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.
Закон сохранения импульса
Из уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:
${∆p_{сист}}↖{→}=m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=const$
Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.
Закон сохранения импульса гласит:
Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.
Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.
Реактивное движение
Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.
Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.
Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.
Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_{p}υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_{газ}·υ_{газ}$ выброшенных газов:
$m_{p}υ_p=m_{газ}·υ_{газ}$
Отсюда следует, что скорость ракеты
$υ_p=({m_{газ}}/{m_p})·υ_{газ}$
Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.
Формула $υ_p=({m_{газ}}/{m_p})·υ_{газ}$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.
Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.
Работа силы
Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.
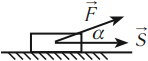
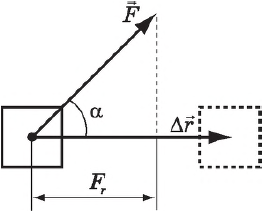
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:
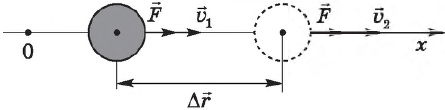
$A=F|∆r↖{→}|cosα$
где $F$ — сила, действующая на тело, $∆r↖{→}$ — перемещение, $α$ — угол между силой и перемещением.
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖{→}$ и $∆r↖{→}$.
Работа — величина скалярная. Если $α < 90°$, то $А > 0$, а если $90° < α < 180°$, то $A < 0$; если же $α = 90°$, то $А = 0$. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. Также при движении спутника по круговой орбите сила тяготения не совершает работу.
При действии на тело нескольких сил полная работа (сумма работ всех сил) равна работе результирующей силы.
Единицей работы в СИ является джоуль ($1$ Дж). $1$ Дж — это работа, которую совершает сила в $1$ Н на пути в $1$ м в направлении действия этой силы. Эта единица названа в честь английского ученого Дж. Джоуля (1818-1889): $1$ Дж = $1$ Н $·$ м. Часто применяются также килоджоули и миллиджоули: $1$ кДж $= 1 000$ Дж, $1$ мДж $= 0.001$ Дж.
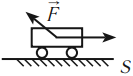
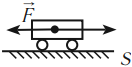
Работа силы тяжести
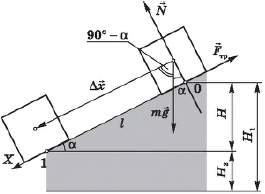
Рассмотрим тело, скользящее по наклонной плоскости с углом наклона $α$ и высотой $Н$.
Выразим $∆x$ через $H$ и $α$:
$∆x={H}/{sinα}$
Учитывая, что сила тяжести $F_т=mg$ составляет угол ($90° — α$) с направлением перемещения, используя формулу $∆x={H}/{sin}α$, получим выражение для работы силы тяжести $A_g$:
$A_g=mg·cos(90°-α)·{H}/{sinα}=mgH$
Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.
Отсюда следует, что:
- работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
- при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).
Работа сил реакции, равна нулю, поскольку сила реакции ($N$) направлена перпендикулярно перемещению $∆x$.
Работа силы трения
Сила трения направлена противоположно перемещению $∆x$ и составляет с ним угол $180°$, поэтому работа силы трения отрицательна:
$A_{тр}=F_{тр}∆x·cos180°=-F_{тр}·∆x$
Так как $F_{тр}=μN, N=mg·cosα, ∆x=l={H}/{sinα},$ то
$A_{тр}=μmgHctgα$
Работа силы упругости
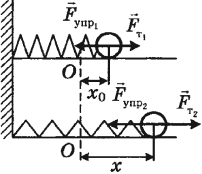
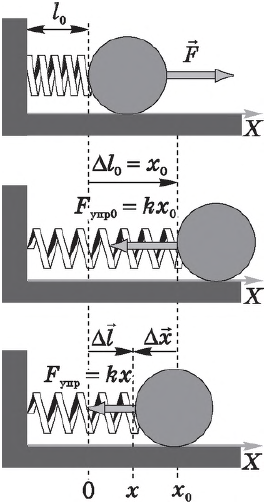
Пусть на нерастянутую пружину длиной $l_0$ действует внешняя сила $F↖{→}$, растягивая ее на $∆l_0=x_0$. В положении $x=x_0F_{упр}=kx_0$. После прекращения действия силы $F↖{→}$ в точке $х_0$ пружина под действием силы $F_{упр}$ сжимается.
Определим работу силы упругости при изменении координаты правого конца пружины от $х_0$ до $х$. Поскольку сила упругости на этом участке изменяется линейно, в законе Гука можно использовать ее среднее значение на этом участке:
$F_{упр.ср.}={kx_0+kx}/{2}={k}/{2}(x_0+x)$
Тогда работа (с учетом того, что направления ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$ совпадают) равна:
$A_{упр}={k}/{2}(x_0+x)(x_0-x)={kx_0^2}/{2}-{kx^2}/{2}$
Можно показать, что вид последней формулы не зависит от угла между ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$. Работа сил упругости зависит лишь от деформаций пружины в начальном и конечном состояниях.
Таким образом, сила упругости, подобно силе тяжести, является консервативной силой.
Мощность силы
Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.
Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за $1$ с).
Мощность определяется формулой:
$N={A}/{∆t}$
где $N$ — мощность, $А$ — работа, совершенная за время $∆t$.
Подставив в формулу $N={A}/{∆t}$ вместо работы $A$ ее выражение $A=F|{∆r}↖{→}|cosα$, получим:
$N={F|{∆r}↖{→}|cosα}/{∆t}=Fυcosα$
Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.
Мощность в системе СИ измеряется в ваттах (Вт). Один ватт ($1$ Вт) — это такая мощность, при которой за $1$ с совершается работа $1$ Дж: $1$ Вт $= 1$ Дж/с.
Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с.), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: $1$ л.с. $= 735.5$ Вт.
В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: $1$ кВт $= 1000$ Вт, $1$ МВт $= 1000000$ Вт.
Кинетическая энергия. Закон изменения кинетической энергии
Если тело или несколько взаимодействующих между собой тел (система тел) могут совершать работу, то говорят, что они обладают энергией.
Слово «энергия» (от греч. energia — действие, деятельность) нередко употребляется в быту. Так, например, людей, которые могут быстро выполнять работу, называют энергичными, обладающими большой энергией.
Энергия, которой обладает тело вследствие движения, называется кинетической энергией.
Как и в случае определения энергии вообще, о кинетической энергии можно сказать, что кинетическая энергия — это способность движущегося тела совершать работу.
Найдем кинетическую энергию тела массой $m$, движущегося со скоростью $υ$. Поскольку кинетическая энергия — это энергия, обусловленная движением, нулевым состоянием для нее является то состояние, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем его кинетическую энергию.
Для этого подсчитаем работу на участке перемещения $∆r↖{→}$ при совпадении направлений векторов силы $F↖{→}$ и перемещения $∆r↖{→}$. В этом случае работа равна
$A=F·∆x,$
где $∆x=∆r$
Для движения точки с ускорением $α=const$ выражение для перемещения имеет вид:
$∆x=υ_1t+{at^2}/{2},$
где $υ_1$ — начальная скорость.
Подставив в уравнение $A=F·∆x$ выражение для $∆x$ из $∆x=υ_1t+{at^2}/{2}$ и воспользовавшись вторым законом Ньютона $F=ma$, получим:
$A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$
Выразив ускорение через начальную $υ_1$ и конечную $υ_2$ скорости $a={υ_2-υ_1}/{t}$ и подставив в $A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$ имеем:
$A={m(υ_2-υ_1)}/{2}·(2υ_1+υ_2-υ_1)$
или
$A={mυ_2^2}/{2}-{mυ_1^2}/{2}$
Приравняв теперь начальную скорость к нулю: $υ_1=0$, получим выражение для кинетической энергии:
$E_K={mυ}/{2}={p^2}/{2m}$
Таким образом, движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую необходимо совершить, чтобы увеличить скорость тела от нуля до значения $υ$.
Из $E_K={mυ}/{2}={p^2}/{2m}$ следует, что работа силы по перемещению тела из одного положения в другое равна изменению кинетической энергии:
$A=E_{K_2}-E_{K_1}=∆E_K$
Равенство $A=E_{K_2}-E_{K_1}=∆E_K$ выражает теорему об изменении кинетической энергии.
Изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за это время силой, действующей на тело.
Потенциальная энергия
Потенциальной энергией называется энергия, определяемая взаимным расположением взаимодействующих тел или частей одного и того же тела.
Поскольку энергия определяется как способность тела совершать работу, то потенциальную энергию, естественно, определяют как работу силы, зависящую только от взаимного расположения тел. Таковой является работа силы тяжести $A=mgh_1-mgh_2=mgH$ и работа силы упругости:
$A={kx_0^2}/{2}-{kx^2}/{2}$
Потенциальной энергией тела, взаимодействующего с Землей, называют величину, равную произведению массы $m$ этого тела на ускорение свободного падения $g$ и на высоту $h$ тела над поверхностью Земли:
$E_p=mgh$
Потенциальной энергией упруго деформированного тела называют величину, равную половине произведения коэффициента упругости (жесткости) $k$ тела на квадрат деформации $∆l$:
$E_p={1}/{2}k∆l^2$
Работа консервативных сил (тяжести и упругости) с учетом $E_p=mgh$ и $E_p={1}/{2}k∆l^2$ выражается следующим образом:
$A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$
Эта формула позволяет дать общее определение потенциальной энергии.
Потенциальной энергией системы называется зависящая от положения тел величина, изменение которой при переходе системы из начального состояния в конечное равно работе внутренних консервативных сил системы, взятой с противоположным знаком.
Знак «минус» в правой части уравнения $A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$ означает, что при совершении работы внутренними силами (например, падение тела на землю под действием силы тяжести в системе «камень — Земля») энергия системы убывает. Работа и изменение потенциальной энергии в системе всегда имеют противоположные знаки.
Поскольку работа определяет лишь изменение потенциальной энергии, то физический смысл в механике имеет только изменение энергии. Поэтому выбор нулевого уровня энергии произволен и определяется исключительно соображениями удобства, например, простотой записи соответствующих уравнений.
Закон изменения и сохранения механической энергии
Полной механической энергией системы называется сумма ее кинетической и потенциальной энергий:
$E=E_k+E_p$
Она определяется положением тел (потенциальная энергия) и их скоростью (кинетическая энергия).
Согласно теореме о кинетической энергии,
$E_k-E_{k_1}=A_p+A_{пр},$
где $А_р$ — работа потенциальных сил, $А_{пр}$ — работа непотенциальных сил.
В свою очередь, работа потенциальных сил равна разности потенциальной энергии тела в начальном $Е_{р_1}$ и конечном $Е_р$ состояниях. Учитывая это, получим выражение для закона изменения механической энергии:
$(E_k+E_p)-(E_{k_1}+E_{p_1})=A_{пр}$
где левая часть равенства — изменение полной механической энергии, а правая — работа непотенциальных сил.
Итак, закон изменения механической энергии гласит:
Изменение механической энергии системы равно работе всех непотенциальных сил.
Механическая система, в которой действуют только потенциальные силы, называется консервативной.
В консервативной системе $А_{пр} = 0$. Отсюда следует закон сохранения механической энергии:
В замкнутой консервативной системе полная механическая энергия сохраняется (не изменяется со временем):
$E_k+E_p=E_{k_1}+E_{p_1}$
Закон сохранения механической энергии выводится из законов механики Ньютона, которые применимы для системы материальных точек (или макрочастиц).
Однако закон сохранения механической энергии справедлив и для системы микрочастиц, где сами законы Ньютона уже не действуют.
Закон сохранения механической энергии является следствием однородности времени.
Однородность времени состоит в том, что при одинаковых начальных условиях протекание физических процессов не зависит от того, в какой момент времени эти условия созданы.
Закон сохранения полной механической энергии означает, что при изменении кинетической энергии в консервативной системе должна меняться и ее потенциальная энергия, так что их сумма остается постоянной. Это означает возможность превращения одного вида энергии в другой.
В соответствии с различными формами движения материи рассматривают различные виды энергии: механическую, внутреннюю (равную сумме кинетической энергии хаотического движения молекул относительно центра масс тела и потенциальной энергии взаимодействия молекул друг с другом), электромагнитную, химическую (которая складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами), ядерную и пр. Из сказанного видно, что деление энергии на разные виды достаточно условно.
Явления природы обычно сопровождаются превращением одного вида энергии в другой. Так, например, трение частей различных механизмов приводит к превращению механической энергии в тепло, т. е. во внутреннюю энергию. В тепловых двигателях, наоборот, происходит превращение внутренней энергии в механическую; в гальванических элементах химическая энергия превращается в электрическую и т. д.
В настоящее время понятие энергии является одним из основных понятий физики. Это понятие неразрывно связано с представлением о превращении одной формы движения в другую.
Вот как в современной физике формулируется понятие энергии:
Энергия — общая количественная мера движения и взаимодействия всех видов материи. Энергия не возникает из ничего и не исчезает, она может только переходить из одной формы в другую. Понятие энергии связывает воедино все явления природы.
Простые механизмы. КПД механизмов
Простыми механизмами называются приспособления, изменяющие величину или направление приложенных к телу сил.
Они применяются для перемещения или подъема больших грузов с помощью небольших усилий. К ним относятся рычаг и его разновидности — блоки (подвижный и неподвижный), ворот, наклонная плоскость и ее разновидности — клин, винт и др.
Рычаг. Правило рычага
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
Правило рычага гласит:
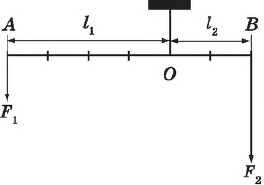
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
${F_2}/{F_1}={l_1}/{l_2}$
Из формулы ${F_2}/{F_1}={l_1}/{l_2}$, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:
$F_1l_1=F_2l_2$
Но $F_1l_1=M_1$ — момент силы, стремящейся повернуть рычаг по часовой стрелке, а $F_2l_2=M_2$ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, $M_1=M_2$, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту $147$ м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу $2.5$ тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).
Неподвижный блок
Действие неподвижного блока аналогично действию рычага с равными плечами: $l_1=l_2=r$. Приложенная сила $F_1$ равна нагрузке $F_2$, и условие равновесия имеет вид:
$F_1=F_2$
Неподвижный блок применяют, когда нужно изменить направление силы, не меняя ее величину.
Подвижный блок
Подвижный блок действует аналогично рычагу, плечи которого составляют: $l_2={l_1}/{2}=r$. При этом условие равновесия имеет вид:
$F_1={F_2}/{2}$
где $F_1$ — приложенная сила, $F_2$ — нагрузка. Применение подвижного блока дает выигрыш в силе в два раза.
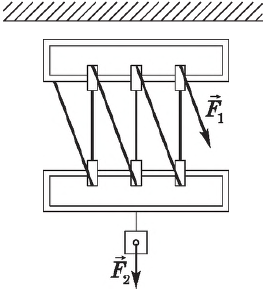
Полиспаст (система блоков)
Обычный полиспаст состоит из $n$ подвижных и $n$ неподвижных блоков. Его применив дает выигрыш в силе в $2n$ раз:
$F_1={F_2}/{2n}$
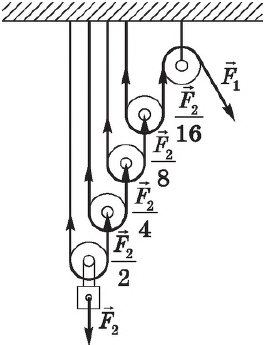
Степенной полиспаст состоит из п подвижных и одного неподвижного блока. Применение степенного полиспаста дает выигрыш в силе в $2^n$ раз:
$F_1={F_2}/{2^n}$
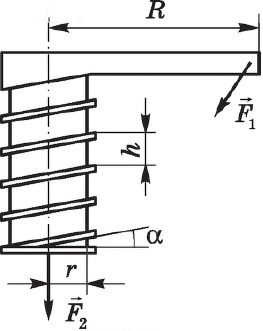
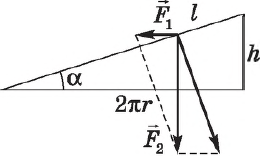
Винт
Винт представляет собой наклонную плоскость, навитую на ось.
Условие равновесия сил, действующих на винт, имеет вид:
$F_1={F_2h}/{2πr}=F_2tgα, F_1={F_2h}/{2πR}$
где $F_1$ — внешняя сила, приложенная к винту и действующая на расстоянии $R$ от его оси; $F_2$ — сила, действующая в направлении оси винта; $h$ — шаг винта; $r$ — средний радиус резьбы; $α$ — угол наклона резьбы. $R$ — длина рычага (гаечного ключа), вращающего винт с силой $F_1$.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — отношение полезной работы ко всей затраченной работе.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой $η$ («эта»):
$η={A_п}/{A_3}·100%$
где $А_п$ — полезная работа, $А_3$ — вся затраченная работа.
Полезная работа всегда составляет лишь часть полной работы, которую затрачивает человек, используя тот или иной механизм.
Часть совершенной работы тратится на преодоление сил трения. Поскольку $А_3 > А_п$, КПД всегда меньше $1$ (или $< 100%$).
Когда КПД немного меньше $1$, можно считать, что затраченная работа примерно равна полезной: $А_3 ≈ А_п$.
Поскольку каждую из работ в этом равенстве можно выразить в виде произведения соответствующей силы на пройденный путь, то его можно переписать так: $F_1s_1≈F_2s_2$.
Отсюда следует, что, выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот. Этот закон называют золотым правилом механики.
Золотое правило механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
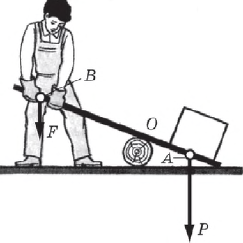
Так, например, благодаря этому правилу сразу можно сказать, что рабочему, изображенному на рисунке, при двукратном выигрыше в силе подъема груза на $10$ см придется опустить противоположный конец рычага на $20$ см.
Столкновение тел. Упругий и неупругий удары
Законы сохранения импульса и механической энергии применяются для решения задачи о движении тел после столкновения: по известным импульсам и энергиям до столкновения определяются значения этих величин после столкновения. Рассмотрим случаи упругого и неупругого ударов.
Абсолютно неупругим называется удар, после которого тела образуют единое тело, движущееся с определенной скоростью. Задача о скорости последнего решается с помощью закона сохранения импульса системы тел с массами $m_1$ и $m_2$ (если речь идет о двух телах) до и после удара:
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=(m_1+m_2)υ↖{→}$
Очевидно, что кинетическая энергия тел при неупругом ударе не сохраняется (например, при ${υ_1}↖{→}=-{υ_2}↖{→}$ и $m_1=m_2$ она становится равной нулю после удара).
Абсолютно упругим называется удар, при котором сохраняется не только сумма импульсов, но и сумма кинетических энергий ударяющихся тел.
Для абсолютно упругого удара справедливы уравнения
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=m_1{υ’_1}↖{→}+m_2{υ’_2}↖{→};$
${m_{1}υ_1^2}/{2}+{m_{2}υ_2^2}/{2}={m_1(υ’_1)^2}/{2}+{m_2(υ’_2)^2}/{2}$
где $m_1, m_2$ — массы шаров, $υ_1, υ_2$ —скорости шаров до удара, $υ’_1, υ’_2$ —скорости шаров после удара.
Тема 30.
Механика (Расчетная задача высокого уровня сложности+обоснование)
30
.
03
Законы сохранения в механике
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
механика (расчетная задача высокого уровня сложности+обоснование)
30.01Кинематика
30.02Динамика
30.03Законы сохранения в механике
30.04Статика
30.05Гидростатика
30.06Механические колебания
Решаем задачи
Показать ответ и решение
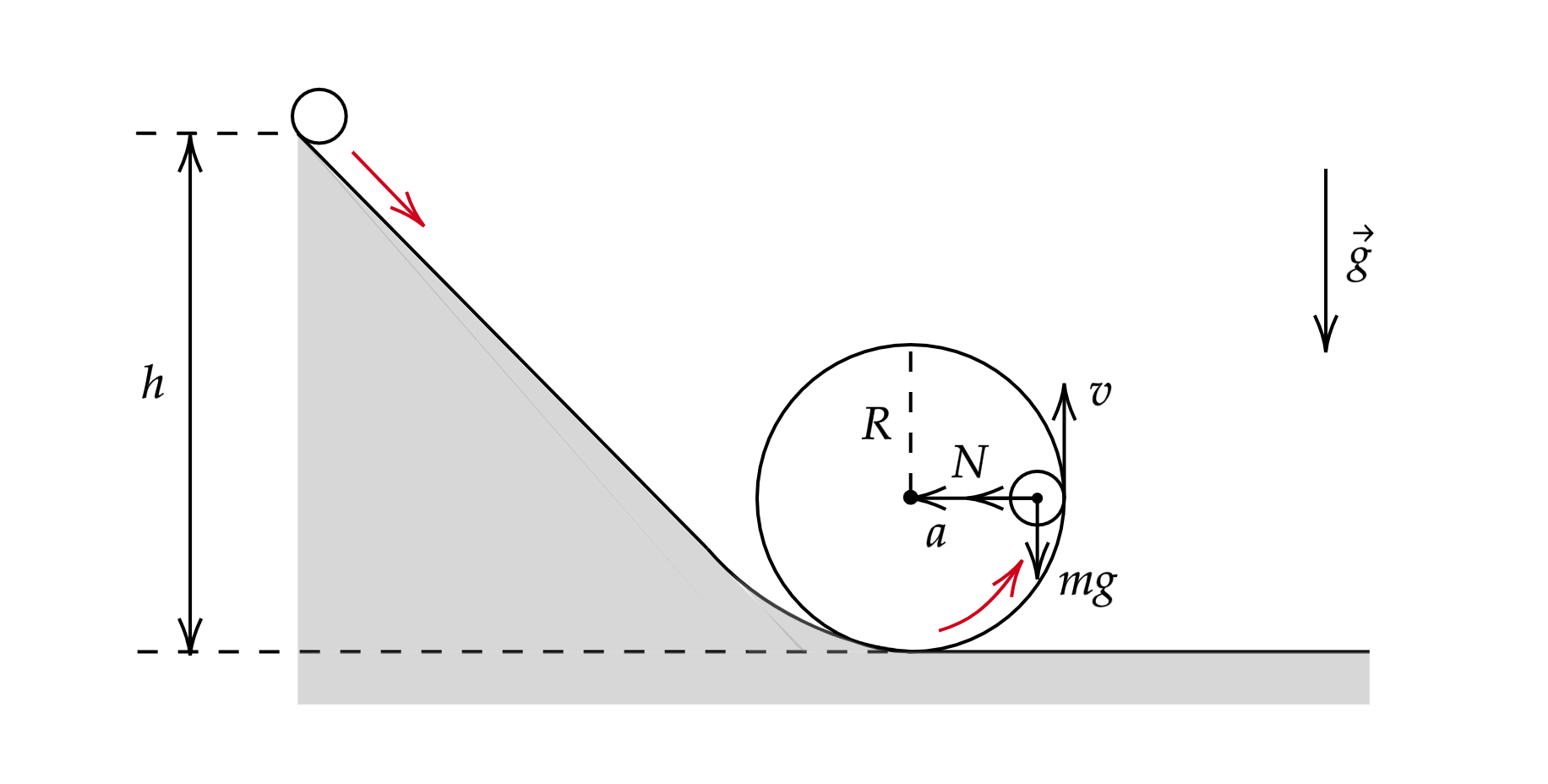
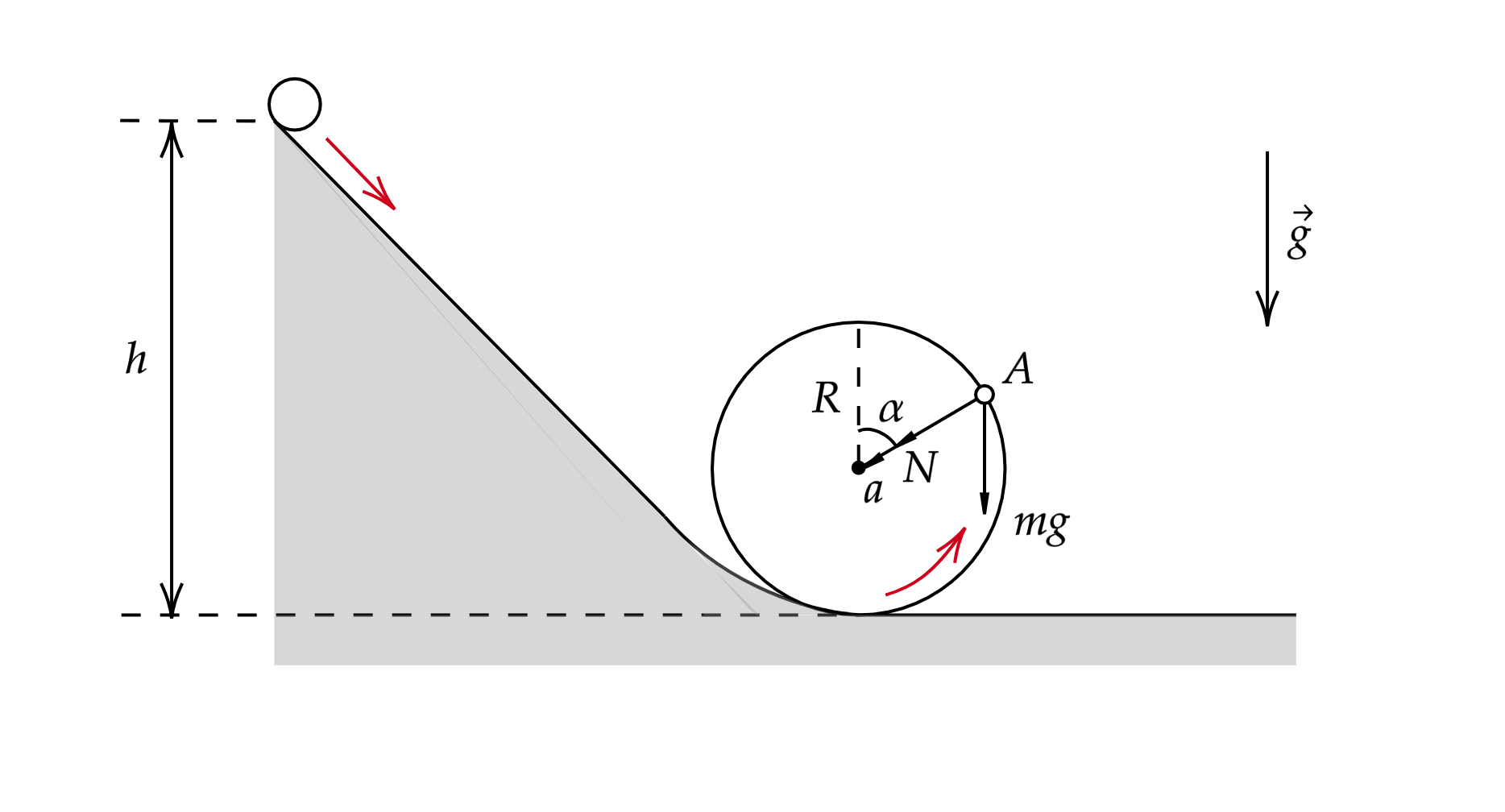
1) Запишем закон сохранения энергии для шайбы:
Отсюда:
2)
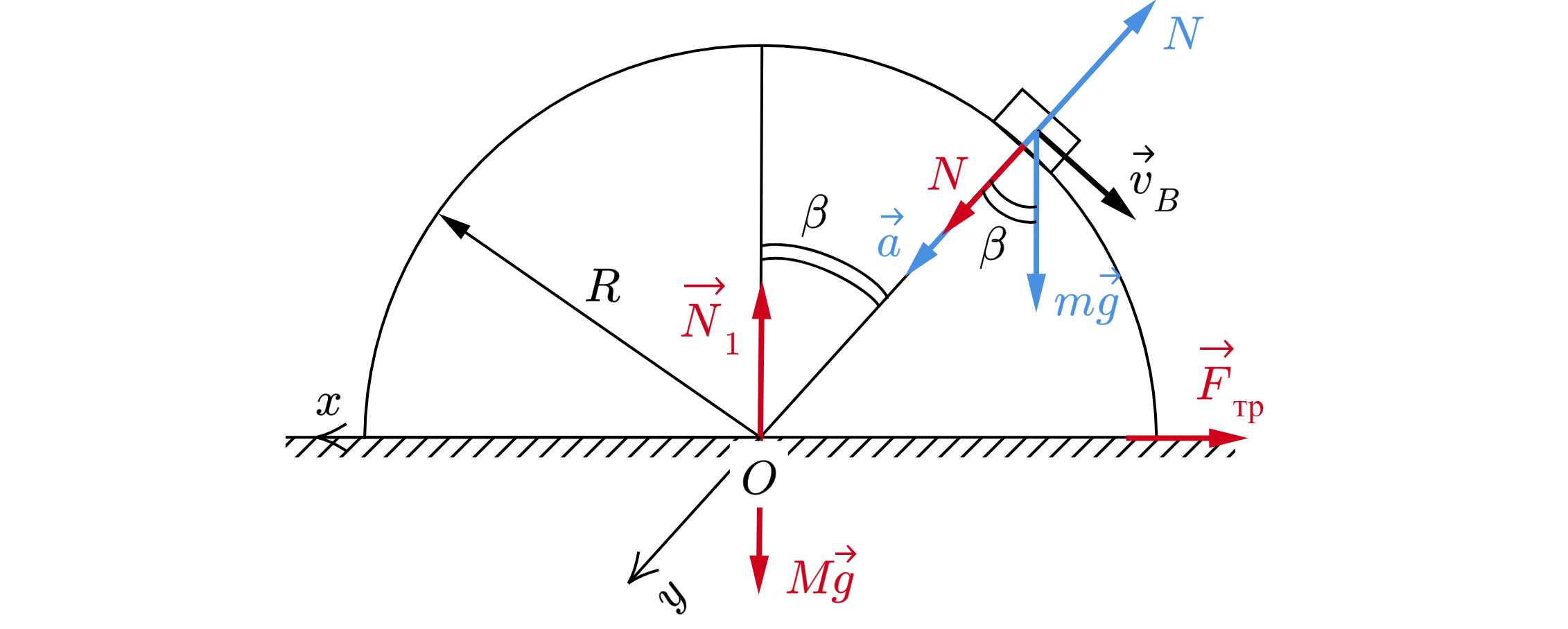
Расставим силы, действующие на шайбу (синим цветом) и полусферу (красным цветом) в точке
Здесь – сила реакции опоры со стороны шайбы, а также из третьего закона Ньютона сила
давления шайбы на полушар, – сила тяжести шайбы,
– сила тяжести полушара,
–
сила реакции опоры со стороны стола, – сила трения между столом и полушаром,
–
центростремительное ускорение Запишем второй закон Ньютона для шайбы:
Спроецируем его на ось :
центростремительное ускорение можно найти по формуле:
тогда
с
учётом (1) и условия
Запишем второй закон Ньютона для полушара:
где
– ускорение полушара.
Так как полушар неподвижен, то . Спроецируем второй закон Ньютона на ось
:
С
учетом, что и (2), имеем:
Показать ответ и решение
1) Запишем закон сохранения энергии
Запишем второй закон Ньютона для шарика:
где
— сила натяжения нити,
– центростремительное ускорение,
– скорость тела,
– длина
нити.
На рисунке красным показаны силы, действующие на брусок, и синим – действующие на
шарик. Запишем второй закон Ньютона на ось, сонаправленную с центростремительным
ускорением
2)
Запишем второй закон Ньютона для бруска:
где
– сила реакции опоры,
– сила трения,
– ускорение бруска.
Расстановка сила показана на рисунке выше красным цветом. Спроецируем второй закон Ньютона на
вертикальную и горизонтальную ось:
в
момент начала скольжения , тогда
Подставляем числа из условия
Маленький шарик массой m подвешен на нити и колеблется в вертикальной плоскости с угловой
амплитудой .
1) Найти минимальную силу натяжения нити при колебаниях.
2) Найти максимальную силу натяжения нити при колебаниях.
3) Найти касательное ускорение шарика в момент, когда сила натяжения нити в 1,5 раза больше её
минимального значения.
(«Физтех», 2016, 10–11 )
Показать ответ и решение
Запишем второй закон Ньютона:
где – сила натяжения нити,
– центростремительное ускорение,
– скорость шарика,
– длина нити.
Пусть – угол между вертикалью и силой натяжения нити. Тогда второй закон Ньютона в проекции
на ось, совпадающую с осью движения шарика, запишется в виде:
Запишем также закон сохранения энергии
Тогда второй закон Ньютона запишется в виде
1) Минимальная сила натяжения будет при
2) Максимальная при
3) По условию . Найдем угол между вертикалью и силой натяжения нитью
,
тогда
Из последних двух уравнений
Откуда
Откуда
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать
второй закон Ньютона относительно ИСО.
4. Так как сумма работ всех сил равняется изменению кинетической энергии тела, то применим
закон изменения кинетической энергии. За нулевой уровень потенциальной энергии выберем уровень, на
котором находится стенка.
Решение
Изобразим силы, действующие на тело в процессе движения вниз (рис. 1) и вверх (рис.
2).
Где – сила трения,
– сила реакции опоры.
Запишем второй закон Ньютона:
Спроецируем второй закон Ньютона на ось для движения вниз и вверх:
Сила трения же равна:
При этом тело остановится у стенки. Запишем закон об изменении кинетической энергии:
где – работа силы реакции опоры,
– работа силы тяжести,
– работа силы
трения.
Работа находится по формуле:
где – сила,
– перемещение,
– угол между силой и перемещением.
Найдём работу каждой силы:
Работа силы тяжести равна изменению потенциальной энергии тела
Работа силы трения отрицательна, так как сила трения направлена противоположно движению
бруска:
Тогда закон об изменении кинетической энергии запишется в виде:
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обоснована возможность использования закона об изменении кинетической энергии
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в
векторной форме и в проекции на координатные оси, формула силы трения скольжения, закон
изменения механической энергии, формула для вычисления работы силы по перемещению
тела).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
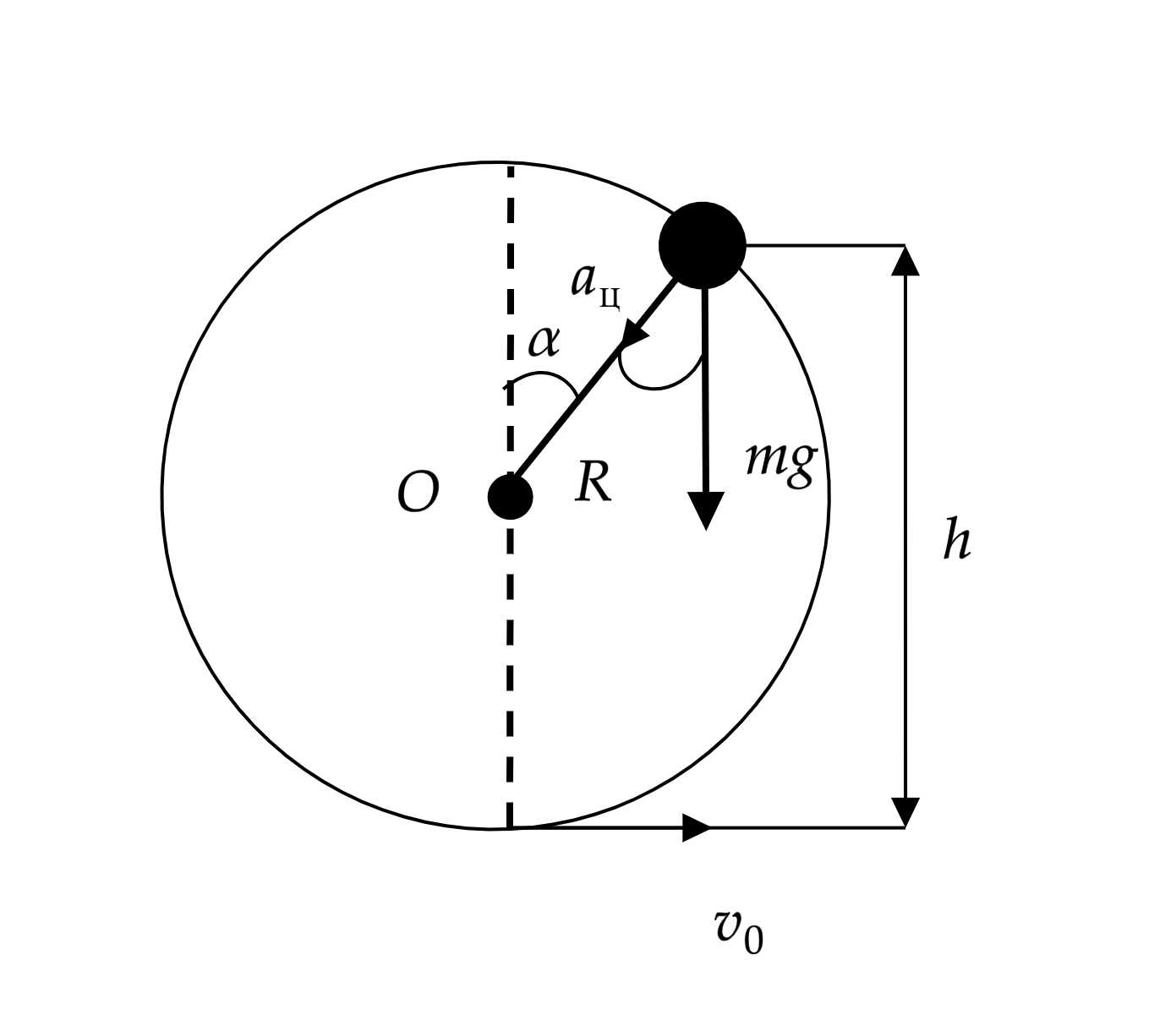
С высоты соскальзывает без начальной скорости небольшой шарик, двигаясь без трения по
жёлобу, расположенному в вертикальной плоскости (см. рисунок). Горизонтальный участок жёлоба
плавно переходит в полуокружность радиуса . Какой максимальной высоты достигнет шарик после
отрыва от жёлоба?
Какие законы Вы используете для решения задачи? Обоснуйте их применение.
МФТИ, 1994
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать
второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не
потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна
вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная
механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень,
на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм
ускорением, направленным к центру окружности вращения.
Решение
Пусть – сила реакции опоры,
– центростремительное ускорение,
– сила тяжести,
–
угол между силой тяжести и центростремительным ускорением.
В момент отрыва от петли будет равна 0, значит второй закон Ньютона запишется в
виде
Найдем скорость тела в момент отрыва, как разность потенциальных энергий
где – высота отрыва шайбы от поверхности,
— потенциальная энергия тела на высоте
,
— кинетическая энергия на высоте
,
— потенциальная энергия на высоте
.
Подставляем (2) в (1) и находим
Откуда высота отрыва
Синус угла
Или тангенс
Скорость направлена перпендикулярно центростремительному ускорению, следовательно
Скорость тела в момент отрыва
Тогда горизонтальная и вертикальная составляющие скорости
После отрыва шайба дополнительно поднимется на высота , пока скорость шайбы на станет
равна нулю. Найдём эту высоту, для этого запишем уравнение кинематики на вертикальную
ось:
где – время движения.
Подъём будет осуществляться, пока вертикальная составляющая скорости не станет равна
нулю.
Тогда высота подъема
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к шарику модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения шарика
4. Обоснована возможность использования закона сохранения энергия для связи состояний
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: закон сохранения
энергии, второй закон Ньютона в векторной форме и в проекции на координатную ось для
момента отрыва тела от петли, формулы центростремительного ускорения, кинетической и
потенциальной энергии, уравнения кинематики для скорости и максимальной высоты подъема
тела).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
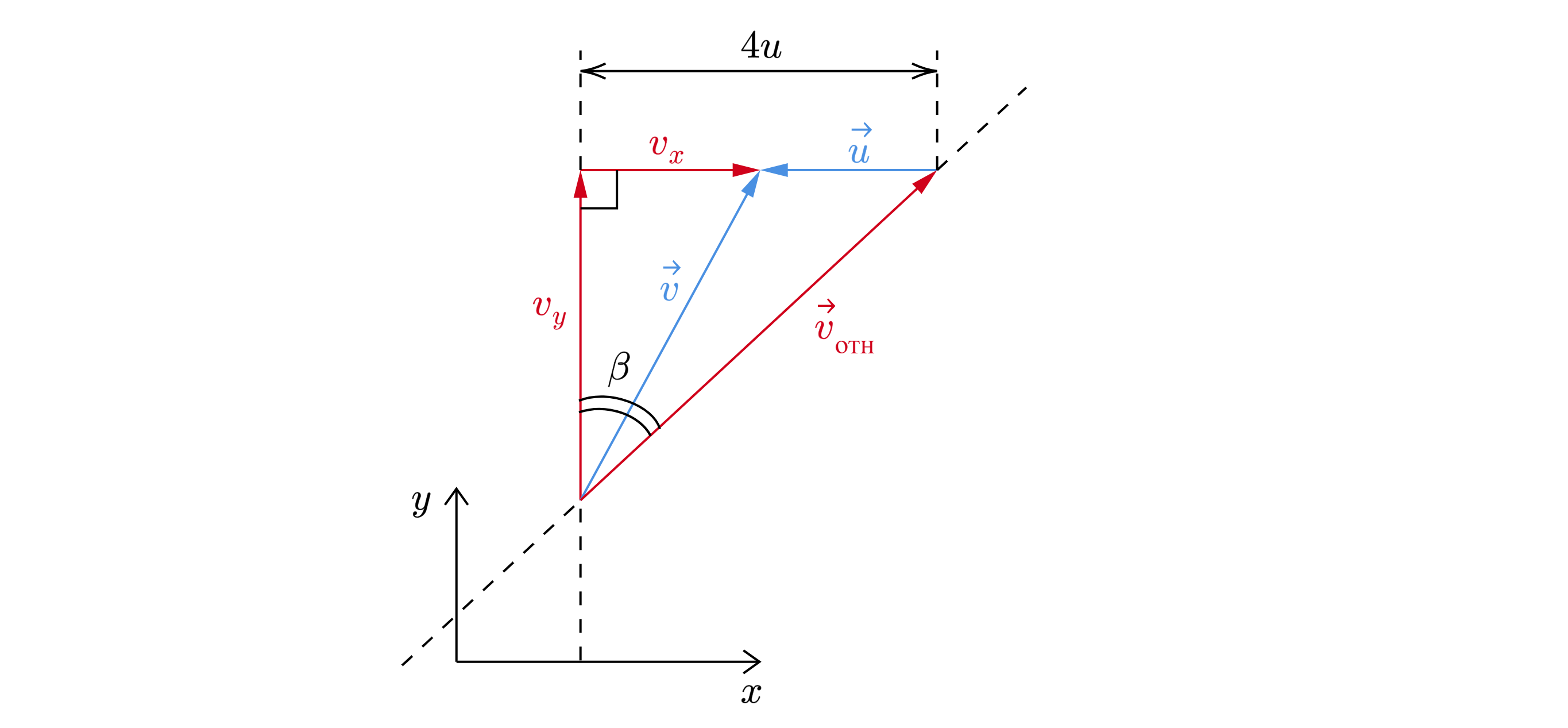
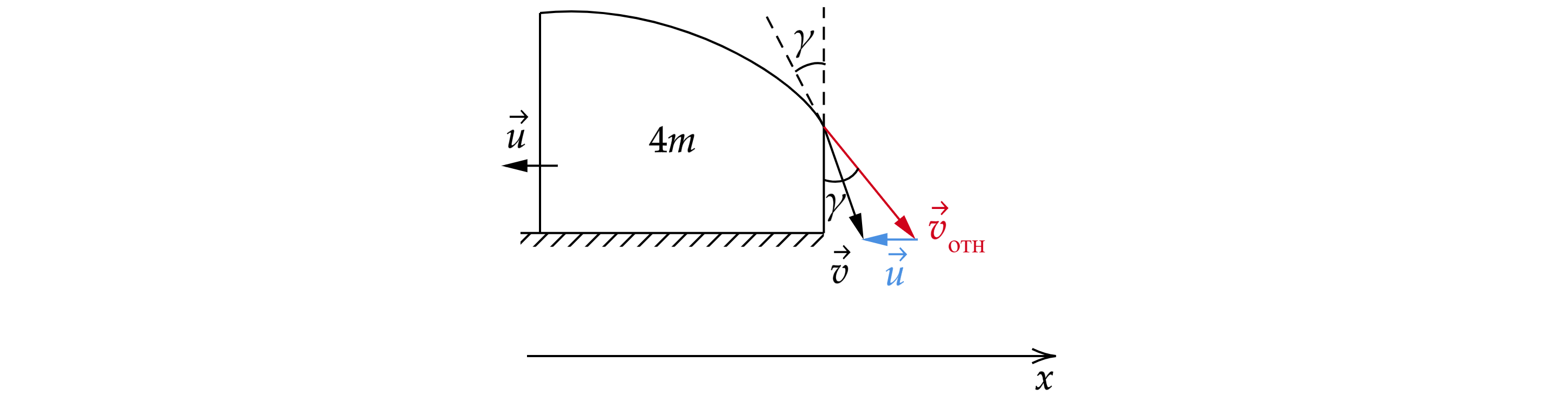
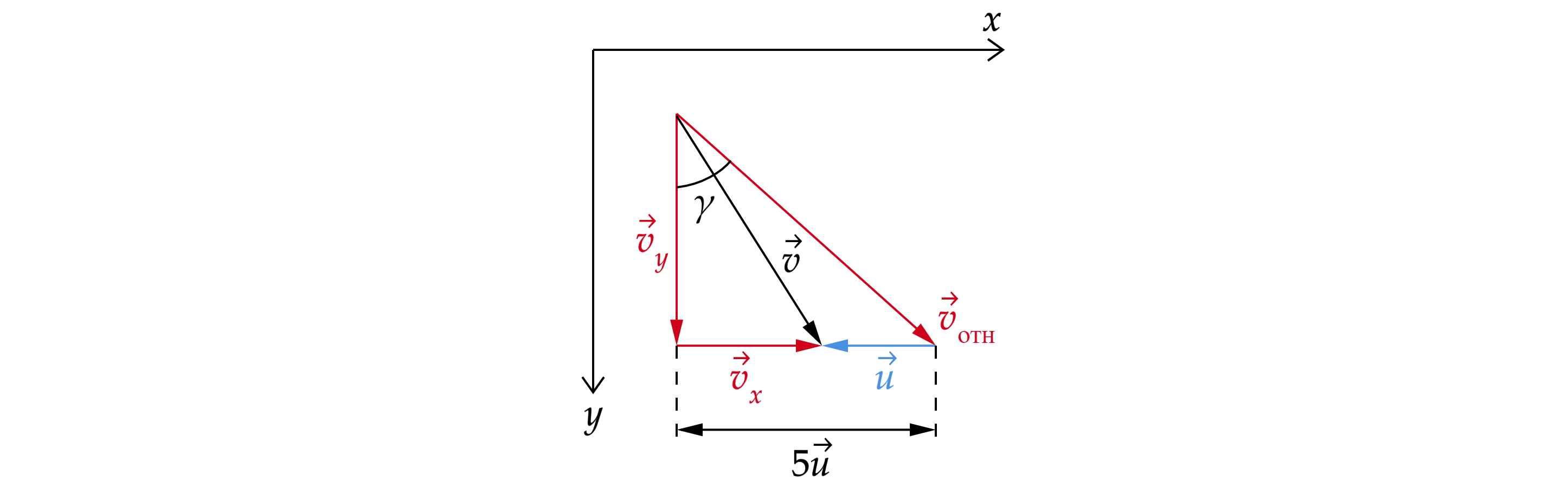
Так как шайба движется без отрыва от горки, то относительная скорость шайбы при вылете с горки
направлена под углом к перпендикуляру (см. рис.).
Изобразим треугольник скоростей
Здесь – скорость шайбы относительно горки,
– скорость горки,
– скорость шайбы в
неподвижной системе отсчёта, и
– проекция скорости
на горизонтальную и вертикальную
оси.
Запишем закон сохранения энергии:
Запишем также закон сохранения импульса для горизонтальной системы отсчёта:
Из
треугольника скоростей можно найти
Из
теоремы Пифагора
Тогда по закону сохранения энергии
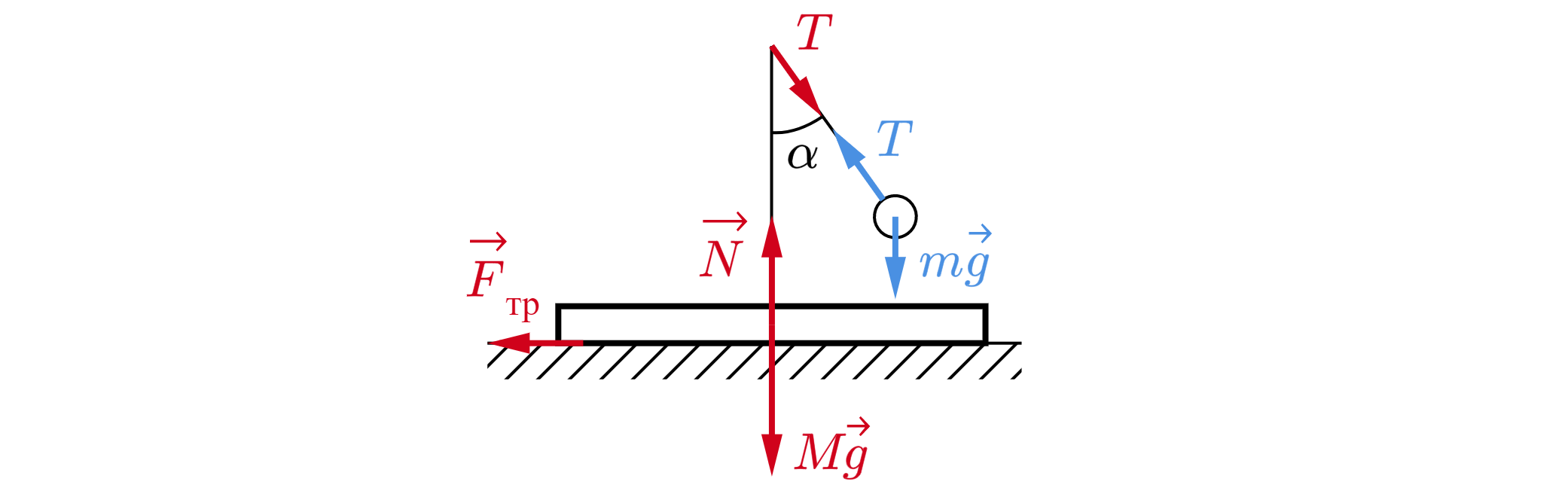
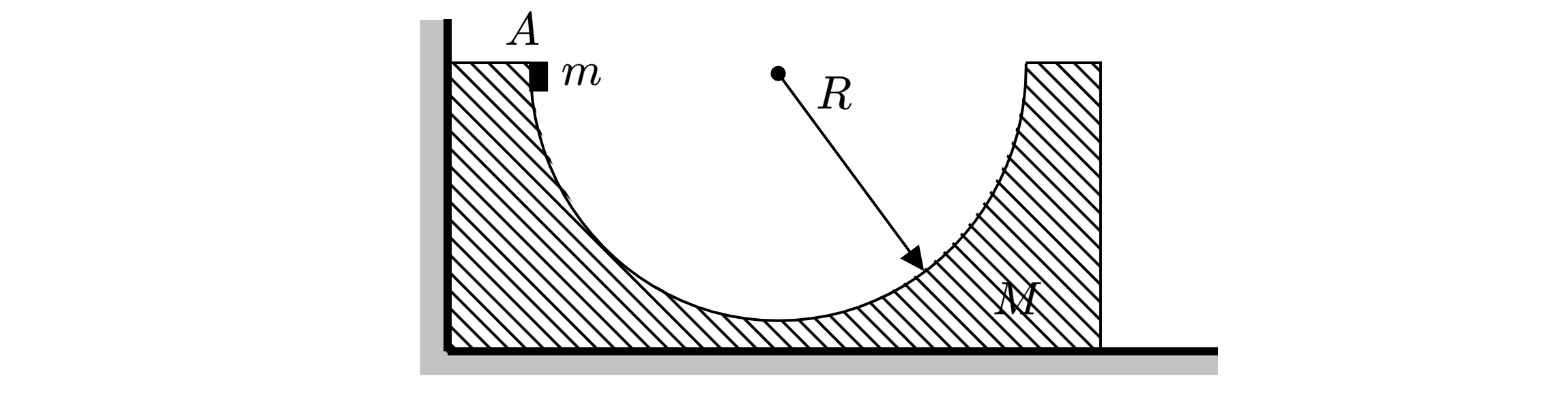
На гладкой горизонтальной поверхности вплотную к вертикальной стенке стоит брусок массой
кг, в котором сделано гладкое углубление полусферической формы радиусом
м. Из
точка А начинает соскальзывать маленькая шайба массой кг. Найдите максимальную высоту
относительно нижней точки полусферы, на которую поднимется шайба при ее последующем
движении. Какие законы Вы используете для решения задачи? Обоснуйте их применение.
ДВИ МГУ 2020
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Шайба движется поступательно, её размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. На максимальной высоте подъёма скорости шайбы и полусферы будут равны и направлены по
горизонтали (вертикальная составляющая скорости шайбы равняется нулю в верхней точке) , не будет
наблюдаться их относительного движения, после этого момента времени, шайба будет скатываться
обратно вниз относительно полусферы.
4. На тело массой и полусферу
действуют силы реакции опоры, так как поверхность
полусферы гладкая, то суммарная работа сил нормальной реакции опоры действующей на шайбу массой
и полусферу
равняется нулю (идеальная связь). За нулевой уровень потенциальной энергии
выберем нижнюю точку полусферы. Выполняется закон сохранения энергии для системы
тел.
5. Так как на систему не действуют внешние силы по горизонтальному направлению, то выполняется
закон сохранения импульса в проекции на эту ось.
Решение
До нижней точки движения шайба будет «давить»на брусок с силой, направленной к стенке,
следовательно, брусок не будет сдвигаться с места. На высоте шайба имеет потенциальную
энергию:
А при движении в нижней точке углубления со скоростью кинетическая энергия шайбы
равна:
Найдем скорость шайбы в нижней точке траектории из закона сохранения энергии движения шайбы
вниз:
Максимальная высота будет достигнута тогда, когда скорость бруска и шайбы будет равна, пусть
она равна . Воспользуемся законом сохранения импульса
в проекции на горизонтальную ось:
Пусть максимальная высота подъёма равна , тогда потенциальная энергия шайбы на этой высоте
равна:
при этом на этой высоте будет и кинетическая энергия шайбы и бруска, равна:
Из закона сохранения энергии для движения шайбы вверх:
с учетом ранее написанных выражений, имеем
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к шайбе модели материальной точки
3. Обосновано применение закона сохранения импульса
4. Обосновано применение закона сохранения энергии для шайбы и системы тел вместе.
5. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения механической энергии,
формулы кинетической энергии точки, потенциальной энергии тела в однородном поле
тяжести. Закон сохранения импульса сначала в векторном виде, после в проекции на выбранные
оси).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Так как шайба движется без отрыва от горки, то относительная скорость шайбы при вылете с горки
направлена под углом к перпендикуляру (см. рис.).
Запишем закон сохранения импульса:
где – скорость шайбы.
В проекции на горизонтальную ось :
Изобразим треугольник скоростей
Здесь – скорость шайбы относительно горки,
– скорость горки,
– скорость шайбы в
неподвижной системе отсчёта, и
– проекция скорости
на горизонтальную и вертикальную
оси.
Из треугольника скоростей можно найти
Из теоремы Пифагора
Запишем также закон сохранения энергии при движении шайбы вниз после отрыва от
горки:
где – искомая конечная скорость.
Откуда
Трубка в виде петли жёстко укреплена на платформе, находящейся на гладкой горизонтальной
поверхности стола. Правый конец трубки горизонтален, его расстояние до стола равно . В трубке на
высоте удерживается шарик массой m, который может скользить по трубке без трения (см.
рисунок). Масса платформы с трубкой . Система покоится. Шарик отпускают. Найти скорость
вылетевшего из трубки шарика, если:
1) платформа закреплена на столе;
2) платформа не закреплена и после вылета шарика движется поступательно.
МФТИ, 1997
Показать ответ и решение
1) Если платформа закреплена на столе, то её скорость равна нулю. Запишем закон сохранения
энергии:
отсюда искомая скорость :
2)
Если платформа не закреплена, то она имеет некоторую скорость. Запишем закон сохранения
импульса:
где – скорость шарика при вылете из трубки,
– скорость платформы при вылете
шарика.
Спроецируем закон сохранения импульса на горизонтальную ось:
Запишем закон сохранения энергии:
Отсюда:
Лягушка массой 100 г сидит на конце доски массой 900 г и длиной 50 см, которая лежит
на гладкой горизонтальной поверхности. Лягушка прыгает под углом вдоль доски.
Какова должна быть начальная скорость лягушки, чтобы она приземлилась на другом конце
доски?
Показать ответ и решение
Пусть за время полёта доска сместится на ,
– масса доски,
– масса лягушки,
– длина
доски, – начальная скорость лягушки,
.
Запишем закон сохранения импульса в проекции на горизонтальную ось
где
– скорость доски после прыжка.
Воспользуемся уравнениями кинематики. По горизонтали лягушка должна пройти ,
тогда
где
– время полёта.
Время полёта можно найти из, уравнения
где
– высота над доской.
При этом при
, тогда
Откуда
движения доски является равномерным, тогда если доска прошла , то должно выполняться
равенство
или с
учётом (2)
Объединим (1) и (4)
Из
(3) выразим
Приравняем два последних уравнения
Или
Подставим в формулу из
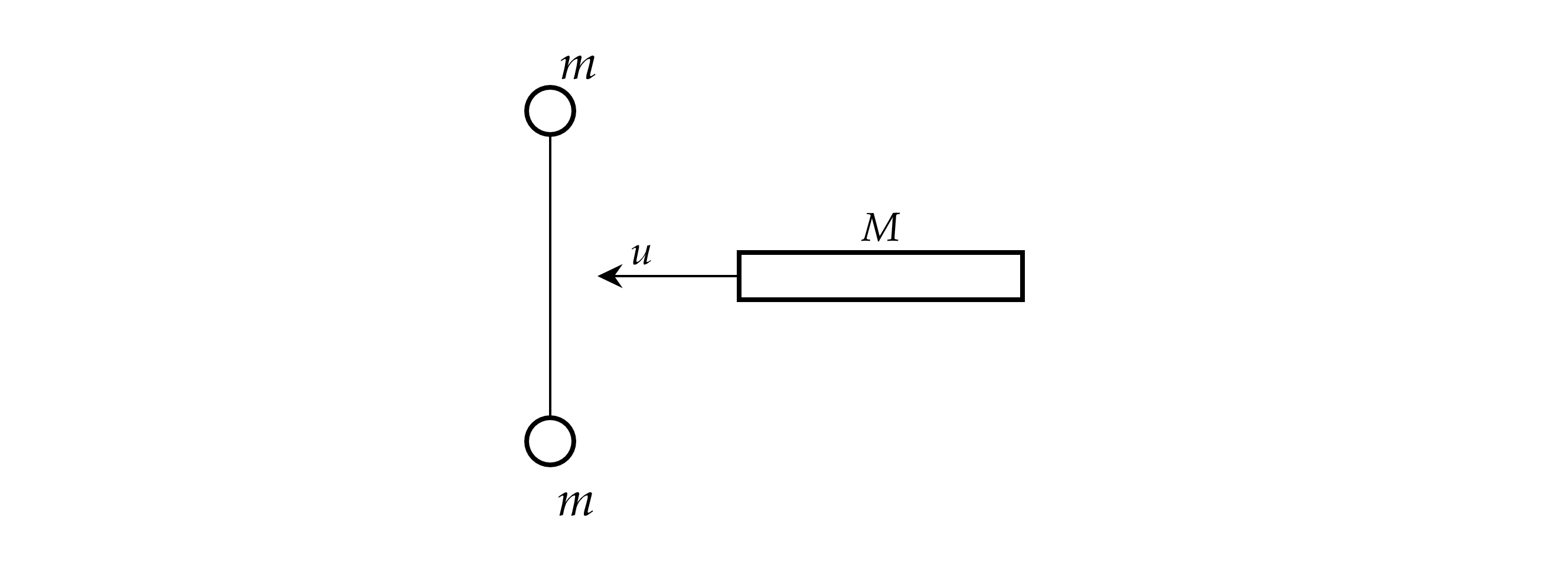
Два одинаковых шара массы каждый связаны прочной нитью и лежат на гладком столе (рис. вид
сверху) . Доска массы налетает со скоростью
м/с на эту систему и ударяет по середине
нити. Найти скорости шаров при ударе о доску. Какие законы Вы используете для решения задачи?
Обоснуйте их применение.
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тела движутся поступательно, их размеры малы по сравнению с размерами установки, будем
описывать тела моделью материальной точки.
3. Будем считать, что время соударения доски и нити мало, а значит нить за это время
не успевает заметно отклониться, поэтому в момент столкновения все силы направлены
вертикально (в плоскость чертежа и от неё). Следовательно, в ИСО при попадании доски в
нить сохраняется горизонтальная составляющая импульса системы тел «шарики m + доска
M».
4. Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил,
приложенных к телу, а в данном случае такой силой является только сила реакции опоры
(сопротивлением воздуха пренебрегаем, поверхность гладкая), при этом в любой точке траектории сила
реакции опоры перпендикулярна скорости, поэтому работа силы реакции опоры равняется нулю и
полная механическая энергия тела M + 2m сохраняется. Выполняется закон сохранения
энергии.
Решение
Пусть проекции скоростей шаров на направление, перпендикулярное направлению движения
доски, а – скорость доски сразу после удара. Из законов сохранения энергии и импульса
имеем
отсюда
Подставим это значение в закон сохранения энергии
Значит полная скорость шариков будет равна:
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телам модели материальной точки
3. Обосновано применение закона сохранения импульса для описания движения тел
4. Обосновано применение закона сохранения энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: закон сохранения импульса в проекции на
горизонтальную ось, закон сохранения энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
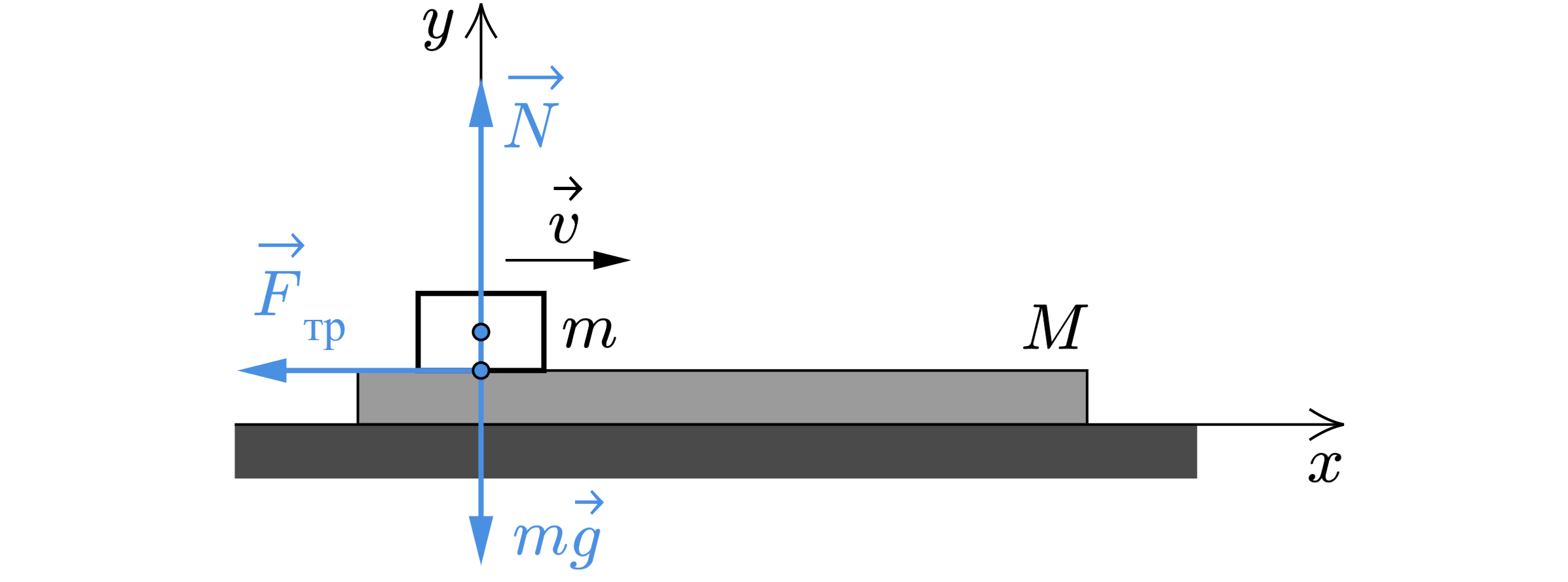
Расставим силы, действующие на шайбу при движении по доске.
Движение шайбы прекратится в тот момент, когда скорость шайбы и доски будет одинакова.
Запишем закон сохранения импульса:
где – скорость системы «шайба+доска».
Спроецируем на ось :
Запишем второй закон Ньютона:
где – сила трения скольжения,
– сила реакции доски,
– ускорение шайбы.
Сила трения скольжения равна:
Спроецируем второй закон Ньютона на вертикальную ось :
И на горизонтальную ось :
Тогда
Движение шайбы по доске является равноускоренным, значит, описывается уравнением:
Подставим (1) и (2) в (3)
Или
Отсюда
Снаряд массой 4 кг, летящий со скоростью 400 м/с в полёте разрывается на две равные части, одна из
которых продолжает движение по направлению движения снаряда, а другая – в противоположную
сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии
взрыва на величину 0,5 МДж. Найдите модуль скорости осколка, движущегося по направлению
движения снаряда
Демоверсия 2022
Показать ответ и решение
Обоснование
Введем инерциальную систему отсчёта, связанную с Землёй, и направим ось Оx системы координат в
направлении начальной скорости движения снаряда. При описании движения снаряда и осколков
используем модель материальной точки. Для описания разрыва снаряда использован закон сохранения
импульса системы тел. Он выполняется в инерциальной системе отсчёта, если сумма внешних сил,
приложенных к телам системы, равна нулю. В данном случае из-за отсутствия сопротивления
воздуха внешней силой является только сила тяжести , которая не равна нулю. Но
этим можно пренебречь, считая время разрыва снаряда малым. За малое время разрыва
импульс каждого из осколков меняется на конечную величину за счёт больших внутренних сил,
разрывающих снаряд при взрыве. По сравнению с этими большими силами конечная сила тяжести
пренебрежимо мала. Так как время разрыва снаряда считаем малым, то можно пренебречь
и изменением потенциальной энергии снаряда и его осколков в поле тяжести в процессе
разрыва.
Решение
Кинетическая энергия тела находится по формуле:
где – масса тела,
– его скорость.
Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения
энергии
где начальная скорость гранаты.
Выразим скорость второго осколка из второго уравнения.
Подставим в первое уравнение системы
Выразим :
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета.
2. Описано рассмотрение тела моделью материальной точки.
3. Описана возможность применения закона сохранения импульса.
4. Описано применение закона сохранения энергии.
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: закон сохранения
импульса, закон сохранения энергии, записана формула импульса, формула кинетического
энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
На горизонтальной поверхности неподвижно закреплена абсолютно гладкая полусфера радиусом
м. С её верхней точки из состояния покоя соскальзывает маленькое тело. В некоторой точке
тело отрывается от сферы и летит свободно. Найдите скорость тела в момент отрыва от сферы.
Сопротивлением воздуха пренебречь. Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать
второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не
потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна
вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная
механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень
горизонтальной поверхности.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм
ускорением, направленным к центру окружности вращения.
Решение
Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это
означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой
тяжести. Запишем второй закон Ньютона
где – масса тела,
– сила реакции опоры,
– центростремительное ускорение.
Так как , то с учетом формулы центростремительного ускорения
где
– скорость
тела, – радиус полусферы.
Тогда второй закон Ньютона на ось
С учетом того, что имеем
Также запишем закон сохранения энергии
где – потенциальная энергия тела на высоте
,
– кинетическая энергия на
высоте ,
– потенциальная энергия на высоте
. Расписав все слагаемые по формулам
получим
Подставим (1) в (2)
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тел
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной
форме и в проекции на радиальное направление для момента отрыва тела, закон сохранения
механической энергии, формулы потенциальной и кинетической энергии, центростремительного
ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Маленький шарик входит в мёртвую петлю радиуса , соскальзывая без начальной скорости с высоты
. На какой высоте шарик оторвётся от поверхности петли? Какие законы Вы используете для
решения задачи? Обоснуйте их применение.
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать
второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не
потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна
вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная
механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень,
на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм
ускорением, направленным к центру окружности вращения.
Решение
Пусть – сила реакции опоры,
– центростремительное ускорение,
– сила тяжести,
–
угол между силой тяжести и центростремительным ускорением.
Запишем второй закон Ньютона:
В момент отрыва от петли будет равна 0, значит второй закон Ньютона запишется в
виде
Найдем скорость тела в момент отрыва, как разность потенциальных энергий
Подставляем (2) в (1) и находим
Откуда высота отрыва
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление для момента прохождения телом точки отрыва, закон
сохранения механической энергии, формулы потенциальной и кинетической энергии, формула
центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Небольшой шарик соскальзывает без начальной скорости и без трения с верхней точки сферы,
закреплённой на горизонтальной поверхности стола.
а) Под каким углом к поверхности стола шарик ударится о стол?
б) На какую максимальную высоту поднимется шарик после упругого удара о стол, если радиус сферы
равен ?
Показать ответ и решение
Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это
означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой
тяжести. Запишем второй закон Ньютона
где
– сила реакции опоры,
– центростремительное ускорение Так как
, то с учетом формулы
центростремительного ускорения где
– скорость тела.
Тогда второй закон Ньютона на ось
С
учетом того, что имеем
Также запишем закон сохранения энергии
где
– потенциальная энергия тела на высоте
,
– кинетическая энергия на
высоте ,
– потенциальная энергия на высоте
,
отсчитывается от центра
сферы. Расписав все слагаемые по формулам получим
Объединим (1) и (2):
При
этом расстояние равно:
Мы
нашли точку отрыва тела от поверхности сферы.
Скорость направлена перпендикулярно центростремительному ускорению, следовательно
Скорость тела в момент отрыва
Тогда горизонтальная и вертикальная составляющие скорости
Горизонтальная составляющая скорости не изменяется во время полета, значит справедливо
равенство:
где
– скорость в нижней точке полёта,
– искомый угол.
Запишем закон сохранения полной энергии при всем движении
Отсюда
Так
как горизонтальная составляющая часть скорость сохраняется при движении тела, то закон сохранения
энергии запишется в виде:
где
– искомая высота.
Тогда
Гладкая сфера радиуса закреплена на горизонтальном столе. Маленький брусок начинает движение
из верхней точки сферы без начальной скорости. На какой высоте над поверхностью стола
брусок оторвётся от сферы? Какие законы Вы используете для решения задачи? Обоснуйте их
применение.
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать
второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной
не потенциальной силой является сила натяжения нити, действующая на тело. Эта сила
перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа
равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень
потенциальной энергии выберем уровень, на котором находится нижняя точка траектории
тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм
ускорением, направленным к центру окружности вращения.
Решение
Запишем второй закон Ньютона в момент, когда шарик оторвется от поверхности сферы, это
означает, что сила реакции опоры будет равна нулю, и ускорение будет создаваться только силой
тяжести. Запишем второй закон Ньютона
где – сила реакции опоры,
– центростремительное ускорение Так как
, то с учетом
формулы центростремительного ускорения где
– скорость тела.
Тогда второй закон Ньютона на ось
С учетом того, что имеем
Также запишем закон сохранения энергии
где – потенциальная энергия тела на высоте
,
– кинетическая энергия
на высоте ,
– потенциальная энергия на высоте
. Расписав все слагаемые по
формулам получим
Объединим (1) и (2):
При этом искомое расстояние равно:
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление, закон сохранения механической энергии, формулы
центростремительного ускорения, кинетической и потенциальной энергии).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Сделаем рисунок сил
Где – сила реакции опоры,
– центростремительное ускорение,
– сила тяжести,
–
скорость шарика.
а) Скорость тела направлена по касательной к окружности, значит, тело должно находиться в
крайней правой (левой) точке петли (см. рис.). Найдем скорость шарика из закона сохранения
энергии
Запишем второй закон Ньютона:
Запишем второй закон Ньютона на вертикальную ось
По
горизонтальной оси у тела присутствует центростремительное ускорение, равное
Откуда полное ускорение
б)
Пусть угол между центростремительным ускорением и силой тяжести равен , тогда скорость на
искомой высоте равна
Рассмотрим два случая. Первый случай, сила тяжести сонаправлена с силой реакции опоры
По
условию , тогда
Откуда высота
Теперь рассмотрим случай разнонаправленности и
Косинус не может быть больше 1, следовательно, такая ситуация невозможна
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать
второй и третий законы Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной не
потенциальной силой является сила реакции опоры, действующая на тело. Эта сила перпендикулярна
вектору скорости в процессе движения, а значит ее мощность и работа равняются нулю, полная
механическая энергия тела не изменяется. За нулевой уровень потенциальной энергии выберем уровень,
на котором находится нижняя точка траектории тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм
ускорением, направленным к центру окружности вращения.
Решение
Сделаем рисунок сил
Где – сила реакции опоры,
– центростремительное ускорение,
– сила тяжести.
Запишем второй закон Ньютона:
Для того, чтобы тело прошло петлю, необходимо, чтобы сила реакции опоры во время прохождения
ни разу не была равна 0, минимальная сила реакции опоры наблюдается в верхней точке движения.
Докажем это
Пусть угол между силой тяжести и силой реакции опоры равен , тогда второй закон Ньютона
запишется в виде
Тогда из закона сохранения энергии
Тогда второй закон Ньютона запишется в виде
Тогда, для того, чтобы было минимально,
должен быть максимален, значит
, что
возможно только в верхней точке.
Из закона сохранения энергии скорость в верхней точке
Примем в верхней точке силу реакции опоры равно 0, тогда
Тогда скорость тела в точке А
Запишем второй закон Ньютона в проекции на ось, направленную в центр траектории:
По третьему закону Ньютона сола давления на опору вточке равняется силе, с которой опора
давит на шарик в этой точке, то есть равна силе реакции опоры в точке .
Критерии оценки
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго и третьего законов Ньютона для описания движения
тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых необходимо
для решения задачи выбранным способом (в данном случае: второй закон Ньютона в векторной форме
и в проекции на радиальное направление для момента прохождения телом токи , третий закон
Ньютона, закон сохранения механической энергии, формулы потенциальной и кинетической энергии,
формула центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Обоснование
1. Введем инерциальную систему отсчёта (ИСО) связанную с землей.
2. Тело движется поступательно, его размеры малы по сравнению с размерами установки, будем
описывать тело моделью материальной точки.
3. Так как тело является материальной точкой, то для описания его движения будем использовать
второй закон Ньютона относительно ИСО.
4. Применим закон сохранения энергии для описания движения тел, так как единственной
не потенциальной силой является сила натяжения нити, действующая на тело. Эта сила
перпендикулярна вектору скорости в процессе движения, а значит ее мощность и работа
равняются нулю, полная механическая энергия тела не изменяется. За нулевой уровень
потенциальной энергии выберем уровень, на котором находится нижняя точка траектории
тела.
5. Так как тело будет двигаться по окружности, то оно будет обладать центростремительнм
ускорением, направленным к центру окружности вращения.
Решение
Второй закон Ньютона для тела запишется в виде:
где – сила натяжения нити,
– центростремительное ускорение.
Ослабление нити означает, что . Пусть в момент ослабления нити скорость равен
, а угол
между вертикалью и нитью равен , тогда второй закон Ньютона на ось, совпадающую с осью нити
можно записать в виде
Также запишем закон сохранения энергии
Здесь — кинетическая энергия в начальный момент времени,
— потенциальная энергия в
точке, где нить ослабнет, — кинетическая энергия в той точке, где нить ослабнет.
Проанализируем начальную скорость, чтобы тело поднялось не выше, чем , его скорость должна
составлять
Следовательно, тело поднялось выше , откуда следует, что высота подъема равна
Подставим (1) и (3) в (2)
Откуда высота подъема
Критерий 1
1 балл ставится если
1. Введена инерциальная система отсчета
2. Обоснована возможность применения к телу модели материальной точки
3. Обосновано применение второго закона Ньютона для описания движения тела
4. Обосновано применение закона сохранения энергии
5. Обосновано наличие центростремительного ускорения
6. Введен нулевой уровень потенциальной энергии
__________________________________________________________________________________________________________________________________
В остальных случаях ставится 0 баллов по данному критерию.
При отсутствии обоснования по данному критерию ставится 0 баллов
Критерий 2
3 балла ставится если:
_________________________________________________________________________________________________________________
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: второй закон Ньютона в
векторной форме и в проекции на радиальное направление для момента ослабления нити, закон
сохранения механической энергии, формулы потенциальной и кинетической энергии, формула
центростремительного ускорения).
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в условии
задачи или представлены в виде констант в КИМ, стандартных обозначений величин, используемых при
написании физических законов.
III) Представлены математические образования, приводящие к верному ответу (в данном случае
последовательное выражение величин с пояснением действий).
IV) Получен верный ответ.
2 балла ставится если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
I) В решении имеются лишние записи, не входящие в решение, которые не отделены от решения и не
зачёркнуты.
II) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги. (Получение
конечной формулы сразу, без последовательного, логического вывода. Пропуск преобразований в
формулах.)
III) Отсутствуют описания вновь вводимых в решение буквенных обозначений физических величин.
IV) Ответ получен неверный или в нём допущена ошибка. (В ответе обязательно указываются единицы
измерений.)
1 балл ставится если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Законы сохранения. Работа и мощность.
(теория и формулы для ЕГЭ)
Законы сохранения
Импульсом тела (материальной точки) называют произведение массы тела на вектор его скорости. Единица модуля импульса тела – 1 кг·м/c.
Импульсом силы называют произведение вектора скорости на интервал времени её действия ∆t. Единица модуля импульса силы – 1 кг·м/c.
[F·∆t] = Н·м.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются друг с другом и движутся дальше как одно тело. Механическая энергия не сохраняется (она частично или полностью переходит во внутреннюю энергию тел).
Закон сохранения импульса.
Замкнутая (изолированная) система – система тел, взаимодействующих только между собой и не взаимодействующих с телами, не входящими в эту систему.
Закон сохранения импульса: векторная сумма импульсов тел, составляющих замкнутую систему, не изменяется.
Энергия – скалярная физическая величина, являющаяся мерой способности тела (или системы тел) совершить работу. Существует кинетическая и потенциальная энергия.
Закон сохранения энергии в механических процессах – сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Е = Еk1 + Ep1 = Еk2 + Ep2 = const при Fтр = 0
Если Fтр≠ 0, механическая энергия переходит во внутреннюю (тепловую) энергию тела:
Q = Е2 – Е1, где Q =Атр
Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными (силы тяжести и силы упругости)
Работа силы.
Механической работой A, совершаемой постоянной силой, называется скалярная физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения.
А = F∙s∙cos α [А] = Дж 1Дж =1Н∙1м
Работа зависит от угла α.
Работа силы тяжести не зависит от формы траектории и равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Атяж. = mg(h1 – h2) = — ( mgh1 — mgh2) = — (Ер2 – Ер1)
Работа силы тяжести по замкнутой траектории равна нулю.
Мощность – скалярная физическая величина, равная отношению совершенной работы к промежутку времени, за который она совершена.
Коэффициент полезного действия механизмов КПД – величина, равная отношению полезной работы к полной работ, выраженная в процентах.
Конспект урока «Законы сохранения. Работа и мощность. Теория и формулы для ЕГЭ».
Еще конспекты для 10-11 классов:
Презентация «Законы сохранения в механике » составлена в соответствии с требованиями к ЕГЭ по физике 2013 года и предназначена для подготовки выпускников к экзамену. Состоит из теоретической и практической части
Скачать:
Подписи к слайдам:
Подготовка к ЕГЭЗаконы сохранения в механике часть 1 Учитель физики Тычкова Н.А.МБОУ СОШ № 91Г. Красноярск Импульс тела
Закон сохранения импульса В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов
Импульс силы – временная характеристика действия силы Абсолютно упругий удар (тело отскакивает с прежней по величине скоростью).
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело. Работа силы Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения A = Fs cos αРабота является скалярной величиной. Она может быть положительной (0° ≤ α < 90°), отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж);Графически работа определяется по площади криволинейной фигуры под графиком Fs(x)Работа всех приложенных сил равна работе равнодействующей силы F. Кинетическая энергия тела массой m, движущегося со скоростью V, равна работе, которую должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.
Теорема о кинетической энергии: работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии:
Кинетическая энергия Потенциальная энергия Кинетическая энергия – это энергия движения. Потенциальная энергия — энергии взаимодействия телПотенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Силы, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями называются консервативными.Работа консервативных сил на замкнутой траектории равна нулю. A = A1a2 + A2b1 = A1a2 – A1b2 = 0Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.Сила трения не является консервативной. Работа силы трения зависит от длины пути
Подписи к слайдам:
Подготовка к ЕГЭЗаконы сохранения в механике часть 3 Учитель физики Тычкова Н.А.МБОУ СОШ № 91Г. Красноярск РЕШЕНИЕ ЗАДАЧ1. Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы?1) 4 кг м/с 2) 8 кг м/с 3) 5,7 кг м/с 4) 11.7 кг м/с 2. Система состоит из двух тел 1 и 2, массы которых равны 0,5 кг и 2 кг. На рисунке стрелками в заданном масштабе указаны скорости этих тел.Чему равен импульс всей системы по модулю?1) 14 кг м/с 2) 10 кг м/с 3) 20 кг м/с 4) 40 кг м/с 3. Если при увеличении модуля скорости материальной точки величина ее импульс увеличилась в 4 раза, то при этом кинетическая энергия1) увеличилась в 2 раза2) увеличилась в 4 раза3) увеличилась в 16 раз4) уменьшилась в 4 раза 4. Танк движется со скоростью , а грузовик со скоростью . Масса танка . Отношение величины импульса танка к величине импульса грузовика равно 2,25. Масса грузовика равна 1) 1 500 кг 2) 3 000 кг 3) 4 000 кг 4) 8 000 кг 5. Две тележки движутся навстречу друг другу с одинаковыми по модулю скоростями . Массы тележек m и 2m. Какой будет скорость движения тележек после их абсолютно неупругого столкновения? 2/3v 3v 2v1/3v 6. Охотник массой 60 кг, стоящий на гладком льду, стреляет из ружья в горизонтальном направлении. Масса заряда 0,03 кг. Скорость дробинок при выстреле 300 м/с . Какова скорость охотника после выстрела?0.5 м/с0.15 м/с0.3 м/с3 м/с ДЕМО 2013
ДЕМО 2011 ДЕМО 2012 Уровень С. ЕГЭ 2008 г Решите самостоятельно Решите самостоятельно Литература http://physics.kgsu.ru/index.php?option=com_content&view=article&id=129&Itemid=72http://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D1%89%D0%BD%D0%BE%D1%81%D1%82%D1%8Chttp://www.alleng.ru/edu/phys3.htmhttp://www.alsak.ru/content/view/200/1/http://www.physics.ru/courses/op25part1/content/chapter1/section/paragraph19/theory.htmlhttp://fipi.ru/view/sections/92/docs/http://www.vixri.ru/d/Kas’janov%20A.V.%20%20_10%20klass.%20Illjustrirovannyj%20Atlas%20po%20fizike.pdfМякишев, Г.Я. и др. Физика. 11 класс [Текст]: учебник для общеобразовательных школ / учебник для общеобразовательных школ Г.Я. Мякишев, Б.Б. Буховцев . –» Просвещение «, 2009. ФИПИ ЕГЭ 2012 Физика Типовые экзаменационные задания Под редакцией М.Ю.Демидовой, Москва Национальное образование 2011
Подписи к слайдам:
Мощность
Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа: Международной системе (СИ) единица мощности называется ватт (Вт)
Закон сохранения механической энергии Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.Ek1 + Ep1 = Ek2 + Ep2. Сумму E = Ek + Ep называют полной механической энергиейЕсли между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).Закон сохранения и превращения энергии: при любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Работа как мера изменения энергии Работа силы тяжести:Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести. Работа этой силы зависит только от вертикального перемещения тела. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком. A = – (Eр2 – Eр1). Работа силы тяжести не зависит от формы траекторииРабота силы тяжести не зависит от выбора нулевого уровня. Работа силы упругости:Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины Зависимость модуля внешней силы от координаты x изображается на графике прямой линиейПотенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
По теме: методические разработки, презентации и конспекты
Открытый урок: «Законы сохранения в механике».
Данный урок дан в рамках методического дня. Урок рассчитан на 90минут. Часто учителя работающие в 10-ых классах не выполняют лабораторную работу по данной теме, потому что она не всегда получается. Ур…
- Мне нравится