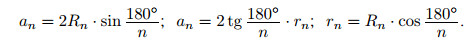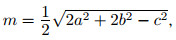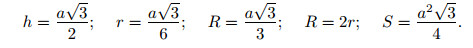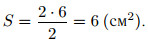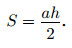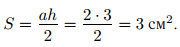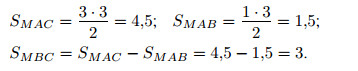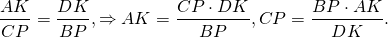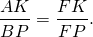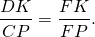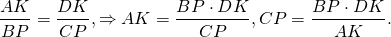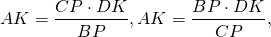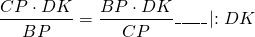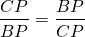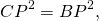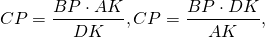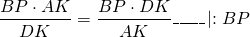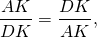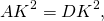Замечательное свойство трапеции
Анна Малкова
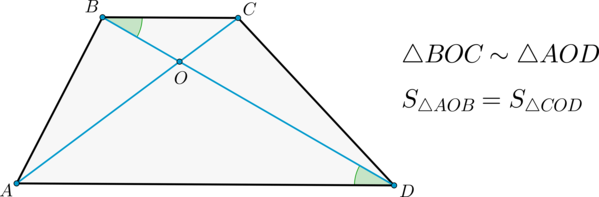
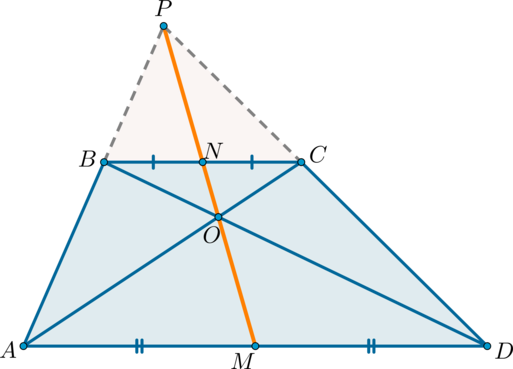
Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии.
Дана трапеция ABCD, , N — середина AD, M — середина BC,
. Докажем, что точки M, N, O, P лежат на одной прямой.
Задача не так уж и проста, да и сама формулировка необычна: доказать, что четыре точки лежат на одной прямой. Как это сделать?
Во-первых, разобьем задачу на две более простых. Во-вторых – немного переформулируем.
1) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения диагоналей.
2) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения продолжений боковых сторон.
Начнем с пункта 1.
Пусть M — середина BC, O – точка пересечения диагоналей трапеции, .
Докажем, что N – середина AD.
по двум углам (
как вертикальные,
как накрест лежащие при параллельных основаниях трапеции), тогда
.
Аналогично, (
как вертикальные,
как накрест лежащие при параллельных основаниях трапеция), отсюда
.
Отсюда . Это значит, что N – середина AD.
Теперь пункт 2.
Проведем PM – медиану треугольника BPC. Пусть прямые AD и PM пересекаются в точке N. Докажем, что N – середина AD
по двум углам (угол P – общий,
как соответственные при параллельных основаниях трапеции), отсюда
.
аналогично,
.
Получим: , значит, N – середина AD.
Таким образом, точки M,O,N,P лежат на одной прямой, что и требовалось доказать.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Замечательное свойство трапеции» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
5 февраля 2018
В закладки
Обсудить
Жалоба
Какие геометрические факты можно использовать на ЕГЭ без доказательства?
Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.
Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.
Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:
→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)
Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть
Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.
Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.
Источник: vk.com/wildmathing
Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.
Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.
Сформулируем это свойство иначе:
Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.
ABCD- трапеция, AD||BC,
AB∩CD=F, AC∩BD=O,
FO∩AD=K, FO∩BC=P
Доказать: K- середина AD,
P- середина BC
Доказательство:
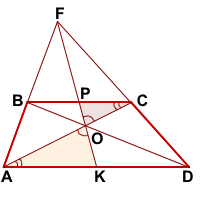
∠AOK=∠COP (как вертикальные),
∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).
Значит, треугольники AOK и COP подобны (по двум углам).
Следовательно,
Аналогично, треугольники DOK и BOP подобны и
Так как правые части этих равенств равны, то левые также равны:
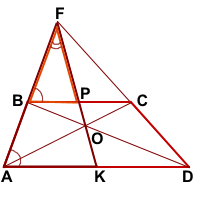
∠F- общий,
∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).
Следовательно, треугольники AFK и BFP подобны (по двум углам).
Отсюда,
Аналогично, треугольники DFK и CFP подобны и
Правые части равенств равны, приравниваем левые части:
Так как
то
По основному свойству пропорции,
а значит, CP=BP, то есть P — середина BC.
Аналогично,
AK=DK, K — середина AD.
Что и требовалось доказать.
Альтернативный вариант.
- Докажем, что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
- Докажем, что точка пересечения диагоналей трапеции и середина её меньшего основания лежат на прямой, проходящей через точку пересечения продолжения боковых сторон трапеции и середину большего основания
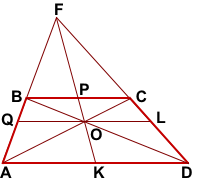
FK — медиана треугольника AFD.
Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.
BC||AD (как основания трапеции), QL||AD (по построению).
О — середина QL.
Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.
И ещё.
Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.
Всего: 10 1–10
Добавить в вариант
Дана трапеция ABCD с основаниями AD и ВС. Диагонали АС и BD пересекаются в точке О, а прямые АВ и CD — в точке К. Прямая КО пересекает стороны ВС и AD в точках М и N соответственно, и угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность.
а) Докажите, что треугольник AKD тупоугольный.
б) Найти отношение площадей треугольника ВКС и трапеции ABCD.
Источник: А. Ларин: Тренировочный вариант № 232.
Боковые стороны KL и MN трапеции KLMN равны 16 и 34 соответственно. Отрезок, соединяющий середины диагоналей, равен 15, средняя линия трапеции равна 30. Прямые KL и MN пересекаются в точке А. Найдите радиус окружности, вписанной в треугольник ALM.
Боковые стороны KL и MN трапеции KLMN равны 16 и 34 соответственно. Отрезок, соединяющий середины диагоналей, равен 15, средняя линия трапеции равна 30. Прямые KL и MN пересекаются в точке А. Найдите радиус окружности, вписанной в треугольник ALM.
В трапеции параллельно основаниям проведены четыре отрезка с концами на боковых сторонах: KL, MN, RS и TQ. Известно, что первый отрезок проходит через точку пересечения диагоналей трапеции, второй — делит ее на два подобных четырехугольника, третий — соединяет середины боковых сторон, четвертый разбивает трапецию на две равновеликие части.
а) Найдите длины этих отрезков.
б) Докажите, что KL < MN < RS < TQ.
Источник: А. Ларин: Тренировочный вариант № 128.
Боковые стороны AB и CD трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке М. Найдите радиус окружности, вписанной в треугольник ВМС.
Боковые стороны KL и MN трапеции KLMN равны 8 и 17 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 17,5. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.
Боковые стороны KL и MN трапеции KLMN равны 8 и 17 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 17,5. Прямые KL и MN пересекаются в точке Найдите радиус окружности, вписанной в треугольник
Боковые стороны AB и CD трапеции ABCD равны 9 и 12 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 37,5. Прямые AB и CD пересекаются в точке М. Найдите радиус окружности, вписанной в треугольник ВМС.
Площадь трапеции ABCD равна 6. Пусть E — точка пересечения продолжений боковых сторон этой трапеции. Через точку E и точку пересечения диагоналей трапеции проведена прямая, которая пересекает меньшее основание BC в точке P, а большее основание AD — в точке Q. Точка F лежит на отрезке EC, причем
а) Докажите, что прямая EQ точками пересечения делит основания трапеции пополам.
б) Найдите площадь треугольника EPF.
Источник: А. Ларин. Тренировочный вариант № 267.
Боковые стороны KL и MN трапеции KLMN равны 7 и 25 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 60. Прямые KL и MN пересекаются в точке А. Найдите радиус окружности, вписанной в треугольник ALM.
Всего: 10 1–10
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 5
МУНИЦИПАЛЬНОГО
ОБРАЗОВАНИЯ
город – курорт АНАПА
Рассмотрено и
рекомендовано к использованию
на заседании МО от _______________
Протокол №______
Подготовка
к ОГЭ и ЕГЭ.
«Формулы
и свойства трапеции»
Методическая разработка
учителя
математики
Снегуровой Амины Мугиновны
2018 год.
Оглавление
Введение 3
1.
Определения 4
2.
Частные случаи трапеции 5
3.
Свойства произвольной трапеции 6-7
4.
Свойства равнобедренной трапеции 8-10
5. Свойства
биссектрисы угла трапеции 10-12
6.
Свойства треугольников, образованных диагоналями трапеции 12-13
7.
Формулы нахождения диагоналей трапеции 13-14
8.
Трапеция и окружность 14-17
9.
Дополнительные построения в трапеции 17-23
10. Для
тех, кому интересно. Теоремы. 23-27
11.
Задачи с решениями.27-35
12. Список используемой литературы.
Введение
Дорогой ученик!
В материалах различных контрольных работ и экзаменов очень часто встречаются
задачи на трапецию, решение которых требует от учащихся знаний
«непрограммных» свойств трапеции. (Программными считаются свойство средней
линии трапеции, свойства диагоналей и углов равнобедренной
трапеции.) Свойства, необходимые для решения задач, отсутствуют в
учебниках или перенесены в задачи и не воспринимаются как теоретические
положения.
Какими же замечательными свойствами обладает трапеция?
Как решать геометрические задачи, требующие глубоких знаний? Трапеция
обладает рядом интересных и полезных для решения задач свойствами. Если
овладеть ими и рассмотреть дополнительные построения в трапеции, то возникает
объективная возможность для решения задач повышенной сложности.
В планиметрии существует целый класс таких задач,
к которым традиционные методы (метод цепочек равных треугольников, метод
геометрических преобразований, векторный метод и др.) либо вовсе не применимы,
либо дают сложные и громоздкие решения. Во многих случаях решать такого рода
задачи помогает введение в чертеж дополнительных линий – так называемое
дополнительное построение. В одних случаях эти построения напрашиваются сами
собой, в других они не так очевидны и требуют от решающего достаточно большого
опыта, изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно
достраивать до фигуры другого типа, можно с многоугольной фигурой связывать
окружность, а можно целью дополнительного построения ставить выделение на
чертеже равных, равновеликих или подобных фигур.
Знание метода дополнительных построений в
большинстве случаев позволяет решать, казалось бы, сложные геометрические
задачи просто, понятно и красиво.
В этой
разработке собраны формулы, свойства и подсказки для решения задач связанных с
трапецией. Надеюсь, что ты здесь найдешь для себя много полезной информации.
1.Определения.
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
Параллельные
стороны
называются её основаниями, а две другие стороны — боковыми
сторонами.
Высотой трапеции называется расстояние между основаниями.

Kаждый
из этих отрезков EF, BM, DK, PQ является высотой трапеции ABCD.
В
формулах используются следующие обозначения:
a,
b — основания трапеции
c,
d — боковые стороны трапеции
d1
d2 — диагонали трапеции
α
β — углы при большем основании трапеции
h—
высота.
2.Частные
случаи трапеции.
Прямоугольной
трапецией называется трапециия, в которой одна из боковых сторон перпендикулярна
основаниям.
У
нее два прямых угла при меньшей боковой стороне.
Эта
сторона одновременно является и высотой трапеции.
произвольная
Трапецией
называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
У
равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при
основании равны.
Трапеция,
у которой боковые стороны равны, называется равнобедренной
(равнобокой,
равнобочной).
3.Свойства произвольной
трапеции.
1. Во всякой трапеции сумма углов , прилежащих к
одной ее боковой стороне, равна 1800.


основаниям, равна полусумме этих оснований и делит диагонали трапеции пополам.

MК =
3.Четыре замечательные
точки трапеции:
Во всякой трапеции середины
оснований, точка пересечения диагоналей и точка пересечения продолжений боковых
сторон лежат на одной прямой.

4. Во всякой трапеции если
сумма углов при большем основании равна 900, то боковые стороны
лежат на перпендикулярных прямых. Длина отрезка, соединяющего середины
оснований, равна полуразности оснований.
5.
Свойства отрезка, соединяющего основания трапеции

соединяющий основания всякой трапеции, и проходящий через точку пересечения
диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований
трапеции.
Если провести отрезок, концы которого лежат на основаниях
трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то
соотношение составляющих его отрезков от стороны основания до точки пересечения
диагоналей ( KO/ON ) будет равно соотношению оснований трапеции:
6.Свойства отрезка, параллельного основаниям всякой трапеции.

провести отрезок, параллельный основаниям трапеции и проходящий через точку
пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
*Заданный отрезок (KM) делится точкой пересечения диагоналей
трапеции пополам, то есть КО=ОМ
*Длина отрезка,
проходящего через точку пересечения диагоналей трапеции и параллельного
основаниям, равна
KM = .
 |
|||
7.Во всякой трапеции с основаниями a и b отрезок, параллельный
основаниям, концы которого лежат на боковых сторонах, равен среднему
геометрическому оснований, если он делит трапецию на две трапеции, подобные
между собой.
8. Во всякой трапеции с основаниями a и b отрезок, параллельный
основаниям, концы которого лежат на боковых сторонах, равен среднему
квадратичному оснований, если он делит трапецию на две трапеции равной площади
(равновеликие).

9.Сумма
квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс
удвоенное произведение ее оснований.
d12
+ d22
= c2 + d2+
2ab, d— боковая сторона. d1 и
d2 –
диагонали.
Свойства
равнобедренной трапеции.
Трапеция является равнобедренной
тогда и только тогда, когда
*углы, прилежащие к одному
основанию, равны
*сумма противолежащих углов 1800;
*диагонали равны;

AC = BD
*отрезки диагоналей, соединяющих точку пересечения
с концами одного основания, равны; BO = OC, AO = OD.

описать окружность.
BC // AD, AB = CD. ABCD – вписанная трапеция.

большее основание на отрезки, один из которых равен полуразности оснований, а
другой полусумме оснований трапеции, т. е. средней линии трапеции.
*если в равнобедренной трапеции диагонали перпендикулярны,
то
1)квадрат ее диагонали равен половине квадрата суммы
оснований, а также удвоенному квадрату высоты и удвоенному квадрату
средней линии.
2)высота трапеции равна полусумме оснований.
3)ее высота равна средней линии.
4)
площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны,
равна квадрату её высоты.
(или квадрату полусуммы оснований, или квадрату средней линии).


диагонали трапеции взаимно перпендикулярны.
BH = HD = h =.
*высота, проведённая через
точку пересечения диагоналей, в
равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две
равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
*в равнобедренной трапеции прямая, проходящая через середины
оснований, перпендикулярна им и является осью симметрии трапеции.


*отрезки, последовательно соединяющие середины смежных сторон
равнобедренной трапеции, образуют ромб.

MNKE – ромб,
то есть
MN=NK=KE=
ME.
*в равнобедренной трапеции квадрат диагонали равен квадрату его
боковой стороны плюс произведение оснований: d2
= c2 + a b

равнобедренной трапеции с радиусом вписанной окружности равным r и углом при
основании α:
S =
Свойства
биссектрисы угла трапеции.
*биссектриса угла отсекает
от трапеции равнобедренный треугольник.



*точка пересечения биссектрис
тупых углов при основании трапеции принадлежит другому основанию.
*если диагональ трапеции является биссектрисой ее острого угла, то
меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.
*биссектриса угла трапеции, пересекающая основание, отсекает от
трапеции равнобедренный треугольник.
*биссектрисы углов при боковой стороне трапеции пересекаются под
прямым углом.
* точка пересечения биссектрис трапеции, прилежащих к боковой
стороне, лежит на средней линии трапеции.
*если биссектриса тупого угла трапеции является диагональю, то
боковая сторона равна большему основанию трапеции.
*если меньшее основание трапеции равно ее
боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой
боковой стороне острого угла.
Если в условии задачи сказано, что основание трапеции равно ее боковой
стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее
угла.
*если меньшее основание трапеции равно ее
боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой
боковой стороне острого угла.

трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой
прилежащего к этой боковой стороне тупого угла.
*если большее основание прямоугольной трапеции
равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла,
прилежащего к меньшему основанию.
* если меньшее основание прямоугольной трапеции
равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла,
прилежащего к большему основанию.
* если меньшее основание прямоугольной трапеции равно ее
большей боковой стороне, диагональ является биссектрисой прилежащего к этой
боковой стороне острого угла.
* если большее основание прямоугольной трапеции
равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к
этой боковой стороне тупого угла.
*если меньшее основание равнобедренной трапеции
равно ее боковой стороне, то диагональ является биссектрисой острого угла
трапеции.
* если большее основание равнобедренной трапеции
равно ее боковой стороне, то диагональ является биссектрисой тупого угла
трапеции.
Свойства
треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой
пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются
вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD
и BC (основания трапеции параллельны между собой) и секущей прямой AC,
следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим
углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для
решения задач по геометрии подобие треугольников используется следующим
образом.
*Если
нам известны значения длин двух соответствующих элементов подобных
треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда
длины всех остальных элементов соотносятся между собой точно таким же
значением.
*В подобных треугольниках
длины всех линейных элементов пропорциональны, а именно:
отношения периметров, радиусы
вписанных окружностей, радиусы описанных окружностей, соответствующих высот, биссектрис,
медиан (проведенных из равных углов) подобных треугольников равны отношению
соответствующих сторон (лежащих против равных углов) или равны коэффициенту
подобия.
*Площади подобных
треугольников относятся как квадраты соответствующих сторон или равно квадрату
коэффициента подобия.

образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
S12= S2 S3
S3: S2 = 2
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции
AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных
сторон у данных треугольников могут быть совершенно различны, но площади
треугольников, образованных боковыми сторонами и точкой пересечения диагоналей
трапеции равны, то есть треугольники являются равновеликими.
Если продлить боковые стороны трапеции в сторону меньшего
основания, то они пересекутся в одной точке с прямой, соединяющей середины
оснований
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами,
углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения
задач по геометрии на тему «диагонали трапеции»

Далее, в формулах используются следующие обозначения:
a, b —
основания трапеции
c, d —
боковые стороны трапеции
d1 d2 —
диагонали трапеции
α β —
углы при большем основании трапеции
h— высота
Формулы нахождения диагоналей трапеции
через основания, боковые стороны и углы при основании

Эта группа формул отражает одно из основных свойств диагоналей
трапеции:
*Сумма квадратов диагоналей трапеции равна
сумме квадратов боковых сторон плюс удвоенное произведение ее оснований.
Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Используем
теорему косинусов.
*Данная
формула получена путем преобразования предыдущей формулы. Квадрат второй
диагонали переброшен через знак равенства, после чего из левой и правой части
выражения извлечен квадратный корень.
*Эта формула
нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что
в левой части выражения оставлена другая диагональ
4.В прямоугольной трапеции разность квадратов диагоналей равна
разности квадратов оснований
d12
— d22
= a2 –
b2
*Если
диагонали трапеции взаимно перпендикулярны, то длина отрезка, соединяющего
середины оснований трапеции равна полусумме оснований.
MH =
BDCE и FAOD прямоугольники, а диагонали
прямоугольника равны.
Трапеция и окружность.
1) Если в равнобокую трапецию можно вписать окружность, то средняя
линия трапеции равна боковой стороне.
Высота равнобедренной трапеции, в которую можно вписать окружность,
является средним геометрическим её оснований
h2
= a ∙ b
2)
Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна
средней линии. Площадь трапеции определяется произведением средней линии на
высоту трапеции.
3. Высота трапеции равна длине диаметра вписанной
окружности или двум ее радиусам.
MK —
высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной
окружности является точкой пересечения биссектрис углов трапеции.
. CF =m,
FD =n, OF = r.

как сумма
внутренних односторонних углов при параллельных прямых AD и BC и секущей CD
равна 1800.
Отсюда
радиус вписанной в трапецию окружности выражается через длины отрезков, как
которые боковая сторона делится точкой касания, как r = .
А так как
высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через
длины этих отрезков: h = 2 .
5.Если в трапецию можно вписать окружность и около трапеции можно
описать окружность, то проекция диагонали на большее основание, равна боковой
стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, в задаче появляется несколько
путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда,
когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма
ее оснований равна сумме боковых сторон.
AB+CD=AD+BC

проведенных из одной точки, равны. Отсюда следует, что
AL=AK BL=BM
CM=CF DF=DK
Описанная окружность.
Когда трапецию можно вписать в
окружность? Четырехугольник можно вписать в окружность тогда и только тогда,
когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать
в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как
радиус окружности, описанной около из одного из двух треугольников, на которые
трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это
зависит от угла между диагональю трапеции и ее боковой стороной.

перпендикулярна ее боковой стороне, то центр окружности, описанной около
трапеции, лежит на середине ее большего основания. Радиус описанной около
трапеции окружности в этом случае равен половине ее большего основания:

боковой стороной острый угол, центр окружности, описанной около трапеции, лежит
внутри трапеции.
3) Если
диагональ трапеции образует с боковой стороной тупой угол, центр описанной
около трапеции окружности лежит вне трапеции, за большим основанием.
4)Радиус описанной около трапеции окружности можно найти по
следствию из теоремы синусов. Из треугольника ACD

Из треугольника ABC
Другой вариант найти радиус описанной окружности —

угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и
ACF:
При решении задач на трапецию, вписанную в окружность, можно
также использовать то, что вписанный угол равен половине соответствующего ему
центрального угла. Например,

Использовать углы COD и CAD можно и для нахождения площади
трапеции. По формуле нахождения площади четырехугольника через его диагонали
5)Если диагонали вписанной в окружность трапеции
(четырехугольника) взаимно перпендикулярны, то сумма квадратов его
противоположных сторон равна квадрату диаметра описанной окружности или
удвоенному квадрату боковой стороны:
a2
+ b2
= 4R2
= 2c2.

вписанной в нее окружности и основание перпендикуляра, опущенного из другой
вершины на основание, лежат на одной прямой.
Дополнительные построения
как прием при решении задач
Дополнительные
построения являются эффективным методом решения геометрических задач. Наиболее
часто используются при решении задач:
1.
Опускание высот из концов одного основания на другое основание
2.
Проведение через вершины трапеции прямой, параллельной боковой стороне, не
содержащей эту вершину
3.
Проведение через середину меньшего основания прямых, параллельных боковым
сторонам
4.
Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей
эту вершину .
5.
Продолжение боковых сторон до пересечения.
Рассмотрим
каждое их них.
При
решении задач на отыскание площади дополнительным построением считается
построение ее высоты или высот. Если построение высоты не помогает решить
задачу, то нужно построить прямую, параллельную одной из ее диагоналей. Потом
найти площадь полученного треугольника, который будет равновеликим исходной
трапеции.
1.
Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей
эту вершину.
При
дополнительном построении, когда переносится диагональ, образуется треугольник,
площадь которого равна площади трапеции.
S1 = S2
Задача.
Найдите
площадь трапеции, дмагонали которой равны 8 и 15, а средняя линия равна 8,5.
Решение.
Построим
CF // BD и
получим SACF = SABCD.
Почему?
ABC
= CDF, так как DF = BC и эти треугольники имеют одинаковую высоту.
Значит,
для того, чтобы найти площадь трапеции нам достаточно найти площадь ACF.
АF
= АD + ВС — сумма оснований трапеции. По условию задачи средняя линия
трапеции 8,5. Значит сумма оснований АF = 8,52=17.
Рассмотрим ACF.
Проверим, является ли он прямоугольным? В этом нам поможет теорема Пифагора:
172
= 82 + 152
289
= 64 + 225.
289
= 289.
ACF
– прямоугольный. SACF = AC*CF
= 8*15 = 60. SABCD=
60.
Если ACF
разносторонний, то его площадь вычислим по формуле Герона.
Ответ:60.
2.
Продолжение боковых сторон до пересечения.
Свойства трапеции,
достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то
точка пересечения сторон будет совпадать с прямой линией, которая
проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до
треугольника. При этом:
*Треугольники, образованные основаниями трапеции с общей вершиной
в точке пересечения продленных боковых сторон являются подобными
*Прямая, соединяющая середины оснований трапеции, является,
одновременно, медианой построенного треугольника.
*Если ABCD равнобедренная трапеция, то KL
является биссектрисой, медианой и высотой одновременно.
Это
дополнительное построение позволяет перейти от трапеции к треугольнику. Если
сумма углов при большем основании равна 900, топродолжив боковые
стороны мы получим прямоугольный треугольник.
Задача.
В
трапеции ABCD основания АD и ВС равны соответственно 72 и 18, а сумма углов при основании АD равна
900. Найдите радиус окружности, проходящей через точки А и В и
касающейся прямой CD, если АВ = 18.
Решение.
Центром
О данной окружности будет точка пересечения серединного
перпендикуляра к АВ и перпендикуляра, возведенного к стороне CD
из точки касания окружности. АВО равнобедренный: АО = ВО. Продлим боковые
стороны трапеции и получим прямоугольный треугольник АМD.
KMNO – прямоугольник, где KM = MN
= NO =КО = R.
BMC AMD.
=
, то есть
и x
= 6. Тогда R = КВ + 6 = 9 + 6 = 15.
Ответ:15.
3. Опускание высот из концов одного основания на другое основание.
Дополнительное
построение 1,2 позволяет разбить трапецию на прямоугольник (стороны которого —
одно из оснований и высота трапеции) и два прямоугольных треугольника (в
которых один из катетов – высота трапеции, а гипотенузы – боковые стороны
трапеции)
Построение
1 Построение 2

Задача. Найдите площадь трапеции с основаниями 8 и 13 и
боковыми сторонами 3 и 4.

Решение.
Проведем ВН и СM — высоты и получим ABD (египетский
треугольник) со сторонами 3,4,5, так как АD – ВС=13 – 8=5.
S= АВ* BD= 6.
Найдем высоту
трапеции: h= 2S:5 = 2*6:5=
2,4.
SABCD= 6+2,4*8=25,2. Ответ:25,2.
4. Проведение
через середину меньшего основания прямых, параллельных боковым сторонам.
Дополнительное построение 4
делит трапецию на параллелограммы и треугольник. Боковые стороны соединяются в
треугольник.


5. Проведение через вершины трапеции прямой, параллельной боковой
стороне, не содержащей эту вершину.
Задача. Основания трапеции равны 30см и 15см, а боковые стороны равны 9 см
и 12 см. Найдите высоту трапеции.
Решение.
Пусть АВСД трапеция, заданная в условии.
Проведем
через вершину С прямую, которая параллельна АВ. Пусть эта прямая пересекает АД
в точке М.
Тогда
АВСМ – параллелограмм и СМ=9, АМ=ДМ=15.
Так
как 92+122=152, то, применив обратную теорему
Пифагора, приходим к выводу, что СМ перпендикулярна СД.
Заметим,
что высота трапеции и треугольника МСД, проведенная из вершины С, совпадают.
Для определения искомой высоты применим метод площадей. Пусть искомая высота
равна х. Тогда для определения х составим уравнение, дважды вычислив площадь
треугольника МСД:
.
Решив
это уравнение находим: х=7,2. Ответ: 7,2.
Задача.
Боковые стороны AB и CD трапеции ABCD равны 15 и 12
соответственно. Найдите градусную величину угла D, если одно из оснований
трапеции на 9 больше другого.
Решение.
Из вершины угла проведем
прямую линию, параллельную стороне. Трапеция разделена данной прямой линией на
параллелограмм и треугольник. Противоположные стороны параллелограмма равны,
значит, длина стороны треугольника равна разности длин оснований трапеции. Данный
треугольник определен по трем сторонам. По теореме косинусов определим искомый
угол. Вычисления показывают, что боковая сторона перпендикулярна к основанию,
искомый угол прямой.

Для
тех, кому интересно.



Теорема.
Задачи с решениями.
Пример
1.Найдите площадь равнобедренной трапеции, описанной около окружности с
радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD —
равнобедренная трапеция, r = 4, AB = 10
Найти: SABCD
1.
AB = CD = 10 по условию.
2.
AB + CD = AD + BC по свойству вписанной
окружности.
3.
AD + BC = 10 + 10 = 20.
4.
FE = 2r = 2 · 4 = 8.
5.
SABCD=1/2(BC + AD)·FE, SABCD = 1/2 · 20
· 8 = 20/2 · 8 = 10 · 8 = 80.
Пример
2.Основания трапеции равны 10 м и 31 м, а боковые стороны —
20 м и 13 м. Найдите высоту трапеции.
Решение.
Пусть HK
= BC = 10 м, BH
= CK = x, AH
= y, тогда KD
= 21 – y
По
теореме Пифагора:x2 +
y2 =
132x2 +
(21 – y)2 =
202x2 +
y2 =
169 (1)
x2 +
441 – 42y + y2 =
400 (2)
Вычтем
из (2) уравнения (1):441 – 42y =
23142y = 210y
= 5AH = 5 м
По
теореме Пифагора:BH2 =
AB2 –
AH2BH2 =
132 – 52BH2 =
169 – 25BH2 =
144
BH
= 12
Пример
3.Большее основание трапеции равно 24. Найдите длину меньшего основания, если
расстояние между серединами диагоналей равно 4.
Решение.

Пример
4.Диагонали AC и BD трапеции ABCD пересекаются в точке O.
Найдите
площадь трапеции, если BC < AD и площади треугольников BOC и ABO равны
соответственно равны 2 и 8.
Анализ.
Рассмотреть подобие
треугольников.
Квадраты соответствующих
сторон относятся как площади треугольников.
Введем параметры
треугольников: стороны оснований и высоты треугольников.
Площади трапеции и
треугольников определим по известным формулам.
Решение.

Пример
5.В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны
боковым сторонам. Найдите площадь трапеции.
Анализ.
Длины диагоналей равны и
перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников
по катету и гипотенузе: ABD
= ACD,
поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для
определения боковой стороны трапеции.
Высоту трапеции определим из
равенства площадей.
Проекцию боковой стороны на
большее основание легче определить из подобия треугольников, чем по теореме
Пифагора.
Длину средней линии в
равнобокой трапеции можно определять как разность большего основания и проекции
боковой стороны на основание.
Площадь трапеции находим как
площадь прямоугольника АМСК, который получим, если достроим трапецию.

Пример
6.Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9.
Найдите длину отрезка, соединяющего середины оснований трапеции.

Задача решается построением.
Достроим прямоугольники и
используем свойство прямоугольника: диагонали прямоугольника равны и в точке
пересечения делятся пополам.
Длина средней линии равна
полусумме длин оснований.
Длина отрезка, соединяющая
середины оснований, равна полусумме длин диагоналей двух построенных
треугольников.
Пример
7.Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного
основаниям и заключенного между боковыми сторонами, который делит трапецию на
две равновеликие части.
Анализ.
Провести из вершины тупого
угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей
трапеций.
Определить отношение при
подобии треугольников.
Рациональные алгебраические
преобразования приведут к результату.
Решение.
Пример
11.Равнобедренная трапеция ABCD описана около окружности. Боковая сторона
трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
Анализ.
Сумма противоположных сторон
трапеции равна между собой — свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине
средней линии.
Применяем теорему Пифагора для
нахождения высоты трапеции.
Площадь трапеции определяем по
доступной формуле.

Пример
8.Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно
вписать окружность, а средняя линия делит ее на части, площади которых
относятся как 5: 11. Найдите длину большего основания трапеции.

Трапеция является описанной.
Сумма длин оснований равна
сумме боковых сторон.
Средняя линия делит трапецию
на две трапеции, высоты которых равны.
Задача сводится к системе
уравнений.
Длина средней линии равна
половине суммы длин боковых сторон.
Пример
9.Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите
среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.

Трапеция равнобедренная.
Длина средней линии равна
боковой стороне.
Площадь трапеции определяется
произведением средней линии на высоту трапеции.
Опустим высоту трапеции из
тупого угла. Через заданный косинус угла определим синус угла.
По синусу угла выразим высоту
трапеции через боковую сторону.

Пример
10.В прямоугольной трапеции, описанной около окружности, большая боковая
сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание
трапеции.
Анализ.
Необходимо использовать
свойство сторон четырехугольника, описанной около окружности: сумма длин
противоположных сторон равна между собой.
Кроме того, длина средней
линии равна полусумме длин сторон оснований.
Проведем из вершины тупого
угла высоту трапеции.
Воспользуемся теоремой
Пифагора и определим проекцию наклонной боковой стороны на основание.
Пример
11.В равнобедренную трапецию, один из углов которой равен 60°, а площадь
равна ,
вписана окружность. Найдите радиус этой окружности.

Анализ.
Важное положение, что трапеция
является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны
равна длине средней линии.
Введем параметр боковой
стороны, из прямоугольного треугольника по заданному углу определим высоту
трапеции, которая является диаметром вписанной окружности. Площадь трапеции
определяется как произведение средней линии на высоту трапеции.
.
Пример
12.Найдите площадь равнобедренной трапеции, у которой большее основание равно
13, средняя линия равна 8, а биссектриса тупого угла является диагональю
трапеции.
Анализ.
При проведении биссектрисы
тупого угла боковая сторона равна большему основанию трапеции. Проекция боковой
стороны равнобедренной трапеции равна полуразности длин оснований.
По теореме Пифагора найдем
высоту трапеции.
Площадь трапеции находим по
формул.
Список используемой литературы
1.
2.
3.
4.
5.
6.
7.
8.
Правильный многоугольник
Пусть an — сторона правильного n-угольника, а rn и Rn — радиусы вписанной и описанной окружностей. Тогда
Формула Герона для четырёхугольника, около которого можно описать окружность:
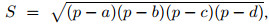 |
где a, b, c, d — стороны этого четырёхугольника, p — полупериметр, а S — площадь. |
Окружность
Окружностью называется геометрическое место точек плоскости, равноудалённых от данной точки, называемой центром окружности.
Основные свойства окружности
1. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
2. Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
3. Серединный перпендикуляр к хорде проходит через центр окружности.
4. Равные хорды удалены от центра окружности на равные расстояния.
5. Хорды окружности, удалённые от центра на равные расстояния, равны.
6. Окружность симметрична относительно любого своего диаметра.
7. Дуги окружности, заключённые между параллельными хордами, равны.
8. Из двух хорд больше та, которая менее удалена от центра.
9. Диаметр есть наибольшая хорда окружности.
Замечательные свойства окружности
1. Геометрическое место точек M, из которых отрезок AB виден под прямым углом (∠AMB = 90°), есть окружность с диаметром AB без точек A и B
2. Геометрическое место точек M, из которых отрезок AB виден под острым углом (∠AMB < 90°), есть внешность круга с диаметром AB без точек прямой AB.
3. Геометрическое место точек M, из которых отрезок AB виден под тупым углом (∠AMB > 90°), есть внутренность круга с диаметром AB без точек отрезка AB
4. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (без концов этих дуг).
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
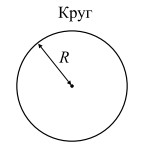 |
R — радиус; |
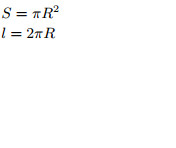 |
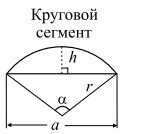 |
r — внутренний радиус; |
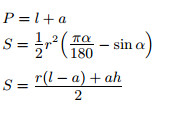 |
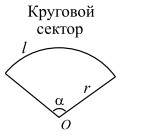 |
r — радиус; |
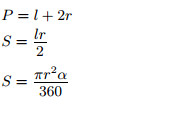 |
Площади круга и сектора
Площадь круга равна произведению числа π на квадрат радиуса:
S = πR2.
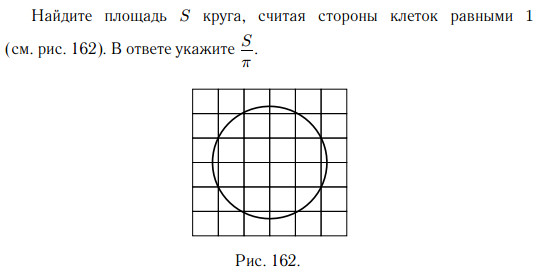
Решение.
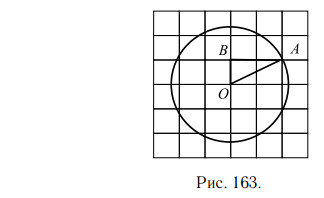
Площадь круга равна произведению числа π на квадрат радиуса. Найдём радиус. Из центра O проведём радиус OA. В треугольнике OAB сторона OA — гипотенуза, катеты равны 1 и 2 (см. рис. 163)
Найдём гипотенузу по теореме Пифагора.
Ответ: 5
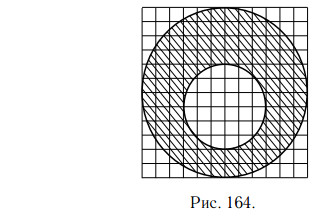
На клетчатой бумаге нарисовано два круга (см. рис. 164). Площадь
внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.
Решение.
Радиус R внутреннего круга — 3 клетки, его площадь равна πR2 = 3.
Радиус внешнего круга — 6 клеток, то есть 2R, поэтому его площадь равна
π · (2R)2 = 3 · 4 = 12. Площадь заштрихованной фигуры равна разности 12 − 3 = 9.
Ответ: 9
Признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.
Признаки равенства прямоугольных треугольников
1. По двум катетам.
2. По катету и гипотенузе.
3. По гипотенузе и острому углу
4. По катету и острому углу
Теорема о сумме углов треугольника и следствия из неё
1. Сумма внутренних углов треугольника равна 180°.
2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
3. Сумма внутренних углов выпуклого n-угольника равна 180°(n − 2).
4. Сумма внешних углов n-угольника равна 360°
5. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.
6. Угол между биссектрисами смежных углов равен 90°.
7. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.
Основные свойства и признаки равнобедренного треугольника
1. Углы при основании равнобедренного треугольника равны.
2. Если два угла треугольника равны, то он равнобедренный.
3. В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.
4. Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, — то он является равнобедренным.
Неравенство треугольника и следствия из него
1. Сумма двух сторон треугольника больше его третьей стороны
2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.
3. Против большего угла треугольника лежит бOльшая сторона.
4. Против большей стороны треугольника лежит больший угол.
5. Гипотенуза прямоугольного треугольника больше катета
6. Если из одной точки проведены к прямой перпендикуляр и наклонные, то
1) перпендикуляр короче наклонных;
2) большей наклонной соответствует большая ´ проекция и наоборот
Средняя линия треугольника.
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Теорема о средней линии треугольника.
Средняя линия треугольника параллельна стороне треугольника и равна её половине.
Теоремы о медианах треугольника
1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины.
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный
3. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы
Свойство серединных перпендикуляров к сторонам треугольника.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника
Теорема о высотах треугольника.
Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Теорема о биссектрисах треугольника.
Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Свойство биссектрисы треугольника.
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам
Признаки подобия треугольников
1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.
3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Площади подобных треугольников
1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.
В прямоугольном треугольнике
1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.
2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.
3. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
4. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.
где a, b — катеты, а c — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружностей соответственно
Теорема Пифагора и теорема, обратная теореме Пифагора
1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный
Средние пропорциональные в прямоугольном треугольнике
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу
Метрические соотношения в треугольнике
1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
3. Формула для медианы треугольника. Если m — медиана треугольника, проведённая к стороне c, то
где a и b — остальные стороны треугольника.
4. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
5. Обобщённая теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
Формулы площади треугольника
1. Площадь треугольника равна половине произведения основания на высоту.
2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
4. Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности.
5. Формула Герона:
где p — полупериметр; a, b, c — стороны треугольника.
Элементы равностороннего треугольника
Пусть h, S, r, R — высота, площадь, радиусы вписанной и описанной
окружностей равностороннего треугольника со стороной a. Тогда
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
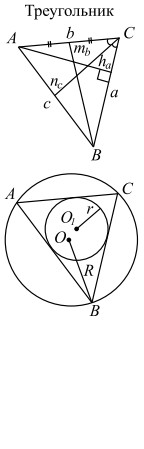 |
a, b, c — стороны; ha, hb, hc — высоты, na, nb, nc — биссектрисы, ba и bc — отрезки, на полусумма медиан; r — радиус вписанной |
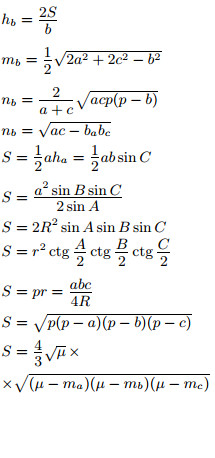 |
Прямоугольный треугольник
Немного полезной информации
В этой главе мы рассмотрим простые виды задач по геометрии, а именно задачи, в которых нужно найти площади плоских фигур, нарисованных
на клетчатой бумаге или расположенных на координатной плоскости.
Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому.
Давайте вспомним эти формулы и разберём примеры их применения.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):
c2 = a2 + b2
Площадь прямоугольного треугольника равна половине произведения его катетов:
S =ab/2.
Напомним, что у прямоугольного
треугольника есть прямой угол, равный 90°. Сторона напротив прямого
угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.
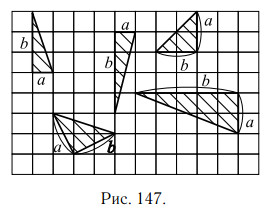
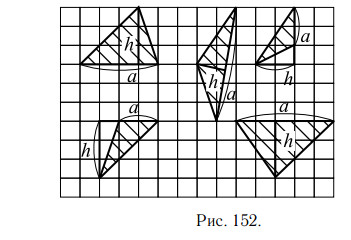
На рисунке 147 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты a и b.
Задачи с решениями
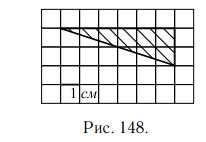
1. На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 148). Найдите его площадь в квадратных сантиметрах.
Решение.
Площадь прямоугольного треугольника равна половине произведения
его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем
по клеточкам), поэтому площадь
Ответ: 6
Площадь треугольника
Немного полезной информации
Площадь произвольного треугольника равна половине произведения длины его стороны (a) на высоту (h), проведённую к этой стороне:
На рисунке 152 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон a и высота, проведённая к этой стороне h.
Как правило, удобно брать ту сторону, которая проходит по линиям
клетчатой бумаги (или же проходит параллельно осям координат).
Задачи с решениями
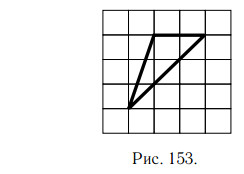
На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 153). Найдите его площадь в квадратных сантиметрах.
Решение.
1-й способ.
Площадь произвольного треугольника равна половине произведения
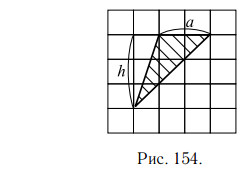
длины его стороны (a) на высоту (h), проведённую к этой стороне. Проведём высоту h. Треугольник тупоугольный, поэтому высота проводится вне
треугольника.
На рисунке 154 сторона a = 2 см, высота h = 3 см
Ответ: 3.
Заметим, что так как клетки имеют размер 1 см × 1 см, то площадь
в квадратных сантиметрах получится, если мы будем по рисунку считать
размер отрезков в клетках. Поэтому единицы длины в этих задачах можно
и не писать.
2-й способ.
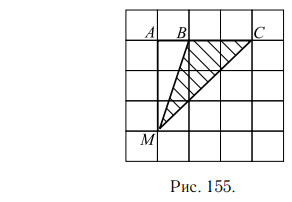
Достроим треугольник BCM до прямоугольного треугольника MCA
(см. рис. 155).
Тогда искомую площадь треугольника BCM можно найти как разность площадей двух прямоугольных треугольников MAC и MAB.
Катеты первого из них равны 3 см и 3 см, катеты второго — 3 см и 1 см.
Площадь прямоугольного треугольника равна половине произведения
его катетов, следовательно,
Ответ: 3.
Четырёхугольник
Параллелограмм.
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Свойство середин сторон четырёхугольника.
Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник.
Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник
Квадрат.
Квадратом называется прямоугольник, все стороны которого равны.
Формулы площади четырёхугольника
1. Площадь параллелограмма равна произведению основания на высоту
2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
Площадь четырёхугольника
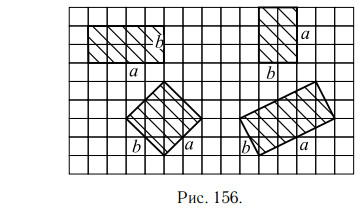
Площадь прямоугольника равна произведению его смежных сторон:
S = ab.
На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b
Ромб
Квадрат.
Квадратом называется прямоугольник, все стороны которого равны.
Свойства и признаки ромба
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам
3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
Площадь ромба равна половине произведения его диагоналей
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции.
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция.
Трапеция называется равнобедренной, если её боковые стороны равны.
Свойства и признаки равнобедренной трапеции
1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
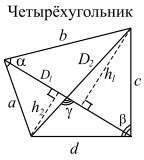 |
a, b, c, d — стороны; |
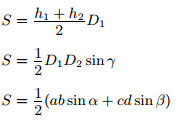 |
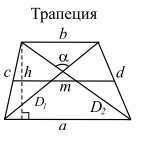 |
a, b — основания; |
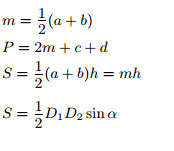 |
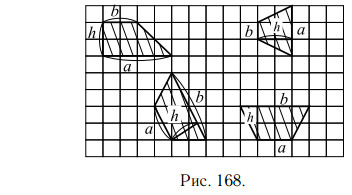
Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):
На рисунке 168 приведены чертежи некоторых трапеций, у каждой из
которых показаны основания a и b и высота h.
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
Замечательное свойство трапеции
Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.
Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.
Сформулируем это свойство иначе:
Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

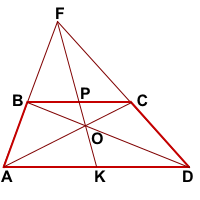
ABCD- трапеция, AD||BC,
Доказать: K- середина AD,

∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).
Значит, треугольники AOK и COP подобны (по двум углам).
Аналогично, треугольники DOK и BOP подобны и
Так как правые части этих равенств равны, то левые также равны:

∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).
Следовательно, треугольники AFK и BFP подобны (по двум углам).
Аналогично, треугольники DFK и CFP подобны и
Правые части равенств равны, приравниваем левые части:
а значит, CP=BP, то есть P — середина BC.
AK=DK, K — середина AD.
Что и требовалось доказать.
- Докажем, что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
- Докажем, что точка пересечения диагоналей трапеции и середина её меньшего основания лежат на прямой, проходящей через точку пересечения продолжения боковых сторон трапеции и середину большего основания

FK — медиана треугольника AFD.
Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.
BC||AD (как основания трапеции), QL||AD (по построению).
Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.
Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.
Замечательное свойство трапеции
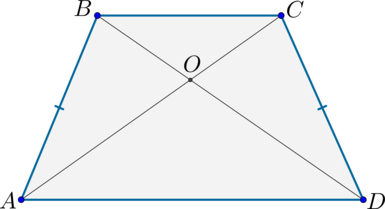
Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии.
Дана трапеция ABCD, , N — середина AD, M — середина BC, . Докажем, что точки M, N, O, P лежат на одной прямой.
Задача не так уж и проста, да и сама формулировка необычна: доказать, что четыре точки лежат на одной прямой. Как это сделать?
Во-первых, разобьем задачу на две более простых. Во-вторых – немного переформулируем.
1) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения диагоналей.
2) Докажем, что середина основания AD лежит на прямой, соединяющей середину основания BC и точку пересечения продолжений боковых сторон.
Начнем с пункта 1.
Пусть M — середина BC, O – точка пересечения диагоналей трапеции, .
Докажем, что N – середина AD.
по двум углам ( как вертикальные, как накрест лежащие при параллельных основаниях трапеции), тогда .
Аналогично, ( как вертикальные, как накрест лежащие при параллельных основаниях трапеция), отсюда .
Отсюда . Это значит, что N – середина AD.
Проведем PM – медиану треугольника BPC. Пусть прямые AD и PM пересекаются в точке N. Докажем, что N – середина AD
по двум углам (угол P – общий, как соответственные при параллельных основаниях трапеции), отсюда .
Получим: , значит, N – середина AD.
Таким образом, точки M,O,N,P лежат на одной прямой, что и требовалось доказать.
Трапеция
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ) .
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. (ADparallel BC) , то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB) , следовательно, (angle BAD +angle ABC=180^circ) .
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD) .
Определение
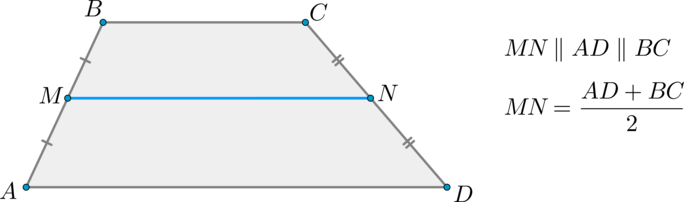
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
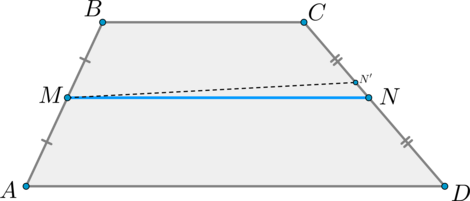
Проведем через точку (M) прямую (MN’parallel AD) ( (N’in CD) ). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB) ) точка (N’) — середина отрезка (CD) . Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
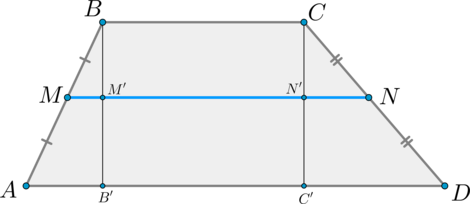
Проведем (BB’perp AD, CC’perp AD) . Пусть (BB’cap MN=M’, CC’cap MN=N’) .
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle ABB’) , (NN’) — средняя линия (triangle DCC’) . Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD) , то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B) . Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC) .
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
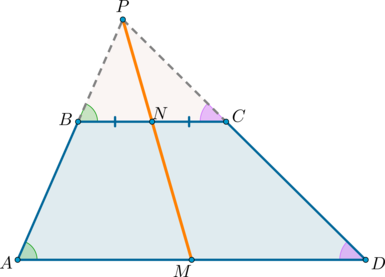
1) Докажем, что точки (P) , (N) и (M) лежат на одной прямой.
Проведем прямую (PN) ( (P) – точка пересечения продолжений боковых сторон, (N) – середина (BC) ). Пусть она пересечет сторону (AD) в точке (M) . Докажем, что (M) – середина (AD) .
Рассмотрим (triangle BPN) и (triangle APM) . Они подобны по двум углам ( (angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac=dfrac]
Рассмотрим (triangle CPN) и (triangle DPM) . Они подобны по двум углам ( (angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac=dfrac]
Отсюда (dfrac=dfrac) . Но (BN=NC) , следовательно, (AM=DM) .
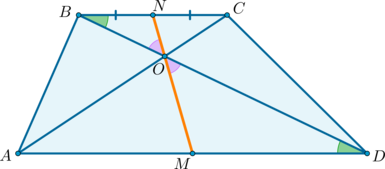
2) Докажем, что точки (N, O, M) лежат на одной прямой.
Пусть (N) – середина (BC) , (O) – точка пересечения диагоналей. Проведем прямую (NO) , она пересечет сторону (AD) в точке (M) . Докажем, что (M) – середина (AD) .
(triangle BNOsim triangle DMO) по двум углам ( (angle OBN=angle ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac=dfrac]
Аналогично (triangle CONsim triangle AOM) . Значит: [dfrac=dfrac]
Отсюда (dfrac=dfrac) . Но (BN=CN) , следовательно, (AM=MD) .
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD) .
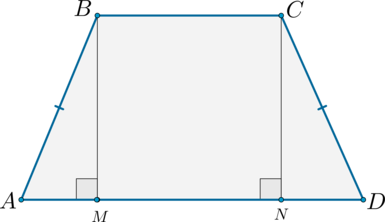
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD) , то (BMparallel CN) ; (ADparallel BC) , тогда (MBCN) – параллелограмм, следовательно, (BM = CN) .
Рассмотрим прямоугольные треугольники (ABM) и (CDN) . Так как у них равны гипотенузы и катет (BM) равен катету (CN) , то эти треугольники равны, следовательно, (angle DAB = angle CDA) .
2)
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD) . Следовательно, (AC=BD) .
3) Т.к. (triangle ABD=triangle ACD) , то (angle BDA=angle CAD) . Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
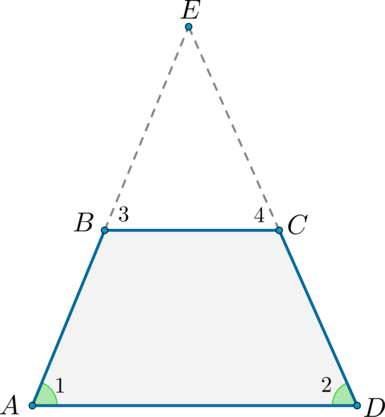
Рассмотрим трапецию (ABCD) , такую что (angle A = angle D) .
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2) , то треугольник (AED) равнобедренный и (AE = ED) . Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB) . Аналогично равны углы (2) и (4) , но (angle 1 = angle 2) , тогда (angle 3 = angle 1 = angle 2 = angle 4) , следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC) .
В итоге (AB = AE — BE = DE — CE = CD) , то есть (AB = CD) , что и требовалось доказать.
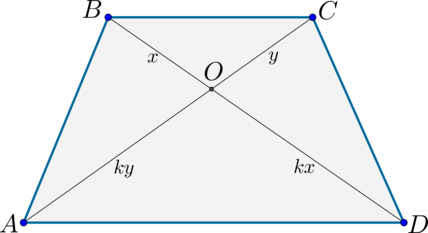
2) Пусть (AC=BD) . Т.к. (triangle AODsim triangle BOC) , то обозначим их коэффициент подобия за (k) . Тогда если (BO=x) , то (OD=kx) . Аналогично (CO=y Rightarrow AO=ky) .
Т.к. (AC=BD) , то (x+kx=y+ky Rightarrow x=y) . Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA) .
Таким образом, по первому признаку (triangle ABD=triangle ACD) ( (AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD) , чтд.
источники:
http://ege-study.ru/materialy-ege/zamechatelnoe-svojstvo-trapecii
http://shkolkovo.net/theory/58