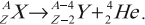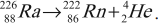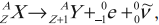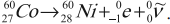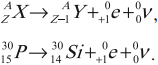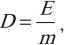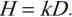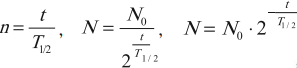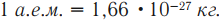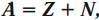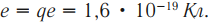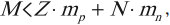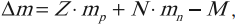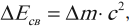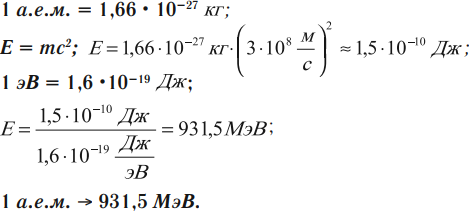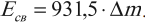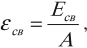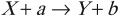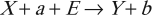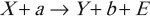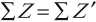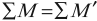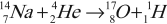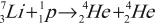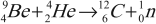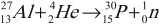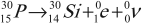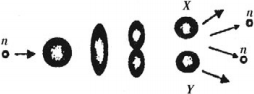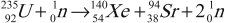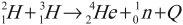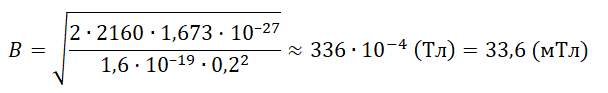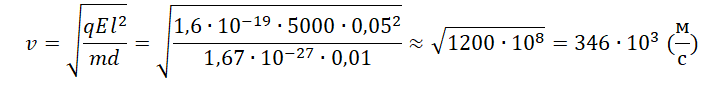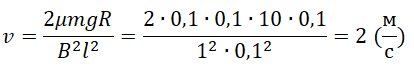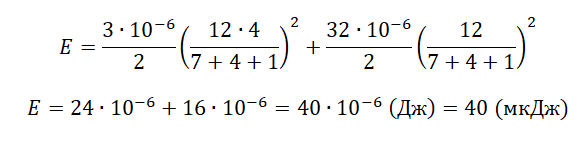Десятичные приставки
| Наименование | Обозначение | Множитель |
| гига | Г | 109 |
| мега | М | 106 |
| кило | к | 103 |
| деци | д | 10–1 |
| санти | с | 10–2 |
| милли | м | 10–3 |
| микро | мк | 10–6 |
| нано | н | 10–9 |
| пико | п | 10–12 |
Физические постоянные (константы)
| число π | π = 3,14 |
| ускорение свободного падения | g = 10 м/с2 |
| гравитационная постоянная | G = 6,7·10–11 Н·м2/кг2 |
| газовая постоянная | R = 8,31 Дж/(моль·К) |
| постоянная Больцмана | k = 1,38·10–23 Дж/К |
| постоянная Авогадро | NA = 6,02·1023 1/моль |
| скорость света в вакууме | с = 3·108 м/с |
| коэффициент пропорциональности в законе Кулона | k = 1/(4πε0) = 9·109 Н·м2/Кл2 |
| модуль заряд электрона | e = 1,6·10-19 Кл |
| масса электрона | me = 9,1·10–31 кг |
| масса протона | mp = 1,67·10–27 кг |
| постоянная Планка | h = 6,62·10-34 Дж·с |
| радиус Солнца | 6,96·108 м |
| температура поверхности Солнца | T = 6000 K |
| радиус Земли | 6370 км |
Соотношение между различными единицами измерения
| температура | 0 К = –273 0С |
| атомная единица массы | 1 а.е.м. = 1,66·10–27 кг |
| 1 атомная единица массы эквивалентна | 931,5 МэВ |
| 1 электронвольт | 1 эВ = 1,6·10-19 Дж |
| 1 астрономическая единица | 1 а.е. ≈ 150 000 000 км |
| 1 световой год | 1 св. год ≈ 9,46·1015 м |
| 1 парсек | 1 пк ≈ 3,26 св. года |
Масса частиц
| электрона | 9,1·10–31кг ≈ 5,5·10–4 а.е.м. |
| протона | 1,673·10–27 кг ≈ 1,007 а.е.м. |
| нейтрона | 1,675·10–27 кг ≈ 1,008 а.е.м. |
Плотность
| воды | 1000 кг/м3 |
| древесины (сосна) | 400 кг/м3 |
| керосина | 800 кг/м3 |
| подсолнечного масла | 900 кг/м3 |
| алюминия | 2700 кг/м3 |
| железа | 7800 кг/м3 |
| ртути | 13 600 кг/м3 |
Удельная теплоёмкость
| воды | 4,2·10 3 Дж/(кг·К) |
| льда | 2,1·10 3 Дж/(кг·К) |
| железа | 460 Дж/(кг·К) |
| свинца | 130 Дж/(кг·К) |
| алюминия | 900 Дж/(кг·К) |
| меди | 380 Дж/(кг·К) |
| чугуна | 500 Дж/(кг·К) |
Удельная теплота
| парообразования воды | 2,3·10 6 Дж/кг |
| плавления свинца | 2,5·10 4 Дж/кг |
| плавления льда | 3,3·10 5 Дж/кг |
Нормальные условия:
| давление | 105 Па |
| температура | 00 C |
Молярная маcса молекул
| азота | 28·10–3 кг/моль |
| аргона | 40·10–3 кг/моль |
| водорода | 2·10–3 кг/моль |
| воздуха | 29·10–3 кг/моль |
| воды | 18·10–3 кг/моль |
| гелия | 4·10–3 кг/моль |
| кислорода | 32·10–3 кг/моль |
| лития | 6·10–3 кг/моль |
| неона | 20·10–3 кг/моль |
| углекислого газа | 44·10–3 кг/моль |
Электрический заряд
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электризация тел, взаимодействие зарядов, два вида заряда, закон сохранения электрического заряда.
Электромагнитные взаимодействия принадлежат к числу наиболее фундаментальных взаимодействий в природе. Силы упругости и трения, давление газа и многое другое можно свести к электромагнитным силам между частицами вещества. Сами электромагнитные взаимодействия уже не сводятся к другим, более глубоким видам взаимодействий.
Столь же фундаментальным типом взаимодействия является тяготение — гравитационное притяжение любых двух тел. Однако между электромагнитными и гравитационными взаимодействиями имеется несколько важных отличий.
1. Участвовать в электромагнитных взаимодействиях могут не любые, а только заряженные тела (имеющие электрический заряд).
2. Гравитационное взаимодействие — это всегда притяжение одного тела к другому. Электромагнитные взаимодействия могут быть как притяжением, так и отталкиванием.
3. Электромагнитное взаимодействие гораздо интенсивнее гравитационного. Например, сила электрического отталкивания двух электронов в раз превышает силу их гравитационного притяжения друг к другу.
Каждое заряженное тело обладает некоторой величиной электрического заряда . Электрический заряд — это физическая величина, определяющая силу электромагнитного взаимодействия между объектами природы. Единицей измерения заряда является кулон (Кл).
Два вида заряда
Поскольку гравитационное взаимодействие всегда является притяжением, массы всех тел неотрицательны. Но для зарядов это не так. Два вида электромагнитного взаимодействия — притяжение и отталкивание — удобно описывать, вводя два вида электрических зарядов: положительные и отрицательные.
Заряды разных знаков притягиваются друг к другу, а заряды разных знаков друг от друга отталкиваются. Это проиллюстрировано на рис. 1; подвешенным на нитях шарикам сообщены заряды того или иного знака.
Рис. 1. Взаимодействие двух видов зарядов
Повсеместное проявление электромагнитных сил объясняется тем, что в атомах любого вещества присутствуют заряженные частицы: в состав ядра атома входят положительно заряженные протоны, а по орбитам вокруг ядра движутся отрицательно заряженные электроны.
Заряды протона и электрона равны по модулю, а число протонов в ядре равно числу электронов на орбитах, и поэтому оказывается, что атом в целом электрически нейтрален. Вот почему в обычных условиях мы не замечаем электромагнитного воздействия со стороны окружающих тел: суммарный заряд каждого из них равен нулю, а заряженные частицы равномерно распределены по объёму тела. Но при нарушении электронейтральности (например, в результате электризации) тело немедленно начинает действовать на окружающие заряженные частицы.
Почему существует именно два вида электрических зарядов, а не какое-то другое их число, в данный момент не известно. Мы можем лишь утверждать, что принятие этого факта в качестве первичного даёт адекватное описание электромагнитных взаимодействий.
Заряд протона равен Кл. Заряд электрона противоположен ему по знаку и равен
Кл. Величина
Кл
называется элементарным зарядом. Это минимальный возможный заряд: свободные частицы с меньшей величиной заряда в экспериментах не обнаружены. Физика не может пока объяснить, почему в природе имеется наименьший заряд и почему его величина именно такова.
Заряд любого тела всегда складывается из целого количества элементарных зарядов:
Если , то тело имеет избыточное количество
электронов (по сравнению с количеством протонов). Если же
, то наоборот, у тела электронов недостаёт: протонов на
больше.
Электризация тел
Чтобы макроскопическое тело оказывало электрическое влияние на другие тела, его нужно электризовать. Электризация — это нарушение электрической нейтральности тела или его частей. В результате электризации тело становится способным к электромагнитным взаимодействиям.
Один из способов электризовать тело — сообщить ему электрический заряд, то есть добиться избытка в данном теле зарядов одного знака. Это несложно сделать с помощью трения.
Так, при натирании шёлком стеклянной палочки часть её отрицательных зарядов уходит на шёлк. В результате палочка заряжается положительно, а шёлк — отрицательно. А вот при натирании шерстью эбонитовой палочки часть отрицательных зарядов переходит с шерсти на палочку: палочка заряжается отрицательно, а шерсть — положительно.
Данный способ электризации тел называется электризацией трением. С электризацией трением вы сталкиваетесь всякий раз, когда снимаете свитер через голову 
Другой тип электризации называется электростатической индукцией, или электризацией через влияние. В этом случае суммарный заряд тела остаётся равным нулю, но перераспределяется так, что в одних участках тела скапливаются положительные заряды, в других — отрицательные.
Рис. 2. Электростатическая индукция
Давайте посмотрим на рис. 2. На некотором расстоянии от металлического тела находится положительный заряд . Он притягивает к себе отрицательные заряды металла (свободные электроны), которые скапливаются на ближайших к заряду участках поверхности тела. На дальних участках остаются нескомпенсированные положительные заряды.
Несмотря на то, что суммарный заряд металлического тела остался равным нулю, в теле произошло пространственное разделение зарядов. Если сейчас разделить тело вдоль пунктирной линии, то правая половина окажется заряженной отрицательно, а левая — положительно.
Наблюдать электризацию тела можно с помощью электроскопа. Простой электроскоп показан на рис. 3 (изображение с сайта en.wikipedia.org).
Рис. 3. Электроскоп
Что происходит в данном случае? Положительно заряженная палочка (например, предварительно натёртая) подносится к диску электроскопа и собирает на нём отрицательный заряд. Внизу, на подвижных листочках электроскопа, остаются нескомпенсированные положительные заряды; отталкиваясь друг от друга, листочки расходятся в разные стороны. Если убрать палочку, то заряды вернутся на место и листочки опадут обратно.
Явление электростатической индукции в грандиозных масштабах наблюдается во время грозы. На рис. 4 мы видим идущую над землёй грозовую тучу.
Рис. 4. Электризация земли грозовой тучей
Внутри тучи имеются льдинки разных размеров, которые перемешиваются восходящими потоками воздуха, сталкиваются друг с другом и электризуются. При этом оказывается, что в нижней части тучи скапливается отрицательный заряд, а в верхней — положительный.
Отрицательно заряженная нижняя часть тучи наводит под собой на поверхности земли заряды положительного знака. Возникает гигантский конденсатор с колоссальным напряжением между тучей и землёй. Если этого напряжения будет достаточно для пробоя воздушного промежутка, то произойдёт разряд — хорошо известная вам молния.
Закон сохранения заряда
Вернёмся к примеру электризации трением — натирании палочки тканью. В этом случае палочка и кусок ткани приобретают равные по модулю и противоположные по знаку заряды. Их суммарный заряд как был равен нулю до взаимодействия, так и остаётся равным нулю после взаимодействия.
Мы видим здесь закон сохранения заряда, который гласит: в замкнутой системе тел алгебраическая сумма зарядов остаётся неизменной при любых процессах, происходящих с этими телами:
Замкнутость системы тел означает, что эти тела могут обмениваться зарядами только между собой, но не с какими-либо другими объектами, внешними по отношению к данной системе.
При электризации палочки ничего удивительного в сохранении заряда нет: сколько заряженных частиц ушло с палочки — столько же пришло на кусок ткани (или наоборот). Удивительно то, что в более сложных процессах, сопровождающихся взаимными превращениями элементарных частиц и изменением числа заряженных частиц в системе, суммарный заряд всё равно сохраняется!
Например, на рис. 5 показан процесс , при котором порция электромагнитного излучения
(так называемый фотон) превращается в две заряженные частицы — электрон
и позитрон
. Такой процесс оказывается возможным при некоторых условиях — например, в электрическом поле атомного ядра.
Рис. 5. Рождение пары электрон–позитрон
Заряд позитрона равен по модулю заряду электрона и противоположен ему по знаку. Закон сохранения заряда выполнен! Действительно, в начале процесса у нас был фотон, заряд которого равен нулю, а в конце мы получили две частицы с нулевым суммарным зарядом.
Закон сохранения заряда (наряду с существованием наименьшего элементарного заряда) является на сегодняшний день первичным научным фактом. Объяснить, почему природа ведёт себя именно так, а не иначе, физикам пока не удаётся. Мы можем лишь констатировать, что эти факты подтверждаются многочисленными физическими экспериментами.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Электрический заряд» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Физика атома
Атом — это наименьшая частица химического элемента, способная к самостоятельному существованию и обладающая его свойствами.
Каждому элементу соответствует определенный род атомов, обозначаемый химическим символом этого элемента. Например, атом кислорода обозначается символом О, атом водорода Н, атом гелия Не.
Атомы могут существовать в свободном состоянии (в виде отдельных атомов) в газах. В жидкостях и твердых телах они существуют в виде молекул, в которых соединяются с атомами того же элемента или других химических элементов (или, как принято говорить, существуют в связанном состоянии).
Со времен Демокрита (ок. 460—370 гг. до н. э.) и до конца XIX в. атом считался неделимой частицей — кирпичиком мироздания. После открытия электрона в 1897 г. английским ученым Дж. Дж. Томсоном стало ясно, что атом — сложная система.
Планетарная модель атома
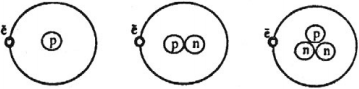
С целью выяснения распределения положительного заряда в атоме английский ученый Э. Резерфорд исследовал рассеяние $α$-частиц фольгой из различных веществ. Большинство а-частиц беспрепятственно, почти без отклонений, проникало через фольгу, и только $1$ из $2000$ частиц отклонялась на углы, большие $90°$. В результате этих экспериментов в 1911 г. Резерфорд предложил следующую модель строения атома.
Атом состоит из положительно заряженного ядра, вокруг которого обращаются электроны, каждый на своей орбите, подобно планетам Солнечной системы, обращающимся вокруг Солнца. Поэтому модель называют планетарной.
Расстояние от электронов до ядра очень велико по сравнению с размерами ядра. Оценки Резерфорда показали, что диаметр ядра составляет порядка $10^{-12}—10^{-13}$ см. Размер самого атома $10^{-8}$ см. Положительный заряд ядра $q_{ядра}$ связан с числом электронов $Z$ в атоме соотношением:
$q_{ядра}=+Z·e$
где $е$ — заряд электрона.
Заряд ядра и число электронов в атоме, соответственно, совпадает с порядковым номером элемента в таблице Д. И. Менделеева.
В целом атом электронейтрален. При отрыве электрона от атома или присоединении электрона к атому (в результате столкновений, например, или при различных химических процессах) могут образоваться положительно или отрицательно заряженные ионы.
Простая и наглядная модель атома Резерфорда прекрасно объясняла результаты его опытов. Однако на основании этой модели нельзя объяснить факт существования атома, его устойчивость. Согласно законам электродинамики Максвелла электрон, движущийся по орбите с немалым ускорением, должен излучать электромагнитные волны с частотой, равной частоте его обращения вокруг ядра, в результате чего в скором времени, потеряв в результате излучения всю энергию, упасть на ядро. Согласно расчетам, основанным на механике Ньютона и электродинамике Максвелла, время это составляет всего $10^{-8}$ с. В действительности ничего подобного не происходит. Нейтральные невозбужденные атомы существуют неограниченно долго.
Это несоответствие опыта выводам теории связано с попыткой применения законов классической физики к внутриатомным явлениям (которые, как оказалось, подчиняются законам квантовой механики).
Выход из создавшейся в теории атома ситуации был найден датским физиком Нильсом Бором.
Состав ядра. Нуклонная модель Гейзенберга-Иваненко
Атомное ядро — это центральная часть атома, состоящая из протонов и нейтронов (которые вместе называются нуклонами).
Ядро было открыто Э. Резерфордом в 1911 г. при исследовании прохождения а-частиц через вещество. Оказалось, что почти вся масса атома ($99.95%$) сосредоточена в ядре. Размер атомного ядра имеет порядок величины $10^{-13}-10^{-12}$ см, что в $10 000$ раз меньше размера электронной оболочки.
Предложенная Э. Резерфордом планетарная модель атома и экспериментальное наблюдение им ядер водорода, выбитых $α$-частицами из ядер других элементов (1919—1920 гг.), привели ученого к представлению о протоне. Термин протон был введен в начале 20-х гг XX ст.
Протон (от protos — первый, символ $p$) — стабильная элементарная частица, ядро атома водорода.
Протон — положительно заряженная частица, заряд которой по абсолютной величине равен заряду электрона $e=1.6·10^{-19}$ Кл. Масса протона в $1836$ раз больше массы электрона. Масса покоя протона $m_p=1.6726231·10^{-27}кг=1.007276470 а.е.м.$
Второй частицей, входящей в состав ядра, является нейтрон.
Нейтрон (от лат. neuter — ни тот, ни другой, символ $n$) — это элементарная частица, не имеющая заряда, т. е. нейтральная.
Масса нейтрона в $1839$ раз превышает массу электрона. Масса нейтрона почти равна (незначительно больше) массе протона: масса покоя свободного нейтрона $m_n=1.6749286·10^{-27}кг=1.0008664902 а.е.м.$ и превосходит массу протона на $2.5$ массы электрона. Нейтрон, наряду с протоном под общим названием нуклон входит в состав атомных ядер.
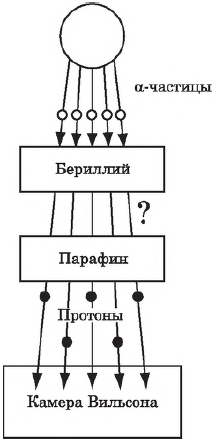
Нейтрон был открыт в 1932 г. учеником Э. Резерфорда Д. Чедвигом при бомбардировке бериллия $α$-частицами. Возникающее при этом излучение с большой проникающей способностью (преодолевало преграду из свинцовой пластины толщиной $10-20$ см) усиливало свое действие при прохождении через парафиновую пластину. Оценка энергии этих частиц по трекам в камере Вильсона, сделанная супругами Жолио-Кюри, и дополнительные наблюдения позволили исключить первоначальное предположение о том, что это $γ$-кванты. Большая проникающая способность новых частиц, названных нейтронами, объяснялась их электронейтральностью. Ведь заряженные частицы активно взаимодействуют с веществом и быстро теряют свою энергию. Существование нейтронов было предсказано Э. Резерфордом за 10 лет до опытов Д. Чедвига. При попадании $α$-частиц в ядра бериллия происходит следующая реакция:
$↙{4}↖{9}Be{+}{}↙{2}↖{4}He{→}{}↙{6}↖{12}C{+}{}↙{0}↖{1}n$
Здесь $↙{0}↖{1}n$ — символ нейтрона; заряд его равен нулю, а относительная атомная масса приблизительно равна единице. Нейтрон — нестабильная частица: свободный нейтрон за время $~15$ мин. распадается на протон, электрон и нейтрино — частицу, лишенную массы покоя.
После открытия Дж. Чедвиком нейтрона в 1932 г. Д. Иваненко и В. Гейзенберг независимо друг от друга предложили протоннонейтронную (нуклонную) модель ядра. Согласно этой модели, ядро состоит из протонов и нейтронов. Число протонов $Z$ совпадает с порядковым номером элемента в таблице Д. И. Менделеева.
Заряд ядра $Q$ определяется числом протонов $Z$, входящих в состав ядра, и кратен абсолютной величине заряда электрона $e$:
$Q=+Ze$
Число $Z$ называется зарядовым числом ядра или атомным номером.
Массовым числом ядра $А$ называется общее число нуклонов, т. е. протонов и нейтронов, содержащихся в нем. Число нейтронов в ядре обозначается буквой $N$. Таким образом, массовое число равно:
$A=Z+N$
Нуклонам (протону и нейтрону) приписывается массовое число, равное единице, электрону — нулевое значение.
Представлению о составе ядра содействовало также открытие изотопов.
Изотопы (от греч. isos — равный, одинаковый и topos — место) — это разновидности атомов одного и того же химического элемента, атомные ядра которых имеют одинаковое число протонов ($Z$) и различное число нейтронов ($N$).
Изотопами называются также ядра таких атомов. Изотопы являются нуклидами одного элемента. Нуклид (от лат. nucleus — ядро) — любое атомное ядро (соответственно атом) с заданными числами $Z$ и $N$. Общее обозначение нуклидов имеет вид $↙{A}↖{Z}X_N$, где $X$ — символ химического элемента, $A=Z+N$ — массовое число.
Изотопы занимают одно и то же место в Периодической системе элементов, откуда и произошло их название. По своим ядерным свойствам (например, по способности вступать в ядерные реакции) изотопы, как правило, существенно отличаются. Химические (и почти в той же мере физические) свойства изотопов одинаковы. Это объясняется тем, что химические свойства элемента определяются зарядом ядра, поскольку именно он влияет на структуру электронной оболочки атома.
Исключением являются изотопы легких элементов. Изотопы водорода $↖{1}H$ — протий, $↖{2}H$ — дейтерий, $↖{3}H$ — тритий столь сильно отличаются по массе, что и их физические и химические свойства различны. Дейтерий стабилен (т. е. не радиоактивен) и входит в качестве небольшой примеси ($1:4500$) в обычный водород. При соединении дейтерия с кислородом образуется тяжелая вода. Она при нормальном атмосферном давлении кипит при $101.2°$С и замерзает при $+3.8°$С. Тритий $β$-радиоактивен с периодом полураспада около $12$ лет.
У всех химических элементов имеются изотопы. У некоторых элементов имеются только нестабильные (радиоактивные) изотопы. Для всех элементов искусственно получены радиоактивные изотопы.
Изотопы урана. У элемента урана есть два изотопа — с массовыми числами $235$ и $238$. Изотоп $↙{92}↖{235}U$ составляет всего ${1}/{140}$ часть от более распространенного $↙{92}↖{238}U$.
Энергия связи нуклонов в ядре. Ядерные силы
Поскольку протоны в ядре имеют одинаковый положительный заряд, они отталкиваются. Для того чтобы удержать их вместе, должны существовать силы, намного превышающие силы электрического и гравитационного взаимодействия. Эти силы называются ядерными силами. Они в $100$ раз превосходят электрические (кулоновские) силы. Это самые мощные силы из всех, которыми располагает природа. Поэтому взаимодействие ядерных частиц относят к сильным взаимодействиям — особому типу взаимодействия, присущему большинству элементарных частиц наряду с электромагнитными взаимодействиями. Ядерные силы заметно проявляются лишь на расстояниях порядка $10^{-13}-10^{-12}$ см, равных по порядку величины размерам ядра, что показали опыты Резерфорда по рассеянию $α$-частиц ядрами.
Устойчивость атомного ядра характеризуется энергией связи ($Е_{св}$). Энергия связи — это энергия, которую надо затратить, чтобы расщепить ядро. Ее принято выражать в мегаэлектронвольтах (МэВ) ($1 МэВ = 1.6·10^{-13}Дж$).
Под энергией связи ядра понимают ту энергию, которая необходима для полного расщепления ядра на отдельные нуклоны. На основании закона сохранения энергии можно также утверждать, что энергия связи равна той энергии, которая выделяется при образовании ядра из отдельных частиц. Энергия связи атомных ядер очень велика. Определить ее можно, применяя соотношение Эйнштейна между массой и энергией: $E=mc^2$.
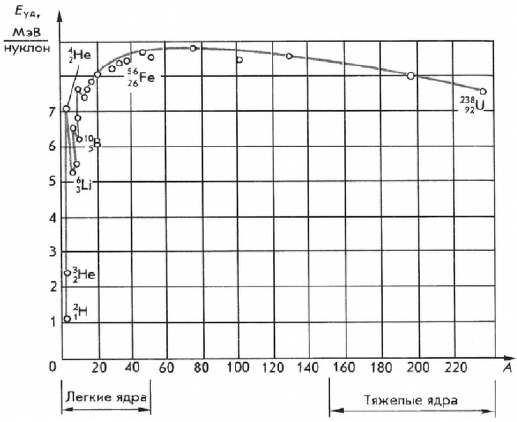
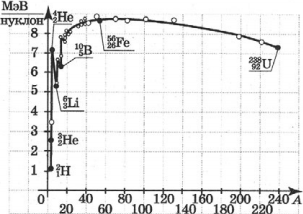
Удельной энергией связи называют энергию связи, приходящуюся на один нуклон ядра. Ее определяют экспериментально. Зависимость $Е_{уд}$ от массового числа $А$ приведена на рисунке. Как видно из рисунка, удельная энергия связи примерно постоянна (не считая самых легких ядер) и равна $8$ МэВ/нуклон. Слабый максимум ($8.6$ МэВ) приходится на элементы с массовыми числами от $50$ до $60$, т. е. на железо и близкие к нему по порядковому номеру элементы. Ядра этих элементов наиболее устойчивы.
У тяжелых ядер удельная энергия связи уменьшается за счет растущей с увеличением $Z$ кулоновской энергии отталкивания протонов. Кулоновские силы стремятся разорвать ядро.
Дефект массы
Точнейшие измерения показывают, что масса покоя ядра $М_я$ всегда меньше суммы масс покоя составляющих ее протонов и нейтронов: $М_я < Zm_p + Nm_n$. Существует положительная разность масс, называемая дефектом массы: $∆M=Zm_p + Nm_n-М_я$. Для гелия масса ядра на $0.75 %$ меньше суммы масс двух протонов и двух нейтронов. Для одного моля гелия $∆M=0.03$ г.
Уменьшение массы при образовании ядра из нуклонов означает, что при этом уменьшается энергия этой системы нуклонов на значение энергии связи $Е_{св}$:
$Е_{св}=∆Mc^2=(Zm_p + Nm_n-М_я)c^2$
Энергия связи переходит в энергию излучаемых при ядерных превращениях $γ$-квантов, которая равна как раз $Е_{св}$, и масса которых $∆M={Е_{св}}/{с^2}$.
Физика атомного ядра
Содержание
- Радиоактивность. Альфа-распад. Бета-распад. Гамма-излучение
- Закон радиоактивного распада
- Нуклонная модель ядра. Заряд ядра. Массовое число ядра
- Энергия связи нуклонов в ядре. Ядерные силы
- Ядерные реакции. Деление и синтез ядер
- Основные формулы по теме «Физика атомного ядра»
Радиоактивность. Альфа-распад. Бета-распад. Гамма-излучение
Радиоактивность – способность некоторых атомных ядер самопроизвольно превращаться в другие ядра с испусканием различных видов радиоактивных излучений.
Виды радиоактивности:
- естественная радиоактивность – это радиоактивность, которая наблюдается у неустойчивых изотопов, существующих в природе и имеющих в таблице Менделеева порядковый номер больше 83;
- искусственная радиоактивность – это радиоактивность, которая наблюдается у изотопов, полученных посредством ядерных реакций в лабораторных условиях.
Явление естественной радиоактивности открыл в 1896 году французский физик А. Беккерель. Проводя опыты с солями урана, он заметил, что они самопроизвольно испускают лучи неизвестной природы, которые проходят через бумагу, дерево, металлические пластины и делают воздух проводником электричества.
Радиоактивность данного химического элемента не зависит от того, является ли химический элемент чистым или входит в состав какоголибо химического соединения. Радиоактивность не зависит от внешних условий: температуры, освещения, давления. Это означает, что радиоактивность представляет собой внутреннее свойство атомов радиоактивного элемента.
Виды радиоактивных излучений
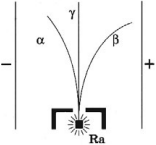
Излучение радиоактивных веществ имеет сложный характер и состоит из трех видов излучений. Если радиоактивное излучение пропустить через электрическое и магнитное поля, то оно распадается на три части, две из них отклоняются в противоположные стороны, а третий не отклоняется.
- ( alpha )-излучение представляет собой ядра атомов гелия ( {}^4_2He ), движущиеся со скоростью 107 м/с, несет положительный заряд;
- ( beta )-излучение представляет собой поток быстрых электронов, движущихся со скоростями, близкими к скорости света, несет отрицательный заряд;
- ( gamma )-излучение представляет собой электромагнитное излучение с длиной волны 10-12 м, заряда не имеет.
При одинаковой энергии частиц разные виды излучений неодинаково взаимодействуют с веществом.
Вследствие сильного ионизирующего действия глубина проникновения ( alpha )-частиц в твердых телах обычно очень мала. ( beta )-частицы менее эффективно взаимодействуют с атомами вещества, поэтому их проникающая способность больше, чем у ( alpha )-частиц. ( gamma )-кванты взаимодействуют с электронными оболочками атомов и имеют самую большую проникающую способность. Для защиты от ( gamma )-излучения необходимы защитные стены или оболочки толщиной несколько десятков сантиметров или даже метров.
Радиоактивный распад – самопроизвольный распад атомов радиоактивного вещества, в результате которого ядра одних химических элементов превращаются в ядра других химических элементов.
Превращения атомных ядер, которые сопровождаются испусканием ( alpha )- и ( beta )-частиц, называются соответственно ( alpha )— и ( beta )-распадом. Термина «( gamma )-распад» не существует, так как ( alpha )— и ( beta )-распад сопровождаются γ-излучением.
Распадающееся ядро Х называется материнским ядром, ядро продукта распада Y – дочерним ядром.
Правила радиоактивного смещения
Это правила, позволяющие установить, какое ядро возникает в результате распада данного материнского ядра.
- ( alpha )-распад:
Если при радиоактивном превращении испускаются ( alpha )-частицы, то в результате такого превращения образуется ядро элемента, находящегося в таблице Менделеева на две клетки раньше исходного ядра плюс ядро атома гелия ( {}^4_2He ) (или ( alpha )-частица):
- ( beta )-распад.
Если при радиоактивном превращении испускаются ( beta )-частицы, то в результате такого превращения образуется ядро элемента, находящегося в таблице Менделеева:
– при ( beta^- )-распаде в следующей после исходного ядра клетке плюс электрон и антинейтрино (частица, не имеющая заряда и масса покоя которой равна нулю):
– при ( beta^+ )-распаде в предшествующей исходному ядру клетке плюс позитрон и нейтрино (частица, не имеющая заряда и масса покоя которой равна нулю):
( gamma )-излучение сопровождает ( alpha )- и ( beta )-распады, а также возникает при ядерных реакциях, торможении частиц, их распаде и т. д.
( gamma )-излучение испускается дочерним ядром, которое в момент своего образования оказывается в возбужденном состоянии, а затем переходит в невозбужденное состояние.
Спектр ( gamma )-излучения является линейчатым.
Биологическое действие радиоактивных излучений
При облучении вещества ( alpha )-, ( beta )-, ( gamma )-частицами происходит возбуждение или ионизация атомов вещества. При этом сами частицы могут тормозиться, что сопровождается рентгеновским излучением. Кроме того, частицы могут упруго или неупруго соударяться с атомами вещества. Все это может привести к изменению свойств облучаемого вещества и к отрицательному воздействию на живые организмы. Вредное действие излучений на организм связано с образованием свободных химических радикалов и с мутацией в клетках, которые могут оказывать влияние на потомство, приводить к лучевой болезни и образованию злокачественных опухолей.
Методы защиты от внешнего радиоактивного облучения:
- удаление от источника излучения на большое расстояние;
- ограничение времени пребывания на загрязненной местности или вблизи радиоактивных источников;
- ограждение радиоактивных источников экранами из материалов, эффективно поглощающих радиоактивные излучения (графит, свинец, кадмий, бор).
Методы защиты от внутреннего радиоактивного облучения:
- дозиметрический контроль воздуха, осадков в близлежащей местности;
- дозиметрический контроль продуктов питания;
- применение веществ, ослабляющих воздействие радиоактивных излучений на организм.
В дозиметрии различают поглощенную и эквивалентную дозы.
Поглощенная доза равна энергии радиоактивного излучения, поглощенного единицей массы вещества.
Обозначение – ( D ), единица измерения в СИ – грей (Гр).
где ( E ) – энергия излучения; ( m ) – масса вещества.
Для характеристики биологического воздействия на организм используется коэффициент качества излучения ( (k) ), или коэффициент относительной биологической активности.
( k ) = 1 для ( gamma )-квантов, ( k ) = 3 для тепловых нейтронов, ( k ) = 10 для нейтронов с энергией порядка 0,5 МэВ.
Эквивалентная доза равна произведению коэффициента качества излучения и поглощенной дозы.
Обозначение – ( H ), единица измерения в СИ – зиверт (Зв).
1 зиверт – это эквивалентная доза, при которой поглощенная доза равна 1 Гр при коэффициенте качества, равном 1.
Естественный фон составляет 2 мЗв за год.
Предельно допустимая доза – 5 мЗв за год.
При дозе 0,5 Зв наступает острое лучевое поражение организма.
При дозе 3–5 Зв – смертельный исход.
Допустимая доза облучения за среднее время жизни человека (70 лет) составляет 0,35 Зв.
Закон радиоактивного распада
Если имеется большое количество одинаковых радиоактивных ядер, то вероятность распада каждого из них в любой момент времени одинакова. Радиоактивный распад любого ядра является случайным процессом, поэтому момент его распада предсказать невозможно.
Однако для большого числа частиц, находящихся в образце вещества, выполняется статистический закон радиоактивного распада.
Закон радиоактивного распада:
число нераспавшихся атомных ядер при естественном радиоактивном распаде экспоненциально уменьшается с течением времени.
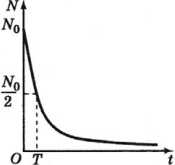
Период полураспада – это время, в течение которого распадается половина способных к распаду ядер.
В начальный момент времени ( t ) = 0, число атомных ядер ( N_0 ).
Через промежуток времени, равный периоду полураспада ( t=T_{1/2} ), число атомных ядер ( N=frac{N_0}{2} ).
Через промежуток времени, равный двум периодам полураспада ( t=2T_{1/2} ), число атомных ядер ( N=frac{N_0}{4}=frac{N_0}{2^2} ).
Через промежуток времени, равный ( n ) периодам полураспада ( t=nT_{1/2} ), число атомных ядер ( N=frac{N_0}{2^n} ).
где ( N ) – число нераспавшихся атомных ядер к моменту времени ( t ); ( N_0 ) – начальное число атомных ядер; ( T_{1/2} ) – период полураспада.
На рисунке период полураспада соответствует времени, в течение которого число радиоактивных ядер (активность) уменьшается вдвое.
Нуклонная модель ядра. Заряд ядра. Массовое число ядра
Элементарные частицы:
- протон
Обозначение – ( p ), заряд ( q_p ) = 1,6·10-19 Кл, масса ( m_p ) = 1,67·10-27 кг. - нейтрон
Обозначение – ( n ), заряд отсутствует, масса ( m_n ) = 1,66·10-27 кг. - электрон
Обозначение – ( e ), заряд ( q_e ) = –1,6·10-19 Кл, масса ( m_e ) = 9,1·10-31 кг.
Нуклон – это частица, входящая в состав атомного ядра.
Атомное ядро любого химического элемента состоит из протонов и нейтронов.
Массовое число – это число, которое определяет количество протонов и нейтронов в ядре и равно округленному до целого значению массы атомного ядра в а.е.м.
Обозначение – ( A ), единица измерения – 1 атомная единица массы (а.е.м.).
Массовое число равно сумме количества протонов и нейтронов в ядре:
где ( A ) – массовое число; ( Z ) – количество протонов в ядре; ( N ) – количество нейтронов в ядре.
Зарядовое число – это число, которое показывает количество протонов в ядре.
Зарядовое число равно сумме зарядов протонов, входящих в состав ядра, выраженной в элементарных электрических зарядах.
Элементарный электрический заряд равен заряду электрона:
( Z ) – порядковый номер химического элемента в периодической таблице Менделеева.
Если некоторый химический элемент обозначить ( {}^A_ZX ), это означает, что в его ядре ( Z ) – протонов и ( N=A-Z ) – нейтронов.
Измерения массы атомов показали, что практически все химические элементы имеют изотопы.
Изотопы – это атомы одного и того же химического элемента, имеющие одинаковое количество протонов, но отличающиеся количеством нейтронов в ядре.
Изотопы имеют:
- одинаковый атомный номер ( Z ) (одинаковое число протонов);
- различные массовые числа ( A ) (различное число нуклонов);
- одинаковое строение электронных оболочек;
- близкие химические свойства.
Изотопы бывают:
- стабильные – это изотопы, которые сохраняются сколь угодно долго;
- радиоактивные – это изотопы, которые превращаются в ядра других элементов с течением времени.
Изотопы водорода: водород имеет два стабильных изотопа – водород ( {}^1_1H ), дейтерий ( {}^2_1H ) и один радиоактивный изотоп тритий ( {}^3_1H ).
Энергия связи нуклонов в ядре. Ядерные силы
Между нуклонами ядра действуют самые мощные силы природы – ядерные силы.
Ядерные силы – это силы притяжения, связывающие протоны и нейтроны в атомном ядре и обеспечивающие существование устойчивых ядер.
Свойства ядерных сил:
- являются силами притяжения;
- являются короткодействующими силами (действуют на малых расстояниях, не превышающих 2·10-15 м; на таком расстоянии ядерные силы больше кулоновских приблизительно в 100 раз);
- обладают свойством зарядовой независимости (ядерные силы, действующие между двумя протонами, двумя нейтронами и между протоном и нейтроном, одинаковы);
- имеют свойство насыщения (каждый нуклон взаимодействует только с ограниченным числом ближайших к нему нуклонов, а не со всеми нуклонами ядра);
- не являются центральными (не действуют по линии, соединяющей центры взаимодействующих нуклонов).
Массу ядра можно точно определить с помощью масс-спектрографов, которые разделяют заряженные частицы с разными удельными зарядами с помощью электрических и магнитных полей.
Опытным путем было установлено, что благодаря действию сил притяжения масса ядра всегда меньше суммы масс протонов и масс нейтронов, входящих в состав этого ядра:
где ( M ) – масса ядра.
Дефект масс – это величина, равная разности суммы масс входящих в ядро нуклонов и массы ядра:
где ( Delta m ) – дефект масс.
Благодаря ядерным силам ядра атомов обладают огромной энергией связи.
Энергия связи – это энергия, которую необходимо затратить, чтобы разделить ядро на составляющие его нуклоны, или энергия, которая выделяется при образовании ядра из отдельных нуклонов:
где ( Delta E_{св} ) – энергия связи, ( c ) – скорость света.
Если в формуле энергии связи массы протона и нейтрона выражены в килограммах, а скорость света – в метрах в секунду, то энергия связи будет измерена в джоулях. Однако в физике атома и атомного ядра энергию ядер и элементарных частиц чаще выражают в мегаэлектронвольтах (МэВ).
Энергетический эквивалент 1 а.е.м.
Поэтому энергию связи можно рассчитать следующим образом:
В этом случае энергия связи измеряется в мегаэлектронвольтах (МэВ).
Для характеристики прочности ядра используется величина, которая называется удельной энергией связи.
Удельная энергия связи – это энергия связи ядра, приходящаяся на один нуклон ядра:
где ( A ) – массовое число.
Удельная энергия связи неодинакова для разных химических элементов и даже для изотопов одного и того же химического элемента. Удельная энергия связи нуклона в ядре меняется в среднем в пределах от 1 МэВ у легких ядер до 8,6 МэВ у ядер средней массы (с массовым числом ( A ) ≈ 100). У тяжелых ядер (( A ) ≈ 200) удельная энергия связи нуклона меньше, чем у ядер средней массы, приблизительно на 1 МэВ, так что их превращение в ядра среднего веса (деление на 2 части) сопровождается выделением энергии в количестве около 1 МэВ на нуклон, или около 200 МэВ на ядро. Превращение легких ядер в более тяжелые ядра дает еще больший энергетический выигрыш в расчете на нуклон.
Зависимость удельной энергии связи от массового числа установили экспериментально. Из рисунка хорошо видно, что, не считая самых легких ядер, удельная энергия связи примерно постоянна и равна 8 МэВ/нуклон. Отметим, что энергия связи электрона и ядра в атоме водорода, равная энергии ионизации, почти в миллион раз меньше этого значения. Кривая на рисунке имеет слабо выраженный максимум. Максимальную удельную энергию связи (8,6 МэВ/нуклон) имеют элементы с массовыми числами от 50 до 60, т. е. железо и близкие к нему по порядковому номеру элементы. Ядра этих элементов наиболее устойчивы.
У тяжелых ядер удельная энергия связи уменьшается за счет возрастающей с увеличением ( Z ) кулоновской энергии отталкивания протонов. Кулоновские силы стремятся разорвать ядро.
Ядерные реакции. Деление и синтез ядер
Атомные ядра при взаимодействиях испытывают превращения. Эти превращения сопровождаются увеличением или уменьшением кинетической энергии участвующих в них частиц.
Ядерные реакции – это изменения атомных ядер при взаимодействии их с элементарными частицами или друг с другом.
Ядерные реакции происходят, когда частицы вплотную приближаются к ядру и попадают в сферу действия ядерных сил. Одноименно заряженные частицы отталкиваются друг от друга, поэтому сближение положительно заряженных частиц с ядрами (или ядер друг с другом) возможно, если этим частицам (или ядрам) сообщена достаточно большая кинетическая энергия. Эта энергия сообщается протонам, ядрам дейтерия, α-частицам и другим более тяжелым ядрам с помощью ускорителей.
Для осуществления ядерных реакций такой метод гораздо эффективнее, чем использование ядер гелия, испускаемых радиоактивными элементами. Во-первых, с помощью ускорителей частицам может быть сообщена энергия порядка 105 МэВ, т. е. гораздо большая той, которую имеют ( alpha )-частицы (максимально 9 МэВ). Во-вторых, можно использовать протоны, которые в процессе радиоактивного распада не появляются (это целесообразно потому, что заряд протонов вдвое меньше заряда α-частиц, и поэтому действующая на них сила отталкивания со стороны ядер тоже в 2 раза меньше). В-третьих, можно ускорить ядра более тяжелые, чем ядра гелия.
Наиболее распространенный вид ядерной реакции:
где ( X ) и ( Y ) – исходное и конечное ядра; ( a ) и ( b ) – бомбардирующая и испускающая частицы.
Эндотермическая реакция – это реакция с поглощением энергии:
Экзотермическая реакция – это реакция с выделением энергии:
При ядерных реакциях выполняются следующие законы.
- Закон сохранения электрического заряда:
сумма электрических зарядов атомных ядер и частиц до реакции равна сумме электрических зарядов атомных ядер и частиц после реакции:
- Закон сохранения массового числа:
сумма нуклонов атомных ядер и частиц до реакции равна сумме нуклонов атомных ядер и частиц после реакции:
- Закон сохранения энергии.
Примеры ядерных реакций
- Первое наблюдавшееся превращение ядра (Ю. Резерфорд, 1919):
- Первая ядерная реакция на быстрых протонах (1932):
- Открытие нейтрона (Дж. Чедвик, 1932):
- Первое искусственное получение радиоактивного распада и открытие позитрона. Радиоактивный распад под действием ( alpha )-частиц наблюдал Ф. Жолио-Кюри:
Изотоп фосфора оказался радиоактивным: его ядро распадается с испусканием позитрона и нейтрино:
Классификация ядерных реакций
Ядерные реакции классифицируются:
- по роду участвующих в них частиц – реакции под действием нейтронов, заряженных частиц, ( gamma )-квантов;
- по энергии вызывающих их частиц – реакции при малых, средних, высоких энергиях;
- по роду участвующих в них ядер – реакции на легких ядрах (А < 50), средних ядрах (50 < А < 100) и тяжелых ядрах (А > 100);
- по характеру происходящих ядерных превращений – реакции с испусканием нейтронов, заряженных частиц, реакции захвата.
Деление ядер – это деление атомного ядра урана на несколько более легких ядер (осколков), чаще всего на два ядра, близких по массе.
- Делиться могут только ядра некоторых тяжелых элементов.
- При делении ядер испускаются нейтроны и ( gamma )-лучи.
- При делении ядер выделяется большая энергия.
Механизм деления ядер (капельная модель)
В тяжелых ядрах действуют значительные ядерные силы, которые удерживают ядро от распада. Под влиянием поглощенного нейтрона ядро возбуждается и начинает деформироваться, приобретая вытянутую форму. Оно растягивается до тех пор, пока силы отталкивания половинок ядра не начинают преобладать над силами притяжения, действующими в перешейке. В результате ядро разрывается на два осколка X и Y.
Под действием сил кулоновского отталкивания осколки разлетаются со скоростью, равной приблизительно 1/30 скорости света. Одновременно испускается излучение высокой частоты.
Цепная ядерная реакция – ядерная реакция деления тяжелых ядер нейтронами, в результате которой число нейтронов возрастает и поэтому может возникнуть самоподдерживающийся процесс деления.
В 1939 году было обнаружено, что при попадании нейтрона в ядро изотопа урана-235 происходит деление ядра на два или три осколка с испусканием 2–3 нейтронов:
Эти нейтроны способны вызвать деление 2–3 новых ядер урана с испусканием 4–9 новых нейтронов и т. д., процесс может продолжаться самостоятельно, вовлекая все большее число новых ядер.
Условия протекания цепной ядерной реакции:
- должны отсутствовать примеси, поглощающие нейтроны;
- количество вещества, способного делиться, должно быть достаточным для того, чтобы образующиеся нейтроны могли соударяться с другими ядрами, не покидая объем, не испытывая взаимодействия;
- скорость нейтронов должна быть достаточной, чтобы вызвать деление ядер.
Минимальное количество вещества, необходимое для осуществления цепной ядерной реакции, называется критической массой.
Устройства, в которых осуществляются управляемые цепные ядерные реакции, называются ядерными реакторами.
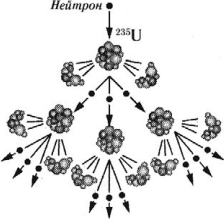
Основные элементы ядерного реактора:
- Ядерное горючее (сырьевые и делящиеся вещества в реакторах – изотопы урана, плутоний, торий).
- Замедлитель и отражатель нейтронов, которые способствуют увеличению числа медленных нейтронов, наиболее эффективных для развития цепной реакции деления (графит, тяжелая или обычная вода).
- Регулирующие стержни, которые вводят в активную зону реактора для поддержания стационарного режима реактора, так как быстрое развитие реакции сопровождается выделением большого количества тепла и перегревом реактора; стержни выполнены из материалов, сильно поглощающих тепловые нейтроны (из бора, кадмия).
- Теплоноситель, который необходим для отвода тепла, образующегося в реакторе (вода, жидкий натрий и др.).
- Защитные устройства, которые применяют для защиты персонала, обслуживающего реактор, от действия на организм нейтронных потоков и ( gamma )-лучей.
Термоядерный синтез
График зависимости удельной энергии связи нуклонов в ядре от массового числа показывает, что кроме реакции деления тяжелых ядер с выделением энергии идут реакции синтеза легких ядер.
Синтез ядер – это слияние ядер в одно ядро, сопровождающееся выделением энергии.
Для осуществления реакции синтеза легких ядер требуются высокие энергии сливающихся частиц, так как необходимо преодолеть кулоновское отталкивание. Этого можно достичь за счет высокой температуры вещества.
Термоядерная реакция – это реакция синтеза легких атомных ядер в более тяжелые, происходящая при сверхвысоких температурах (порядка 107 К и выше).
В природе термоядерные реакции происходят в недрах звезд.
При термоядерном синтезе энергетический выход на единицу массы топлива оказывается выше, чем при реакции деления тяжелых ядер урана.
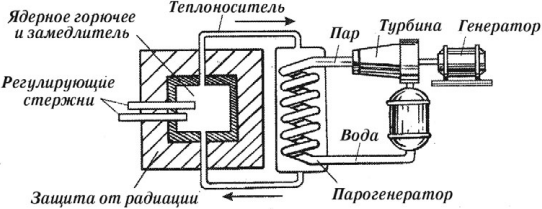
Пример реакции синтеза:
Синтез гелия из тяжелых изотопов водорода – дейтерия и трития – происходит при температуре около 5·107 К.
При синтезе 1 г гелия из дейтерия и трития выделяется 4,2·1011 Дж – такая же энергия выделяется при сгорании 10 т дизельного топлива.
Термоядерный синтез может стать одним из возможных альтернативных источников энергии. Поиск таких источников энергии важен, так как запасы нефти и газа на Земле ограничены.
В настоящее время ведется испытание установок для осуществления управляемых термоядерных реакций синтеза гелия из водорода. Запасы водорода на Земле практически неисчерпаемы. Количество дейтерия в океанической воде составляет примерно 4·1011 т, чему соответствует энергетический запас 1017 МВт·год. Наиболее заманчивой является возможность извлечения энергии дейтерия, содержащегося в обычной воде.
Основные формулы по теме «Физика атомного ядра»
Физика атомного ядра
3.1 (61.41%) 128 votes
Для решения задания № 31 требуется полное знание курса электродинамики. При этом может потребоваться как использование простейших формул – для силы Кулона, напряженности и т.д., – так и связанных со сложными явлениями, в том числе с исследованием многофункциональных эл электрических цепей.
Задание EF17621
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Лоренца.
3.Выразить модуль вектора магнитной индукции.
4.Определить недостающие величины.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Напряжение на обкладках конденсатора: U = 2160 В.
• Радиус окружности, по которой движется протон в однородном магнитном поле: R = 20 см.
• Масса протона: m = 1,673·10–27 кг.
• Заряд протона: q = 1,6·10–19 Кл.
20 см = 0,2 м
Сила Лоренца определяется формулой:
FЛ=|q|vBsinα
По условию задачи протон движется перпендикулярно вектору магнитной индукции. Поэтому синус угла между вектором скорости и вектором магнитной индукции будет равен 1. А протон имеет положительный заряд. Тогда:
FЛ=qvB
Сила Лоренца сообщает протону центростремительное ускорение, равное:
a=v2R
Применим второй закон Ньютона:
F=ma
qvB=mv2R
Отсюда модуль вектора магнитной индукции равен:
B=mv2qvR=mvqR
Энергия заряда, движущегося в электрическом поле, определяется формулой:
W=qU
Но энергию заряда также можно выразить как кинетическую энергию движения:
W=Eк=mv22
Приравняем правые части выражений и получим:
qU=mv22
Отсюда ускорение протона равно:
v=√2qUm
Конечная формула для определения модуля вектора магнитной индукции:
B=mvqR=mqR√2qUm=√2UmqR2
Ответ: 33,6
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18703
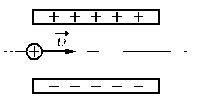
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.
3.Выяснить, при каком условии протон успеет вылететь из конденсатора.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса протона: m = 1,67∙10–27 кг.
• Заряд протона: q = 1,6∙10–19 Кл.
• Расстояние между обкладками конденсатора: d = 1 см.
• Длина пластин конденсатора: l = 5 см.
• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.
1 см = 0,01 м
5 см = 0,05 м
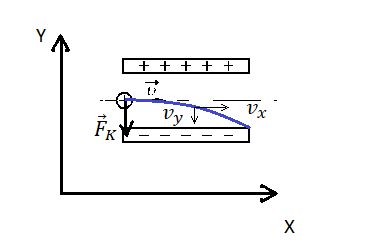
Сделаем рисунок:
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350
pазбирался: Алиса Никитина | обсудить разбор | оценить
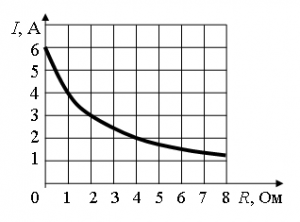
Задание EF17550
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для определения мощности тока, выделяемой на внутреннем сопротивлении источника, и выразить из нее сопротивление.
3.С помощью закона Ома для полной цепи найти неизвестные величины.
4.Выполнить решение в общем виде.
5.Выполнить вычисления, подставив известные и найденные данные.
Решение
Запишем исходные данные:
• Внутренне сопротивление источника тока: r.
• Мощность тока, выделяемая на внутреннем сопротивлении источника: Pвнутр = 8 Вт.
Мощность тока, выделяемая на внутреннем сопротивлении источника, определяется формулой:
Pвнутр=(εR+r)2r
Выразим отсюда сопротивление реостата:
R=ε√rPвнутр−r
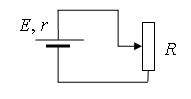
Запишем закон Ома для полной цепи:
I=εR+r
Согласно графику, при нулевом сопротивлении реостата, сила тока, равна 6 Амперам. Следовательно:
I(0 Ом)=εr=6
Но при сопротивлении реостата в 4 Ом сила тока равна 2 Амперам. Следовательно:
I(4 Ом)=ε4+r=2
Получили систему уравнений:
{εr=6ε4+r=2)
ε=6r
6r4+r=2
6r=8+2r
4r=8
r=2 (Ом)
ε=6·2=12 (В)
Теперь можем вычислить искомое сопротивление:
R=12√28−2=4 (Ом)
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18453
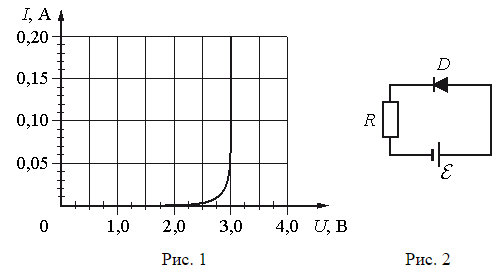
На рис. 1 изображена зависимость силы тока через светодиод D от приложенного к нему напряжения, а на рис. 2 – схема его включения. Напряжение на светодиоде практически не зависит от силы тока через него в интервале значений 0,05 А<I<0,2 А. Этот светодиод соединён последовательно с резистором R и подключён к источнику с ЭДС E1=6 В. При этом сила тока в цепи равна 0,1 А. Какова сила тока, текущего через светодиод, при замене источника на другой с ЭДС E2=4,5 В? Внутренним сопротивлением источников пренебречь.
Алгоритм решения
1.Записать исходные данные.
2.С помощью закона Ома для участка и для полной цепи определить сопротивление на светодиоде.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС первого источника тока: ε1=6 В.
• Сила тока, проходящая через светодиод, подключенный к первому источнику тока: I1 = 0,1 А.
• ЭДС второго источника тока: ε2=4,5 В.
Из рисунка 1 следует, что при силе тока, равной I1 = 0,1 А напряжение на светодиоде равно UD = 3 В. По закону Ома для участка цепи напряжение на резисторе, будет равно:
U1=I1R
По закону Ома для полной (замкнутой) цепи, имеем:
ε1=U1+UD
Следовательно:
U1=ε1−UD
Тогда сопротивление резистора равно:
R=ε1−UDI1
Напряжение на светодиоде не зависит от силы тока, проходящего через него в интервале значений (это следует из графика рис. 1), поэтому U2=ε2−UDдля любой силы тока из этого интервала значений, следовательно, сила тока в цепи при изменении ЭДС источника:
I2=U2R=ε2−UDR=I1ε2−UDε1−UD
I2=0,14,5−36−3=0,05 (А)
Ответ: 0,05
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17725
Алгоритм решения
1.Сделать список известных данных.
2.Определить, при каком условии рамка с током будет вращаться вокруг стороны CD.
3.Выполнить решение в общем виде.
Решение
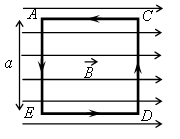
По условию задачи известными данными являются:
• Сторона квадратной рамки с током: a.
• Вектор магнитной индукции однородного горизонтального магнитного поля, в котором лежит рамка: B.
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
FA1=FA2=IaB
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
MA=Ia2B
Момент силы тяжести относительно оси CD:
Mmg=−12mga
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
MA+Mmg>0
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Ia2B>12mga
Отсюда выразим силу тока:
I>mga2a2B
I>mg2aB
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18860
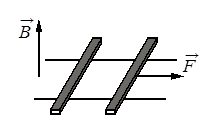
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать закон электромагнитной индукции для двигающихся стержней.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса стержней: m1=m2=m=100 г.
• Сопротивление стержней: R1=R2=R=0,1 Ом.
• Расстояние между рельсами: l = 10 см.
• Коэффициент трения между стержнями и рельсами: μ = 0,1.
• Модуль вектора магнитной индукции магнитного поля: B = 1 Тл.
• Угол между вектором магнитной индукцией и вектором скорости стержней: α = 90 градусов (синус прямого угла равен «1»).
100 г = 0,1 кг
10 см = 0,1 м
Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:
εi=vBlsinα
Причем v — это разность скоростей стержней (v2 – v1), которая характеризует скорость изменения площади проводящего контура.
Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:
εi=IRк
где Rк — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:
Rк=2R
Отсюда закон Ома принимает вид:
εi=2IR
Тогда ток в контуре равен:
I=εi2R=vBlsinα2R
С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):
Fтр=FА
μmg=BIlsinα
Подставим сюда выражение, полученное для силы тока в контуре:
μmg=BvBlsinα2Rlsinα=vB2l2sin2α2R
Отсюда скорость равна:
v=2μmgRB2l2sin2α
Так как синус угла равен «1»:
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17724
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Установить величину электромагнитного поля катушки и электрического поля конденсатора.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
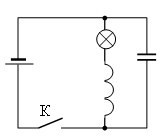
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: r = 1 Ом.
• Емкость конденсатора: C = 2 мФ.
• Индуктивность катушки: L = 36 мГн.
• Сопротивление лампы: R = 5 Ом.
2 мФ = 2∙10–3 Ф
36 мГн = 36∙10–3 Гн
Пока ключ замкнут, через катушку L течёт ток определяемый внутренним сопротивлением источника и сопротивлением лампочки. Его можно вычислить, используя закон Ома для полной цепи:
I=εR+r
При этом конденсатор будет заряжен до напряжения U, которое определяется законом Ома для участка цепи:
U=IR
Подставив в это выражение закон Ома для полной цепи, получим:
U=εRR+r
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22=C2(εRR+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR+r)2
После размыкания ключа начинаются затухающие электромагнитные колебания, и вся энергия, запасённая в конденсаторе и катушке, выделится на лампе:
E=Wкон+Wкат=C2(εRR+r)2+L2(εR+r)2
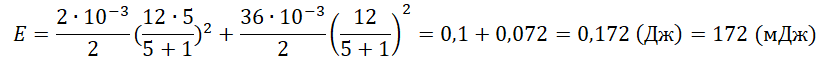
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF22800
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать закон электромагнитной индукции для двигающихся стержней.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: R = 1 Ом.
• Сопротивление первого резистора: R1 = 7 Ом.
• Сопротивление второго резистора: R2 = 4 Ом.
• Электроемкость конденсатора: C = 3 мкФ.
• Индуктивность катушки: L = 32 мкГн.
3 мкФ = 3∙10–6 Ф
32 мкГн = 32∙10–6 Гн
До размыкания ключа электрический ток протекает через последовательно соединённые резисторы R1, R2 и катушку L. После размыкания ключа вся накопленная в элементах цепи энергия выделится в виде тепла на резисторе R2:
E=Wкон+Wкат
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22
Напряжение U на конденсаторе можно выразит из закона Ома для участка цепи:
U=IR2
Чтобы выразить силу тока, потребуется записать закон Ома для полной цепи:
I=εR+r
Так как в цепи есть два последовательно соединенных резистора, общее сопротивление цепи будет равно сумме их сопротивлений:
R=R1+R2
Тогда закон Ома для полной цепи примет вид:
I=εR1+R2+r
Тогда напряжение на конденсаторе равно:
U=εR2R1+R2+r
Следовательно, энергия электрического поля в конденсаторе будет равна:
Wкон=C2(εR2R1+R2+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR1+R2+r)2
Следовательно, на втором резисторе выделится энергия, равная:
E=C2(εR2R1+R2+r)2+L2(εR1+R2+r)2
Ответ: 40
pазбирался: Алиса Никитина | обсудить разбор | оценить
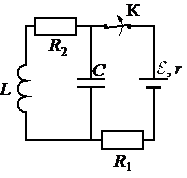
Задание EF22801
Период свободных электромагнитных колебаний в идеальном колебательном контуре, состоящем из конденсатора и катушки индуктивности, равен 6,3 мкс. Амплитуда колебаний силы тока Im=5 мА. В момент времени t сила тока в катушке равна 3мА. Найдите заряд конденсатора в этот момент. Ответ округлите до целых и запишите в нКл.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать закон сохранения энергии в колебательном контуре.
3.Записать формулу Томсона.
4.Выполнить решение задачи в общем виде.
5.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Период колебаний в гармоническом контуре: T = 6,3 мкс.
• Амплитуда колебаний силы тока: Imax = 5 мА.
• Сила тока в катушке в момент времени t: i = 3 мА.
6,3 мкс = 6,3∙10–6 с
5 мА = 5∙10–3 А
3 мА = 3∙10–3 А
Закон сохранения энергии в колебательном контуре имеет вид:
W=Li22+q22C=LI2max2
Запишем формулу Томсона:
T=2π√LC
Выразим из закона сохранения энергии заряд конденсатора:
q2=2С(LI2max2−Li22)=CL(I2max−i2)
q=√CL(I2max−i2)
Выразим емкость конденсатора из формулы Томсона:
√LC=T2π
C=1L(T2π)2
q=⎷1L(T2π)2L(I2max−i2)=T2π√I2max−i2
4·10−9 (Кл)=4 (нКл)
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18735
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
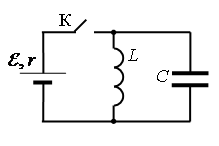
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF19015
На дне бассейна с водой находится небольшая лампочка. На поверхности воды плавает круглый плот – так, что центр плота находится точно над лампочкой. Определите глубину бассейна Н, если минимальный радиус плота, при котором свет от лампочки не выходит из воды, R = 2,4 м. Сделайте рисунок, поясняющий решение. Толщиной плота пренебречь. Показатель преломления воды n = 4/3.
Алгоритм решения
1.Записать исходные данные.
3.Записать закон полного отражения.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Радиус круглого плота: R = 2,4 м.
• Показатель преломления воды: n = 4/3.
Выполним рисунок. Проведем перпендикуляры к поверхности: перпендикуляр от точечного источника света, а также нормали, проведенные через края плота.
Чтобы свет лампочки не выходил из воды, лучи света от лампочки, направленные к границе между краем плота и поверхностью воды, должны полностью отражаться. Это возможно только при выполнении следующего условия:
sinα=1n
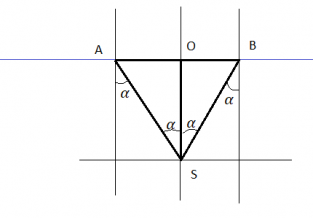
Поскольку вершина S треугольника ABS лежит строго под центром круглого плота, этот треугольник является равнобедренным. Причем перпендикуляр, восстановленный к основанию треугольника AB — SO — делит это основание на 2 равные стороны. Одновременно он делит угол S этого треугольника на 2 равные части, так как он является одновременно перпендикуляром, медианой и биссектрисой.
Пусть α — угол падения луча. Тогда угол OSB будет равен этому углу как накрест лежащие углы.
Треугольник OSB — прямоугольный. Причем искомая величина — глубина бассейна — является одним из его катетов. Из курса геометрии известно, что катет равен произведения второго катета на котангенс прилежащего угла. Второй катет в нашем случае — радиус круглого плота. Прилежащий угол равен углу падения. Следовательно:
H=Rcotα
Котангенс угла определяется как отношение косинуса этого угла к его синусу:
cotα=cosαsinα
Косинус угла можем выразить из основного тригонометрического тождества:
sin2α+cos2α=1
Следовательно:
cosα=√1−sin2α
Отсюда котангенс равен:
cotα=√1−sin2αsinα
Тогда глубина бассейна:
H=Rcotα=R√1−sin2αsinα
Из закона полного отражения вспомним, что синус угла падения есть величина, обратная показателю преломления воды. Тогда эта формула примет вид:
H=R√1−(1n)21n=Rn√1−1n2
Подставим известные данные и получим:
H=2,4·43⎷1−1(43)2=3,2√1−916=3,2√74≈0,8·2,65=2,12 ⎛⎜⎜⎝м⎞⎟⎟⎠
Ответ: 2,12
pазбирался: Алиса Никитина | обсудить разбор | оценить
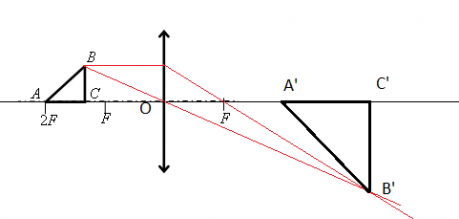
Задание EF17760

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF19112
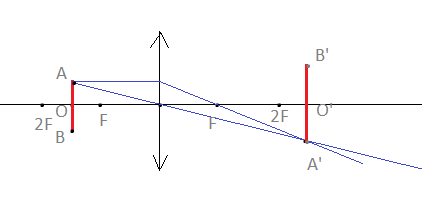
В плоскости, параллельной плоскости тонкой собирающей линзы, по окружности со скоростью v = 5 м/с движется точечный источник света. Расстояние между плоскостями d = 15 см. Центр окружности находится на главной оптической оси линзы. Фокусное расстояние линзы F = 10 см. Найдите скорость движения изображения точечного источника света. Сделайте пояснительный чертёж, указав ход лучей в линзе. Ответ запишите в м/с.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
3.Записать формулу тонкой линзы и определить из нее расстояние от изображения до линзы.
4.Записать формулу линейного увеличения линзы двумя способами для вычисления радиусов окружностей, по которым движутся точка и ее изображение.
5.Выполнить решение в общем виде.
6.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Фокусное расстояние линзы: F = 10 см.
• Расстояние от линзы до плоскости, в которой вращается точка: d = 15 см.
• Скорость вращения точки: v = 5 м/с.
10 см = 0,1 м
15 см = 0,15 м
Выполним рисунок. Для его построения достаточно найти изображение точки А. Затем в противоположную сторону отложим перпендикуляр и на таком же расстоянии от главной оптической оси будет находиться изображение точки B.
Глядя со стороны, мы будем видеть вместо окружности, которую описывает точка, линию AB. Она равн диаметру окружности, по которой движется точка. Обозначим ее радиус OA за r. Изображением окружности будет окружность. Вместо нее мы со стороны также увидим отрезок — A´B´. Обозначим радиус O´A´ за R.
Запишем формулу тонкой линзы и выразим из нее расстояние от изображения до линзы:
1d+1f=1F
1f=1F−1d=d−FFd
f=dFd−F
Формулу линейного увеличения линзы можно определить как отношение радиуса окружности, по которой движется точка-изображение, к радиусу окружности, по которой движется сама точка:
Γ=Rr
Линейное увеличение также определяется формулой:
Γ=fd
Следовательно:
Rr=fd
Подставим сюда выражение, найденное для расстояния от изображения до линзы из формулы тонкой линзы:
Rr=dFd(d−F)=Fd−F
Так как изображение будет двигаться вслед за точкой, то угловые скорости этой точки и изображения будут равны. Поэтому:
ω=vr=VR
Отсюда линейная скорость движения изображения равна:
V=Rvr=Fvd−F=0,1·50,15−0,1=10 (мс)
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор | оценить
Подготовка к ЕГЭ по физике
| A 17: Атом Бора содержит … | |
| A 18: Дан график изменения числа ядер … | |
| A 19: Радиоактивный полоний 21684Po, испытав один α-распад … | |
| Сколько нейтронов содержит ядро |
Пишите в комментариях какую ещё задачу нужно решить.
Сколько нейтронов содержит ядро
Рассмотрим пример.
Атом Полония 21284Po содержит 84 протона. Это сразу же видно из нижнего индекса.
Также он содержит 128 нейтронов.
Как я это узнал — просто вычел из 212 84.
212 — 84 = 128.
A 17
Условие:
Атом бора 85B содержит:
Варианты ответа
1) 8 протонов 5 нейтронов и 13 электронов
2) 8 протонов 13 нейтронов и 8 электронов
3) 5 протонов 3 нейтрона и 5 электронов
4) 5 протонов, 8 нейтронов и 13 электронов
Как решать
Чтобы решать такие задачи, нужно понимать из чего состоят атомы.
1) Самый простой факт, который легко запомнить: в нейтральных атомах
количество протонов и электронов одинаково.
То есть, если в условии не сказано, что атом имеет заряд (т.е. это не простой атом а ион).
мы считаем, что электронов столько же сколько и протонов.
2) Нижний индекс это количество протонов.
3) Верхний индекс это сумма протонов и нейтронов
4) Как дополнительную информацию можно держать в уме, что в лёгких ядрах
нейтронов меньше чем протонов, с ростом массы количество нейтронов догоняет
количество протонов и в тяжёлых ядрах нейтронов может быть намного больше.
Пример
Атом бора 85B содержит:
1) 8 протонов 5 нейтронов и 13 электронов
2) 8 протонов 13 нейтронов и 8 электронов
3) 5 протонов 3 нейтрона и 5 электронов
4) 5 протонов, 8 нейтронов и 13 электронов
85B
Нижний индекс — это число протонов (см. пункт 2).
Значит протонов в этом атоме 5
Про заряд атома ничего не сказано, значит он нейтральный.
Следовательно электронов столько же сколько протонов — их тоже пять.
Уже этих знаний достаточно чтобы выбрать ответ номер 3.
Для проверки смотрим, что 5 протонов плюс 3 нейтрона это 8. То есть
верхний индекс должен равняться 8. Сходится.
Ответ: 3.
A 18
Условие:
Дан график изменения числа ядер находящегося в пробирке радиоактивного
изотопа с течением времени. Период полураспада этого изотопа —
Сначала проговорим условие и решение без конкретного графика. Затем разберём пример.
Варианты ответа
1) 1 месяц 2) 2 месяца 3) 3 месяца 4) 4 месяца или любой другой отрезок времени.
Как решать такие задачи в общем случае
1) Период полураспада, это такое время за которое количество ядер уменьшается в два раза.
2) Смотрим на график. Ищем где ось, по которой отложено количество ядер.
3) Ищем любой удобный участок на котором количество изменилось в два раза.
4) Отмечаем две точки — первая это точка на которой количество больше.
Вторая — это точка в которой количество ядер в два раза меньше чем в первой.
5) Помним, что у каждой точки графика есть две координаты: количество ядер и
время.
6) После того как мы отметили точки — смотрим какие значения времени им соответсвуют.
7) Вычитаем из большего времени меньшее — это и будет период полураспада.
Замечание: вполне возможна, что графике можно выбрать несколько удобных
пар точек, если график правильный то ответ, меняться не будет.
Как решать конкретно этот пример
Условие: Дан график изменения числа ядер находящегося в пробирке радиоактивного
изотопа с течением времени. Период полураспада этого изотопа —
1) 1 месяц 2) 2 месяца 3) 3 месяца 4) 4 месяца
График:
2) Смотрим на график. Ищем где ось, по которой отложено количество ядер.
В нашем случае это ось ординат. Подчёркнута оранжевым.
3) Ищем любой участок на котором количество изменилось в два раза.
Например, выберем участок, на котором количество ядер уменьшилось
с 6 до 3.
Для этого проведём две прямые. Красная будет соответствовать количеству 6 * N18
а зелёная 3 * N18
Теперь нужно найти и отметить точки, в которых эти прямые пересекают наш график.
Примечание:
Если Вы решаете задачу не про радиоативный распад, а про что-то другое
таких точек может быть много — нужно выбрать две соседние. В нашем случае их будет всего две.
4) Отмечаем две точки — первая это
точка, на которой количество больше.
Вторая — это
точка, в которой количество ядер в два раза меньше чем в первой.
5) Помним, что у каждой точки графика есть две координаты: количество ядер и
время.
6) После того как мы отметили точки — смотрим какие значения времени им соответсвуют.
В нашем случае это 0 месяцев и 1 месяц
7) Вычитаем из большего времени меньшее — это и будет период полураспада.
1 месяц — 0 месяцев = 1 месяц
Ответ: 1 месяц
A 19
Условие:
Радиоактивный полоний 21684Po, испытав один α-распад и два
электронных β-распада, превратился в изотоп
Варианты ответа
1) свинца 21282Pb
2) полония 21284Po
3) висмута 21283Bi
4) таллия 20881Po
Как решать вообще не вникая в суть
Если совсем примитивно: альфа распад вычитает 4 из
верхнего индекса и 2 из нижнего. Ничего никуда не добавляет.
Электронный бета распад не трогает верхний индекс но добавляет 1 к нижнему.
Буква зависит от нижнего индекса, если нижний индекс не изменился, то элемент остался
собой и буква не поменяется.
216 — 4 = 212
84 — 2 + 1*2 = 84
Разбираемся в сути происходящего
1) Альфа частица это два протона
вместе с двумя нейтронам.
Т.е. всего частиц (адронов) четыре.
Записать её можно следующей формулой 42α2
2) α-распад: Альфа распад это процесс при котором из ядра вылетает альфа частица.
Т.е.
в ядре становится на два протона и на два нейтрона меньше.
3) Нижний индекс это число протонов в ядре.
21684Po т.е.
в нашем ядре 84 протона
4) Верхний индекс это сумма протонов и нейтронов в ядре.
21684Po в нашем ядре
84 протона и, следовательно, 216 — 84 = 132 нейтрона.
5) Один α-распад это минус 4 из верхнего индекса и минус 2 из нижнего.
6) электронный β-распад или β— — распад это процесс при котором нейтрон превращается
в протон и излучает ещё пару частиц, которые
не остаются в ядре.
7) β— — распад не изменяет верхний индекс, но увеличивает на 1 нижний
Решаем наш пример
21684 минус альфа частица это 21282
то есть это свинец
21282Pb
Два электронных бета распада увеличивают нижний индекс на 2.
Получаем
21284 и это полоний 21284Po
| ФФ: | |
| Как выбрать кафедру физфака | |
| Болонский процесс | |
| Жизнь студентов 1 — 7 курсы | |
| Впечатления немцев от ПУНКа | |
| ПУНК + РЖД | |
| Справка | |
| О физ-факе | |
| Как выбрать кафедру версия Максима Николаевича |