Знание позиционных систем счисления егэ

На уроке рассматривается 14 задание, решение и объяснение ЕГЭ по информатике

Содержание:

  • Объяснение заданий 14 ЕГЭ по информатике
    • Перевод числа из любой системы счисления в десятичную
    • Особенности при переводах в разные системы счисления
  • Решение заданий 14 ЕГЭ по информатике
    • Определите наибольшее/наименьшее значение x, y
    • Сколько цифр или сумма цифр
    • Найти основание системы счисления и уравнения

14-е задание: «Операции в системах счисления»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

  
Проверяемые элементы содержания: Знание позиционных систем счисления

До ЕГЭ 2021 года — это было задание № 16 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Основные ошибки связаны с невнимательностью при выполнении арифметических действий
в недесятичных системах счисления. Например, вычитания единицы в ситуации типа: 10100002 – 1»

ФГБНУ «Федеральный институт педагогических измерений»

С основами темы можно ознакомиться в теории к заданию 1.

Перевод числа из любой системы счисления в десятичную

Чтобы перевести, например, 10045N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной разряду этой цифры:
перевод в десятичную систему счисления

Особенности при переводах в разные системы счисления

Некоторые правила, которые нужно знать, при работе с системами счисления:

  • последняя цифра (крайняя справа) в записи числа в системе счисления с основанием N – представляет собой остаток от деления этого числа на N:
    • 710 = 1112
7/2 = остаток 1
  • две крайние справа цифры числа в системе счисления с основанием N – это остаток от деления этого числа на N², и так далее:
    • 710 = 1112
112=310
7/22 = остаток 310 (112)
  • десятичное число 10N записывается как единица и N нулей:

    • 1_1

  • тогда как десятичное число 2N в двоичной системе записывается как единица и N нулей:

    • 2

  • а десятичное число 3N записывается в троичной системе в виде единицы и N нулей:

    • 2

  • можно сделать аналогичные выводы для любой системы счисления с основанием a; общее правило:

    • 3

  • десятичное 10N-1 записывается как N девяток:

    • 1_11

  • тогда как десятичное число 2N-1 в двоичной системе записывается как N единиц:

    • 3

  • а десятичное число 3N-1 записывается в троичной системе как N двоек:

    • объяснение 14 задания егэ

  • значит есть общее правило: число aN-1 в системе счисления с основанием a записывается как N старших цифр этой системы, то есть, цифр (a-1)

    • 1_1

  • десятичное число 10N-10M = 10M * (10N-M – 1) записывается как N-M девяток, за которыми стоят M нулей:

    • 1

  • тогда как десятичное число 2N – 2K при K < N в двоичной системе записывается как N – K единиц и K нулей:

    • 1

  • то есть, существует общее правило:

    • 1_11

  • Также следует знать, что верны равенства:

    • 1
    1_1
    1_11

Решение заданий 14 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Определите наибольшее/наименьшее значение x, y

14_14:

Операнды арифметического выражения записаны в системе счисления с основанием 15.

82x19₁₅ – 6x073₁₅

В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

✍ Решение:

    ✎ Решение с использованием программирования:

    PascalABC.net:

    1
2
3
4
5
6
7
8
9
10
11
12
13
14

    uses school;
begin
  foreach var x in '0123456789abcde' do
  begin
    var a := dec('82'+ x +'19', 15);
    var b :=dec('6' + x +'073', 15);
    var sum := a - b;
    if sum mod 11 = 0 then
    begin
      print(sum / 11);
      break;
    end
  end;
end.
    Python:
    С++:

Ответ: 7806

Сколько цифр или сумма цифр

14_12:

Значение арифметического выражения 

43∙7103 – 21∙757 + 98

записали в системе счисления с основанием 7.
Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.

✍Решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

1
2
3
4
5
6
7
8
9
10
11
12

begin
  var x,s: Biginteger;
  x := 43*Biginteger.Pow(7, 103) - 21*Biginteger.Pow(7, 57) + 98;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  s:=0;
  while x > 0 do
  begin
    s:=s+ x mod 7; // добавляем цифру правого разряда
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(s);
end.
PascalABC.net, Решение 2:

1
2
3
4
5
6
7
8
9
10
11
12

uses school;
 
begin
  var n: bigInteger;
  n := 43 * Biginteger.Pow(7, 103) - 21 * Biginteger.Pow(7, 57) + 98;
  print(n.ToString.ToBase(7).CountOf('1') +
    n.ToString.ToBase(7).CountOf('2') * 2 + 
    n.ToString.ToBase(7).CountOf('3') * 3 +
    n.ToString.ToBase(7).CountOf('4') * 4 +
    n.ToString.ToBase(7).CountOf('5') * 5 +
    n.ToString.ToBase(7).CountOf('6') * 6);
end.
Python:

1
2
3
4
5
6
7

x = 43*7**103 - 21*7**57 + 98
s = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    s+= x % 7 # добавляем цифру к сумматору
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( s )
С++:

Результат: 276

14_1:

Значение арифметического выражения:
21024 + 464 — 64
записали в системе счисления с основанием 2.

Сколько цифр «1» содержится в этой записи?

Типовые задания для тренировки

✍Решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

1
2
3
4
5
6
7
8
9
10
11
12

begin
  var k := 0;
  var x: Biginteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  // в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
  while x > 0 do
  begin
    if x mod 2 = 1 then k += 1; // если цифра = 1, то считаем ее
    x := x div 2; // убираем разряд числа в 2-й системе сч.
  end;
  println(k);
end.
PascalABC.net, Решение 2:

1
2
3
4
5
6
7

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  print(x.ToString.ToBase(2).CountOf('1'));
end.
Python:

1
2
3
4
5
6
7
8

x = 2**1024 + 4**64 - 64
k = 0
# в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
while x: 
    if x % 2 == 1: # если цифра = 1, то считаем ее
        k += 1
    x //= 2 # убираем разряд числа в 2-й системе сч.
print( k )
С++:

✎ Решение теоретическое:

  • Существует правило:

    • 2N = 10..02(1 единица и N нулей)

  • Чтобы воспользоваться этим правилом, преобразуем общее выражение к степеням двойки:
    • 21024 + (22)64 - 26 = 21024 + 2128 - 26
  • При переводе в двоичную систему получим:
    • 10...0 (1024 нуля) + 10...0 (128 нулей) - 10...0 (6 нулей)
  • Обратим внимание, что разница между числами большая. Т.е. при выполнении сложения в столбик, единицы в одном и том же разряде быть не могут. Так:
    •  10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0
  • Из первого слагаемого 10…0 (1024 нуля) запомним одну единицу в старшем бите, остальные нули нас не интересуют, так как далее мы воспользуемся другим правилом — для разницы:
    •  10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0  - запомним единицу
  • Существует также правило:

    • 2N — 2K = 1…1 (N - K единиц)0…0(K нулей)

  • По формуле выполним вычитание 2128 — 26: получим 1..1 (122 единицы) 0..0(6 нулей):
    •  10..0000000  - 128 нулей
-
     1000000  
_________________________
 11..1000000  - 122 единицы и 6 нулей
  • Прибавим к 122 получившимся единицам еще одну из первого слагаемого (10…0 (1024 нуля)) и получим:
    • 122 + 1 = 123 единицы

Результат: 123

Также можно посмотреть видео решения 14 задания ЕГЭ по информатике (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_3: 14 задание. Демоверсия ЕГЭ 2018 информатика:

Значение арифметического выражения:
4910 + 730 – 49
записали в системе счисления с основанием 7.

Сколько цифр «6» содержится в этой записи?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net, решение 1:

1
2
3
4
5
6
7
8
9
10
11
12

begin
  var x: Biginteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  var k:=0;
  while x > 0 do
  begin
    if x mod 7 = 6 then k+=1; // если цифра = 6, то считаем ее
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(k);
end.
PascalABC.net, решение 2:

1
2
3
4
5
6
7

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  print(x.ToString.ToBase(7).CountOf('6'));
end.
Python:

1
2
3
4
5
6
7
8

x = 49**10 + 7**30 - 49
k = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    if x % 7 == 6: # если цифра = 6, то считаем ее
        k += 1
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( k )
С++:

✎ Решение теоретическое:

  • Приведем все числа к степеням 7:
    • 720 + 730 - 72
  • Расставим операнды выражения в порядке убывания степеней:
    • 730 + 720 - 72
  • Вспомним две формулы для работы со системами счисления:
    • 1.
an = 10..0a
       n
2.
an - am = (a-1)..(a-1)0..0a
              n-m       m
  • Переведем первое число согласно формуле 1:
    • 730 = 10..0
        30
  • В данном числе нет цифры 6, как и в остальных числах.
  • Цифра 6 появляется при выполнении вычитания.
  • Подсчитаем все «6», используя формулу 2:
    • 0 + (20 - 2) = 18
  • Получаем шестерок: 18

Результат: 18

Подробное решение 14 задания демоверсии ЕГЭ смотрите на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_2:

Значение арифметического выражения:
4500 + 3*42500 + 16500 — 1024
записали в системе счисления с основанием 4.

Сколько цифр «3» содержится в этой записи?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net:

1
2
3
4
5
6
7

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,500) + 3*Biginteger.Pow(4,2500) + Biginteger.Pow(16,500) - 1024;
  print(x.ToString.ToBase(4).CountOf('3'));
end.
Python:

1
2
3
4
5
6
7
8

x = 4**500 + 3*4**2500 + 16**500 - 1024
k = 0
# в получившемся числе рассматриваем каждую цифру в 4-й системе сч.
while x: 
    if x % 4 == 3: # если цифра = 3, то считаем ее
        k += 1
    x //= 4 # убираем разряд числа в 4-й системе сч.
print( k )
С++:

Результат: 496

Подробное решение данного 14 задания ЕГЭ по информатике можно посмотреть на видео (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

14_5:

Значение арифметического выражения: 81024 + 832 – 65 – записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?

Типовые задания для тренировки

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net:

1
2
3
4
5
6
7

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(8,1024) + Biginteger.Pow(8,32) - 65;
  print(x.ToString.ToBase(8).CountOf('7'));
end.
Python:

1
2
3
4
5
6
7
8

x = 8**1024 + 8**32 - 65
k = 0
# в получившемся числе рассматриваем каждую цифру в 8-й системе сч.
while x: 
    if x % 8 == 7: # если цифра = 7, то считаем ее
        k += 1
    x //= 8 # убираем разряд числа в 8-й системе сч.
print( k )
С++:

✎ Решение теоретическое:

  • Приведем все числа к степеням восьмерки:
    • 65 = 64 + 1 = 82 + 80;
  • Получаем:
    • 81024 + 832 - (82 + 80);
81024 + 832 - 82 - 80
  • Вспомним две формулы для работы с системами счисления:
    • 1.
an = 10..0a
       n
2.
an - am = (a-1)..(a-1)0..0a
              n-m       m
  • Переведем первое число согласно формуле 1:
    • 81024 = 10..0
        1024
  • В данном числе нет цифры 7, как и в остальных числах.
  • Цифра 7 появляется при выполнении вычитания. У нас два таких действия, идущих подряд. Это неудобно. Необходимо, чтобы действия чередовались (a + b — c + d — e…)
  • Вспомним еще одну формулу:
    • 3.

    -2n = -2n+1 + 2n

    
! Формула предназначена для чисел в двоичной системе счисления,
но для подсчета цифр "7" в 8-й (или "6" в 7-й и т.п.) ее можно использовать
(для поиска единиц или нулей она не подходит!!!)
  • В нашем случае заменим часть выражения:
    • -82 = -83 + 82
! обратите внимание, что тождество неверно, но
при поиске количества "7" этой формулой можно воспользоваться
(для поиска единиц или нулей она не подходит!)


Получаем:

81024 + 832 - 83 + 82- 80
  • Получили чередование операций «+» и «-«.
  • Теперь посчитаем все «7», используя формулу 2:
    • 0 + (32 - 3) + (2 - 0) = 31
  • Получаем семерок: 31

Результат: 31

14_13:

Сколько значащих нулей в двоичной записи числа 4350 + 8340 – 2320 – 12?

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net, решение 1:

1
2
3
4
5
6
7
8
9
10
11
12
13

begin
  var b2 := biginteger(2);
  var numb := (2 * b2) ** 350 + (4 * b2) ** 340 - (1 * b2) ** 320 - 12;
  var digit: biginteger;
  var n := 0;
  while numb > 0 do
  begin
    digit := numb mod 2;
    if digit = 0 then n += 1;
    numb := numb div 2
  end;
  print(n)
 end.
PascalABC.net, решение 2:

1
2
3
4
5
6
7

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,350) + Biginteger.Pow(8,340) - Biginteger.Pow(2,320) - 12;
  print(x.ToString.ToBase(2).CountOf('0'));
end.
Python:

1
2
3
4
5
6
7

x = 4**350 + 8**340 - 2**320 - 12
print(x)
k = 0
while x:
  if x % 2 == 0: k += 1
  x //= 2
     print( k )
С++:

✎ Решение теоретическое:

    4350 + 8340 – 2320 – 12

  • По возможности приведем каждое слагаемое к степеням 2. Получим:
    • (22)350 + (23)340 - 2320 - 3*22 =
(22)350 + (23)340 - 2320 - 12 =
2700 + 21020 - 2320 - (23 + 22)
  • Далее рассуждаем так: количество нулей можно найти, если из общего количества цифр в результирующем числе вычесть количество не нулей (любых других цифр).
  • Расположим операнды по убыванию:
    • 21020 + 2700 - 2320 - 23 - 22
  • Наибольшее число 21020, в нем 1021 разряд в двоичной с.с. (одна единица и 1020 нулей). То есть всего 1021 знаков.
  • Для того, чтобы избежать два подряд идущих минуса, воспользуемся правилом -2n = -2n+1+2n и преобразуем выражение:
    • 21020 + 2700 - 2321+ 2320- 24 + 23 - 22
  • Посчитаем количество не нулей в каждом операнде:
    • 21020 -> один не ноль
2700 - 2321 -> 379 не нулей
2320- 24 -> 316 не нулей 
23 - 22 -> один не ноль
Итого: 1+ 379+316 +1 = 697
  • Получаем нулей:
    • 1021 - 697 = 324

    Результат: 324

    Найти основание системы счисления и уравнения

    14_7:

    Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.

    Типовые задания для тренировки

    ✍ Решение:

    • Для начала достаточно перевести первое и последнее число предложенного интервала в троичную систему счисления. Сделаем это:
      • 1.
 13 | 3 
 12   4 | 3 
  1   3   1   
      1
1310 = 1113

2.
23 | 3 
21   7 | 3 
2    6   2
     1
2310 = 2123
    • Теперь добавим промежуточные числа в троичной системе счисления (прибавляя единицу к каждому очередному полученному числу), не забывая, что в троичной системе всего три цифры (0, 1 и 2):
      • 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212
    • На всякий случай стоит посчитать количество полученных чисел и сравнить их с количеством чисел в исходной последовательности.
    • Теперь осталось посчитать количество цифр 2 в полученной последовательности. Их 13:
      • 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212

    Ответ: 13

    ✍ Решение:

    • Разделим уравнение на три части и вычислим каждую часть отдельно (выделим части разным цветом):
      • 204N+1 = 204N + 2616
 1       2     3
    • Используем формулу разложения числа по степеням основания:
      • 1. 
210
204N+1

По формуле получаем:
2*(N+1)2 + 0*(N+1)1 + 4*(N+1)0 =
= 2*(N2 + 2N + 1) + 0 + 4 = 2N2 + 4N + 6
    • Выполним то же самое для остальных двух частей:
      • 2.
210
204N

По формуле получаем:
2*N2 + 0*N1 + 4*N0 =
= 2N2 + 4

      3.
2616 = 3810
    • Подставим результаты всех частей в уравнение:
      • 2N2 + 4N + 6 = 2N2 + 4 + 38;
4N = 36;
N = 9

    Результат: 9

    ✍ Решение:

    • Вместо обозначения искомой системы счисления введем неизвестное x:
      • 144x + 24x = 201x
    • Запишем формулу перевода в десятичную систему счисления каждого из слагаемых и сумму исходного равенства:
      • 144 + 24 = 201
1*x2 + 4*x1 + 4*x0 + 2*x1 + 4*x0 = 2*x2 + 0*x1 + 1*x0
    • Упростим полученное уравнение:
      • x2 - 6x - 7 = 0
    • Решим уравнение:
      • D = b2 - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
x = 7

    Ответ: 7

    14_9:

    В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.

    Типовые задания для тренировки

    ✍ Решение:

    • Вспомним правило:

      • Последняя цифра записи числа в системе счисления с основанием X — это остаток от деления этого числа на X

    • Примем искомую систему счисления за x. Тогда, исходя из приведенного правила имеем:
      • 94 / x = некоторое число и остаток 3
и
68 / x = некоторое число и остаток 3
    • Поскольку x должно быть целым числом, то следующее деление должно выполняться без остатка:
      • 91/x 
65/x
    • Иными словами x — наибольший общий делитель чисел 91 и 65.
    • Найдем НОД, например, по алгоритму Евклида: 
      • 91 - 65 = 26
65 - 26 = 39
39 - 26 = 13
26 - 13 = 13
    • Получаем результат 13.

    Ответ: 13

    14_10:

    Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:

    X = *516 = *0*8

    Сколько чисел соответствуют условию задачи?

    Типовые задания для тренировки

    ✍ Решение:

    • Данные числа с утерянными символами переведем из 16-й и из 8-й системы счисления в двоичную. Перевод будем делать триадами и тетрадами, неизвестные позиции оставим пустыми:
      • 1. *516
    *   |    5  16

* * * * | 0 1 0 1 2

2. *0*8
  *  |  0  |  *  8
* * *|0 0 0|* * * 2
    • Сопоставим известные и неизвестные биты в обеих получившихся масках:
      • * * 0 0 0 1 0 1
    • Неизвестными остались 7-й и 8-й бит. Они не могут быть одновременно нулями, так как для *0*8 тогда исчезнет старший разряд. Поэтому оставшиеся варианты будут такими:
      • 1. 01000101
2. 10000101
3. 11000101
    • Итого 3 варианта.

    Ответ: 3

    Предлагаем посмотреть видео решения данного 14 задания ЕГЭ (аналитическое решение):

      
    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь

    14_4:

    Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.

    Типовые задания для тренировки

    ✍ Решение:

    • Так как 75 должно оканчиваться на 13, то имеем два общих случая:
      • 1. 7510 = 13N 
2. 7510 = ...13N (число оканчивается на 13)
    • Рассмотрим подробно каждый случай.

      • 1 случай:

    • Остаток должен быть равен 3 (последнее число в неизвестной системе), а частное должно равняться 1 (предпоследнее число в неизвестной системе):
      •  75|N 
  N|1  отсюда имеем => 75 - N = 3; т.е. N = 72
  3
    • Таким образом, мы получили одно из искомых оснований (72).

      • 2 случай:

    • Искомое оканчивается на цифру 3, значит:
      •  75|N 
 72|y  отсюда имеем => 75 = Ny + 3, где N - целое, неотриц.
  3
    • и далее, частное от деления — 1 (предпоследнее число):
      •  75|N  
 72|  y |N   => y = Nz + 1, где z - целое, неотриц.
  3  y-1|z
       1
    • Получаем два равенства (систему уравнений):
      • 75 = Ny + 3
y = Nz + 1
    • Подставим y из второго равенства в первое:
      • 75 = N (Nz + 1) + 3;
75 = N2z + N + 3;
75 = N2z + N
    • Выразим z:
      • z = (72 - N)/N2
    • Учитывая то, что z — целое неотрицательное число, то 72 — N должно быть кратно N2, т.е. в числителе не может быть простого числа.
    • Простое число 67 получается путем вычитания из 72 числа 5. Соответственно, 5 нам не подходит: N ≠ 5:
      • 72 - 5 / 52 = 67 / 25  не делится, - не подходит!
    • Еще одно простое число — 71 получится при вычитании 72 — 1. Единица не подходит, так как при переводе в конце числа никак не останется 13: N ≠ 1.
    • Раз в знаменателе N2, то отбросим все числа, квадрат которых больше 72: 9, 10, … и т.д. до бесконечности: N < 9
    • Раз в итоговом числе есть число 13, значит основание системы счисления больше 3 (т.е. цифра три присутствует в системах, начиная с 4-й): N >= 4
    • Проверим оставшиеся варианты — 4, 6, 7, 8:
      •  75 | 4 
 72 | 18| 4 
  3   16| 2
       2  => не подходит! должна быть единица

       75 | 6 
 72 | 12| 6 
  3   12| 1
       0  => не подходит! должна быть единица

       75 | 7 
 70 
  5 => не подходит! должна быть 3 

       75 | 8 
 72 | 9| 8 
  3   8| 1
       1  => подходит!

    Результат: 8,72

    Видеоразбор решения (аналитический способ):

    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь

    14_11:

    Выражение 25*325 записано в троичной системе счисления. Определите, сколько в этой записи цифр 0, 1 и 2.

    ✍ Решение:

      Рассмотрим каждый сомножитель отдельно.

    • Первый сомножитель:
      • 25 = 32

Переведем в троичную систему счисления (делением на 3, переписываем остатки).
Результат:
3210 = 10123
    • Для рассмотрения второго сомножителя будем использовать правило:

    • Получим:
      • 325 = 10..0{25 нулей}3
    • Выполним произведение, но для простоты счета, представим, что нулей не 25, а только 3:
      •    1000 x
   1012 =
   ----
   2000
  1000
 0000
1000
-------
1012000
    • В исходном числе было 3 нуля, стало 4. Значит если было 25 нулей, то станет 25 + 1 = 26.
    • Единиц = 2, двоек = 1.

    Ответ: «0»=26, «1»=2, «2»=1

    Смотрите видео разбора на нашем канале (аналитическое решение):
    📹 YouTube здесь
    📹 Видеорешение на RuTube здесь

    Источник

    Всего: 185    1–20 | 21–40 | 41–60 | 61–80 …

    Добавить в вариант

    Запись числа N в системе счисления с основанием 7 содержит две цифры, запись этого числа в системе счисления с основанием 6 содержит три цифры, а запись в системе счисления с основанием 11 заканчивается на 2.

    Чему равно N?

    К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.

    Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?

    Ответ записать в виде целого числа.

    Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?

    Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 7?

    В системе счисления с некоторым основанием десятичное число 144 записывается в виде 264. Укажите это основание.

    Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?

    Источник: Демонстрационная версия ЕГЭ—2013 по информатике.

    Десятичное число 81 в некоторой системе счисления записывается как 144. Определите основание системы счисления.

    Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.

    Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?

    Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.

    Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.

    Запись числа 6810 в системе счисления с основанием N оканчивается на 2 и содержит 4 цифры. Чему равно основание этой системы счисления N?

    Решите уравнение:

    1005 + x = 2004.

    Ответ запишите в семеричной системе (основание системы счисления в ответе писать не нужно).

    Решите уравнение:

    608 + x = 2005.

    Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).

    В системе счисления с некоторым основанием десятичное число 15 записывается в виде 30. Укажите это основание.

    Источник: ЕГЭ по информатике 08.07.2013. Вторая волна. Вариант 602.

    Решите уравнение:

    608 + x = 609

    Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).

    Восьмеричное число 77 в некоторой системе счисления записывается как 53. Определите основание системы счисления.

    Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10104

    Запишите натуральное число, десятичная запись которого состоит из двух цифр, шестнадцатеричная запись заканчивается цифрой B, а пятеричная  — цифрой 3.

    Запишите натуральное число, десятичная запись которого состоит из двух цифр, шестнадцатеричная запись заканчивается цифрой A, а пятеричная  — цифрой 3.

    Всего: 185    1–20 | 21–40 | 41–60 | 61–80 …

    Источник

    Подготовка к ЕГЭ – 2021, Занятие 1.

    Позиционные системы счисления, задание 14

    Презентацию по теме можно посмотреть здесь.

    На уроках информатики мы никогда ничего не зубрим! Ученики должны понимать все, о чем говорится на уроках, и запоминать новое путем повторений пройденного, сравнений и ассоциаций с уже знакомыми темами и понятной информацией.

    Для максимально быстрого и однозначно верного решения задач мы придерживаемся принципа: чем меньше вычислений и другой работы мы делаем, тем меньше времени тратиться на решение задачи и тем меньшую вероятность появления ошибок получаем в результате. При этом, соглашаясь с Аристотелем, что «Ум заключается не только в знании, но и в умении прилагать знания на деле», я настаиваю на способах решений, соответствующих этому принципу, хотя существуют и другие варианты. На своих уроках я придерживаюсь изложения темы именно в этом ключе. Сначала это бывает сложно, особенно тем, кто приходит ко мне на уроки уже знакомым с иначе излагаемым материалом и не желающим переучиваться. Но хочу научить Вас решать быстро и без ошибок, экономя время и силы для новых задач. Поверьте, этому несложно научиться, нужно только поверить в свои силы — и все получится! При этом проверочные работы и тесты проводятся мной на время с расчетом решения задач именно по такому принципу.

    При изучении этой темы обращаю особое внимание на таблицу степеней двойки и на ряд закономерностей. При этом знание таблицы является необходимым и достаточным условием для максимально быстрого и однозначно точного решения, а дополнительное знание закономерностей позволит выполнить все еще быстрее и точнее.

    Ниже приведена таблица степеней двойки, где n – это степень, а 2n – результат возведения числа 2 в степень n:

    n

    0

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    2n

    1

    2

    4

    8

    16

    32

    64

    128

    256

    512

    1024

    2048

    4096

    Таблицу не обязательно заранее учить наизусть. Нужно при решении задач пользоваться ею, но при этом заглядывать в нее все реже и реже, пытаясь сначала вспомнить значение степени. Тогда эта таблица сама «уляжется» в голове и очень поможет на экзамене в этой и в других темах!

    Теперь перейдем к теории рассматриваемой темы.

    Система счисления или нумерация – это способ записи (обозначения) чисел.

    Возьмем это за основу работы с разными системами счисления, поскольку только способ записи у них будет разный, а все закономерности одинаковые. Поэтому в случае возникновения трудностей в понимании темы обращаемся к десятичной системе счисления и переносим аналог на остальные.

    Символы, при помощи которых записываются числа, называются цифрами, а их совокупность – алфавитом системы счисления. Количество цифр, составляющих алфавит, называется основанием (размерностью) системы счисления. Число в любой системе счисления состоит из цифр, входящих в алфавит этой системы.

    В системе счисления, которой мы пользуемся в повседневной жизни – 10 цифр (от 0 до 9), и поэтому такая система счисления называется десятичной.

    Аналогично, если в системе счисления будет две цифры (0 и 1), то она называется двоичной, восемь цифр (от 0 до 7) – восьмеричной и т.д.

    Основание алфавита указывается в виде индекса числа, записанного в десятичной системе счисления, например: 10112, 1528, 1А716.

    При этом основание десятичной системы счисления можно не указывать (будем использовать то, что всем нам привычно — «по умолчанию»).

    Обратим внимание, что

    • наименьшей цифрой в алфавите любой системе счисления является ноль, а наибольшая цифра всегда на единицу меньше основания

    Системы счисления бывают двух видов — позиционные и непозиционные.

    Система счисления называется позиционной, если количественный эквивалент цифры зависит от ее положения (позиции) в записи числа.

    Например, запишем одинаковыми цифрами несколько разных чисел:

    1234 = 1 тысяча + 2 сотни + 3 десятка + 1 единица

    3124 = 3 тысячи + 1 сотня + 2 десятка + 4 единицы

    4321 = 4 тысячи + 3 сотни + 2 десятка +1 единица.

    Таким образом, числа, составленные из одних и тех же цифр, но стоящих в числах на разных позициях, имеют различные значения (математический вес).

    Как и в привычной нам десятичной, так и в любой другой позиционной системе счисления значение числа образуется суммой результатов умножения цифр на «веса» (степени основания) соответствующих разрядов.

    Например,

    3948 = 3*1000+9*100+4*10+8*1 = 3*103+9*102+4*101+8*100

    10112 = 1*23+0*22+1*21+1*20 или 10112 = 1*20+1*21+0*22+1*23

    (далее будем пользоваться последней приведенной в примере формой записи, чтобы не делать лишних действий и не нумеровать степени двойки слева направо для их правильного использования).

    При этом форма записи числа в виде 3948 называется свернутой, а в виде 3*103+9*102+4*101+8*100 – развернутой формой записи числа.

    Примером непозиционных систем могут служить древнеегипетская, древнеславянская или римская система счисления. 
    Самым ярким примером непозиционной системы счисления является известная всем римская система счисления, в которой каждый символ обозначает всегда одно и тоже число независимо от его позиции в числе. Так в римской системе счисления из двух цифр X — десять и I — один можно составить числа: XI (одиннадцать), IX (девять), XIX (девятнадцать) или другие, но во всех них значения цифр в зависимости от занимаемых позиций не меняются, а значение числа получается разным при смене порядка следования цифр друг за другом.

    Будем называть позиционные системы счисления дружественными (родственными), если в основании у них лежит одно и то же число, но в разных степенях. При этом «дружат» они через систему счисления с основанием в первой степени.

    Например, двоичная, четверичная, восьмеричная и шестнадцатеричная системы счисления «дружат» через двоичную, т.к. в основании у них лежит число 2, но в разных степенях:

    2=21, 4=22, 8=23, 16=24

    Будем считать, что десятичная система счисления не дружит ни с какой другой, так как ближайшая к ней система счисления с основанием 100 в практических вычислениях нам не встречается.

    Правила перевода между различными системами счисления делятся на две группы – перевод между дружественными и недружественными системами.

    Перевод между недружественными системами счисления всегда выполняется через десятичную систему следующим образом:

    • из десятичной системы счисления в любую – делением исходного числа на основание системы счисления, в которую переводим; при этом остатки от деления и последнее частное должны быть меньше этого основания. Частное и остатки от деления собираются справа налево.

    • из любой системы счисления в десятичную — умножением цифр на «веса» (степени основания) соответствующих разрядов и все полученные значения складываются.

    Например, переведем десятичное число 25 в двоичную систему счисления (рис.1):

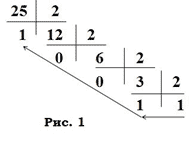
    Тогда 2510 = 110012

    и обратно 110012 = 1*20+0*21+0*22+1*23+1*24

    2510 = 2213

    и обратно 2213 = 1*30+2*31+2*32

    2510 = 416 и обратно 416 = 1*60+4*61

    Для быстрого и точного перевода между дружественными (причем только между ними!) двоичной, восьмеричной и шестнадцатеричной системами счисления построим таблицу соответствия десятичных, восьмеричных и шестнадцатеричных чисел двоичным, и назовем эту таблицу таблицей «дружбы» (рис.2). Левая часть этой таблицы включает цифры восьмеричной системы счисления, а правая дополняет ее для всех цифр шестнадцатеричной системы счисления.

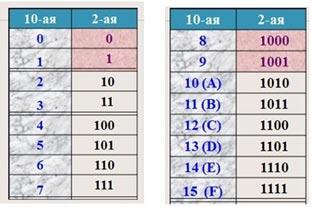
    Рис. 2

    Заметим, что так как каждая цифра в любой системе счисления занимает только одну позицию (один разряд числа), то в шестнадцатеричной системе счисления для записи цифр со значением больше 9 (10, 11 и т.д. здесь – это цифры!) используют латинские заглавные буквы от A до F .

    Данная таблица разделена двойными линиями в местах условного ее разделения на дружественные системы счисления (двоичную, четверичную, восьмеричную и шестнадцатеричную).

    Обратите внимание, что длина чисел в двоичной системе счисления зависит от степени двойки в основании дружественной системы счисления:

    • т.к. 8=23, то при переводе из восьмеричной системы счисления в двоичную мы записываем каждое двоичное число тремя разрядами (триадами);

    • т.к. 16=24, то при переводе из восьмеричной системы счисления в двоичную мы записываем каждое двоичное число четырьмя разрядами (тетрадами);

    Именно это позволяет легко осуществлять перевод между дружественными системами счисления, записывая каждую цифру исходного числа соответствующей ему в таблице двоичной цифрой с учетом того, чтобы длина двоичной цифры при этом строго соответствовала степени двойки основания исходной системы счисления:

    • 8=23, то меняем одну восьмеричную цифру на три двоичные — триады,

    • 16 = 24, тогда меняем каждую шестнадцатеричную цифру на четыре двоичные — тетрады,

    дополняя их при необходимости до нужной длины незначащими нулями слева (добавление нулей справа от исходного числа является результатом умножения числа на 10, 100 и т.д., т.е. изменяет исходное число).

    Например,

    1528 = 001 101 0102 = 1 101 0102

    (при этом первые два нуля не указываются, т.к. они незначащие), а

    15216 = 0001 0101 00102 = 1 0101 00102

    (при этом первые три нуля также не указываются).

    Выполним перевод из восьмеричной системы счисления в шестнадцатеричную и обратно через двоичную систему счисления.
    Перегруппировка двоичных разрядов по четыре и по три во второй части выражений выполняется справа налево по количеству разрядов в степени результирующей системы счисления, а дальнейшая запись числа – как обычно, слева направо.

    Например,

    1528 = 1 101 0102 = 110 10102 = 6А16

    15216 = 1 0101 00102 = 101 010 0102 = 5228

    Теперь обратим внимание еще на несколько закономерностей, которые можно заметить в вышеприведенной таблице «дружбы» и аналогичных ей таблицах других систем счисления, в том числе и десятичной.

    Закономерность № 1

    • Любое основание в своей системе счисления выглядит как 10, т.е.

    N10 = 10n

    (210=102 – посмотрите в таблице, 810=108, 1610=1016 и т.д.).

    Закономерность № 2.

    • Степень любого основания в своей системе счисления выглядит как единица и количество нулей, равных степени, т.е.

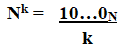
    (посмотрите в таблице: 4=22=1002, 8=23 =10002, тогда 16=24=100002).

    Закономерность № 3.

    • Число, стоящее перед k-й степенью основания, в своей системе счисления выглядит как последовательность из k самых больших цифр этой системы счисления, т.е.

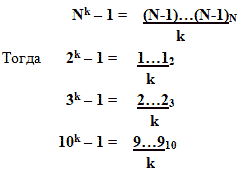
    (посмотрите в таблице: 3=22 – 1=112, 7=23 — 1=1112, тогда 15=24-1=11112).

    Закономерность № 4.

    • Длина числа при переводе десятичного числа в любую систему счисления легко определяется по формуле:

    где Ch – исходное число,

    L — длина после перевода в систему счисления с основанием N.

    (например: 22 ≤ 5 23, тогда при переводе в двоичную систему счисления длина числа будет равна 3, посмотрите в таблице: 5=1012;

    23 ≤ 13 24, тогда при переводе в двоичную систему счисления длина числа будет равна 3, посмотрите в таблице: 13=10112).

    Если закономерности 1, 2 и 3 применяются для быстрого и точного перевода чисел между системами счисления, то закономерность 4 удобно использовать для первичной проверки правильности перевода чисел из десятичной системы счисления в любую другую, что позволит сэкономить время на проверке результата перевода и даст возможность избежать ошибок).

    Но использование закономерностей дает нам еще ряд преимуществ!

    Так, помня о нашем принципе быстрых и точных вычислений и в соответствии с закономерностями 1 и 3, рекомендуется выполнять перевод из десятичной системы счисления в двоичную разложением числа на степени двойки следующим образом. Вычитаем из числа степень двойки, которая меньше числа, но максимально приближенную к нему, Затем с остатком проделываем те же действия до тех пор, пока не разложим все число на степени двойки.

    Например:

    25 = 16 + 8 + 1 = 24 + 23 + 20

    (25 – 16 = 9 ; 9 = 8 + 1)

    После этого, заменяем присутствующие степени двойки единицами (в соответствии с закономерностью 2), а пропущенные – нулями в порядке следования степеней, получая двоичную запись числа:

    25 = 16 + 8 + 1 = 24 + 23 + 20 = 110012

    (отсутствующие вторую и первую степени двойки заменяем нулями).

    На чем еще можно сэкономить время и избежать ошибок?

    Например, для перевода большого двоичного числа в десятичную систему счисления можно использовать в качестве промежуточной восьмеричную или шестнадцатеричную системы счисления:

    1100111012 = 110 011 1012 = 6358 = 5*80+3*81+6*82 = 5 + 24 + 384 = 413

    1100111012 = 1 1001 11012 = 19D16= 13*160+9*161+1*162 = 13 + 144 + 256 = 413

    ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

    Решим несколько задач по этой теме с использованием изложенных выше закономерностей.

    Примечание. Так как любое число в нулевой степени равно единице, а любое число в первой степени равно самому числу, то при решении задач можно не писать степень в разряде единиц и десятков.

    1. Переведите двоичное число 1110101 в десятичную систему счисления.

    Решение:

    11101012= 1 110 1012 = 1658 = 5+6*81+1*82 =5+48+64=117

    Или:

    11101012= 111 01012 = 7516 = 5+7*161=5+112=117

    Ответ: 117

    2. Переведите двоичное число 1100011 в десятичную систему счисления.

    Решение:

    11000112 = 110 00112 = 7316 = 3+6*161=3+96=99

    Ответ: 99

    3. Переведите число 135 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

    Решение:

    135 = 128+4+2+1= 27 + 22 + 21 + 20

    Ответ: 4

    Заметим, что этот ответ получен без окончательного перевода числа в двоичную систему счисления, достаточно посчитать количество двоек в степенях. Это позволило сэкономить время решения задачи и избежать возможных ошибок при дальнейшей записи.

    4. Переведите число 125 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

    Решение:

    125 = 127 – 2 = 11111112 -102 = 11111012

    Ответ: 6

    5. Переведите число FE из шестнадцатеричной системы счисления в двоичную систему счисления.

    Решение:

    FE16 = 1111 11102 (используем запись тетрадами из таблицы «дружбы»).

    Ответ: 11111110

    6. Переведите число 143 из десятичной системы счисления в двоичную систему счисления. Сколько значащих нулей содержит полученное число? В ответе укажите одно число — количество нулей.

    Решение:

    143 = 128+8+4+2+1 = 27 + 23 + 22 + 21 + 20,

    то пропущены всего три (6, 5 и 4 степени двойки, которые при записи двоичного числа заполняются нулями.

    Ответ: 3

    7. Переведите число 305 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.

    Решение:

    305 = 256 + 32 + 16 + 1

    (305-256=49, 49 — 32=17=16+1)

    (т.к. в сложении участвуют всего 4 степени двойки, то результат будет содержать всего 4 единицы. Степени можно даже не писать)

    Ответ: 4

    8. Вычислите: 101010102 – 2528 + 716. Ответ запишите в десятичной системе счисления.

    Решение: Для решения задач такого типа нужно сначала перевести все числа в одну систему счисления, а уже потом выполнять действия между ними.

    Переведем первое число в восьмеричную систему счисления:

    101010102 = 2528

    Тогда получаем выражение: 2528 – 2528 + 716 = 716 = 710

    Ответ: 7

    9. Вычислите значение выражения B916 − 2718. В ответе запишите вычисленное значение в десятичной системе счисления.

    Решение: Переведем первое число в восьмеричную систему счисления:

    В916 = 1011 10012 = 10 111 0012 = 2718. Тогда 2718 — 2718 = 0.

    Ответ: 0

    10. Вычислите значение выражения EB16 − 3528. Ответ запишите в десятичной системе счисления.

    Решение: Переведем первое число в восьмеричную систему счисления:

    EB16= 111010112= 3528

    Тогда разница между двумя исходными числами равна 1.

    Ответ: 1

    11. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 5 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.

    Решение: Наименьшее двоичное число, содержащее 5 единиц, равно 111112.

    Но чтобы восьмеричное число было четырехзначным нужно, чтобы оно состояло из 4 триад (из 12 цифр). При этом первой цифрой двоичного числа обязательно должна быть 1 (два незначащих нуля в начале можно не писать), а остальные единицы будут занимать последние разряды числа. Тогда получаем:

    001 000 001 1112 = 10178

    Ответ: 1017

    12. Найдите значение выражения 1116 + 118 : 112. Ответ запишите в двоичной системе счисления.

    Решение: В таких задачах, где нужно выполнять быстро и без ошибок вычисления в различных системах счисления, а результат требуется получить в десятичной, то и решение быстрее и проще выполнить в десятичной системе счисления. Поэтому переводим туда все исходные числа и считаем:

    1116 = 16+1 = 17

    118 = 8+1 = 9

    112 = 2+1 = 3

    Тогда 17 + 9 : 3 = 20

    20 = 16 + 4 = 24 + 22 = 101002

    Ответ: 10100

    13. Даны 4 целых числа, записанные в двоичной системе:

    10001011, 10111000, 10011011, 10110100.

    Сколько среди них чисел, больших, чем A416+208?

    Решение: Для выполнения действий над числами, представленными в разных системах счисления, нужно сначала перевести их в наиболее удобную для вас систему счисления, и только потом решать задачу. Для меня наиболее удобной является восьмеричная система счисления:

    100010112 = 2138, 101110002 = 5608, 100110112 = 2338, 101101002 = 2468

    A416 = 101001002 = 2448, и 2448+208=2648.

    Тогда из предложенных чисел подходит только второе число.

    Ответ: 1

    14. Запись числа 6910 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Чему равно основание этой системы счисления N?

    Решение: Для решения этой задачи используем две закономерности.

    Во-первых, последней цифрой числа при переводе из одной системы счисления в другую всегда является первый остаток от деления числа на основание системы счисления, куда переводим. Тогда искомое основание N должно быть кратно 68 (69=х*N+1, то х*N=68): 2, 4, 7 и т.д. Во-вторых, по закономерности 4, получаем N3 ≤ 69 4.

    Тогда при выполнении этих условий искомое число N будет равно 4.

    Ответ: 4

    15. В системе счисления с основанием N запись числа 4110 оканчивается на 2, а запись числа 13110 — на 1. Чему равно число N?

    Решение: Т.к. в остатках чисел у нас есть цифры 2 и 1, то N ≤3. При этом N нужно найти число, кратное числам 39 и 130. Следовательно, N = 13.

    Ответ: 13

    16. В какой системе счисления выполняется равенство 12 · 13 = 211? В ответе укажите число – основание системы счисления.

    Решение: При переводе числа 211N в десятичную систему счисления получаем уравнение:

    211N = 2*N3 + 1*N +1

    Для перевода множителей 12 и 13 в десятичную систему счисления вспомним закономерность 1. Тогда 12N = N+2, 13N = N+3.

    Следовательно, получаем уравнение:

     (N+2)(N+3) = 2*N2 + N +1

    Корнями данного уравнения являются 5 и -1. Но т.к. основание системы счисления является натуральным числом, то N = 5.

    Ответ: 5

    17. Укажите наименьшее основание системы счисления, в которой запись числа 50 трехзначна.

    Решение: По закономерности 4 получаем N2 ≤ 50 3.

    Следовательно, нам нужно найти наименьшее число, куб которого больше 50.

    Ответ: 4

    Источник

    Понравилась статья? Поделить с друзьями:
  • Знаки препинания на стыке союзов егэ
  • Злостный взгляд надзирателя выдавал недоброе намерение егэ
  • Земельный кадастр вопросы к экзамену
  • Зеленая лампа грин анализ для итогового сочинения
  • Звук сдачи экзамена