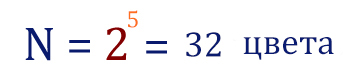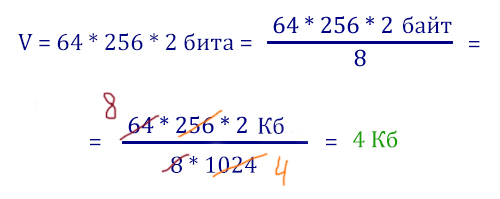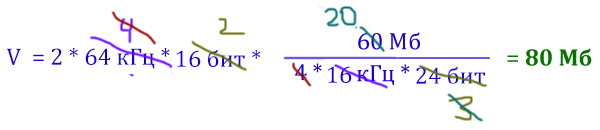Звукозапись егэ информатика - Помощь в подготовке к экзаменам и поступлению

Урок посвящен разбору задания 7 ЕГЭ по информатике

Содержание:

Объяснение заданий 7 ЕГЭ по информатике
- Кодирование текстовой информации
- Кодирование графической информации
- Кодирование звуковой информации
- Определение скорости передачи информации
Решение заданий 7 ЕГЭ по информатике
- Тема: Кодирование изображений
- Тема: Кодирование звука
- Тема: Кодирование видео
- Тема: Скорость передачи данных

7-е задание: «Кодирование графической и звуковой информации, объем и передача информации»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Умение определять объём памяти, необходимый для хранения графической и звуковой информации

До ЕГЭ 2021 года — это было задание № 9 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Если вычисления получаются слишком громоздкими, значит, Вы неправильно решаете задачу. Удобно выделить во всех множителях степени двойки, тогда умножение сведётся к сложению
показателей степеней, а деление – к вычитанию»

ФГБНУ «Федеральный институт педагогических измерений»

Кодирование текстовой информации

I = n * i

где:

n — количество символов

i — количество бит на 1 символ (кодировка)

Кодирование графической информации

Рассмотрим некоторые понятия и формулы, необходимые для решения ЕГЭ по информатике данной темы.

Пиксель – это наименьший элемент растрового изображения, который имеет определенный цвет.
Разрешение – это количество пикселей на дюйм размера изображения.
Глубина цвета — это количество битов, необходимое для кодирования цвета пикселя.
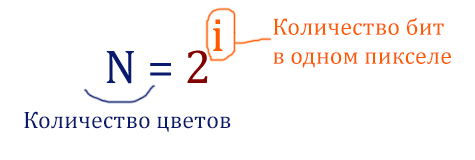
Если глубина кодирования составляет i битов на пиксель, код каждого пикселя выбирается из 2ⁱ возможных вариантов, поэтому можно использовать не более 2ⁱ различных цветов.

Формула для нахождения количества цветов в используемой палитре:

i = log₂N

N — количество цветов
i — глубина цвета
В цветовой модели RGB (красный (R), зеленый (G), синий (B)): R (0..255) G (0..255) B (0..255) -> получаем 2⁸ вариантов на каждый из трех цветов.
R G B: 24 бита = 3 байта — режим True Color (истинный цвет)

Найдем формулу объема памяти для хранения растрового изображения:

I = M * N * i

где:

I — объем памяти, требуемый для хранения изображения
M — ширина изображения в пикселях
N — высота изображения в пикселях
i — глубина кодирования цвета или разрешение

Или можно формулу записать так:

I = N * i битов

где N – количество пикселей (M * N) и i – глубина кодирования цвета (разрядность кодирования)

* для указания объема выделенной памяти встречаются разные обозначения (V или I).

Следует также помнить формулы преобразования:

1 Мбайт = 2²⁰ байт = 2²³ бит,
1 Кбайт = 2¹⁰ байт = 2¹³ бит

Кодирование звуковой информации

Познакомимся с понятиями и формулами, необходимыми для решения заданий 7 ЕГЭ по информатике.

Оцифровка или дискретизация – это преобразование аналогового сигнала в цифровой код.

Дискретизация, объяснение задания 7 ЕГЭ

T – интервал дискретизации (измеряется в с)
ƒ — частота дискретизации (измеряется в Гц, кГц)

* Изображение взято из презентации К. Полякова

Частота дискретизации определяет количество отсчетов, т.е. отдельных значений сигнала, запоминаемых за 1 секунду. Измеряется в герцах, 1 Гц (один герц) – это один отсчет в секунду, а, например, 7 кГц – это 7000 отсчетов в секунду.
Разрядность кодирования (глубина, разрешение) — это число битов, используемое для хранения одного отсчёта.

Разрядность кодирования

* Изображение взято из презентации К. Полякова

Получим формулу объема звукового файла:

Для хранения информации о звуке длительностью t секунд, закодированном с частотой дискретизации ƒ Гц и глубиной кодирования β бит требуется бит памяти:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

S для моно = 1, для стерео = 2, для квадро = 4

Пример: при ƒ=8 кГц, глубине кодирования 16 бит на отсчёт и длительности звука 128 с. потребуется:

✍ Решение:

I = 8000*16*128 = 16384000 бит
I = 8000*16*128/8 = 2³ * 1000 * 2⁴ * 2⁷ / 2³ = 2¹⁴ / 2³ =2¹¹ =
= 2048000 байт

Определение скорости передачи информации

Канал связи всегда имеет ограниченную пропускную способность (скорость передачи информации), которая зависит от свойств аппаратуры и самой линии связи(кабеля)

Объем переданной информации I вычисляется по формуле:

I = V * t

I — объем информации
v — пропускная способность канала связи (измеряется в битах в секунду или подобных единицах)
t — время передачи

* Вместо обозначения скорости V иногда используется q
* Вместо обозначения объема сообщения I иногда используется Q

Скорость передачи данных определяется по формуле:

V = I/t

и измеряется в бит/с

Егифка ©:

Решение заданий 7 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Тема: Кодирование изображений

7_1:

Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 160 х 160 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Используем формулу нахождения объема:
Подсчитаем каждый сомножитель в формуле, стараясь привести числа к степеням двойки:
M x N:

160 * 160 = 20 * 2³ *  20 * 2³ = 400 * 2⁶ = 
= 25 * 2⁴ * 2⁶

Нахождение глубины кодирования i:

256 = 2⁸ 
т.е. 8 бит на пиксель  (из формулы кол-во цветов = 2ⁱ)

Находим объем:

I = 25 * 2⁴ * 2⁶ * 2³ = 25 * 2¹³ - всего бит на всё изображение

Переводим в Кбайты:

(25 * 2¹³) / 2¹³ = 25 Кбайт

Результат: 25

Детальный разбор задания 7 ЕГЭ по информатике предлагаем посмотреть в видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.2:

Рисунок размером 128 на 256 пикселей занимает в памяти 24 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:
где M * N — общее количество пикселей. Найдем это значение, используя для удобства степени двойки:

128 * 256 = 2⁷ * 2⁸ = 2¹⁵

В вышеуказанной формуле i — это глубина цвета, от которой зависит количество цветов в палитре:
Найдем i из той же формулы:

i = I / (M*N)

Учтем, что 24 Кбайт необходимо перевести в биты. Получим:

2³ * 3 * 2¹⁰ * 2³:
i = (2³ * 3 * 2¹⁰ * 2³) / 2¹⁵ = 
= 3 * 2¹⁶ / 2¹⁵ = 6 бит

Теперь найдем количество цветов в палитре:

2⁶ = 64 вариантов цветов в цветовой палитре

Результат: 64

Смотрите видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.3:

После преобразования растрового 256-цветного графического файла в 4-цветный формат его размер уменьшился на 18 Кбайт. Каков был размер исходного файла в Кбайтах?

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей,
а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

i можно найти, зная количество цветов в палитре:

до преобразования: i = 8 (2⁸ = 256)
после преобразования: i = 2 (2² = 4)

Составим систему уравнений на основе имеющихся сведений, примем за x количество пикселей (разрешение):

I = x * 8
I - 18 = x * 2

Выразим x в первом уравнении:

x = I / 8

Подставим во второе уравнение и найдем I (объем файла):

I - 18 = I / 4
4I - I = 72
3I = 72
I = 24

Результат: 24

Подробный разбор 7 задания ЕГЭ смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.4:

Цветное изображение было оцифровано и сохранено в виде файла без использования сжатия данных. Размер полученного файла – 42 Мбайт. Затем то же изображение было оцифровано повторно с разрешением в 2 раза меньше и глубиной кодирования цвета увеличили в 4 раза больше по сравнению с первоначальными параметрами. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной оцифровке.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

В такого рода задачах необходимо учесть, что уменьшение разрешения в 2 раза, подразумевает уменьшение в 2 раза пикселей отдельно по ширине и по высоте. Т.е. в целом N уменьшается в 4 раза!
Составим систему уравнений на основе имеющихся сведений, в которой первое уравнение будет соответствовать данным до преобразования файла, а второе уравнение — после:

42 = N * i
I = N / 4 * 4i

Выразим i в первом уравнении:

i = 42 / N

Подставим во второе уравнение и найдем I (объем файла):

[ I= frac {N}{4} * 4* frac {42}{N} ]

После сокращений получим:

I = 42

Результат: 42

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.5:

Изображение было оцифровано и сохранено в виде растрового файла. Получившийся файл был передан в город А по каналу связи за 72 секунды. Затем то же изображение было оцифровано повторно с разрешением в 2 раза больше и глубиной кодирования цвета в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 3 раза выше, чем канала связи с городом А.
Сколько секунд длилась передача файла в город Б?

Типовые задания для тренировки

✍ Решение:

По формуле скорости передачи файла имеем:

где I — объем файла, а t — время

По формуле объема файла изображения имеем:

где N — общее количество пикселей или разрешение,
а i — глубина цвета (количество бит, выделенное на 1 пиксель)

Для данной задачи, необходимо уточнить, что разрешение на самом деле имеет два сомножителя (пикселей по ширине * пикселей по высоте). Поэтому при увеличении разрешения в два раза, увеличатся оба числа, т.е. N увеличится в 4 раза вместо двух.
Изменим формулу получения объема файла для города Б:

[ I= frac {2*N * i}{3} ]

Для города А и Б заменим значения объема в формуле для получения скорости:

Город А:

[ V= frac {N*i}{72} ]

Город Б:

[ 3*V= frac{frac {4*N*i}{3}}{t} ]

или:

[ t*3*V= frac {4*N*i}{3} ]

Подставим значение скорости из формулы для города А в формулу для города Б:

[ frac {t*3*N*i}{72}= frac {4*N*i}{3} ]

Выразим t:

t = 4 * 72 / (3 * 3) = 32 секунды

Результат: 32

Другой способ решения смотрите в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

ЕГЭ по информатике задание 7.6:

Камера делает фотоснимки размером 1024 х 768 пикселей. На хранение одного кадра отводится 900 Кбайт.
Найдите максимально возможное количество цветов в палитре изображения.

Типовые задания для терировки

✍ Решение:

Количество цветов зависит от глубины кодирования цвета, которая измеряется в битах. Для хранения кадра, т.е. общего количества пикселей выделено 900 Кбайт. Переведем в биты:

900 Кбайт = 2² * 225 * 2¹⁰ * 2³ = 225 * 2¹⁵

Посчитаем общее количество пикселей (из заданного размера):

1024 * 768 = 2¹⁰ * 3 * 2⁸

Определим объем памяти, необходимый для хранения не общего количества пикселей, а одного пикселя ([память для кадра]/[кол-во пикселей]):

[ frac {225 * 2^{15}}{3 * 2^{18}} = frac {75}{8} approx 9 ]

9 бит на 1 пиксель

9 бит — это i — глубина кодирования цвета. Количество цветов = 2ⁱ:

2⁹ = 512

Результат: 512

Смотрите подробное решение на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование изображений:

7_8: Демоверсия ЕГЭ 2018 информатика:

Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится.
Какое максимальное количество цветов можно использовать в палитре?

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Посмотрим, что из формулы нам уже дано:

I = 320 Кбайт, 
N = 640 * 420 = 307200 = 75 * 2¹² всего пикселей, 
i - ?

Количество цветов в изображении зависит от параметра i, который неизвестен. Вспомним формулу:

количество цветов = 2ⁱ

Поскольку глубина цвета измеряется в битах, то необходимо объем перевести из Килобайт в биты:

320 Кбайт = 320 * 2¹⁰ * 2³ бит  = 320 * 2¹³ бит

Найдем i:

[ i = frac {I}{N} = frac {320 * 2^{13}}{75 * 2^{12}} approx 8,5 бит ]

Найдем количество цветов:

2ⁱ = 2⁸ = 256

Результат: 256

Подробное решение данного 7 (9) задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

7_21: : ЕГЭ по информатике задание 7.21:

Для хранения в информационной системе документы сканируются с разрешением 300 ppi. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 5 Мбайт. В целях экономии было решено перейти на разрешение 150 ppi и цветовую систему, содержащую 16 цветов. Средний размер документа, отсканированного с изменёнными параметрами, составляет 512 Кбайт.

Определите количество цветов в палитре до оптимизации.

Типовые задания для тренировки

✍ Решение:

По формуле объема файла изображения имеем:

I = N * i

где N — общее количество пикселей или разрешение, а i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель).

Так как по заданию имеем разрешение, выраженное в пикселях на дюйм, то фактически это означает:

I = значение ppi² * N * i

Формула количества цветов:

количество цветов = 2ⁱ

Посмотрим, что из формулы нам уже дано до экономного варианта и при экономном варианте:

Неэкономный вариант:
I = 5 Мбайт = 5 * 2²³ бит, 
N - ?, 
i - ?
300 ppi

Экономный вариант:
I = 512 Кбайт = 2⁹ * 2¹³ бит = 2²² бит, 
N - ?, 
i = 4 бит (2⁴ = 16)
150 ppi

Так как в экономном режиме нам известны все составляющие формулы, кроме разрешения (N), то найдем разрешение:

N = I / (i * 150*150 ppi)
N = 2²² / (4 * 22500)

Подставим все известные значения, включая найденное N, в формулу для неэкономного режима:

I = N * 300*300 ppi * i
5 * 2²³ = (2²² * 300 * 300 * i) / (22500 * 4);

Выразим i и вычислим его значение:

i = (5 * 2²³ * 22500 * 4) / (2²² * 300 * 300) = 9000 / 900 = 10 бит

По формуле нахождения количества цветов в палитре имеем:

2¹⁰ = 1024

Результат: 1024

Тема: Кодирование звука

7_7:

На студии при четырехканальной (квадро) звукозаписи с 32-битным разрешением за 30 секунд был записан звуковой файл. Сжатие данных не производилось. Известно, что размер файла оказался 7500 Кбайт.

С какой частотой дискретизации (в кГц) велась запись? В качестве ответа укажите только число, единицы измерения указывать не нужно.

Типовые задания для тренировки

✍ Решение:

По формуле объема звукового файла получим:

I = β * t * ƒ * S

Из задания имеем:

I= 7500 Кбайт
β= 32 бита
t= 30 секунд
S= 4 канала

ƒ — частота дискретизации — неизвестна, выразим ее из формулы:

[ ƒ = frac {I}{S*B*t} = frac {7500 * 2^{10} * 2^3 бит}{2^7 * 30}Гц = frac { 750 * 2^6}{1000}КГц = 2^4 = 16 ]

2⁴ = 16 КГц

Результат: 16

Для более детального разбора предлагаем посмотреть видео решения данного 7 задания ЕГЭ по информатике:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_9:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.

Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Для решения понадобится формула нахождения скорости передачи данных формулы:

V = I/t

Вспомним также формулу объема звукового файла:

I = β * ƒ * t * s

где:
I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — кол-во каналов (если не указывается, то моно)

Выпишем отдельно, все данные, касающиеся города Б (про А практически ничего не известно):

город Б: 
β - в 2 раза выше
ƒ - в 3 раза меньше
t - 15 секунд, 
пропускная способность (скорость V) - в 4 раза выше

Исходя из предыдущего пункта, для города А получаем обратные значения:

город А: 
β_Б / 2
ƒ_Б * 3
I_Б / 2
V_Б / 4
t_Б / 2, t_Б * 3, t_Б * 4  -  ?

Дадим объяснения полученным данным:
так как глубина кодирования (β) для города Б выше в 2 раза, то для города А она будет ниже в 2 раза, соответственно, и t уменьшится в 2 раза:

t = t/2

так как частота дискретизации (ƒ) для города Б меньше в 3 раза, то для города А она будет выше в 3 раза; I и t изменяются пропорционально, значит, при увеличении частоты дискретизации увеличится не только объем, но и время:

t = t * 3

скорость (V)(пропускная способность) для города Б выше в 4 раза, значит, для города А она будет ниже в 4 раза; раз скорость ниже, то время выше в 4 раза (t и V — обратно пропорциональная зависимость из формулы V = I/t):

t = t * 4

Таким образом, с учетом всех показателей, время для города А меняется так:

[ t_А = frac {15}{2} * 3 * 4 ]

90 секунд

Результат: 90

Подробное решение смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7.10:

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 30 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.

Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S -количество каналов

Выпишем отдельно, все данные, касающиеся первого состояния файла, затем второго состояния — после преобразования:

1 состояние:
S = 2 канала
I = 30 Мбайт

2 состояние:
S = 1 канал
β = в 2 раза выше
ƒ = в 1,5 раза ниже
I = ?

Так как изначально было 2 канала связи (S), а стал использоваться один канал связи, то файл уменьшился в 2 раза:

I = I / 2

Глубина кодирования (β) увеличилась в 2 раза, то и объем (I) увеличится в 2 раза (пропорциональная зависимость):

I = I * 2

Частота дискретизации (ƒ) уменьшилась в 1,5 раза, значит, объем (I) тоже уменьшится в 1,5 раза:

I = I / 1,5

Рассмотрим все изменения объема преобразованного файла:

I = 30 Мбайт / 2 * 2 / 1,5 = 20 Мбайт

Результат: 20

Смотрите видеоразбор данной задачи:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звуковых файлов:

ЕГЭ по информатике задание 7_11:

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 100 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 4 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 15 секунд.

✍ Решение:

Вспомним формулу объема звукового файла:

I = β * ƒ * t * S

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время

Выпишем отдельно, все данные, касающиеся файла, переданного в город А, затем преобразованного файла, переданного в город Б:

А:
t = 100 c.

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.

✎ 1 способ решения:

Скорость передачи данных (пропускная способность) зависит от времени передачи файла: чем больше время, тем ниже скорость. Т.е. во сколько раз увеличится время передачи, во столько раз уменьшится скорость и наоборот.
Из предыдущего пункта видим, что если мы вычислим, во сколько раз уменьшится или увеличится время передачи файла в город Б (по сравнению с городом А), то мы поймем, во сколько раз увеличится или уменьшится скорость передачи данных в город Б (обратная зависимость).
Соответственно, представим, что преобразованный файл передается в город А. Объем файла изменился в 3/4 раза (глубина кодирования (β) в 3 раза выше, частота дискретизации (ƒ) в 4 раза ниже). Объем и время изменяются пропорционально. Значит и время изменится в 3/4 раза:

 t_{A для преобразов.} = 100 секунд * 3 / 4 = 75 секунд

Т.е. преобразованный файл передавался бы в город А 75 секунд, а в город Б 15 секунд. Вычислим, во сколько раз снизилось время передачи:

75 / 15 = 5

Раз время передачи в город Б снизилось в 5 раз, соответственно, скорость увеличилась в 5 раз.

Ответ: 5

✎ 2 способ решения:

Выпишем отдельно все данные, касающиеся файла, переданного в город А:
```
А:
t_А = 100 c.
V_А = I / 100
```
Поскольку увеличение или уменьшение во сколько-то раз разрешения и частоты дискретизации приводит к соответствующему увеличению или уменьшению объема файла (пропорциональная зависимость), то запишем известные данные для преобразованного файла, переданного в город Б:

Б:
β = в 3 раза выше
ƒ = в 4 раза ниже
t = 15 c.
I_Б = (3 / 4) * I
V_Б = ((3 / 4) * I) / 15

Теперь найдем соотношение V_Б к V_А:

[ frac {V_Б}{V_А} = frac {3/_4 * I}{15} * frac {100}{I} = frac {3/_4 * 100}{15} = frac {15}{3} = 5 ]

(((3/4) * I) / 15) * (100 / I)= (3/4 * 100) / 15 = 15/3 = 5

Результат: 5

Подробный видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

ЕГЭ по информатике задание 7_12:

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

✍ Решение:

Вспомним формулу объема звукового файла:

I — объем
β — глубина кодирования
ƒ — частота дискретизации
t — время
S — количество каналов

Для простоты расчетов пока не будем брать во внимание количество каналов. Рассмотрим, какие данные у нас есть, и какие из них необходимо перевести в другие единицы измерения:

β = 32 бита
ƒ = 32кГц = 32000Гц
t = 2 мин = 120 с

Подставим данные в формулу; учтем, что результат необходимо получить в Мбайтах, соответственно, произведение будем делить на 2²³ (2³ (байт) * 2¹⁰ (Кбайт) * 2¹⁰(Мбайт)):

(32 * 32000 * 120) / 2²³ = 
=( 2⁵ * 2⁷ * 250 * 120) / 2²³ = 
= (250*120) / 2¹¹ = 
= 30000 / 2¹¹ = 
= (2⁴ * 1875) / 2¹¹ =
= 1875 / 128 ~ 14,6

Полученный результат значения объема умножим на 4 с учетом количества каналов связи:

 14,6 * 4 = 58,5

Ближайшее число, кратное 10 — это 60.

Результат: 60

Смотрите подробное решение:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_19: Государственный выпускной экзамен ГВЭ 2018 (информатика ГВЭ ФИПИ, задание 7):

Производится двухканальная (стерео) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду, для записи каждого значения используется 32 бит. Запись длится 5 минут, её результаты записываются в файл, сжатие данных не производится.

Какая из приведённых ниже величин наиболее близка к размеру полученного файла?

1) 14 Мбайт
2) 28 Мбайт
3) 55 Мбайт
4) 110 Мбайт

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения:

I = 48000 * 32 * 300 * 2

Поскольку значения большие, необходимо числа 48000 и 300 выразить в степенях двойки:

48000 | 2
24000 | 2
12000 | 2
 6000 | 2     = 375 * 2⁷
 3000 | 2
 1500 | 2
  750 | 2 
  375 | 2 - уже не делится
 187,5

300 | 2     = 75 * 2²
150 | 2
 75 | 2 - уже не делится 
37,5

Получим:

I = 375 * 75 * 2¹⁵

В предложенных вариантах ответа видим, что результат везде в Мбайт. Значит, необходимо разделить полученный нами результат на 2²³ (2³ * 2¹⁰ * 2¹⁰):

I = 375 * 75 * 2¹⁵ / 2²³ = 28125 / 2⁸

Найдем приближенное к числу 28125 значение в степени двойки:

Получаем:

2¹⁰ * 2⁵ = 2¹⁵ = 32768
2¹⁰ * 2⁴ = 2¹⁴ = 16384

Число 28125 лежит между этими значениями, значит берем их:

2¹⁵ / 2⁸ = 2⁷ = 128
2¹⁴ / 2⁸ = 2⁶ = 64

Выбираем ответ, значение в котором находится между двумя этими числами: вариант 4 (110 Мбайт)

Результат: 4

Подробное решение ГВЭ задания 7 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование звука:

7_20:

Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.

✍ Решение:

По формуле объема звукового файла имеем:

I — объем
β — глубина кодирования = 32 бита
ƒ — частота дискретизации = 48000 Гц
t — время = 5 мин = 300 с
S — количество каналов = 2

Подставим в формулу имеющиеся значения. Для удобства будем использовать степени двойки:

ƒ = 4 кГЦ = 4 * 1000 Гц ~ 2² * 2¹⁰
B = 64 бит = 2⁶ / 2²³ Мбайт
t = 1 мин = 60 c = 15 * 2² c
S = 2

Подставим значения в формулу объема звукового файла:

I = 2⁶ * 2² * 2¹⁰ * 15 * 2² * 2¹ / 2²³ = 15/4 ~ 3,75

Ближайшее целое, кратное двум — это число 4

Результат: 4

Видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Кодирование видео

7_22:

Камера снимает видео без звука с частотой 120 кадров в секунду, при этом изображения используют палитру, содержащую 2²⁴ = 16 777 216 цветов. При записи файла на сервер полученное видео преобразуют так, что частота кадров уменьшается до 20, а изображения преобразуют в формат, использующий палитру из 256 цветов. Другие преобразования и иные методы сжатия не используются. 10 секунд преобразованного видео в среднем занимают 512 Кбайт.

Сколько Мбайт в среднем занимает 1 минута исходного видео?

Типовые задания для тренировки

✍ Решение:

Посмотрим, как изменялись параметры файла до преобразования и после:

ДО:
ƒ = 120, 
i = 24 бит

ПОСЛЕ:
ƒ = 20, 
i = 8 бит (2⁸ = 256)
t = 10 секунд
I = 512 Кбайт = 2⁹ Кбайт

Поскольку после преобразования количество кадров в секунду уменьшилось в 6 раз (120 / 20 = 6), а количество бит на пиксель уменьшилось в 3 раза (24 / 8 = 3), то и объем уменьшился в целом в 18 раз (6 * 3 = 18).
Вычислим объем файла, передаваемого за 10 секунд, до его преобразования:

за 10 секунд: I * 18 = 2⁹ * 18 Кбайт = (2⁹ * 18) . 2¹⁰ Мбайт = 9 Мбайт

Чтобы получить объем, переданный за 1 минуту, необходимо полученное значение умножить на 6:

за 1 мин: 9 * 6 = 54 Мбайт

Результат: 54

Тема: Скорость передачи данных

ЕГЭ по информатике задание 7_13:

Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту.

Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Что нам известно из формулы (для удобства решения будем использовать степени двойки):

V = 128000 бит/с = 2¹⁰ * 125 бит/с
t = 1 мин = 60 с = 2² * 15 с
1 символ кодируется 16-ю битами
всего символов - ?

Если мы найдем, сколько бит необходимо для всего текста, тогда, зная что на 1 символ приходится 16 бит, мы сможем найти сколько всего символов в тексте. Таким образом, найдем объем:

Q = 2¹⁰ * 125 * 2² * 15 = 
= 2¹² * 1875 бит на все символы

Когда мы знаем, что на 1 символ необходимо 16 бит, а на все символы 2¹² * 1875 бит, то можем найти общее количество символов:

кол-во символов = 2¹² * 1875 / 16 = 2¹² * 1875 / 2⁴ = 
= 2⁸ * 1875 = 480000

Результат: 480000

Разбор 7 задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_14:

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 2¹⁷ бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 2¹⁶ бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных.

Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Определим, что нам известно:

Вася: V = 2¹⁷ бит/с
Петя: V = 2¹⁶ бит/с
Общий объем Q = 8 Мбайт

Для начала переведем объем в биты:

Q = 8Мбайт = 8 * 2²³ бит = 2³ * 2²³ = 2²⁶ бит

Также известно, что сначала 1024 Кбайта будут передаваться по скоростному каналу Васи со скоростью 2¹⁷ бит/с (примем за t1), а затем все 8 Мбайт будут передаваться по низкоскоростному каналу (примем за t2). Найдем время по двум промежуткам:

t1 = 1024 Кбайт / 2¹⁷ = 2¹⁰ * 2¹³ бит / 2¹⁷ = 
= 2¹⁰ / 2⁴ = 64 с

t2 = 2²⁶ / 2¹⁶ = 2¹⁰ = 1024 c

Найдем общее время:

t = t1 + t2 = 64 + 1024 = 1088

Результат: 1088

Подробный разбор смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_15:

Сколько секунд потребуется модему, передающему сообщения со скоростью 32000 бит/с, чтобы передать 16-цветное растровое изображение размером 800 x 600 пикселей, при условии, что в каждом байте закодировано максимально возможное число пикселей?

Типовые задания для тренировки

✍ Решение:

Вспомним формулу скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

Отсюда получаем формулу для времени:
Для нахождения времени вычислим объем сообщения по формуле:

N — общее количество пикселей или разрешение, 
i — глубина кодирования цвета (количество бит, выделенное на 1 пиксель)

Q = 4 * 480000

Теперь найдем время:

t = 4 * 480000 / 32000 = 60 секунд

Результат: 60

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_16:

Каково время (в минутах) передачи полного объема данных по каналу связи, если известно, что передано 9000 Мбайт данных, причем треть времени передача шла со скоростью 60 Мбит в секунду, а остальное время – со скоростью 90 Мбит в секунду?

✍ Решение:

Формула скорости передачи данных:

* Вместо Q можно использовать обозначение I (для объема файла)

V - скорость
Q - объем
t - время

При 1/3 t скорость (V) равна 60 Мбит/c
При 2/3 t скорость(V) равна 90 Мбит/c
Объем переданных данных выразим в Мбитах:

1 Мбайт = 8 Мбит

 Q = 9000 Мбайт * 8 = 72000 Мбит

Из формулы выразим объем:
Так как общий объем данных у нас известен, получим уравнение:

(60 * 1/3t)  + (90 * 2/3t) = 72000
вынесем t за скобки, получим уравнение:
t * (20 + 60) = 72000
выразим t:
t = 72000 / 80 = 900 с = 15 мин

Результат: 15

Решение задания можно посмотреть и на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7.17:

Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2¹⁸ бит в секунду,
объем сжатого архиватором документа равен 20% от исходного,
время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

Типовые задания для тренировки

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 5 Мбайт * 0.2 = 1 Мбайт = 1 * 2²³ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Получим t с учетом времени на сжатие и распаковку:

t = Q / V + 7 + 1 = 8 + 2²³ / 2¹⁸ = 8 + 2⁵ = 40 c

Рассмотрим способ Б:

Для этого способа можно сразу найти время (по формуле):

t = Q / V = 5 * 2²³ / 2¹⁸ = 5 * 2⁵ = 5 * 32 = 160 c

Получаем, что способ А быстрее; вычислим насколько быстрее:

160 с - 40 с = 120 с

Результат: А120

Решение также можно посмотреть в видеоуроке:

📹 YouTube здесьздесь

Тема: Скорость передачи информации:

ЕГЭ по информатике задание 7_18:

Документ объёмом 20 Мбайт можно передать с одного компьютера на другой двумя способами:
А) сжать архиватором-1, передать архив по каналу связи, распаковать;
Б) сжать архиватором-2, передать архив по каналу связи, распаковать;

Какой способ быстрее и насколько, если

средняя скорость передачи данных по каналу связи составляет 2²⁰ бит в секунду,
объём документа, сжатого архиватором-1, равен 20% от исходного,
на сжатие документа архиватором-1 требуется 15 секунд, на распаковку — 2 секунды,
объём документа, сжатого архиватором-2, равен 10% от исходного,
на сжатие документа архиватором-2 требуется 20 секунд, на распаковку — 4 секунды?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.

✍ Решение:

Рассмотрим способ А:

Сначала найдем объем документа, зная, что он составляет 20% от исходного:

Q (объем) = 20 Мбайт * 0.2  = 4 Мбайт = 2² * 2²³ бит  = 2²⁵ бит

Формула времени передачи данных:

V - скорость
Q - объем
t - время

Найдем время для способа А с учетом времени на сжатие и распаковку:

t_A = 2²⁵ / 2²⁰ + 17 с = 2⁵ + 17 = 49 с

Рассмотрим способ Б:

Сначала найдем объем документа, зная, что он составляет 10% от исходного:

Q (объем) = 20 Мбайт * 0.1  = 2 Мбайт = 2¹ * 2²³ бит  = 2²⁴ бит

Найдем общее время с учетом потраченного времени на сжатие и распаковку:

t_Б = 2²⁴ / 2²⁰ + 24 с = 2⁴ + 24 = 40 с

Получили, что второй способ (Б) быстрее. Выясним насколько быстрее:

49 - 40 = 9 с

Результат: Б9

Тема: Скорость передачи информации:

Решение 7 ЕГЭ по информатике, задание 7_19:

Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за 1 минуту и 40 секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит 30 секунд. При этом на упаковку и распаковку данных всего ушло 10 секунд. Размер исходного документа 45 Мбайт.

Чему равен размер упакованного документа (в Мбайт)?

✍ Решение:

Выпишем исходные данные для двух состояний документа, используя неизвестное x для искомого параметра — объема:

неупакованный:

I₁ = 45 Мбайт
t₁ = 100 секунд (60 секунд + 40 секунд = 100)

упакованный:

I₂ = x Мбайт
t₂ = 20 секунд (30 секунд - 10 секунд = 20)

Получим систему уравнений:

45 = 100
х = 20

Выразим x, т.е. объем упакованного документа:

х = (45 * 20) / 100 = 9 Мбайт

Результат: 9

Источник

Всего: 92 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Для проведения эксперимента записывается звуковой фрагмент в формате квадро (четырёхканальная запись) с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записываются в файл, сжатие данных не производится; дополнительно в файл записывается служебная информация, необходимая для эксперимента, размер полученного файла 97 Мбайт. Затем производится повторная запись этого же фрагмента в формате моно (одноканальная запись) с частотой дискретизации 16 кГц и 16-битным разрешением. Результаты тоже записываются в файл без сжатия и со служебной информацией, размер полученного файла 7 Мбайт. Объём служебной информации в обоих случаях одинаков. Укажите этот объём в мегабайтах. В ответе укажите только число (количество Мбайт), единицу измерения указывать не надо.

Для проведения эксперимента записывается звуковой фрагмент в формате стерео (двухканальная запись) с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записываются в файл, сжатие данных не производится; дополнительно в файл записывается служебная информация, необходимая для эксперимента, размер полученного файла 42 Мбайт. Затем производится повторная запись этого же фрагмента в формате моно (одноканальная запись) с частотой дискретизации 16 кГц и 16-битным разрешением. Результаты тоже записываются в файл без сжатия и со служебной информацией, размер полученного файла 7 Мбайт. Объём служебной информации в обоих случаях одинаков. Укажите этот объём в мегабайтах. В ответе укажите только число (количество Мбайт), единицу измерения указывать не надо.

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 48 кГц и 24-битным разрешением. В результате был получен файл размером 5625 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное 5.

Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 3 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное пяти.

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 3 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное пяти.

Производится четырёхканальная звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись производилась в течение 3 минут. Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

Источник: ЕГЭ 16.06.2016 по информатике. Основная волна.

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 64-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла в мегабайтах. В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10303

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 64-битным разрешением. Запись длится 3 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла ( в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10304

Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла (в мегабайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10203

Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записи записываются в файл, сжатие данных не производится; размер полученного файла  — 90 Мбайт. Определите приблизительно время записи ( в минутах). В качестве ответа укажите ближайшее ко времени записи целое число.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10103

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записи записываются в файл, сжатие данных не производится; размер полученного файла  — 90 Мбайт. Определите приблизительно время записи (в минутах). В качестве ответа укажите ближайшее к времени записи целое число.

Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10104

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 24-битным разрешением. В результате был получен файл размером 48 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее к времени записи целое число.

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 16-битным разрешением. В результате был получен файл размером 32 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее к времени записи целое число.

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 30 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.

Источник: ЕГЭ 05.05.2015. Досрочная волна.

Производилась четырехканальная (квадро) звукозапись с частотой дискретизации 24 кГц и 16-битным разрешением. В результате был получен файл размером 1800 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько минут производилась запись.

В качестве ответа укажите ближайшее к времени записи целое число минут.

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 32-битным разрешением. В результате был получен файл размером 60 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись?

В качестве ответа укажите ближайшее к времени записи целое число.

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 16-битным разрешением. В результате был получен файл размером 60 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись?

В качестве ответа укажите ближайшее к времени записи целое число.

Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записи записываются в файл, сжатие данных не производится; размер полученного файла  — 45 Мбайт. Определите приблизительно время записи (в минутах). В качестве ответа укажите ближайшее к времени записи целое число.

Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 2 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла в Мбайт. В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

Всего: 92 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Тема 7.

Передача данных. Размеры файлов.

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

передача данных. размеры файлов.

7.01Изображение

7.02Звукозапись

7.03Видеофайлы

7.04Текстовые файлы

7.05Передача по каналу связи

7.06Сравнение двух способов передачи данных

7.07Смешанное

7.08Измерение информации

Решаем задачи

Показать ответ и решение

Размер исходного файла равен , тогда размер нового файла равен
Кбайт.

Показать ответ и решение

Размер отправленного файла равен Кбайт.

Анатолий решил поздравить Тамару Петровну с юбилеем. Для этого он записал в формате стерео 4-ёх минутное аудио
поздравление с частотой дискретизации 32 кГц при глубине кодирования 16 бит.

Затем, полученный файл был сжат в 2 раза и отправлен Тамаре Петровне по электронной почте.

Укажите размер отправленного файла в Кбайтах. В ответе укажите только целое число, единицу измерения писать не
нужно.

Показать ответ и решение

Напишем основную формулу для объема музыкального файла , где — частота дискретизации, —
разрешение (глубина кодирования), — количество каналов, — время звучания.

сек

Найдем объем поделим на 2 и переведем в Кбайт.

32000⋅16⋅2-⋅240
I = 2⋅213 = 15000

Показать ответ и решение

Выразим время: I
t =------
f ⋅k⋅r

23
--60⋅2-----
t = 64000 ⋅4⋅32 = 61,44 сек.

В минутах ответ равен .

Анатолий заядлый меломан, но у него очень плохая память. Поэтому, когда он записывает аудио на флешку, он
прикрепляет к ней бумажку со всеми параметрами записи.

Но вот беда: у композиции “Белый ветер” отсутствует время записи. Известно лишь, что производилась одноканальная
цифровая звукозапись. Значение сигнала фиксировалось 32000 раз в секунду, а для записи каждого значения
использовалось 12 бит. Весь файл занимает на флешке 4800000 Байт.

Помогите Анатолию найти время записи в секундах. В ответе укажите только целое число, единицу измерение писать не
нужно.

Показать ответ и решение

сек.

64000⋅32⋅4 ⋅240
I = -------23------= 234,375
2

Ближайшее целое число 230 кратное 10

Показать ответ и решение

Найдём размер аудиозаписи:
Округлим до целого и запишем ответ .

Алексей Рамилевич открыл своё антикафе и хочет записывать музыку для проигрывания в своём антикафе в формате
стерео, с частотой дискретизации 12 кГц, использовав 16-битное разрешение. Но у него есть только флешка со свободным
местом в 2,15 Гбит.

Какое максимальное целое количество минут может длиться запись? В ответе укажите целое число.

Показать ответ и решение

Чтобы найти максимальную длительность записи решим уравнение:

Переведём в минуты: .

Олег и Валентин подключились к разным каналам связи на 223 бит/секунду и на 225 бит в секунду соответственно. Олег
имеет возможность выйти в Интернет, а канал связи Валентина позволяет обмениваться данными только с Олегом
(подключен к нему напрямую).

Валентин хочет послушать аудиокнигу, которая весит 480 Мбайт, поэтому попросил Олега помочь ему: Олег будет
скачивать аудиокнигу и одновременно ретранслировать её Валентину. Валентин сможет начать слушать аудиокнигу только
после завершения загрузки.

Через сколько минут Валентин сможет начать слушать аудиокнигу? В ответе укажите только целое
число.

Но вот беда: у композиции «Белый ветер» отсутствует время записи. Известно лишь, что производилась одноканальная
цифровая звукозапись. Значение сигнала фиксировалось 000 раз в секунду, а для записи каждого значения
использовалось бит. Весь файл занимает на флешке 800 000 Байт.

Анатолий решил поздравить Тамару Петровну с юбилеем. Для этого он записал в формате стерео -ёх минутное аудио
поздравление с частотой дискретизации кГц при глубине кодирования бит.

Затем полученный файл был сжат в раза и отправлен Тамаре Петровне по электронной почте.

Показать ответ и решение

сек

Найдем объем, поделим на и переведем в Кбайт.

32000⋅16⋅2-⋅240
I = 2⋅213 = 15000

Показать ответ и решение

Выразим глубину кодирования: I
r =------
f ⋅k⋅t

23
--160⋅2-----
r = 80000⋅4⋅205 = 20

Ответ не может быть , так как нам бы не хватило выделенной памяти

Показать ответ и решение

Выразим время: I
t =------
f ⋅k⋅r

23
--60⋅2-----
t = 64000 ⋅4⋅32 = 61,44 сек.

Ответ в минутах равен

Показать ответ и решение

Напишем эту же формулу, но после изменений

Показать ответ и решение

Напишем эту же формулу, но после изменений

Максим Олегович спел песню ко дню победы и записал её в аудиофайл. Известно, что запись
производилась минуты секунд в стерео формате с частотой дискретизации кГц и количеством
уровней квантования 256. Сжатие данных не производилось.

Укажите размер отправленного файла в Мбайт. В ответе укажите только значение, единицу
измерение писать не нужно.

Показать ответ и решение

Для хранения информации о звуке длительностью секунд, закодированном с частотой дискретизации
Гц и глубиной кодирования бит с каналами записи требуется бит
памяти.

(Гц) — частота дискретизации определяет количество отсчетов, запоминаемых за
секунду.

(бит) — глубина кодирования — это количество бит, которые выделяются на один отсчет.

Итак, давайте выпишем что нам дано:

t = 128 с;

k = 2 канала;

Для 8
256 = 2 уровней квантования необходимо B = 8 бит;

Гц.

Все данные у нас есть, подставим в формулу:

Мбайт.

Макар открыл свой магазин и хочет записать музыку для проигрывания в своём магазине в формате
стерео, частотой дискретизации 44,1 кГц использовав -битное разрешение. Но у него в
распоряжении есть только флешка на 2, 55 Гбайт.

Какое максимальное целое количество минут может длиться запись? В ответе укажите только целое
число.

Показать ответ и решение

f(Гц) — частота дискретизации определяет количество отсчетов, запоминаемых за
секунду.

— глубина кодирования — это количество бит, которые выделяются на один отсчет.

Итак, давайте выпишем что нам дано:

k = 2 канала;

B = 24 бит;

Гц.

бит.

Все данные у нас есть, подставим:

33
t ⋅ 2 ⋅ 44100 ⋅ 24 ≤ 2,55 ⋅ 2 ⇒ t ∼ 10347 с. ∼ 172 м.

Михаил открыл свой магазин и хочет записать музыку для проигрывания в своём магазине в формате
стерео, частотой дискретизации кГц использовав 8-битное разрешение. Но у него в распоряжении
есть только флешка на 500 Мбайт.

Какое максимальное целое количество минут может длиться запись? В ответе укажите только целое
число.

Показать ответ и решение

(Гц) — частота дискретизации определяет количество отсчетов, запоминаемых за
секунду.

(бит) — глубина кодирования — это количество бит, которые выделяются на один отсчет.

Итак, давайте выпишем что нам дано:

с.

k = 2 канала;

B = 8 бит;

Гц.

бит.

Все данные у нас есть, подставим:

23
t ⋅ 2 ⋅ 32000 ⋅ 8 ≤ 500 ⋅ 2 ⇒ t = 8192 с. ∼ 136 м.

Рэп-исполнитель заказал у битмейкера бит. Битмейкер всю ночь писал бит, но из-за усталости записал
музыкальный фрагмент с неправильным темпом и разрешением. Он записал его с темпом равным
240BP M и -битным разрешением без использования сжатия данных. Размер файла составил 1,8
МБайт.

Утром битмейкер обнаружил ошибку и перезаписал данный фрагмент с -битным разрешением и
уменьшил темп до Сжатие данных не производилось.

Укажите размер конечной композиции, которую утром перезаписал композитор, в Мбайтах. В ответе
укажите только значение, единицу измерение писать не нужно.

Источник

1. Общие сведения

2. Пример задания

3. Советы учителям и ученикам

4. Задачи для самостоятельного решения

5. Дополнение. Некоторые сведения о цифровой звукозаписи.

6. Решения задач с сайта ege.yandex.ru

7. История

1. Общие сведения

Сложность: базовая.

Примерное время решения (для тех, кто будет выполнять часть 2): 2 минуты

Тема: Создание и обработка графической и мультимедийной информации

Подтема: Цифровая звукозапись

Что проверяется: Умение оценивать количественные характеристики процесса записи звука.

Краткие теоретические сведения: Поскольку данный тип задания является новым в КИМ ЕГЭ, приведем (пока без обоснования, обоснование ниже) математическую модель процесса звукозаписи:

N = k F * L T (1)

где

• N – размер файла (в битах) , содержащего запись звука;
• k — количество каналов записи (например, 1 – моно, 2 – стерео, 4 – квадро и т.д.);
• F – частота дискретизации (в герцах), т.е. количество значений амплитуды звука фиксируемых за одну секунду;
• L – разрешение, т.е. число бит, используемых для хранения каждого измеренного значения;
• T – продолжительность звукового фрагмента (в секундах).

Как может выглядеть задание? Например, так: Заданы значения всех требуемых параметров процесса звукозаписи, кроме одного. Требуется оценить значение оставшегося параметра, например, размер файла или продолжительность звукового фрагмента.

Пример условия:

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

Варианты ответов:

1) 0,2 Мбайт

2) 2 Мбайт

3) 3 Мбайт

4) 4 Мбайт

2. Пример задания

2.1. Условие задачи.

Задача 2012-А8-1.

1) 0,2 Мбайт 2) 2 Мбайт 3) 3 Мбайт 4) 4 Мбайт

2.2. Решение.

Приводим исходные данные к размерности биты-секунды-герцы и проводим расчеты по формуле (1):

Дано:

k = 1, т.к. одноканальная (моно) звукозапись;

F = 16 кГц = 16 000 Гц;

L = 24;

T = 1 мин = 60 с.

Найти N

Подставляем значение известных параметров в формулу (1)

N = 1*16000*24*60 =(16*1000)* (8*3) * (4*15)=

= 2⁴*(2³*125)*(2³*3)* )*(2²* 15) = 2¹²*5625 (бит)=

= 2¹²*5625 бит = (2¹²*5625)/2³ байт = 2⁹*5625 байт =

= (2⁹*5625)/ 2²⁰Мбайт = 5625/2¹¹Мбайт = 5625/2048 Мбайт.

Число 5625/2048 находится между числами 2 и 3. При этом оно ближе к 3, чем к 2, т.к. 3 * 2048 – 5625 < 1000; 5625 — 2 * 2048 > 1000.

Правильный вариант ответа: №3 (3 Мбайт)

Замечание. Другая идея решения приведена в п.3.3

3. Советы учителям и ученикам

3.1 Какие знания/умения/навыки нужны ученику, чтобы решить эту задачу

1) Не следует «зазубривать» формулу (1). Ученик, представляющий суть процесса цифровой звукозаписи, должен быть способен самостоятельно её сформулировать.

2) Необходимо умение записывать значения параметров в требуемой размерности, а также элементарные арифметические навыки, в т.ч. оперирование со степенями двойки.

3.2. Рекомендации для учителей: как разбирать задачу с учениками

Эти рекомендации – не догма, а попытка сделать выводы из собственного опыта. Ждем комментариев и Ваших рекомендаций.

А. Сильные ученики.

1. Скорее всего, они и так решат эту задачу.

2. Можно дать задание ученикам проверить формулу (1) на практике, записывая в файл звук с микрофона. При этом следует учесть, что она справедлива только в том случае, если записываемая информация не подвергается сжатию (формат WAV (PCM) без сжатия). Если используются аудиоформаты со сжатием (WMA, MP3), то объем получившегося файла будет по понятным причинам существенно меньше расчетного. Для экспериментов с цифровой звукозаписью можно использовать свободно распространяемый аудиоредактор Audacity (http://audacity.sourceforge.net/).

3. Целесообразно подчеркнуть концептуальную общность растрового представления звука и изображения, являющихся разновидностями одного и того же процесса приближенного представления непрерывного сигнала последовательность коротких дискретных сигналов, т.е. оцифровывания на основе дискретизации. В случае растрового изображения производится двумерная дискретизизация яркости в пространстве, в случае звука – одномерная дискретизация по времени. И в том, и в другом случае повышение частоты дискретизации (количества пикселей или звуковых отсчетов) и/или увеличение количества битов для представления одного отсчета (разрядность цвета или звука) ведет к повышению качества оцифровки, при одновременном росте размера файла с цифровым представлением. Отсюда – необходимость сжатия данных.

4. Желательно упомянуть об альтернативных способах оцифровки звука – запись «партий» инструментов в MIDI-формате. Здесь уместно провести аналогию с растровым и векторным представлением изображений.

Б. Не столь сильные ученики.

1. Необходимо обеспечить усвоение соотношения (1). Рекомендуется дать задания типа «Как изменится объем файла, если время записи звучания увеличить/уменьшить в p раз? »,

«Во сколько раз можно увеличить/уменьшить продолжительность записи, если максимальный размер файла увеличить/уменьшить в p раз? », «Как изменится объем файла, если количество бит для записи одного значения увеличить/уменьшить в p раз?» и т.д.

2. Необходимо убедиться, что учащиеся свободно оперируют размерностями, знают, что в Мбайте 2²³ бит и т.д.

3. Необходимо убедиться, что учащиеся достаточно арифметически грамотны, свободно владеют устным счетом со степенями двойки (умножение, деление, выделение сомножителей, представляющих собой 2ⁿ).

4. Придумывайте свои подходы и пробуйте их.

3.3. Полезный прием.

В подобных задачах часто возникают степени двойки. Перемножать и делить степени проще, чем произвольные числа: умножение и деление степеней сводится к сложению и вычитанию показателей.

Заметим, что числа 1000 и 1024 отличаются менее, чем на 3%, числа 60 и 64 отличаются менее, чем на 7%. Поэтому можно поступить так. Провести вычисления, заменив 1000 на 1024 = 2¹⁰ и 60 на 64 = 2⁶, используя преимущества операций со степенями. Ближайший к полученному числу ответ и будет искомым. Можно после этого перепроверить себя, проведя точные вычисления. Но можно учесть, что общая погрешность вычислений при нашем приближении не превышает 10%. Действительно, 60*1000 = 60000; 64*1024=65536;

60000 > 0.9 * 65536 = 58982.4

Таким образом, правильный результат умножений по формуле (1) немного больше, чем 90% от полученного приближенного результата. Если учет погрешности не меняет результата – можно не сомневаться в ответе.

Пример. (ege.yandex.ru, вариант 1).

Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 30 Мбайт 2) 60 Мбайт 3) 75 Мбайт 4) 90 Мбайт

Решение. Размер записи в битах равен

2*16*1000*32*12*60

С учетом замены 1000 на 1024=2¹⁰ и 60 на 64=2⁶ получим:

2¹*2⁴*2¹⁰*2⁵*3*2²*2⁶=3*2²⁸

Как известно, 1 Мбайт = 2²⁰ байт = 2²³ бит. Поэтому 3*2²⁸ бит = 3*32 = 96 Мбайт. Уменьшив это число на 10%, получим 86.4 Мбайт. В обоих случаях ближайшей величиной является 90 Мбайт.

Правильный ответ: 4

3.4. Рекомендации для учеников: как решать подобные задачи

1. Прочитайте условие задачи. Выразите неизвестный параметр через известные. Особое внимание обратите, на размерность известных параметров. Она должна быть – биты-секунды-герцы (напомним, что 1 Гц = с^-1). При необходимости, приведите значения параметров к нужной размерности, так же как это делается в задачах по физике.

2. Проводите вычисления, стараясь выделять степени двойки.

3. Обратите внимание, что в условии требуется выбрать наиболее подходящий ответ, поэтому высокая точность вычислений до знаков после запятой не требуется. Как только стало ясно, какой из вариантов ответов наиболее близок к вычисляемому значению, вычисления следует прекратить. Если расхождение со всеми вариантами ответов очень велико (в разы или на порядок), то вычисления надо перепроверить.

Удачи!

4. Задачи для самостоятельного решения

4.1. Клоны задачи 2012-А8-1.

Ниже приведены еще четыре варианта задачи 2012-А8-1.

А) Производится одноканальная (моно) звукозапись с частотой дискретизации 32 кГц и 24-битным разрешением. Запись длится 15 секунд, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 1,5 Мбайт 2) 3 Мбайт 3) 6 Мбайт 4) 12 Мбайт

Б) Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 24-битным разрешением. Запись длится 30 секунд, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 1,5 Мбайт 2) 3 Мбайт 3) 6 Мбайт 4) 12 Мбайт

В) Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 2 Мбайт 2) 4 Мбайт 3) 8 Мбайт 4) 16 Мбайт

Г) Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 4 минуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 2 Мбайт 2) 4 Мбайт 3) 8 Мбайт 4) 16 Мбайт

Правильные ответы:

А:1; Б:3; В:3; Г:4.

4.2. Задача 2012-А8-2(обратная к предыдущей).

A) Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, размер которого не может превышать 8 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

Б) Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, размер которого не может превышать 8 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

В) Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и 8-битным разрешением. Результаты записываются в файл, размер которого не может превышать 2,5 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

Г) Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и 16-битным разрешением. Результаты записываются в файл, размер которого не может превышать 5 Мбайт, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к максимально возможной длительности записываемого звукового фрагмента?

1) 1минута 2) 30 секунд 3) 3 минуты 4) 90 секунд

Правильные ответы:

А:3; Б: 4 ; В: 1; Г:1 .

5.Дополнение. Некоторые сведения о цифровой звукозаписи.

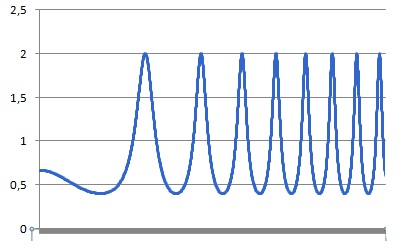
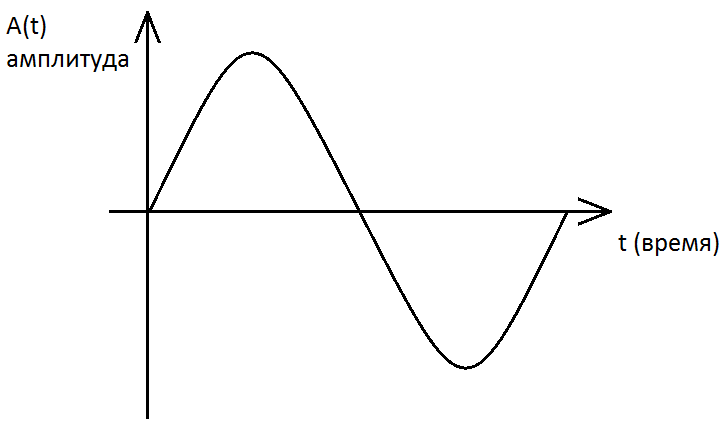
Распространение звука в воздухе можно рассматривать как распространение колебаний давления. Микрофон преобразует колебания давления в колебания электрического тока. Это аналоговый непрерывный сигнал. Звуковая плата обеспечивает дискретизацию входного сигнала от микрофона. Это делается следующим образом – непрерывный сигнал заменяется последовательностью измеренных с определенной точностью значений.

Пример:

График аналогового сигнала:

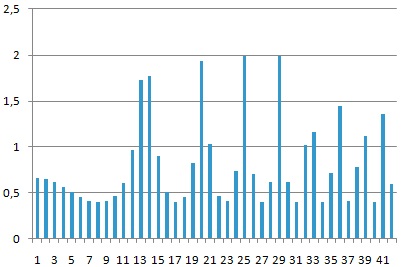
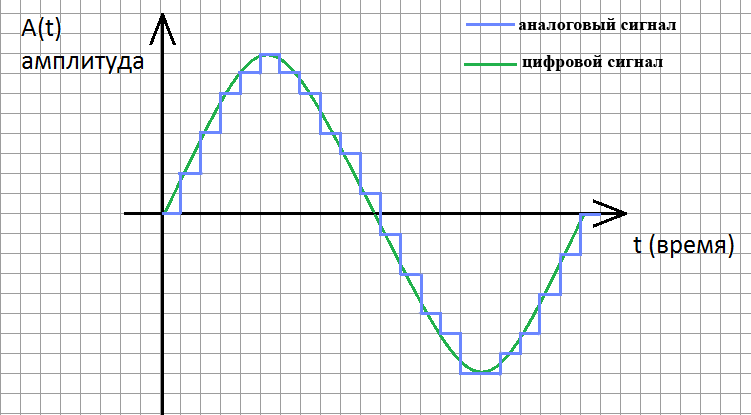
Дискретное представление этого же сигнала (41 измеренное значение):

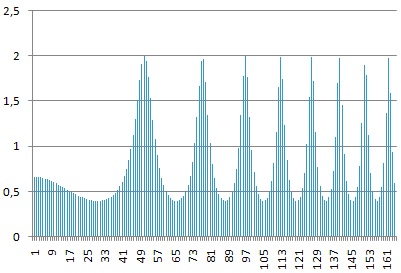
Дискретное представление этого же сигнала (161 измеренное значение, более высокая частота дискретизации):

Видно, что чем выше частота дискретизации, тем выше качество приближенного (дискретного) сигнала. Кроме частоты дискретизации, на качество оцифрованного сигнала влияет количество двоичных разрядов, отводимых для записи каждого значения сигнала. Чем больше бит отводится под каждое значение, тем более точно можно оцифровать сигнал.

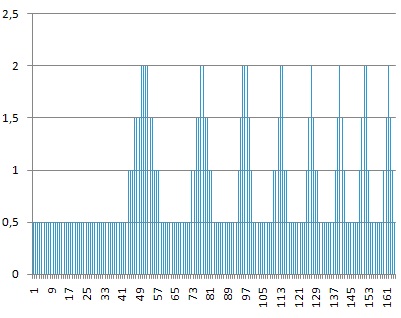
Пример 2-х битного представления этого же сигнала (двумя разрядами можно пронумеровать только 4 возможных уровня величины сигнала):

Теперь можно выписать зависимость для размера файла с оцифрованным звуком

размер_файла = (количество_значений,_фиксируемых_за_1_секунду)*

*( количество_двоичных_разрядов_для_записи_одного_значения )*

*(число_секунд_записи).

Учитывая возможность одновременной записи звука с нескольких микрофонов (стерео-, квадро- запись и т.д.), что делается для усиления реалистичности при воспроизведении, получаем формулу (1).

При воспроизведении звука цифровые значения преобразуются в аналоговые. Электрические колебания, передаваемые на динамики, преобразуются ими снова в колебания давления воздуха.

Источник

Автор материалов — Лада Борисовна Есакова.

При оцифровке звука в памяти запоминаются только отдельные значения сигнала. Чем чаще записывается сигнал, тем лучше качество записи.

Частота дискретизации f – это количество раз в секунду, которое происходит преобразование аналогового звукового сигнала в цифровой. Измеряется в Герцах (Гц).

Глубина кодирования (а также, разрешение) – это количество бит, выделяемое на одно преобразование сигнала. Измеряется в битах (Бит).

Возможна запись нескольких каналов: одного (моно), двух (стерео), четырех (квадро).

Обозначим частоту дискретизации – f (Гц), глубину кодирования – B(бит), количество каналов – k, время записи – t(Сек).

Количество уровней дискретизации d можно рассчитать по формуле: d = 2^B.

Тогда объем записанного файла V(бит) = f * B * k * t.

Или, если нам дано количество уровней дискретизации,

V(бит) = f * log₂d * k * t.

Единицы измерения объемов информации:

1 б (байт) = 8 бит

1 Кб (килобайт) = 2¹⁰ б

1 Мб (мегабайт) = 2²⁰ б

1 Гб (гигабайт) = 2³⁰ б

1 Тб (терабайт) = 2⁴⁰ б

1 Пб (петабайт) = 2⁵⁰ б

При оцифровке графического изображения качество картинки зависит от количества точек и количества цветов, в которые можно раскрасить точку.

Если X – количество точек по горизонтали,

Y – количество точек по вертикали,

I – глубина цвета (количество бит, отводимых для кодирования одной точки), то количество различных цветов в палитре N = 2^I. Соответственно, I = log₂N.

Тогда объем файла, содержащего изображение, V(бит) = X * Y * I

Или, если нам дано количество цветов в палитре, V(бит) = X * Y * log₂N.

Скорость передачи информации по каналу связи (пропускная способность канала) вычисляется как количество информации в битах, переданное за 1 секунду (бит/с).

Объем переданной информации вычисляется по формуле V = q * t, где q – пропускная способность канала, а t – время передачи.

Кодирование звука

Пример 1.

Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 30 2) 45 3) 75 4) 90

Решение:

V(бит) = f(Гц)* B(бит) * k * t(Сек),

где V – размер файла, f – частота дискретизации, B – глубина кодирования, k – количество каналов, t – время.

Значит, V(Мб) = (f * B * k * t ) / 2²³

Переведем все величины в требуемые единицы измерения:

V(Мб) = (16*1000 * 32 * 2 * 12 * 60 ) / 2²³

Представим все возможные числа, как степени двойки:

V(Мб) = (2⁴ * 2³ * 125 * 2⁵ * 2 * 2² * 3 * 15 * 2²) / 2²³ = (5625 * 2¹⁷) / 2²³ = 5625 / 2⁶ =

5625 / 64 ≈ 90.

Ответ: 4

!!! Без представления чисел через степени двойки вычисления становятся намного сложнее.

!!! Частота – это физическая величина, а потому 16 кГц = 16 * 1000 Гц, а не 16 * 2¹⁰. Иногда этой разницей можно пренебречь, но на последних диагностических работах она влияла на правильность ответа.

Пример 2.

В течение трех минут производилась четырёхканальная (квадро) звукозапись с частотой дискретизации 16 КГц и 24-битным разрешением. Сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 25 Мбайт

2) 35 Мбайт

3) 45 Мбайт

4) 55 Мбайт

Решение:

V(бит) = f(Гц)* B(бит) * k * t(Сек),

где V – размер файла, f – частота дискретизации, B – глубина кодирования (или разрешение), k – количество каналов, t – время.

Значит, V(Мб) = (f * B * k * t ) / 2²³= (16 * 1000 * 24 * 4 * 3 * 60) / 2²³ = (2⁴ * 2³ * 125 * 3 * 2³ * 2² * 3 * 15 * 2²) / 2²³ = (125 * 9 * 15 * 2¹⁴) / 2²³ = 16875 / 2⁹ = 32, 96 ≈ 35

Ответ: 2

Пример 3.

Аналоговый звуковой сигнал был записан сначала с использованием 64 уровней дискретизации сигнала, а затем с использованием 4096 уровней дискретизации сигнала. Во сколько раз увеличился информационный объем оцифрованного звука?

1) 64

2) 8

3) 2

4) 12

Решение:

V(бит) = f * log₂d * k * t, где V – размер файла, f – частота дискретизации, d – количество уровней дискретизации, k – количество каналов, t – время.

V₁= f * log₂64 * k * t = f * 6 * k * t

V₂= f * log₂4096 * k * t = f * 12 * k * t

V₂ / V₁ = 2

Правильный ответ указан под номером 3.

Ответ: 3

Кодирование изображения

Пример 4.

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64×64 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

V(бит) = X * Y * log₂N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.

V (Кб) = (64 * 64 * log₂256) / 2¹³ = 2¹² * 8 / 2¹³ = 4

Ответ: 4

Пример 5.

Для хранения растрового изображения размером 64×32 пикселя отвели
1 килобайт памяти. Каково максимально возможное число цветов в палитре изображения?

Решение:

log₂N = V /( X*Y) = 2¹³ / (2⁶* 2⁵) = 4

N = 16

Ответ:16

Сравнение двух способов передачи данных

Пример 6.

Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:

А) Сжать архиватором, передать архив по каналу связи, распаковать.

Б) Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если

– средняя скорость передачи данных по каналу связи составляет 2¹⁸ бит в секунду,

– объем сжатого архиватором документа равен 80% от исходного,

– время, требуемое на сжатие документа – 35 секунд, на распаковку – 3 секунды?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.

Решение:

Способ А. Общее время складывается из времени сжатия, распаковки и передачи. Время передачи t рассчитывается по формуле t = V / q, где V — объём информации, q — скорость передачи данных.

Объем сжатого документа: 5 * 0,8 = 4 Мб =4 * 2²³ бит.

Найдём общее время: t = 35 с + 3 с + 4 * 2²³ бит / 2¹⁸ бит/с = 38 + 2⁷ с = 166 с.

Способ Б. Общее время совпадает с временем передачи: t = 5 * 2²³ бит / 2¹⁸ бит/с = 5 * 2⁵ с = 160 с.

Способ Б быстрее на 166 — 160 = 6 с.

Ответ: Б6

Определение времени передачи данных

Пример 7.

Скорость передачи данных через ADSL─соединение равна 128000 бит/c. Через данное соединение передают файл размером 625 Кбайт. Определите время передачи файла в секундах.

Решение:

Время t = V / q, где V — объем файла, q — скорость передачи данных.

t = 625 * 2¹⁰ байт / (2 ⁷ * 1000) бит/c = 625 * 2¹³ бит / (125 * 2¹⁰) бит/c = 5 * 2³ с = 40 с.

Ответ: 40

Пример 8.

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 2¹⁷ бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 2¹⁵ бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 4 Мбайта по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Решение:

Нужно определить, сколько времени будет передаваться файл объемом 4 Мбайта по каналу со скоростью передачи данных 2¹⁵ бит/с; к этому времени нужно добавить задержку файла у Васи (пока он не получит 512 Кбайт данных по каналу со скоростью 2¹⁷ бит/с).

Время скачивания данных Петей: t₁= 4*2²³ бит / 2¹⁵ бит/с = 2¹⁰ c.

Время задержки: t₂ = 512 кб / 2¹⁷ бит/с = 2^{(9 + 10 + 3) — 17} c = 2⁵ c.

Полное время: t₁ + t₂ = 2¹⁰ c + 2⁵ c = (1024 + 32) c = 1056 c.

Ответ: 1056

Пример 9.

Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 2¹⁹ бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 2²⁰ бит в секунду. Задержка в пункте Б (время между окончанием приема данных из пункта А и началом передачи в пункт В) составляет 25 секунд. Сколько времени (в секундах) прошло с момента начала передачи данных из пункта А до их полного получения в пункте В? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Решение:

Полное время складывается из времени передачи из пункта А в пункт Б (t₁), задержки в пункте Б (t2) и времени передачи из пункта Б в пункт В (t₃).

t₁= (60 * 2²³) / 2¹⁹ =60 * 16 = 960 c

t₂ = 25 c

t₃ = (60 * 2²³) / 2²⁰ =60 * 8 = 480 c

Полное время t₁ + t₂ +t₃ = 960 + 25 + 480 = 1465 c

Ответ: 1465

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №9. Кодирование звуковой и графической информации. Передача информации, Время записи звукового файла, время передачи данных, определение объема информации.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник

Седьмое задание из ЕГЭ по информатике 2022. Отличное задание, которое нужно решать!

Данное задание проверяет умение определять объём памяти, необходимый для хранения графической и звуковой информации.

Приступим к примерным вариантам из ЕГЭ по информатике.

Задача (классика, количество цветов изображения)

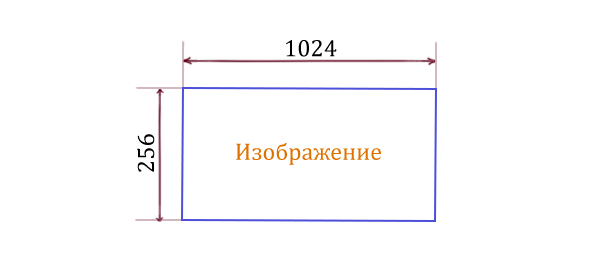
Какое максимальное количество цветов может быть в палитре неупакованного растрового изображения, имеющего размер 1024 * 256 пикселей и занимающего на диске не более 165 кб.

Решение:

1. Найдём сколько будет весить один пиксель! У нас всего 1024 * 256 пикселей. Берём максимально возможный объём картинки (165 Кб) и разделим его на количество пикселей.

Важно: Мы не пытаемся сразу вычислить, например, количество пикселей во всём изображении. А записываем сначала в виде действия 1024 * 256. Когда уже получается дробь, пытаемся сократить эту дробь по максимуму. Это позволяет экономить силы при решении седьмого задания из ЕГЭ по информатике 2022.

Нам нужно найти: сколько именно целых бит занимает один пиксель. Округляем количество бит в меньшую сторону, потому что мы не можем «перевалить» за максимальную отметку 165 Кб для всего изображения.

Применим формулу, которую нужно твёрдо знать для решения 7 задания из ЕГЭ по информатике.

Ответ: 32

Задача (Резервирование памяти)

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64 * 256 пикселей при условии, что в изображении могут использоваться 4 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

Задача обратная предыдущей. Первый вопрос на который нужно ответить: сколько весит 1 пиксель? Снова используется формула N = 2 ⁱ.

Видно, что 1 пиксель имеет объём i = 2 бита. Количество пикселей в изображении равно 64 * 256. Важно опять умножать эти два числа не сразу. Тогда объём картинки будет равен: количество пикселей (64 * 256) умножить на объём одного пикселя (2 бита).

В подобных задачах из ЕГЭ по информатике фишка в том, чтобы составить дробь и потом сократить её, тем самым вычисление делается без калькулятора и без лишних усилий.

Ответ: 4

Задача (работа со звуком)

Производится звукозапись музыкального фрагмента в формате квадро (четырёхканальная запись) с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, сжатие данных не производится; размер полученного файла 60 Мбайт. Затем производится повторная запись этого же фрагмента в формате стерео (двухканальная запись) с частотой дискретизации 64 кГц и 16-битным разрешением. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

Общая формула для решения 7-ого задания на тему звуковых файлов из ЕГЭ по информатике.

Её легко запомнить. Объём записанного файла равен произведению всех остальных параметров. Важно соблюдать единицы измерения.

Распишем формулу дискретизации для первой звукозаписи и для второй. В первом случае у нас режим квадро, значит, нужно к произведению добавить ещё 4. Во втором случае режим стерео, значит, должны поставить коэффициент 2. Т.к. производилась запись этого же фрагмента, то время в обоях случаях одинаковое.

Выражаем время из первого уравнения и подставляем во второе.

Опять удобно решать с помощью сокращение дробей.

Ответ: 80

Закрепим результат, решив ещё одну тренировочную задачу из ЕГЭ по информатике 2021.

Задача (ЕГЭ по информатике 2020, Досрочная волна)

Музыкальный фрагмент был записан в формате квадро (четырёхканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла без учёта размера заголовка файла – 12 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер в Мбайт файла, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно. Искомый объём не учитывает размера заголовка файла.

Решение:

Вначале выписываем формулу для первого файла и для второго файла. Подставляем всё, что нам известно.

Для второго звукового файла коэффициенты все переносим в одну сторону.

Выражаем из первого уравнения произведение M * i * t и подставляем его во второе уравнение.

После небольших сокращений получаем 4 Мб для второго звукового файла.

Время было для обоих файлов одинаковым, потому что было сказано, что тот же музыкальный файл перезаписали второй раз с другими параметрами.

Ответ: 4

Удачи при решении 7 задания из ЕГЭ по информатике 2022!

Источник

Формула записи звука в егэ по информатике

Обработка звуковой информации. Вариант задания №9 ЕГЭ

Определение параметров звукового файла является одним из возможных вариантов Задания №9 ЕГЭ по информатике и ИКТ.

В этом типе задачи, обычно, проверяются умения выпускников оценивать объем памяти необходимый для хранения данных или время звучания звукового файла. Для ее успешного решения необходимо знать:

Принципы кодирования звуковой информации Единицы измерения информации и связь между ними.

Рассмотрим возможные варианты задания, встречающиеся в тренировочных и досрочных вариантах КИМов по информатике и ИКТ.

Задание №9. Производится четырёхканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Запись длится 3 минуты, её результаты записываются в файл, сжатие данных не производится.

Определите приблизительно размер полученного файла в Мбайт. В качестве ответа укажите ближайшее к размеру файла целое число, кратное 10.

Представим данные в удобной для расчетов форме. Из условия задачи нам известно:

частота дискретизации ν = 32 кГц = 2 5 × 10 3 Гц = 2 5 × 10 3 с -1 глубина кодирования звука (разрешение) i = 2 5 бит время звучания файла (время записи) t = 3 мин. = 3 × 60 с = 3 × 15 × 2 2 с Поскольку запись четырехканальная, то k = 4 = 2 2

При решении данной задачи будем считать 1000 ≈ 1024 = 2 10

Рассчитаем информационный объем звукового файла
I = i × ν × t × k = 2 5 бит × 2 5 × 10 3 с -1 × 3 × 15 × 2 2 с × 2 2 = 45 ×* 2 14 × 10 3 бит ≈ 45 × 2 × 2 23 бит = 90 Мбайт

Решим задачу №9 из майской тренировочной работы по информатике и ИКТ 2016 — 2017 учебного года.

Задание №9. Производится звукозапись музыкального фрагмента в формате стерео (двухканальная запись) с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записываются в файл, сжатие данных не производится; размер полученного файла 40 Мбайт. Затем производится повторная запись этого же фрагмента в формате моно (одноканальная запись) с частотой дискретизации 16 кГц и 16-битным разрешением. Сжатие данных не производилось.

Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Запишем данные из условия задачи:
I1 = 40 Мбайт = 40 × 2 23 бит, i1 =2 5 бит, ν1 = 2 5 × 10 3 Гц = 2 5 × 10 3 с -1 , k1 = 2
I2 =2 4 бит, ν2 = 2 4 × 10 3 Гц = 2 4 × 10 3 с -1 , k2 = 1
Поскольку манипуляции идут с одним и тем же музыкальным фрагментом, то
T1 = t2 = t

Рассчитаем размер файла полученного при повторной записи:
I2 = 2 4 бит × 2 4 × 10 3 с -1 × 1 × 40 × 2 23 бит / (2 5 бит × 2 5 × 10 3 с -1 × 2) = 5 × 2 23 бит = 5 Мбайт

Производится звукозапись музыкального фрагмента в формате стерео двухканальная запись с частотой дискретизации 32 кГц и 32-битным разрешением.

Informatics-lesson. ru

29.02.2020 5:57:47

2020-02-29 05:57:47

Источники:

Http://informatics-lesson. ru/ege/task-sound. php

Кодирования звука. » /> » /> .keyword { color: red; } Формула записи звука в егэ по информатике

Кодирования звука

Кодирования звука.

Звук – это звуковая волна, у которой непрерывно меняется амплитуда и частота. При этом амплитуда определяет громкость звука, а частота — его тон. Чем больше амплитуда звуковых колебаний, тем он громче. А частота писка комара больше частоты сигнала автомобиля. Частоту измеряют в Герцах. 1Гц — это одно колебание в секунду.

Кодирование звука.

Компьютер является мощнейшим устройством для обработки различных типов информации, в том числе и звуковой. Но аналоговый звук непригоден для обработки на компьютере, его необходимо Преобразовать в цифровой. Для этого используются специальные устройства — Аналого-цифровые преобразователи или АЦП. В компьютере роль АЦП выполняет Звуковая карта. Каким же образом АЦП преобразует сигнал из аналогового в цифровой вид? Давайте разберемся.

Пусть у нас есть источник звука с частотой 440Гц, пусть это будет гитара. Сначала звук нужно превратить в электрический сигнал. Для этого используем микрофон. На выходе микрофона мы получим электрический сигнал с частотой 440Гц. Графически он выглядит таким образом:

Следующая задача — преобразовать этот сигнал в цифровой вид, то есть в последовательность цифр. Для этого используется Временная дискретизация — аналоговый звуковой сигнал разбивается на отдельные маленькие временные участки и для каждого такого участка устанавливается определенная величина интенсивности звука, которая зависит от амплитуды. Другими словами через какие-то промежутки времени мы измеряем уровень аналогового сигнала. Количество таких измерений за одну секунду называется частотой дискретизации. Частота дискретизации измеряется в Герцах. Соответственно, если мы будет измерять наш сигнал 100 раз в секунду, то частота дискретизации будет равна 100Гц.

Вот примеры некоторых используемых частот дискретизации звука:

8 000 Гц — телефон, достаточно для речи; 11 025 Гц; 16 000 Гц; 22 050 Гц — радио; 32 000 Гц; 44 100 Гц — используется в Audio CD; 48 000 Гц — DVD, DAT; 96 000 Гц — DVD-Audio (MLP 5.1); 192 000 Гц — DVD-Audio (MLP 2.0); 2 822 400 Гц — SACD, процесс однобитной дельта-сигма модуляции, известный как DSD — Direct Stream Digital, совместно разработан компаниями Sony и Philips; 5,644,800 Гц — DSD с удвоенной частотой дискретизации, однобитный Direct Stream Digital с частотой дискретизации вдвое больше, чем у SACD. Используется в некоторых профессиональных устройствах записи DSD.

В итоге наш аналоговый сигнал превратится в цифровой, а график станет уже не гладким, а ступенчатым, дискретным:

Глубина кодирования звука — это количество возможных уровней сигнала. Другими словами глубина кодирования это точность измерения сигнала. Глубина кодирования измеряется в битах. Например, если количество возможных уровней сигнала равно 255, то глубина кодирования такого звука 8 бит. 16-битный звук уже позволяет работать с 65536 уровнями сигнала. Современные звуковые карты обеспечивают Глубину кодирования в 16 и даже 24 бита, а это возможность кодирования 65536 и 16 777 216 различных уровней громкости соответственно.

Зная Глубину кодирования, можно Легко узнать количество уровней сигнала цифрового звука. Для этого используем формулу:

Где N — количество уровней сигнала, а i — глубина кодирования.

Например, мы знаем, что глубина кодирования звука 16 бит. Значит количество уровней цифрового сигнала равно 2 16 =65536.

Чтобы определить глубину кодирования если известно количество возможных уровней применяют эту же формулу. Например, если известно, что сигнал имеет 256 уровней сигнала, то глубина кодирования составит 8 бит, так как 2 8 =256.

Как понятно из данного вышеприведенного рисунка, чем чаще мы будем измерять уровень сигнала, т. е. Чем выше частота дискретизации и чем точнее мы будем его измерять, тем более график цифрового сигнала будет похож на аналоговый график, соответственно, Тем выше качество цифрового звука мы получим. И Тем больший объем будет иметь файл.

Кроме того, мы рассматривали Монофонический (одноканальный) звук, если же звук Стереофонический, то размер файла увеличивается в 2 раза, так как он содержит 2 канала.

Рассмотрим пример задачи.

Какой объем будет иметь звуковой монофонический файл содержащий звук, если длительность звука 1 минута, глубина кодирования 8 бит, а частота дискретизации 22050Гц?

Зная частоту дискретизации и длительность звука легко установить количество измерений уровня сигнала за все время. Если частота дискретизации 22050Гц — значит за 1 секунду происходит 22050 измерений, а за минуту таких измерений будет 22050*60=1 323 000.

На одно измерение требуется 8 бит памяти, следовательно на 1 323 000 измерений потребуется 1 323 000*8 = 10 584 000 бит памяти. Разделив полученное число на 8 получим объем файла в байтах — 10584000/8=1 323 000 байт. Далее, разделив полученное число на 1024 получим объем файла в килобайтах — 1 291,9921875 Кбайт. А разделив полученное число еще раз на 1024 и округлив до сотых получим размер файла в мегабайтах — 1 291,9921875/1024=1,26Мбайт.

Кодирования звука.

Вот примеры некоторых используемых частот дискретизации звука:

Где N — количество уровней сигнала, а i — глубина кодирования.

Для этого используется временная дискретизация аналоговый звуковой сигнал разбивается на отдельные маленькие временные участки и для каждого такого участка устанавливается определенная величина интенсивности звука, которая зависит от амплитуды.

Easyinformatics. ru

27.05.2018 2:26:28

2018-05-27 02:26:28

Источники:

Https://easyinformatics. ru/uroki/kodirovaniya-zvuka

Информатика 11 класс пробный вариант №1 ЕГЭ 2022 задания с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } Формула записи звука в егэ по информатике

Информатика 11 класс пробный вариант №1 ЕГЭ 2022 задания с ответами

1)На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите длину дороги между пунктами А и Б, если известно, что длина дороги между Г и Д меньше длины дороги между Г и Е. Передвигаться можно только по указанным дорогам.

Правильный ответ: 10

2)Логическая функция F задаётся выражением ((a ∧ b) ≡ c) ∧ (b → d). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d. В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Правильный ответ: cadb

3)В файле 3-40.xls приведён фрагмент базы фрагмент базы данных «Города и страны», описывающей различные страны, города и языки. База данных состоит из трех таблиц. Таблица «Страны» (код, название, континент, регион, площадь, год получения независимости, население, ОПЖ – ожидаемая продолжительность жизни, ВНД – валовый национальный доход, предыдущее значение ВНД, форма правления, идентификатор столицы). Таблица «Города» (идентификатор, название, код страны, район, население). Таблица «Языки» (код языка, код страны, название, является ли официальным, процент использования в стране). По некоторым значениям данных нет, в этом случае в таблице внесено значение NULL. На рисунке приведена схема базы данных. Используя информацию из приведённой базы данных, определите среднее население городов, расположенных в странах, население столицы которых превышает 1 000 000 человек, а одним из официальных языков является английский (English). В ответе запишите только целую часть числа. Используя информацию из приведённой базы данных, определите среднее население городов, расположенных в странах, население столицы которых превышает 1 000 000 человек, а одним из официальных языков является английский (English). В ответе запишите только целую часть числа.

Правильный ответ: 319862

4)Для кодирования некоторой последовательности, состоящей из букв П, О, Е, Х, А, Л, И, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв О, Е, А, И использовали соответственно кодовые слова 01, 110, 1010, 001. Найдите наименьшую возможную суммарную длину всех кодовых слов.

Правильный ответ: 21

5)Автомат обрабатывает десятичное натуральное число N по следующему алгоритму: 1) Строится двоичная запись числа N. 2) К этой записи справа дописывается 0, если число нечетное, и слева 1 в обратном случае. 3) Если единиц в двоичном числе получилось четное количество, справа дописывается 1, иначе 0. Например, двоичная запись 1010 числа 10 будет преобразована в 110100. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма. Укажите минимальное число N, для которого результат работы алгоритма будет больше 228. В ответе это число запишите в десятичной системе счисления.

Правильный ответ: 50

6)Какое максимальное значение переменной s, подаваемого на вход программе, для которого в результате работы программы на экран будет выведено значение 46?

Правильный ответ: 425

7)Найдите битовую глубину кодирования растрового изображения размером 512×300 пикселей, которое занимает 600 Кбайт. В ответе запишите только целое число, единицу измерения писать не нужно.

Правильный ответ: 32

8)Все 4-буквенные слова, составленные из букв П, Р, В, Д, А, записаны в алфавитном порядке и пронумерованы. Вот начало списка: 1. АААА 2. АААВ 3. АААД 4. АААП 5. АААР 6. ААВА … Найдите номер первого слова в этом списке, которое не содержит гласных и одинаковых букв.

Правильный ответ: 195

9)Откройте файл электронной таблицы 9-130.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек могут перестановкой образовать геометрическую прогрессию с отличным от единицы знаменателем прогрессии.

Правильный ответ: 133

10)В файле 10-141.docx приведена книга Н. В. Гоголя «Вечера на хуторе близ Диканьки». Сколько раз местоимение «я» (со строчной буквы) встречается в тексте повести «Страшная месть» (не считая сносок)? В ответе укажите только число.

Правильный ответ: 81

11)Автомобильный номер состоит из одиннадцати букв русского алфавита A, B, C, E, H, K, M, O, P, T, X и десятичных цифр от 0 до 9. Каждый номер состоит из двух букв, затем идет 3 цифры и еще одна буква. Например, АВ901С. В системе каждый такой номер кодируется посимвольно, при этом каждая буква и каждая цифра кодируются одинаковым минимально возможным количеством бит. Укажите, на сколько бит можно уменьшить размер памяти, выделенной для хранения одного номера, если кодировать с помощью минимально возможного количества бит каждую из трех групп – первые две буквы, три цифры и последняя буква.

Правильный ответ: 3

12)Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. 1. заменить (v, w) 2. нашлось (v) Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Дана программа для исполнителя Редактор: ПОКА нашлось(42) или нашлось(32) ЕСЛИ нашлось(42) ТО заменить(42, 51) ИНАЧЕ заменить(32, 61) КОНЕЦ ПОКА На вход программе подана строка, содержащая только 20 двоек, 15 троек и 10 четверок. Порядок символов заранее неизвестен. Определите максимально возможную сумму всех цифр в конечной строке.

Правильный ответ: 155

13)На рисунке представлена схема дорог, связывающих города A, B, C, D. По каждой дороге можно двигаться только один раз в направлении стрелки. По дороге из B в D можно двигаться в любую сторону, но лишь один раз. Сколько существует различных путей из города A в город C, проходящих либо через В (но не D), либо через D (но не B), либо через B и D одновременно?

Правильный ответ: 100

14)Значение выражения (64 25 + 4 10 ) – (16 20 + 32 3 ) записали в системе счисления с основанием 4. В каком разряде четверичной записи числа при просмотре справа налево впервые встречается цифра 2?

Правильный ответ: 7

15)На числовой прямой даны два отрезка: P=[10,29] и Q=[13,18]. Укажите наибольшую возможную длину такого отрезка A, что формула ((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Правильный ответ: 19

16)Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 1, F(1) = 3 F(n) = F(n–1) – F(n–2) + 3n, при чётном n > 1 F(n) = F(n–2) – F(n–3) + 2n, при нечётном n > 1 Чему равно значение функции F(40)? В ответе запишите только целое число.

Правильный ответ: 84

17)В файле 17-204.txt содержится последовательность целых чисел, которые принимают значения от -10000 до 10000 включительно. Тройка идущих подряд чисел последовательности называется уникальной, если только второе из них является положительным числом, заканчивающимся на 9. Определите количество уникальных троек чисел, а затем – максимальную из всех сумм таких троек.

Правильный ответ: 206 23427

Правильный ответ: 721 640

19-21)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит одна куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может а) убрать из кучи половину камней, если количество камней в куче делится на 2; иначе убрать из кучи два камня; б) убрать из кучи две трети камней, если количество камней в куче делится на 3; иначе убрать из кучи три камня. Например, пусть в куче 10 камней, тогда можно убрать половину или только три камня. А если в куче 12 камней, то можно убрать половину или две трети камней. Игра завершается в тот момент, когда в куче останется ровно 1 камень. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет ровно 1 камень. В начальный момент в куче было S камней, 1 ≤ S ≤ 37.

Правильный ответ: 19- 4, 20- 7 18, 21-9

22)Ниже на трёх языках программирования записан алгоритм. Получив на вход число X, этот алгоритм печатает одно число. Укажите наименьшее число Х, большее 80, при вводе которого алгоритм печатает число 17.

Правильный ответ: 97

23)Исполнитель Калькулятор преобразует число, записанное на экране. У исполнителя есть две команды, которым присвоены номера: 1. Вычти 8 2. Раздели нацело на 2 Первая команда уменьшает число на 8, вторая – вдвое. Программа для исполнителя – это последовательность команд. Сколько существует таких программ, которые исходное число 102 преобразуют в число 5 и при этом траектория вычислений программы содержит число 43?

Правильный ответ: 8

24)Текстовый файл 24-179.txt содержит строку из заглавных букв A, B, C, D, E, F, всего не более чем из 10 6 символов. Определите, сколько встречается комбинаций вида CB*BC, где на месте «*» может стоять любая буква, кроме A, B и F. В ответе укажите сначала букву, которая чаще всего встречается на месте «*», затем общее количество подходящих комбинаций.

Правильный ответ: С6347

25)Среди чисел, больших 520000, найти такие, сумма всех делителей которых, не считая единицы и самого числа, образует число-палиндром (например, число 1221: если его «перевернуть», получается то же самое число). Вывести первые пять чисел, удовлетворяющих вышеописанному условию, справа от каждого числа вывести его максимальный делитель.

26)Организация купила для своих сотрудников все места в нескольких подряд идущих рядах на концертной площадке. Известно, какие места уже распределены между сотрудниками. Найдите ряд с наибольшим номером, в котором есть два соседних места, таких что слева и справа от них в том же ряду места уже распределены (заняты). Гарантируется, что есть хотя бы один ряд, удовлетворяющий условию. Входные данные представлены в файле 26-59.txt следующим образом. В первой строке входного файла находится одно число: N – количество занятых мест (натуральное число, не превышающее 10 000). В следующих N строках находятся пары чисел: ряд и место выкупленного билета, не превышающие 100000. В ответе запишите два целых числа: номер ряда и наименьший номер места из найденных в этом ряду подходящих пар. В данном примере есть следующие свободные места, удовлетворяющие условию: 7 и 8 в ряду 5, 4 и 5 в ряду 16, а также 7 и 8 в ряду 16. Выбираем наибольший номер ряда: 16 и наименьший номер места: 4. В ответе нужно указать: 16 4.

27)Набор данных состоит из групп натуральных чисел, каждая группа записана в отдельной строке. В любой группе содержится не менее двух чисел. Из каждой группы выбрали два числа и нашли их наименьшее общее краткое (НОК). Затем все полученные таким образом значения НОК сложили. Определите наибольшую сумму, кратную числу 5 или 7 (но не одновременно двум этим числам), которая может быть получена таким образом. Входные данные. Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 100000). В каждой из следующих N строк файлов записан сначала размер группы K (N

12 Исполнитель Редактор получает на вход строку цифр и преобразовывает её.

100ballnik. com

29.10.2018 19:23:48

2018-10-29 19:23:48

Источники:

Https://100ballnik. com/%D0%B8%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0-11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%BF%D1%80%D0%BE%D0%B1%D0%BD%D1%8B%D0%B9-%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82-%E2%84%961/

Источник

Кодирование текстовой информации

Кодирование графической информации

Кодирование звуковой информации

Определение скорости передачи информации

Решение заданий 7 ЕГЭ по информатике

Тема: Кодирование изображений

Тема: Кодирование звука

Тема: Кодирование видео

Тема: Скорость передачи данных

N = k * F * L *T (1)

Обработка звуковой информации. Вариант задания №9 ЕГЭ

Источники:

Кодирования звука

Кодирования звука.

Кодирование звука.

Рассмотрим пример задачи.

Кодирования звука.

Источники:

Информатика 11 класс пробный вариант №1 ЕГЭ 2022 задания с ответами

Информатика 11 класс пробный вариант №1 ЕГЭ 2022 задания с ответами

Источники:

N = k F * L T (1)